Содержание
Введение
Глава 1. Аспекты создания анимационных программ по физике
1.1Обучающие программы
1.2Классическая теория теплоемкости твердых тел (кристаллов)
1.3Тепловые свойства твердых тел
Вывод
Глава 2. Реализация анимационной обучающей программы для определения удельной теплоемкости твердых тел (проверка выполнимости закона Дюлонга и Пти)
2.1Алгоритм программы
2.2Блок – схема
2.3Листинг программы
2.4Результаты работы программы
Заключение
Литература
Введение
В настоящее время информационные технологии проникают во все новые сферы жизнедеятельности человека. Особенно бурное развития информационные технологии получают в сфере образования. Применение компьютерной техники в образовательной процессе дает неоспоримое преимущество позволяя получить всесторонние знания по данному предмету.
Последние достижения в вычислительной технике и программном обеспечении позволяют перевести физические опыты из практической (материальной) сферы в виртуальную, реализованную на компьютере. Сейчас уже известны программы, моделирующие различные физические процессы и явление которые моделируются с помощью математических и физических моделей.
На основании этого вычислительна техника становится незаменимым инструментом в образовательном процессе позволяя создавать компьютерные модели приборов и физических явлений, проводить различные опыты, а также получать результаты опытов.
Дополнительный преимуществом таких программ является применение анимации, что делает весь эксперимент наглядным и позволяет совмещать в одном интерфейсе графическую, текстовую и звуковую информацию, тем самым позволяя рассмотреть явление в различных ракурсах.
Также значительным преимуществом является, то что реальные физические эксперименты требуют дорогостоящего оборудование и материалов, а иногда они не безопасны для здоровья. При использовании же обучающих анимационных программ эти недостатки устраняются.
На основании этого вытекает востребованность программ подобного класса, а из востребованности вытекает актуальность задачи.
Глава 1. Аспекты создания анимационных программа по физике
1.1 Обучающие программы
Общие требования к созданию анимационно–обучающей программе.
Реклама

Основной показатель высокого качества обучающей программы - эффективность обучения. Богатейшие демонстрационные возможности и высокая степень интерактивности системы само по себе не могут служить основанием для того, чтобы считать обучающую программу полезной. Эффективность программы целиком и полностью определяется тем, насколько она обеспечивает предусмотренные цели обучения, как ближайшие, так и отдаленные. При решении любого вопроса, начиная с использования графики и кончая индивидуализацией обучения, во главу угла должны быть поставлены учебные цели. Богатейшие возможности компьютера должны быть проанализированы с точки зрения психологии и дидактики и использованы тогда, когда это необходимо с педагогической точки зрения. Не следует гнаться за внешним эффектом, обучающая система должна быть не эффектной, а эффективной.
Вопрос о том, насколько эффективна обучающая программа, может быть решен только после ее апробации. Тем не менее можно наметить ряд психолога - педагогических требований, которым должна удовлетворять обучающая программа.
Обучающая система должна:
Позволять строить содержание учебной деятельности с учетом основных принципов педагогической психологии и дидактики;
Допускать реализацию любого способа управления учебной деятельностью, выбор которого обусловлен, с одной стороны, теоретическими воззрениями разработчиков обучающей программы, а с другой — целями обучения;
Стимулировать все виды познавательной активности учащихся, включая, естественно и продуктивную, которые необходимы для достижения основных учебных целей – как ближайших, так и отдаленных;
Учитывать в содержании учебного материала и ученых задач уже приобретенные знания, умения и навыки учащихся;
Стимулировать высокую мотивацию учащихся к учению, причем оно не должно идти за счет интереса к самому компьютеру. Необходимо обеспечить учебные мотивы, интересы учащихся к познанию;
Обеспечивать диалог как внешний, так и внутренний, причем диалог должен выполнять следующие функции:
· активизировать познавательную деятельность учащихся путем включения их в процесс рассуждения;
· моделировать совместную (субъект субъектную) деятельность;
· способствовать пониманию текста;
· содержание учебного предмета и трудность учебных задач должны соответствовать возрастным возможностям и строиться с учетом индивидуальных особенностей учащихся;
· обратная связь должна быть педагогически оправданной.
Реклама

1.2 Классическая теория теплоемкости твердых тел (кристаллов)
Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы, принимаемые за материальные точки. Атомы совершают тепловые колебания около положений равновесия. Если колебания малы, то они будут гармоническими. Энергия каждого – атома слагается из кинетической и потенциальной. На каждую степень свободы приходится в среднем кинетическая энергия 1
/2
kT. Как было показано в параграфе 63, при гармонических колебаниях на одну степень свободы приходится в среднем такая же потенциальная энергия, т. е. 1
/2
kT. Таким образом, среднее значение полной энергии, приходящейся на одну колебательную степень свободы, равно
εкол
= εкин
+ εпот
= kT. (1.1)
Теперь легко рассчитать теплоемкость кристаллической решетки. Для простоты будем считать, что все атомы одинаковы. Каждый атом обладает тремя колебательными степенями свободы, а потому на него приходится средняя энергия 3kT. Умножив эту величину на число Авогадро N, найдем внутреннюю энергию грамм – атома твердого тела U = N * 3kT = 3kT. Теплоемкость одного грамм – атома называется атомной теплоемкостью. Для нее получаем
Cν
= dU/dt = 3R ≈ 24.9 Дж / (К * моль) ≈ 6 кал/(К * моль). (1.2)
Еще в 1819 г. Дюлонг (1785 - 1838) и Пти (1791 - 1820) установили эмпирическое правило, согласно которому произведение удельной теплоемкости химического элемента в твердом состоянии на его атомный вес приблизительно одинаково для всех элементов и составляет около 6 кал/(град * моль). Мы видим, что правило Дюлонга и Пти находит простое объяснение в классической теории теплоемкостей. Вывод показывает, что в правиле Дюлонга и Пти речь идет об атомной теплоемкости при постоянном объеме. В табл. 1 приведены атомные теплоемкости некоторых элементов в твердом состоянии в температурном интервале от 15 до 100 0
С.
Таблица 1.1.
| Элемент |
CV
, Кал / (К * моль) |
Элемент |
CV
, Кал / (К * моль) |
С
B
Al
Ca
Ag
|
1,44
2,44
5,51
5,60
6,11
|
Pt
Au
Pb
U
|
6,11
5,99
5,94
6,47
|
2. Пусть теперь твердое тело является химическим соединением, например, NaCl. Его кристаллическая решетка построена из атомов различных типов. Молекулярной или молярной теплоемкостью называется теплоемкость одного моля химического соединения; она равна произведению удельной теплоемкости на молекулярный вес. Очевидно, молекулярный вес химического соединения равен сумме атомных весов всех атомов, из которых состоит молекула этого соединения. Для применимости теоремы о равномерном распределении энергии по степеням свободы не имеет значения, одинаковы или различны атомы. Каждый атом обладает тремя колебательными степенями свободы, и на него в среднем приходится энергия 3kT. Если в молекуле n атомов, то на молекулу придется в среднем энергия 3nkT. Молекулярная теплоемкость будет 3nkN = 3nR, т. е. она равна атомной теплоемкости, умноженной на число атомов в молекуле. Иными словами, молекулярная теплоемкость твердого соединения равна сумме – атомных теплоемкостей элементов из которых оно состоит. Это правило было найдено эмпирически и называется законом Джоуля и Коппа. Джоуль высказал – его в 1844 г. Но только в 1864 г. закон был окончательно сформулирован Коппов и подтвержден громадным множеством фактов, полученных самим Коппом. Заметим, что закон Джоуля – Коппа в приведенной выше формулировке: «Молекулярная теплоемкость твердого соединения приблизительно равна сумме атомных теплоемкостей» – обладает большей общностью, чем правило Дюлонга и Пти. Правило Дюлонга и Пти может нарушаться, т. е. атомные теплоемкости химических элементов, входящих в соединение, могут отличаться друг от друга, но тем не менее закон Джоуля и Коппа может оставаться справедливым. Именно это и было установлено Коппом.
Недостаточность классической теории теплоемкостей.
Понятие о квантовой теории – (качественное рассмотрение).
1.Сравнение классической теории теплоемкости с опытом показывает, что она в основном правильно описывает определенный круг явлений. Однако многие явления она не объясняет. Ряд опытных фактов находится в резком противоречии с этой теорией.
Прежде всего, классическая теория не дает объяснения зависимости теплоемкости тел от температуры. В табл. 2 приведены для примера молярные теплоемкости газообразного водорода при различных температурах.
Таблица 2.2.
| т. К |
CV
, Кал / (К * моль) |
т, к |
CV
, Кал / (К * моль) |
35
100
290
600
800
1000
|
2,98
3,10
4,90
5,08
5,22
5,36
|
1200
1600
1800
2000
2500
|
5,49
5,76
5,92
6,06
6,40
|
Можно было бы попытаться объяснить зависимость теплоемкости от температуры не гармоничностью колебательных степеней свободы при больших амплитудах колебаний. Например, в случае молекулы водорода взаимодействие атомов приводит к их колебаниям вдоль оси YY. Для не гармонических колебаний средняя кинетическая энергия, приходящаяся на одну степень свободы, уже не равна соответствующей средней потенциальной энергии. Соотношение между ними зависит от амплитуды колебаний, т. е. в конце концов от температуры газа. При высоких температурах учет колебаний улучшает дело, поскольку теплоемкость, связанная с колебательной степенью свободы, меняется с изменением температуры. Однако эти соображения теряют силу при низких температурах, где расхождения классической теории с опытом проявляются особенно резко. При низких температурах, согласно представлениям классической теории, амплитуды колебаний малы, а потому сами колебания могут считаться гармоническими. В этом случае для теплоемкости CV
по классической теории мы получили бы 7 кал / (К * моль) вместо экспериментального значения 3 кал / (К * моль). Опыт показывает, что ниже 100 К водород начинает вести себя как одноатомный газ. К этому следует добавить экспериментально установленный факт, что при приближении к абсолютному нулю теплоемкости CV
и СP
всех тел стремятся к нулю.
2. Классическая теория непоследовательна. По теореме о равномерном распределении кинетической энергии все степени свободы равноправны. Поэтому требуется лишь подсчитать полное число степеней свободы, совсем не обращая внимания на их природу. Между тем классическая теория по каким-то непонятным причинам учитывает одни и отбрасывает другие степени свободы. Так, атом одноатомного газа классическая теория рассматривает как материальную точку с тремя степенями свободы и этим достигает известного согласия с опытом. Но атом – не точка. Если его принять за твердое тело, то получится шесть степеней свободы – три поступательные и три вращательные. Теоретическая теплоемкость CV
одноатомного газа возрастет до 6 кал / (К * моль). Атом не является также твердым телом, а имеет внутреннюю структуру. Число степеней свободы его много больше шести. Поэтому при последовательном рассмотрении теплоемкость CV
одноатомного газа по классической теории должна была бы быть много больше 6 кал / (К * моль), а это противоречит фактам.
Возьмем, далее, двухатомную молекулу. Классическая теория учитывает вращения ее вокруг осей ХХ и ZZ, но не принимает во внимание вращение вокруг оси YY. Последнее в классической теории исключается на том основании, что не имеет смысла говорить о вращении материальных точек 1 и 2 вокруг соединяющей прямой 12. Но такая аргументация формальна и неубедительна, так как атомы не являются материальными точками. Если атомы 1 и 2 рассматривать как твердые тела, то каждый из них будет иметь 6, а вся молекула – 12 степеней свободы. Им соответствует в среднем кинетическая энергия 6kT. К этой энергии следует прибавить еще среднюю потенциальную энергию колеблющихся атомов вдоль прямой 12, которая равна 1
/2
kT. Всего мы получаем, следовательно, 13
/2
kT, а потому теплоемкость CV
для такой модели двухатомного газа должна быть равна 13 кал / (К * моль). При учете внутренней структуры атомов это значение еще больше возрастет.
3. Определенное согласие с опытом достигается в классической теории благодаря использованию механических моделей с наложенными связями, ограничивающими свободу движения. Идея связей заимствована из теоретической механики. Там она служит искусственным приемом для решения различных задач о равновесии и движении идеализированных макроскопических телах никаких связей не существует. Тем более их не существует в атомных системах. Двухатомная молекула, например, часто рассматривается как неизменяемая система двух материальных точек, скрепленных жестким невесомым стержнем. На самом деле это, конечно, не так – никаких жестких стержней, скрепляющих атомы в молекулах, нет. Речь идет об идеализированной макроскопической модели атомной системы. Для макроскопических систем физика в состоянии раскрыть физическую природу связей и установить, когда можно пользоваться такой идеализацией. Но классическая физика не может ответить на вопрос, почему в определенной области явлений атомные системы приближенно ведут себя как макроскопические модели с наложенными связями.
4. Рассмотрим, наконец, теплоемкость металлов. Металл состоит из положительно заряженных ионов, совершающих тепловые колебания вокруг узлов кристаллической решетки. Между ними движутся так называемые свободные электроны, т. е. электроны, сравнительно слабо связанные с ионами решетки. Они ведут себя подобно электронному газу. Наличием свободных электронов объясняется высокая электропроводность металлов. По значению электропроводности можно оценить концентрацию свободных электронов. Она оказалась того же порядка, что и концентрация ионов, образующих кристаллическую решетку. Классическая теория теплоемкости отвлекается от наличия электронного газа. Она учитывает тепловые колебания одних только ионов и благодаря этому приходит к правильному значению для теплоемкости CV
= 6 кал / (К * моль) (правило Дюлонга и Пти). Между тем следовало бы учесть также вклад в теплоемкость, вносимый электронами. Если электроны принять за материальные точки, то на каждый свободный электрон будет приходиться средняя кинетическая энергия 3
/2
kT. Поэтому по классической теории теплоемкость электронного газа должна была бы быть сравнимой с теплоемкостью решетки. Опыт показывает, однако, что свободные электроны практически не вносят никакого вклада в теплоемкость металлов.
5. Таким образом, опытные факты приводят к заключению, что всегда явления протекают так, что эффективный вклад в теплоемкость вносят не все, а только некоторые степени свободы. При понижении температуры некоторые степени свободы становятся малоэффективными и, наконец, совсем выпадают из игры. Про такие степени свободы говорят, что они «заморожены». Наоборот, при повышении температуры начинают проявляться все новые и новые степени свободы, которые ранее были либо малоэффективны, либо совсем заморожены. Это значит, что классический закон равномерного распределения кинетической энергии по степеням свободы не справедлив и требует уточнения. Парадоксально, что успехи самой классической теории связаны с тем, что она в применении к конкретным системам фактически отказывалась от этого закона. Она исключала некоторые степени свободы путем наложения на систему идеально жестких связей. Фактически это эквивалентно тому, что такие степени свободы считаются замороженными.
6. Трудности такого рода были преодолены после того, как теория теплоемкости была построена на квантовой основе. Не вдаваясь в детали, ограничимся здесь немногими качественными указаниями. В параграф 58 уже говорилось, что внутренняя энергия атомных систем может принимать лишь дискретные значения. Приведем в качестве примера гармонический осциллятор, т. е. частицу, которая по классическим представлениям может совершать гармонические колебания под действием квазиупругой силы – силы, пропорциональной отклонению частицы из положения равновесия. Двухатомная молекула, когда речь идет о малых колебаниях ее атомов относительно друг друга, может рассматриваться как гармонический осциллятор. Как доказывается в квантовой механике, возможные значения колебательной энергии такой системы представляются формулой
en
= (n + 1/2) * hn, (2.1)
где n - частота осциллятора, n – целое число, которое может принимать значения 1, 2, 3, …, h – универсальная постоянная, называемая постоянной Планка. По современным данным
h = (6,626186 +
0,000057) * 10-34
Дж * с = (6,626186 +
0,000057) * 10-27
эрг * с.
Таким образом, энергетический спектр гармонического осциллятора состоит из бесконечного множества равноотстоящих уровней. Расстояние между соседними уровню соответствует энергия e0
= 1
/2
hn. Она называется нулевой энергией. Наличие нулевой энергии означает, что даже в состоянии с наименьшей энергией колебания осциллятора не прекращаются. Такие колебания называются нулевыми. Воздействуя на осциллятор, его можно возбудить, т. е. перевести на один из возможных более высоких уровней энергии. Ближайшим является энергетический уровень с n = 1 и энергией e1
=3
/2
hn.
 7. Допустим теперь, что газ состоит из гармонических осцилляторов, например, двухатомных молекул. Предположим, что температура газа настолько низка, что kT << hn. Средняя энергия теплового движения молекулы порядка kT. Такой энергии недостаточно, чтобы возбудить осциллятор, т. е. перевести его с нулевого уровня на ближайший – первый – энергетический уровень. Возбужденные может происходить только при столкновениях с молекулами, энергия которых значительно больше средней. Однако таких молекул относительно мало, так что практически все осцилляторы останутся на нижнем энергетическом уровне. Эта картина сохранится при дальнейшем повышении температуры газа, пока соблюдается условие kT << hn. При выполнении этого условия колебательная энергия осцилляторов практически не зависит от температуры и по причине не влияет на теплоемкость газа. Вот почему при условии kT << hn в теории теплоемкости двухатомных газов можно не учитывать колебания атомов 1 и 2 (см. рис. 47) вдоль соединяющей их прямой. Отличие квантовой от формальной классической теории состоит здесь в том, что согласно квантовой теории должны происходить нулевые колебания, тогда как формальная классическая теория совсем исключает их, считая молекулы абсолютно жесткими. Однако это различие не может сказаться на величине теплоемкости, так как энергия нулевых колебаний не зависит от температуры. Моделью жесткой двухатомной молекулы в теории теплоемкости можно пользоваться лишь при соблюдении условия kT<< hn. Если это условие не соблюдается, то классическая модель становится неприменимой. При повышении температуры, когда величина kT становится сравнимой с hn, начинает возбуждаться первый, а затем и более высокие колебательные уровни двухатомной молекулы. Температура 7. Допустим теперь, что газ состоит из гармонических осцилляторов, например, двухатомных молекул. Предположим, что температура газа настолько низка, что kT << hn. Средняя энергия теплового движения молекулы порядка kT. Такой энергии недостаточно, чтобы возбудить осциллятор, т. е. перевести его с нулевого уровня на ближайший – первый – энергетический уровень. Возбужденные может происходить только при столкновениях с молекулами, энергия которых значительно больше средней. Однако таких молекул относительно мало, так что практически все осцилляторы останутся на нижнем энергетическом уровне. Эта картина сохранится при дальнейшем повышении температуры газа, пока соблюдается условие kT << hn. При выполнении этого условия колебательная энергия осцилляторов практически не зависит от температуры и по причине не влияет на теплоемкость газа. Вот почему при условии kT << hn в теории теплоемкости двухатомных газов можно не учитывать колебания атомов 1 и 2 (см. рис. 47) вдоль соединяющей их прямой. Отличие квантовой от формальной классической теории состоит здесь в том, что согласно квантовой теории должны происходить нулевые колебания, тогда как формальная классическая теория совсем исключает их, считая молекулы абсолютно жесткими. Однако это различие не может сказаться на величине теплоемкости, так как энергия нулевых колебаний не зависит от температуры. Моделью жесткой двухатомной молекулы в теории теплоемкости можно пользоваться лишь при соблюдении условия kT<< hn. Если это условие не соблюдается, то классическая модель становится неприменимой. При повышении температуры, когда величина kT становится сравнимой с hn, начинает возбуждаться первый, а затем и более высокие колебательные уровни двухатомной молекулы. Температура
TV
= hn / k, (2.2)
Называется характеристической температурой. При T >
TV
 колебания существенно влияют на теплоемкость двухатомного газа. При T << TV
происходят только нулевые колебания, не сказывающиеся на теплоемкости. Для водорода TV
~ 6000 K. колебания существенно влияют на теплоемкость двухатомного газа. При T << TV
происходят только нулевые колебания, не сказывающиеся на теплоемкости. Для водорода TV
~ 6000 K.
8. Совершенно аналогично влияет на теплоемкость газов и вращение молекул. Энергия вращения также квантуется. Ее возможные значения по квантовой механике определяются формулой
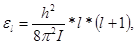 (2.3) (2.3)
где I – момент инерции молекулы, а l – целое число, которое может принимать значения 0, 1, 2, 3, …Расстояния между уровнями энергии не постоянны, а возрастают в арифметической прогрессии. В состоянии с наименьшей энергией l = 0 вращения не возбуждены. В состоянии с l = 1 энергия вращения равна
    (2.4) (2.4)
 Если kT << e1
, то средней тепловой энергии молекулы недостаточно для возбуждения вращение. В этом случае при вычислении теплоемкости вращения можно не учитывать. В противоположном случае, когда kT >> e1
, возбуждается много вращательных уровней. Тогда дискретность энергетических уровней слабо сказывается на теплоемкости. Для вращение становится приближенно применимой классическая теорема о равномерном распределении кинетической энергии по степеням свободы. Характеристическая температура для вращения определяется формулой Если kT << e1
, то средней тепловой энергии молекулы недостаточно для возбуждения вращение. В этом случае при вычислении теплоемкости вращения можно не учитывать. В противоположном случае, когда kT >> e1
, возбуждается много вращательных уровней. Тогда дискретность энергетических уровней слабо сказывается на теплоемкости. Для вращение становится приближенно применимой классическая теорема о равномерном распределении кинетической энергии по степеням свободы. Характеристическая температура для вращения определяется формулой
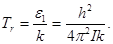 (2.5) (2.5)
При T >> Tr
справедлива классическая теория, при T << Tr
вращения не возбуждены и не оказывают влияния на теплоемкость. Для водорода при вращении молекул вокруг осей ХХ и ZZ (см. рис. 47) характеристическая температура Tr
~ 175 K. Вращения вокруг оси ХХ не возбуждены из – за малости соответствующего момента инерции. По той же причине не возбуждены вращения атомов одноатомных газов.
9. Изложенные соображения применимы не только к колебаниям гармонических осцилляторов и вращением жестких молекул, но и к любым квантовым системам. Они показывают, что дискретность энергетических уровней не совместима с классической теоремой о равномерном распределении энергии по степеням свободы. Только тогда, когда средняя энергия теплового движения kT велика по сравнению с разностями между высшими энергетическими уровнями и наинизшим из них, возбуждается много энергетических уровней. При таком условии дискретность уровней становится малосущественной, и атомная система ведет себя как классическая, в которой энергия меняется непрерывно. Отсюда следует, что чем выше температура, тем лучше оправдывается классическая теорема о равномерном распределении энергии по степеням свободы.
10. Мы не рассматриваем здесь квантовую теорию теплоемкости с количественной стороны. Об этом будет идти речь в гл. VI. Однако уже качественное рассмотрение показывает, что одного представления о дискретности энергетических уровней достаточно, чтобы выяснить, в каких случаях можно и в каких нельзя пользоваться классической теорией теплоемкости и ее грубыми механическими моделями. В качестве первого примера оценим молекулярную теплоемкость кислорода, нагретого до температуры 1000 эВ и выше. При комнатной температуре все атомы находятся в основном – низшем – состоянии, электронные уровни не возбуждены. Не возбуждены также колебания атомов в молекуле – молекула кислорода ведет себя как жесткая двухатомная молекула. При нагревании молекулы кислорода сначала диссоциируют, т. е. распадаются на два атома. Затем начинается процесс ионизации, т. е. отрыв электронов от атомов. Сначала оторвутся внешние электроны, наименее прочно связанные с атомными ядрами. При дальнейшем нагревании начнется отрыв и внутренних электронов. Для отрыва последнего электрона требуется энергия порядка 870 эВ. При температурах 1000 эВ и выше практически все электроны окажутся оторванными от атомных ядер. Вещество перейдет в состояние полностью ионизованной плазмы, состоящей из электронов и «голых» атомных ядер. Из каждого атома образуется 9 частиц: ядро и 8 электронов; из каждой молекулы – 18 частиц: два ядра и 16 электронов. Если пренебречь потенциальной энергией взаимодействия частиц, то вся внутренняя энергия сведется к кинетической энергии теплового движения электронов и атомных ядер. Средняя энергия одной частицы 3
/2
kT, средняя энергия частиц, образовавшихся из молекулы, 18 * 3
/2
kT = 27kT, внутренняя энергия одного моля U = 27NkT = 27RT, а молекулярная теплоемкость CV
= 27R » 54 кал / (К * моль).
11. В качестве второго примера возьмем вращательное броуновское движение, рассмотренное в параграф 65. Выясним, применима ли к такому движению классическая теорема о равномерном распределении кинетической энергии по степеням свободы. Зеркальце можно рассматривать как гармонический осциллятор с собственной частотой
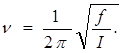
Если взять I ~ 0,01 г * см2
, то получится n~ 1,5 * 10-4
с-1
, hn~ 10-31
эрг, тогда как средняя энергия теплового движения kT ~ 4 * 10-14
эрг. Таким образом, 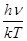 ~ 2,5 * 10-18
, т. е. с громадным запасом kT << hn. Применимость теоремы о равномерном распределении энергии здесь не вызывает сомнений. ~ 2,5 * 10-18
, т. е. с громадным запасом kT << hn. Применимость теоремы о равномерном распределении энергии здесь не вызывает сомнений.
1.3 Тепловые свойства твердых тел
Тепловое движение в твердых телах. Уже упоминалось, что тепловые движения частиц в твердом теле не таковы, как в жидкости и газе. Частицы твердого тела, связанные друг с другом силами взаимодействия, зависящими от межатомных расстояний, могут совершать только колебания около некоторого равновесного положения в узлах кристаллической решетки. Так как вещество может быть твердым только при достаточно низких температурах, когда энергия тепловых движений, т. е. kT, много меньше, чем потенциальная энергия взаимодействия частиц между собой, то колебания атомов около положений равновесия являются малыми колебаниями. Энергия этих колебаний и представляет собой внутреннюю энергию твердого тела, которая определяет его температуру.
При абсолютном нуле температуры всякие атомные движения замирают. Кристалл должен быть вполне упорядочен, так, чтобы его энтропия была равна нулю. Однако квантовая теория привод к выводу, что и при абсолютном нуле частицы обладают некоторой энергией, тем большей, чем меньше масса частицы. Эта энергия ни при каких условиях не может быть отнята у частиц. Наличие такой нулевой энергии не мешает тому, чтобы энтропия твердого тела при абсолютном нуле была равна нулю, так как энтропия связана с беспорядочными тепловыми движениями, а нулевая энергия не является тепловой. И если кристалл лишен дефектов, то его энтропия стремится к нулю при приближении к абсолютному нулю.
Нулевая энергия обычно значительно меньше энергии взаимодействия между частицами, так что она не мешает отвердеванию вещества. И только в одном-единственном случае, именно, в случае гелия, нулевая энергия играет настолько важную роль, что без действия внешнего давления отвердевание гелия становится невозможным. Все другие вещества отвердевают раньше, чем нулевая энергия сможет оказать существенное влияние на их свойства.
Теплоемкость твердых тел. Итак, твердое тело представляет собой совокупность колеблющихся частиц, осцилляторов. При подводе тепла к телу оно расходуется на увеличение энергии колебаний осцилляторов, которая складывается из кинетической и потенциальной энергий. Если колебания гармонические, обе эти части полной энергии равны друг другу.
Каждое колебание можно разложить на три составляющие по осям координат, и энергия каждой составляющей также выражается суммой равных друг другу потенциальной и кинетической энергии.
Из кинетической теории газов мы знаем, что. средняя кинетическая энергия атома вдоль одной из осей равна l
/z
kT. Это — кинетическая энергия, приходящаяся на одну степень свободы. Но поскольку потенциальная энергия осциллятора равна кинетической, то полная энергия, приходящаяся на одну степень свободы, равна 2 х V3
kT = kT.
Так как каждый атом (осциллятор) обладает тремя степенями свободы, и если принять, как это мы делали в теории идеальных газов, что на каждую степень свободы приходится одна и та же кинетическая энергия ]
lz
kT, то полная энергия одного атома твердого тела равна 3 х 2 х l
lz
kT = 3 kT.
Если тело содержит N атомов, то внутренняя энергия тела равна 3NkT, Внутренняя энергия одного моля равна, таким образом, 3 NQ
kT = 3RT, где NQ
—число Авогадро.
При подводе тепла в условиях постоянного объема все тепло уходит на увеличение внутренней энергии. Поэтому атомная теплоемкость при постоянном объеме определяется равенством
СV
= (dU / dT)V
= 3R » 6 кал/К- моль »25,12 Дж/К * моль. (1.1)
Это вдвое больше молярной теплоемкости идеального газа (одноатомного). Достаточно, значит, перевести вещество из газообразного состояния в твердое, чтобы его молярная теплоемкость удвоилась. Из сказанного выше ясно, что удвоение теплоемкости происходит потому, что при нагревании твердого тела подводимая теплота расходуется на увеличение не только кинетической, но и потенциальной энергии частиц.
Из формулы (1.1) следует, что атомная теплоемкость (т. е. теплоемкость грамм-атома) твердых тел есть величина постоянная, одинаковая для всех веществ и не зависящая от температуры. Это утверждение называется законом Дюлонга и Пти.
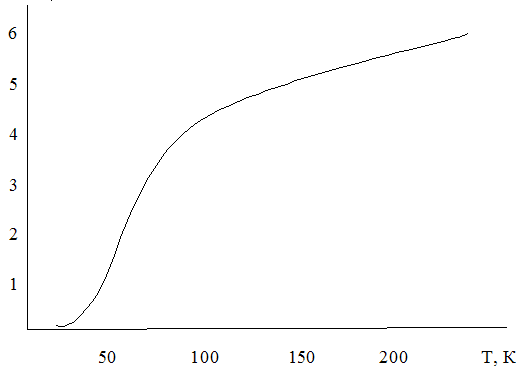
Рис. 1.1.
Опыт показывает, что при обычных температурах атомная теплоемкость большинства твердых тел (химических элементов) в самом деле близка к значению б кал/К. -моль и почти не зависит от температуры. Существуют, однако, исключения. У четырех химических элементов —бериллия, бора, кремния и алмаза—теплоемкость при обычных температурах значительно меньше, чем ЗЯ, и заметно зависит от температуры. С повышением температуры теплоемкость этих веществ растет, стремясь все же к значению 3R.
Это не единственное отклонение от закона Дюлонга и Пти. При низких (значительно ниже комнатной) температурах теплоемкость всех веществ, в том числе и тех, которые при обычных температурах следуют закону Дюлонга и Пти, быстро падает, стремясь к нулю при абсолютном нуле температуры. На рис. 1.1 приведена экспериментальная кривая зависимости теплоемкости Ср (именно теплоемкость при постоянном давлении определяется на опыте) от температуры для серебра.
Многочисленные опыты показали, что общей для всех твердых тел закономерностью является не закон Дюлонга и Пти, а отклонения от него. В действительности теплоемкость твердых тел зависит от температуры и притом так, что с понижением температуры она уменьшается пропорционально кубу температуры и стремится к нулю при абсолютном нуле. Значит, элементы бериллий, бор, кремний и алмаз являются не исключением, а правилом, но для них комнатная температура является уже низкой температурой.
Закон Дюлонга и Пти является, как мы видели, следствием закона равномерного распределения энергии по степеням свободы. Поэтому тот факт, что твердые тела в действительности не следуют закону Дюлонга и Пти при низких температурах, показывает, что гипотеза о равномерном распределении энергии по степеням свободы является приближением.
Наблюдаемая на опыте зависимость теплоемкости от температуры может быть объяснена на основе квантовых представлений.
Выше было указано, что молекулы твердого тела — осцилляторы. Согласно квантовой теории энергия осциллятора есть целое кратное величины a.v, где v — частота колебаний осциллятора, h — универсальная постоянная Планка, равная 6,6-10~27
эрг -сек. Таким образом, энергия колеблющейся молекулы может быть записана в виде:
W=nhv, (1.2)
где п — любое целое число. У разных молекул твердого тела v может быть различным, и соответственно этому и энергия их различна, Мы для простоты предполагаем, как это сделал Эйнштейн, что все молекулы колеблются с одинаковой частотой, что в действительности неверно.
Какова же средняя энергия w одной молекулы?
Воспользовавшись формулой Больцмана, можно найти, какая часть молекул обладает энергией w — nhv:
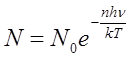
Тогда средняя энергия молекулы w, равная отношению суммы энергий к сумме числа молекул, определяется выражением:
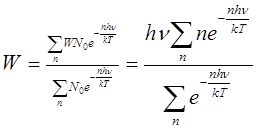
или, обозначив hv/kT = x, получаем:
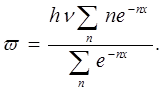
При большом п
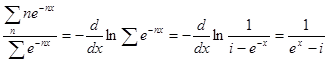
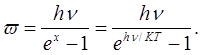
Таким образом, в отличие от классической теории, по которой средняя энергия одной молекулы w — kT, согласно квантовой теории она равна:
 (1.3) (1.3)
Легко убедиться в том, что при высоких температурах, когда kT>>hv, оба выражения совпадают. Действительно, если ограничиться первыми двумя членами разложения в ряд функции ehv/kT
, получаем:
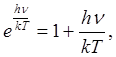
и (1.3) приводится к выражению
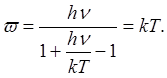
Энергия одного моля вместо значения 3A/0
feT по классической теории принимает значение
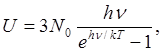
а теплоемкость
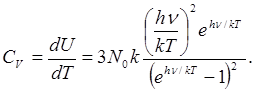 (1.4) (1.4)
При больших Т выражение (1.4.) дает для. теплоемкости Cv значение, равное 3R, т. е. закон Дюлонга и Пти, а при Т = 0 теплоемкость оказывается равной нулю, в полном соответствии с опытом.
Температурная зависимость теплоемкости, вычисленная из теории Эйнштейна, в общем близка к экспериментально наблюдаемой, и только при низких температурах расхождения между теорией и опытом оказываются весьма значительными. Эти расхождения объясняются, конечно, произвольностью допущения, что все колебания молекул твердого тела совершаются с одинаковой частотой v. Эта частота подбирается так, чтобы вычисленные по (1.4.) значения теплоемкости Cv
были по возможности близки к опытным данным. Неудивительно, что для всех температур это сделать не удается.
Дебай, сохранив основную идею Эйнштейна, существенно усовершенствовал теорию, предположив, что в твердом теле существует целый набор частот колебаний. Набор частот колебаний системы называется спектром. Колебания, о которых здесь идет речь, — это те упругие колебания, которые ответственны за распространение звука в твердом теле, а скорость звука равна в первом приближении 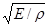 (Е — модуль Юнга, р — плотность тела). (Е — модуль Юнга, р — плотность тела).
Со спектром частот мы встречаемся, например, при рассмотрении колебаний струны, которые представляют собой результат наложений колебаний бесконечного числа обертонов на основной тон струны.
В квантовой теории энергию.звуковых колебаний kv рассматривают как особые частицы фононы (см. ниже). Число возможных частот колебаний бесконечно велико. Число же атомов в твердом теле хотя и очень велико (порядка 1022
в 1 см3
), но конечно; поэтому необходимо принять, как это и сделал Дебай, что в твердом теле спектр колебаний ограничен некоторой максимальной частотой vm
. Из теории Дебая следует, что, начиная с некоторой температуры 6 (характеристическая температура Дебая), теплоемкость начинает быстро убывать с понижением температуры. Это та температура, при которой энергия тепловых движений k® становится равной максимальной энергии осцилляторов:
kQ = hvm
,
отсюда
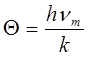 . .
При температурах, значительно меньших в, теплоемкость убывает пропорционально третьей степени температуры («закон Т3
»), что, как мы видели, соответствует опытным данным.
Температура Дебая Q может считаться (и не только по отношению к теплоемкости) границей между высокими и низкими температурами.
С точки зрения квантовой теории теплоемкости тот факт, что некоторые вещества (алмаз, бор и др.) не подчиняются закону Дюлонга и Пти даже при комнатных температурах, объясняется именно тем, что у этих веществ характеристическая температура Дебая настолько высока, что комнатная температура должна считаться низкой температурой. Так, если для серебра в = 210°С, для алюминия » 400°С, для свинца » 90°С, то характеристическая температура для алмаза равна 2000°С.
Измерения теплоемкости и ее температурного хода играют большую роль в исследованиях твердых тел. Это связано с тем, что теплоемкость непосредственно определяется колебаниями атомов в кристаллической решетке. Ясно, что характер этих колебаний должен зависеть от структуры решетки, от ее симметрии и т. д. Благодаря этому во многих случаях превращения, которые могут происходить в веществе, сопровождаются различными аномалиями теплоемкости.
В частности, фазовые переходы второго рода, при которых скрытая теплота перехода не выделяется (и не поглощается), сопровождаются скачком теплоемкости, разрывом в ее монотонном изменении с температурой. Исследуя температурный ход теплоемкости, можно обнаружить такие превращения.
Отметим в заключение, что непосредственному измерению доступна только теплоемкость при постоянном давлении, а не при постоянном объеме, так как из-за теплового расширения нельзя обеспечить постоянство объема тела. Однако вследствие малости изменения объема при нагревании различие между теплоемкостями Су и Ср мало.
Измерение теплоемкости
Теплоемкость определяется, как известно, отношением количества теплоты AQ, подведенного к телу, к вызванному этим теплом повышению температуры:
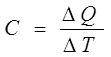
Следовательно, для определения теплоемкости С нужно подвести к исследуемому образцу точно измеренное количество теплоты DQ и измерить последовавшее за этим изменение температуры DT.
Измерение DТ не встречает серьезных трудностей. Современные методы измерения температур позволяют легко измерять небольшую разность температур с точностью до 0,001°, и этого обычно вполне достаточно. Можно также с большой точностью измерять и подводимое количество теплоты. Но при этом необходимо быть уверенным, что подведенное точно измеренное количество теплоты действительно поглощено образцом, так что измеренное изменение температуры DТ вызвано именно измеренным количеством теплоты DQ. Между тем подводимое к образцу тепло может не полностью им поглощаться. Кроме того, образец может получать тепло от других источников или терять его, поэтому всегда существует некоторая неопределенность в значении величины DQ и, следовательно, погрешность в определении С. Усилия экспериментаторов и направлены на то, чтобы уменьшить эти погрешности в измерениях.,
Приборы, служащие для измерения теплоемкости, называются калориметрами (при известной теплоемкости они служат для измерения количества теплоты).
Известно очень большое число различных по своему устройству и даже по принципу действия калориметров. В качестве примера мы приведем здесь схему одного из видов калориметров, довольно часто используемых при измерении теплоёмкости (главным образом при низких температурах).
Прибор состоит из собственно калориметра, которым является образец из исследуемого вещества А с намотанным на нем электрическим нагревателем R, и оболочки В, окружающей образец. Нагреватель R является в то же время термометром сопротивления, контактирующим с образцом. Роль оболочки сводится к тепловой изоляции исследуемого образца от окружающей среды. Изоляция достигается тем, что пространство внутри оболочки откачивается до высокого вакуума. Образец подвешивается на тонких металлических нитях, служащих в то же время для подвода тока к нагревателю. В идеальном калориметре оболочка должна вполне надежно ограждать образец от теплового взаимодействия с окружающей калориметр средой, так чтобы образец не получал от нее и не отдавал ей тепла. Устройства для подвода тепла и для измерения температуры не должны нарушать этой изоляции..
В таком идеальном калориметре измерения сводились бы к следующим простым операциям. Сначала, не создавая вакуума внутри калориметра, его помещают в термостат (например, в электрическую печь, в сосуд с жидкостью заданной/температуры и т. д.), так чтобы образец был доведен до той температуры, при которой должны быть проведены измерения. После этого пространство внутри калориметра откачивают и тем самым изолируют образен от термостата. Затем через нагреватель в течение определенного времени (точно измеряемого) пропускают электрический ток, измеряя при этом разность потенциалов на его концах и силу тока в нем. Измерив теперь вызванное действием нагревателя повышение температуры, можно вычислить теплоемкость образца. Разделив полученное значение С на массу образца, выраженную в граммах или в молях, получают соответствен но удельную или молярную теплоемкость вещества," из которого изготовлен образец.
Тепловое расширение твердых тел.
Общеизвестно, что твердые тела при нагревании увеличивают свой объем. Это — тепловое расширение. Рассмотрим причины, приводящие к увеличению объема тела при нагревании.
Очевидно, что объем кристалла растет с увеличением среднего расстояния между атомами. Значит, повышение температуры влечет за собой увеличение среднего расстояния между атомами кристалла. Чем же обусловлено увеличение расстояния между атомами при нагревании?
Повышение температуры кристалла означает увеличение энергии теплового движения, т. е. тепловых колебаний атомов в решетке, а следовательно, и рост амплитуды этих колебаний.
Но увеличение амплитуды колебаний атомов не всегда приводит к увеличению среднего расстояния между ними.
Если бы колебания атомов были строго гармоническими, то каждый атом настолько же приближался бы к одному из своих соседей, насколько удалялся от другого, и увеличение амплитуды его колебаний не привело бы к изменению среднего межатомного расстояния, а значит, и к тепловому расширению.
В действительности атомы в кристаллической решетке совершают ангармонические (т. е. не гармонические) колебания. Это обусловлено характером зависимости сил взаимодействия между атомами от расстояния между ними. Как было указано в начале настоящей главы, зависимость эта такова, что при больших расстояниях между атомами силы взаимодействия между атомами проявляются как силы притяжения, а при уменьшении этого расстояния меняют свой знак и становятся силами отталкивания, быстро возрастающими с уменьшением расстояния.
Это приводит к тому, что при возрастании «амплитуды» колебаний атомов вследствие нагревания кристалла рост сил отталкивания между атомами преобладает над ростом сил притяжения. Другими словами, атому «легче» удалиться от соседа, чем приблизиться к другому. Это, конечно, должно привести к увеличению среднего расстояния между атомами, т. е. к увеличению объема тела при его нагревании.
Отсюда следует, что причиной теплового расширения твердых тел является ан гармоничность колебаний атомов в кристаллической решетке.
Количественно тепловое расширение характеризуется коэффициентами линейного и объемного расширения, которые определяются следующим образом. Пусть тело длиной I при изменении температуры на DТ градусов изменяет свою длину на Dt. Коэффициент линейного расширения определяется из соотношения
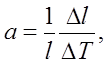
т. е. коэффициент линейного расширения равен относительному изменению длины при изменении температуры на один градус. Точно так же коэффициент объемного расширения Ә5 определяется формулой
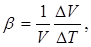
т. е. коэффициент р равен относительному изменению объема DV/V, отнесенному к одному градусу.
Из этих формул следует, что длина lТ
и объем VT
при некоторой температуре, отличающейся от начальной на DТ градусов, выражаются формулами (при малом DT):
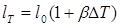 и и 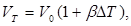
где /о и V0
— начальные длина и объем тела.
Вследствие анизотропии кристаллов коэффициент линейного расширения а может быть различным в разных направлениях. Это означает, что если из данного кристалла выточить шар, то после его нагревания он потеряет свою сферическую форму. Можно показать, что в самом общем случае такой шар при нагревании превращается в трехосный эллипсоид, оси которого связаны с кристаллографическими осями кристалла.
Коэффициенты теплового расширения по трем осям этого эллипсоида называются главными коэффициентами расширения кристалла.
Если их обозначить соответственно через a1
, a2
и a3
, то коэффициент объемного расширения кристалла
b = a1
+ a2
+ a3
.
Для кристаллов с кубической симметрией, так же как и для изотропных тел,
a1
= a2
= a3
= a и b = 3a.
Шар, выточенный из таких тел, остается шаром и после нагревания (разумеется, большего диаметра).
В некоторых кристаллах (например, гексагональных)
a1
= a2
иb = a1
+ a3
.
Коэффициенты линейного и объемного расширения практически остаются постоянными, если интервалы температур, в которых они измеряются, малы, а сами температуры высокие. Вообще же коэффициенты теплового расширения зависят от температуры и притом так же, как теплоемкость, т. е. при низких температурах коэффициенты a и b уменьшаются с понижением температуры пропорционально кубу температуры, стремясь, как и теплоемкость, к нулю при абсолютном нуле. Это неудивительно, так как и теплоемкость, и тепловое расширение связаны с колебаниями решетки: теплоемкость дает количество теплоты, необходимое для увеличения средней энергии тепловых колебаний атомов, зависящей от амплитуды колебаний, коэффициент же теплового расширения непосредственно связан со средними расстояниями между атомами, которые тоже зависят от амплитуды атомных колебаний.
Отсюда следует важный закон, открытый Грюнейзеном: отношение коэффициента теплового расширения к 'атомной теплоемкости твердого тела для данного вещества есть величина постоянная (т. е. не зависящая от температуры).
Коэффициенты 'теплового расширения твердых тел обычно очень малы, как это видно из табл. 3.1. Приведенные в этой таблице значения коэффициента а относятся к интервалу температур между О и 100°С.
Таблица 3.1. Коэффициенты теплового расширения твердых тел
| Вещество |
a |
Вещество |
a |
Алюминий
|
26*10-6
|
Латунь
|
19*10-6
|
Серебро
|
19*10-6
|
Дюралюминий
|
22,6*10-6
|
Кремний
|
7*10-6
|
Молибден
|
5*10-6
|
Железо
|
12*10-6
|
Фосфор
|
124*10-6
|
Вольфрам
|
4 *10-6
|
Медь
|
17*10-6
|
Натрий
|
80*10-6
|
Цинк
|
28*10-6
|
Некоторые вещества имеют особенно малый коэффициент теплового расширения. Таким свойством отличается, например, кварц (а = 0,5-Ю"6
). Другим примером может служить сплав никеля и железа (36% Ni), известный под названием инвар (а = 1 -Ю"0
). Эти вещества получили широкое применение в точном приборостроении.
Теплопроводность
Если в твердом теле существует разность температур между различными его частями, то подобно тому, как это происходит в газах и жидкостях, тепло переносится от более нагретой к менее нагретой части.
В отличие от жидкостей и газов, в твердом теле не может возникнуть конвекция, т. е. перемещения массы вещества вместе с теплом. Поэтому перенос тепла в твердом теле осуществляется только теплопроводностью.
Механизм переноса тепла в твердом теле вытекает из характера тепловых движений в нем. Твердое тело представляет собой совокупность атомов, совершающих колебания. Но колебания эти не независимы друг от друга. Колебания могут передаваться (со скоростью звука) от одних атомов к другим. При этом образуется волна, которая и переносит энергию колебаний. Таким распространением колебаний и осуществляется перенос тепла.
Количественно перенос тепла в твердом теле описывается так же, как и в газе. Если через единицу площади сечения перпендикулярно к его плоскости в единицу времени переносится количество тепла q, то оно связано с разностью температур, вызывающей перенос, соотношением [см. (4.3)]:
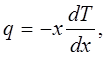 (4.1) (4.1)
где dTldx — градиент температуры в направлении X. Величина q называется потоком тепла. Величина коэффициента теплопроводности к не может быть вычислена так, как это делается для газа — системы более простой, состоящей из невзаимодействующих частиц.
Приближенно коэффициент теплопроводности твердого тела можно вычислить с помощью квантовых представлений.
Фононы. Квантовая теория позволяет сопоставить распространяющимся в твердом теле со скоростью звука колебаниям некоторые фиктивные частицы —фононы. Каждая частица характеризуется энергией, равной известной уже нам постоянной Планка, умноженной на ту величину, которая в классической физике называется частотой колебания v. Энергия фонона равна, значит, hv.
Если пользоваться представлением о фононах, то можно сказать, что тепловые движения в твердом теле обусловлены именно ими, так что при абсолютном нуле фононы отсутствуют, а с повышением температуры их число возрастает, но не линейно, а по более сложному закону (при низких температурах пропорционально кубу температуры).
Твердое тело мы можем теперь рассматривать как сосуд, содержащий газ из фонопов, газ, который при не очень высоких температурах может считаться идеальным газом. Как и в случае обычного газа, перенос тепла в фононном газе осуществляется столкновениями фононов с атомами решетки, и все рассуждения, которые были проведены при вычислении коэффициента теплопроводности идеальных газов, справедливы и здесь. Поэтому коэффициент теплопроводности твердого тела может быть выражен совершенно такой же формулой [см. (4.3)]:
 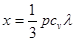 c, c,
где р —плотность тела, су —его удельная теплоемкость, ас — скорость звука в нем.
Несколько сложнее вычислить длину свободного пробега фононов λ. Оценка показывает, что эта величина обратно пропорциональна, абсолютной температуре. Поэтому и коэффициент теплопроводности х обратно пропорционален температуре:
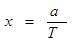 , ,
где а — некоторая константа, различная для, различных веществ.
В металлах, помимо колебаний решетки, в переносе тепла участвуют и заряженные частицы — электроны, которые вместе с тем являются и носителями электрического тока в металле, При высоких температурах электронная часть теплопроводности много больше решеточной. Этим объясняется высокая теплопроводность металлов по сравнению с неметаллами, в.которых фононы — единственные переносчики тепла.
Так, коэффициент теплопроводности алюминия равен 238 Вт/м*К, в то время как у кварца он не превышает 5. Напомним, что коэффициент теплопроводности газов при нормальных условиях ~ 10-3
Вт/м *К. При более низких (но не самых низких) температурах начинает преобладать решеточная теплопроводность, так как она растет с понижением температуры, а электронная от температуры не зависит. При самых низких температурах электронная часть теплопроводности вновь начинает преобладать.
Однако в сверхпроводниках, в которых электрический ток не встречает сопротивления, электронная теплопроводность практически отсутствует: электроны, без сопротивления переносящие электрический ток, в переносе тепла не участвуют, и теплопередача в сверхпроводниках — чисто решеточная.
Измерение теплопроводности. Из уравнения теплопроводности
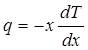
видно, что для определения коэффициента теплопроводности нужно измерить количество тепла q, протекающего через единицу площади сечения тела в единицу времени, и градиент температуры вдоль тела.
При такого рода измерениях встречаются те же трудности, что и при измерении теплоемкости. Ведь и в том и в другом случае нужно измерять количество теплоты и изменение температуры. В обоих случаях подводимое количество теплоты может теряться и таким образом не участвовать в изучаемом процессе. Поэтому при измерении теплопроводности, так же как и теплоемкости, главное внимание нужно обращать на устранение погрешности, возникающей из-за того, что не все тепло передается через исследуемое тело путем теплопроводности, а частично может передаваться окружающей среде через боковые поверхности.
На рис. 4.1 представлена простейшая схема измерения теплопроводности твердого тела.
Исследуемое вещество в виде стержня А нагревается с одного конца каким-нибудь источником тепла (электрическим нагревателем, парами кипящей жидкости), а с другой стороны поддерживается при постоянной температуре {например, проточной водой).
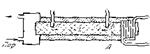
Рис. 4.1.
Стержень на всей его длине окружается изолирующей оболочкой для уменьшения отдачи тепла через боковые поверхности.
Для этой же цели рекомендуется поверхность стержня полировать.
В двух точках стержня а и b специальных углублениях помещаются термометры или термопары.
Через некоторое время после включения нагревателя устанавливается стационарное состояние, при котором градиент температуры становится одинаковым по всей длине стержня. Поэтому он может быть определен как (Т1
— T2
)/ l, где Т1
и Т2
—температуры в точках а и b, а / — расстояние между этими точками. Коэффициент теплопроводности определяется из равенства
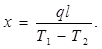
Мощность нагревателя q легко определяется из измерений силы тока и - разности потенциалов.
Приведем еще один пример установки для измерения коэффициента теплопроводности, используемой для исследования веществ, плохо проводящих тепло. В этом случае исследуемому образцу удобно придать форму пластины или диска. Схема опыта представлена на рис.4.2.
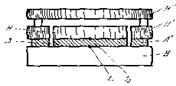
Рис.4.2.
Пластина А исследуемого вещества помещается на массивной охлаждаемой пластине В. Над образцом располагается пластина-нагреватель Я, обогреваемая электрическим током.
Чтобы устранить влияние краев образца, он окружается кольцом из того же материала А'. Защитным кольцом Я' окружается и нагреватель. Наконец, над нагревателем помещается еще один нагреватель Я", температура которого поддерживается такой, чтобы верхняя и нижняя поверхности основного нагревателя H имели одинаковую температуру. Это значит, что тепло, идущее от Я вверх, компенсируется теплом от Я". При таком устройстве прибора можно считать, что тепло от нагревателя Я целиком передается через исследуемый образец, а сам образец не отдает тепла в сторону, так как он защищен кольцом, обогреваемым так же, как и сам образец.
С помощью термометров t1
и t2
измеряются температуры T1
и Т2
обеих поверхностей образца.
Из измерений мощности нагревателя q и разности температур коэффициент теплопроводности вычисляется по формуле
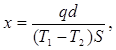
где d—толщина пластины Л, а 5—площадь ее поверхности.
Отдачу образцом тепла в сторону можно, также устранить, изготовляя образец в форме полого цилиндра или сферы и помещая нагреватель на оси цилиндра или в центре сферы.
Диффузия в твердых телах
Несмотря на то, что для твердого тела характерно упорядоченное расположение атомов в кристаллической решетке, перемещение атомов возможно и в нем. Тепловые движения, которые в основном имеют характер малых колебаний, в некоторых случаях приводят к тому, что атомы вовсе покидают свои места в решетке. О возможности таких срывов атомов свидетельствует уже тот факт, что твердые тела могут испаряться. Правда, при испарении отрыв атомов происходит в поверхностном слое, но нет оснований утверждать, что такой отрыв невозможен и внутри тела.
Именно благодаря тому, что атомы покидают свои места в узлах решетки, возникают некоторые дефекты в кристаллах —такие, как дефекты типа Шоттки и Френкеля. С этими срывами атомов и их последующим перемещением в кристалле связана и диффузия в твердых телах.
Так же, как в газах, частицы в твердых телах имеют различные энергии тепловых движений. И при любой температуре имеется определенная часть атомов, энергия которых значительно превосходит среднюю и достаточно велика для того, чтобы они могли покинуть свое место в решетке и перейти в новое положение. Чем выше температура, тем таких атомов больше, и поэтому коэффициент диффузии D с повышением температуры быстро возрастает (по экспоненциальному закону). Но так как число атомов с достаточно большой энергией всегда мало (если температура много ниже температуры плавления), то процесс диффузии в твердом теле оказывается еще более медленным процессом, чем в газах и жидкостях. Например, коэффициент диффузии меди в золото при300°С равен 1,5-10-13
см2
/с. Для сравнения укажем, что при диффузии водного раствора метилового спирта в воду D = 1,3 –10-5
см2
/с, а диффузия аргона в гелий идет с D = 0,7 см2
/с. Тем не менее диффузия в твердых телах играет большую роль в целом ряде процессов. Она наблюдается как в однокомпонентном (в этом случае говорят о само диффузии), так и в многокомпонентных веществах, в моно- и в поликристаллах.
Опыт (в частности, исследования с помощью так называемых меченых атомов) показывает, что диффузия в твердых телах осуществляется главным образом следующими тремя способами:
1. Соседние атомы в решетке обмениваются местами в решетке. Обмен этот может, например, явиться следствием поворота участвующей в ней пары атомов вокруг средней точки.
2. Атом, находящийся на «своем» месте в узле решетки, покидает его и располагается в междоузлии, а затем мигрирует в междоузлиях.
3. Атомы из узлов решетки переходят в незанятые узлы, так называемые вакансии. Этот последний процесс возможен только в дефектных кристаллах, так как вакансии являются, конечно, дефектами кристалла. Очевидно, что переход атомов на вакантные места эквивалентен перемещению самих вакансий в правлении, обратном направлению движения атомов.
Наиболее важную роль играет, по-видимому, последний механизм диффузии. Для его осуществления в твердом теле должен существовать градиент плотности вакансий, так что атомы (а значит и вакансии) чаще перемещаются в одном направлении, чем в другом. В поликристаллах важную роль играет процесс заполнения вакансий на границах кристалликов (зерен). По-видимому, в процессе создания вакансий, без которых невозможна диффузия, важную роль играют дислокации.
При экспериментальном изучении диффузии в твердых телах исследуемые вещества приводятся в надежный контакт друг с другом и затем длительное время выдерживаются при той или иной температуре опыта. После такой выдержки снимаются последовательно тонкие слои, перпендикулярные к направлению диффузии, и исследуются концентрации про диффундировавших веществ в зависимости от расстояния до места контакта.
В последнее время широко используются искусственные радиоактивные вещества, присутствие которых легко обнаруживается по их излучению.
Этот метод (метод - меченых атомов) позволяет исследовать и явление самодиффузии, т. е. диффузии в твердом теле атомов самого этого тела.
Общий закон диффузии в твердых телах — такой же, как в газах и жидкостях. Это — закон Физика, о котором мы не раз упоминали.
Что касается коэффициента диффузии D, то выражение для него можно получить из соображений, сходных системы, которые были приведены на стр. 318 в связи с вопросом о диффузии в жидкостях. Ведь диффузия в твердом теле тоже осуществляется скачками атомов из их положений равновесия в узлах кристаллической решетки. Но теперь о дальности скачка можно, вполне определенно сказать, что она равна постоянной решетки а.
Необходимо, однако, иметь в виду, что при вакансионном механизме диффузии атом из узла решетки может совершить скачок только в том случае, если соседний узел пустует, если он представляет собой вакансию. Но даже и при таком соседстве атому необходима добавочная энергия q, чтобы скачок в вакансию состоялся. Ведь в узле решетки потенциальная энергия атома минимальна. Поэтому любое смещение атома из узла, включая и смещение в соседнюю вакансию, требует добавочную энергию, которую он с некоторой вероятностью может получить в результате флуктуации. Эта вероятность, как всегда, определяется законом Больцмана:
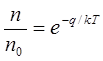
Здесь q — энергия, необходимая для скачка из узла решетки, энергия перемещения атома в вакансию.
По соображениям, приведенным на стр. 318, коэффициент само диффузии в твердом теле может быть записан в виде:
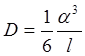
где а — постоянная решетки и t — среднее время пребывания атома в узле решетки. Это время, очевидно, тем меньше, чем больше вероятность образования вакансии рядом с атомом и чем больше вероятность того, что атом получит энергию перемещения д. На стр. 319 мы видели, что вероятность образования вакансии равна e-w/kT
. Теперь мы видим, что вероятность того, что атом получит энергию q, равна eW/kT
. Поэтому выражение для коэффициента диффузии может быть записано в виде:
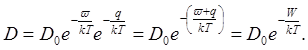
Множитель do (так называемый пред экспоненциальный множитель) — постоянная, характерная для данного вещества. Величина W, равная сумме энергии образования вакансии w и энергии q перемещения атома в вакансию, называется энергией активации диффузии и тоже является величиной, характерной для вещества.
Коэффициент диффузии в твердых телах очень мал. Для золота, например, при комнатной температуре он порядка 10-35
. Даже вблизи температуры плавления золота он достигает значения лишь в 10-8
см2
/с. Это показывает, как сильно зависит коэффициент диффузии от температуры.
Малость коэффициента диффузии в твердых телах объясняется тем, что для того, чтобы диффузионный скачок атома в вакансию состоялся, необходимо, чтобы практически одновременно произошли два, вообще говоря, маловероятных события; чтобы рядом с атомом образовалась вакансия и чтобы сам атом получил в результате флуктуации энергию, достаточную для скачка.
При других механизмах диффузии, при диффузии одних веществ в другие, коэффициент диффузии вычисляется иначе. Об этом читатель узнает из специальных курсов. Но во всех случаях коэффициенты диффузии по абсолютному значению малы. Так, например, коэффициент диффузии серы в железо даже при температуре, близкой к 1000°С, равен приблизительно 2,7 -КН3
м2
/с. Но несмотря на малость коэффициентов диффузии в твердых телах, роль диффузии в твердых телах очень велика. Именно диффузия обеспечивает такие явления и процессы в твердых телах, как отжиг для устранения неоднородностей в сплавах, насыщение поверхностей деталей углеродом, азотом и т. д., спекание порошков и другие процессы обработки металлов.
теплоемкость твердое тело анимационная программа
Глава 2. Реализация анимационной обучающей программы для определения удельной теплоемкости твердых тел (проверка выполнимости закона Дюлонга и Пти)
2.1 Алгоритмизация
Определение удельной теплоемкости твердых тел.
Цель работы: проверка выполнимости закона Дюлонга и Пти для ряда исследуемых веществ.
Согласно классической теории теплоемкости при не слишком низких температурах, молярная теплоемкость химически простых веществ в кристаллическом состоянии одинакова и равна 25 Дж/(моль*К). Это утверждение составляет содержание закона Дюлонга и Пти, установленного опытным путем.
Между частицами, образующими кристаллическую решетку твердых тел, существуют силы взаимодействия. Расположение частиц в узлах кристаллической решетки отвечает минимуму их взаимной потенциальной энергии. При смещении частиц из положения равновесия в любом направлении появляется сила, стремящаяся вернуть частицу в первоначальное положение, вследствие чего возникают ее колебания.
При точном рассмотрении задачи необходимо учитывать, что частицы в решетке взаимодействуют друг с другом и их колебания надо рассматривать как связанные. Однако при достаточно высоких температурах, когда энергия становится большой, колебания частиц можно рассматривать приближенно как независимые друг от друга.
Полная энергия частицы U равна сумме кинетической Ек
и потенциальной Еn
:
U = Ek
+ En
.
Колебания частиц в решетке приближенно являются гармоническими. При этом как кинетическая, так и потенциальная энергии гармонических колебаний частицы являются периодическими функциями времени и их средние значения (Ек
) и (Еn
) равны друг другу: (Ек
) = (Еn
). Поэтому среднее значение полной энергии
(U) = (Ek
). (1)
С другой стороны, из кинетической теории идеального газа известно, что средняя кинетическая энергия одноатомных молекул (изолированных частиц)
(Ek
) = 3 / 2 * kT. (2)
где k – постоянная Больцмана, Т – абсолютная температура.
Поскольку, как было отмечено, атомы или ионы кристаллической решетки при достаточно высоких температурах колеблются независимо друг от друга, к ним также применима формула (2). Тогда из (1) и (2) имеем
(U) = 3kT. (3)
 C C
  3R 3R
 Т Т
Рис. 1
Полную внутреннюю энергию одного моля твердого тела получим, умножив среднюю энергию одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле, т. е, на постоянную Авогадро NA
:
U = (U) NA
= 3NA
kT = 3RT, (4)
Где R – молярная газовая постоянная.
Для твердых тел вследствие малого коэффициента теплового расширения теплоемкости при постоянном давлении и постоянном объеме практически не различаются. Поэтому общее выражение теплоемкости твердого тела совпадает с значением молярной теплоемкости при V = const: Cm
= dU / dT. Из формулы (4) окончательно следует, что
Сm
= 3R.
Подставляя численное значение молярной газовой постоянной, получаем
Cm
= 25 Дж / (моль * К). (5)
Это равенство выполняется с довольно хорошим приближением для многих веществ при комнатной температуре. Для более низких температур наблюдаются отклонения от него (рис. 1). Вблизи абсолютного нуля молярная теплоемкость всех тел пропорционально Т3
, и только при достаточно высокой, характерной для каждого вещества температуре начинает выполняться равенство (5).
Строгая теория теплоемкости твердых тел создана Эйнштейном и Дебаем. Она учитывает, что колебания частиц в кристаллической решетке не являются независимыми и что энергия колебательного движения квантована.
Описание установки.
ПРИБОРЫ и ПРИНАДЛЕЖНОСТИ: исследуемые тела, калориметр, автотрансформатор с вольтметром, амперметр, мост постоянного тока.
В настоящей работе для определения молярной теплоемкости различных веществ используется калориметр особой конструкции, схема которого представлена на рис. 2.
Калориметр представляет собой латунный корпус 2 с коническим отверстием 3, куда вставляются испытуемые тела 9, изготовленные из исследуемых материалов и представляющие собой конические цилиндры, притертые к отверстию в корпусе. В корпусе калориметра уложены нагревательная спираль 4 и спираль термометра сопротивления 5.
Снаружи корпус калориметра теплоизолирован слоями асбеста 6 и пенопласта 7 и закрыт алюминиевым кожухом 8. После помещения в калориметр испытуемого тела он закрывается крышкой 10. Винт 1 предназначен для выталкивания испытуемых тел из калориметра по окончании опыта. Для этой же цели можно использовать и специальный крючок, зацепив им тело за предназначенную для этого петлю 9’.
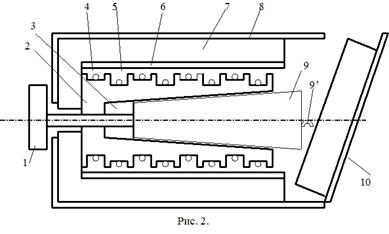
Рис. 2.
Электрическая схема калориметра представлена на рис. 3.
Нагревание обмотки 4 производится от сети переменного тока 2. Напряжение нагревателя регулируется лабораторным автотрансформатором. Измерения амперметром 3 и вольтметром 1. Термометр сопротивления 5 включен в мост постоянного тока 6. Методика измерения сопротивления с помощью моста постоянного тока дана в приложении.
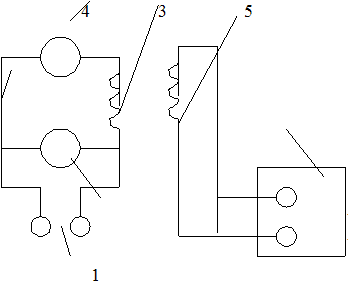
Рис 3.
Если нагрет на ∆Т градусов калориметр с помещенным в него исследуемым телом, то энергия электрического тока пойдет на нагревание исследуемого тела и калориметра
IUt1
= mk
ck
∆Т + mT
cT
∆Т+d. (6)
Здесь I и U – ток и напряжение на нагревателе, t1
- время нагревания, mk
и mT
- массы калориметра и нагреваемого тела, ck
и сT
– удельные теплоемкости калориметра и нагреваемого тела, d - потери тепла.
Для того чтобы вычислить и исключить из уравнения (6) тепло, идущее на нагрев калориметра, и потери тепла в окружающее пространство, можно нагреть пустой калориметр на те же ∆Т градусов. Потери тепла в обоих случаях будут одинаковыми, так как они зависят только от разности температур ∆Т но этот процесс потребует меньшего времени нагревания t2
:
IUt2
= mk
ck
∆Т + d. (7)
Из равенства (6) и (7) следует
где ∆Т = t1
- t2
. Величину можно определить по графикам зависимости ∆Т от t для пустого калориметра и калориметра с исследуемым телом (рис. 73). Температура нагрева измеряется в данной установке при помощи термометра сопротивления, т. е. металлической проволоки.

t2
t1
Рис. 4
Сопротивление металла изменяется температурой по закону
R = R0
(1 + at)?, (9)
где R0
– сопротивление при температуре t, a - температурный коэффициент сопротивления, tкоторый в узком диапазоне температуру можно считать постоянным.
Измерив температуру воздуха в комнате tn
по ртутному термометру и сопротивление RB
измерительной обмотки при помощи моста постоянного тока, можно из формулы (9) рассчитать R0
:
где a - температурный коэффициент сопротивления меди.
Приведенная формула (9) позволяет также по известному сопротивлению R0
обмотки термометра сопротивления и измеренному приращению сопротивления DR = R – RB
подсчитать DT:
DT = Dt = DR / (aR0
) (11).
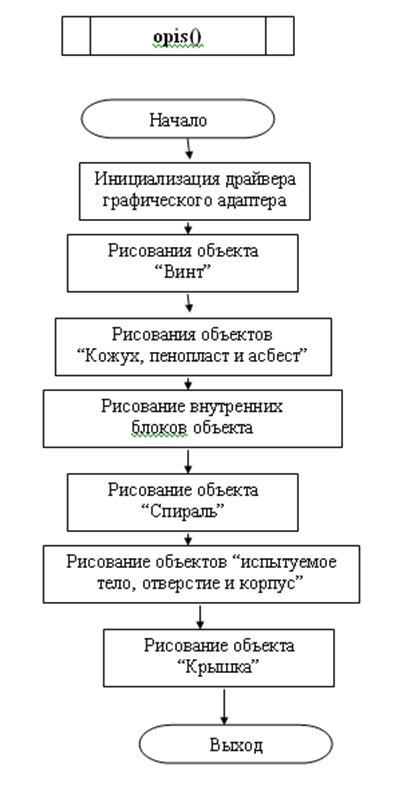
3.2 Блок – схема программы
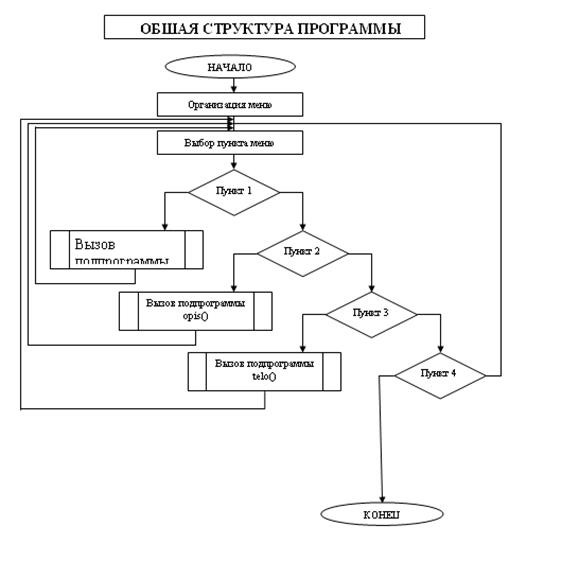
Блок-схема подпрограммы opis()
Блок-схема подпрограммы teoria()
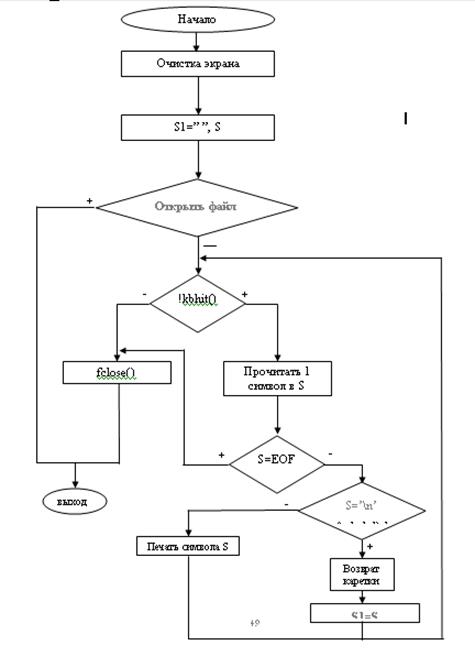

Блок схема подпрограммы Telo()

3.3 Листинг программа
#include <graphics.h>
#include <stdlib.h>
#include <stdio.h>
#include <conio.h>
#include <dos.h>
#include <ctype.h>
#include "steps.h"
int main(void)
{
int gdriver = DETECT, gmode, errorcode,i;
initgraph(&gdriver, &gmode, "");
errorcode = graphresult();
if (errorcode != grOk)
{ printf("Graphics error: %s\n", grapherrormsg(errorcode));
printf("Press any key to halt:");
getch(); exit(1); }
menu:
cleardevice();
setbkcolor(BLACK);
settextjustify(LEFT_TEXT, LEFT_TEXT);
settextstyle(DEFAULT_FONT, HORIZ_DIR, 1);
setfillstyle(SOLID_FILL,15);
setcolor(WHITE);
rectangle(0,0,getmaxx(),getmaxy());
setcolor(RED);
outtextxy(20,64,"-, + - перемещение, Enter - Выбор");
settextstyle(DEFAULT_FONT, HORIZ_DIR, 2);
settextjustify(0, 1);
setcolor(BLUE);
outtextxy(10,12,"");
outtextxy(180,30,"*** M E НЮ***");
outtextxy(10,45,"‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑‑");
setcolor(RED);
outtextxy(30,100,"1.Теория и выполнение работы");
outtextxy(30,150,"2.Описание установок");
outtextxy(30,200,"3.Практика");
outtextxy(30,250,"4.Выход");
int y=80,y1=120;
char x;
setcolor(14);
rectangle(15,y,620,y1);
m1:
x=getch();
switch (toascii(x))
{
case 43: if (y==230)
{
setcolor(BLACK);
rectangle(15,y,620,y1);
y=80; y1=120;
setcolor(14);
rectangle(15,y,620,y1);
goto m1;
}
setcolor(BLACK);
rectangle(15,y,620,y1);
y=y+50;
y1=y1+50;
setcolor(14);
rectangle(15,y,620,y1);
goto m1;
case 45: if (y==80)
{
setcolor(BLACK);
rectangle(15,y,620,y1);
y=230;
y1=270;
setcolor(14);
rectangle(15,y,620,y1);
goto m1;
}
setcolor(BLACK);
rectangle(15,y,620,y1);
y=y-50;
y1=y1-50;
setcolor(14);
rectangle(15,y,620,y1);
goto m1;
case 13: for (i=0;i<1;i++)
{
setcolor(BLUE);
rectangle(15,y,620,y1);
sound(100);
delay(100);
setcolor(14);
rectangle(15,y,620,y1);
sound(200);
delay(100);
}
nosound();
switch(y)
{ case 80: teoria();
goto menu;
case 130: opis();
goto menu;
case 180: telo();
goto menu;
case 230: goto door;
}
goto m1;
default:
goto m1;
}
door:
closegraph();
return 0;
}
ФайлSteps.h
void step1()
{
setcolor(15);
int a10[10]={395,372, 403,378, 548,194, 540,188, 395,372};
drawpoly(5,a10);
int a11[8]={404,361, 382,345, 509,183, 531,199};
drawpoly(4,a11);
setfillstyle(9,7);
floodfill(383,345,15);
setfillstyle(2,9);
floodfill(396,372,15);
}
void step2()
{
setcolor(15);
int a11[10]={395,370, 405,375, 480,165, 470,160,395,370};
drawpoly(5,a11);
int a10[8]={400,355, 375,345, 440,165, 465,175};
drawpoly(4,a10);
setfillstyle(9,7);
floodfill(383,345,15);
setfillstyle(2,9);
floodfill(396,369,15);
}
void step3()
{
setcolor(15);
setfillstyle(9,7);
rectangle(366,355,395,165);
floodfill(370,340,15);
setfillstyle(2,9);
rectangle(395,148,405,372);
floodfill(396,150,15);
}
void step11()
{
setcolor(GREEN);
setfillstyle(SOLID_FILL,GREEN);
int a10[10]={395,372, 403,378, 548,194, 540,188, 395,372};
fillpoly(5,a10);
int a11[8]={404,361, 382,345, 509,183, 531,199};
fillpoly(4,a11);
}
void step22()
{
setcolor(GREEN);
setfillstyle(SOLID_FILL,GREEN);
int a11[10]={395,370, 405,375, 480,165, 470,160,395,370};
fillpoly(5,a11);
int a10[8]={400,355, 375,345, 440,165, 465,175};
fillpoly(4,a10);
}
void step33()
{
setcolor(GREEN);
setfillstyle(SOLID_FILL,GREEN);
bar3d(366,355,395,165,0,0);
bar3d(395,148,405,372,0,0);
}
void voice()
{ sound(25);
delay(4);
nosound(); }
void teoria()
{
int x,i;
cleardevice();
FILE *file1;
char s, s1=' ';
if ((file1=fopen("tr.txt","r"))==NULL)
{ perror("Не могу открыть файл! \n");
exit(1); }
while (!kbhit())
{ s=fgetc(file1);
if (s==EOF) break;
if (s=='\n' && s1=='\n') delay(1500);
printf("%c", s);
voice(); delay(10); s1=s; }
fclose(file1);
getch();
}
void telo(void)
{
int i,j,I,U,M,t,T;
setbkcolor(GREEN);
cleardevice();
settextjustify(LEFT_TEXT, LEFT_TEXT);
settextstyle(DEFAULT_FONT, HORIZ_DIR, 1);
setcolor(15); setfillstyle(SOLID_FILL,15);
printf(" ВХОДНЫЕДАННЫЕ");
printf("\n Силатока(1-3): ");
scanf("%d",&I);
printf(" Напряжение(110-220): ");
scanf("%d",&U);
printf(" Масса(100-300): ");
scanf("%d",&M);
printf(" Время нагревания(1-3): ");
scanf("%d",&t);
printf(" Начальная температура(15-25): ");
scanf("%d",&T);
//VINT
bar3d(85,254,185,266,0,0); bar3d(67,237,85,283,0,0);
int a1[10]={376,215, 185,239, 185,281, 376,305, 376,215};
fillpoly(5,a1);
//kryuchok
arc(381,260,270,180,5);
arc(381,260,270,180,4);
//Blok
int a2[14]={95,140, 395,140, 395,148, 103,148, 103,245, 95,245, 95,140};
drawpoly(7,a2);
int a3[12]={365,148, 365,172, 127,172, 127,250, 103,250, 103,245};
drawpoly(6,a3);
line(365,172,365,180);
line(365,180,127,180);
int a4[14]={95,380, 395,380, 395,372, 103,372, 103,275, 95,275, 95,380};
drawpoly(7,a4);
int a5[12]={365,372, 365,348, 127,348, 127,270, 103,270, 103,275};
drawpoly(6,a5);
line(365,348,365,340); line(365,340,127,340);
setfillstyle(5,9);
floodfill(97,142,15); floodfill(100,372,15);
setfillstyle(9,7);
floodfill(105,162,15); floodfill(125,300,15);
setfillstyle(4,3);
floodfill(355,178,15); floodfill(360,342,15);
//Vnut blok
int a6[12]={348,188, 348,215, 157,239, 157,254, 127,254, 127,250};
drawpoly(6,a6);
int a7[12]={348,332, 348,305, 157,281, 157,266, 127,266, 127,270};
drawpoly(6,a7);
int a8[68]={127,188, 140,188, 140,195, 153,195, 153,188, 166,188, 166,203, 179,203, 179,188, 192,188, 192,195, 205,195, 205,188, 218,188, 218,203, 231,203, 231,188, 244,188, 244,195, 257,195, 257,188, 270,188, 270,203, 283,203, 283,188, 296,188, 296,195, 309,195, 309,188, 322,188, 322,203, 335,203, 335,188, 348,188};
drawpoly(34,a8);
setfillstyle(6,8);
floodfill(130,190,15);
int a9[68]={127,332, 140,332, 140,317, 153,317, 153,332, 166,332, 166,325, 179,325, 179,332, 192,332, 192,317, 205,317, 205,332, 218,332, 218,325, 231,325, 231,332, 244,332, 244,317, 257,317, 257,332, 270,332, 270,325, 283,325, 283,332, 296,332, 296,317, 309,317, 309,332, 322,332, 322,325, 335,325, 335,332, 348,332};
drawpoly(34,a9);
setfillstyle(6,8);
floodfill(130,330,15);
//spiral
setcolor(BLUE);
for(i=146,j=173;i<=310;i=i+52,j=j+52)
{ circle(i,191,3);
circle(j,329,3); }
for(i=172,j=146;i<=340;i=i+52,j=j+52)
{ circle(i,199,3);
circle(j,321,3);}
//krishka
step1();
//move
int k;
for(k=0;k<19;)
{
setcolor(GREEN);
setfillstyle(SOLID_FILL,15);
bar3d(85-k,254,185-k,266,0,0); bar3d(67-k,237,85-k,283,0,0);
a1[0]=376-k; a1[2]=185-k; a1[4]=185-k; a1[6]=376-k; a1[8]=376-k;
fillpoly(5,a1);
arc(381-k,260,270-k,180,5); arc(381-k,260,270-k,180,4);
k++;
setcolor(15);
bar3d(85-k,254,185-k,266,0,0); bar3d(67-k,237,85-k,283,0,0);
arc(381-k,260,270-k,180,5); arc(381-k,260,270-k,180,4);
a1[0]=376-k; a1[2]=185-k; a1[4]=185-k; a1[6]=376-k; a1[8]=376-k;
fillpoly(5,a1);
delay(100);
}
delay(1000);
step11();
step2();
delay(1000);
step22();
step3();
delay(2000);
setcolor(YELLOW);
for(i=146,j=173;i<=310;i=i+52,j=j+52)
{ circle(i,191,3);
circle(j,329,3); }
for(i=172,j=146;i<=340;i=i+52,j=j+52)
{ circle(i,199,3);
circle(j,321,3);}
delay(2000);
setcolor(RED);
for(i=146,j=173;i<=310;i=i+52,j=j+52)
{ circle(i,191,3);
circle(j,329,3); }
for(i=172,j=146;i<=340;i=i+52,j=j+52)
{ circle(i,199,3);
circle(j,321,3);}
delay(2000);
setcolor(LIGHTRED);
for(i=146,j=173;i<=310;i=i+52,j=j+52)
{ circle(i,191,3);
circle(j,329,3); }
for(i=172,j=146;i<=340;i=i+52,j=j+52)
{ circle(i,199,3);
circle(j,321,3);}
delay(2000);
step33();
step2();
delay(1000);
step22();
step1();
for(k=25;k>0;)
{
setcolor(GREEN);
setfillstyle(SOLID_FILL,15);
bar3d(85-k,254,185-k,266,0,0); bar3d(67-k,237,85-k,283,0,0);
a1[0]=376-k; a1[2]=185-k; a1[4]=185-k; a1[6]=376-k; a1[8]=376-k;
fillpoly(5,a1);
arc(381-k,260,270-k,180,5); arc(381-k,260,270-k,180,4);
k--;
setcolor(15);
bar3d(85-k,254,185-k,266,0,0); bar3d(67-k,237,85-k,283,0,0);
arc(381-k,260,270-k,180,5); arc(381-k,260,270-k,180,4);
a1[0]=376-k; a1[2]=185-k; a1[4]=185-k; a1[6]=376-k; a1[8]=376-k;
fillpoly(5,a1);
delay(100);
}
for(i=1;i<25;i++) printf("\n");
printf(" ВЫХОДНЫЕ ДАННЫЕ");
printf("\n Сила тока: %d",I);
printf("\n Напряжение: %d",U);
printf("\n Масса: %d",M);
printf("\n Время нагревания: %d min",t);
printf("\n Начальная температура: %d C",T);
printf("\n Конечная температура: %d C",T+t*9);
printf("\n Удельная теплоемкость: %d",((T+t*9)-T)*2);
getch();
}
void opis(void)
{
int i,j,I,U,M,t,T;
setcolor(15); setfillstyle(SOLID_FILL,15);
cleardevice();
settextjustify(LEFT_TEXT, LEFT_TEXT);
settextstyle(DEFAULT_FONT, HORIZ_DIR, 1);
setbkcolor(GREEN);
//VINT
rectangle(85,254,185,266);
rectangle(67,237,85,283);
int a1[10]={376,215, 185,239, 185,281, 376,305, 376,215};
drawpoly(5,a1);
line(70,250,50,250);
outtextxy(10,250,"Винт");
//kryuchok
arc(381,260,270,180,5);
arc(381,260,270,180,4);
line(381,260,420,160);
outtextxy(420,160,"Кручок");
//Blok
int a2[14]={95,140, 395,140, 395,148, 103,148, 103,245, 95,245, 95,140};
drawpoly(7,a2);
int a3[12]={365,148, 365,172, 127,172, 127,250, 103,250, 103,245};
drawpoly(6,a3);
line(365,172,365,180);
line(365,180,127,180);
int a4[14]={95,380, 395,380, 395,372, 103,372, 103,275, 95,275, 95,380};
drawpoly(7,a4);
int a5[12]={365,372, 365,348, 127,348, 127,270, 103,270, 103,275};
drawpoly(6,a5);
line(365,348,365,340);
line(365,340,127,340);
setfillstyle(5,9);
floodfill(97,142,15);
floodfill(100,372,15);
setfillstyle(9,7);
floodfill(105,162,15);
floodfill(125,300,15);
setfillstyle(4,3);
floodfill(355,178,15);
floodfill(360,342,15);
line(300,100,300,145);
outtextxy(300,100,"Кожух");
line(280,120,280,155);
outtextxy(280,120,"Пенопласта");
line(250,80,250,175);
outtextxy(250,80,"Асбест");
//Vnut blok
int a6[12]={348,188, 348,215, 157,239, 157,254, 127,254, 127,250};
drawpoly(6,a6);
int a7[12]={348,332, 348,305, 157,281, 157,266, 127,266, 127,270};
drawpoly(6,a7);
int a8[68]={127,188, 140,188, 140,195, 153,195, 153,188, 166,188, 166,203, 179,203, 179,188, 192,188, 192,195, 205,195, 205,188, 218,188, 218,203, 231,203, 231,188, 244,188, 244,195, 257,195, 257,188, 270,188, 270,203, 283,203, 283,188, 296,188, 296,195, 309,195, 309,188, 322,188, 322,203, 335,203, 335,188, 348,188};
drawpoly(34,a8);
setfillstyle(6,8);
floodfill(130,190,15);
int a9[68]={127,332, 140,332, 140,317, 153,317, 153,332, 166,332, 166,325, 179,325, 179,332, 192,332, 192,317, 205,317, 205,332, 218,332, 218,325, 231,325, 231,332, 244,332, 244,317, 257,317, 257,332, 270,332, 270,325, 283,325, 283,332, 296,332, 296,317, 309,317, 309,332, 322,332, 322,325, 335,325, 335,332, 348,332};
drawpoly(34,a9);
setfillstyle(6,8);
floodfill(130,330,15);
//spiral
setcolor(4);
for(i=146,j=173;i<=310;i=i+52,j=j+52)
{ circle(i,191,3);
circle(j,329,3); }
// setcolor(4);
for(i=172,j=146;i<=340;i=i+52,j=j+52)
{ circle(i,199,3);
circle(j,321,3);}
setcolor(15);
line(146,192,146,100);
outtextxy(146,100,"Спираль");
line(136,200,136,80);
outtextxy(136,80,"Корпус");
line(170,250,170,450);
outtextxy(170,450,"Отверстье");
line(370,250,370,450);
outtextxy(370,450,"Испытуемоетело");
//krishka
int a10[10]={395,372, 403,378, 548,194, 540,188, 395,372};
drawpoly(5,a10);
int a11[8]={404,361, 382,345, 509,183, 531,199};
drawpoly(4,a11);
setfillstyle(9,7);
floodfill(383,345,15);
setfillstyle(2,9);
floodfill(396,372,15);
line(470,250,470,400);
outtextxy(470,400,"Крышка");
getch(); getch();
}
3.4 Описание работы программы
Рис. 1. Главное меню программы.
На первом рисунке показано меню программы. С помощью клавиш “-” и “+” пользователь может передвигаться по пунктам меню и с помощью клавиши “Enter” выбрать необходимый пункт. При этом управление передается соответствующей подпрограмме которая выполняет функции соответствующие выбранному меню.
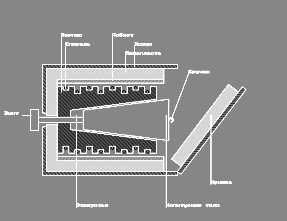
Рис. 2. Вид раздела “Теория и выполнение работы”
После выбора первого раздела меню “Теория и выполнение работы”, управление передается соответствующей подпрограмме которая показывает внешний вид установки. Результат работы показан на рис.2.
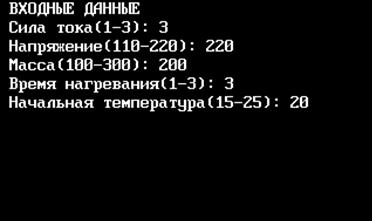
Рис. 3. Вид окна ввода параметров опыта.
При выборе пункта меню “Практика” управление передается подпрограмме выполняющей эмуляцию работы установки. Сначала с пользователем осуществляется диалог, в ходе которого он вводит параметры предстоящего опыта, см. рис.3.
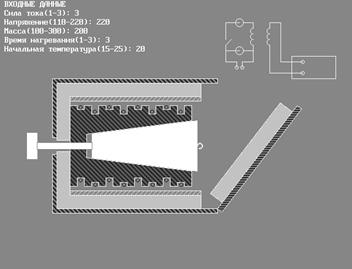
Рис. 4. Визуализация опыта.
После ввода пользователем параметров опыта, эти данные передаются подпрограмме визуализирующей процесс протекания опыта. Результат работы подпрограммы представлен на рис.4.
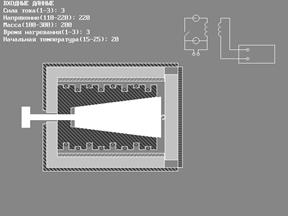
Рис. 5. Визуализация процесса протекания опыта.
Первый шаг визуализации это закрытие крышки калориметра, что показывается ни рис.5.
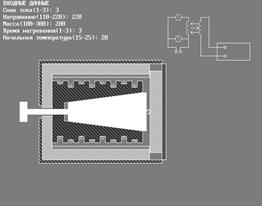
Рис. 6. Визуализация подачи напряжения на катушку.
Следующим шагом протекания опыта является подача тока на катушку и нагревания следствии этого спирали которая нагревает заготовку.
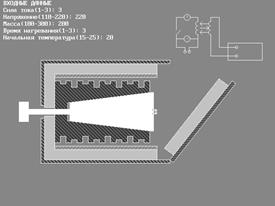
Рис. 7. Визуализация окончания опыта- открытие крышки калориметра.
Следующим шагом опыта является выключение подачи тока к спирали вследствие чего спираль перестает нагревать болванку и затем открывается крышка калориметра для извлечения болванки из него (см.рис.7.).
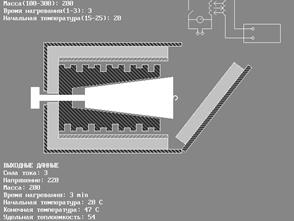
Рис. 8. Извлечение болванки из калориметра.
Завершение опыта – извлечение болванки из калориметра и выдача результата опыта (см. Рис. 8.).

Рис. 9. Результат выбора пункта «Теория».
В результате выбора пункта меню «Теория» пользователю выводится текстовая информация описывающая установку и сам опыт как показано на рис.9.
Заключение
Достижение вычислительной техники за последнее время позволяют внедрять ее в те сферы жизнедеятельности человека, где ранее это было невозможно. Так острой проблемой отечественных школ является острая нехватка физических лабораторий и приборов. При этом, практически во всех школах республики имеются современные компьютерные классы, что позволяют решить проблемы отсутствия лабораторий и приборов путем создания виртуальных анимационных лабораторий.
Создавая анимационно - обучающие программы ученикам представляется возможность всесторонне изучить процессы и влияние, получать практические навыки по физике. Эксплуатация программного комплекса показала большой педагогический эффект, что доказывает актуальность данной тематики.
Список используемой литературы
1. Ливенцев Н.М. Практикум по физике для медицинских вузов. Москва 1972г.
2. М.М. Архангельский. Курс физики. Механика. Москва. 1975г.
3. А.К. Кикоин. Молекулярная физика. Наука. 1976г.
4. А.Ф. Шевченко, Е.А. Безденежных. Физика. 1978г.
5. А.Н. Ремизов. Медицинская и биологическая физика.1987г.
6. М.А. Эссаулова и др. Руководство к лабораторным работам.
7. А.Н. Ремизов. Сборник задач по медицинской и биологической физике. 1987г.
8. О.Ф. Владимиров, Д.М. Ращупкин и др. Биофизика.
9. А.Н. Матвеев. Молекулярная физика. Высшая школа. Москва. 1981г.
10. А.Ф. Шевченко, Е.А. Безденежных. Физика.1978г.
11. Д.В. Сивухин. Общий курс физики. Том 2. Термодинамика и молекулярная физика. Наука. 1975г.
12. Г.С. Ландсберга. Элементарный учебник физики. Том 1. Москва. 1973г.
|