ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
Государственное образовательное учреждение
высшего профессионального образования
"ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"
Химический факультет
Кафедра аналитической и физической химии
Дипломная работа
ТЕРМОДИНАМИКА ХИМИЧЕСКОЙ И ЭЛЕКТРОХИМИЧЕСКОЙ УСТОЙЧИВОСТИ СПЛАВОВ Ni-Si
Челябинск 2009г.
Содержание
Введение
1. Литературный обзор
1.1 Никель-кремниевые сплавы. Их свойства и промышленное применение. Силициды никеля
1.2 Диаграмма состояния Ni - Si. Фазовые превращения в системе Ni-Si
1.3 Термодинамическое моделирование свойств твердых металлических растворов. Обобщенная теория "регулярных" растворов
1.4 Моделирование термодинамических свойств системы Ni-Si
1.5 Термодинамические функции образования интерметаллидов
1.6. Фазовые диаграммы состояния систем Ni-O и Si-O
1.7 Диаграммы электрохимического равновесия систем
2. Экспериментальная часть
2.1 Согласование и прогнозирование свойств системы Ni-Si в области низких температур
2.2 Расчет активностей компонентов системы Ni-Si при 250
С
2.3 Расчет диаграммы состояния системы Ni-Si-O при 25 0
С. Анализ химической устойчивости
2.4 Расчет диаграммы состояния системы Ni-Si-H2
O при 250
С. Анализ химической устойчивости
2.5 Обсуждение результатов
Выводы
Список литературы
Сплавы кремния с никелем относятся к группе аморфных металлических сплавов [1]. Следствием их аморфной структуры являются необычные магнитные, механические, электрические свойства и высокая коррозионная стойкость сплавов. Благодаря этим свойствам они являются перспективными электродными и магнитными материалами. Поэтому анализ их химической и электрохимической устойчивости - важная научная и практическая задача.
Целью работы является термодинамическое описание химических и фазовых равновесий в системе Ni-Siпри низких температурах, анализ химической и электрохимической устойчивости сплавов на основе этих элементов.
Аморфными называют металлы и металлические сплавы, у которых отсутствует дальний порядок в расположении атомов [2]. Они получили также название металлических стекол или некристаллических сплавов. Для их приготовления используют различные методы, в основе которых лежит быстрый переход компонентов сплава из жидкого или газообразного состояния в твердое. При этом затвердевание происходит настолько быстро, что атомы вещества оказываются замороженными в тех положениях, которые они занимали, находясь в жидком состоянии. Существуют убедительные свидетельства, как структурные, так и следующие из различных свойств, того, что в большинстве аморфных кристаллических сплавов действительно существует ближний порядок.
Реклама

Обычно выделяют три класса магнитных аморфных сплавов [2]: это сплавы переходных металлов с металлоидами (ПМ-М), редкоземельных металлов с переходными (РЗМ-ПМ) и переходных металлов с цирконием и гафнием.
Сплавы типа ПМ-М обычно содержат около 80 % (ат.) Fe, Coили Niи в качестве остального - такие элементы, как B, C, Si, Pили Al. Производятся они в основном путем быстрого охлаждения расплава, хотя не исключается использование и других способов - таких, как напыление, электроосаждение или химическое осаждение. Входящие с состав сплавов металлоиды необходимы для того, чтобы понизить температуру плавления и обеспечить достаточно быстрое охлаждение расплава ниже его температуры стеклования, чтобы в результате образовалась аморфная фаза. Стабилизируя аморфное состояние, те же металлоиды радикальным образом изменяют магнитные, механические и электрические свойства сплава в результате перехода части их электронов в d-зону сплава [1].
Установлено, что вследствие магнитных свойств аморфные сплавы являются перспективными материалами для изготовления сердечников больших трансформаторов, а необычное сочетание их магнитных и механических свойств может быть использовано в головках магнитных записывающих устройств, в некоторых типах магнитопроводов в электронике, а также в разнообразных датчиках [2].
Достаточно перспективными электродными материалами являются интерметаллические и металлоподобные соединения, многие из которых обладают уникально высокой коррозионной стойкостью и низким перенапряжением водорода. Были изучены основные закономерности анодного растворения и катодного поведения силицидов металлов подгруппы железа [3] в кислых и щелочных электролитах и детально изучено влияние внешних и внутренних факторов на механизм и кинетику анодного растворения. Установлено, что стойкость силицидов металлов подгруппы железа в кислых электролитах в области потенциалов активного растворения, активно-пассивного перехода и в пассивной области существенно выше, нежели соответствующих чистых металлов и она зависит от соотношения количества "металл: кремний" в силицидах.
Реклама

Полученные результаты дают основание полагать, что низшие силициды подгруппы железа являются перспективными материалами для разработки коррозионностойких катодов для электрохимического получения высокочистого водорода. Наряду с невысоким перенапряжением выделения водорода, они обладают высокой коррозионной стойкостью, хорошими механическими характеристиками.
В сущности, проблемой является ответ на вопрос о том, каким образом аморфность атомной структуры влияет на все разнообразие свойств. Одним из благоприятных моментов при исследовании аморфных сплавов является возможность непрерывного изменения их химического состава в рамках однофазного состояния. Это позволяет получить гомогенные сплавы и исследовать концентрационную и температурную зависимость свойств, не опасаясь сложностей, связанных со структурными превращениями [1].
Свойства силицидов никеля [3].
Теплопроводность λ силицидов никеля (Ni2
Si, NiSi) сравнительно невелика и с повышением температуры практически не меняется. Для Ni3
Si, Ni3
Si2
, NiSi2
наблюдается более сложный характер изменения теплопроводности. Для некоторых силицидов эта величина была установлена при 40 0
С:
λэ
(Ni3
Si) =7,7 Вт/ (м*град),
λэ
(NiSi2
) =6,5 Вт/ (м*град).
В широких пределах (20-1000 0
С) измерены электрофизические свойства силицидов никеля. Для Ni2
Siи NiSiустановлен металлический тип проводимости во всем исследованном интервале температур. Судя по температурной зависимости, основными носителями зарядов являются электроны. Для Ni3
Si, Ni3
Si2
, NiSi2
линейная зависимость электросопротивления наблюдается от 20 до 800, 700 и 5800
С соответственно. Дальнейшее повышение температуры приводит к падению электросопротивления и повышению λ.
По характеру температурной зависимости можно предположить, что у NiSi электроперенос осуществляется отрицательными зарядами, а у Ni3
Si2
- смешанная проводимость. У NiSi2
для переноса электричества служат дырки в интервале 20-8000
С, а затем положительные носители тока заменяются отрицательными.
Силицид Ni2
Si реагирует с фтором при комнатной температуре с воспламенением, с хлором - при 600-7000
С. Газообразные HF, HCl, HBr и HI разлагают его с образованием галогенидов никеля и кремния. Пары воды разлагают Ni2
Si в тех же условиях. Плавиковая кислота растворяет его очень легко, а остальные кислоты - труднее. В смеси HCl и HNO3
силицид Ni2
Si растворяется полностью. Водные растворы щелочей не взаимодействуют с ним, расплавленные щелочи разлагают с образованием растворимых силикатов щелочей и осадка окислов никеля, аналогично действуют на него смеси H2
CO3
и KNO3
, но при более низких температурах.
Высший силицид никеля NISi2
полностью разлагается в смеси концентрированной HNO3
и HF. Некоторые минеральные кислоты (H2
SO4
, H3
PO4
) при одночасовом кипячении растворяют NISi2
незначительно. Прибавление к серной кислоте окислителей (перекись водорода, надсернокислый аммоний) не увеличивает скорость разложения. Органические кислоты, растворы окислителей и комплексообразователей не разлагают силицид, растворы щелочей различной концентрации разлагают его незначительно [3].
Сведения о термическом расширении силицидов никеля весьма немногочисленны. Первая информация по этому вопросу была получена Нешпором и Резниченко, выполнившим дилатометрическое исследование Ni3
Si и Ni2
Si в области температур от 20 до 10700
С [3]. При этом авторы установили, что коэффициенты термического расширения силицидов меняются с ростом температуры как показано в таблице 1.1.:
Таблица 1.1.
Коэффициенты термического расширения силицидов
| Силицид |
Интервал температур, 0
С |
α 106
град-1
|
| Ni3
Si |
20-370
370-770
770-1070
|
9,0
11,5
14,85
|
| Ni2
Si |
20-870
870-1070
|
16,5
19,0
|
На рис.1.1 приведена фазовая диаграмма состояния Ni-Si [4].
В системе определены следующие фазы: β1
, β3
, γ, δ, θ, έ, NiSi и NiSi2
. Из них три фазы γ, θ и NiSi плавятся конгруэнтно при 1242, 1306 и 992 0
С соответственно. Фазы β3
, δ и βNiSi2
образуются по перитектическим реакциям при 1170, 1255 и 993 0
С соответственно. В твердом состоянии по перитектоидным реакциям образуются фазы β1
(1035 0
С) и έ (845 0
С). Три фазы имеют высоко - и низкотемпературные модификации: β3
↔ β2
(1115 0
С), έ↔ε (830 0
С) и βNiSi2
↔αNiSi2
(981 0
С). Максимальная растворимость Si в Ni достигает 15,8 % (ат.) при 1143 0
С (эвтектическая температура). Кристаллическая структура соединений приведена в табл.1.2 [4]
Таблица 1.2.
Кристаллическая структура соединений системы Ni-Si
| Соединение |
Прототип |
Параметры решетки, нм |
| a |
b |
c |
| β (Ni3
Si) |
AuCu3
|
0,350 |
─ |
─ |
| β2
*1
|
(GePt3
?) |
0,697 |
0,625 |
0,507 |
| β3
*2
|
(GePt3
?) |
0,704 |
0,626 |
0,508 |
| δ (Ni2
Si) |
Co2
Si |
0,706 |
0,499 |
0,372 |
| θ*3
|
─ |
0,3805 |
─ |
0,489 |
| ε (Ni3
Si2
) *4
|
─ |
1,2229 |
1,0805 |
0,6924 |
| NiSi |
MnP |
0,562 |
0,518 |
0,334 |
| αNiSi2
|
CaF2
|
0,546 |
─ |
─ |
*1
β=48,74о
*2
β=48,84о
*4
Ромбическая сингония
|

Рис.1.1 Диаграмма состояния системы Ni - Si.
Регулярный раствор образуется из компонентов с выделением или поглощением тепла, а энтропия смешения его такая же, как и в совершенном растворе. Проблема аналитического представления концентрационной и температурной зависимости термодинамических свойств сводится к поиску соответствующего выражения для избыточной энергии Гиббса GE
[5]. Обычно в качестве нулевого приближения к теории реальных растворов применяется модель идеального раствора, где GE
=0. В настоящей модели за нулевое приближение принята теория регулярных растворов.
Понятие "регулярный раствор" включает в себя как частные случаи понятия "идеальный" и "предельно разбавленный" раствор, а закон граничной регулярности, согласно которому любой раствор можно считать регулярным до определенного предела, справедлив для более широкого диапазона концентраций, чем законы Рауля и Генри [5].
Для регулярного раствора:
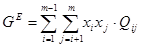 , (1.1) , (1.1)
где xi
и xj
- мольные доли компонентов,
Qij
-
энергия взаимообмена (смешения).
В рамках модели строго регулярного раствора энергии взаимообмена являются константами. В реальных системах энергии взаимообмена (как эмпирические параметры модели) зависят от состава и температуры.
Для субрегулярных растворов:
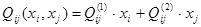 ; (1.2) ; (1.2)
Для квазирегулярных растворов:
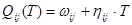 ; (1.3) ; (1.3)
где: 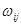 и и 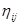 - соответственно теплота и избыточная энтропия смешения компонентов. Выражения (1.2) и (1.3), очевидно, можно рассматривать как частные случаи неизвестной функции для концентрационной и температурной зависимостей энергии смешения компонентов, получаемой путем разложения - соответственно теплота и избыточная энтропия смешения компонентов. Выражения (1.2) и (1.3), очевидно, можно рассматривать как частные случаи неизвестной функции для концентрационной и температурной зависимостей энергии смешения компонентов, получаемой путем разложения 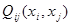 и и 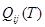 в ряд Тейлора. Если ограничиться несколькими первыми членами ряда: в ряд Тейлора. Если ограничиться несколькими первыми членами ряда:
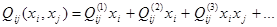 ; (1.4) ; (1.4)
то получится представление функции 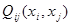 полиномом. В свою очередь, каждый из параметров полиномом. В свою очередь, каждый из параметров 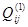 , , 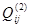 , , 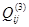 ,…, ,…, 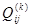 может зависеть от температуры: может зависеть от температуры:
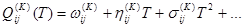 ; (1.5) ; (1.5)
Многочлены (1.4) и (1.5) - приближенное выражение неизвестной функции 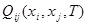 . Качество приближения определяется величиной остатка рядов - той ее части, которая отбрасывается. Чтобы наше приближение удовлетворительно описывало термодинамические свойства раствора, нужно, чтобы остаток был невелик по сравнению с ошибкой экспериментов. Тогда дальнейшее уточнение функции теряет смысл. . Качество приближения определяется величиной остатка рядов - той ее части, которая отбрасывается. Чтобы наше приближение удовлетворительно описывало термодинамические свойства раствора, нужно, чтобы остаток был невелик по сравнению с ошибкой экспериментов. Тогда дальнейшее уточнение функции теряет смысл.
Как показывает математическая обработка экспериментальных данных, для бинарных растворов достаточно трех параметров 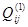 , , 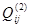 , , 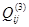 , чтобы в большинстве случаев корректно аппроксимировать термодинамические функции смешения системы. Поэтому концентрационную (конфигурационную) энергию взаимообмена компонентов в дальнейшем будем представлять тремя членами ряда (1.4), а избыточную энергию Гиббса любой фазы с областью гомогенности будем описывать уравнением: , чтобы в большинстве случаев корректно аппроксимировать термодинамические функции смешения системы. Поэтому концентрационную (конфигурационную) энергию взаимообмена компонентов в дальнейшем будем представлять тремя членами ряда (1.4), а избыточную энергию Гиббса любой фазы с областью гомогенности будем описывать уравнением:
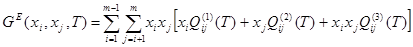 ; (1.6) ; (1.6)
где 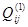 и и 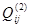 - термодинамические характеристики областей регулярности двойной системы вблизи чистых компонентов; - термодинамические характеристики областей регулярности двойной системы вблизи чистых компонентов;
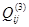 - параметр, учитывающий отклонение от "регулярности". - параметр, учитывающий отклонение от "регулярности".
Умножив части уравнения (1.6) на общее число молей 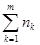 компонентов в растворе, получим избыточную энергию Гиббса компонентов в растворе, получим избыточную энергию Гиббса 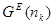 произвольного количества фазы. Откуда: произвольного количества фазы. Откуда:
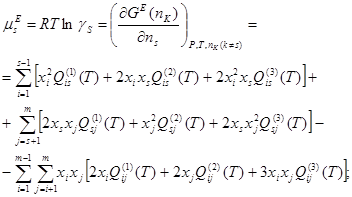 (1.7) (1.7)
Активности компонентов двойной системы:
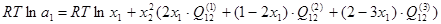 ; (1.8) ; (1.8)
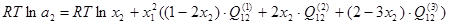 ; (1.9) ; (1.9)
Обобщенная теория "регулярных" растворов позволяет успешно описать термодинамические свойства металлических, неметаллических и смешанных систем [5].
сплав кремний никель интерметаллид
Для описания термодинамических свойств фаз переменного состава твердых растворов применялась обобщенная теория "регулярных" растворов в однопараметрическом приближении.
Энергетические параметры γ-фазы (Ni) определялись из условия равновесия интерметаллида Ni3
Siс твердым раствором:
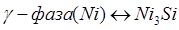 ; (1.10) ; (1.10)
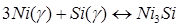 ; (1.11) ; (1.11)
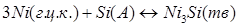 ; (1.12) ; (1.12)
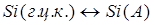 ; (1.13) ; (1.13)
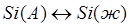 ; (1.14) ; (1.14)
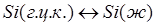 ; (1.15) ; (1.15)
Комбинируя реакции, получим:
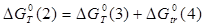 ; (1.16) ; (1.16)
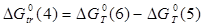 ; (1.17) ; (1.17)
Величины энергия образования реакций (1.14) и (1.15):
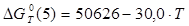 ; ;
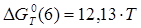 ; ;
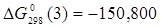 кДж/моль. кДж/моль.
Отсюда:
 , ,
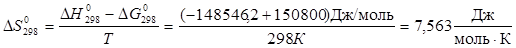

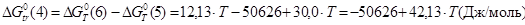
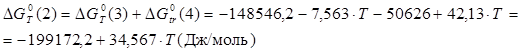
В рамках однопараметрического приближения теории "регулярных" растворов:
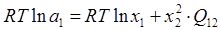 , ,
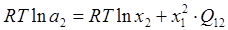 ; (1.18) ; (1.18)
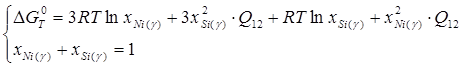 ; (1.19) ; (1.19)
Мольные доли компонентов и температуру определили из диаграммы состояния системы Ni-Si. Они представлены в табл.1.3:
Таблица 1.3
Состав γ-фазы по диаграмме состояния Ni-Si
| T, 0
С |
T, К |
xS
i (γ)
|
xNi (γ)
|
| 793 |
1066 |
0,100 |
0,900 |
| 821 |
1094 |
0,105 |
0,895 |
| 870 |
1143 |
0,110 |
0,890 |
| 910 |
1183 |
0,115 |
0,885 |
| 933 |
1206 |
0,120 |
0,880 |
| 953 |
1226 |
0,125 |
0,875 |
| 974 |
1247 |
0,130 |
0,870 |
| 988 |
1261 |
0,135 |
0,865 |
| 1005 |
1278 |
0,140 |
0,860 |
| 1020 |
1293 |
0,145 |
0,855 |
| 1033 |
1306 |
0,150 |
0,850 |
Решая систему уравнений (1.19), получаем значения энергий смешения (табл.1.4). Q12
<0, следовательно, раствор имеет отрицательные отклонения от закона идеальности.
Таблица 1.4
Энергии смешения для γ-фазы
| № |
T, К |
Q12
, Дж/моль |
| 1 |
1066 |
-165626,7 |
| 2 |
1094 |
-165257,0 |
| 3 |
1143 |
-163418,7 |
| 4 |
1183 |
-162127,0 |
| 5 |
1206 |
-161927,6 |
| 6 |
1226 |
-161878,5 |
| 7 |
1247 |
-161708,6 |
| 8 |
1261 |
-161963,2 |
| 9 |
1278 |
-161961,2 |
| 10 |
1293, |
-162043,7 |
| 11 |
1306 |
-162211,6 |

Рис.1.2 Зависимость энергии смешения от температуры.
Строим зависимость энергии смешения от температуры, аппроксимируем полученную функцию по частям (рис.1.2)
в области низких температур при мольной доле кремния 0,1-0,12 функцию зависимости энергии смешения аппроксимировали линейно:
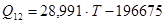 , R2
=0,9802; (1.20) , R2
=0,9802; (1.20)
при мольной доле от 0,12 до 0,15 полиномиальная аппроксимация:
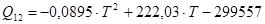 , R2
=0,8098; (1.21) , R2
=0,8098; (1.21)
Согласование энергий Гиббса образования бинарных интерметаллидов систем Ni - Si.
В системе Ni-Siпри низких температурах термодинамически устойчив твердый раствор кремния в никеле с решеткой г. ц. к., существуют интерметаллидные фазы β1 (
Ni3
Si), δ (Ni2
Si), ε (Ni3
Si2
), αNiSi2
и NiSi. Стандартные энергии Гиббса образования этих интерметаллидов приведены в таблице 1.5 [6].
Таблица 1.5.
Стандартные энергии Гиббса образования интерметаллидов
| Соединение |
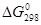 , кДж/моль , кДж/моль |
| β1 (
Ni3
Si) |
-150,800 |
| δ (Ni2
Si) |
-143,100 |
| ε (Ni3
Si2
) |
-232,000 |
| αNiSi2
|
-94, 200 |
| NiSi |
-89,600 |
Методы расчета фазовых диаграмм состояния металл-кислород.
Химическая устойчивость металлов в окислительной газовой среде, например, на воздухе, определяется их стойкостью к окислению кислородом. Лучшим способом представления термодинамической информации об окислении металлических материалов являются фазовые диаграммы состояния систем металл-кислород.
На фазовых диаграммах Ме-О представлены различные химические равновесия, играющие роль в процессе окисления металла. Они характеризуют растворимость кислорода в данном металле, состав оксидных форм, образующихся в результате окислении металла кислородом, и устойчивость фаз в зависимости от различных параметров системы: температуры, давления, состава и др.
Состав системы выражается содержанием металла и кислорода в атомных процентах, либо в процентах по массе.
Для более сложных систем, содержащих третий компонент - другой металл, существуют аналогичные диаграммы состояния Ме1
-Ме2
-О. Они позволяют разобраться в вопросах состава и структуры окалины (слоев окислов) на поверхности бинарных сплавов. В литературе накоплен огромный справочный материал по термодинамическим свойствам неорганических веществ, сформулированы общие принципы фазовых равновесий в гетерогенных системах (правило фаз Гиббса), предложены различные модели, интерполирующие свойства компонентов и металлических, и оксидных растворов (теории совершенных и "регулярных" растворов) и т.п. Все это позволило расчетным путем выявить вид и характерные особенности интересующих нас диаграмм состояния [7].
Согласно закону равновесия фаз - правилу фаз Гиббса, в трехкомпонентной системе при постоянных внешних параметрах (P,T=const):
f=3-Ф; (1.22)
где f - число термодинамических степеней свободы, или вариантность системы, то есть количество параметров (температура, давление, концентрации компонентов в фазах), которые являются независимыми,
Ф - количество фаз в системе, находящихся в равновесии.
Из физических соображений следует, что f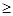 0. Таким образом, в указанной системе возможны равновесия с участием одной, двух или максимум трех фаз: 0. Таким образом, в указанной системе возможны равновесия с участием одной, двух или максимум трех фаз:
однофазные равновесия (f=2); отдельные фазы (вещества) термодинамически устойчивы в определенном интервале составов и, соответственно, парциальных давлений кислорода;
двухфазные (моновариантные) равновесия (f=1);
трехфазные (нонвариантные) равновесия (f=0).
В условиях трехфазного равновесия система не имеет степеней свободы, т.е. данное состояние системы полностью описывается законами действующих масс гетерогенных химических реакций и условиями нормировки составов фаз. Для однозначного расчета составов фаз в условиях двухфазового равновесия необходимо задаваться одним из параметров системы.
Для записи законов действующих масс (выражений для констант равновесий) химических реакций необходимо определить активности компонентов в фазах. Активность кислорода в газовой фазе при давлении 1 атм может быть принята его парциальному давлению. Для конденсированных фаз в рамках модели регулярных растворов справедливо выражение:
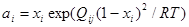 ; (1.23) ; (1.23)
где 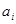 - активность компонента в растворе; - активность компонента в растворе;
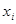 - мольная (атомная) доля компонента в растворе; - мольная (атомная) доля компонента в растворе;
 - энергия смешения компонентов при образовании раствора. - энергия смешения компонентов при образовании раствора.
Формула применима к двухкомпонентным растворам.
Для конденсированных фаз в рамках модели идеального (совершенного раствора) 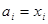 . .
Валовый состав тройной системы Ме1
-Ме2
-О можно записать как
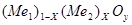 ; ;
где 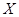 - атомная доля металла - атомная доля металла 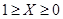 ; ;
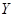 - степень окисленности системы - степень окисленности системы
(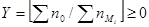 .) .)
Тогда изотермические сечения диаграммы состояния этой системы удобно представить графически на плоскости в координатах 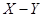 . .
В соответствии с теорией химического сродства Вант-Гоффа термодинамическим критерием возможности окисления элементов в сплаве служит стандартное изменение свободной энергии Гиббса 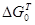 для реакции: для реакции:
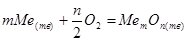 ; (1.24) ; (1.24)
или давление кислорода 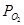 . Эти показатели взаимосвязаны уравнением: . Эти показатели взаимосвязаны уравнением:
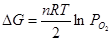 ; (1.25) ; (1.25)
Чем отрицательнее величина изобарно-изотермического потенциала реакции (1.24), или ниже 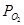 , тем выше избирательность окисления данного металла. , тем выше избирательность окисления данного металла.
Итак, представление фазовых диаграмм вида Ме-О, Ме1
-Ме2
-О может быть различно и зависеть от выбора термодинамических параметров как координат (Р, Т составов и др.) Но в любом случае эти диаграммы могут служить термодинамической основой при изучении вопросов об устойчивости систем, в частности, при рассмотрении вопросов об окислении металлов [8].
Фазовая диаграмма состояния системы Si-O
Фазовая диаграмма состояния системы Si-Oпредставлена на рис.1.3 [7]. Как следует из диаграммы, в системе образуется одна устойчивая оксидная фаза - SiO2
(кремнезем). Таким образом, при температурах ниже 14000
С в системе реализуются следующие фазовые равновесия:
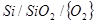
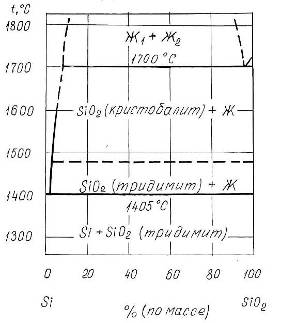
Рис.1.3 Диаграмма состояния системы Si-O.
Фазовая диаграмма состояния Ni-Oприведена на рис.1.4 [5].
Из нее следует, что при температурах ниже 200 0
С в системе никель - кислород наблюдается следующая последовательность равновесий:
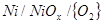
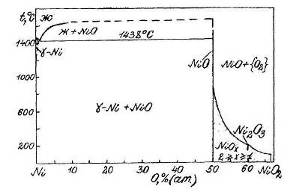
Рис.1.4 Диаграмма состояния Ni - O.
Здесь 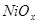 - фаза нестехиометрического состава, непрерывный ряд твердых растворов между NiO и NiO2
(1<x<2). - фаза нестехиометрического состава, непрерывный ряд твердых растворов между NiO и NiO2
(1<x<2).
Ni-H2
Oи Si-H2
О. Общие положения. Применение диаграммы рН-потенциал. Электрохимическая устойчивость металлов и сплавов определяется их стойкостью к коррозии в водной среде. Лучшим способом представления термодинамической информации о химической и электрохимической устойчивости металлических систем в водных растворах являются диаграммы рН-потенциал. Впервые такие диаграммы в системе элемент-вода для чистых металлов при температуре 250
С были построены Марселем Пурбе и использованы им для описания термодинамических коррозионных процессов.
На диаграммах Пурбе представлены различные химические и электрохимические равновесия, играющие роль в процессе коррозии металлов. Они характеризуют прежде всего состав водного раствора и устойчивость твердых фаз в зависимости от двух переменных: электродного потенциала и рН раствора для реально устанавливающихся равновесий. Электродные потенциалы φ выражены в вольтах по водородной шкале.
Диаграммы состоят из областей, разграниченных между собой кривыми равновесия. В случае жидких фаз положение границы зависит от активности не только ионов водорода, но и других ионов, участвующих в равновесии. В таких случаях, вместо одной кривой на рисунке нанесено семейство кривых, каждая из которых отвечает определенной активности соответствующих ионов (при этом для каждой кривой указано значение логарифма активности 0, - 2, - 4, - 6 и т.п.) [5].
На всех диаграммах рН-потенциал наносятся две основные линии диаграммы состояния воды (они наносятся пунктиром и обозначаются буквами а и b). Эти линии отвечают электрохимическим равновесиям воды продуктами ее восстановления - водородом (линия а) и окисления - кислородом (линия b). Область, заключенная между этими двумя линиями, является областью устойчивости воды. При потенциалах, лежащих вне этой области, т.е. выще линии b или ниже линии а, вода термодинамически неустойчива; выше линии b вода окисляется, а ниже линии а - восстанавливается.
Диаграммы Пурбе служат термодинамической основой при решении вопросов об устойчивости того или иного состояния системы и о возможности протекания в ней какой-либо реакции. В частности, ими можно пользоваться при рассмотрении вопросов об окислении металлов (как самопроизвольном, так и анодном) [10].
Методика расчетов диаграмм рН-потенциал
Для расчета и построения диаграмм рН-потенциал необходимо располагать сведениями об основных реакциях (окисления и восстановления, комплексообразования и осаждения), возможных в данной системе, об их количественных характеристиках (энергии Гиббса, произведение растворимости и т.д.) и передать графически в координатах рН-потенциал.
Линии на диаграмме рН-потенциал рассчитываются по равновесию, записанному в общей форме:
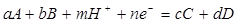 ; (1.26) ; (1.26)
для которого можно записать уравнение равновесного потенциала:
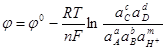 ; (1.27) ; (1.27)
где 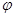 - равновесный потенциал системы; - равновесный потенциал системы;
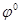 - стандартный потенциал системы; - стандартный потенциал системы;
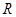 - универсальная газовая постоянная; - универсальная газовая постоянная;
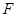 - постоянная Фарадея; - постоянная Фарадея;
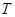 - температура, К; - температура, К;
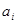 - активность иона в растворе. - активность иона в растворе.
Введя общепринятое обозначение 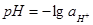 , получим: , получим:
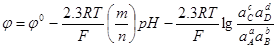 ; (1.28) ; (1.28)
Для того чтобы построить диаграмму рН-потенциал по уравнению (1.28), выбирают фиксированные значения 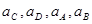 так, чтобы последний член имел постоянную величину. Затем строят прямую линию с одинаковой так, чтобы последний член имел постоянную величину. Затем строят прямую линию с одинаковой 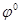 при рН=0 и наклоном при рН=0 и наклоном 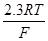 . При 25 0
С значение . При 25 0
С значение 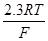 равно 0,0591 В, тогда наклон прямой равен равно 0,0591 В, тогда наклон прямой равен 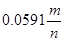 . .
Наклонные линии (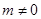 и и 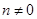 ) отображают равновесия, в которых участвуют ионы Н+
и ОН -
совместно с электронами; горизонтальные линии (m=0) - равновесия, в которых участвуют электроны, но не принимают участия ионы Н+
и ОН-
; вертикальные линии (n=0) - равновесия, в которых принимают участие ионы Н+
и ОН-
, но не учавствуют электроны. Последнее равновесие является химическим, поэтому не может быть рассчитано по формуле (1.28). ) отображают равновесия, в которых участвуют ионы Н+
и ОН -
совместно с электронами; горизонтальные линии (m=0) - равновесия, в которых участвуют электроны, но не принимают участия ионы Н+
и ОН-
; вертикальные линии (n=0) - равновесия, в которых принимают участие ионы Н+
и ОН-
, но не учавствуют электроны. Последнее равновесие является химическим, поэтому не может быть рассчитано по формуле (1.28).
Вместо него применяют уравнение:
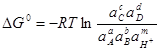 ; (1.29) ; (1.29)
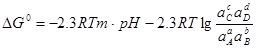 ; (1.30) ; (1.30)
Затем определяют значение рН для вертикальной линии по уравнению:
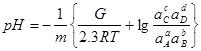 ; (1.31) ; (1.31)
Как ранее упоминалось, на полные диаграммы рН-потенциал наносят семейства линий при активностях ионов в растворе равных 100
, 10-2
, 10-4
, 10-6
моль, соответственно обозначаемые 0, - 2, - 4, - 6.
Для характеристики коррозионных процессов можно использовать упрощенные диаграммы рН-потенциал. Для этого или объединяют отдельные кривые, соответствующие различным активностям (проводят усредненную кривую), в одну, либо строят диаграмму только для одной из активностей ионов в растворе.
Диаграмма рН-потенциал системы Si-H2
O и Ni-O
Диаграмма электрохимического равновесия системы Si-H2
O представлена на рис.1.5 [7].

Рис.1.5 Диаграмма рН-потенциал для системы Si-H2
O при 25 0
С,
1 атм. (воздух) и 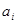 =1. =1.
Линии "а" и "b" на диаграмме ограничивают область термодинамической устойчивости воды. В области 1 кремний находится в виде оксида кремния SiO2
.
Основные химические и электрохимические равновесия приведены в таблице 1.6.
Таблица 1.6.
Основные химические и электрохимические равновесия в системе Si-H2
O при 25 0
С, 1 атм. (воздух) и ai
=1
| № на рис. |
Электродная реакция |
Равновесный потенциал (В)
или рН раствора
|
| a |
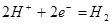 ; ; 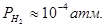
(0,01 об. % возд.)
|
0,186-0,0591рН |
| b |
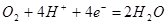 ; ; 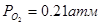 , (21об. % возд.) , (21об. % возд.) |
1,219-0,0591рН |
| 1 |
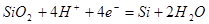 |
-1,151-0,0591рН |
| 2 |
 |
-0,739-0,0887рН |
| 3 |
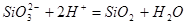 |
рН 13,94 |
Линии "а" и "b" на диаграмме ограничивают область термодинамической устойчивости воды. В области 1 кремний находится в виде оксида кремния SiO2
.
Диаграмма рН-потенциал системы Ni-H2
Oприведена на рис.1.6 [10].
На диаграмме можно выделить 4 области преобладания различных фаз:
I - Ni - область иммунности
II - Ni2+
- область активной коррозии
III - NiOx
- область пассивности
IV - 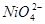 - область транспассивности. - область транспассивности.
Основные химические и электрохимические равновесия указаны в табл.1.7.
Таблица 1.7.
Основные химические и электрохимические равновесия в системе Ni-H2
Oпри 25 0
С, 1 атм. (воздух) и ai
=1 моль/л (негидратированная форма оксидов)

Рис.1.6. Диаграмма рН-потенциал системы Ni-H2
Oпри 25 0
С,
1 атм. (воздух) и 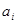 =1 моль/л (негидратированная форма оксидов). =1 моль/л (негидратированная форма оксидов).
Справочные данные для расчетов системы Ni-Si-O [6].
Таблица 2.1.
Стандартные энтальпии образования и энтропии некоторых веществ
| Элемент или соединение |
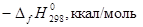 |
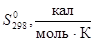 |
| Ni (г. ц. к.) |
0 |
7,12 ± 0,05 |
| O2
(г) |
0 |
49,005 ± 0,008 |
| NiO (т) |
57,2 ± 0,1 |
9,1 ± 0,1 |
Таблица 2.2.
Стандартные энергии Гиббса образования некоторых соединений
| Соединение |
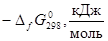 |
Соединение |
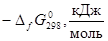 |
| SiO2
|
918,472 |
Ni (г. ц. к.) |
8,878 |
| Ni2
SiO4
|
1317,270 |
O2
(г) |
61,107 |
| NiO (т) |
250,695 |
Таблица 2.3.
Стандартные электродные потенциалы
| № |
Электродная реакция |
Равновесный потенциал, В |
| a |
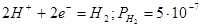 атм. атм. |
0,186-0,0591рН |
| b |
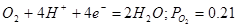 атм. атм. |
1,219-0,0591рН |
В разделе 1.4 нами была получена модель термодинамических свойств системы Ni-Si, которая описывалась с помощью обобщенной теории "регулярных" растворов в однопараметрическом приближении. Проверяем адекватность полученной модели, решая обратную задачу: рассчитываем мольные доли компонентов раствора, задавая температуру, энергию Гиббса и рассчитанные нами энергии смешения Q12
по уравнениям (1.20) и (1.21). При этом экстраполируем зависимость до комнатных температур. На рис.2.1 точками обозначены исходные данные из диаграммы Ni-Si, а сплошной линией показана полученная модель.
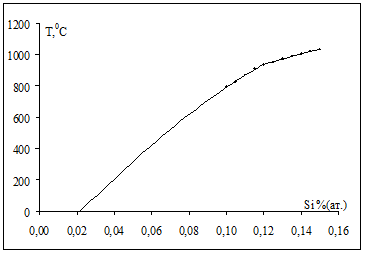
Рис.2.1 Проверка адекватности модели.
Как видно из графика, при 00
С растворимость Siв Niсоставляет около 0,022 % (ат.).
В соответствии с обобщенной теорией "регулярных" растворов, активности компонентов двойной системы можно рассчитать по следующим уравнениям:
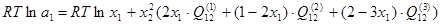 ; (2.1) ; (2.1)
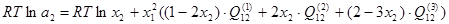 ; (2.2) ; (2.2)
В рамках однопараметрического приближения теории "регулярных" растворов и непосредственно для системы Ni-Siэти уравнения перепишутся следующим образом:
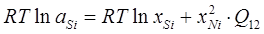 , ,
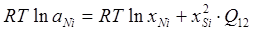 . .
Результаты расчетов предоставлены в таблице 2.4.
Таблица 2.4.
Состав и активности компонентов системы Ni-Si при 250
С
| Компонент |
xi
|
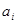 |
| Si |
0,0228 |
7,370*10-29
|
| Ni |
0,9772 |
0,9394 |
Как следует из экспериментальных данных по системе никель-кремний (рис.1.1), никель-кислород (рис.1.3) и кремний-кислород (рис.1.4) схема фазовых равновесий в системе никель-кремний-кислород при 298 К и 1 атм. имеет вид (рис.2.2).

Рис.2.2 Фазовая диаграмма состояния системы Ni-Si-O при 25 0
С.
Поскольку химическое сродство кремния к кислороду выше, чем никеля, то можно предположить, что почти при любом составе сплава Ni-Si в первую очередь будет реализовываться равновесие сплав - SiO2
.
На диаграмме 2.2 можно выделить области, в которых присутствуют следующие фазы:
1. Si (γ) - NiSi2
- SiO2
; (I)
2. NiSi2
- NiSi - SiO2
; (II)
3. NiSi - Ni3
Si2
- SiO2
; (III)
4. Ni3
Si2
- Ni2
Si - SiO2
; (IV)
5. Ni2
Si - Ni3
Si - SiO2
; (V)
6. Ni3
Si - γ-фаза - SiO2
; (VI)
7. γ - фаза - Ni2
SiO4
- NiO; (VII)
8. γ-фаза - Ni2
SiO4
- NiO; (VIII)
9. Ni2
SiO4
- NiOх
, 1<x<1,346; (IX)
10. Ni2
SiO4
- SiO2
- NiOx
, 1,346<x<1,903; (XI)
Примеры расчета:
а) Фазовое равновесие VII:
γ-фаза - Ni2
SiO4
- SiO2
было описано независимыми реакциями образования SiO2
и Ni2
SiO4
из компонентов γ-фазы (Ni, Si) и компонентов газовой фазы O2
:
(1) 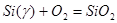 ; ;
(2) 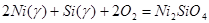 ; ;
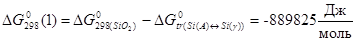
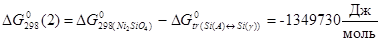
Константы равновесия реакций 1 и 2:
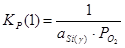 ; (2.3), ; (2.3), 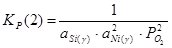 ; (2.4) ; (2.4)
Для определения состава γ-фазы исключим 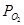 из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в квадрат и поделим полученное на уравнение (2.4), получим: из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в квадрат и поделим полученное на уравнение (2.4), получим:
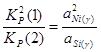 ; (2.5) ; (2.5)
Это уравнение можно переписать в виде:
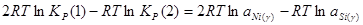 ; (2.6) ; (2.6)
Из уравнения изотермы химической реакции:
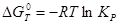 ; (2.7) ; (2.7)
уравнение (2.3.4) можно переписать:
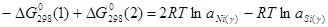 ; (2.8) ; (2.8)
Данное трансцендентное уравнение можно решить только численным методом. Обозначив xSi
=x, xNi
=x-1, получим:
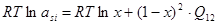 ; (2.9) ; (2.9)
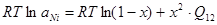 ; (2.10) ; (2.10)
Подставив уравнения (2.9) и (2.10) в (2.8) решаем численным методом, находим значение х. Исходя из уравнений (2.3) или (2.4) определяем величину 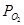 . .
Для остальных трехфазных равновесий расчет производился тоже исходя из константы равновесия. Например, для равновесия IV:
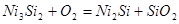
Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:
 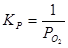 ; (2.11) ; (2.11)
Результаты расчетов приведены в таблице 2.5.
Таблица 2.5.
Характеристики фазовых равновесий системы Ni-Si-O при 25 0
С
| № |
Равновесие |
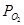 , атм. , атм. |
Равновесный состав фаз |
| I |
Si (γ) - NiSi2
- SiO2
|
1,07*10-156
|
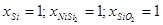 |
| II |
NiSi2
- NiSi - SiO2
|
3,35*10-150
|
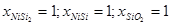 |
| III |
NiSi - Ni3
Si2
- SiO2
|
1,48*10-144
|
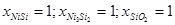 |
| IV |
Ni3
Si2
- Ni2
Si - SiO2
|
2,00*10-135
|
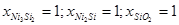 |
| V |
Ni2
Si - Ni3
Si - SiO2
|
1,27*10-128
|
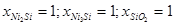 |
| VI |
Ni3
Si - γ-фаза - SiO2
|
3,04*10-129
|
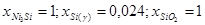 |
| VII |
γ - фаза - Ni2
SiO4
- SiO2
|
2,44*10-81
|
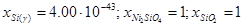 |
| VIII |
γ - фаза - Ni2
SiO4
- NiO |
8,68*10-75
|
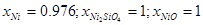 |
| IX |
Ni2
SiO4
- NiOх
, 1<x<1,346 |
0,21 |
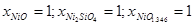 |
| X |
Ni2
SiO4
- SiO2
- NiOx
, 1,346<x<1,903 |
0,21 |
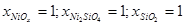 |
| XI |
NiO1,903 -
NiO2
- SiO2
|
9,48*1030
|
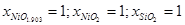 |
б) Расчет равновесия NiOx
- Ni2
SiO4
- SiO2
Окисление Ni2
SiO4
на воздухе завершится образованием фазы NiOx
. Для нахождения значения x решим уравнение:
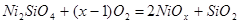 ; (2.12), ; (2.12), 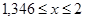
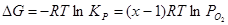 ; (2.13) ; (2.13)
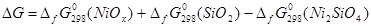 ; (2.14) ; (2.14)
Чтобы знать в явном виде зависимость 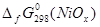 от х воспользуемся функциональной зависимостью между стандартной энергией образования оксидов данного металла из элементов и стехиометрическим составом оксидов: от х воспользуемся функциональной зависимостью между стандартной энергией образования оксидов данного металла из элементов и стехиометрическим составом оксидов:
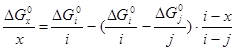 ; (2.15), ; (2.15),
где i, j - степени окисленности оксидов металла, для которых существуют наиболее достоверные термодинамические данные,
х - степень окисленности неизвестного оксида.
Наиболее достоверные термодинамические данные для никеля получены для оксида NiO:
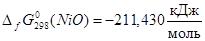
Данные для оксида Ni2
O3
получены расчетным путем: 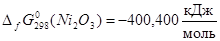 . Поскольку для гипотетического оксида NiO1,5
энергия Гиббса образования вдвое меньше, то . Поскольку для гипотетического оксида NiO1,5
энергия Гиббса образования вдвое меньше, то 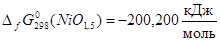 . Таким образом, . Таким образом, 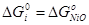 , , 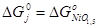 , , 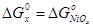 , i=1, j=1,5 и энергия Гиббса оксида NiOx
: , i=1, j=1,5 и энергия Гиббса оксида NiOx
:
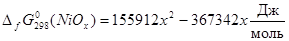 ; (2.16) ; (2.16)
Подставляя (2.3.13) в (2.3.12) и полученное выражении для 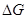 в (2.3.11), находим значение x, соответствующее максимальной степени окисленности никеля в оксиде, полученного окислением Ni2
SiO4
на воздухе: х=1,903. в (2.3.11), находим значение x, соответствующее максимальной степени окисленности никеля в оксиде, полученного окислением Ni2
SiO4
на воздухе: х=1,903.
Из результатов расчета следует, что химическое сродство кремния к кислороду намного выше, чем у никеля. Вплоть до содержания кремния в γ - фазе - 10-40
моль единственной оксидной фазой (продуктов окисления сплава) является кремнезем. Окисление сплавов начинается при давлении кислорода большем чем 10-156
атм, поэтому сплавы будут окисляться кислородом воздуха при 250
С. Так как для образования NiO2
требуется давление кислорода в газовой фазе над сплавом большее, чем 9,48*1030
, то при окислении сплавов кислородом воздуха NiO2
образовываться не будет. Окисления никеля завершится образованием фазы NiOx
.
Диаграммы рН-потенциал строят, зафиксировав активности компонентов, находящихся в растворе. В данной работе построены диаграммы рН-потенциал для системы Ni-Si-H2
O при активностях ионов в растворе равных 1 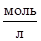 , 10-3 , 10-3
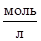 , 10-6 , 10-6
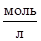 . Они представлены соответственно на рис.2.3, 2.4, 2.5 Основные химические и электрохимические равновесия указаны в табл.2.6. . Они представлены соответственно на рис.2.3, 2.4, 2.5 Основные химические и электрохимические равновесия указаны в табл.2.6.
При построении диаграмм были использованы данные из табл.1.5 и табл.2.2-2.3. В качестве примера рассмотрим расчеты некоторых равновесий:
1) Электрохимическое равновесие 3:
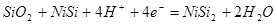
рассчитывалось комбинацией следующих реакций:
а) 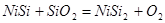 , ,
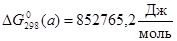 ; ;
б) 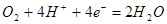 , ,
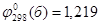 В; Так как В; Так как 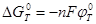 , (2.17) , (2.17)
то свободная энергия Гиббса электрохимической реакции (б) будет равна:
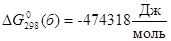 . .
По закону Гесса 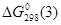 будет равна: будет равна:
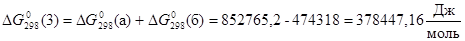 . .
Согласно уравнению (2.17): 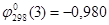 В. В.
Таблица 2.6.
Основные химические и электрохимические равновесия в системе Ni-Si-H2
Oпри 25 0
С, 1 атм. (воздух)
| №линии |
Электродная реакция |
Равновесный потенциал (В) или рН раствора |
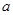 |
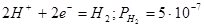 атм. атм. |
0,186-0,0591рН |
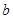 |
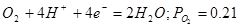 атм. атм. |
1,219-0,0591рН |
| 1 |
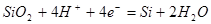 |
-1,151-0,0591рН |
| 2 |
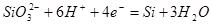 |
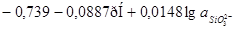 |
| 3 |
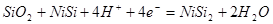 |
-0,980-0,0591рН |
| 4 |
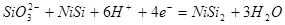 |
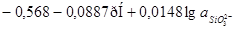 |
| 5 |
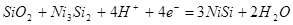 |
-0,897-0,0591рН |
| 6 |
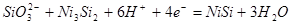 |
 |
| 7 |
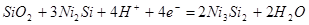 |
-0,762-0,0591рН |
| 8 |
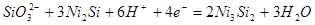 |
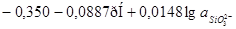 |
| 9 |
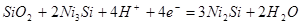 |
-0,714-0,0591рН |
| 10 |
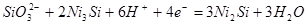 |
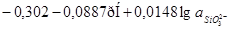 |
| 11 |
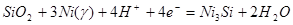 |
-0,645-0,0591рН |
| 12 |
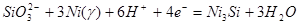 |
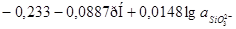 |
| 13 |
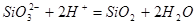 |
рН 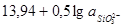 |
| 14 |
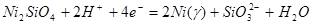 |
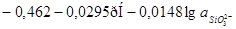 |
| 15 |
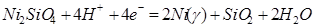 |
-0,49-0,0591рН |
| 16 |
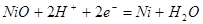 |
0,133-0,0591рН |
| 17 |
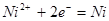 |
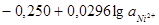 |
| 18 |
 |
рН 3,4 |
| 19 |
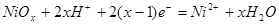 |
(0,806х2
-0,67х-0,0591хрН) / (х-1) |
| 20 |
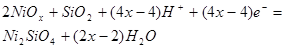 |
1,602-0,0591рН |
| 21 |
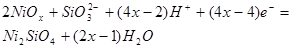 |
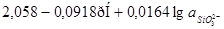 |
| 22 |
 |
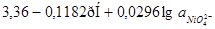 |
Подставив значение 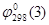 в уравнение (1.27) или (1.28) и учитывая, что в уравнение (1.27) или (1.28) и учитывая, что 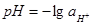 , получим равновесный потенциал реакции (3): , получим равновесный потенциал реакции (3):
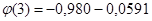 рН. рН.
2) Электрохимическое равновесие 4:
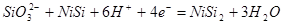
рассчитывалось сложением равновесий 3 и 13:
а) 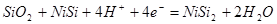 , ,
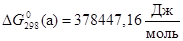 ; ;
б) 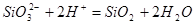 , рН 13,94. , рН 13,94.
Используя уравнение (1.31), найдем энергию Гиббса реакции (б):
  . .
Тогда энергия Гиббса равновесия 4:
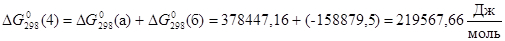 , ,
Отсюда 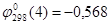 . .
Равновесный потенциал реакции 4:
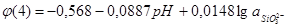
Аналогичным образом были рассчитаны остальные фазовые равновесия. Результаты расчетов приведены в табл.2.6.
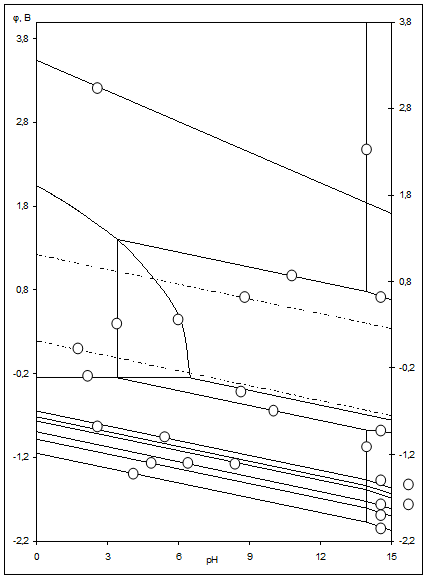
Рис.2.3 Диаграмма рН-потенциал системы Ni-Si-H2
Oпри 25 0
С, 1 атм. (воздух) и 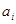 =1 =1 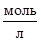 . .
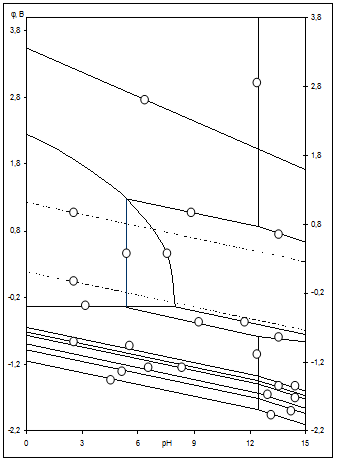
Рис.2.4 Диаграмма рН-потенциал системы Ni-Si-H2
Oпри 25 0
С, 1 атм. (воздух) и 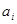 =10-3 =10-3
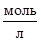 . .
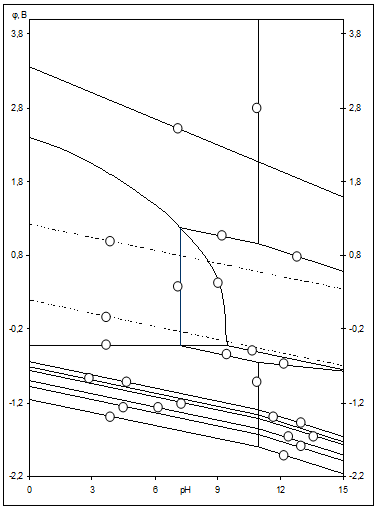
Рис.2.5 Диаграмма рН-потенциал системы Ni-Si-H2
Oпри 25 0
С, 1 атм. (воздух) и 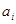 =10-6 =10-6
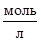 . .
На диаграмме можно выделить 21 область преобладания различных фаз:
I. 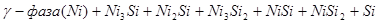
II. 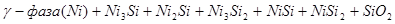
III. 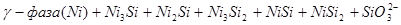
IV. 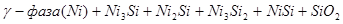
V. 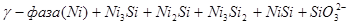
VI. 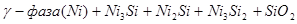
VII. 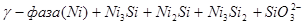
VIII. 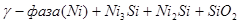
IX. 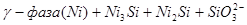
X. 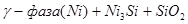
XI. 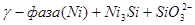
XII. 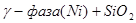
XIII. 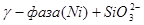
XIV. 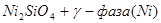
XV. 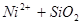
XVI. 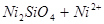
XVII. 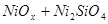
XVIII. 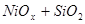
XIX. 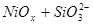
XX. 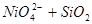
XXI. 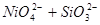
Область I - область иммунности γ-фазы, интерметаллидов и чистого кремния, когда сплав не подвергается коррозии. Выше линии 1 кремний термодинамически неустойчив и окисляется до кремнезема ( ) в кислых средах и до ) в кислых средах и до 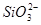 в щелочных средах, интерметаллиды и γ-фаза остаются термодинамически устойчивыми фазами. Выше линии 3 происходит последовательное диспропорционирование в щелочных средах, интерметаллиды и γ-фаза остаются термодинамически устойчивыми фазами. Выше линии 3 происходит последовательное диспропорционирование 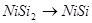 , , 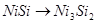 и так далее вплоть до и так далее вплоть до 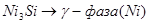 . Области XIV, XVIи XVII - области термодинамической устойчивости . Области XIV, XVIи XVII - области термодинамической устойчивости 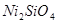 . В кислых средах он неустойчив и распадается с образованием . В кислых средах он неустойчив и распадается с образованием 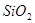 и свободных ионов никеля и свободных ионов никеля 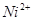 . Области XVII, XVIII и XIX отвечают образованию оксидов никеля . Области XVII, XVIII и XIX отвечают образованию оксидов никеля 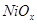 . В областях транспассивности - XX и XXI - происходит перепассивация сплава по никелю. Коррозия сплава происходит во всех областях, находящихся правее линии 13, а также избирательная коррозия в областях XVи XVI. . В областях транспассивности - XX и XXI - происходит перепассивация сплава по никелю. Коррозия сплава происходит во всех областях, находящихся правее линии 13, а также избирательная коррозия в областях XVи XVI.
Состав образующейся пассивационной пленки может быть разным. Если в сплаве достаточно много кремния, то образуется сплошная пассивационная оксидная пленка в виде  . Если кремния недостаточно для образования сплошной пленки из кремнезема, пассивационная пленка представляет из себя . Если кремния недостаточно для образования сплошной пленки из кремнезема, пассивационная пленка представляет из себя 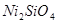 . В случае недостатка кремния даже для образования . В случае недостатка кремния даже для образования 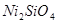 , в качестве пассивационной пленки выступает оксид никеля , в качестве пассивационной пленки выступает оксид никеля 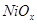 с включениями из с включениями из  . Сравнение диаграмм, построенных при различных значениях активностей ионов в растворе, показывает, что с уменьшением активностей ионов снижаются потенциалы растворения компонентов сплава и потенциал перепассивации сплава по никелю. Области активной коррозии расширяются, а области пассивности наоборот уменьшаются и сдвигаются в более кислую область. Области устойчивости . Сравнение диаграмм, построенных при различных значениях активностей ионов в растворе, показывает, что с уменьшением активностей ионов снижаются потенциалы растворения компонентов сплава и потенциал перепассивации сплава по никелю. Области активной коррозии расширяются, а области пассивности наоборот уменьшаются и сдвигаются в более кислую область. Области устойчивости 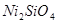 XIVи XVIтоже имеют тенденцию к уменьшению. Линии XIVи XVIтоже имеют тенденцию к уменьшению. Линии 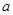 и и 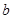 на диаграммах (рис.2.3-2.5) определяют электрохимическое поведение воды (см. табл.2.5). В области ниже линии на диаграммах (рис.2.3-2.5) определяют электрохимическое поведение воды (см. табл.2.5). В области ниже линии 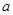 происходит катодное восстановление воды с выделением водорода. Область между линиями происходит катодное восстановление воды с выделением водорода. Область между линиями 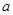 и и 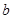 определяет электрохимическую устойчивость воды. Выше линии определяет электрохимическую устойчивость воды. Выше линии 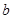 происходит окисление воды с выделением кислорода на аноде. происходит окисление воды с выделением кислорода на аноде.
Построена диаграмма состояния Ni-Si-Oи проанализирована химическая устойчивость никель-кремниевых сплавов. Установлено, что никель-кремниевые сплавы окисляются кислородов воздуха в нормальных условиях. Подтверждено, что окисление никеля из сплава на воздухе заканчивается образованием фазы нестехиометрического состава NiOx
, что подтверждается диаграммой состояния Ni-O (см. рис.1.4.). Однако установлено, что в нормальных условиях и при повышенной температуре оксид NiO2
не образуется, а его образование возможно лишь при давлениях порядка 1030
атм.
Построены диаграммы рН-потенциал системы Ni-Si-H2
O и проанализирована электрохимическая устойчивость сплавов Ni-Si. Они свидетельствуют о высокой коррозионной стойкости никель-кремниевых сплавов. Установлено, что область активного растворения сплава при высоких активностях ионов достаточно мала и сплав подвергается коррозии в сильно щелочных средах, а в кислых и нейтральных на его поверхности образуется пассивирующая пленка.
1) В рамках обобщенной теории "регулярных" растворов рассчитаны температурные зависимости энергий смешения компонентов бинарной системы Ni-Si.
2) Определены равновесные характеристики фаз в области комнатных температур, проверена адекватность полученной модели.
3) Рассчитаны активности компонентов системы Ni - Siпри 250
С.
4) На основании построенной при 250
С диаграммы состояния Ni-Si-O проанализирована химическая устойчивость никель-кремниевых сплавов.
5) На основании постоенных диаграмм рН-потенциал системы Ni-Si-H2
O при 25 0
С и различных активностях ионов в растворе проанализирована электрохимическая устойчивость сплавов Ni-Si, определены области различного коррозионного поведения.
1. Аллотропные металлические сплавы, под ред. Ф.Е. Люборского. М.: Металлургия, 1987.584 с.
2. Глезер А.М., Молотилов Б.В. Структура и механические свойства аморфных сплавов. М.: Металлургия, 1992.207 с.
3. Самсонов Г.В., Дворина Л.А., Рудь Б.М. Силициды. М.: Металлургия, 1979.272 с.
4. Диаграммы состояния двойных металлических систем: Справ. изд. в 3 томах, под общей редакцией Н.П. Лякишева. М.: Машиностроение, 1997-2000 гг
5. Тюрин А.Г. Термодинамика химической и электрохимической устойчивости сплавов, часть I. Челябинск, 2004.86 с.
6. Тюрин А.Г. Термодинамика химической и электрохимической устойчивости сплавов, часть II, Челябинск, 2004.90 с.
7. Мосунова Т.В. Термодинамика химической и электрохимической устойчивости сплавов системы Co-Si: дипломная работа // рук. Тюрин А.Г. Челябинск, 2001.56 с.
8. Тюрин А.Г. Моделирование термодинамических свойств растворов: Учебное пособие; Челябинск: ЧелГУ, 1997.74 с.
9. Тимошенко Т.А. Химические и фазовые равновесия в системе Al - Mn. Курсовая работа, рук. Тюрин А. Г.; Челябинск: ЧелГУ, 2006.25 с.
10. Николайчук П.А. Термодинамика химической и электрохимической устойчивости медно-никелевых сплавов: дипломная работа // рук. Тюрин А.Г. Челябинск, 2007.67 с.
11. Рузинов Л.П., Гуляницкий Б.С. Равновесные превращения металлургических реакций. М.: Металлургия, 1975.416 с.
12. Гельд П.В., Сидоренко Ф.А. Силициды переходных металлов четвертого периода. М.: Металлургия, 1971.582 с.
|