Министерство образования Российской Федерации
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Обратимые матрицы над кольцом Zn
Выполнила:
Студентка V курса
Математического факультета
Сычева О. Г.
Научный руководитель:
д.ф.-м.н., профессор
Вечтомов Е. М.
Рецензент:
к.ф.-м.н., доцент
Чермных В. В.
Допущена к защите в ГАК
Зав.кафедрой Вечтомов Е М.
« »
Декан факультета Варанкина В. И.
« »Киров 2003
Содержание:
Введение………………………………………….…………………….2 стр.
§1 Основные понятия………………………………………………….3 стр.
§2 Обратимые матрицы над полем Zp
п.1 формула для подсчета обратимых матриц порядка 2 ……….10 стр.
п.2 формула для подсчета обратимых матриц порядка 3 ……….11 стр.
п.3 общая формула подсчета обратимых матриц над полем Zp
..16 стр.
§3 Обратимые матрицы над Z
n
………………………………………17 стр.
Литература …………………………………………………………….27 стр.
Введение
Теория матриц является одним из основных вопросов линейной алгебры.
Цель данной работы: подсчитать количество обратимых матриц над кольцом вычетов и по возможности получить формулу для их вычисления. Для вычисления количества обратимых матриц воспользовались теорией определителей и полным перебором всех возможных вариантов получения элементов в кольцах вычетов.
Вся работа разбита на два этапа:
В §2 показан метод построения обратимых матриц второго и третьего порядков над полем Zp
. В конце параграфа построена гипотеза формулы подсчета количества обратимых матриц n–го порядка над полем Zp
.
В §3 приведен алгоритм построения обратимых матриц второго порядка над некоторыми кольцами вычетов (приведены конкретные примеры). В конце параграфа построена гипотеза формулы подсчета количества обратимых матриц второго порядка над кольцом классов вычетов Z
n
.
§1. Основные определения.
Матрицей называется прямоугольная таблица, заполненная некоторыми математическими объектами. Чаще всего рассматриваются матрицы, заполненные элементами из некоторого поля P
.
Элементы матрицы обозначаются одной буквой с двумя индексами, указывающими "адрес" элемента - первый индекс дает номер строки, содержащий элемент, второй - номер столбца. Если матрица имеет m
строк и n
столбцов, то говорят, что матрица имеет размерность 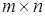 (или - размеров (или - размеров 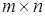 ). Мы будем обозначать матрицы заглавными латинскими буквами, а ее элементы - такими же буквами, но строчными. Таким образом, матрица (размеров ). Мы будем обозначать матрицы заглавными латинскими буквами, а ее элементы - такими же буквами, но строчными. Таким образом, матрица (размеров 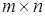 ) записывается в форме: ) записывается в форме:
Реклама

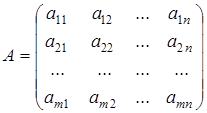 . .
Матрица, состоящая из одних нулей, называется нулевой.
Будем обозначать ее 0
.
Матрица, имеющая одно и то же число n
строк и столбцов, называется квадратной. Число n
называется порядком квадратной матрицы.
Элементы матрицы, у которых оба индекса равны (i
=
j
) называются диагональными, а воображаемая прямая, соединяющая все диагональные элементы матрицы называется главной диагональю.
Квадратная матрица, у которой все элементы, за исключением элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается Е.
:
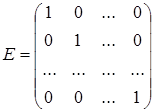
Две матрицы считаются равными, если они одного размера и у них совпадают соответствующие элементы.
Две матрицыA
=(a
ij
) и B
=(b
ij
) одного и того же размера 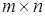 можно складывать, их суммой будет матрица того же размера C
=(c
i
j
), можно складывать, их суммой будет матрица того же размера C
=(c
i
j
), 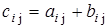 , т.е. чтобы получить сумму двух матрицы достаточно сложить соответственные элементы этих матриц. , т.е. чтобы получить сумму двух матрицы достаточно сложить соответственные элементы этих матриц.
Произведение элемента c
из поля на матрицу A
=(a
ij
) определяется следующим образом: cA
=
(caij
).
Для любой матрицы A
существует противоположная -
A
такая, что
A
+
(-
A
)=0
.
Все перечисленные свойства непосредственно следуют из определений и свойств операций в поле.
Рассмотрим матрицу A
=(a
ij
) размером 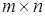 и матрицу B
=(b
ij
) размером и матрицу B
=(b
ij
) размером 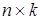 (т.к. произведение матриц определено лишь в том случае, когда число столбцов в первой матрице равно числу строк во второй). Для таких матриц введем действие умножения матрицы на матрицу, в результате чего получается матрица C
=
(cij
) размером (т.к. произведение матриц определено лишь в том случае, когда число столбцов в первой матрице равно числу строк во второй). Для таких матриц введем действие умножения матрицы на матрицу, в результате чего получается матрица C
=
(cij
) размером 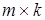 , где , где 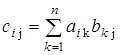 . .
Итак, матрицы можно складывать, умножать их на скаляр, а также умножать матрицу на матрицу. Эти действия обладают свойствами:
По сложению:
1. (A
+
B
)+
C
=
A
+
(B
+
C
) – ассоциативность;
2. A
+
B
=
B
+
A
– коммутативность;
3. Существует нейтральный элемент – матрица 0:
A
+ 0 = 0 +
A
=
A
;
4. Для матрицы A
существует обратный элемент -
A
:
A
+
(-
A
)=0
;
По умножению матриц на скаляр:
5. 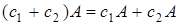 ; ;
6. 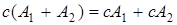 ; ;
7. 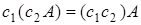 ; ;
8.  ; ;
По умножению матриц:
9. Произведение матриц в общем случае не коммутативно, т.е. AB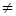 ВА
;
ВА
;
10. (AB
)C
=
A
(BC
) – ассоциативность;
11. (cA
)B
=
A
(cB
)=
cAB
;
Реклама

12. Дистрибутивность умножения относительно сложения (правая и левая)(A
1
+
A
2
)B
=
A
1
B
+
A
2
B
, A
(B
1
+
B
2
)=
AB
1
+
AB
2
;
13. Существует единственный нейтральный элемент E
(если A
– квадратная): EA
=
AE
=
A
.
Если же A
размером 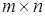 , то , то
Em
A
=
AEn
=
A
.
14. Произведение матрицы А
на нулевую матрицу дает в результате так же нулевую матрицу (существуют случаи, когда нулевая матрица получается в результате перемножения ненулевых матриц).
Для квадратных матриц фиксированного порядка n действия сложения и умножения определены всегда, и их результатами являются квадратные матрицы того же порядка. Таким образом, квадратные матрицы фиксированного порядка образуют кольцо.
Определителем n
-го порядка квадратной матрицы А
, называется алгебраическая сумма n
!
членов, которыми являются всевозможные произведения по n
элементов, взятых по одному и только по одному из каждой строки и каждого столбца, причем член берется со знаком плюс, если его индексы составляют четную перестановку, и со знаком минус – если нечетную перестановку.
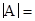 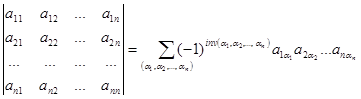 , ,
где (a
1
,
a
2
, ...,
a
n
) пробегает все перестановки чисел 1, 2, ..., n
; множитель 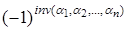 равен +1, если (a
1
,
a
2
, ...,
a
n
) - четная перестановка, и равен –1, если нечетная. равен +1, если (a
1
,
a
2
, ...,
a
n
) - четная перестановка, и равен –1, если нечетная.
Минором элемента aij
называется определитель (n
-1) – порядка, полученный из данного определителя n
-го порядка, путем вычеркивания i
-
й строки и j
-
го столбца.
Минор aij
элемента обозначается М
ij
.
Алгебраическим дополнением элемента aij
называется минор этого элемента, взятый со знаком (-1)i
+
j
.
Алгебраическое дополнение элемента обозначается А
ij
=
(-1)i
+
j
×
М
ij
.
Матрица B
называется обратной для матрицы A
, если AB
=
BA
=
E
,
где E
- единичная матрица. Равенство AB
=
BA
показывает (нетрудно видеть, используя правило умножения матриц), что число строк и столбцов матрицы A должно быть одинаково.
Таким образом, обратная матрица имеет смысл только для квадратных матриц. Далее мы будем рассматривать только квадратные матрицы.
Если матрица А
имеет обратную, то она единственна.
Покажем это. Пусть АВ=СА=Е
и С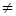 В,
тогда заметим: С=СЕ=С
(АВ
)=
(СА
)В=ЕВ=В.
Что противоречить условию. В,
тогда заметим: С=СЕ=С
(АВ
)=
(СА
)В=ЕВ=В.
Что противоречить условию.
Определитель произведения любых двух матриц n
-
го порядка равен произведению их определителей.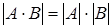
Докажем. Рассмотрим единичные столбцы n
-
го порядка:
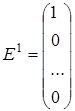 , , 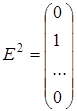 , …, , …, 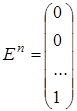
Возьмем произведение матрицы АВ
на столбец единичных столбцов (т.е. столбец из n
n
-мерных столбцов)
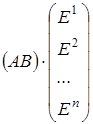
Тогда 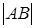 = =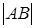 ×1= ×1=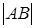 × ×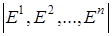 = =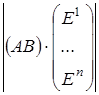 = =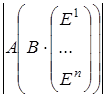
=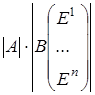 = =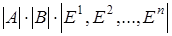 = =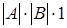 = =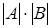 . .
Что требовалось доказать.
Заключение данной теоремы также выполняется и для случая, когда элементы матриц взяты из кольца вычетов Zn
.
Квадратная матрица называется вырожденной, если ее определитель равен нулю и не вырожденной в противном случае.
Для всякой невырожденной матрицы существует обратная матрица.
Покажем это. ПустьA
=(a
ij
) –невырожденная квадратная матрица (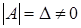 ). Рассмотрим матрицу А
*
= ). Рассмотрим матрицу А
*
=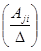 , где Аij
– алгебраическое дополнение элементов определителя
, где Аij
– алгебраическое дополнение элементов определителя 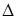 , причем алгебраические дополнения i
-й сроки стоят в i
-ом столбце. , причем алгебраические дополнения i
-й сроки стоят в i
-ом столбце.
Найдем произведение С=АА
*
, где С=
(с
ij
)
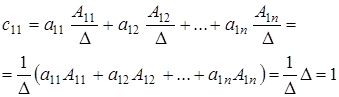
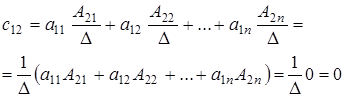
и т.д.
Найдя все элементы матрицы С
по описанному выше алгоритму,
в итоге, получим следующее: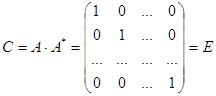 , т.е. , т.е. 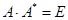 . Значит матрица А
*
- обратная к невырожденной матрице А
. . Значит матрица А
*
- обратная к невырожденной матрице А
.
Для вырожденной матрицы обратной матрицы не существует. Иначе если вырожденная матрица А
(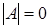 ) имеет обратную А
*
, тогда верными будут следующие равенства: А
·А
*
=Е
, ) имеет обратную А
*
, тогда верными будут следующие равенства: А
·А
*
=Е
,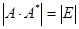 , , 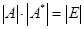 , , 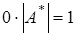 . .
Что в принципе не верно.
Нужно отметить, что невырожденной матрицей над Zn
называется матрица, определитель которой является обратимым элементом в Zn
.
§2
. Обратимые матрицы над полем Z
p
В данном параграфе попытаемся вывести формулу для подсчета количества обратимых матриц в поле Zp
, где p – простое.
1. Формула для подсчета обратимых матриц порядка 2.
Будем рассматривать матрицы 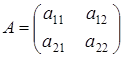 . .
Алгебраическое дополнение к элементу 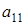 есть определитель матрицы есть определитель матрицы 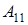 порядка 1, т.е. порядка 1, т.е. 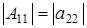 . Алгебраическое дополнение к элементу . Алгебраическое дополнение к элементу 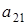 есть определитель матрицы есть определитель матрицы 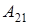 порядка 1, т.е. порядка 1, т.е. 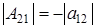 . .
Нужно найти количество всех невырожденных матриц
(когда 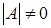 ). При этом ). При этом
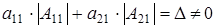 (1.1) (1.1)
Формулу выведем в 2 этапа.
1) Пусть  (р-1 штук), (р-1 штук), 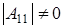 (р-1 штук), (р-1 штук),
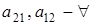 (по р штук) (1.2)
. (по р штук) (1.2)
.
Тогда количество матриц, удовлетворяющих данным условиям, вычисляется по формуле
(р-1)2
р2
(1.3)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что  , , 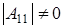 . .
В условии (1.2)
не учитываются матрицы вида 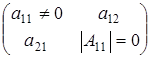 с неравным нулю определителем, количество которых нужно прибавить. с неравным нулю определителем, количество которых нужно прибавить.
Но сосчитали матрицы вида 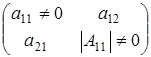 с определителем обращающимся в нуль, количество которых нужно вычесть. с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково.
а) 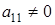 (р-1 штук), (р-1 штук), 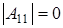 и и 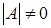 . Из (1.1)
получаем равенство . Из (1.1)
получаем равенство 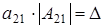 . Значит . Значит 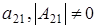 . При заданном . При заданном 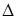 (где (где 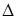 =1,2…р-1) элемент =1,2…р-1) элемент 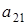 однозначно выражается через однозначно выражается через 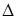 и и 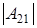 (количество невырожденных матриц (количество невырожденных матриц 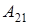 – р-1). Поэтому количество матриц удовлетворяющих этим условиям (р-1)3
штук. – р-1). Поэтому количество матриц удовлетворяющих этим условиям (р-1)3
штук.
б) 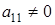 , , 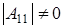 и и 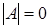 . Значит . Значит 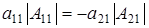 . Отсюда . Отсюда 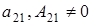 . Элемент . Элемент 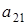 однозначно выражается через однозначно выражается через 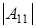 , , 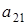 , , 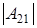 , которые принимаю не нулевые значения. Поэтому количество матриц удовлетворяющих этим условиям (р-1)3
штук , которые принимаю не нулевые значения. Поэтому количество матриц удовлетворяющих этим условиям (р-1)3
штук
Значит формула (1.3)
при условии (1.2)
верна.
2) Пусть 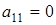 . Тогда . Тогда 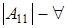 , а из (1.1)
получаем что , а из (1.1)
получаем что 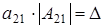 и и 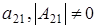 (как в первом этапе, случае а). Тогда количество таких матриц вычисляется по формуле (как в первом этапе, случае а). Тогда количество таких матриц вычисляется по формуле
(р-1)2
×р (1.4)
Этими этапами мы перебрали все случаи невырожденных матриц.
Складывая формулы (1.3)
и (1.4)
полученные в этапах 1) и 2) получаем формулу для нахождения количества обратимых матриц порядка 2 над полем Zp
(р-1)2
×р×(р+1) (1.5)
2. Формула для подсчета обратимых матриц порядка 3.
Будем рассматривать матрицы 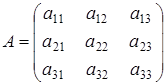 . .
Алгебраические дополнения к элементам 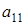 , ,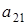 и и 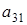 есть определители матриц есть определители матриц 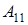 , , 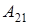 и и 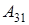 соответственно, порядка 2, при чем соответственно, порядка 2, при чем 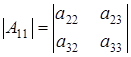 , , 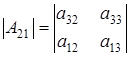 и и 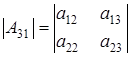 . .
Нужно найти количество всех невырожденных матриц (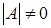 ). ).
При этом
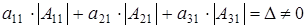 (2.1) (2.1)
Формулу выведем в 3 этапа.
1) Пусть  (р-1 штук), (р-1 штук), 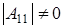 (их количество по формуле (1.5)
), (их количество по формуле (1.5)
), 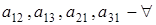 (по р штук) (2.2)
. (по р штук) (2.2)
.
Тогда количество таких матриц вычисляется по формуле
(р-1)3
р5
(р+1) (2.3)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что  , , 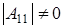 . .
При условии (2.2)
не учитываются матрицы вида 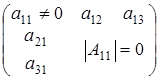 с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида 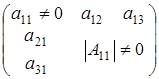 с определителем обращающимся в нуль, количество которых нужно вычесть. с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково:
а) 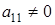 (р-1 штук), (р-1 штук), 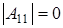 и и 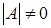 . Из (2.1)
получаем равенство . Из (2.1)
получаем равенство 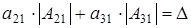 . .
а1) Пусть 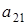 =0. Тогда =0. Тогда 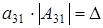 и и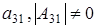 . Значит элементов . Значит элементов 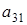 всего р-1 штук, количество невырожденных матриц всего р-1 штук, количество невырожденных матриц 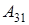 - (р-1)2
р(р+1). Т.к - (р-1)2
р(р+1). Т.к 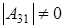 то из выражения то из выражения 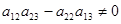 получаем равенство получаем равенство 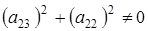 , т.е. хотя бы один из этих элементов не равен нулю. Пусть , т.е. хотя бы один из этих элементов не равен нулю. Пусть  . Из того, что . Из того, что 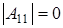 получаем получаем 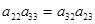 .Элементом .Элементом 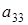 , принимающим любое значение, можем однозначно задать элемент , принимающим любое значение, можем однозначно задать элемент 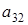 . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4
×р2
×(р+1) штук. . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4
×р2
×(р+1) штук.
а2) Если 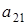 ¹0, ¹0, 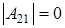 .Тогда .Тогда 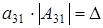 и и 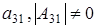 . Значит элементов . Значит элементов 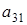 всего р-1 штук, количество невырожденных матриц всего р-1 штук, количество невырожденных матриц 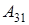 - (р-1)2
р(р+1). Т.к - (р-1)2
р(р+1). Т.к 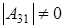 , то, из выражения , то, из выражения 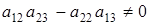 получаем получаем 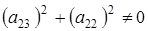 . Пусть . Пусть  . Домножим равенство . Домножим равенство 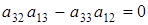 ( (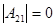 ) на ) на  . Заменим . Заменим 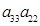 на на 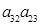  (из того, что (из того, что 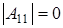 ). Получим равенство ). Получим равенство 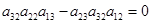 . Вынесем . Вынесем 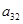 за скобки за скобки 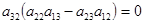 и т.к. и т.к. 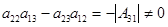 делаем вывод, что делаем вывод, что 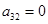 . Значит и . Значит и 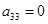 ( (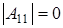 ). Поэтому количество матриц удовлетворяющих этим условиям (р-1)5
×р×(р+1) штук. ). Поэтому количество матриц удовлетворяющих этим условиям (р-1)5
×р×(р+1) штук.
а3) Если 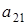 ¹0, ¹0, 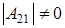 и и 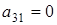 получаем (р-1)4
×р2
×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1) получаем (р-1)4
×р2
×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а1)
а4) Если 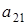 ¹0, ¹0, 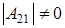 , , 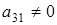 и и 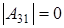 получаем получаем
(р-1)5
×р×(р+1) штук матриц удовлетворяющих этим условиям (рассуждение как в пункте а2)
а5) Если 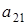 ¹0, ¹0, 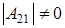 , , 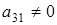 и и 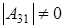 . Из того, что . Из того, что 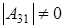 получаем получаем 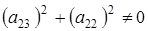 . Пусть . Пусть  . Равенство . Равенство 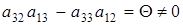 ( (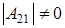 ) умножим на ) умножим на  и заменим и заменим 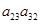 на на 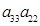 ( (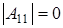 ). Получим равенство ). Получим равенство 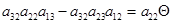 . Вынося . Вынося 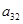 за скобки ( за скобки (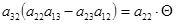 ), замечаем, что элемент ), замечаем, что элемент 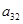 однозначно выражается через однозначно выражается через 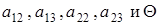 ( (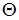 - р-1 штук). Но тогда - р-1 штук). Но тогда 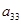 тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)6
×р×(р+1)штук. тоже выражается через эти элементы. Поэтому количество матриц удовлетворяющих этим условиям (р-1)6
×р×(р+1)штук.
Таким образом, общее количество матриц удовлетворяющих условию пункта а) подсчитывается по формуле
(р-1)4
×р×(р+1)×(р2
+2р-1) (получается суммированием формул полученных в пунктах а1-а5).
б) 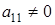 (р-1 штук), (р-1 штук), 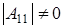 ((р-1)2
×р×(р+1)) штук). Т.к. ((р-1)2
×р×(р+1)) штук). Т.к. 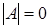 , значит , значит 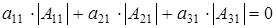 (2.4) (2.4)
б1) Пусть 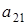 =0. Тогда из (2.4) выводится равенство =0. Тогда из (2.4) выводится равенство
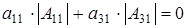 (2.5) (2.5)
а из (2.5)
получим 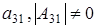 . Распишем (2.5)
: . Распишем (2.5)
: 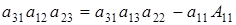 . Т.е. . Т.е. 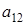 однозначно выражается через элемент однозначно выражается через элемент 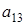 , которых может быть р штук, и через элементы , которых может быть р штук, и через элементы 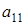 , , 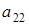 , , 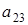 , , 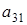 , , 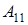 . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4
×р2
×(р+1). . Поэтому количество матриц удовлетворяющих этим условиям (р-1)4
×р2
×(р+1).
б2) Если 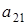 ¹0, ¹0, 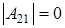 .Тогда получим опять равенство (2.5)
и из него .Тогда получим опять равенство (2.5)
и из него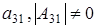 . Элементов . Элементов 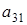 всего р-1 штук. Т.к всего р-1 штук. Т.к 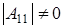 , то получаем что , то получаем что 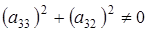 . Пусть . Пусть 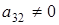 . Умножив равенство (2.5) на . Умножив равенство (2.5) на 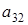 , выражая , выражая 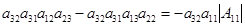 и произведя замену и произведя замену 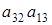 на на 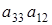 получим равенство получим равенство 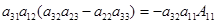 . А т.к. . А т.к. 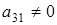 и и 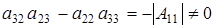 делаем вывод, что делаем вывод, что 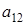 и и 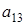 выражаются через все остальные элементы матрицы. Поэтому количество матриц удовлетворяющих этим условиям выражаются через все остальные элементы матрицы. Поэтому количество матриц удовлетворяющих этим условиям
(р-1)5
×р×(р+1) штук.
б3) Если 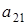 ¹0, ¹0, 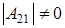 и и 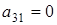 получаем (р-1)4
×р2
×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в получаем (р-1)4
×р2
×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в
пункте б1)
б4) Если 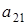 ¹0, ¹0, 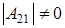 , , 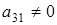 и и 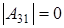 получаем получаем
(р-1)5
×р×(р+1) матриц удовлетворяющих этим условиям (рассуждения как в пункте б2)
б5) Пусть 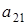 ¹0, ¹0, 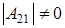 , , 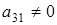 и и 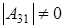 . Из того, что . Из того, что 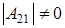 , получаем , получаем 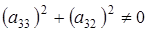 . Пусть . Пусть 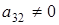 . Тогда преобразовывая (2.4)
получаем, что . Тогда преобразовывая (2.4)
получаем, что 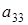 однозначно выражается через однозначно выражается через 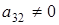 и все остальные элементы. и все остальные элементы.
Поэтому количество матриц удовлетворяющих этим условиям (р-1)6
×р×(р+1) штук.
Таким образом, общее количество матриц удовлетворяющих условию пункта б) подсчитывается по формуле
(р-1)4
×р×(р+1)×(р2
+2р-1) (получается суммированием формул полученных в пунктах б1-б5).
Значит формула (р-1)3
р5
(р+1) для случая 1) при условии (2.2)
верна.
2) Пусть 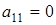 , , 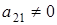 (количество их р-1), (количество их р-1), 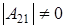 (количество высчитывается по формуле (1.5)
) и (количество высчитывается по формуле (1.5)
) и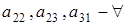 (по р штук). Тогда из (2.1)
получаем (по р штук). Тогда из (2.1)
получаем
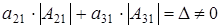 . .
Тогда количество таких матриц вычисляется по формуле
(р-1)3
р4
(р+1) (2.6)
Мы утверждаем, что по этой же формуле вычисляется количество матриц, определитель которых не обращается в нуль, при условии, что 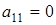 , , 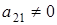 и и 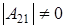 . .
Но при этих условиях не учитываются матрицы вида 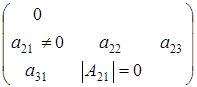 с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида с неравным нулю определителем, количество которых нужно прибавить. Но сосчитали матрицы вида 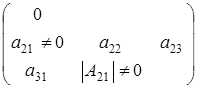 с определителем обращающимся в нуль, количество которых нужно вычесть. с определителем обращающимся в нуль, количество которых нужно вычесть.
Докажем, что количество матриц в обоих случаях одинаково:
а) 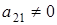 , , 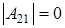 и и 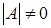 . Из (2.1)
получаем равенство . Из (2.1)
получаем равенство 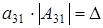 , , 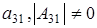 , а из того что , а из того что 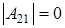 получаем что, например, элемент получаем что, например, элемент 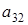 однозначно выражается через элемент однозначно выражается через элемент 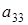 (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4
р2
(р+1). (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4
р2
(р+1).
б) 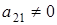 , , 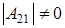 и и 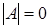 . Из (2.1) получаем равенство . Из (2.1) получаем равенство 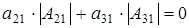 , , 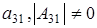 . А из . А из 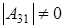 можем однозначно выразить, например, элемент можем однозначно выразить, например, элемент 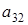 через элемент через элемент 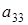 (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4
р2
(р+1). (р штук) и все остальные элементы. А значит количество матриц с данными условиями (р-1)4
р2
(р+1).
3) Пусть 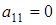 , , 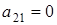 , , 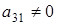 (количество их p-1), (количество их p-1), 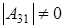 (количество высчитывается по формуле (1.5)) и (количество высчитывается по формуле (1.5)) и 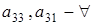 (по р штук). (по р штук).
Тогда количество таких матриц вычисляется по формуле
(р-1)[(р-1)2
р(р+1)]×р×р×р (2.7)
Этими этапами мы перебрали все случаи невырожденных матриц порядка 3. складывая формулы (2.3), (2.6)
и (2.7),
полученные в этапах 1), 2) и 3) получаем формулу для нахождения количества обратимых матриц порядка 3матриц над полем Zp
(р-1)3
р3
(р+1)(р2
+р+1) (2.8)
3. Общая формула для подсчета обратимых матриц над полем Zp
.
Используя алгоритм, описанный в предыдущих пунктах, для выведения формулы подсчета количества обратимых матриц, можем получить частные формулы для матриц произвольных порядков.
Например:
Для матриц порядка 4:
(р-1)4
р6
(р+1)(р2
+р+1)(р3
+р2
+р+1).
Для матриц порядка 5:
(р-1)5
р10
(р+1)(р2
+р+1)(р3
+р2
+р+1)( р4
+р3
+р2
+р+1), и т.д.
Анализируя полученные результаты, можем сделать выводы, что общая формула для получения количества обратимых матриц порядка n над полем Zp
выглядит так:
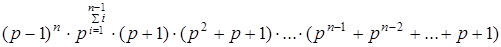
Данную формулу тождественными преобразованиями можно привести к виду:
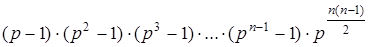
§3. Обратимые матрицы над кольцом
Zn
Из теоремы доказанной в § 1 следует, что для определителей матриц A и B выполняется равенство |A·B|=|A|·|B|.
Для обратимых матриц A и B следует A·
B=E.Следовательно |A·
B|=|A|·
|B|=|E|=1.
Таким образом, получаем: определитель обратимой матрицы является обратимым элементом.
Попытаемся сосчитать количество обратимых матриц над некоторыми кольцами вычетов по составному модулю.
Обратимые матрицы над
Z4
.
| * |
0 |
1 |
2 |
3 |
| 0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
| 2 |
0 |
2 |
0 |
2 |
| 3 |
0 |
3 |
2 |
1 |
Всего различных матриц второго порядка над Z4
: 44
=256.
В Z
4
обратимыми элементами являются 1и3. Рассмотрим сколько обратимых матриц с определителем равным 1: |A|=ad-bc=1.
Разобьем на следующие варианты:
1. ad=3. Возможные случаи:
1) a=1 Ù d=3,
2) a=3 Ù d=1,
bc=2. Возможные случаи:
1) b=1 Ù c=2,
2) b=2 Ù c=1,
3) b=2 Ù c=3,
4) b=3 Ù c=2.
Получили с данным условием 8 обратимых матриц.
2. ad=2.Возможно 4 случая (см. предыдущий пункт).
bc=1. Возможные случаи:
1) b=c=1,
2) b=c=3.
Получили с данным условием 8 обратимых матриц.
3. ad=1. Возможно 2 случая (см. предыдущий пункт).
bc=0. Возможные случаи:
1) b=0 Ù c=1,
2) b=0 Ù c=2,
3) b=0 Ù c=3,
4) b=1 Ù c=0,
5) b=2 Ù c=0,
6) b=3 Ù c=0,
7) b=c=0,
8) b=c=2.
Получили сданным условием 16 обратимых матриц.
4. ad=0. Возможно 8 случаев (см. предыдущий пункт).
bc=3. Возможно 2 случая (см. первый пункт).
Получили с данным условием 16 обратимых матриц.
Таким образом, по данной классификации получаем 8+8+16+16+16=48 обратимых матриц, определитель которых равен 1. Аналогичную классификацию можно составить для обратимых матриц с определителем равным 3, и число таких матриц будет также равно 48.
Следовательно, из 256 квадратных матриц второго порядка над Z4
обратимыми являются 96.
Обратимые матрицы над
Z6
.
| * |
0
|
1
|
2
|
3
|
4
|
5
|
| 0
|
0 |
0 |
0 |
0 |
0 |
0 |
| 1
|
0 |
1 |
2 |
3 |
4 |
5 |
| 2
|
0 |
2 |
4 |
0 |
2 |
4 |
| 3
|
0 |
3 |
0 |
3 |
0 |
3 |
| 4
|
0 |
4 |
2 |
0 |
4 |
2 |
| 5
|
0 |
5 |
4 |
3 |
2 |
1 |
Всего различных матриц второго порядка над Z6
: 64
=1296.
В Z
6
обратимыми элементами являются 1 и 5. Аналогично рассмотрим, сколько обратимых матриц с определителем равным 1:
|A|=ad-bc=1.
Разобьем на следующие варианты:
1. ad=5. Возможные случаи:
1) a=1 Ù d=5,
2) a=5 Ù d=1,
bc=4. Возможные случаи:
1) b=1 Ù c=4,
2) b=4 Ù c=1,
3) b=2 Ù c=5,
4) b=5 Ù c=2,
5) b=c=2,
6) b=c=4.
Получили с данным условием 12 обратимых матриц.
2. ad=4.Возможно 6 случаев (см. предыдущий пункт).
bc=3. Возможные случаи:
1) b=3 Ù c=1,
2) b=1 Ù c=3,
3) b=3 Ù c=5,
4) b=5 Ù c=3,
5) b=c=3.
Получили с данным условием 30 обратимых матриц.
3. ad=3. Возможно 5 случаев (см. предыдущий пункт).
bc=2. Возможные случаи:
1) b=2 Ù c=1,
2) b=1 Ù c=2,
3) b=2 Ù c=4,
4) b=4 Ù c=2,
5) b=4 Ù c=5,
6) b=5 Ù c=4.
Получили с данным условием 30 обратимых матриц.
4. ad=2. Возможно 6 случаев (см. предыдущий пункт).
bc=1. Возможные случаи:
1) b=c=1,
2) b=c=5.
Получили с данным условием 12 обратимых матриц.
5. ad=1. Возможно 2 случая (см. предыдущий пункт).
bc=0. Возможные случаи:
1) b=0 Ù c=1,
2) b=0 Ù c=2,
3) b=0 Ù c=3,
4) b=0 Ù c=4,
5) b=0 Ù c=5,
6) b=1 Ù c=0,
7) b=2 Ù c=0,
8) b=3 Ù c=0,
9) b=4 Ù c=0,
10) b=5 Ù c=0,
11) b=2 Ù c=3,
12) b=3 Ù c=2,
13) b=3 Ù c=4,
14) b=4 Ù c=3,
15) b=c=0.
Получили с данным условием 30 обратимых матриц.
6. ad=0. Возможно 15 случаев (см. предыдущий пункт).
bc=5. Возможно 2 случая (см. первый пункт).
Получили с данным условием 30 обратимых матриц.
Таким образом по данной классификации получаем 12+30+30+12+30+30=144 обратимых матриц, определитель которых
равен 1. Аналогичную классификацию можно составить для обратимых матриц с определителем равным 5, и число таких матриц будет также равно 144.
Следовательно, из 1296 квадратных матриц второго порядка над Z6
обратимыми являются 288.
Обратимые матрицы над
Z8
| * |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 0
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 2
|
0 |
2 |
4 |
6 |
0 |
2 |
4 |
6 |
| 3
|
0 |
3 |
6 |
3 |
4 |
7 |
2 |
5 |
| 4
|
0 |
4 |
0 |
4 |
0 |
4 |
0 |
4 |
| 5
|
0 |
5 |
2 |
7 |
4 |
1 |
6 |
3 |
| 6
|
0 |
6 |
4 |
2 |
0 |
6 |
4 |
2 |
| 7
|
0 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Всего различных матриц второго порядка над Z8
: 84
=4096.
В Z
8
обратимыми элементами являются 1, 3, 5 и 7. Аналогично рассмотрим, сколько обратимых матриц с определителем равным 1
|A|=ad-bc=1.
Аналогично предыдущим пунктам будем придерживаться той же классификации:
1. ad=7. Возможно 4 случая.
bc=6. Возможно 8 случаев.
Получили с данным условием 32 обратимых матрицы.
2. ad=6. Возможно 8 случаев.
bc=5. Возможно 4 случая.
Получили с данным условием 32 обратимых матрицы.
3. ad=5. Возможно 4 случая.
bc=4. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
4. ad=4. Возможно 12 случаев.
bc=3. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
5. ad=3. Возможно 4 случая.
bc=2. Возможно 8 случаев.
Получили с данным условием 32 обратимых матрицы.
6. ad=2. Возможно 8 случаев.
bc=1. Возможно 4 случая.
Получили с данным условием 32 обратимых матрицы.
7. ad=1.Возможны 4 случая .
bc=0. Возможно 20 случаев.
Получили с данным условием 80 обратимых матриц.
8. ad=0. Возможно 20 случаев.
bc=7. Возможно 4 случая.
Получили с данным условием 80 обратимых матриц.
Таким образом, обратимых матриц, определитель которых
равен 1 —384.
Следовательно, из 4096 квадратных матриц второго порядка над Z8
обратимыми являются 1536.
Обратимые матрицы над
Z9
| * |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| 0
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 2
|
0 |
2 |
4 |
6 |
8 |
1 |
3 |
5 |
7 |
| 3
|
0 |
3 |
6 |
0 |
3 |
6 |
0 |
3 |
6 |
| 4
|
0 |
4 |
8 |
3 |
7 |
2 |
6 |
1 |
5 |
| 5
|
0 |
5 |
1 |
6 |
2 |
7 |
3 |
8 |
4 |
| 6
|
0 |
6 |
3 |
0 |
6 |
3 |
0 |
6 |
3 |
| 7
|
0 |
7 |
5 |
3 |
1 |
8 |
6 |
4 |
2 |
| 8
|
0 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Всего различных матриц второго порядка над Z9
: 94
=6561.
В Z
9
обратимыми элементами являются 1, 2, 4, 5, 7 и 8.
1. ad=8. Возможно 6 случаев.
bc=7. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
2. ad=7. Возможно 6 случаев.
bc=6. Возможно 12 случаев.
Получили с данным условием 72 обратимых матриц.
3. ad=6. Возможно 12 случаев.
bc=5. Возможно 6 случаев.
Получили с данным условием 72 обратимых матриц.
4. ad=5. Возможно 6 случаев.
bc=4. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
5. ad=4. Возможно 6 случаев.
bc=3. Возможно 12 случаев.
Получили с данным условием 72 обратимых матриц.
6. ad=3. Возможно 12 случаев.
bc=2. Возможно 6 случаев.
Получили с данным условием 72 обратимых матриц.
7. ad=2. Возможно 6 случаев.
bc=1. Возможно 6 случаев.
Получили с данным условием 36 обратимых матриц.
8. ad=1. Возможно 6 случаев.
bc=0. Возможно 21 случай.
Получили с данным условием 126 обратимых матриц.
9. ad=0. Возможно 21 случай.
bc=8. Возможно 6 случаев.
Получили с данным условием 126 обратимых матриц.
Таким образом, обратимых матриц, определитель которых равен 1 -648.
Следовательно, из 6561 квадратных матриц второго порядка над Z9
обратимыми являются 3888.
Обратимые матрицы над
Z10
| * |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| 0
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 2
|
0 |
2 |
4 |
6 |
8 |
0 |
2 |
4 |
6 |
8 |
| 3
|
0 |
3 |
6 |
9 |
2 |
5 |
8 |
1 |
4 |
7 |
| 4
|
0 |
4 |
8 |
2 |
6 |
0 |
4 |
8 |
2 |
6 |
| 5
|
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
| 6
|
0 |
6 |
2 |
8 |
4 |
0 |
6 |
2 |
8 |
4 |
| 7
|
0 |
7 |
4 |
1 |
8 |
5 |
2 |
9 |
6 |
3 |
| 8
|
0 |
8 |
6 |
4 |
2 |
0 |
8 |
6 |
4 |
2 |
| 9
|
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
Всего различных матриц второго порядка над Z10
: 104
=1000.
В Z
10
обратимыми элементами являются 1, 3, 7 и 9.
1. ad=9. Возможно 4 случая.
bc=8. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
2. ad=8. Возможно 12 случаев.
bc=7. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
3. ad=7. Возможно 4 случая.
bc=6. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
4. ad=6. Возможно 12 случаев.
bc=5. Возможно 9 случаев.
Получили с данным условием 108 обратимых матриц.
5. ad=5. Возможно 9 случаев.
bc=4. Возможно 12 случаев.
Получили с данным условием 108 обратимых матриц.
6. ad=4. Возможно 12 случаев.
bc=3. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
7. ad=3. Возможно 4 случая.
bc=2. Возможно 12 случаев.
Получили с данным условием 48 обратимых матриц.
8. ad=2. Возможно 12 случаев.
bc=1. Возможно 4 случая.
Получили с данным условием 48 обратимых матриц.
9. ad=1. Возможно 4 случая.
bc=0. Возможно 27 случаев.
Получили с данным условием 108 обратимых матриц.
10. ad=0. Возможно 27 случаев.
bc=9. Возможно 4 случая.
Получили с данным условием 108 обратимых матриц.
Таким образом, обратимых матриц, определитель которых
равен 1 —720.
Следовательно, из 10000 квадратных матриц второго порядка над Z10
обратимыми являются 2880.
Используя выше изложенный метод, было также вычислено количество обратимых матриц для колец вычетов по модулям:10, 12, 14, 15, 16, 18, 20, 21. В результате всех вычислений были получены следующие данные (ниже также использованы формулы полученные в §
2):
| Z
n
|
формула |
количество |
| 2
|
(p-1)2
p(p+1) |
6 |
| 3
|
(p-1)2
p(p+1) |
48 |
| 4
|
- |
96 |
| 5
|
(p-1)2
p(p+1) |
480 |
| 6
|
- |
288 |
| 7
|
(p-1)2
p(p+1) |
2016 |
| 8
|
- |
1536 |
| 9
|
- |
3888 |
| 10
|
- |
2880 |
| 11
|
(p-1)2
p(p+1) |
13200 |
| 12
|
- |
4608 |
| 13
|
(p-1)2
p(p+1) |
26208 |
| 14
|
- |
12096 |
| 15
|
- |
23040 |
| 16
|
- |
24576 |
| 17
|
(p-1)2
p(p+1) |
78336 |
| 18
|
- |
23328 |
| 19
|
(p-1)2
p(p+1) |
123120 |
| 20
|
- |
43520 |
| 21
|
- |
96768 |
В итоге анализа полученных результатов эмпирическим путем была получена следующая формула для вычисления количества обратимых матриц второго порядка над кольцом вычетов по произвольному модулю.
Пусть Z
n
-
кольцо вычетов по модулю n
, причем n
=
p
1
k
1
p
2
k
2
…
pm
km
,
Тогда количество обратимых матриц второго порядка равно:
(p1
-1)2
(p2
-1)2
…(pm
-1)2
p1
p2
…pm
(p1
+1)(p2
+1)…(pm
+1)(p1
4
)k
1-1
(p2
4
)k
2-1
…(pm
4
)km
-1
Литература
1. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966.
2. Куликов Л.Я. Алгебра и теория чисел. М.: Высшая школа, 1979.
3. Курош А. Г. Курс высшей алгебры. М.: Наука, 1975.
|