| МОДЕЛЮВАННЯ НА ЕОМ ВИПАДКОВИХ ВЕЛИЧИН І ВИПАДКОВИХ ПРОЦЕСІВ
Содержание
Вступ
1. Принципи моделювання на ЕОМ випадкових елементів
2. Моделювання випадкових величин із заданими ймовірнісними характеристиками
Моделювання випадкових величин, що приймають дискретні значення
Моделювання випадкових величин із заданими щільностями імовірностей методом обернених функцій
Моделювання випадкових величин із заданими щільностями імовірностей методом суперпозиції
Моделювання гаусових випадкових величин методом сумації
Моделювання випадкових величин із експоненціальним розподілом та розподілом Релея
Вступ
При статистичному моделюванні на ЕОМ систем та мереж зв’язку виникає необхідність моделювання різних випадкових елементів - одержання на ЕОМ реалізацій випадкових величин та випадкових процесів, які описують реальні фізичні явища, події та процеси функціювання цих систем. Розглянемо основні принципи, методи та алгоритми моделювання на ЕОМ типових випадкових величин та випадкових процесів, що можуть бути використані для статистичних випробовувань при моделюванні систем та мереж зв’язку на ЕОМ.
При моделюванні випадкових елементів (ВЕ) на ЕОМ розглядають три об'єкти: реальний фізичний об'єкт, його математичну модель, алгоритм моделювання на ЕОМ реалізацій ВЕ на основі вибранної математичної моделі. Наприклад, в системах та мережах зв'язку такими реальними фізичними об'єктами можуть бути повідомлення, сигнали-переносчики, модульовані сигнали, завади, потоки заявок, процеси обслуговування заявок, процеси комутації. Математичні моделі цих фізичних процесів - це різні класи випадкових процесів з імовірнісними характеристиками, що відповідають реальним фізичним процесам. Результатом моделювання на ЕОМ є вибірки реалізацій процесів, що одержуються за допомогою спеціальних моделюючих алгоритмів. Моделювання ВЕ базується на таких принципах:
ВЕ визначається (“конструюється”) як відповідна борелівська функція від найпростіших базових випадкових величин (БВВ);
повинна бути забезпечена близькість (за вибраним критерієм) імовірнісних характеристик реальних фізичних процесів та змодельованих реалізацій випадкових процесів.
БВВ одержують в результаті проведення на ЕОМ найпростішого випадкового експерименту.
Реклама

Експеримент полягає в “киданні точки навмання“ в інтервал [0,1) (мал.1). Математичною моделлю такого експерименту є ймовірнісний простір 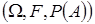 , де , де 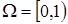 - це простір незалежних елементарних подій - це простір незалежних елементарних подій 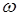 ; ; 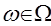 - це елементарна подія, яка полягає в тому, що координата кинутої точки дорівнює - це елементарна подія, яка полягає в тому, що координата кинутої точки дорівнює 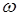 ; ; 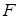 -
це -
це 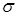 -алгебра, що породжена напівінтервалами з простору -алгебра, що породжена напівінтервалами з простору 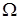 ; ; 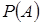 - це імовірнісна міра, яка визначена для підмножин - це імовірнісна міра, яка визначена для підмножин 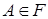 і збігається з мірою Лебега, так що і збігається з мірою Лебега, так що 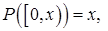 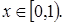
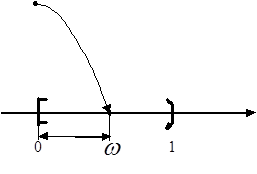
Рисунок 1 - Графічне пояснення найпростішого випадкового експерименту для одержання реалізацій БВВ
Випадкова величина 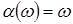 , що задана на просторі , що задана на просторі 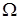 , породжує інший імовірнісний простір , породжує інший імовірнісний простір 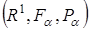 , де , де 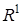 - це множина значень на числовій осі; - це множина значень на числовій осі; 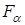 - борельова - борельова 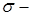 алгебра, алгебра, 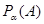 - індуктована імовірнісна міра. Фактично, - індуктована імовірнісна міра. Фактично, 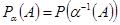 - це функція розподілу БВВ - це функція розподілу БВВ 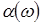 , що у даному випадку має вигляд , що у даному випадку має вигляд
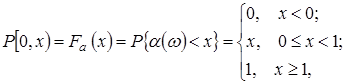 (1) (1)
Відповідна їй щільність розподілу рівномірна на півінтервалі [0,1]
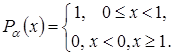 (2) (2)
На рис.2 наведені графічні зображення функції і щільності розподілу ВВ 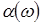 . .
моделювання випадкова величина алгоритм
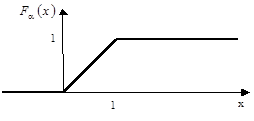 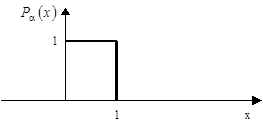
а б
Рисунок 2 - Графічне зображення функції розподілу (а) та щільності розподілу (б) БВВ.
У кожній ЕОМ є генератори (спеціальні програми) одержання випадкових величин, що мають вказані ймовірнісні характеристики. При послідовному звертанні 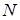 раз до таких програм моделюється вибірка із раз до таких програм моделюється вибірка із 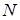 незалежних реалізацій БВВ незалежних реалізацій БВВ 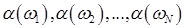 , яка в подальшому використовується для побудови ВЕ із необхідними ймовірнісними характеристиками. , яка в подальшому використовується для побудови ВЕ із необхідними ймовірнісними характеристиками.
При моделюванні на ЕОМ складних ВЕ, зокрема, випадкової величини (ВВ) або випадкового процесу (ВП) з заданими ймовірнісними характеристиками розглядається складний випадковий експеримент, що полягає в проведенні 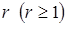 раз описаного вище найпростішого експерименту. Цей складний експеримент описується імовірнісним простором раз описаного вище найпростішого експерименту. Цей складний експеримент описується імовірнісним простором 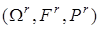 , де , де 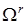 - декартовий добуток: - декартовий добуток: 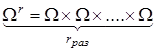 ; ; 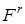 - найменша - найменша 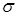 - алгебра, що побудована на - алгебра, що побудована на 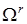 ; ; 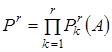 - імовірнісна міра, отримана як добуток імовірнісних мір для найпростішого експерименту. - імовірнісна міра, отримана як добуток імовірнісних мір для найпростішого експерименту.
В результаті проведення такого складного експерименту отримуємо 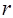 БВВ. Далі відповідно до першого принципу моделювання ВЕ на ЕОМ будь-який складний випадковий елемент БВВ. Далі відповідно до першого принципу моделювання ВЕ на ЕОМ будь-який складний випадковий елемент 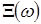 отримується як борелівська функція від отримується як борелівська функція від 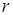 БВВ БВВ
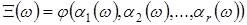 . (4) . (4)
Підбирають функцію 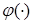 і число і число 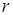 таким, щоб імовірнісні характеристики отриманого ВЕ таким, щоб імовірнісні характеристики отриманого ВЕ 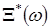 збігалися з імовірнісними характеристиками оригіналу, що моделюється. Існують різні критерії близькості імовірнісних характеристик ВЕ - оригіналу і ВЕ, отриманого при моделюванні, зокрема, критерій Пірсона, критерій Колмогорова. збігалися з імовірнісними характеристиками оригіналу, що моделюється. Існують різні критерії близькості імовірнісних характеристик ВЕ - оригіналу і ВЕ, отриманого при моделюванні, зокрема, критерій Пірсона, критерій Колмогорова.
Реклама

Оскільки моделювання випадкових процесів на ЕОМ зводиться до моделювання послідовності випадкових величин із заданими ймовірнісними характеристиками, спочатку розглянемо особливості моделювання деяких випадкових величин.
Розглянемо моделювання випадкових величин 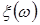 , що приймають , що приймають 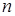 дискретних значень дискретних значень  із заданими ймовірностями із заданими ймовірностями 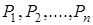 ( (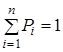 ). Моделювання таких ВВ може бути зведене до моделювання повної групи ). Моделювання таких ВВ може бути зведене до моделювання повної групи 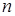 незалежних подій, які відбуваються з імовірностями незалежних подій, які відбуваються з імовірностями 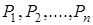 . Для цього використовується датчик БВВ із математичною моделлю . Для цього використовується датчик БВВ із математичною моделлю 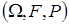 . .
Введемо систему таких підмножин 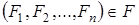 , щоб їх можна було розглядати як повну групу незалежних подій на , щоб їх можна було розглядати як повну групу незалежних подій на 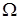 . При цьому повинні задовольнятись умови . При цьому повинні задовольнятись умови 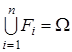 ; ; 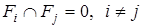 ; ; 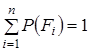 . Визначимо ці підмножини так . Визначимо ці підмножини так
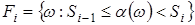 , (5) , (5)
де 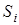 і і 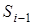 - це межі інтервалів, які визначаються за формулою - це межі інтервалів, які визначаються за формулою
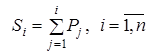 , причому , причому 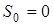 . (6) . (6)
Зважаючи на те, що БВВ розподілена рівномірно на інтервалі 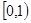 , імовірності підмножин , імовірності підмножин 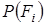 визначаються через щільність розподілу БВВ відповідним спввідношенням визначаються через щільність розподілу БВВ відповідним спввідношенням
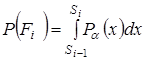 . (7) . (7)
Це означає, що імовірність попадання значення БВВ в інтервал 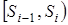 дорівнює довжині цього інтервалу (рис.3). дорівнює довжині цього інтервалу (рис.3).
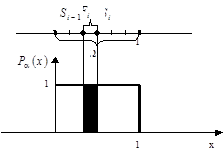
Рисунок 3 - Геометричне пояснення моделювання групи незалежних подій з допомогою БВВ
Таким чином, моделювання ВВ 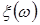 , яка приймає дискретні значення, полягає у виборі значення БВВ за допомогою генератора, перевірки попадання значення БВВ до однієї з підмножин , яка приймає дискретні значення, полягає у виборі значення БВВ за допомогою генератора, перевірки попадання значення БВВ до однієї з підмножин 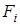 і винесенні рішення про те, що модельоване ВВ приймає значення і винесенні рішення про те, що модельоване ВВ приймає значення 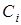
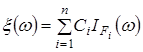 , (8) , (8)
де 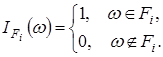 - це характеристична функція множини. (9) - це характеристична функція множини. (9)
Розглянемо моделювання ВВ 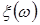 із заданою щільністю ймовірності із заданою щільністю ймовірності 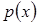 та функцією розподілу та функцією розподілу
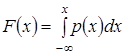 . (10) . (10)
Якщо функція 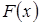 є строго монотонно зростаючою, то із рівняння є строго монотонно зростаючою, то із рівняння 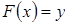 можна знайти обернену функцію можна знайти обернену функцію
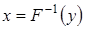 . (11) . (11)
Підставивши замість 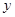 БВВ БВВ 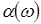 , можна одержати алгоритм моделювання ВВ із заданим розподілом: , можна одержати алгоритм моделювання ВВ із заданим розподілом:
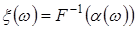 . (12) . (12)
Таким чином, для моделювання на ЕОМ ВВ 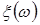 із заданою щільністю ймовірності, потрібно виконати такі операції: із заданою щільністю ймовірності, потрібно виконати такі операції:
знайти функцію розподілу, користуючись заданою щільністю ймовірності;
знайти функцію, що буде оберненою до функції розподілу;
одержувати реалізації БВВ 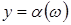 ; ;
обчислювати значення ВВ 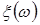 як значення знайденої функції як значення знайденої функції 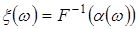 . .
Виконуючи ці операції 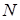 - разів, одержимо вибірку реалізацій - разів, одержимо вибірку реалізацій 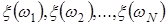 . Скориставшись нею, можна побудувати гістограму розподілу і порівняти її з заданою щільністю ймовірності. . Скориставшись нею, можна побудувати гістограму розподілу і порівняти її з заданою щільністю ймовірності.
Даний метод моделювання має недоліки тому, що не завжди вдається аналітично розрахувати для заданої щільності ймовірностей 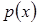 інтеграл для одержання інтеграл для одержання 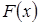 , і не для всякої функції розподілу вдається одержати обернену функцію. , і не для всякої функції розподілу вдається одержати обернену функцію.
Цей метод базується на зображенні складних щільностей ймовірностей 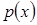 через простіші. Зокрема, можна подати будь-яку щільність ймовірності випадкової величини через простіші. Зокрема, можна подати будь-яку щільність ймовірності випадкової величини 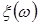 у вигляді суміші простих розподілів у вигляді суміші простих розподілів
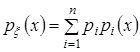 , (13) , (13)
де 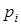 - деякі коефіцієнти, причому - деякі коефіцієнти, причому 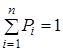 , а , а 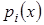 - щільності розподілу ВВ, для яких досить просто виконати моделювання на ЕОМ. - щільності розподілу ВВ, для яких досить просто виконати моделювання на ЕОМ.
В основі моделювання лежить такий математичний апарат. Нехай існують ВВ 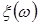 і і 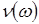 незалежні між собою і задані на тому самому імовірнісному просторі незалежні між собою і задані на тому самому імовірнісному просторі 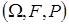 . Нехай . Нехай 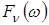 - це функція розподілу ВВ - це функція розподілу ВВ 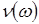 і і 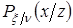 - це умовна щільність ймовірності ВВ - це умовна щільність ймовірності ВВ 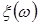 за умови, що ВВ за умови, що ВВ 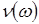 прийняла якесь значення прийняла якесь значення 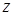
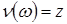 . (14) . (14)
Тоді безумовна щільність ймовірності ВВ 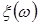
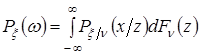 . (15) . (15)
Припустимо, що 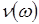 - це ВВ, яка приймає дискретні значення - це ВВ, яка приймає дискретні значення 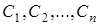 з імовірностями з імовірностями
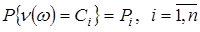 . (16) . (16)
У цьому випадку 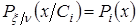 , отже приходимо до раніше наведеної суміші розподілу. У ролі щільностей ймовірності найпростішого типу можуть виступати: гаусові, прямокутні, трикутні розподіли. , отже приходимо до раніше наведеної суміші розподілу. У ролі щільностей ймовірності найпростішого типу можуть виступати: гаусові, прямокутні, трикутні розподіли.
На рис.6 для прикладу показано, як за допомогою гаусових розподілів апроксимується щільність розподілу складнішого виду
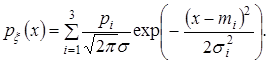 (17) (17)
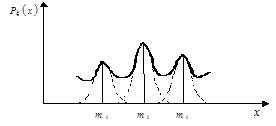
Рисунок 6 - Апроксимація складної щільності ймовірності за допомогою гаусових розподілів
Таким чином, алгоритм моделювання ВВ методом суперпозиції містить у собі такі етапи:
вибір вигляду найпростішої щільності розподілу, за допомогою якої апроксимується задана щільність ймовірності;
моделюється реалізація ВВ, яка приймає дискретні значення 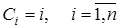 з заданими імовірностями з заданими імовірностями 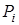 ; ;
для отриманого значення i
моделюються реалізація ВВ з 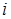 -
тою щільністю ймовірності; -
тою щільністю ймовірності;
з нову моделюється реалізація ВВ, яка приймає дискретні значення 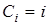 ; ;
потім виконується процес моделювання реалізації ВВ із новим номером щільності ймовірності;
зазначені етапи моделювання повторюються доти, доки не буде отримана вибірка реалізацій ВВ необхідного обсягу.
Введемо стандартну гаусову ВВ 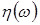 із нульовим математичним сподіванням із нульовим математичним сподіванням 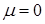 і одиничною дисперсією і одиничною дисперсією 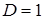
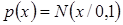 , (18) , (18)
де 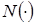 - символ гаусової щільності ймовірності. - символ гаусової щільності ймовірності.
У математичній статистиці доведено, що сумма значного числа незалежних між собою і рівномірно розподілених ВВ має гаусовий закон розподілу. Тому стандартну гаусову ВВ можна моделювати відповідно до виразу:
 , (19) , (19)
де 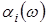 - незалежні між собою БВВ. - незалежні між собою БВВ.
У загальному випадку довільних 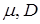 гаусову ВВ можна записати як гаусову ВВ можна записати як
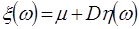 , (20) , (20)
де 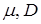 - це необхідні математичне сподівання і дисперсія ВВ. - це необхідні математичне сподівання і дисперсія ВВ.
Таким чином, алгоритм моделювання гаусової ВВ із заданими математичним сподіванням і дисперсією містить такі операції:
одержання 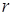 незалежних реалізацій БВВ і виконання над ними перетворення відповідно до зазначеного співвідношення (19);
незалежних реалізацій БВВ і виконання над ними перетворення відповідно до зазначеного співвідношення (19);
виконання перетворень (20) для одержання ВВ із заданими 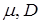 . .
Для моделювання вказаних ВВ використовуються стандартні гаусові випадкові величини 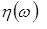 . Спочатку виконується моделювання ВВ згідно виразу . Спочатку виконується моделювання ВВ згідно виразу
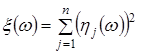 , (21) , (21)
де 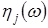 - стандартні ВВ із гаусовим розподілом ( - стандартні ВВ із гаусовим розподілом (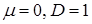 ). ).
Випадкова величина 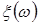 (21) має (21) має 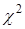 -розподіл з -розподіл з 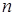 ступенями свободи ступенями свободи
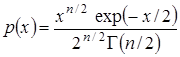 , (22) , (22)
де 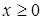 , , 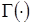 - це гамма-функція. - це гамма-функція.
В окремому випадку 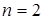 ця ВВ має експоненціальний розподіл з параметром ця ВВ має експоненціальний розподіл з параметром 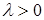
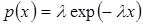 . (23) . (23)
ВВ, що визначається співвідношенням
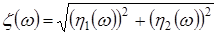 , (24) , (24)
має розподіл Релея
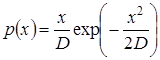 . .
Тут 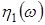 , , 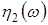 - незалежні між собою стандартні гаусові ВВ. - незалежні між собою стандартні гаусові ВВ.
Наведені співвідношення для одержання ВВ фактично є моделюючими алгоритмами, що містять такі етапи:
моделювання 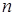 стандартних гаусових ВВ ( стандартних гаусових ВВ (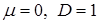 ); );
виконання операцій обчислення ВВ згідно (21) (для 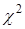 -розподілу); -розподілу);
для експоненційного розподілу алгоритм той же, тільки 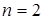 ;
;
для розподілу Релея (24) моделювання згідно (24).
|