СОДЕРЖАНИЕ
Введение
1. Многочлены Лежандра
2. Многочлены Чебышева
3. Преобразование Лапласа
4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4.1 Постановка задачи
4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра
4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.
Заключение
преобразование смещенный многочлен исчисление
ВВЕДЕНИЕ
Математический анализ – раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела.
Начало математическому анализу положил в 1665 И.Ньютон и (около 1675) независимо от него Г.Лейбниц, хотя важную подготовительную работу провели И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма (1601–1665), Дж.Валлис (1616–1703) и И.Барроу (1630–1677).
Операционное исчисление –раздел математики, занимающийся главным образом алгебраическими операциями, производимыми над символами операции (или преобразования).
Во многих задачах математического анализа рассматриваются ситуации, в которых каждая точка одного пространства ставится в соответствие некоторой точке другого (или того же) пространства. Пространства могут быть абстрактными, в которых «точки» в действительности являются функциями. Соответствие между двумя точками устанавливается с помощью преобразования или оператора. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления. Обычно теорию операторов применяют к пространствам, в которых допускается сложение или умножение точек, т.е. линейным пространствам, группам, кольцам, полям и т.д.
Операционное исчисление позволяет осуществить абстрактные постановки задач и обобщить такие разделы математического анализа, как теория дифференциальных и интегральных уравнений. Мощным стимулом для развития теории операторов стали современные проблемы квантовой теории. Наиболее полные результаты получены для дистрибутивных операторов в т.н. гильбертовом пространстве. Интерес к этой области во многом связан с представлением таких операторов интегральными преобразованиями.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
В середине XIX века появился ряд сочинений, посвящённых так называемому символическому исчислению и применению его к решению некоторых типов линейных дифференциальных уравнений. Сущность символического исчисления состоит в том, что вводятся в рассмотрение и надлежащим образом интерпретируются функции оператора дифференцирования.
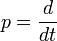 . .
Среди сочинений по символическому исчислению следует отметить вышедшую в 1862 году в Киеве обстоятельную монографию русского математика М. Е. Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений». В ней поставлены и разрешены основные задачи того метода, который в дальнейшем получил название операционного.
В 1892 году появились работы английского учёного О. Хевисайда, посвящённые применению метода символического исчисления к решению задач по теории распространения электрических колебаний в проводах.
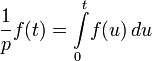
В отличие от своих предшественников, Хевисайд определил обратный оператор однозначно, полагая и считая f
(u
) = 0 для u
< 0. Труды Хевисайда положили начало систематическому применению символического, или операционного, исчисления к решению физических и технических задач.
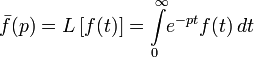
Однако широко развитое в трудах Хевисайда операционное исчисление не получило математического обоснования, и многие его результаты оставались недоказанными. Строгое обоснование было дано значительно позже, когда была установлена связь между функциональным преобразованием Лапласа и оператором дифференцирования
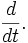
если существует производная 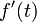 , для которой , для которой
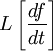
существует и f
(0) = 0, то
 . .
Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований. Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач теории упругости, теплопроводности, электродинамики и других разделов математической физики. Использование интегральных преобразований позволяет свести дифференциальное, интегральное или интегро-дифференциальное уравнение к алгебраическому, а также, в случае дифференциального уравнения в частных производных, уменьшить размерность.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Интегральные преобразования задаются формулой
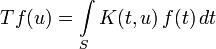 , (1) , (1)
где функции 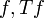 называются оригиналом и изображением соответственно, и являются элементами некоторого функционального пространства называются оригиналом и изображением соответственно, и являются элементами некоторого функционального пространства 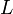 , при этом функция , при этом функция 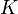 называется ядром интегрального преобразования. называется ядром интегрального преобразования.
Большинство интегральных преобразований являются обратимыми, то есть по известному изображению можно восстановить оригинал, зачастую также интегральным преобразованием:
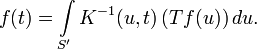 (2) (2)
Хотя свойства интегральных преобразований достаточно обширны, у них довольно много общего.
преобразование смещенный многочлен исчисление
1. Многочлены Лежандра
Многочлены Лежандра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке 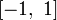 по мере Лебега. Многочлены Лежандра могут быть получены из многочленов по мере Лебега. Многочлены Лежандра могут быть получены из многочленов 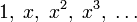 ортогонализацией Грама ― Шмидта. ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
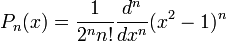 (3) (3)
часто записываемой в виде:
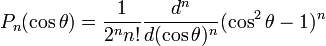 (4) (4)
Многочлены Лежандра также определяются по следующим формулам:
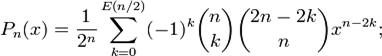
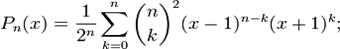
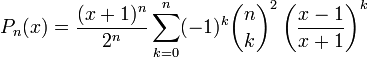 , если , если  ; ;
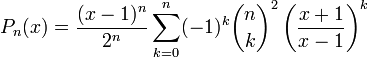 , если , если 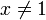 . .
Они также могут быть вычислены по рекуррентной формуле:
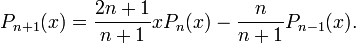
Первые многочлены Лежандра равны:
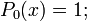
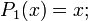
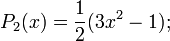
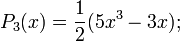
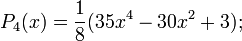
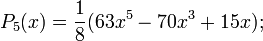
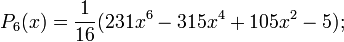
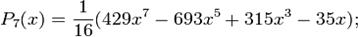
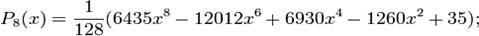
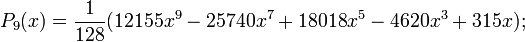
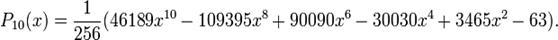
2.
Многочлены Чебышева
Многочлены Чебышева — две последовательности многочленов Tn
(x
) и Un
(x
), 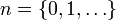 названные в честь Пафнутия Львовича Чебышева. названные в честь Пафнутия Львовича Чебышева.
Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода используются в качестве узлов в интерполяции алгебраическими многочленами.
Многочлен Чебышева первого рода Tn
(x
) характеризуется как многочлен степени n
со старшим коэффициентом 2n
- 1
, который меньше всего отклоняется от нуля на интервале [ − 1,1]. Впервые рассмотрены самим Чебышёвым.
Многочлены Чебышева первого рода Tn
(x
) могут быть определены с помощью рекуррентного соотношения:
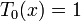
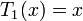
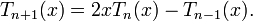
Многочлены Чебышева первого рода 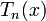 могут быть также определены с помощью равенства: могут быть также определены с помощью равенства:
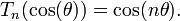
или, что почти эквивалентно,
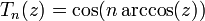
Несколько первых многочленов Чебышева первого рода
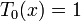
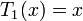
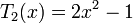
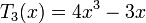
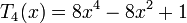
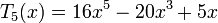
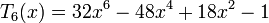
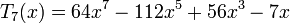

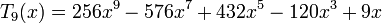
Многочлены Чебышева обладают следующими свойствами:
Ортогональность по отношению к соответствующим скалярному произведению (с весом 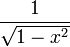 для многочленов первого рода и для многочленов первого рода и 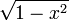 для многочленов второго рода). для многочленов второго рода).
Среди всех многочленов, значения которых на отрезке [ − 1,1] не превосходят по модулю 1, многочлен Чебышева имеет: наибольший старший коэффициент наибольшее значение в любой точке за пределами [ − 1,1] если 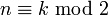 , то , то 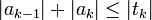 , где tk
— коэффициент многочлена Чебышева первого рода, ak
— коэффициент любого из рассматриваемых полиномов. , где tk
— коэффициент многочлена Чебышева первого рода, ak
— коэффициент любого из рассматриваемых полиномов.
Нули полиномов Чебышева являются оптимальными узлами в различных интерполяционных схемах. Например, в методе дискретных особенностей, который часто используется при исследовании интегральных уравнений в электродинамике и аэродинамике.
3.
4.
Преобразование Лапласа
Преобразование Лапласа — интегральное преобразование, связывающее функцию 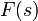 комплексного переменного (изображение) с функцией комплексного переменного (изображение) с функцией 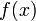 действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Интеграл Лапласа имеет вид:
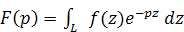 (5) (5)
где интегрирование производится по некоторому контуру Lв
плоскости комплексного переменного z, ставящий в соответствие функции f(z), определенной на L,
аналитическую функцию F(p) комплексного переменного p=s+it. Многие интегралы вида (5) были рассмотрены П. Лапласом.
В узком смысле под преобразованием Лапласа подразумевают одностороннее преобразование Лапласа
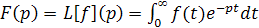 , (6) , (6)
называемое так в отличие от двустороннего преобразования Лапласа
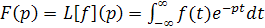 (7) (7)
Преобразование Лапласа – частный вид интегральных преобразований;. преобразования вида (6) или (7) тесно связаны с Фурье преобразованием.
Двустороннее преобразование Лапласа (7) можно рассматривать как преобразование Фурье функции 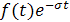 , одностороннее преобразование Лапласа (6) - как преобразование Фурье функции j(t) равной , одностороннее преобразование Лапласа (6) - как преобразование Фурье функции j(t) равной 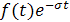 при 0 < t < ∞ и равной нулю при -∞ < t < 0. при 0 < t < ∞ и равной нулю при -∞ < t < 0.
Подынтегральная комплексная локально суммируемая функция f(t) называется функцией-оригиналом, или просто оригиналом; в приложениях часто удобно трактовать переменное t как время. Функция F(p)=L[f], (р) называется также преобразованием Лапласа оригинала f(t) или изображением по Лапласу. Интеграл (6) понимается, вообще говоря, как условно сходящийся на бесконечности.
Априори возможны три случая:
1) существует действительное число 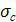 такое, что интеграл (6) сходится при такое, что интеграл (6) сходится при 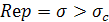 , а при , а при 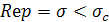 – расходится; это число σс
называется абсциссой (условной) сходимости; – расходится; это число σс
называется абсциссой (условной) сходимости;
2) интеграл (6) сходится при всех р,
в этом случае полагают 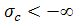 ; ;
3) интеграл (6) расходится при всех р, в этом случае полагают 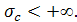
Если 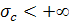 , то интеграл (6) представляет однозначную аналитическую функцию F(p) в полуплоскости сходимости , то интеграл (6) представляет однозначную аналитическую функцию F(p) в полуплоскости сходимости 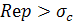 . Обычно ограничиваются рассмотрением абсолютно сходящихся интегралов (6). Точная нижняя грань тех s, для которых существует интеграл . Обычно ограничиваются рассмотрением абсолютно сходящихся интегралов (6). Точная нижняя грань тех s, для которых существует интеграл 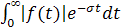 , называется абсциссой абсолютной сходимости , называется абсциссой абсолютной сходимости 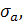 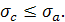
Если а – есть нижняя грань тех s, для которых 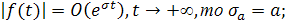 число а иногда называют показателем роста оригинала f(t). число а иногда называют показателем роста оригинала f(t).
При некоторых дополнительных условиях оригинал f(t) однозначно восстанавливается по своему F(p).
Например, если f(t) имеет ограниченную вариацию в окрестности точки t0
или если f(t) кусочногладкая, то имеет место формула обращения преобразования Лапласа:
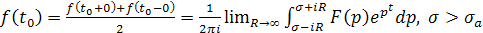 (8) (8)
Формулы (6) и (8) позволяют получить ряд соотношений между операциями, производимыми над оригиналами и изображениями, а также таблицу изображений для часто встречающихся оригиналов. Все это составляет элементарную часть операционного исчисления.
В математической физике важные применения находит многомерное преобразование Лапласа:
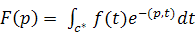 (9) (9)
где t
= (
t
1
, ……,
tn
)
-точка re-мерного евклидова пространства
Rn
,
p
= (
p
1
, ……,
pn
) =
σ
+
iτ
= (
σ
1
, ……, σ
n
) + (τ1
, ……, τ
n
)
-точка комплексного пространства
Cn
,
n
≥1, (
p
,
t
) = (
σ
,
t
)+
i
(
τ
,
t
) =
p
1
t
1
+ … +
pn
tn
-скалярное произведение, dt
=
dt
1
…
dtn
- элемент объема в Rn
. Комплексная функция f(t) в (9) определена и локально суммируема в области интегрирования
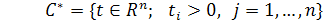
-положительном координатном угле пространства Rn
. Если функция f(t) ограничена в C*
, то интеграл (9) существует во всех точках 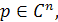 удовлетворяющих условию Re
(
p
,
t
)>0
, удовлетворяющих условию Re
(
p
,
t
)>0
, 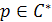 , которое определяет снова положительный координатный угол , которое определяет снова положительный координатный угол
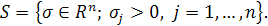
Интеграл (9) определяет голоморфную функцию комплексных переменных p
= (
p
1
,-
pn
)
в трубчатой области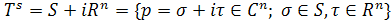 пространства пространства 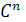 с основанием S.
В более общем случае в качестве области интегрирования с основанием S.
В более общем случае в качестве области интегрирования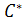 в (9) и основания Sтрубчатой области можно взять любую пару сопряженных замкнутых выпуклых острых конусов в пространстве в (9) и основания Sтрубчатой области можно взять любую пару сопряженных замкнутых выпуклых острых конусов в пространстве 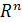 с вершиной в начале координат. При n=1 формула (9) переходит в (6), причем с вершиной в начале координат. При n=1 формула (9) переходит в (6), причем 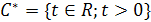 - положительная полуось и - положительная полуось и 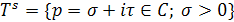 - правая полуплоскость. Преобразование Лапласа (9) определено и голоморфно и для функций f(t) гораздо более широких классов. Элементарные свойства преобразования Лапласа с соответствующими изменениями остаются справедливыми и для многомерного случая. - правая полуплоскость. Преобразование Лапласа (9) определено и голоморфно и для функций f(t) гораздо более широких классов. Элементарные свойства преобразования Лапласа с соответствующими изменениями остаются справедливыми и для многомерного случая.
Численное преобразование Лапласа - численное выполнение преобразования (6), переводящего оригинал f
(
t
), 0<
t
<∞
в изображение F(p),
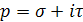 ,
а также численное обращение преобразования Лапласа, т. е. численное нахождение f(t) из интегрального уравнения (6) либо по формуле обращения (8). ,
а также численное обращение преобразования Лапласа, т. е. численное нахождение f(t) из интегрального уравнения (6) либо по формуле обращения (8).
Необходимость применения численного преобразования Лапласа возникает вследствие того, что таблицы оригиналов и изображений охватывают далеко не все встречающиеся в практике случаи, а также вследствие того, что оригинал или изображение зачастую выражаются слишком сложными, неудобными для применений формулами.
Проблема обращения преобразования Лапласа, как задача отыскания решения f(x) интегрального уравнения первого рода (6), относится к классу некорректных задач и может быть решена, в частности, посредством регуляризирующего алгоритма.
Задачу численного обращения преобразования Лапласа можно также решать методами, основанными на разложении функции-оригинала в функциональный ряд. Сюда в первую очередь можно отнести разложение в степенной ряд, в обобщенный степенной ряд, в ряд по показательным функциям, а также в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра, Якоби и Лагерра. Задача разложения оригинала в ряды по многочленам Чебышева, Лежандра, Якоби в окончательном своем виде сводится к проблеме моментов на конечном промежутке. Пусть известно преобразование Лапласа F(p) функции β(
t
)
f
(
t
):
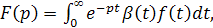
где f(t) - искомая функция, а β(t) - неотрицательная, интегрируемая на [0,∞) функция. Предполагается, что функция f(t) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L
2
(β(
t
), 0, ∞).
По изображению F(р).функции β(t), f(t), функция f(t) строится в виде ряда по смещенным многочленам Якоби, в частности по смещенным многочленам Лежандра, Чебышева первого и второго рода, коэффициенты которого ak
вычисляются по формуле.
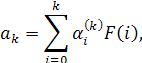
где 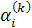 - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде - коэффициенты смещенного многочлена Лежандра, Чебышева первого и второго рода соответственно, записанных в виде 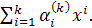
Другим приемом численного обращения преобразования Лапласа является построение квадратурных формул для интеграла обращения (8).
4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4.1
Постановка задачи
Задачу преобразования Лапласа можно решать методами, основанными на разложении оригинала в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра и Якоби.Эта задача, которая в окончательном своем виде сводится к проблеме моментов на конечном промежутке, была подвергнута изучению в работах многих авторов.
Рассмотрим постановку этой задачи в таком виде, как это сделано в работах В.М. Амербаева и в книге В.А. Диткина и А.П. Прудникова [2].
Пусть известно преобразование Лапласа F
(
p
)
функции β(
t
)
f
(
t
):
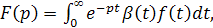 (10) (10)
Где f(t
) –
искомая функция, а β(t
) – неотрицательная, абсолютно интегрируемая на [0,∞) функция. Предположим, что функция f(t
) интегрируема на любом конечном отрезке [0, Т] и принадлежит классу L
2
(β(
t
), 0, ∞):
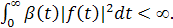 (11) (11)
Требуется по изображению F(р
) функции β(t)f(t),
построить функцию f(t
).
В интеграле (10) введем замену переменной x
=
e
-
t
; тогда он приведется к виду
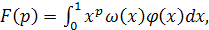 (12) (12)
где

В силу условий, которые наложены на функции f(t
) и β(t
), интеграл (12) сходится всюду в плоскости Re
p
≥,0,
поэтому переменной р
можно придать значения 0, 1, 2, … и получить «взвешенные моменты» функции 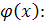
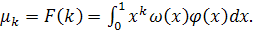 (13) (13)
После этого решаемую задачу можно сформулировать так: найти функцию 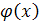 по ее «взвешенным моментам» по ее «взвешенным моментам» 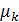 , или, что тоже самое, найти функцию f(t
) по значениям изображения функции β(t)f(t)
в целочисленных точках p
=
k
(
k
= 0, 1, 2, …).
В частном случае эту задачу можно упростить и по первым п + 1 «
взвешенным моментам» искать многочлен , или, что тоже самое, найти функцию f(t
) по значениям изображения функции β(t)f(t)
в целочисленных точках p
=
k
(
k
= 0, 1, 2, …).
В частном случае эту задачу можно упростить и по первым п + 1 «
взвешенным моментам» искать многочлен 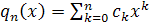 , такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции , такой, чтобы его «взвешенные моменты» совпадали с заданными моментами функции 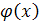 , то есть чтобы выполнялись равенства , то есть чтобы выполнялись равенства
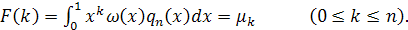 (14) (14)
4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра
Рассмотрим частный случай весовой функции
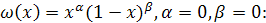 (15) (15)
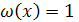 или или 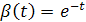 . .
Многочленами, ортогональными на отрезке [0,1] с весом 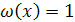 , будут смещены многочлены Лежандра , будут смещены многочлены Лежандра 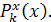
Они задаются формулой
 при при 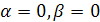
или же формулой
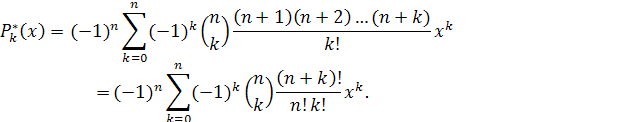
Величина rn
в этом случае равна
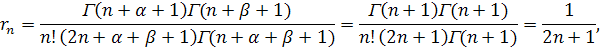
и разложение функции f(t
) по смещенным многочленам Лежандра имеет вид
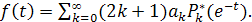 (16) (16)
Величины αk
вычисляются по формуле
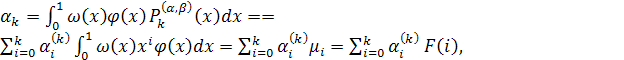 (17) (17)
в которой 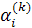 - коэффициенты смещенного многочлена Лежандра - коэффициенты смещенного многочлена Лежандра 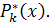
4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.
Положим теперь 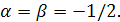 Весовая функция имеет вид Весовая функция имеет вид
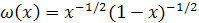 и и 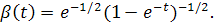
Смещенные многочлены Чебышева первого рода 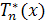 являются ортогональной системой на [0,1] по весу являются ортогональной системой на [0,1] по весу 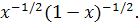
Многочлены Якоби 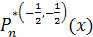 отличаются от отличаются от 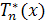 только численным множителем, а именно только численным множителем, а именно
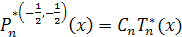 , ,
где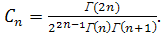
Многочлены 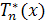 имеют вид имеют вид
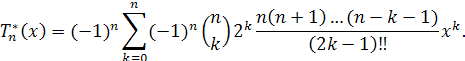
Значения rn
вычисляются по формулам
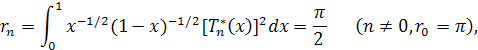
а разложение функции f(t
) по смещенным многочленам Чебышева первого рода имеет вид
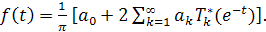 (18) (18)
Коэффициенты ak
(
k
=0, 1, …)
вычисляются по формуле (17), в которой 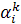 - коэффициенты смещенного многочлена Чебышева первого рода - коэффициенты смещенного многочлена Чебышева первого рода 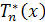 . .
В вычислениях удобнее пользоваться тригонометрической записью многочленов 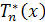 , а именно: , а именно: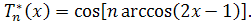
Сделав замену переменной 2
x
– 1 =
cosθ
(0≤θ≤π)
и учитывая, что 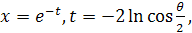 разложение (18) можно переписать в виде: разложение (18) можно переписать в виде:
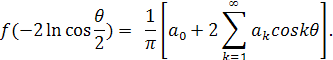
ЗАКЛЮЧЕНИЕ
Одним из наиболее мощных средств решения дифференциальных уравнений, как обыкновенных, так, особенно, в частных производных, является метод интегральных преобразований.
Преобразования Фурье, Лапласа, Ганкеля и другие применяются для решения задач теории упругости, теплопроводности, электродинамики и других разделов математической физики.
Преобразование Лапласа — интегральное преобразование, связывающее функцию 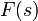 комплексного переменного (изображение) с функцией комплексного переменного (изображение) с функцией 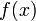 действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
Интеграл Лапласа имеет вид:
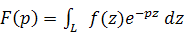
где интегрирование производится по некоторому контуру Lв
плоскости комплексного переменного z, ставящий в соответствие функции f(z), определенной на L,
аналитическую функцию F(p) комплексного переменного p=s+it.
Численное преобразование Лапласа - численное выполнение преобразования
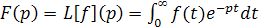 , ,
переводящего оригинал f
(
t
), 0<
t
<∞
в изображение F(p),
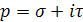 ,
а также численное обращение преобразования Лапласа. ,
а также численное обращение преобразования Лапласа.
Необходимость применения численного преобразования Лапласа возникает вследствие того, что таблицы оригиналов и изображений охватывают далеко не все встречающиеся в практике случаи, а также вследствие того, что оригинал или изображение зачастую выражаются слишком сложными, неудобными для применений формулами.
Задачу численного обращения преобразования Лапласа можно также решать методами, основанными на разложении функции-оригинала в функциональный ряд. Сюда в первую очередь можно отнести разложение в степенной ряд, в обобщенный степенной ряд, в ряд по показательным функциям, а также в ряды по ортогональным функциям, в частности по многочленам Чебышева, Лежандра, Якоби и Лагерра. Задача разложения оригинала в ряды по многочленам Чебышева, Лежандра, Якоби в окончательном своем виде сводится к проблеме моментов на конечном промежутке. Пусть известно преобразование Лапласа F(p) функции β(
t
)
f
(
t
):
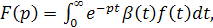
где f(t) - искомая функция, а β(t) - неотрицательная, интегрируемая на [0,∞) функция.
СПИСОК ЛИТЕРАТУРЫ
1. Ван дер Поль Б., Бремер Х. Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: Издательство иностранной литературы, 1952. — 507 с.
2. Диткин В.А., Прудников А. П. Интегральные преобразования и операционное исчисление. — М.: Главная редакция физико-математической литературы издательства «Наука», 1974. — 544 с.
3. Кожевников Н.И., Краснощекова Т. И., Шишкин Н. Е. Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1964. — 184 с.
4. Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращения преобразования Лапласа. – М.: Наука, 1974. – 226 с.
|