Файл: MENTOR
© Н.М. Козий, 2007
Авторские права защищены
свидетельствами Украины
№ 23145 и № 27312
ОБЩЕЕ ДОКАЗАТЕЛЬСТВО
ГИПОТЕЗЫ БИЛЯ, ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА
И ТЕОРЕМЫ ПИФАГОРА
ДОКАЗАТЕЛЬСТВО ГИПОТЕЗЫ БИЛЯ
Гипотеза Биля формулируется следующим образом: неопределенное уравнение
Аx +Вy= Сz/1/
не имеет решения в целых положительных числах А, В, С, x, y и z при условии, что x, y и z больше 2.
Суть гипотезы Биля не изменится, если уравнение /1/ запишем следующим образом:
Аx = Сz - Вy/2/
Уравнение /2/ рассматриваем как параметрическое уравнение с параметром Aи переменными Bи С.
Уравнение /2/ запишем в следующем виде:
Аx = (С0,5z) 2 -(В0,5y) 2 /3/
Обозначим:
В0,5y =V/4/
С0,5z =U/5/
Отсюда:
Вy=V2 /6/
Сz =U2 /7/
В =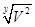 /8/ /8/
С =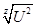 /9/ /9/
Тогда из уравнений /2/, /6/ и /7/ следует:
Аx = Сz-Вy =U2-V2 /10/
Уравнение /10/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:
Аx= (U-V) ∙(U+V) /11/
Для доказательства гипотезы Биля используем метод замены переменных. Обозначим:
U-V=X/12/
Из уравнения /12/ имеем:
U=V+X/13/
Из уравнений /11/, /12/ и /13/ имеем:
Аx= X· (V+X+V) =X(2V+X) =2VХ+X2 /14/
Из уравнения /14/ имеем:
Аx - X2=2VХ /15/
Отсюда:
V=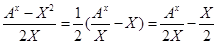 /16/ /16/
Из уравнений /13/ и /16/ имеем:
U= 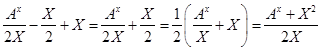 /17/ /17/
Из уравнений /8/, /9/, /16/ и /17/ имеем:
B=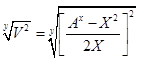 /18/ /18/
C =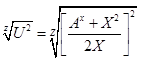 /19/ /19/
Из уравнений / 18/ и /19/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа Аxна число X, т.е. число Xдолжно быть одним из множителей, входящих в состав множителей числа Аx. Другими словами, число Аxдолжно быть, например, равно:
Ax = (abc) x, /20/
где: a, b, c - простые или составные целые положительные числа.
При этом должно быть, например:
X=сm; X2=c2m. /21/
В любым случае должно соблюдаться соотношение: 2m ≤ x.
Из уравнений / 18/ и /19/ следует, что необходимым условием для того чтобы числа В и С были целыми, является также одинаковая четность чисел Aи X: оба числа должны быть четными или оба нечетными.
Из уравнений / 18/, /19/ и /20/ следует:
В=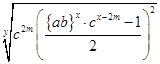 /22/ /22/
C=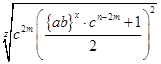 /23/ /23/
Обозначим:
P = 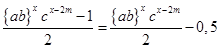 /24/ /24/
Q = 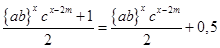 /25/ /25/
Тогда:
B = 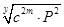 /26/ /26/
С =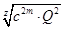 /27/ /27/
Из уравнений /24/ и /25/ имеем:
Q =  /28/ /28/
Таким образом, из уравнений /27/ и /28/ следует:
С =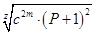 /29/ /29/
Из анализа уравнений /26/ и /29/ следует, что поскольку разность между числами Qи Pравна всего лишь:
Реклама

Q- P = P + 1 - P = 1, /30/
то, по меньшей мере, одно из чисел В или С является дробным числом.
Допустим, что число В - целое число.
ПРИМЕР: c=5; P = 612 = 3721; y = 4; m=2; 2m=4.
По формуле /25/ имеем:
B = 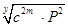 = =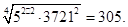
Тогда:
при z=3: С = 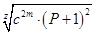 = = 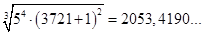 - дробное число. - дробное число.
при z=4: С = 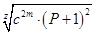 = = 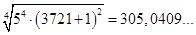 - дробное число. - дробное число.
при z=5: С = 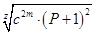 = = 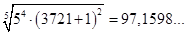 - дробное число. - дробное число.
при z=6: С = 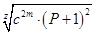 = = 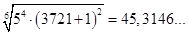 - дробное число. - дробное число.
Очевидно, что если
(dm) 2 = d2m, то (dm + 1) 2 ≠ e2m,
где: d- целое число;
e- целое число.
Таким образом, если допустить, что В - целое число, то С - дробное число.
Следовательно, гипотеза Биля не имеет решения в целых положительных числах.
ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА
Если в уравнении /1/ гипотезы Биля принять, что показатели степени равны между собой, т.е. x = y = z = n, то оно преобразуется в уравнение великой теоремы Ферма:
Аn +Вn= Сn/31/
Тогда уравнения /2/, /6/ - /11/, /16/ - /20/ примут вид:
Аn = Сn- Вn/32/
Вn =V2 /33/
Сn =U2 /34/
В =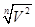 /35/ /35/
С =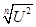 /36/ /36/
Аn = Сn- Вn = U2-V2 /37/
Аn = (U-V) ∙(U+V) /38/
V=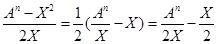 /39/ /39/
U=  /40/ /40/
B =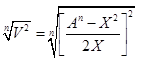 /41/ /41/
C =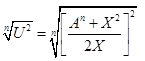 /42/ /42/
Пусть: An = (abc) n, /43/
где: a, b, c - простые или составные целые положительные числа.
При этом должно быть, например:
X=сm; X2=c2m. /44/
В любом случае должно соблюдаться соотношение: 2m ≤ n.
Из уравнений / 41/ и /42/ следует, что необходимым условием для того чтобы числа В и С были целыми, является также одинаковая четность чисел Aи X: оба числа должны быть четными или оба нечетными.
Из уравнений / 41/, /42/ и /43/ следует:
В=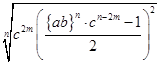 /45/ /45/
C=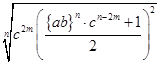 /46/ /46/
Обозначим:
P = 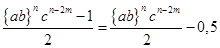 /47/ /47/
Q = 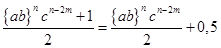 /48/ /48/
Тогда:
B = 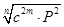 /49/ /49/
С =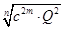 /50/ /50/
Из уравнений /47/ и /48/ имеем:
Q = 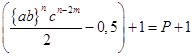 /51/ /51/
Таким образом, из уравнений /50/ и /51/ следует:
С =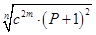 /52/ /52/
Из анализа уравнений /49/ и /52/ следует, что поскольку разность между числами Qи Pравна всего лишь:
Q- P = P + 1 - P = 1, /53/
то, по меньшей мере, одно из чисел В или С является дробным числом.
Допустим, что число В - целое число.
ПРИМЕР: c=5; P = 612 = 3721; n =2m = 4; m=2.
По формуле /49/ имеем:
B = 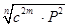 = =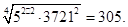
Тогда:
С = 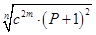 = = 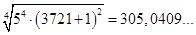 - дробное число. - дробное число.
Очевидно, что если (dm) 2 = d2m, то (dm + 1) 2 ≠ e2m,
где: d- целое число; e- целое число.
Таким образом, если допустить, что число В - целое число, то С - дробное число.
Следовательно, великая теорема Ферма не имеет решения в целых положительных числах.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА
Если в уравнении /1/ гипотезы Биля принять, что показатели степени равны между собой и равны: x = y = z = 2, то оно преобразуется в уравнение теоремы Пифагора:
А2 +В2= С2 /54/
Тогда уравнения /2/, /6/ - /11/, /16/ и /17/ примут вид:
Реклама

А2 = С2 - В2/55/
В2 =V2 /56/
С2 =U2 /57/
В =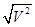 = V/58/ = V/58/
С =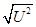 = U/59/ = U/59/
А2 = С2 - В2 = U2-V2 /60/
А2 = (U-V) ∙(U+V) /61/
B = V=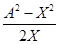 /62/ /62/
C = U= 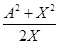 /63/ /63/
По уравнениям /62/ и /63/ и заданному значению числа A определяются пары чисел B и С, которые с числом Aобразуют тройки пифагоровых чисел.
ПРИМЕРЫ
Пример 1: А=3∙5=15; n=2; М=3.
В=Х=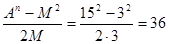 ; С=Y= ; С=Y=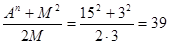
А2=С2-В2=392-362=225; А=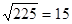 или: А2 +В2=152+362=1521=392= С2 или: А2 +В2=152+362=1521=392= С2
Пример 2: А=3∙5=15; n=2; М=5.
В=Х=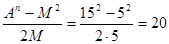 ; С=Y= ; С=Y=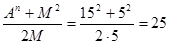
А2 =С2-В2=252-202=225=152 или: А2+В2=152+202=625=252= С2
Пример 3: А=2∙3∙13=78; n=2; М=2∙13=26.
В=Х=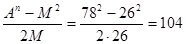 ; С=Y= ; С=Y=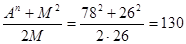
А2=С2-В2=1302-1042=6084=782, или: А2 + В2=782+1042=16900=1302= С2
Пример 4: А=2∙3∙13=78; n=2; М=2∙3=6.
В=Х=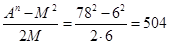 ; С=Y= ; С=Y=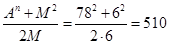
А2=С2-В2=5102-5042=6084=782, или: А2 + В2=782+5042=260100=5102= С2
Таким образом, из уравнения /60/ следует, что любое целое положительное число в квадрате всегда равно разности квадратов одной пары или нескольких пар целых положительных чисел.
ВЫВОДЫ
Из анализа гипотезы Биля, великой теоремы Ферма и теоремы Пифагора следует, что в основе их лежит одно и тоже уравнение:
Аx +Вy= Сz
При этом:
в уравнении гипотезы Биля показатели степени x, y, z больше 2 и не равны между собой;
в уравнении великой теоремы Ферма показатели степени x, y, z больше 2 и равны между собой: x= y= z = n;
в уравнении теоремы Пифагора показатели степени x, y, zравны между собой и равны: x= y= z = n=2.
Таким образом:
уравнение теоремы Пифагора является частным вариантом уравнения великой теоремы Ферма;
уравнение великой теоремы Ферма является частным вариантом уравнения гипотезы Биля.
Доказательства гипотезы Биля, великой теоремы Ферма и теоремы Пифагора выполнены одним методом: методом решения параметрических уравнений в сочетании с методом замены переменных. Тот факт, что использованный метод доказательства теоремы Пифагора дает возможность для любого числа А находить пары пифагоровых чисел В и С, позволяет сделать вывод, что и доказательства гипотезы Биля и великой теоремы Ферма, выполненные тем же методом, достоверны.
|