МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
КИРОВОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. Винниченка
КУРСОВАЯ РАБОТА
по курсу «Математика»
на тему : «Нестандартный анализ»
Кировоград
2003
СОДЕРЖАНИЕ
ВСТУПЛЕНИЕ……………………………………………………………………………3
1. ЛЕЙБНИЦ И “ДРЕВНЯЯ ИСТОРИЯ” НЕСТАНДАРТНОГО АНАЛИЗА ….…4
2. РОБИНСОН И «НОВАЯ ИСТОРИЯ» НЕСТАНДАРТНОГО АНАЛИЗА……...8
3. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ…………………………………………….10
4. ГИПЕРДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ……………………………………………16
5. ПРИМЕР НЕАРХИМЕДОВОЙ ЧИСЛОВОЙ СИСТЕМЫ………………….……..18
6. НОВЫЕ ТРЕБОВАНИЯ К ГИПЕРДЕЙСТВИТЕЛЬНЫМ ЧИСЛАМ И ОСНОВНАЯ ГИПОТЕЗА………………………………………………………………21
7. СЛЕДСТВИЯ ОСНОВНОЙ ГИПОТЕЗЫ………………………………………….24
8. ПОСТРОЕНИЕ СИСТЕМЫ ГИПЕРДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ………………27
ЛИТЕРАТУРА………………………………………………………………………..….33
ВСТУПЛЕНИЕ
Нестандартный анализ возник в 1960 году, когда Абрахам Робинсон, специалист по теории моделей, понял, каким образом методы математической
логики позволяют оправдать классиков математического анализа XVII и XVIII вв., поставив на строгую основу их рассуждения, использующие “бесконечно большие” и бесконечно малые величины. Таким образом, речь идет не о каких-то новых “нестандартных” методах, не имеющих ничего общего с традиционной математикой, а о развитии новых средств внутри стандартной (теоретико-множественной) математики.
Нестандартный анализ остался бы любопытным курьезом, если бы единственным его приложением было обоснование рассуждений классиков математического анализа. Он оказался полезным и при развитии новых математических теорий. Нестандартный анализ можно сравнить с мостом, переброшенным через реку. Постройка моста не расширяет доступной нам территории, но сокращает путь с одного берега на другой. Подобным образом нестандартный анализ делает доказательства многих теорем короче.
Однако, быть может, главное значение нестандартного анализа состоит в другом. Язык нестандартного анализа оказался удобным средством построения математических моделей физических явлений. Идеи и методы нестандартного анализа могут стать важной частью будущей физической картины мира. Во всяком случае уже сейчас многие специалисты по математической физике активно используют нестандартный анализ в своей работе.
Нестандартный анализ позволяет с новой точки зрения посмотреть на многие рассуждения классиков математического анализа, кажущиеся нестрогими, но приводящие к успеху, и путем относительно небольших уточнений сделать их удовлетворяющими современным критериям строгости.
Реклама

1. ЛЕЙБНИЦ И “ДРЕВНЯЯ ИСТОРИЯ” НЕСТАНДАРТНОГО АНАЛИЗА
Возраст нестандартного анализа колеблется (в зависимости от точки зрения) от двух с половиной десятков до трех сотен лет. Два с половиной десятка получится, если считать, что нестандартный анализ зародился осенью 1960 г., когда его основатель, Абрахам Робинсон, сделал доклад на одном нз семинаров Принстонского университета о возможности применения методов математической логики к обоснованию математического анализа. Триста лет получится, если считать началом нестандартного анлиза появление символов бесконечно малых dx, dy трактате Лейбница “Новый метод”.
Трудно сказать с уверенностью, насколько в действительности Лейбниц был близок к идеям нестандартного анализа. Как пишет сам Робинсон “история предмета обычно пишется в свете его позднейшего развития. Уже более чем полвека все обзоры истории дифференциального и интегрального исчислений основывались на уверенности в том, что понятие бесконечно малых и бесконечно больших, если даже и непротиворечиво, бесполезно для развития анализа. В результате в работах этого периода заметно различие между строгостью, с которой рассматриваются идеи Лейбница и его последователей, и снисходительностью, проявляемой к провозвестникам идеи предела”. Характерно, например, следующее высказывание Анри Лебега от 3 декабря 1926 г. “Бесконечно малые были когда-то туманными сущностями, встречавшимися в неясных и неточных формулировках. Все разъяснилось впоследствии благодаря понятию предела”.
Считая, что идеи Лейбница и идеи сторонников понятия предельного перехода мерились двойным стандартом при несправедливом склонении весов правосудия в пользу предела, Робинсон предлагает во многом пересмотреть общую картину возникновения и развития математического анализа от Ньютона и Лейбница до Коши и Вейерштрасса. Этот пересмотр приводит к более полному признанию заслуг Лейбница, и сам Лейбниц перемещается, таким образом, из разряда гениев третьего класса в разряд гениев второго класса (классификация, предложенная Станиславом Лемом: в этой классификации гении третьего класса получают прижизненное, а гении более высокого класса – лишь посмертное признание).
Изложим историко-математические взгляды Робинсона. Робинсон резюмирует стандартный взгляд на историю развития математического анализа в следующих словах: “После длительного периода, в течение которого были определены площади, объемы и касательные в различных частных случаях, во второй половине семнадцатого столетия Ньютоном и (несколько позже, но независимо) Лейбницем была построена общая теория дифференцирования и интегрирования. Касаясь обоснования введенных им понятий, Ньютон обращался то к бесконечно малым, то к пределам, то непосредственно к физической интуиции; его непосредственные последователи предпочитали последнее. С другой стороны, Лейбниц и его последователи развивали теорию исходя из дифференциалов первого и следующих порядков. Технические удобства обозначений, использовавших дифференциалы, привели к быстрому развитию Анализа и его приложений в Европе, где они были приняты. Однако внутренние противоречия этой концепции привели к осознанию того, что необходимы какие-то другие основания. Лагранж считал, что ему удалось найти подходящий путь, взяв за основу тейлоровское разложение функции. Но первое строгое обоснование математического анализа было дано лишь Коши. Основой теории Коши было понятиепредела, которое, будучи впервые выдвинуто Ньютоном, впоследствии поддерживалось Даламбером. Более формальное изложение методов Коши было дано Вейерштрассом (которого в некоторой степени предвосхитил Больцано). После создания теория пределов использование бесконечно больших и бесконечно малых превратилось в оборот речи, применяемый в выражениях типа “... стремится к бесконечности”. Дальнейшее развитие теории неархимедовых полей было целиком предоставлено алгебре.”
Реклама

Этот стандартный вгляд, но мнению Робинсона, в некоторых отношениях “должен быть дополнен или даже изменен”. В доказательсто этого Робинсон приводит большое количество выдержек из сочинений Лейбница и других упомянутых выше авторов. Как считает Робинсон, “... отношение Лейбница к бесконечно большим и бесконечно малым величинам в Анализе в основном оставалось неизменным в течение двух последних десятилетий его жизни. Он полностью одобрял их введение, но считал их “идеальными элементами, подобными мнимым числа. Эти идеальные элементы подчиняются тем же законам, что и обычные числа. Тем не менее они представляют собой не более чем удобные фикции, необходимые для облегчения рассуждений и открытий. Всегда, при желании, можно исключить их использование и вернуться к стилю античных математиков, рассуждая в терминах величин, достаточно больших (или малых) для того, чтобы ошибка была меньше любой наперед заданной. Все это отчетливо и неоднократно утверждается в сочинениях Лейбница”.
Приведем теперь некоторые из высказываний Лейбница, цитируемых Робинсоном.
“... Нужно воспринимать бесконечное подобно тому, как это делается в оптике, когда солнечные лучи считаются приходящими из бесконечно удаленной точки и поэтому параллельными... И когда имеются различные порядки бесконечного или бесконечно малых, то понимаются они в том же смысле, в каком земной шар считается точкой по сравнению с расстоянием до неподвижных звезд, а шарик в наших руках — точкой по сравнению с радиусом земного шара, так что расстояние до неподвижных звезд является бесконечно бесконечным или бесконечностью бесконечности по отношению к диаметру шарика. Вместо бесконечно большого или бесконечно малого количества можно взять количество настолько большое или малое, насколько это нужно, чтобы ошибка не превышала заданной. Отличие от архимедовского стиля рассуждений лишь в выражениях, которые у нас более непосредственные и лучше приспособлены для искусства изобретать”.
“...Если кто-то не желает рассматривать бесконечно большие и малые в строго метафизическом смысле, как реально существующие, он можег пользоваться ими как «идеальными понятиями», которые сокращают рассуждения, подобно мнимым корням в обычном анализе... Таким же образом представляют более трех измерений...— все это для установления идей, способных сокращать рассуждения и основывающихся на реальностях.
Не следует все же воображать, что наука о бесконечном унижается этим объяснением и сводится к фикциям, ибо постоянно остается, говоря языком схоластики, синкатегорематическая бесконечность. Например, остается верным, что 2 равно 1/1+1/2+1/4+1/8+1/16+1/32 и т. д., что есть бесконечный ряд, в котором содержатся сразу все дроби с числителем 1 и со знаменателями, образующими удваивающуюся геометрическую прогрессию, хотя здесь употребляют все время лишь обыкновенные числа и хотя не вводят никакой бесконечно малой дроби или дроби с бесконечным знаменателем... Правила конечного сохраняют силу в бесконечном, как если бы существовали атомы..., хотя они вовсе не существуют, ибо материя в действительности делима без конца и, наоборот, правила бесконечного сохраняют силу в конечном, как если бы имелись метафизические бесконечно малые, хотя в них и нет нужды и хотя деление материи никогда не приходит к бесконечно малым частицам. Это объясняется тем, что все управляется разумом и что иначе совсем не было бы ни науки, ни правила, а это не согласовалось бы с природой верховного начала”. (Это высказывание Лейбница можно при желании рассматривать как формулировку принципа переноса, что дает еще одно основание называть его также “принципом Лейбница”.)
“...Несравнимыми величинами я называю такие, одна из которых никогда не сможет превзойти другую, на какое конечное число ее бы ни помножили, так же как это понимает Евклид...”.
Приведем еще несколько цитат (на этот раз отсутствующих в монографии Робинсона).
“...новый Анализ бесконечных рассматривает не линии и не числа, но величины вообще, как это делает обыкновенная Алгебра. Этот Анализ содержит новый алгоритм, т. е. новый способ складывать, вычитать, умножать, делить, извлекать корни, соответствующий несравнимым величинам, т. е. тем, которые бесконечно велики или бесконечно малы в сравнении с другими...”
Методы Лейбница господствовали в Европе в течение более чем 50 лет. Однако во второй половине XVIII столетия начались поиски альтернативных путей построения анализа. Лагранж предлагал рассматривать разложения функций в степенные ряды, предполагая, что любая или почти любая функция может быть разложена в такой ряд. Даламбер предлагал понятие предела в качестве исходного для построения математического анализа. Он писал:
“Говорят, что одна величина лявляется пределом другой, если вторая может приблизиться к первой ближе, чем на любую заданную величину... Теория пределов является основанием подлинной Метафизики дифференциального исчисления... В дифференциальном исчислении речь идет не о бесконечно малых величинах, как это обычно утверждают; речь идет лишь о переделах конечных величин... Термином “бесконечно малая» пользуются лишь как сокращением …»
Эти высказывания даламбера выглядят как изложение современной точки зрения на пределе. Можно было бы предположить, что с этого времени понятие бесконечно малых будет полностью устранено. Это, однако, не так. Коши, рассматриваемый обычно как основатель современного подхода к построению анализа, использует понятие бесконечно малой величины. Пытаясь объяснить в современных терминах, что Коши называет “величиной”, можно предположить, что величина — это функция с действительными значениями, определенная на упорядоченном множестве без наибольшего элемента. Коши, однако, отнюдь не сводит величины к функциям. Наоборот, он говорит о функции как о соотношении, связывающем две величины. В его изложении бесконечно малые и пределы фигурируют как равноправные компоненты обоснования анализа.
2. РОБИНСОН И «НОВАЯ ИСТОРИЯ» НЕСТАНДАРТНОГО АНАЛИЗА
В 1961 г. появилась статья А. Робинсона «Нестандартный анализ» в Трудах Нидерландской академии наук. В статье намечены как основные положения нестандартного анализа, так и некоторые его приложения (например, к аналитической механике). В этой статье Робинсон, в частности, писал: “Наша главная цель – показать, что эти модели дают естественный подход к старой почтенной проблеме построения исчисления, включающего бесконечно большие и бесконечно малые количества. Как хорошо известно, использование бесконечно малых, настойчиво защищаемое Лейбницем и без колебании принимаемое Эйлером, было дезавуировано с появлением методов Кошн, поставивших математический анализ на твердую основу”.
Итак, до 1961 г. понятие бесконечно малой поятоянной величины, бесконечно малого числа, интерпретировалось как в лучшем случае нестрогое, а в худшем — бессмысленное. Робинсон впервые обнаружил, что этому понятию можно придать точный математический смысл.
В течение последующих восьми лет вышли в свет три монографии, излагающие нестандартную теорию: в 1962 г.– книга У. Л. Дж. Люксембурга “Нестандартный анализ. Лекции о робинсоновой теории бесконечно малых и бесконечно больших чисел”, в 1966 г.— книга самого А. Робинсона “Нестандартный анализ”, в 1969 г. — книга М. Маховера и Дж. Хиршфелда “Лекции о нестандартном анализе”] (из 77 страниц этих “Лекций” действительной прямой отведено немногим болеее двух: «нестандартный анализ» понимается здесь в самом широком смысле).
Наибольший резонанс вызвала книга Робинсона. В девяти первых главах этой монографии содержалось как построение необходимого логико-математического аппарата, так и многочисленные приложения – к дифференциальному и интегральному исчислению, к общей топологии, к теории функций комплексного переменного, к теории групп Ли, к гидродинамике и теории упругости.
В 1966 г. появилась статья А.Р. Бернстейна и А. Робинсона, в которой впервые методами нестандартного анализа было получено решение проблемы инвариантных пространств для полиномиально компактных операторов. В очерке П.Р. Халмоша “Взгляд в гильбертово пространство” в качестве проблемы фигурирует поставленная К.Т. Смитом задача о существовании инвариантного подпространства для таких операторов Т в гильбертовом пространстве 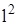 , для которых оператор , для которых оператор 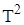 компактен. А.Р. Бернстейном и А. Робинсоном методами нестандартного анализа было доказано, что любой полиномиально компактный оператор в гильбертовом пространстве имеет нетривиальное инвариантное замкнутое подпространство. компактен. А.Р. Бернстейном и А. Робинсоном методами нестандартного анализа было доказано, что любой полиномиально компактный оператор в гильбертовом пространстве имеет нетривиальное инвариантное замкнутое подпространство.
Приложения нестандартного анализа в математике охватывают обширную область от топологии до теории дифференциальных уравнений, теории мер и вероятностей. Что касается внематематических приложений, то среди них мы встречаем даже приложения к математической экономике. Многообещающим выглядит использование нестандартного гильбертова пространства для построения квантовой механики. А в статистической механике становится возможным рассматривать системы из бесконечного числа частиц. Помимо применений к различным областям математики, исследования в области нестандартного анализа включают в себя и исследование самих нестандартных структур.
В 1976 г. вышли сразу три книги по нестандартному анализу: “Элементарный анализ” и “Основания исчисления бесконечно малых” Г. Дж. Кейслера и “Введение в теорию бесконечно малых” К. Д. Стройана и В. А. Дж. Люксембурга.
Быть может, наибольшую пользу нестандартые методы могут принести в области прикладной математики. В 1981 г. вышла книга Р. Лутца и М. Гозе “Нестандартный анализ: практическое руководство с приложениями”. В этой книге после изложения основных принципов нестандартного анализа рассматриваются вопросы теории возмущений.
В настоящее время нестандартный анализ завоёвывает всё большее признание. Состоялся ряд международных симпозиумов, специально посвященных нестандартному анализу и его приложениям. В течении последнего десятилетия нестандартный анализ (точнее, элементарный математический анализ, но основанный на нестандартном подходе) преподавался в ряде высших учебных заведений США.
3. БЕСКОНЕЧНО МАЛЫЕ ВЕЛИЧИНЫ
Один из наиболее принципиальных моментов нестандартного анализа состоит в том, что бесконечно малые рассматриваются не как переменные величины (т. е. не как функции, стремящиеся к нулю, как учат современные учебники), а как величины постоянные. Такой подход хорошо согласуется как с интуицией естествоиспытателя, так и с реальной историей зарождения математического анализа. Что касается интуиции, то достаточно раскрыть любой учебник физики, чтобы натолкнуться на бесконечно малые приращения, бесконечно малые объемы и т.п. Все эти величины мыслятся, разумеется, не как переменные, а просто как очень маленькие, почти равные нулю. Было бы неправильно считать подобного рода интуицию присущей лишь авторам учебников физики. Вряд ли какой-то математик воспринимает (наглядно) элемент дуги ds иначе, чем “очень маленькую дугу”. Любой математик, составляя соответствующее дифференциальное уравнение, скажет, что за бесконечно малое время dt точка прошла бесконечно малый путь dx,
а количество радиоактивного вещества изменилось на бесконечно малую величину dN.
Что же касается истории математического анализа, то в наиболее явной форме излагаемый подход проявился у одного из основоположников этой науки — Лейбница. В мае 1984 г. исполнилось 300 лет с того дня, как символы dx и dy впервые появились на страницах математических публикаций, а именно в знаменитом мемуаре Лейбница “Новый метод...”. Именно Лейбниц яснее других ощущал бесконечно малые величины постоянными (хотя и воображаемыми, идеальными) величинами особого рода, и именно Лейбниц сформулировал правила оперирования с бесконечно малыми в виде исчисления.
Какие положительные числа следует называть бесконечно малыми?
Первый ответ таков: положительное число e называется бесконечно малым, если оно меньше всех положительных чисел. Однако бесконечно малых в этом смысле положительных чисел не бывает: ведь если число меньше всех положительных чисел и само положительно, оно должно быть меньше самого себя. Попытаемся исправить положение, потребовав, чтобы e было меньше всех других
положительных чисел, но больше нуля, т. е. чтобы e было наименьшим в множестве положительных чисел. На числовой оси такое e должно изобразиться самой левой точкой множества (0, +¥). К сожалению, числа e с указанными свойствами тоже нет и не может быть: если e положительно, то число e/2 будет положительным числом, меньшим e. (Согласно обычным свойствам неравенств для всякого а
> 0 выполняются неравенства 0 < а/2 < а
). Так что если мы не хотим отказываться от привычных нам свойств действительных чисел (например, от возможности разделить любое число на 2 или от возможности умножить любое неравенство на положительное число), но хотим иметь бесконечно малые числа, то приведенное определение бесконечной малости не годится.
Более изощренное определение бесконечной малости числа e > 0, которое мы будем использовать в дальнейшем, таково. Будем складывать число e с самим собой, получая числа e, e + e, e + e+ e, e + e + e +e и т. д. Если все полученные числа окажутся меньше 1,
то число e и будет называться бесконечно малым. Другими словами, если e бесконечно мало, то сколько раз ни откладывай отрезок длины e вдоль отрезка длины 1, до конца не дойдешь. Наше требование к бесконечно малому e можно переписать и в такой форме (поделив на e): 1<1/e, 1+1<1/e, 1+1+1<1/e,…
Таким образом, если число число e бесконечно мало, то число 1/e бесконечно велико в том смысле, что оно больше любого из чисел 1, 1+1, 1+1+1, 1+1+1+1 и т. д. Так что если мы начнем измерять отрезок длиной 1/e с помощью эталона длины (т.е. откладывая последовательно отрезки единичной длины), то процесса измерения никогда не закончим.
Из вышеизложенного следует, что существование бесконечно малых противоречит так называемой аксиоме Архимеда, которая утверждает, что для любых двух отрезков А
и В
можно отложить меньший из них (А)
столько раз, чтобы в сумме получить отрезок, превосходящий по длине больший отрезок (В).
Приведенная формулировка касается отрезков; если считать (как это обычно делается), что длины отрезков являются числами, мы приходим к такой формулировке аксиомы Архимеда: для любых двух чисел а
и b
,
для которых 0 < а <
b
,
одно из неравенств а + а >
b
,
a
+ а +
a
>
b
,
... обязательно выполнено. В дальнейшем, говоря об аксиоме Архимеда, мы будем иметь в виду именно эту формулировку. Из нее видно, что в множестве действительных чисел (где эта аксиома выполняется) бесконечно малых нет: чтобы убедиться в этом, достаточно положить a
=
e
,
b
=1.
Мы увидим в дальнейшем, что на самом деле аксиома Архимеда равносильна утверждению об отсутствии бесконечно малых элементов, не равных нулю.
Вывод – если мы хотим рассматривать бесконечно малые, нужно расширить множество R действительных чисел до некоторого большего множества *R. Элементы этого нового множества будем называть гипердействительными числами.
В нем аксиома Архимеда не выполняется и существуют бесконечно малые (в смысле последнего определения) числа — такие, что сколько их ни складывай с собой, сумма будет все время оставаться меньше 1. Подобно тому как обычный (или стандартный) математический анализ занимается изучением множества действительных чисел R, нестандартный анализ изучает множество гипердействи-тельных чисел *R. Полученные при этом результаты используются для исследования свойств R. (Таким образом могут быть получены “нестандартные” доказательства свойств обыкновенных действительных чисел.)
Порядок на R архимедов, а на *R неархимедов: это значит, что в R аксиома Архимеда выполняется, а в *R не выполняется. По этой причине стандартный (обычный) анализ, изучающий R, называется еще архимедовым,
а нестандартный анализ, изучающий *R, называют неархимедовым.
Для построения нестандартного анализа необходимо расширить множество действительных чисел до более широкого множества гипердействительных чисел.
Но прежде поговорим о самих действительных числах и их происхождении.
До сих пор мы предполагали известным понятие действительного числа. Понятие действительного числа имеет долгую историю, начавшуюся еще в древней Греции (о чем напоминает название “аксиома Архимеда”) и закончившуюся лишь вXIX веке. Самой первоначальной и основной числовой системой является, конечно, система натуральных чисел. Натуральных чисел, однако, оказывается мало: пытаясь решить уравнение 3 + х
= 2 в натуральных числах, мы обнаруживаем, что оно не имеет решений и наше желание определить операцию вычитания оказывается неудовлетворенным. Поэтому мы расширяем множество натуральных чисел до множества целых чисел. В этой процедуре для нас сейчас важно следующее: каким образом мы определим сложение и умножение на целых числах? То, что 2 + 2 == 4, можно увидеть, сложив две кучи по два яблока в одну. Но почему мы считаем, что (-2)+(-2)=(-4)? Почему мы считаем, что (-1)(-1)=1?
Эти вопросы не так тривиальны, как может показаться. Найти правильный ответ будет легче, если сформулировать вопрос иначе: что плохого произойдет, если мы будем считать, например, что (-1)(-1)=(-1)? Ответ прост: в этом случае хорошо известные свойства сложения и умножения натуральных чисел (коммутативность, ассоциативность и др.) не будут выполняться для целых чисел. Можно показать, что обычное определение операций над отрицательными числами единственно возможное, если мы хотим сохранить привычные свойства операций сложения и умножения.
Тут следует остановиться: какие же именно свойства сложения и умножения мы хотим сохранить? Ведь если бы мы хотели сохранить все свойства, то введение отрицательных чисел было бы не только излишне, но и вредно: свойство “уравнение х+3=2
не имеет решений”, верное для натуральных чисел, становится неверным для целых! Если же мы ничего не хотим сохранить, то задача становится столь же легкой, сколь и пустой: можно определить операции с отрицательными числами как угодно.
Возвращаясь к истории развития понятия числа, мы видим, что введение отрицательных чисел не доставляет полного удовлетворения: уравнение 2x=3 по-прежнему не имеет решения. Это побуждает ввести рациональные (дробные) числа. Но и этого недостаточно: от рациональных чисел приходится перейти к действительным. В результате получается последовательность множеств NÌZÌQÌR (натуральных, целых, рациональных и действительных чисел; А
Ì
В
означает, что всякий элемент множества А
принадлежит множеству B
. В этой последовательности каждое следующее множество включает в себя предыдущее, при этом имевшиеся в предыдущем операции продолжаются на следующее, более широкое, множество, сохраняя свои полезные свойства.
Мы хотим продолжить эту последовательность еще на одни член, получив последовательность NÌZÌQÌRÌ*R, где *R – множество гипердействительных чисел. Новый шаг расширения будет иметь много общего с предыдущими: мы продолжим на *R имеющиеся в R операции, сохранив их полезные свойства. Но будут и 2 важных отличия.
Во-первых, если расширение (переход от Rк *R) можно выполнить многими различными способами: можно построить существенноразличные множества *R, ни одно из которых ничем не выделяется среди остальных. В то жо время, все предыдущие шаги нашего расширения числовой системы от N к R были в некотором смысле однозначны.
Во-вторых, есть различие в наших целях. Если прежде (двигаясь от N к R) мы строили новую числовую систему прежде всего для того, чтобы исследовать ее свойства и ее применения, то построенная система *R предназначается не столько для того, чтобы исследовать ее свойства, сколько для того, чтобы с ее помощью исследовать свойства R. Впрочем различие и не так велико: и раньше расширение числовой системы было одним из способов получения новых знаний о старых объектах. Кроме того, множество *R можно рассматривать, быть может, как соответствующее физической реальности в не меньшей (и даже в большей) степени, чем R.
Итак, необходимо расширить множество R действительных чисел до большего множества *R, содержащего бесконечно малые, сохранив при этом все полезные свойства R. Центральный вопрос состоит в том, какие именно свойства действительных чисел мы желаем сохранить. Ответим на этот вопрос не сразу, начав с наиболее простых свойств действительных чисел.
Прежде всего, мы хотим, чтобы гипердействительные числа можно было складывать, умножать, вычитать и делить, чтобы эти операции обладали обычными свойствами, называемыми «аксиомами поля». Сформулируем их.
Среди гипердействительных чисел должны быть выделены числа 0 и 1; определены операции сложения, умножения взятия противоположного, а также операция взятия обратного. При этом должны выполняться такие свойства:
(1) a+b=b+a (2) a+(b+c)=(a+b)+c (3) a+0=a (4) a+(-a)=0 (5) ab=ba
(6) a(bc)=(ab)c (7) a*1=a (8) a(b+c)=ab+ac (9) a*(1/a)=1 при a<>0.
Множество с операциями, обладающими этими свойствами, называется полем. Требования (1)-(9) можно сформулировать так: *R должно быть полем.
Кромеарифметических операций, зададим на гипердействительных числах порядок. Для любых двух различных гипердействительных чисел должно быть определено какое из них больше. При этои должны выполняться такие свойства:
(10) если a>b, b>c, то a>c
(11) если a>b, то a+c>b+cдля любого с
(12) если a>b, c>0, то ac>bc
если a>b, c<0, то ac<bc
Поле, в котором введен порядок с такими свойствами, называется упорядоченным полем
. Требования (10)-(12) можно сформулировать так: *R должно быть упорядоченным полем.
Мы хотим, чтобы среди гипердействиетльных чисел были все действительные. При этом операции и порядок на R и на *R должны быть соглсованы. Это требование можно сформулировать так: упорядоченное поле *R должно быть расширением упорядоченного поля R.
Что же нового мы ожидаем от *R? Бесконечно малых.
Определение. Элемент e>=0 упорядоченного поля называется бесконечно малым, если e<1, e+e<1. e+e+e<1 и т.д. Отрицательное e называется бесконечно малым, если –e бесконечно мало.
Существование ненулевых бесконечно малх равносильно нарушению аксиомы Архимеда для гипердействительных чисел. Упорядоченные поля, в которых справедлива аксиома Архимеда и нет бесконечно малых, называют архимедово упорядоченными. Те поля, в которых аксиома Архимеда невернаи есть бесконечно малые, называют неархимедово упорядоченными (неархимедовым).
В этих терминах треюования можно сформулировать так: система гипердействительных чисел должна быть неархимедово упорядоченным полем, являющимся расширением упорядоченного поля действительных чисел.
4. ГИПЕРДЕЙСТВИТЕЛЬНАЯ ПРЯМАЯ
Предположим, что неархимедово расширение упорядоченного поля действительных чисел существует. Исследуем его свойства.
Пусть *R – неархимедово расширение R. Его элементы называются гипердействительными числами. Среди них содержатся и все действительные числа. Для отличия тех гипердействительных чисел, которые не являются действительными (элементы R) назовем их стандартными, а остальнгые гипердействительные (элементы *R\R) – нестандартными. Тогда бесконечно малые являются нестандартными, так как среди действительных чисел бесконечно малых нет.
Бесконечно малые положительные числа меньше всех стандартных положительных чисел. Аналогичным образом отрицательные бесконечно малые числа больше всех стандартных отрицательных чисел. Таким образом, если пытаться изобразить бесконечно малые числа на числовой прямой, то пришлось бы втиснуть их настолько близко к нулю, чтобы все положительные стандартные числа оказались справа, а отрицательные – слева.
Указанное свойство может служить определением бесконечной малости: если число e>0 меньше всех стандартныхположительных чисел, то оно бесконечно мало.
Определение. Гипердействительное число А>0
называется бесконечно большим,
если А>1, А>1+1, А > 1+1+1, .…(Отрицательное число В
называется бесконечно большим, если таков его модуль)
Положительное бесконечно большое число А
больше любого стандартного.
Аналогичным образом всякое отрицательное бесконечно большое гипердействительное число меньше любого стандартного.
Определение.
Гипердействительные числа, не являющиеся бесконечно большими, будут называться конечными.
Утверждение.
Если s – конечное гипердействительное число, то найдутся стандратное v и бесконечно малое e, для которых s=v+e. Такое представление единственно.
Определение.
Стандартной частью st(x) конечного гипердействительного числа x называется такое стандартное v, что x=v+e для бесконечно малого e.
Гипердействительная прямая разбивается на 3 части (слева направо): отрицательные бесконечно большие, конечные, положительные бесконечно большие. Рассмотрим «конечную часть» гипердейсьвительной прямой. Рядом с каждым стандартным действительным числом а
расположено множество бесконечно близких к нему гипердействительных чисел, для которых а
является стандратной частью. Это множество называют монадой стандартного числа а
. Множество конечных гипердействительных чисел разбито на непересекающиеся классы – монады, соответствующие стандартным действительным.
Сумма и разность бесконечно малых бесконечно малы, произведение бесконечно малого и конечного гипердействительных чисел бесконечно мало.
Определение. Два гипердействительных числа называются бесконечно близкими, если их разность бесконечно мала.
Из приведенных выше свойств бесконечно малых следует, что отношение бесконечной близости есть отношение эквивалентности. Это означает, что отношение бесконечно близости рефлексивно (каждое x бесконечно близко самому себе), симметрично (если x бесконено близко к y, то y бесконечно близко к x) и транзитивно (если x бесконено близко к y, а y бесконечно близко к z, то x бесконечно близко к z). Всякое отношение эквивалентности разбивает множество, на котором оно определено на непересекающиеся классы, причем любые два элемента одного класса эквивалентны, а любые два элемента разных классов не эквивалентны. В частности, наше отношение разбивает *R на непересекающиеся классы, причем элементы одного класса бесконечно близки друг к другу, а элементы разных классов — нет. Классы, содержащие стандартные действительные числа, представляют собой упоминавшиеся выше «монады».
5. ПРИМЕР НЕАРХИМЕДОВОЙ ЧИСЛОВОЙ СИСТЕМЫ
До сих пор речь шла о гипердействительной прямой (а точнее, любом неархимедовом расширении упорядоченного поля действительных чисел). Возникает вопрос – существует ли хотя бы одно такое распшрение. Построим такое расширение.
Основная идея этого построения может быть описана в одной фразе так: у нас нет объектов, но есть имена для них; так объявим же имена объектами! Эта (часто применяемая в математической логике) идея конкретизируется в нашем случае следующим образом.
Мы знаем, что в нашем (пока еще не построенном и неизвестно существующем ли) расширении должно быть хотя бы одно бесконечно малое положительное гипердействительное число. Обозначим его через e. Поскольку гипердействительные числа можно умножать друг на друга (и, в частности, на действительные числа), то наряду с e в нашем расширении будут и числа 2e, 0,5e и вообще все числа вида a
e, где а
– произвольное стандартное действительное число. Более того, число e можно умножать и на себя, поэтому в нашем расширении будут иметься e2
, e3
, 2e2
, Зe2
+2e+1, ... и вообще все гипердействительные числа вида Р(e), где P – многочлен со стандартными действительными коэффициентами.
Множество чисел такого вида замкнуто относительно сложения, вычитания и умножения. Это значит, что, складывая, вычитая или перемножая два числа такого вида, мы вновь получим число такого же вида. Но для гипердействительных чисел определено еще и деление. Поэтому в расширении будут и числа вида Р(e)/Q(e), где P и Q – многочлены со стандартными действительными коэффициентами. После этого мы получаем множество гипердействптельных чисел, замкнутое относительно всех арифметических операций: складывая, вычитая, умножая или деля две дроби указанного вида по обычным правилам, получаем дробь такого же вида.
Таким образом, не имея пока искомого расширения, мы уже смогли назвать некоторые его элементы, дать им имена. Этими именами являются записи вида P(e)/Q(e), где e – некоторый символ. Более того, мы можем судить и о том, какая из двух записей обозначает большее число. В самом деле, достаточно уметь определять, обозначает ли данная запись положительное, отрицательное или нулевое число (поскольку а >
b
тогда и только тогда, когда a
-
b
>0
). Знак дроби можно определить по знакам числителя и знаменателя, следовательно достаточно уметь определять знак P(e), где Р – многочлен. Это делается так. Легко видеть, что знак величины a0
+a1
e+… совпадает со знаком a0
, если a0
<>0. В
самом деле, добавка a1
e+… бесконечно мала, а складывая положительное (отрицательное) число с бесконечно малым, мы получаем положительное (соответственно отрицательное) число. Возможен, однако, случай a0
=0. Будем считать для определенности, что e – положительное бесконечно малое. Вынесем из нашего многочлена e в наибольшей возможной степени, т. е. представим его в виде ek
(ak
+ak
+1
e+…), где ak
уже отлично от 0. Знак всего выражения определяется знаком выражения в скобках (при умножении на положительное число знак не меняется), а знак выражения в скобках (как мы уже видели) определяется знаком числа ak
..
По существу, мы уже построили искомое неархимедово расширение. Нужно лишь посмотреть на наши рассуждения с другой позиции. До сих пор выражения P(e)/Q(e) рассматривались нами как имена «настоящих» гипердействительных чисел (взятых неизвестно откуда). А теперь они станут самими гипердействительными числами. Рассмотрим формальные выражения вида P(e)/Q(e), где e – некоторый символ, P, Q – многочлены с действительными коэффициентами, причем Q<>0. Провозглашая, что объектами, а в данном случае гипердействительными числами, мы объявим имена, а в данном случае выражения, или записи вида P(e)/Q(e), мы были не совсем точны. Дело в том, что, очевидно, две различные записи могут выражать одно и то же число (иными словами, быть двумя различными именами одного и того же числа): так, например, естественно считать, что запись (e2
-1)/(e-1) выражает то же самое число, что и (e+1)/1.
Будем называть два выражения P(e)/Q(e) и R(e)/S(e) эквивалентными, если P(e)*S(e)=R(e)*Q(e) (равенство понимается как равенство многочленов, т. е. как равенство коэффициентов при одинаковых степенях). Легко проверить, что это определение действительно задает отношение эквивалентности, разбивающее все выражения вида P(e)/Q(e) на классы. Эти классы мы и будем называть гипердействительными числами. Сложение, вычитание, умножение и деление гипердействительных чисел определяются по обычным правилам. Так, например, если a – класс, содержащий P/Q, а b – класс, содержащий R/S,
то их суммой называется класс, содержащий (PS+RQ)/SQ, а произведением — класс, содержащий PR/QS.
Легко проверить, чтоэто определение корректно, т. е. не зависит от выбора элементов P/Q в классе a и R/S в классе b (в результате получаются разные представители одного и того же класса). Аналогичным образом можно определить взятие обратного и противоположного, нуль и единицу. Нетрудно проверить, что все аксиомы поля при этом будут выполнены. Изложенная конструкция хорошо известна в алгебре: построенное поле называется полем рациональных функций с коэффициентами в R и обозначается R(e).
Осталось определить только порядок, указав, как выбрать из двух различных гипердействительных чисел (т. е. из двух различных классов эквивалентных дробей) большее. Для этого нужно вычесть одно число из другого и определить, будет ли разность (отличная от нуля, поскольку числа различны) положительной или отрицательной. Чтобы определить, будет ли отличное от нуля число a положительным или отрицательным, возьмем его представитель P/Q.
Здесь P, Q отличны от 0 (Q отлично от нуля по определению, Р – потому что, по нашему предположению, разность не равна 0). Вынесем в числителе и в знаменателе e в наибольшей возможной степени:
P=ek
(ak
+ak
+1
e+…), Q=el
(bl
+bl
+1
e+…), ak
, bl
отличны от 0.
Число a будет положительным, если ak
, bl
имеют одинаковые знаки, и отрицательным, если они имеют разные знаки.
Построенное упорядоченное поле R(e) можно рассматривать как расширение поля R: достаточно отождествить действительное число х
с классом эквивалентных дробей, содержащим дробь x/1. Осталось лишь показать, что аксиома Архимеда не выполняется, предъявив бесконечно малый элемент. Этим элементом будет, конечно, e (точнее, класс, содержащий e/1). В самом деле, e+e+ ... +e <1, так как разность 1-ne положительна (знак определяется свободным членном, а 1 > 0).
Искомое расширение построено.
6. НОВЫЕ ТРЕБОВАНИЯ К ГИПЕРДЕЙСТВИТЕЛЬНЫМ ЧИСЛАМ И ОСНОВНАЯ ГИПОТЕЗА
Мы построили неархимедово расширение R(e) поля действительных чисел. Новым требованием к гипердействительным числам яляется следующее. Нужно уметь вычислять «значения» стандартных функций (заданных первоначально как функции с действительными аргументами и значениями) на гипердействительных аргументах. Другими словами, для каждой функции f: R®R необходимо иметь ее «гипердействптельный аналог» *f: R®R. При этом, значения *f на стандартных числах должны совпадать с соответствующими значениями функции f. Другими словами, *f должно быть продолжением f. Такие аналоги были у нас для операций сложения, вычитания, умножения и деления. Но этого мало: нужны такие аналоги и для других функций.
Итак, для каждой стандартной функции f (функции с действительными аргументами и значениями) нам нужно иметь ее гипердействительное продолжение *f. Если от *f ничего не требовать, то это тривиально: можно считать, что во всех действительных точках *f принимает те же значения, что и f, а в нестандартных точках *f имеет какие угодно значения (например, нули). Ясно, однако, что от такого продолжения никакого толку нет:
Нужно выделить некоторый класс свойств — класс тех свойств, которые мы хотим сохранить. Правильный выбор этого класса имеет решающее значение для успеха нашего построения системы гипердействительных чисел. Если этот класс будет слишком узок, то от наличия продолжений *f не будет пользы. Если же, напротив, он будет слишком широк, то сама возможность построения системы гипердействительпых чисел и определения продолжений окажется под угрозой.
Наша главная задача – описать, какие свойства стандартных функций мы хотим сохранить при переходе от действительных чисел к гипердействительным. Есть две возможности это сделать. Первая возможность состоит в применении методов математической логики. Можно сказать, что при переходе от действительных чисел к гипердействительным сохраняются все свойства, которые можно выразить на «языке первого порядка». Вторая возможность позволяет обойтись более «кустарными» средствами и не прибегать к сведениям из логики. Конечно, при этом мы будем испытывать некоторые неудобства, использовать обходные маневры и т. п., но зато не потребуется знакомство с математической логикой.
Мы предполагаем, что помимо поля R действительных чисел имеется более широкое упорядоченное поле *R гипердействительных чисел, включающее R как подмножество (еще раз подчеркнем, что существование *R с нужными свойствами является пока только гипотезой, а не доказанным фактом). Пусть для каждой функции f с действительными аргументами имеется ее естественное распространение, ее «гипердействительный аналог» — функция с гипердействительными аргументами и значениями. При этом функция f может быть функцией не только одного действительного аргумента, но и двух, трех и т. д.; функция *f, разумеется, должна иметь то же самое число аргументов. Для простоты мы пока не будем рассматривать частичных функций и будем считать, что f (соответственно *f) определена при всех действительных (соответственно гипердействительных) аргументах. Сформулируем теперь наше требование («аналоги обладают теми же свойствами, что и исходные функции») более точно.
Будем рассматривать системы уравнений вида t=sи неравенств вида t¹s, левые и правые части которых содержат какие-то действительные функции действительных аргументов, действительные константы и переменные — что-нибудь вроде
sin(cos(x))=y+exp(z), z¹y-2x, [z]=y
Эта система содержит переменные x, y, z, одноместные функции sin,cos,exp [ ] (целая часть), двуместные функции (сложение, вычитание, умножение) и константу 2 (константы для единообразия мы будем считать функциями нуля аргументов). Все входящие в систему функции имеют по нашему предположению гипердействительные аналоги. Обозначим их *sin, *cos, *exp, *[ ], *+, *–, и напишем систему
*sin(*cos(x))=y*+*exp(z), z¹y*–2*x, *[z]=y
которую естественно назвать «гипердействительным аналогом исходной».
В качестве возможных значении переменных этой системы могут фигурировать любые гипердействительные числа. Тем самым приобретает смысл вопрос о наличии или отсутствии гипердействительных решений этой системы. Поскольку мы предполагаем, что входящие в нее функции являются продолжениями соответствующих функций действительного аргумента, то всякое (действительное) решение исходной системы будет одновременно решением новой системы. Таким образом, если исходная система имеет решения, то и ее гипердействительный аналог имеет решения. Мы потребуем и обратного:
всякая система уравнений и неравенств, гипердействительный аналог которой имеет (гипердействительные) решения, должна иметь действительные решения.
Введем понятие терма. Выберем счетный набор символов, элементы которого будем называть переменными.
Будем называть термом
любую переменную, любое действительное число, а также любое выражение вида f(t1
, ..., tn
), где f – функция п
действительных аргументов, а t1
, ..., tn
– построенные ранее термы.
Системой (точнее, системой уравнений и неравенств) назовем конечный набор записей вида t=sили t¹s, где t, s – термы. Определим теперь понятие решения
системы. Еслп в терм подставить действительные числа вместо переменных, то он приобретет некоторое действительное значение. Решение системы – это такой набор значений переменных, при котором левая и правая части любою равенства I
t=s, входящего в систему, приобретают одно и то же значение, а левая и правая части любого неравенства t¹s, входящего в систему,— разные.
По нашему предположению всякая функция с действительными аргументами н значениями имеет гппердействительный аналог («естественное продолжение»). Понятие гипердействительного аналога легко распространяется на термы — чтобы получить аналог терма t,
надо просто заменить все входящие в него функции на их гипердействительпые аналоги. Проделав эту операцию со всеми термами, входящими в какую-то систему S,
мы получим систему *S, которую естественно также назвать гипердействительным аналогом системы S.
Поскольку в нее входят функции с гипердействительными аргументами и значениями, вместо переменных можно подставлять произвольные гипердействительные числа. Гппердейст-вительным решением системы *S назовем такой набор гипердействительпых значений переменных, при которых выполнены все входящие в нее уравнения и неравенства. Теперь можно сформулировать наше требование к системе гипердействительных чисел и к гипердействительным аналогам следующим образом.
Пусть
S
— произвольная система уравнений и неравенств, *
S
– ее гипердействительный аналог. Если *
S
имеет (гипердействительные} решения, то
S
должна иметь действительные решения.
Возможность построения неархимедова упорядоченного расширения *R поля R и таких гипердействительных аналогов *f для всех действительных функций f, которые бы удовлетворяли сформулированному требованию, остается пока всего, лишь гипотезой. (Мы будем называть эту гипотезу Основной гипотезой.)
7. СЛЕДСТВИЯ ОСНОВНОЙ ГИПОТЕЗЫ
Приведем несколько примеров, показывающих, какие следствия можно вывести из сформулированной Основной гипотезы. Оказывается, что несмотря на то, что сформулированное нами требование одновременной разрешимости систем уравнений и неравенств кажется весьма частным, оно имеет самые разнообразные следствия и достаточно для обоснований значительной части рассуждений с ги-пердействительными числами.
Пример 1. Пусть f – функция одного действительного аргумента, принимающая только значения 0 и 1. Докажем, что функция *f принимает только значения 0 и 1. Для этого рассмотрим систему
f(x)
¹
0, f(x)
¹
1,
которая по предположению не имеет действительных решений. Следовательно, не имеет (гипердействительных) решений и ее аналог — система
*f(x)
¹
0, *f(x)
¹
1,
Пример 2. Пусть f и g – функции одного действительного аргумента, причем множества их нулей совпадают. (Множество нулей функции – множество тех зна-чений аргумента, при которых значение функции равно 0) В этом случае и множества гипердействительных чисел, являющиеся множествами нулей функций *f и *g, совпадают. Докажем это. В самом деле, каждая из систем
(1) f(x)=0, g(x)
¹
0,
(2) g(x)=0, f(x)
¹
0,
не имеет действительных решений. Следовательно, не имеют гииердействительных решений и их аналоги. Потому любой гипердействительный нуль функции *f обя-зан (чтобы не быть решением аналога системы (1)) быть нулем и для *g и наоборот.
Этот пример позволяет определить гипердействительные аналоги не только для функций, но и для множеств.
Пусть А
– произвольное множество действительных чисел. Рассмотрим произвольную функцию f, для которой А
– множество нулей. (Такая есть: достаточно положить, например, f(x)=0 при х
Î
А
и f(x)=1 при xÏA). Рассмотрим теперь гипердействительный аналог *f функции f и множество *А
его (гипердействительных) нулей. Как мы видим, множество *А
не зависит от выбора функции f. Его мы и назовем гипердействительным аналогом множества А.
Пример 3. Мы можем теперь разрешить включать системы наряду с равенствами t=s и неравенствами t¹s и записи видаsÎA,
где s представляет собой терм, а А –
множество действительных чисел. При этом решениями будут такиенаборы (действительных или гипердействительных) значений переменных, при которых выполнены все равенства и неравенства, а значение s принадлежит множеству А.
Гипердействительным аналогом sÎA будет *sÎ*A, где *s – гипердей-ствительный аналог терма s,
а *
A
— аналог множества А
(в указанном смысле). Таким образом, у всякой системы равенств, неравенств и включений (т. е. записей вида sÎA)
появляется гипердействительный аналог. Для таких систем остается в силе свойство одновременной разрешимости: если гипердействительный аналог системы имеет (гипердействительные) решения, то исходная система имеет (действительные) решения. Чтобы увидеть это, достаточно заменить s
Î
A
на a
(
s
)=0,
где a
– функция с действительными аргументами и значениями, множеством нулей которой является A
. Аналогичным образом можно добавлять в систему и утверждения вида sÏA (что заменяется на a
(
s
)
¹
0
).
Пример 4. Пусть А
– пустое множество. Докажем, что *A – пустое множество.
В самом деле, система
х
Î
А
не имеет действительных решений, поэтому и система х
Î
*А
не имеет (гипердействительных) решений. Рассмотрев систему х
Ï
А,
получаем аналогичным образом, что если А
содержит все действительные числа, то *А
содержит все гипердействительные числа. Таким образом, гипердействительным аналогом множества R будет множество *R, так что наши обозначения согласованы.
Вдальнейшем, вместо того чтобы говорить о системе S и ее действительных решениях, а также о системе *S и ее гипердействительных решениях, будем говорить о действительных и гипердействительных решениях системы S (говоря о гипердойствительных решениях системы S,
мы на самом деле будем иметь в виду гипердействительные решения системы *S).
Пример 5. Если A=BÇC, то *A=*BÇ*C. В самом деле, каждая из систем
х
Î
B
, х
Î
С, х
Ï
А;
х
Î
A
, х
Ï
B
;
х
Î
A
, х
Ï
С.
не имеет действительных, и, следовательно, гипердействительных решений. (Точнее, следовало бы говорить об аналогах этих систем) Отсюда получаем, что *В
Ç*С
Ì
*
A
(первая система), *АÌ*С (вторая) и *AÌ*C (третья), откуда вытекает, что *AÌ*BÇ*C.
Наши требования к системе гипердействительных чисел состояли из двух частей. Во-первых, *R должно быть упорядоченным неархимедовым полем, расширяющим R. Во-вторых, должны существовать аналоги для всех действительных функций, удовлетворяющие требованию одновременной разрешимости систем уравнений. Эти требования оказываются избыточными:
тот факт, что гипердействительные аналоги сложения, умножения и т. п. превращают *R в поле, можно вывести из требования одновременной разрешимости систем уравнений.
8. ПОСТРОЕНИЕ СИСТЕМЫ ГИПЕРДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Рассмотрим вопрос о существовании гипердействительных чисел. Точнее этот вопрос следует сформулировать так: можно ли построить расширение множества действительных чисел, для которого выполнялась бы Основная гипотеза. Основная гипотеза требует, чтобы:
(1) имелось некоторое множество R
,
для которого RÌ*R;
(2) для каждой функции f: Rn
®R имелась некоторая функция *f: *Rn
®*R являющаяся продолжением исходной;
(3) любая система уравнений и неравенств, гипердействительный аналог который имеет (гипердействительные) решения, имела действительные решения;
(4) *R содержало бесконечно малые элементы, отличные от нуля.
Покажем, каким образом этим требованиям можно удовлетворить. Рассмотрим один из возможных вариантов перехода от Q (множества рациональных чисел) к R (множеству действительных чисел). Рассматриваются всевозможные фундаментальные последовательности рациональных чисел, т. е. такие последовательности, что для любого e > 0 существует отрезок длины e, содержащий все члены последовательности, кроме конечного числа. Две такие последовательности xn
и yn
называют эквивалентными,
если xn
–yn
стремится к 0 при п
®
¥
. Это отношение эквивалентности разбивает фундаментальные последовательности на классы, которые и называются действительными числами.
Мы достигнем цели, если от последовательностей перейдем к классам последовательностей, считая, что две последовательности x0
,x1
,x2
,…. и y0
,y1
,y2
,… задают одно и то же гипердействительное число, если xn
=yn
“для большинства натуральных чисел n”.
Для наглядности будем представлять себе, что проводится голосование по вопросу “считать ли последовательности xn
и yn
совпадающими”. В нем голосующими являются натуральные числа, причем число п
голосует “за”, если
xn
=yn
, и “против”, если xn
¹yn
.
Будем считать последовательности xn
и yn
совпадающими, если большинство натуральных чисел голосуют за это. Нужно объяснить лишь, какова система подсчета голосов, т. е. какие множества натуральных чисел мы считаем “большими” (содержащими “большинство” натуральных чисел), а какие “малыми” (содержащими “меньшинство” натуральных чисел). Перечислим те свойства, которым должна удовлетворять система подсчета голосов, т. с. деление множеств натуральных чисел на большие и малые.
1. Любое множество натуральных чисел является либо большим, либо малым. Ни одно множество не является большим и малым одновременно. (Голосование должно всегда давать ответ.)
2. Множество всех натуральных чисел большое, пустое множество малое. (Предложение, за которое голосуют все, принимается.)
3. Дополнение (до N) любого малого множества является большим, дополнение любого большого множества – малым. (Из двух противоположных законопроектов получает большинство голосов ровно одни.)
4. Любое подмножество малого множества является малым, любое надмножество большого множества – большим. (Утратив часть голосов, отвергнутый законопроект не может стать принятым.)
5. Объединение двух малых множеств является малым, пересечение двух больших множеств является большим. (Если каждая из двух групп голосующих не образует большинства, то они и вместе не образуют большинства (“невозможность коалиции”); если каждая из групп составляет большинство, то голосующие, входящие одновременно в обе группы, уже составляют большинство.)
Эти требования весьма сильны. Чтобы понять это, рассмотрим случай конечного множества голосующих (получающийся заменой N на некоторое конечное множество М).
Можно ли тогда удовлетворить этим требованиям? Один способ почти очевиден. Выберем одного из “голосующих” т
Î
М
и назовем большими все множества, содержащие m, а малыми – все множества, не содержащие т (
“диктатура” m).
При таком определении легко проверить все свойства 1–5. Оказывается, что этим исчерпываются все возможности удовлетворить требованиям 1–5 для случая конечного множества M. В самом деле, , пусть имеется разбиение всех множеств на большие и малые, удовлетворяющее требованиям 1–5. Рассмотрим тогда все большие множества и выберем из них множество M0, содержащее наименьшее возможное число элементов (среди больших множеств). Множество M0 непусто. Если оно содержит ровно один элемент m, то в силу свойства 4 все множества, содержащие т,
будут большими, а в силу свойства 3 все множества, не содержащие m, будут малыми. Осталось показать, что M0 не может содержать более одного элемента. В самом деле, в этом случае его можно было бы разбить на две непустые непересекающиеся части M1 и M2. Эти части должны быть малыми (так как содержат меньше элементов, чем M0), а их объединение M0 является большим, что противоречит требованию 5.
Оказывается, однако, что при счетном числе голосующих возможны системы голосования, удовлетворяющие требованиям 1–5 и не сводящиеся к упомянутому тривиальному случаю. Другими словами, можно так разбить все подмножества натурального ряда на большие и малые, чтобы выполнялись свойства 1–5 и любое одноэлементное множество было малым. Тогда (в силу свойства 5) и любое конечное множество будет малым, а (в силу свойства 3) всякое множество с конечным дополнением (до N) – большим. Таким образом, к требованиям 1–5 можно без противоречия добавить и такое:
6. Всякое конечное множество является малым, всякое множество с конечным
дополнением — большим. (При голосовании мнение конечного числа голосующих несущественно.)
Разбиение всех подмножеств натурального ряда на большие и малые, удовлетворяющее требованиям 1–6, называется нетривиальным ультрафильтром
на множестве натуральных чисел.
Покажем теперь, что такое разбиение позволяет построить систему гипердействительных чисел, удовлетворяющую требованиям Основной гипотезы. Итак, пусть фиксировано разбиение, удовлетворяющее требованиям 1–6. Назовем две последовательности xn
и yn
эквивалентными,
если множество тех n, при которых xn
=yn
является большим. В силу требования 2 всякая последовательность эквивалентна самой себе.
Мы видим, что введенное отношение рефлексивно, симметрично (это очевидно из определения) и транзитивно и, следовательно, разбивает все последовательности действительных чисел на классы эквивалентности, т. е. такие классы, что любые две последовательности одного класса эквивалентны, а любые две последовательности из разных классов – нет. Эти классы мы и назовем гипердействительными числами. Что еще нам нужно? Нужно, чтобы множество действительных чисел было подмножеством множества гипердействительных. Нужно уметь для каждой функции с действительными аргументами и значениями строить ее гипердействительный аналог. Нужно проверить, что любая система уравнений и неравенств, гипердействительный аналог которой имеет гипердействительные решения, имеет действительные решения. И, наконец, нужно убедиться, что среди гипердействительных чисел (рассматриваемых как упорядоченное поле) существуют бесконечно малые, отличные от нуля.
Чтобы сделать R подмножеством *R, отождествим каждое действительное число х
с последовательностью х, х, х,
..., точнее, с содержащим ее классом. При этом разным действительным числам соответствуют разные классы: х,
x
,х
… не эквивалентно у,у,
y
... (множество тех n, при которых n-е члены совпадают, пусто и, следовательно, является малым).
Пусть f: R®R – функция с действительными аргументами и значениями. Определим ее гипердействительныйаналог *f: *R® *R. Пусть x – произвольное гипердействительное число, т.е. класс эквивалентных последовательностей действительных чисел. Рассмотрим произвольную последовательность x0
, x1
, x2
,… из этого класса и применим f ко всем ее членам. Класс, содержащий полученную последоваетльность f(x0), f(x1), f(x2), … и будем считать значением f на х.
Полученный класс не зависит от выбора последовательности x0
, x1
, x2
,… в классе x (определение корректно).
Аналогично определяются и гипердействительные аналоги для функций нескольких аргументов. Пусть, например, f – функция двух действительных аргументов с действительными значениями. Определим ее гипердействительный аналог *f. Чтобы применить *fк двум гипердействительным числам х
и y, возьмем последовательности x0
, x1
, x2
,… и y0
, y1
, y2
,… , им принадлежащие, и в качестве *f(х, у)
рассмотрим класс последовательности f(x0,y0), f(x1,y1), f(x2,y2),… Определение корректно.
Нужно проверить, что построенное гипердействительные аналоги будут продолжениями исходных функций с действительными аргументами и значениями. Это очевидно следует из определений. Проверим теперь, что всякая система уравнений и неравенств, имеющая гипердействительные решения, имеет и действительные решения. Пусть, например, система
f(g(x,y),z)=z, h(x)¹h(y)
имеет гипердействительные решения x, y, z. Рассмотрим последовательности x0,x1,x2,…; y0,y1,y2,…; z0,z1,z2,…, принадлежащие соответствующим классам эквивалентности. Тогда g(x0,y0), g(x1,y1),… принадлежит классу g(x,y),
а f(g(x0,y0),z0), f(g(x1,y1),z1),… – классу f(g(x,y),z). Поскольку x,
y,
z
по предположению являются решениями системы, то f(g(xn
,yn
),zn
)=zn
для большинства п.
Поскольку h(x)¹h(y), последовательности h(x0),h(x1),… и h(y0),h(y1),… не эквивалентны и множество тех п,
при котором h(xn
)=h(yn
) малое. Тогда множество тех п,
при котором h(xn
)¹h(yn
) является большим. Так как пересечение двух больших множеств является большим, то множество тех n, при котором
f(g(xn
,yn
),zn
)=zn
, h(xn
)¹h(yn
)
является большим. Значит, оно непусто. Таким образом, система имеет и действительные решения.
Осталось проверить, что среди гипердействительных чисел существуют бесконечно малые, отличные от нуля. Положительным бесконечно малым гипердействительным числом будет, например, класс последовательности 1, 1/2, 1/3, .,. (или любой другой последовательности положительных действительных чисел, сходящейся к 0). Нам нужно проверить, что это гипердействительное число (обозначим его через e) положительно, но меньше любого стандартного положительного числа. Чтобы доказать это, мы должны вспомнить, как определяется порядок на множестве гипердействительных чисел. Он определяется в соответствии с общей схемой построения гипердействительного аналога для любого отношения на множестве действительных чисел. Нужно взять функцию f двух действительных аргументов, для которой свойства f(x,y)=0 и х
<у
равносильны, и рассмотреть ее гипердействительный аналог *f. Гипердействительное число х
называется меньшим гипердействительного числа у,
если *
f
(
x
,
y
)=0
. Посмотрим, что дает нам эта конструкция для построенной описанным способом системы гипердействительных чисел. Если х –
класс последовательности x0,x1,x2,…, а y – класс последовательности y0,y1,y2,…, то *f(x,y) есть класс последовательности f(x0,y0), f(x1,y1), f(x2,y2), … Равенство этого класса нулю (т. е. классу последовательности 0, 0, 0, ...) означает, что f(xn,yn)=0 для большинства n, т. е. что xn<yn для большинства п.
Таким образом, чтобы выяснить, верно ли х
<у
для гипердействительных чисел х
и y, нужно взять последовательности x0,x1,x2,…, и y0,y1,y2,… в классах х
и у
и выяснить, является ли множество тех п,
при которых xn<yn большим.
Нам нужно было проверить, что 0<e и что e<р
для любого стандартного положительного р
(e —класс последовательности 1, 1/2, 1/3, ...). Это просто:
0<e, так как 0<1/п
при всех п
(а множество N большое), e<р,
так как 1/n<р
для всех натуральных n, кроме конечного числа, а всякое множество с конечным дополнением малое (свойство 6 “системы подсчета голосов”). Отметим, что здесь мы впервые воспользовались свойством 6, до сих пор все наши рассуждения были справедливы и в случае “диктатуры” (когда большими считаются те и только те множества, которые содержат некоторое натуральное число N).
В этом случае две последовательности эквивалентны, если совпадают их N-е
члены, и все гипердействительные числа стандартны (класс последовательности x0,x1,x2,… совпадает со стандартным числом xN
).
ЛИТЕРАТУРА
1. Успенский В.А. Что такое нестандартный анализ? – М., Наука, 1987. – 128с.
2. Девис М. Прикладной нестандартный анализ. – М., Мир, 1980.
3. Успенский В.А. Нестандартный, или неархимедов, анализ. – М., Знание, 1983. 61 с. (Новое в жизни, науке, технике. Сер. “Математика, кибернетика” № 8 ).
4. Успенский В.А. Нестандартный анализ // Наука и жизнь, 1984. – №1. – с. 45-50.
5. Робинсон А. Введение в теорию моделей и математику алгебры. пер. с англ. – М., Наука, 1967.
|