План
Вступ
1 Означення невласних інтегралів
2 Обчислення
3 Приклади
Висновок
Список літератури
Вступ
Математика — одна з найдавніших наук, що зародилась на світанку цивілізації. Вона постійно збагачувалася, час від часу істотно оновлювалася і все більше утверджувалась як засіб пізнання закономірностей навколишнього світу. Розширюючи і зміцнюючи свої багатогранні зв'язки з практикою, математика допомагає людству відкривати і використовувати закони природи і є у наш час могутнім рушієм розвитку науки і техніки.
Саме нашому часу видаються особливо співзвучними пророчі слова великого Леонардо да Вінчі про те, що ніякі людські дослідження не можна назвати справжньою наукою, якщо вони не пройшли через математичні доведення.
Елементи інтегрального числення закладено у працях математиків Стародавньої Греції. Основні поняття і початки теорії інтегральногочислення, насамперед зв'язок його з диференціальним числення,а також застосування їх до розв'язування практичних задач, розроблені в кінці 17 ст. Ньютоном і Лейбніцем. Далі історичний розвитокінтегрального числення пов'язаний зіменами Л. Ейлера,О. Коші, Б. Рімана та інших вчених.
Інтеграл — одне з центральних понять математичного і всієї математики. Воно виникло у зв'язку з двома основними задачами:
1) про відновлення функції по заданій її похідній;
2) про обчислення площі, обмеженої графіком функції у=f(х), х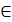 [a;b]прямими х = а, х = b і віссю Ох (подібні задачі дістаємо при обчисленні багатьох інших величин, наприклад роботи, яку виконує сила протягом деякого часу, тощо). Термін «інтеграл» ввів Я.Бернулі у 1690 р. Цікаво, що в історії математики цей термін пов’язують з двома латинськими словами: integro — відновляти та integer – цілий. [a;b]прямими х = а, х = b і віссю Ох (подібні задачі дістаємо при обчисленні багатьох інших величин, наприклад роботи, яку виконує сила протягом деякого часу, тощо). Термін «інтеграл» ввів Я.Бернулі у 1690 р. Цікаво, що в історії математики цей термін пов’язують з двома латинськими словами: integro — відновляти та integer – цілий.
Вказані дві задачі приводять до двох пов'язаних між собою видів інтегралів: невизначеного і визначеного. Вивчення властивостейі обчислення цих інтегралів і складають основну задачу інтегрального числення. Введений визначений інтеграл як границя інтегральних сум, передбачаючи при цьому, що відрізок інтегрування скінченний, а інтегральна функція на цьому відрізку обмежена. Якщо хоча б а з цих умов порушується, то наведене вище означення визначеного інтеграла стає неприйнятним: у випадку нескінченного проміжку інтегрування його не можна розбити на п частинних відрізків скінченної довжини, а у випадку необмеженої функції інтегральна сума явно не має скінченної границі. Узагальнюючи поняття визначеного інтеграла на ці випадки, приходимо до невласного інтеграла — інтеграла від функції на необмеженому проміжку або від необмеженої функції. Тому в цій курсовій роботі розглянемо невласні подвійні інтеграли.
Реклама

Метою роботи є вивчення умов існування, властивостей, методів обчислення невласних подвійних інтегралів.
Відповідно до мети поставлені наступні завдання:
1. Ввести поняття невласного подвійного інтегралу.
2. Навчитися класифікувати невласні подвійні інтеграли.
3. Визначити способи розв’язку невласного подвійного інтегралу.
1 Поняття невласного подвійного інтегралу
Поняття подвійного інтеграла узагальнюється на випадок необмеженої області, або на випадок необмеженої функції.
Зупинимося спочатку на випадку необмеженої області (Р).
Прикладом такої області може бути вся площина або її частина, яка знаходиться за деяким кругом або іншою обмеженою плоскою фігурою, який-небудь кут і тому подібне. Що стосується границі цієї області, то вона передбачається такою, що має площу 0 (наприклад, що складається з кусково-монотонних кривих ) у кожній обмеженій своїй частині. Нехай в області (Р)
задана деяка функція f(x,y)
, яку передбачимо інтегрованою в звичайному сенсі слова в кожній обмеженій і квадратичній частині області (Р).
Провівши допоміжну криву (К')
(теж з площею 0), відсічемо від області (Р)
обмежену зв'язну її частину (Р'),
в якій існує інтеграл:
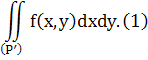
Будемо віддаляти криву (К)
всіма її точками в нескінченність, так, щоб найменша відстань R
від початку до точок цієї кривої зростала до нескінченності. Тоді відокремлена нею змінна область (Р')
поступово охоплюватиме всі точки області (Р)
: кожна точка з (Р)
належатиме (Р')
при достатньо великому R
.
Границя (скінченного або нескінченного) інтеграла
(1)при R
→∞називають (невласним
)
інтегралом від функції
f
(
х,у
) в необмеженій області (Р)
і позначають символом
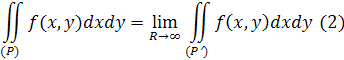
В разі існування скінченної границі інтеграл (2) називається збіжним,
в іншому випадку – розбіжним
. Функція, для якої інтеграл (2) збігається, називається інтегрованою
в області (Р).
У випадку додатної функції f(x,y)
досить, розглянувши яку-небудь певну послідовність, нескінченно віддалених кривих
Реклама

(К1
),(К2
),…,(К
n
)
,
…
і областей, що відсікаються ними
(
P
1
),(Р2
),…,(Р
n
),… ,
передбачити існування скінченної границі

щоб звідси вже випливала збіжність інтеграла (2).
Дійсно, яку б область (Р')
не відокремити кривою (
К'
)
від (Р),
при достатньо великому п
ця область цілком буде міститися в ( Р
n
),
так що
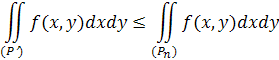
і, тим паче,
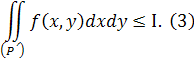
З іншого боку, по заданому 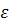 >0
можна знайти таке n
0
,
щоб було >0
можна знайти таке n
0
,
щоб було
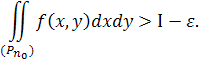
При достатньо великому R
, в свою чергу, область (Р')
охопить (
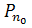 ),
отже ),
отже
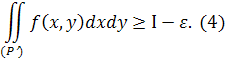
Нерівності (3) і (4) в сукупності доводять, що число І
задовольняє визначенню подвійного інтеграла.
Далі, якщо зберегти відносно функції f(x,y)
попередні припущення, то із збіжності інтеграла від
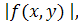 поширеного на необмежену область (Р)
, випливає збіжність подібного ж інтеграла для функції
f(x,y). поширеного на необмежену область (Р)
, випливає збіжність подібного ж інтеграла для функції
f(x,y).
Для доведення цього розглянемо дві функції:
f
+
(
x
,
y
)
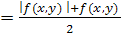 ,
f
-
(
x
,
y
) ,
f
-
(
x
,
y
)
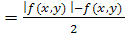 ; ;
очевидно,
f
+
(
x
,
y
)
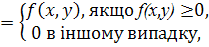
f
-
(
x
,
y
)
=
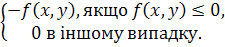
З інтегрованості функції 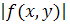 випливає збіжність інтегралів для функцій випливає збіжність інтегралів для функцій
f
+
(
x
,
y
)
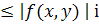 f
-
(
x
,
y
) f
-
(
x
,
y
)
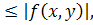
а отже, і для функції
f
(
x
,
y
)=
f
+
(
x
,
y
)-
f
-
(
x
,
y
)
Вельми чудовий той факт, що і навпаки: із збіжності
інтеграла від функції
f(x,y), поширеного на необмежену область (Р),
випливає збіжність інтеграла і для
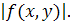 Цьому твердженню немає аналога в теорії одновимірних невласних інтегралів: відомо, що можуть існувати і інтеграли, що не абсолютно збіжні. Цьому твердженню немає аналога в теорії одновимірних невласних інтегралів: відомо, що можуть існувати і інтеграли, що не абсолютно збіжні.
Теорема про абсолютну збіжність невласного подвійного інтеграла.
Кожнийзбіжний інтеграл
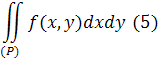
необхідно і абсолютно збіжний,
тобтоодночасно з нимзбіжний і інтеграл
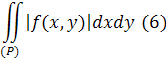
Для доведення цієї теореми будемо користуватись методом доведення від супротивного. Візьмемо послідовність областей {(Р
n
)
}, 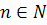 так, щоб вони, розширюючись, поступово охоплювали всю область (Р),
матимемо так, щоб вони, розширюючись, поступово охоплювали всю область (Р),
матимемо
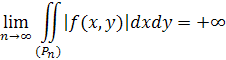
Ми можемо припустити, що при кожному значенні п
виконується нерівність
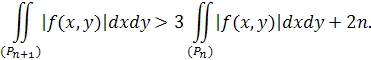
Цього можна досягти, розріджуючи (в разі потреби) послідовність {(Р
n
)
}, тобто витягуючи з неї часткову послідовність і заново нумеруючи її.
Позначимо через (
pn
)
різницю областей (
P
n
+1
)
і (
Pn
),
очевидно, що
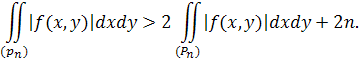
Але
|
f
(
x
,
y
)|=
f
+
(
x
,
y
)+
f
-
(
x
,
y
),
Отже
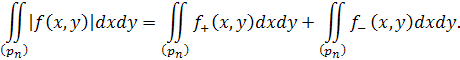
Нехай з двох інтегралів з права більшим буде, наприклад, перший. Тоді
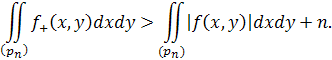
Замінюючи подвійний інтеграл зліва досить близькою до нього нижньою сумою Дарбу, збережемо нерівність
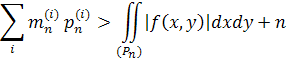
В цій сумі залишаємо лише ті доданки, яким відповідають
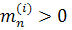 позначивши сукупність відповідних елементів позначивши сукупність відповідних елементів 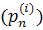 через ( через (
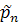 ),
отримаємо, ),
отримаємо,
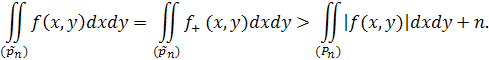
Позначимо через (P
̃
n
)
область, складену з (Р
n
)
і (
р̃
n
);
такяк
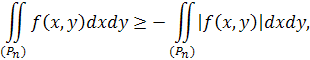
то, складаючи почленно цю нерівність з попередньою, знайдемо
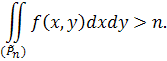
Область (р̃
n
),
а з нею і (Р̃
n
),
можна деформувати так, щоб з останньої вийшла зв'язна область (Р'
n
),
і притому за площею, що настільки мало різниться від (Р̃
n
), що все ж зберігається нерівність
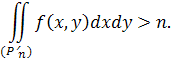
Цього легко досягти, сполучаючи відірвані частини області вузькими «коридорами» з довільно малою загальною площею.
Звідси вже ясно, що інтеграл (5) не може бути збіжним, всупереч припущенню; це протиріччя і доводить теорему.
Відмітимо, що принципова різниця між одновимірним і двовимірним випадками пов'язана саме із завершальною частиною проведеного міркування. Незв'язну лінійну область, що складається з окремих проміжків, вже не можна довільно малою деформацією перетворити в цілісний проміжок.
Доведена теорема зводить питання про збіжність і обчислення невласного інтеграла від довільної функції до такого ж питання для додатної (від’ємної) функції.
Інтеграли
від необмежених функцій.
Нехай функція f
(
x
,
y
)
задана в обмеженій області (Р),
але сама виявляється необмеженою в околі окремих точок М1,
М2,…
в будь - якій частині області (Р),
що не містить цих точок.
Виділимо тепер особливі точки М1,
М2,…
оточивши їх кривими (К
1
),
(К
2
)
,
...
Якщо видалити з області (Р)
обмежені цими кривими околи особливих точок, то ми отримаємо область (Р'),
для якої по припущенню інтеграл
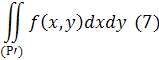
є збіжний. Будемо «стягувати» криві (
К
1
)
,(
K
2
),
...
у вказані точки так, щоб найбільша з відстаней точок цих контурів (К)
до відповідних точок M
(позначимо її через ρ) прямувала до нуля . Відмітимо, що при цьому і площі даних околів (менші ніж πρ2
), також прямуватимуть до нуля.
Інтеграл
(
невласний
) від необмеженої функції f(x,
y
) по області (Р) визначається як
границя
інтеграла
(7) при
ρ→0:
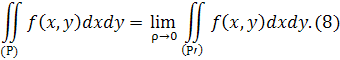
Особливі точки можуть лежати і уздовж деяких особливих ліній, які ми завжди будемо передбачати такими, що мають площу 0. В цьому випадку доводиться оточувати ці лінії околами, що «стискуються» до них.
Проте точна характеристика граничного процесу, що мається на увазі тут, вимагає ще деяких пояснень. Нехай особлива лінія (l
) оточена околом з контуром (К).
Якщо узяти точку А
на (К),
то з відстаней цієї точки від різних точок В
на (l
) існує найменша, ρА
;з іншого боку, якщо змінювати положення А
на (К),
то зі всіх ρА
знайдеться найбільше, ρ. Це число в деякому розумінні і характеризує міру віддаленості контура (К)
від кривої (l
), і граничний процес виражається умовою: ρ → 0. (За наявності декількох кривих під ρ зрозуміло найбільше з подібних чисел.) Тут також можна довести, що разом з ρ прямує до нуля і площа даного околу.
Нарешті, визначення невласного інтеграла легко поширюється на випадок необмеженої області і визначеної в ній функції, яка на скінченній відстані має особливі точки.
З а у в а ж е н н я. Якби при побудові невласного інтеграла, окрім особливих точок (або ліній), ми стали виділяти і деякі такі точки (або лінії), які на ділі не є особливими, то ця обставина ніяк не могла б відбитися ні на існуванні, ні на величині тієї межі, якою представляється інтеграл. Насправді, припустимо, наприклад, до особливих точок додається неособлива точка А
і, крім того, що необхідне визначення невласного інтеграла, - ми виділяємо ще околицю цієї точки А.
Алепоблизу А
функція обмежена, і інтеграл по згаданому околі, разом з її площею, прямує до 0.
Приведення подвійного інтеграла до повторного.
Обмежимося спочатку припущенням, що функція f(x,y)
невідємна. Якщо ця функція задана в необмеженій області будь-якої форми, то, вважаючи її додатною поза цією областю рівною нулю, завжди можна звести справу до випадку необмеженої прямокутної області. Припустимо, що йдеться про нескінченний в одному напрямі прямокутник [a
,
b
;
c
,+∞
] (a
,
b
,
c
-граничні числа, причому b
>
а).
Передбачимо, що в кожному граничному прямокутнику [а,
b
;
c
,
d
](при будь-якому d>c
)
існують як подвійний інтеграл, так і одновимірний інтеграл по y
-
обоє увласному сенсі, так що має місце формула
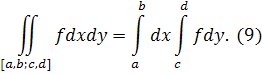
Бажаючи встановити подібну формулу для нескінченного прямокутника, тобто для випадку d
=+∞,
припустим
о
,
що збігається повторний інтеграл
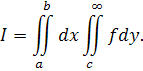
Оскільки при будь-якому d>c
маємо
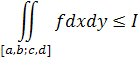
то по попередньому матеріалузвідси вже випливає збіжність подвійного інтеграла
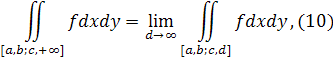
який, вочевидь, не перевершує I
. Залишається лише довести, що подвійний інтеграл рівний I
.
Якщо інтеграл 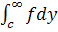 є функцією від х,
інтегровану у власному сенсі, отже, обмежену деякою постійною L
,
то і поготів є функцією від х,
інтегровану у власному сенсі, отже, обмежену деякою постійною L
,
то і поготів
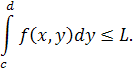
В такому разі
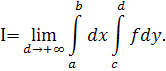
Зіставляючи це з (9) і (10), приходимо до необхідного результату.
Встановлений факт зберігає силу і в тому випадку, якщо інтегралI
збігається, як невласний. Припустимо, наприклад, b
єєдиною особливою точкою для функції 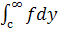 від х.
Тоді подоведеному, при від х.
Тоді подоведеному, при 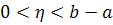 , ,
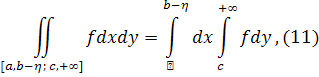
і обидві частини рівності при 𝜂→0 прямують до І
. Беручи до уваги, що
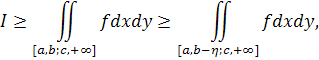
знову говоримо про рівність подвійного і повторного інтегралів за прямокутником [а,
b
;
c
,+∞
].
Відмітимо, що якби невласний повторний інтеграл мав нескінченне значення, то, як видно з попередніх двох співвідношень, таке ж було б і значення подвійного інтеграла.
Отже, маємо подібно (9)
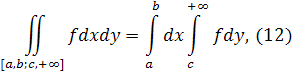
причому з існування повторного інтеграла з права вже випливає існування подвійного інтеграла. Рівність зберігається навіть у тому випадку, коли інтеграл з права рівний +∞.
Звернемося, нарешті, до розгляду прямокутника [а,
+∞;
c
,+∞
], що тягнеться в нескінченність по двох взаємно перпендикулярних напрямках. І тут передбачимо, що в кожному кінцевому прямокутнику [а,
b
;
c
,
d
](при будь-яких b>a
і
d>c
)існують у власному сенсі подвійний інтеграл і простий інтеграл по y.
Для даного випадку також може бути встановлена формула
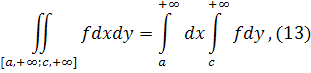
у припущенні, що повторний інтеграл з права збігається. Це легко випливає з (12) переходом до межі при b
→+∞
,
на кшталт того, як вище ми (12) отримали з (11). І тут подвійний інтеграл виявляється рівним +∞
, якщо таке значення повторного інтеграла.
Скажемо тепер декілька слів відносно випадку, коли функція f(x,
y
)
міняє знак; обмежимося для визначеності формулою (12). У граничному прямокутнику [а,
b
;
c
, d
](при d>c
)ми зберігаємо колишні припущення, але, разом із збіжністю повторного інтеграла від самої функції:
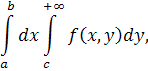
ми цього разу допустимо збіжність повторного інтеграла і від її абсолютної величини:

Тоді подібні ж повторні інтеграли існуватимуть і для функцій f
+
(x
,
y
)
і f
-
(x
,
y
)
. Застосовуючи до цих негативних функцій порізно доведену формулу (12) і віднімаючи результати, переконаємося в справедливості цієї формули і для даної функції f(x,
y
).
2 Обчислення
Заміна змінних
в невласних інтегралах.
Нехай в площинах ху
і ξ𝜂 маємо, відповідно, обмежені області (D) і (∆), зв'язані формулами перетворення:
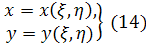
або зворотними їм:
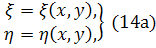
з дотриманням всіх умов.
Нехай, далі, в області (D) задана функція 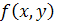 неперервна усюди, за винятком граничного числа окремих точок або навіть кривих, де вона звертається в нескінченність. неперервна усюди, за винятком граничного числа окремих точок або навіть кривих, де вона звертається в нескінченність.
Покажемо, що за цих умов рівність
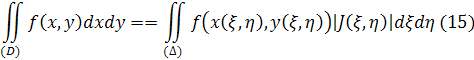
має місце, якщо лише збігається один з цих інтегралів; збіжність іншого звідси вже випливатиме.
Дійсно, якщо особливі точки і особливі лінії першого інтеграла в області (D) виділити їх околами, то відповідними околами в області (∆) виділяться особливі точки і особливі лінії другого інтеграла. Нехай при цьому вийдуть область (D') на площині ху
і область (∆') на площині ξ𝜂. Тоді
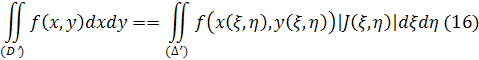
Передбачаючи неперервність відповідності між областями (D) і (∆) в обидві сторони , легко побачити, що при «стисканні» околів на площині ху
до оточених ними точок або ліній такий же процес відбуватиметься і з околами на площині і навпаки. Звідси ясно, що, переходячи в попередньому співвідношенні до границі, із збіжності одного з інтегралів ми дійсно можемо говорити про збіжність іншого і в той же час про наявність рівності (15).
Можна було б допустити навіть, що в окремих точках області (∆) або уздовж окремих лежачих в ній ліній (не пересікають раніше розглянутих в цій області особливих ліній) звертається в нескінченність якобіан J(ξ,𝜂), а з ним і підінтегральна функція другого з інтегралів. Хоча відповідні точки і лінії на площині ху
не є особливими для першого інтеграла, але їх виділення, по зауваженню, не створює скрути, так що при нових припущеннях висновок залишається в силі.
Відмітимо ще, що і в даному випадку часто доводиться стикатися з порушенням неперервності або взаємної однозначності відповідності в окремих точках або уздовж окремих ліній.
Нарешті, звернемося до випадку, коли хоч одна з областей (D),
(∆)є необмеженою.
Якщо ці області тягнуться в нескінченність, причому точки їх, що знаходяться на кінцевій відстані, зв'язані відповідністю (14) або (14а), то, відокремивши (відповідними) кривими обмежені частини цих областей, (Dʹ) і (∆ʹ), ми при дотриманні вказаних вище умов матимемо рівність (16). Оскільки згадані криві, вочевидь, можуть віддалятися в нескінченність лише одночасно, то залишається лише перейти в (16) до межі, аби отримати (15), причому знову із збіжності одного з інтегралів випливає збіжність іншого.
Нехай тепер, скажімо, область (D) прямує в нескінченність, а область (∆) ні, і точки області (D) зв'язані відповідністю зі всіма точками області (∆), за винятком окремої точки (або кривої), яка, так би мовити, відповідає нескінченно видаленій частині контура області (D).
Відокремивши
кривою обмежену частину області (D), ми відповідній кривій в області (∆) виділимо згадану точку (або криву) і тим отримаємо області (Dʹ) і (∆ʹ), до яких вже прикладені колишні міркування. Відмітимо, що заміна змінних разом з переходом до повторного інтегралу є вельми зручним засобом для встановлення існування невласних подвійних інтегралів.
3 Приклади
1) Встановити умови збіжності інтегралів (m>0);
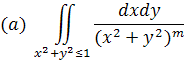
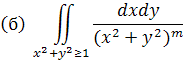
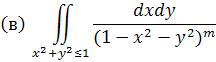
Рішення. У полярних координатах ці інтеграли зведуться до наступних:
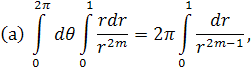
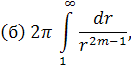
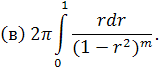
Вочевидь, умови збіжності будуть:
(а)m<1, (б) m>1, (в) m<1.
2) Аналогічне питання по відношенню до інтегралів (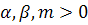 ) )
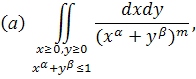
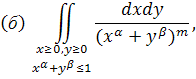
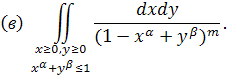
Вказівка. Вдатися до підстановки
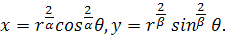
Відповідь. (а)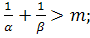 (б) (б)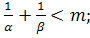 (в) (в) 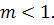
Ті ж відповіді вийдуть і у разі, коли зміна змінних в задачах 1), 2) обмежується сектором між променями θ = θ0
і θ = θ1
.
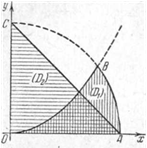
3) Якщо область (D1
) зміни змінних х
,y
криволінійний трикутник АОВ, обмежений відрізком АO осі х
, дугою ОВ параболи y
= х2
і дугою ВА кола x
2
+
y
2
= 1, то інтеграл
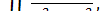
для якого початок як і раніше слугує особливою точкою, все ж існує (хоча не існує для круга!). Дійсно, при переходідо полярних координат інтеграл утворюється до вигляду
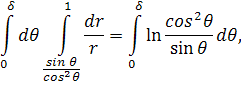
звідки і витікає сказане.
 4) Аналогічно, взявши за область трикутник АОС
(той же малюнок), можна встановити існування інтеграла 4) Аналогічно, взявши за область трикутник АОС
(той же малюнок), можна встановити існування інтеграла

для якого особливими будуть точки А і С
. Так як в полярних координатах рівняння лінії АС
буде 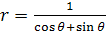 , то запропонований інтеграл зводиться до наступного: , то запропонований інтеграл зводиться до наступного:
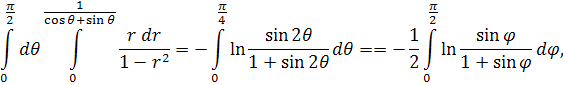
який явно існує.
5)На порівнянні з інтегралами, розглянутими в 1),ґрунтується наступна ознака збіжності:
Якщо (
D
)
є: (а) обмежена область, що містить початкову точку, або (б) область, що тягнеться в нескінченність, не містить початкової точки, то інтеграл від функціїf
(
x
,
y
)
в (
D
)
збігається, оскільки f
(
x
,
y
)
в (
D
)
може бути представлена у вигляді
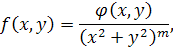
де 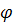 обмежена і, відповідно випадку,(а) т<
1 або (б) m
>1. обмежена і, відповідно випадку,(а) т<
1 або (б) m
>1.
Легко перефразувати цю ознаку для випадку, коли початкова точка замінена будь-якою точкою (х0
, у0
).
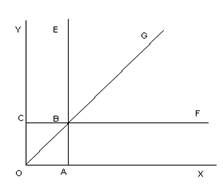
6) Перевірити збіжність подвійного інтеграла від функції
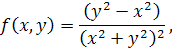
поширеного на: (а) трикутник ОВС
, (б) квадрат ОАВС,
(в)нескінченну смугу Y
СВЕ,
(г)нескінченний трикутник ЕВ
G
,
(д)нескінченний квадрат E
В
F
.
Через 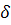 позначений кут променя OB
зполярною віссю. позначений кут променя OB
зполярною віссю.
Відповідь.
У випадках (а), (г) інтеграл не сходиться (тим більше це справедливо для випадків (б)і(д)!); у випадку (в) інтеграл збігається, він рівний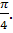
7) Подвійний інтеграл
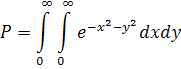
існує,або існує повторний:
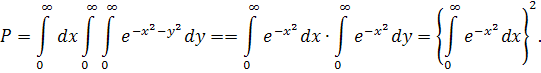
Його легко обчислити, якщо перейти до полярних координат; перший квадрант, на площині ху
перетвориться при цьому в смугу на площині r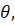 обмежену прямими обмежену прямими 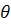 = 0, r = 0 і = 0, r = 0 і 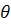 = =  . Таким чином, . Таким чином,
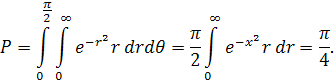
Тому, що
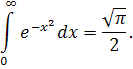
Відповідь.
Інтеграл рівний 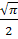 . .
Висновок
У цій курсовій роботі розглянуто означення і основні властивості невласного подвійного інтеграла, особливості і відмінності від інших визначених інтегралів.
Вказані задачі приводять до двох пов'язаних між собою видів інтегралів: невизначеного і визначеного. Вивчення властивостейі обчислення цих інтегралів і складають основну задачу інтегрального. числення. Введений визначений інтеграл як границя інтегральних сум, передбачаючи при цьому, що відрізок інтегрування скінченний, а інтегральна функція на цьому відрізку обмежена. Якщо хоча б одна з цих умов порушувалась, то наведене вище означення визначеного інтеграла стає неприйнятним: у випадку нескінченного проміжку інтегрування його не можна розбити на п частинних відрізків скінченної довжини, а у випадку необмеженої функції інтегральна сума явно не має скінченної границі. Узагальнюючи поняття визначеного інтеграла на ці випадки, приходимо до невласного інтеграла — інтеграла від функції на необмеженому проміжку або від необмеженої функції.
За допомогою курсової роботи ми навчилися визначати умови існування, методи, способи обчислення невласних подвійних інтегралів і розглянули деякі приклади. Отже, можемо стверджувати, що невласні подвійні інтеграли є самостійним інструментом для розв’язку певного класу задач.
Список літератури
1. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: А.С.К., 2001. - 648 с. .: іл.: іл.
2. Шкіль М. І. Математичний аналіз: Підручник: У 2ч. Ч.1- 3-тє вид., переробл. і доповн. – К .: Вища шк.. , 2005. – 447с.: іл.
3. Фіхтенгольц Г. М. Основи математичного аналізу. Том 1:Учебник. – М.:Печатный двор, 1957г. – 440с.:илл.
4. Фихтенгольц Г. М. Курс дифференциального и интегрального исчесления. Том 3: Учебн. пособиэ. – М.: Наука, 1969г. – 656с.:илл.
5. Лиман В.Ф., Власенко В.Ф., Петренко С.В., Одінцова О.О., Семеніхіна О.В. Вища математика: Навч. посібник. У2 ч. – Суми: ВТД «Університетська книга», 2005. – 614с.:іл.
6. Кудрявцев Л.Д. Курс математического анализа, т.2.  М.: Высшая школа, 1965. – 369с М.: Высшая школа, 1965. – 369с
7. Градштейнб Рыжик И.М. Таблицы интегралов, сумм, рядовпроизведений. М.: Наука, 1963 – 312с. М.: Наука, 1963 – 312с.
8. Давидов М.О. Курс математчного анализу. Ч. 1. – К.:Вища школа, 1990. – 350с.
9. Канторович Л.В., Акилов Г.Л. Функциональный анализ. – М.: ИЛ, 1961 – 321с.
|