Вариант 10
(для студентов, номера личных дел которых оканчиваются цифрой 0)
Контрольная работа №3
1. На первом станке обработано 20 деталей, из них семь с дефектами, на втором - 30, из них четыре с дефектами, на третьем - 50 деталей, из них 10 с дефектами. Все детали сложены вместе. Наудачу взятая деталь оказалась без дефектов.
Какова вероятность того, что она обработана на третьем станке?
Для решения этой задачи воспользуемся формулой Байеса:
Пусть Н1
, Н2
, … Нn
– полная группа попарно несовместных событий гипотезы, А – случайное событие, тогда:
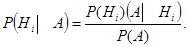
Введем гипотезы: Н1
– деталь обработана на первом станке, Н2
– деталь обработана на втором станке, Н3
– деталь обработана на третьем станке.
Введем событие А – купленная деталь оказалась без дефектов.
Тогда, по условию задачи:
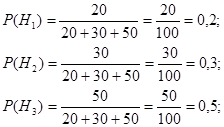
Так как на первом станке было изготовлено 20-7 = 13 деталей без дефектов, то
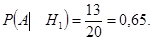
На втором станке было изготовлено 30-4 = 26 деталей без дефектов, то
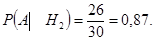
А на третьем станке было изготовлено 50-10 = 40 деталей без дефектов, то
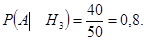
По формуле полной вероятности получаем:
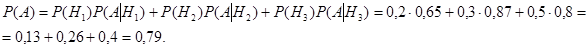
По формуле Байеса:
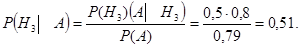
Ответ: 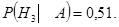
2. Сколько семян следует взять, чтобы с вероятностью не менее чем 0,9545 быть уверенным, что частость взошедших семян будет отличаться от вероятности р - 0,9 не более чем на 2% (по абсолютной величине)?
Решение
По условию, р=0,9, тогда q=0,1. Необходимо найти n. Необходимо, чтобы условие
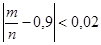
выполнялось с вероятностью, не меньшей, чем 0,9545. Раскроем модуль и найдем границы для m:
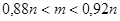
По теореме Муавра-Лапласа:
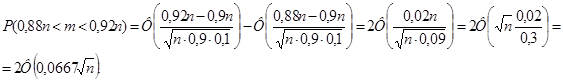
По условию, 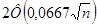 ≥0,9545. ≥0,9545.
По математико-статистическим таблицам находим приближенное значение функции Лапласса:
Ф(Х) = 0,9545, где Х=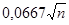 . .
Имеем: Ф(Х) = 2,0 , отсюда
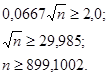
Итак, следует взять не менее 900 семян.
3. Завод «Пино» (г. Новороссийск) отправил в Москву 2000 бутылок вина « Каберне». Вероятность того, что в пути может разбиться бутылка, равна 0,002.
Какова вероятность того, что в пути будет разбито не более пяти бутылок?
Если проводится n независимых испытаний, в каждом из которых событие А может наступить с одной и той же вероятностью, тогда вероятность Рn
(m) того, что событие наступило m раз в этой серии испытаний можно найти:
Р(А) = 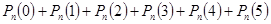 , ,
так как число n=2000 велико, а вероятность р=0,002 мала, то найдем:
Реклама

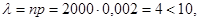 то воспользуемся формулой Пуассона: то воспользуемся формулой Пуассона:
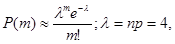
Искомая вероятность приближенно равна:
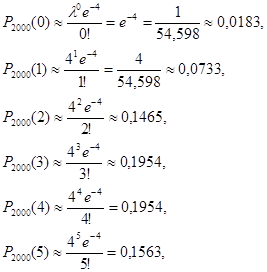
P = P2000
(0)+ P2000
(1)+ P2000
(2)+ P2000
(3)+ P2000
(4)+ P2000
(5)≈0,0183+0,0733+0,1465+0,1954+0,1954+0,1563 = 0,7852
Ответ: Р≈0,7852
4. Одна из случайных величин (X) задана законом распределения:
а другая (У) имеет биномиальное распределение с параметрами п=2,р=0,4.
Составить закон распределения их разности. Найти математическое ожидание и дисперсию этой случайной величины.
Найдем закон распределения для величины (Y):
| y |
0 |
1 |
2 |
| p |
p0
=0,36 |
p1
=0,48 |
p2
=0,16 |
Z11
= X1
- Y1
= 0-0 = 0; p(Z11
) = 0,2·0,36=0,072;
Z12
= X1
- Y2
= 0-1 = -1; p(Z12
) = 0,2·0,48=0,096;
Z13
= X1
- Y3
= 0-2 = -2; p(Z13
) = 0,2·0,16=0,032;
Z21
= X2
- Y1
= 1-0 = 1; p(Z11
) = 0,3·0,36=0,108;
Z22
= X2
- Y2
= 1-1 = 0; p(Z11
) = 0,3·0,48=0,144;
Z23
= X2
- Y3
= 1-2 = -1; p(Z11
) = 0,3·0,16=0,048;
Z31
= X3
- Y1
= 3-0 = 3; p(Z11
) = 0,5·0,36=0,018;
Z32
= X3
- Y2
= 3-1 = 2; p(Z11
) = 0,5·0,48=0,024;
Z33
= X3
- Y3
= 3-2 = 1; p(Z11
) = 0,5·0,16=0,08.
Итак, закон распределения разности имеет вид:
| Z |
-2 |
-1 |
0 |
1 |
2 |
3 |
| P |
0,032 |
0,096+0,048=0,144 |
0,072+0,144=0,216 |
0,108+0,08=0,188 |
0,24 |
0,18 |
Мат. ожидание:
М(Z) = -2·0,032-1·0,144+0·0,216+1·0,188+2·0,24+3·0,18= -0,02+0,48+0,54 = 1
Проверка:
М(Х) = 0,3+1,5 = 1,8
М(Y) = np = 0,8
M(X-Y) = M(X) – M(Y) = 1,8-0,8 = 1.
Дисперсия:
D(Z) = M(Z2
)-[M(Z)]2
M(Z2
)=0,128+0,144+0+0,188+0,96+1,62 = 3,04
D(Z) = 3,04-1 = 2,04.
5. Полагая, что длина изготавливаемой детали есть нормально распределенная случайная величина с математическим ожиданием М{Х) = 10 и средним квадратическим отклонением δ = 2, найти вероятность того, что длина наугад взятой детали заключена в интервале (5; 6).
В каких границах (симметричных относительно М(Х)) будет заключена длина наугад взятой детали с вероятностью 0,95?
1. 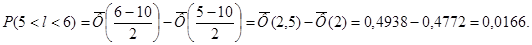
2 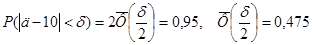
Используя таблицу значений нормированной функции Лапласса, имеем:
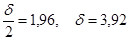
Список использованной литературы
1. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. — 2-е изд., перераб. и доп.— М.: ЮНИТИ-ДАНА, 2004. - 573 с.
|