Електричнi кола при синусоїднiй дiї
Зміст
1. Змiнний струм та його основнi характеристики
2. Синусоїдний струм та його основнi параметри
3 Подання синусоїдних коливань у виглядi проекцiй векторiв, що обертаються
4. Синусоїдний струм в опорi
5. Синусоїдний струм в iндуктивностi
6. Синусоїдний струм в ємності
На рис.1 зображено часовi дiаграми миттєвих значень струму, значення якого змiнюються за часом. Друга та третя дiаграми вiдповiдають перiодичному струмовi.
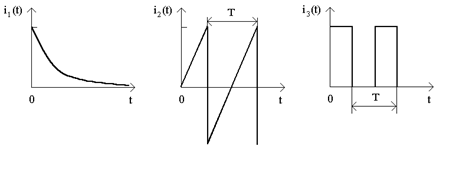
Рисунок 1
Перiодичний струм (напруга, ЕРС) - електричний струм, миттєвi значення якого повторюються через однаковi iнтервали часу.
Перiод T
- найменший iнтервал часу, через який миттєве значення перiодичного електричного струму (ЕРС, напруги) повторюється.
Частота електричного струму F
(f
) - величина, обернена до перiоду електричного струму. Одиницi вимiру - 1/с (Гц), кГц, МГц.
Змiнний струм (напруга) - перiодичний струм (напруга), середнє значення якого за перiод дорiвнює нулю:
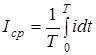 . .
Пульсний струм - перiодичний струм, середнє значення якого за перiод не дорiвнює нулю. На рис.1 на другiй дiаграмi показано змiнний струм, на третiй - пульсний струм.
Дiюче (ефективне) значення перiодичного струму - середньоквадратичне значення струму за перiод. Аби з'ясувати це поняття, розглянемо вплив перiодичного струму i
та постiйного струму I
на один i той самий постiйний резистор R
за час t
= T
.
Енергiя, що видiляється постiйним струмом на опорi R
за час перiоду змiнного струму T
, визначається за формулою:
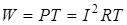 . .
При змiнному струмi за перiод Т
витрачається енергiя 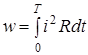 . Дiюче значення струму знайдемо за умови рiвностi W
= w
: . Дiюче значення струму знайдемо за умови рiвностi W
= w
:
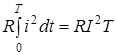 ; ; 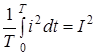 ; ;
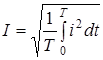 , (1) , (1)
де i
- миттєве значення перiодичного струму; I
- дiюче значення.
Отже, дiючим значенням перiодичного струму називається таке значення постiйного струму, яке за перiод змiнного струму при даному опорi видiляє стiльки ж тепла, скiльки видiляє перiодичний струм за той самий час.
Синусоїдний струм (напруга, ЕРС) - це електричний струм, який є синусоїдною функцiєю часу. У лiтературi також застосовується назва гармонiчний струм - який змiнюється за синусоїдним чи косинусоїдним законами. На рис.2 показано часову дiаграму синусоїдного струму, миттєве значення якого визначається за формулою:
Реклама

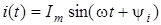 , ,
де 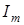 - амплiтуда; - амплiтуда; 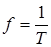 - частота, Гц; - частота, Гц; 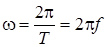 - кутова частота, Рад/с; - кутова частота, Рад/с; 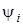 - початкова фаза, Рад. - початкова фаза, Рад.
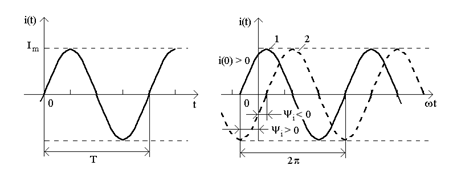
а) б)
Рисунок 2
Початкова фаза синусоїдного електричного струму - значення фази синусоїдного струму в початковий момент часу (t
=0). Iнакше, початкова фаза вiдповiдає абсцисi найближчої точки переходу з вiд'ємної пiвхвилi до додатної. На рис.2а початкова фаза коливання дорiвнює нулю, на рис.2б перша крива має початкову фазу 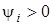 ( (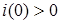 ), а друга крива - ), а друга крива - 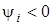 ( (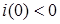 ). ).
Якщо розглядати змiнний струм, який змiнюється за косинусоїдним законом 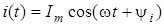 , то як початкова фаза використовується абсциса найближчого додатного максимуму (рис.3а). Рис.3б iлюструє спiввiдношення початкових фаз при синусоїднiй та косинусоїднiй формах запису: , то як початкова фаза використовується абсциса найближчого додатного максимуму (рис.3а). Рис.3б iлюструє спiввiдношення початкових фаз при синусоїднiй та косинусоїднiй формах запису:
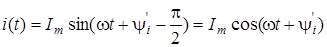 . .
Таким чином, при переходi вiд синусоїдної до косинусоїдної форми запису початкова фаза зменшується, при зворотньому переходi - збiльшується.
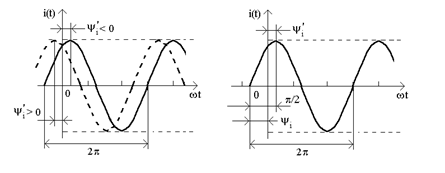
а) б)
Рисунок 3
Нехай для деякої дiлянки електричного кола струм та напруга становлять: 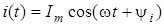 ; ; 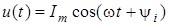 , тодi величина , тодi величина 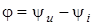 зветься зсувом фаз мiж напругою та струмом. Це поняття встановлюється для характеристики двох коливань однакової частоти. зветься зсувом фаз мiж напругою та струмом. Це поняття встановлюється для характеристики двох коливань однакової частоти.
Отже, зсув фаз мiж напругою та струмом - це алгебраїчна величина, що дорiвнює рiзницi фаз напруги та струму.
Якщо 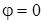 , коливання (тобто струм i напруга) синфазнi; , коливання (тобто струм i напруга) синфазнi;
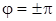 , коливання протифазнi; , коливання протифазнi;
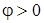 , , 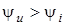 - напруга випереджає струм на величину - напруга випереджає струм на величину 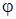 ; ;
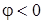 , , 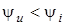 - напруга вiдстає вiд струму на величину - напруга вiдстає вiд струму на величину 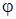 . .
Цi спiввiдношення справедливi також i для синусоїдної форми запису. Аргумент синуса (косинуса) являє собою миттєву або поточну фазу 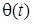 : : 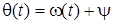 . Зв'язок мiж кутовою частотою . Зв'язок мiж кутовою частотою 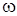 та поточною фазою та поточною фазою 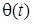 встановлюється спiввiдношеннями: встановлюється спiввiдношеннями:
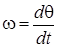 ; ; 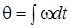 . .
На рис.4а показано залежнiсть 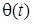 при при 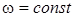 та та 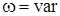 . .
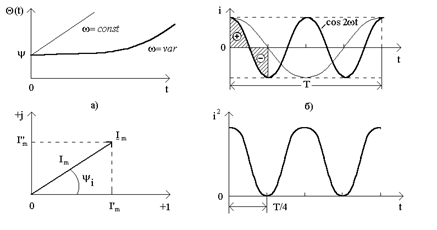
в) г)
Рисунок 4
Аби визначити дiюче значення синусоїдного струму, скористуємось формулою (1) та косинусоїдною формою запису 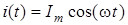 . .
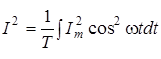 . .
Замiнимо 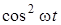 на на 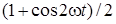 та проiнтегруємо здобутий вираз: та проiнтегруємо здобутий вираз:
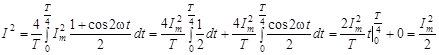 . .
Другий iнтеграл дорiвнює нулю, оскiльки функцiя 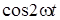 на iнтервалi на iнтервалi
0¸T
/4 має однаковi додатну та вiд'ємнi площi (рис.4б).
Таким чином, дiюче значення пов'язане з амплiтудним: 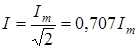 , тобто амплiтудне значення завжди бiльше, нiж дiюче. Для дiючих значень також виконується закон Ома: , тобто амплiтудне значення завжди бiльше, нiж дiюче. Для дiючих значень також виконується закон Ома:
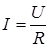 ; ; 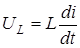 ; ; 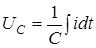 . .
Дiюче значення синусоїдного струму характеризує його енергетичну дiю. Вольтметри та амперметри у колах змiнного струму показують дiюче значення ЕРС, напруги та струму. Наприклад, якщо амплiтуда напруги у колi U
= 311 В, то вольтметр на затискачах кола покаже 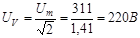 . .
Для розрахунку електричних кiл синусоїдного струму застосовують метод комплексних амплiтуд (або символiчний метод), який дозволяє розраховувати цi кола алгебраїчним способом, аналогiчно колам постiйного струму. Комплексний метод оснований на замiнi синусоїдних функцiй часу векторами, що обертаються.
Реклама

Вiдомо, що кожна точка на комплекснiй площинi визначається вектором, початок якого знаходиться в т.0, а кiнець - у точцi, що вiдповiдає даному комплексному числу. Комплексне число можна виразити в трьох формах: у показниковiй -
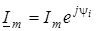 - -
де 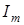 - модуль комплексного числа; - модуль комплексного числа; 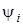 - аргумент (рис.4г); - аргумент (рис.4г);
у тригонометричнiй -
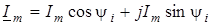 ; ;
в алгебраїчнiй -
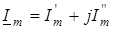 , ,
де 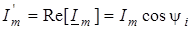 - дiйсна частина; - дiйсна частина;
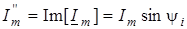 - уявна частина комплексного числа. - уявна частина комплексного числа.
Очевидно, що
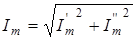 ; ; 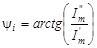 . .
Вектор, який обертається у додатному напрямi (тобто проти годинникової стрiлки) з кутовою швидкiстю 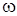 , можна подати як , можна подати як
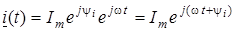 , (2) , (2)
де 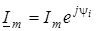 - комплексна амплiтуда; - комплексна амплiтуда; 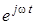 - оператор повороту (обертання). - оператор повороту (обертання).
Отже, комплексна амплiтуда синусоїдного струму (напруги) - це комплексна величина, модуль та аргумент якої дорiвнюють вiдповiдно амплiтудi та початковiй фазi синусоїдного струму (напруги).
Комплексна амплiтуда не залежить вiд часу, тобто є нерухомим вектором. Множення комплексної амплiтуди 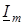 на на 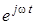 означає поворот вектора означає поворот вектора 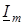 на комплекснiй площинi у позитивному напрямi. на комплекснiй площинi у позитивному напрямi.
Записуючи комплексно-часову функцiю (2) у тригонометричнiй формi
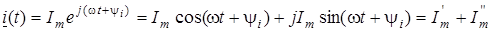 , ,
бачимо, що синусоїдна функцiя i
(t
) може розглядатися як уявна частина (2) або як проекцiя вектора 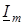 на уявну вiсь: на уявну вiсь:
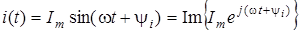 . .
Позначення Im
означає, що застосовується уявна частина ("image").
Аналогiчно косинусоїдна функцiя може розглядатися як дiйсна частина або проекцiя на дiйсну вiсь:
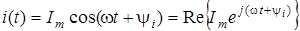 . .
Символ Re
означає операцію взяття дiйсної частини ("real").
Подання синусоїдної функцiї за допомогою векторiв та їх проекцiй iлюструється на рис.5.
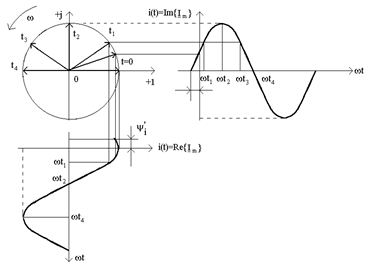
Рисунок 5
Розглянемо коло з резистором, який має активний опiр R. Нехай у колi протікає струм 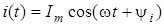 . Тодi за законом Ома напруга на затискачах резистора становить: . Тодi за законом Ома напруга на затискачах резистора становить:
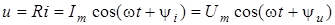 . .
Як бачимо, 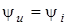 ; ; 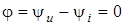 , тобто напруга i струм у колi з активним опором збiгаються за фазою. , тобто напруга i струм у колi з активним опором збiгаються за фазою.
Крiм того, при проходженнi синусоїдного струму крiзь опiр не тiльки миттєвi значення, але й амплiтуди та дiючi значення пов'язанi за законом Ома:
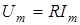 ; ; 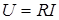 . .
Подамо миттєвi значення напруги та струму через комплекснi амплiтуди:
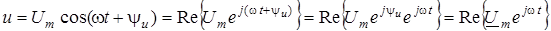 ; ;
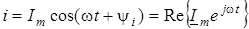 . .
Пiдставимо цi значення до виразу 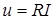 : :
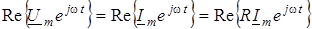 . .
Якщо рiвнi мiж собою реальнi частини, то рiвнi й вектори: 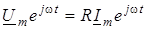 . Скоротивши на множник . Скоротивши на множник 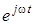 , матимемо , матимемо
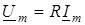 - (3) - (3)
закон Ома в комплекснiй формi.
Запишемо комплекснi дiючi значення струму та напруги:
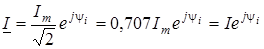 ; ; 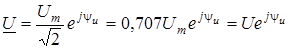 . .
На рис.6 зображено вектори  , , 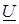 , , 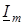 , , 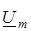 на комплекснiй площинi. на комплекснiй площинi.
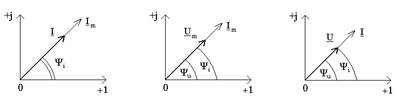
Рисунок 6
Визначимо миттєву потужнiсть, яка витрачається в опорi. При цьому врахуємо, що 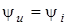 . .
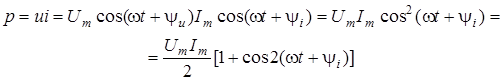 . .
Оскiльки 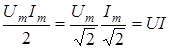 , отримуємо , отримуємо
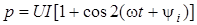 . .
Залежнiсть миттєвих значень u
, i
, p
від t
(або 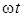 ) показано на рис.7. Визначимо активну потужнiсть P
, яка дорiвнює середньому за перiод значенню миттєвої потужностi: ) показано на рис.7. Визначимо активну потужнiсть P
, яка дорiвнює середньому за перiод значенню миттєвої потужностi:
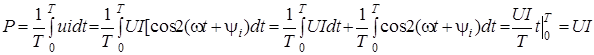 . .
Другий iнтеграл дорiвнює нулю, оскiльки на iнтервалi часу, що кратний перiоду, додатнi та вiд'ємнi площi синусоїдної функцiї однаковi.
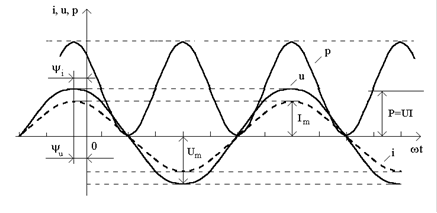
Рисунок 7
Нехай через iндуктивнiсть протiкає струм 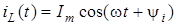 . ЕРС самоiндукцiї визначається за формулою . ЕРС самоiндукцiї визначається за формулою
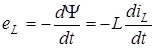 . .
Оскільки 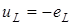 , матимемо , матимемо
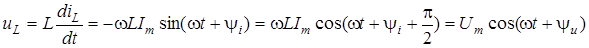 . .
Цей вираз дозволяє зробити такi висновки:
1) 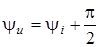 ; ; 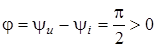 , отже напруга випереджає струм в iндуктивностi на кут , отже напруга випереджає струм в iндуктивностi на кут 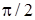 ; ;
2) амплiтуди, так само як i дiючi значення напруги та струму, пов'язанi законом Ома: 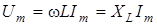 ; ; 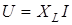 . .
Величина 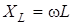 , яка має розмiрнiсть опору, зветься iндуктивним опором; обернена до неї величина , яка має розмiрнiсть опору, зветься iндуктивним опором; обернена до неї величина 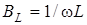 зветься iндуктивною провiднiстю. Тодi зветься iндуктивною провiднiстю. Тодi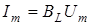 ; ; 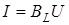 . .
Миттєва потужнiсть, яка надходить до iндуктивностi, становить:
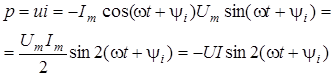 . .
Очевидно, що активна потужнiсть P =
0 (як середнє значення синусоїдної функцiї на iнтервалi часу T
). Визначимо енергiю магнiтного поля в iндуктивностi:
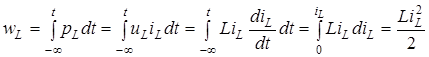 . .
(Замiна змiнних у межах: при 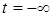 , , 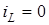 ; при ; при 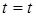 , , 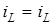 ). ).
Отже
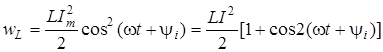 . .
Залежностi миттєвих значень u
, i
, p
, 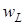 в iндуктивностi за часом зображено на рис.8. Проаналiзуємо цi часовi дiаграми: протягом першої чвертi перiоду (вiдлiк вiд точки t*
), коли струм у колi збiльшується, має мiсце заряд iндуктивностi, тобто накопичення енергiї в магнiтному полi за рахунок джерела. Миттєва потужнiсть при цьому додатна i досягає максимального значення в iндуктивностi за часом зображено на рис.8. Проаналiзуємо цi часовi дiаграми: протягом першої чвертi перiоду (вiдлiк вiд точки t*
), коли струм у колi збiльшується, має мiсце заряд iндуктивностi, тобто накопичення енергiї в магнiтному полi за рахунок джерела. Миттєва потужнiсть при цьому додатна i досягає максимального значення 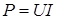 . .
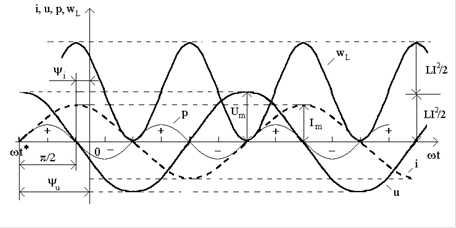
Рисунок 8
У момент часу 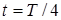 ( (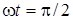 ) енергiя, накопичена в магнiтному полi, також досягає максимального значення ) енергiя, накопичена в магнiтному полi, також досягає максимального значення 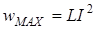 . Пiсля цього впродовж другої чвертi перiоду вiдбувається зменшення струму та миттєвої енергiї, тобто розряд iндуктивностi; миттєва потужнiсть у цi моменти вiд'ємна. Оскiльки енергiя в системi не витрачається (P =
0), то зменшення . Пiсля цього впродовж другої чвертi перiоду вiдбувається зменшення струму та миттєвої енергiї, тобто розряд iндуктивностi; миттєва потужнiсть у цi моменти вiд'ємна. Оскiльки енергiя в системi не витрачається (P =
0), то зменшення 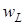 означає, що енергiя повертається до джерела. Далi процес повторюється. Таким чином, вiдбувається коливання енергiї мiж джерелом та iндуктивнiстю, причому активна потужнiсть, яка надходить до iндуктивностi, дорівнює нулю. означає, що енергiя повертається до джерела. Далi процес повторюється. Таким чином, вiдбувається коливання енергiї мiж джерелом та iндуктивнiстю, причому активна потужнiсть, яка надходить до iндуктивностi, дорівнює нулю.
Подамо миттєвi значення струму та напруги через комплекснi амплiтуди:
 ; ; 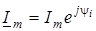 . .
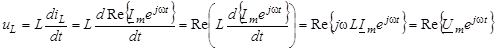 . .
З останнього виразу можна зробити такi висновки:
1) операцiя диференцiювання дiйсної функцiї часу за t
еквiвалентна множенню на величину 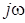 комплексно-часової функцiї; комплексно-часової функцiї;
2) оскiльки рiвнi мiж собою реальнi частини, рiвнi також i вектори: 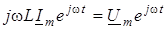 . Тодi маємо закон Ома в комплекснiй формi: . Тодi маємо закон Ома в комплекснiй формi:
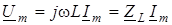 , (4) , (4)
де 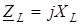 - комплексний опiр iндуктивностi. - комплексний опiр iндуктивностi.
Розглянемо фазовi спiввiдношення комплексних амплiтуд струму та напруги в iндуктивностi. Для цього запишемо 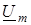 у показниковiй формi: у показниковiй формi:
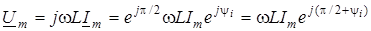 . .
Цей вираз пiдтверджує висновок щодо фазового зсуву мiж комплексними амплiтудами 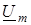 та та 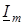 на кут на кут 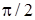 (рис.9а). Нагадаємо, що фазовi кути вiдраховують вiд осi +1 проти ходу годинникової стрiлки. (рис.9а). Нагадаємо, що фазовi кути вiдраховують вiд осi +1 проти ходу годинникової стрiлки.
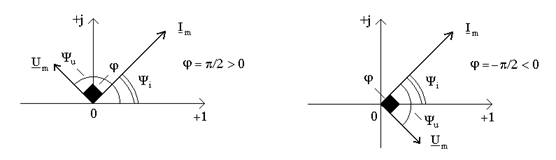
а) б)
Рисунок 9
Знайдемо вираз для комплексної амплiтуди струму, користуючись спiввiдношенням: 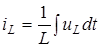 . .
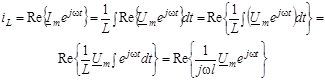 . .
Скоротивши вираз на множник 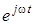 , отримуємо ще один запис закону Ома в комплекснiй формi: , отримуємо ще один запис закону Ома в комплекснiй формi:
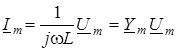 , ,
де 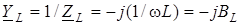 - комплексна провiднiсть iндуктивностi. - комплексна провiднiсть iндуктивностi.
Зазначимо, що операцiя iнтегрування дiйсної функцiї часу при переходi до комплексно-часової функцiї замiнюється операцiєю дiлення на величину 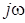 . .
Нехай через ємнiсть протiкає струм 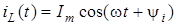 . Миттєвi значення струму та напруги в ємностi пов'язанi спiввiдношеннями: . Миттєвi значення струму та напруги в ємностi пов'язанi спiввiдношеннями:
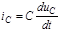 ; ; 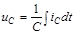 . Тодi . Тодi
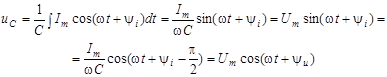 . .
Аналiз останнього виразу показує:
1) 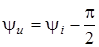 ; ; 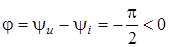 , отже напруга в ємностi вiдстає вiд струму за фазою на кут , отже напруга в ємностi вiдстає вiд струму за фазою на кут 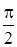 ; ;
2) амплiтуди, так само як i дiючi значення напруги та струму, пов'язанi законом Ома:  ; ; 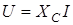 . Величина . Величина 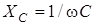 , яка має розмiрнiсть опору, зветься ємнiсним опором; обернена до неї величина , яка має розмiрнiсть опору, зветься ємнiсним опором; обернена до неї величина 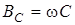 зветься ємнiсною провiднiстю. зветься ємнiсною провiднiстю.
Тодi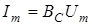 ; ; 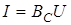 . .
Миттєва потужнiсть, яка надходить до ємностi, становить:
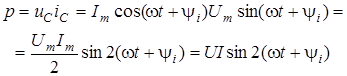 . .
Активна потужнiсть P
= 0, так само як i для iндуктивностi. Енергiя електричного поля в ємностi визначається за формулою:
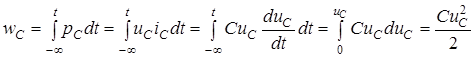 ; ;
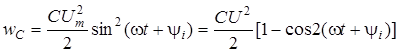 . .
Залежностi миттєвих значень u
, i
, p
, 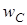 в ємностi за часом зображено на рис.10. Так само як i в iндуктивностi, вiдбувається коливання енергiї мiж джерелом електричної енергiї та ємнiстю, причому активна потужнiсть дорiвнює нулю. в ємностi за часом зображено на рис.10. Так само як i в iндуктивностi, вiдбувається коливання енергiї мiж джерелом електричної енергiї та ємнiстю, причому активна потужнiсть дорiвнює нулю.
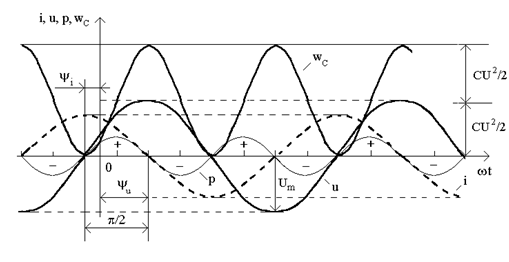
Рисунок 10
Якщо перейти до комплексно-часових функцiй  ; ; 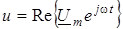 та подати за їх допомогою миттєвi значення, можна знайти вирази для комплексних амплiтуд струму та напруги: та подати за їх допомогою миттєвi значення, можна знайти вирази для комплексних амплiтуд струму та напруги:
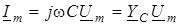 ; ; 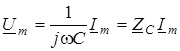 , (5) , (5)
де 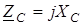 ; ; 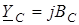 - комплекснi опiр та провiднiсть ємностi. - комплекснi опiр та провiднiсть ємностi.
Здобутi вирази - це закон Ома в комплекснiй формi для ємностi. Аби роз-глянути фазовi спiввiдношення, запишемо комплексну амплiтуду 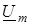 в показниковiй формi: в показниковiй формi:
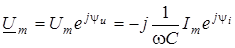 . .
Подамо множник - j
в показниковiй формi 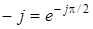 . Тодi . Тодi
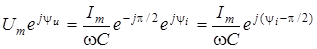 . .
Цей вираз пiдтверджує висновок, що в ємностi напруга вiдстає за фазою вiд струму на кут 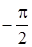 (рис.9б). (рис.9б).
|