Министерство образования Российской Федерации
Министерство образования Кыргызской Республики
Кыргызско-Российский Славянский Университет
Факультет Архитектуры Дизайна и Строительства
Кафедра «Архитектура Промышленных и Гражданских Зданий»
Расчетно-графическое задание по дисциплине:
«Железобетонные конструкции»
Выполнил: Гиндин В.Б.
стд. гр. ПГС-1-06
Проверила: Адыракаева Г.Д.
Бишкек 2010
Исходные данные для проектирования
Шаг колонн в поперечном направлении l
1
= 6,4м;
Шаг колонн в продольном направлении l2
= 5,5м;
Размеры здания - 3l
1
х 8l
2
;
Направление ригелей – поперечное;
Временная равномерно распределенная нагрузка - 6600 Н/м2
= 6,6 кН/м2
;
Число этажей – 8;
Высота этажа – 3м;
Толщина кирпичной стены - 1,5 кирпича = 380 мм.
Класс бетона: В 25, ρ=2500 кг/м3
.
Район строительства – г. Санкт – Петербург.
Содержание
1. Расчет и компоновка плит перекрытия
2. Расчет панели по предельным состояниям 1-й группы
3. Расчет панели по предельным состояниям 2-й группы
4. Статический расчет ригеля
5. Расчет колонны
6. Расчет железобетонного фундамента
Список литературы
1. Расчет и компоновка плит перекрытия
Т.к заданная временная равномерно распределенная нагрузка составляет значение 6600 Н/м2
, согласно таблице 3.4 (п. №1, см. Литература
), в качестве перекрытия будем использовать ребристые плиты.
Размеры связевых принимаем шириной 1,2 м. Тогда:
1. Размеры плит в крайних ячейках l
1
х l
2
:
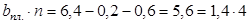
2. Размеры плит в средней ячейке l
1
х l
2
:
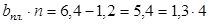 . .
где 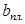 - ширина плиты, - ширина плиты, 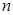 - число плит в ячейке l
1
х l
2. - число плит в ячейке l
1
х l
2.
Данные для проектирования плиты:
1. Проектируемая плита междуэтажного перекрытия будет эксплуатироваться при нормальной температуре (отапливаемое помещение), в неагрессивной среде с влажностью не выше 75%.
2. Способ изготовления конструкций - агрегатно-поточная заводская технология.
3. Вид железобетона - предварительно напряженный.
4. Способ натяжения – электротермическое натяжение на упоры опалубочной стальной формы.
5. Условия твердения бетона - термовлажностная обработка при атмосферном давлении, прогрев бетона выполняется совместно с силовой (опалубочной) формой.
6. Бетон – тяжелый, класса В 25.
По таблице 2 (п.2 см Литература
):
Реклама

- Коэффициент условия работы бетона γв2
= 0,9;
- Призменная прочность Rbn
=18,5 МПа (нормативная), Rb
=14,5 МПа (расчетная);
- Сопротивление на растяжение Rbtn
=1,6 МПа (нормативное), Rbt
=1,05 МПа (расчетное);
- Начальный модуль упругости Ев
=27х103
МПа.
7. Арматура:
По таблице 2 (п.2 см Литература
):
Напрягаемая
,(в продольных ребрах плиты), класса A – IV:
- Нормативное сопротивление растяжению Rsn
=590 МПа;
- Расчетное сопротивление растяжению Rs
=510 МПа;
- Модуль упругости Еs
=190х103
МПа.
Ненапрягаемая
,(сварные сетки), класса Вр - I:
- Нормативное сопротивление растяжению Rsn
=405 МПа;
- Расчетное сопротивление растяжению Rs
=370 МПа;
- Модуль упругости Еs
=170х103
МПа.
8. Требования предельных состояние 2-й группы:
- К трещиностойкости предъявляется 3-я категория требований, предельно допустимая ширина кратковременного и длительного раскрытия трещин должна составлять соответственно:
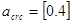 мм и мм и 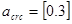 мм. мм.
- Предельно допустимый прогиб должен составлять 2,5 см в соответствии
с таблицей 2 СНиП 2.03-01-84.
Расчетный пролет и нагрузки.
Плита рассчитывается по схеме однопролетной балки с шарнирным опиранием на действие равномерно распределенной нагрузки. Будем производить расчет плиты, которая опирается на 2 ригеля.
Для установления расчетного пролета плиты предварительно задаемся размерами сечения ригеля:
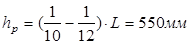 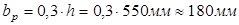
Тогда расчетный пролет, при опирании панели поверху:
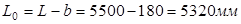
Сбор нагрузок на 1м2
перекрытия приведен в таблице 1
.
Таблица 1
. Вертикальная нагрузка на 1м2
перекрытия.
Вид нагрузки
|
Нормативная нагрузка:
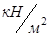
|
Коэффициент надежности по нагрузке 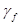 |
Расчетная нагрузка:
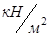
|
| 1. Постоянная
|
Керамическая плитка,
δ=0,008м; 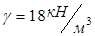
|
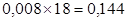 |
1,2 |
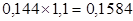 |
Цементно-песчаная стяжка,
δ=25мм, 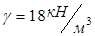
|
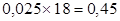 |
1,3 |
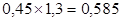 |
| Ребристая панель перекрытия |
2,5 |
1,1 |
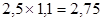 |
| Итого
|
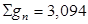
|
-
|
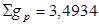
|
2. Временная нагрузка на проектирование.
Включает в себя:
|
6,6 |
1,2 |
7,92 |
| Длительная (70% от временной) |
4,62 |
1,2 |
5,544 |
| Кратковременная (30% от временной) |
1,98 |
1,2 |
2,376 |
| 3. Полная
|
9,694
|
- |
11,4134
|
Нагрузка на 1 м. п. длины при номинальной ширине панели 1,4 м с учетом коэффициента надежности по нагрузке по назначению при II классе ответственности 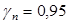 : :
Расчетная: Нормативная:
Постоянная: 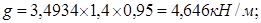
Постоянная: 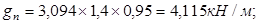
Полная: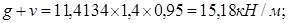
Полная: 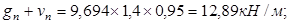
Постоянная и длительная: 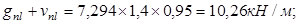
Определение усилий от внешних нагрузок.
Усилия от полной нормативной нагрузки:
- изгибающий момент в середине пролета: - поперечная сила на опоре:
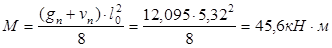
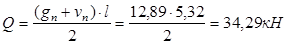
Усилия от полной расчетной нагрузки:
- изгибающий момент в середине пролета: - поперечная сила на опоре:
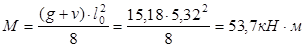
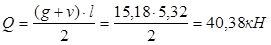
Изгибающий момент от постоянной и длительной нагрузок:
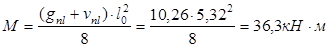
Компоновка поперечного сечения панели.
По опыту проектирования ребристых панелей, высоты рекомендуется принимать равной:
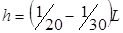 . .
Принимаем высоту 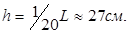 Тогда рабочая высота сечения: Тогда рабочая высота сечения: 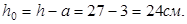 ,
где а
– толщина защитного слоя. ,
где а
– толщина защитного слоя.
Реклама

В соответствии с рекомендациями на стр. 410 (п. №1, см. Литература
), принимаем размеры плиты:
- ширина продольных ребер по низу – 7см;
- то же по верху – 8 см;
- ширина ребра расчетного таврового сечения 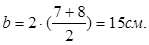
- толщина полки hf
’=5см
;
- ширина полки по верху 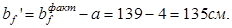
2. Расчет панели по предельным состояниям 1-й группы
Расчет прочности панели по сечению, нормальному к продольной оси.
Расчетное сечение панели принимаем тавровое с полкой в сжатой зоне. В расчет вводится вся ширина полки.
Определяем положение границы сжатой зоны бетона из условия:
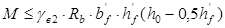
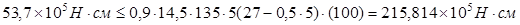
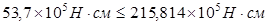
Следовательно, граница сжатой зоны проходит в полке, расчет плиты ведем как для прямоугольного сечения размерами 135см х 27см.
Вычисляем коэффициент 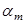 по формуле: по формуле:
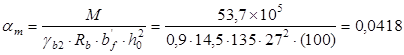
Из таблицы 1.16 (п.1 см. Литература
) находим коэффициенты ξ=0,04 и η=0,98.
Вычислим характеристику сжатой зоны ώ
по формуле:
ώ
=0,85 – 0,008γb
2
Rb
= 0,85 – 0,008∙0,9∙14,5=0,7456
Определим граничную высоту сжатой зоны:
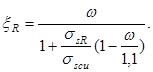 Здесь σscu
= 500 мПа; σs
R
= Rs + 400 – σs
P
- ∆σs
P Здесь σscu
= 500 мПа; σs
R
= Rs + 400 – σs
P
- ∆σs
P
Предварительное напряжение арматуры σs
P
= 0,6Rs
n
= 0,6∙590=354мПа.
Значение предварительного напряжения арматуры вводится с коэффициентом точности натяжения γs
P
.
Его предельное отклонение ∆γs
P
при электромеханическом способе натяжения определяется по формуле:
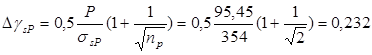 , ,
где np
– число стержней в панели.
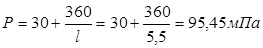 , ,
где l – длина натягиваемого стержня; (=5,5м).
Тогда значение коэффициента точности натяжения равно:
γs
P
= 1- ∆γs
P
= 1 – 0,232=0,768
Следовательно значение предварительного напряжение с учетом коэффициента точности натяжения будет равно:
∆σs
P
= 0,768∙354=271,872мПа.
Отсюда σs
R
= 590 + 400 – σs
P
- ∆σs
P
= 590 + 400 – 354 – 271,872 = 364,128 мПа.
Граничная высота сжатой зоны:
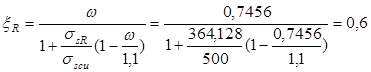
ξ=0,039 < ξR
=0,6. Следовательно, площадь сечения растянутой арматуры можно определить по формуле:
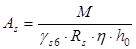
 - коэффициент условия работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести. Определяется согласно формуле: - коэффициент условия работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести. Определяется согласно формуле:
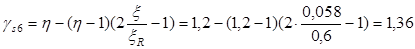 > η > η
η
= 1,2 для арматуры класса A – IV. Принимаем 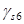 = η
=1,2 = η
=1,2
Площадь арматуры:
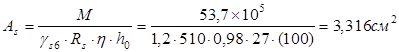
Принимаем 2 стержня ø16 с фактической площадью 4,02 см2
.
Расчет полки на местный изгиб.
Полка панели рассчитывается как балочная плита, частично защемленная в продольных ребрах панели, на действие равномерно распределенной нагрузки.
Расчетный пролет – расстояние в свету между продольными ребрами) при ширине ребер по верху 8 см равен:
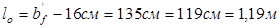
Определим нагрузку, действующую на 1м2
плиты. Она будет составлять: 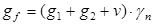 , где: g
1
= 0,1584+0,585=0,7434 кН/м2
– нагрузка от пола. , где: g
1
= 0,1584+0,585=0,7434 кН/м2
– нагрузка от пола.
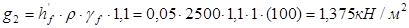 - нагрузка от собственной массы полки v
= 7,2 кН/м2
– временная. - нагрузка от собственной массы полки v
= 7,2 кН/м2
– временная.
Итого: 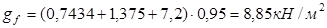 . .
Для расчета условно вырезаем из полки полосу шириной 1м. В этом случае погонная нагрузка на полку будет равна 8850 Н/м. Тогда изгибающий момент в полосе с учетом частичного защемления полки в ребрах, в сечении расположенном в середине пролета будет равен:
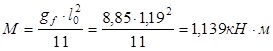
Рабочая высота сечения равна 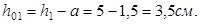
Вычисляем коэффициент 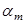 по формуле: по формуле:
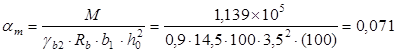
Из таблицы 1.16 (п.1 см. Литература
) находим коэффициенты ξ=0,074 и η=0,963
Определяем граничную высоту сечения:
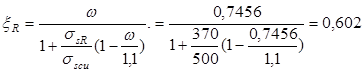 σs
R
=
Rs
=370 мПа. σs
R
=
Rs
=370 мПа.
ξ=0,074 < ξR
=0,602.
Следовательно, площадь арматуры на 1 м.п. можно определить по формуле:
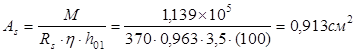
Принимаем сетку с поперечной рабочей арматурой С – 1 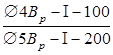 шириной 1140мм. шириной 1140мм.
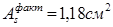 , при шаге стержней 200мм. , при шаге стержней 200мм.
Гнутая сетка С-2 применяется той же марки, что и С-1, но с шириной
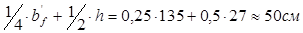
Расчет прочности панели по сечению, наклонному к продольной оси.
Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами при действии поперечной силы Q = 40,38 кН. С помощью формулы:
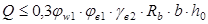
где 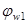 - коэффициент, учитывающий влияние хомутов. Определяется по формуле: - коэффициент, учитывающий влияние хомутов. Определяется по формуле:
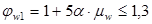 , где , где 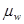 - коэффициент поперечного армирования. Ориентировочно = 0,001. - коэффициент поперечного армирования. Ориентировочно = 0,001. 
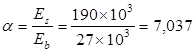
Тогда: 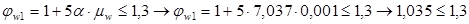
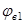 - коэффициент, определяется по формуле: - коэффициент, определяется по формуле:
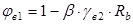 , где , где 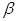 - для тяжелого бетона = 0,01. - для тяжелого бетона = 0,01.
Тогда 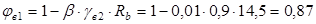
Проверяем:
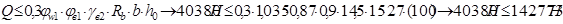
Условие удовлетворяется. Следовательно, размеры поперечного сечения панели достаточны.
Проверяем необходимость постановки расчетной поперечной арматуры из условия:
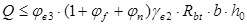
где 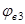 – коэффициент. =0,6 – для тяжелого бетона. – коэффициент. =0,6 – для тяжелого бетона.
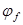 – коэффициент, учитывающий влияние полок в тавровых элементах. – коэффициент, учитывающий влияние полок в тавровых элементах.
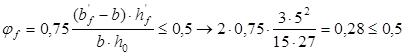
При условии, что 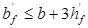 . Учитывается наличие 2-х ребер в панели. . Учитывается наличие 2-х ребер в панели.
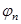 - коэффициент, учитывающий влияние продольных сил. Определяется по формуле: - коэффициент, учитывающий влияние продольных сил. Определяется по формуле:
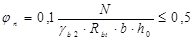
Вместо величины N подставим в формулу значение усилия обжатия с учетом коэффициента точности натяжения (но без учета потерь!) (см. выше):
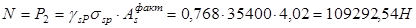
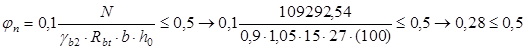
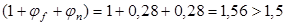 . .
Поэтому принимаем 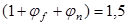
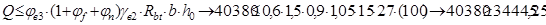
Условие необходимости постановки расчетной поперечной арматуры не удовлетворяется. Следовательно необходима установка поперечной арматуры по расчету.
Расчет поперечной арматуры на действие поперечной силы для обеспечения прочности по наклонной трещине по наклонному сечению, будем производить по условию (1.64) (п.1 см. Литература
). При отсутствии отгибов, условие имеет вид:
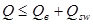
где 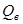 - величина поперечного усилия, воспринимаемого бетоном; - величина поперечного усилия, воспринимаемого бетоном;
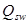 - то же, воспринимаемое поперечными хомутами. - то же, воспринимаемое поперечными хомутами.
Величина 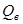 определяется по формуле (1.65) (п.1 см. Литература
): определяется по формуле (1.65) (п.1 см. Литература
):
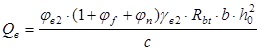
где с
– максимальная длинна проекции опасного сечения на продольную ось элемента.
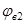 - коэффициент, учитывающий влияние вида бетона Таблица
1.17 (п.1 см. Литература
) - коэффициент, учитывающий влияние вида бетона Таблица
1.17 (п.1 см. Литература
)
Для тяжелого бетона 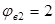
По условию (1.66) (п.1 см. Литература
) поперечное усилие должно быть не менее
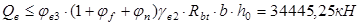 (см. выше) (см. выше)
Подставив минимальное значение в (1.65) получим:
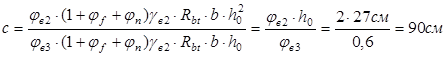
Определим величину поперечных усилий воспринимаемых хомутами:
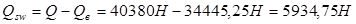
Для хомутов выполнятся условие: Усилие в хомутах на единицу длины равно:
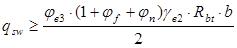 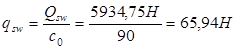
Проверяем:
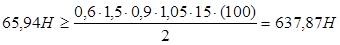 . Не удовлетворяется. . Не удовлетворяется.
В этом случае принимаем 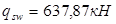
Определим фактическую длину проекции опасной наклонной трещины на продольную ось элемента:
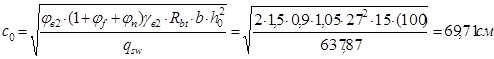
Но так как 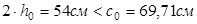 . То принимаем фактическую длину . То принимаем фактическую длину 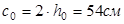
Уточняем величину 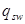 , с учетом , с учетом 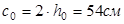 . .
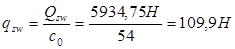 < <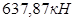
В связи с этим, окончательно принимаем 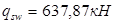 . .
Из условия сварки продольных ребер панели класса А-I с продольной конструктивной ненапрягаемой арматурой (d=8мм), принимаем в качестве поперечной арматуры арматуру класса Вр-I диаметром 4мм 0,126 см2
(по табл. 1.12 (п.1 см. Литература
) 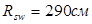 ). ).
Т.к число каркасов составляет по одному в каждом из 2-х ребер, площади поперечного сечения хомутов 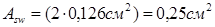
Определим шаг поперечных хомутов на приопорных (четверть пролета) участках:
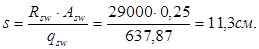
Согласно требований СНиП 2.03.01-84* п.3.31 , при расчете железобетонных элементов с поперечной арматурой, должна также обеспечиваться прочность по наклонному сечению в пределах участка между хомутами. Максимальный шаг поперечных хомутов определяется по формуле:
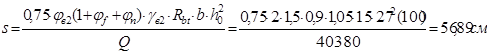
Также, поперечная арматура должна удовлетворять конструктивным требованиям СНиП 2.03.01-84* (5.26-5.28):
- на приопорных участках, при h<45 см, 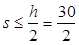 , т.е , т.е 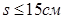 ; ;
- на остальной части пролета при h>30см, 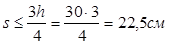 . .
Принимаем окончательные значения шага поперечных хомутов (кратны 5):
- на приопорных участках – 10 см;
- на остальной части пролета – 20см.
Теперь повторно проверим начальное условие 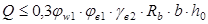 , при известном коэффициенте поперечного армирования: , при известном коэффициенте поперечного армирования:
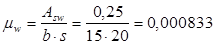
Т.к фактическое значение  меньше принятого ранее ориентировочно меньше принятого ранее ориентировочно 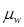 =0,001. То при =0,001. То при 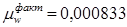 условие условие 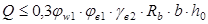 также будет удовлетворятся. также будет удовлетворятся.
3. Расчет панели по предельным состояниям 2-й группы
Определение геометрических характеристик приведенного сечения.
Определим отношение модулей упругости бетона и арматуры:
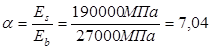
Зная это отношение, определим площадь приведенного сечения:
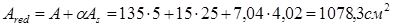
Теперь находим статический момент приведенного сечения относительно нижней грани:
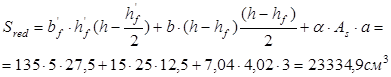
Тогда расстояние от нижней грани сечения до центра его тяжести:

Определяем момент инерции приведенного сечения относительно его центра тяжести:
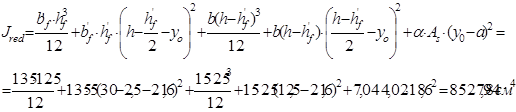
Зная это, находим моменты сопротивления:
- в нижней зоне: 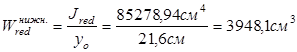
- в верхней зоне: 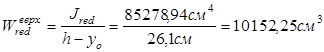
Теперь определяем величину r
–
расстояниеот центра тяжести приведенного сечения до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Для изгибаемых, предварительно напрягаемых элементов r
определяется по формуле:
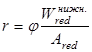 , ,
где 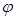 для предварительно напрягаемых элементов равен для предварительно напрягаемых элементов равен 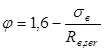
где 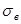 - максимальное нормальное напряжение в бетоне от внешней нагрузки и величины усилия предварительного напряжения. Определяется по формуле: - максимальное нормальное напряжение в бетоне от внешней нагрузки и величины усилия предварительного напряжения. Определяется по формуле:
Rb
,
ser
– нормативная прочность бетона.
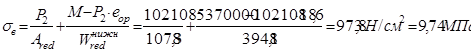
, где М
– изгибающий момент от полной нормативной нагрузки;
P2
– усилие обжатия с учетом полых потерь;
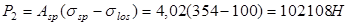
(все полные потери ориентировочно приняты 100 МПа)
eop
– эксцентриситет приложения усилия обжатия; 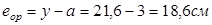
Теперь находим 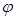 : Величина r: : Величина r:
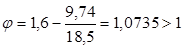 принимаем принимаем 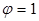 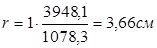
Определим величину rinf
–
расстояниеот центра тяжести приведенного сечения до ядровой точки, наименее удаленной от растянутой зоны:
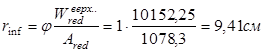
Определим упругопластический момент сопротивления по растянутой зоне согласно формуле:
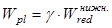
Для таврового сечения с полкой в сжатой зоне 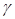 принимается =1,75. принимается =1,75.
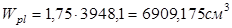
и упругопластический момент сопротивления растянутой зоны в стадии изготовления и обжатия элемента:
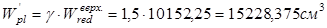
Для таврового сечения с полкой в растянутой зоне, с размерами полки:
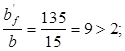 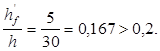
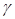 примется =1,5. примется =1,5.
Потери предварительного напряжения арматуры.
Для расчета потерь принимаем коэффициент точности натяжения арматуры 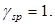
Первые потери (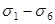 ).
Потеринапряжения ( ).
Потеринапряжения (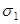 )
наступают от его релаксации. По таблице 1.4 (п.1 см. Литература
) при электротермомеханическом способе натяжения арматуры потери от релаксации напряжений равны: )
наступают от его релаксации. По таблице 1.4 (п.1 см. Литература
) при электротермомеханическом способе натяжения арматуры потери от релаксации напряжений равны:
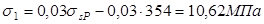
Потери от температурного перепада между натянутой арматурой и упорами (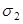 )
равны нулю, так как при агрегатно-поточной технологии изготовления форма с упорами при пропаривании нагревается вместе с плитой. )
равны нулю, так как при агрегатно-поточной технологии изготовления форма с упорами при пропаривании нагревается вместе с плитой.
Потери от деформации анкеров ( )
и формы ( )
и формы (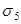 )
, трения об огибающие приспособления ( )
, трения об огибающие приспособления (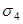 )
так же равны нулю. )
так же равны нулю.
Усилия обжатия с учетом потерь 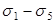 определяем с помощью формулы:
определяем с помощью формулы:
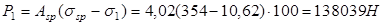
Эксцентриситет приложения усилия рассчитан в предыдущем пункте.
По данным таблицы 1.4 (п.1 см. Литература
) потери от быстронатекающей ползучести 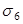 (для бетона подвергнутого тепловой обработке) определяется исходя из сравнения соотношения
(для бетона подвергнутого тепловой обработке) определяется исходя из сравнения соотношения 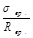 с коэффициентом
с коэффициентом 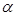 . .
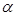 -
коэффициент определяемый: -
коэффициент определяемый: 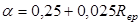 . .
Определяем необходимые для сравнения величины:
1. 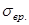 - напряжение в бетоне возникающие при обжатии усилием Р
1
, на уровне центра тяжести напрягаемой арматуры. Определяется по формуле: - напряжение в бетоне возникающие при обжатии усилием Р
1
, на уровне центра тяжести напрягаемой арматуры. Определяется по формуле:
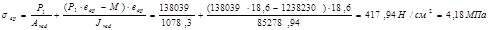
Здесь М – изгибающий момент, возникающий от действия собственного веса панели (2,5 кН/м2
).
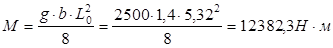
2. 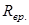 - передаточная прочность бетона, в соответствии с требованиями п2.6 СНиП 2.03.01-84* должна иметь значении не менее 50% прочности принятого класса бетона (В25). Исходя из этих требований, принимаем - передаточная прочность бетона, в соответствии с требованиями п2.6 СНиП 2.03.01-84* должна иметь значении не менее 50% прочности принятого класса бетона (В25). Исходя из этих требований, принимаем 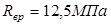 . .
3.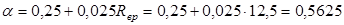 . .
Сравниваем: 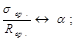
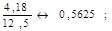 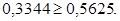
Если 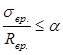 ,
потери от быстронатекающей ползучести ,
потери от быстронатекающей ползучести 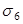 (с учетом теплового воздействия на бетон (введение коэффициента 0,85)) определяется по формуле:
(с учетом теплового воздействия на бетон (введение коэффициента 0,85)) определяется по формуле:

Первые потери: 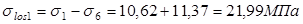
Потери от усадки бетона (таблица 1.4 (п.1 см. Литература
)): 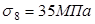
Потери от ползучести бетона (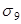 )
определяется исходя из сравнения )
определяется исходя из сравнения
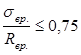
Здесь 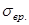 - напряжение в бетоне возникающие при обжатии усилием Р
1
(с учетом всех первых потерь) , на уровне центра тяжести напрягаемой арматуры. - напряжение в бетоне возникающие при обжатии усилием Р
1
(с учетом всех первых потерь) , на уровне центра тяжести напрягаемой арматуры.
Усилия обжатие с учетом всех первых потерь:
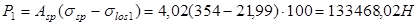
Определяем 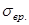 : :
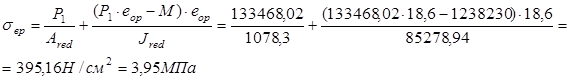
Сравниваем: 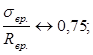 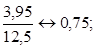 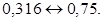
При 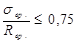 потери от ползучести бетона (
потери от ползучести бетона (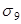 )
определяется по формуле: )
определяется по формуле:
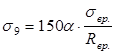 , где
, где 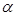 =
0,85 (при тепловой обработке бетона). =
0,85 (при тепловой обработке бетона).
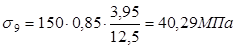
Вторые потери: 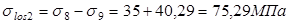
Полные потери: 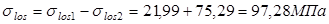 . .
Расчет по образованию трещин, нормальных к продольной оси.
Для элементов, к трещиностойкости которых предъявляются требования 3-й категории, коэффициент надежности по нагрузке 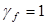 . .
Расчет производится из условия: 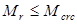
, где 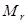 -момент, возникающий от действия внешних сил -момент, возникающий от действия внешних сил
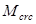 -момент воспринимаемый сечением, нормальным к продольной оси. Определяется по формуле: -момент воспринимаемый сечением, нормальным к продольной оси. Определяется по формуле:
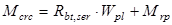 . . 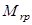 - момент, возникающий от усилия обжатия. - момент, возникающий от усилия обжатия.
Определяем 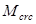 : :
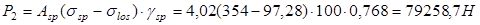
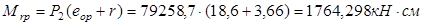
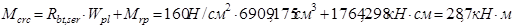
Сравниваем: 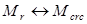 ; ; 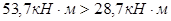 . Условие не выполняется. . Условие не выполняется.
Поскольку условие трещиностойкости не выполняется, в растянутой зоне образуются трещины, а следовательно, необходим расчет по раскрытию трещин.
Проверим образование трещин в верхней зоне
панели в стадии изготовления. Усилия обжатия вводится в расчет с учетом первых потерь и предельного отклонения коэффициента точности натяжения: 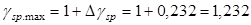
Условия не раскрытия трещин в верхней зоне панели, с учетом её собственной массы:
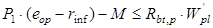 , где , где 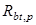 - сопротивление бетона растяжению, соответствующее передаточной прочности (таблица 12.1. (СНиП 2.03.01-84*)). Для 12,5 МПа
, - сопротивление бетона растяжению, соответствующее передаточной прочности (таблица 12.1. (СНиП 2.03.01-84*)). Для 12,5 МПа
, 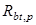 = 1 МПа
. = 1 МПа
.
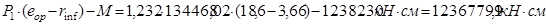
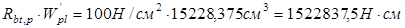
Сравниваем:  . .
Условие удовлетворяется, трещин в верхней зоне не образуется.
Расчет по раскрытию трещин, нормальных к продольной оси при 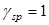 . .
К трещиностойкости предъявляется 3-я категория требований, предельно допустимая ширина кратковременного и длительного раскрытия трещин должна составлять соответственно: 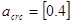 мм и мм и 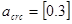 мм. мм.
Определим приращение напряжений в растянутой арматуре от действия постоянной и длительной нагрузок по формуле:
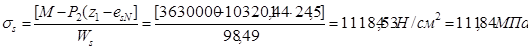
, где 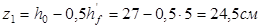 - плечо внутренней пары сил. - плечо внутренней пары сил.
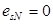 , т.к усилие обжатия приложено к центру тяжести напрягаемой арматуры. , т.к усилие обжатия приложено к центру тяжести напрягаемой арматуры.
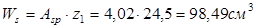 -момент сопротивления сечения растянутой арматуры. -момент сопротивления сечения растянутой арматуры.
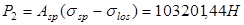 - усилие обжатия, с учетом полных потерь при - усилие обжатия, с учетом полных потерь при 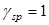 . .
Приращение напряжений в растянутой арматуре от действия полной нагрузки:
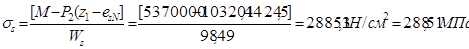
Вычисляем ширину раскрытия трещин:
- от непродолжительного действия всей нагрузки:
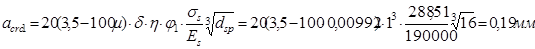
коэффициенты: 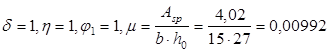
- от непродолжительного действия постоянной и длительной нагрузок:
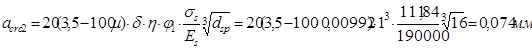
- от продолжительного действия постоянной и длительной нагрузок:
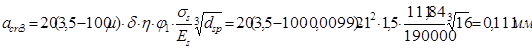
,коэффициент 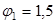 продолжительного действия.
продолжительного действия.
Непродолжительная ширина раскрытия трещин:
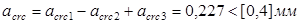
Продолжительная ширина раскрытия трещин:
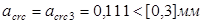
Требования удовлетворяются.
Расчет прогиба плиты.
Прогиб от нормативного значения постоянной и длительной нагрузок, предельное значение 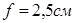 . .
Для вычисления прогиба необходимы значения следующих величин:
1. Момент от постоянной и длительной нагрузок; 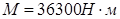
2. Продольное усилие равно усилию обжатия с учетом всех потерь, при 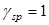 . . 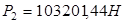 ; ;
3. Эксцентриситет 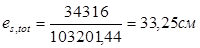
4. Коэффициент, учитывающий длительность действия нагрузки 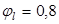
5. 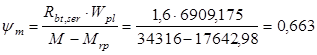 ; ;
6. Коэффициент, характеризующий неравномерность деформаций растянутой арматуры на участках между трещинами, определяется по формуле:
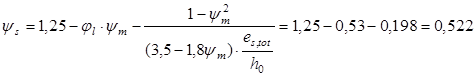
Вычисляем кривизну оси при изгибе:
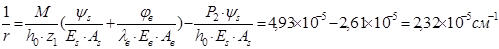
, где 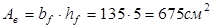 - площадь сечения полки.
- площадь сечения полки.
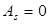 т.к арматура в растянутой зоне отсутствует.
т.к арматура в растянутой зоне отсутствует.
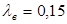 , , 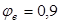 -
коэффициенты, учитывающие длительность действия нагрузки -
коэффициенты, учитывающие длительность действия нагрузки
Прогиб определяем по формуле:
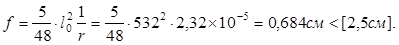
Требования удовлетворяются.
4. Статический расчет ригеля
В данном расчете ригель рассматривается как многопролетная балки (с рядом допущений). Опирание балки – шарнирное. Ригель состоит из отдельных сборных железобетонных элементов, объединяемых в неразрезную систему при монтаже.
Расчетный размер крайних пролетов ригеля принимается равным расстоянию от оси опоры его на стене до оси колонны:
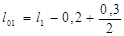 , ,
где 0,2 – расстояние от внутренней грани колонны до разбивочной оси;
0,3 – величина заделки ригеля в стену.
Расчетный размер промежуточных пролетов ригеля равен расстояниям между разбивочными осями.
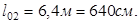
Нагрузка на ригель от ребристых плит перекрытия считается равномерно распределенной, при числе ребер более 4-х.
Ширина грузовой полосы равна шагу колонн в поперечной направлении – 5,5м.
Определяем нагрузку на 1 м длинны ригеля:
Постоянная:
- вес панелей перекрытия с учетом коэффициента надежности 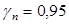 :
:
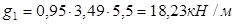
-
собственный вес ригеля сечением 18х55см с учетом коэффициента надежности 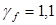 :
:
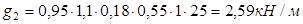
Полная постоянная: 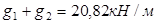
Временная:
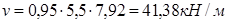
Полная расчетная нагрузка
: 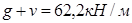
Определение внутренних усилий M
и Q
.
Изгибающие моменты и поперечные силы определяются с учетом перераспределения усилий.
Первоначально внутренние усилия определяются по формулам:
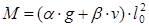
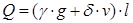 . .
Коэффициенты в этих формулах учитывают вид нагрузки, комбинации загружения и количество пролетов в балке.
Внутренние усилия определяются отдельно от действия постоянной и различных комбинаций временной нагрузок.
Схемы нагружения и значения M
и Q
в серединах пролета и опорах приведены в таблицах (см. ниже).
Далее производим перераспределение изгибающих моментов. Расчет заключается в снижении максимальных усилий моментов примерно на 30% (исходя из опыта проектирования железобетонных конструкций, снижение усилий на такую величину не приводит к превышению ширины раскрытия трещин предельно допустимых величин).
Эпюра фактических моментов ригеля:
Выровненное на 30% значение максимального момента:
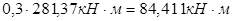 - выравнивающее значение - выравнивающее значение
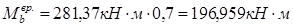 - выровненное значение - выровненное значение
Эпюра выровненных моментов:
Эпюра после перераспределения усилий:
Моменты, на гранях колонн:
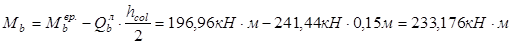
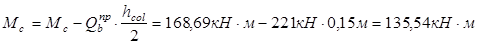
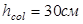 - высота сечения колонны в направлении пролета ригеля. - высота сечения колонны в направлении пролета ригеля.
Расчет прочности ригеля по сечениям нормальным к продольной оси.
Подбор высоты сечения ригеля.
Высота сечения подбирается по опорному моменту, при оптимальном значении относительной высоты сжатой зоны 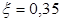 . Этому значению соответствует значение коэффициента . Этому значению соответствует значение коэффициента 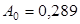 . .
Определяем граничную высоту сжатой зоны:
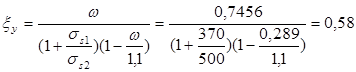
Вычислим характеристику сжатой зоны ώ
по формуле:
ώ
=0,85 – 0,008γb
2
Rb
= 0,85 – 0,008∙0,9∙14,5=0,7456
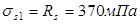
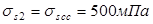
Рабочая высота сечения ригеля определяется по формуле:
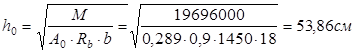
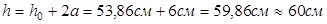
Проверяем принятое сечение по значению пролетного момента:
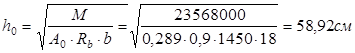
- меньше принятой высоты сечения.
Подбор сечения арматуры на участке первого пролета.
Максимальный момент на участке первого пролета: 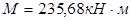
Вычисляем: 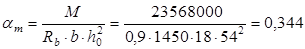
При 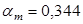 , ,
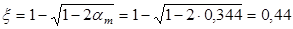 ; ;
тогда 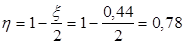
Требуемый диаметр арматуры:
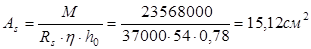
Принимаем 4 стержня ø22 с фактической площадью 15,2 см2
.
Подбор сечения арматуры на участке второго пролета.
Максимальный положительный момент на участке второго пролета: 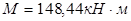
Вычисляем: 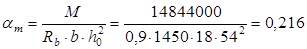
При 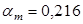 , ,
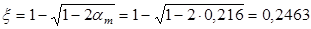 ; ;
тогда 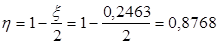
Требуемый диаметр арматуры:
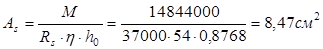
Принимаем 2 стержня ø18 и 2 стержня ø16 фактической площадью 9,1 см2
Максимальный отрицательный момент на участке второго пролета: 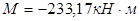
Минимальный отрицательный момент на участке второго пролета: 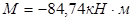
Вычисляем: 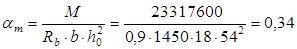
При 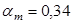 , ,
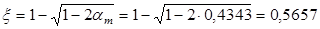 ; ;
тогда 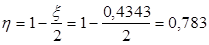
Требуемый диаметр арматуры:
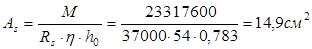
Принимаем 2 стержня ø25 и 2 стержня ø18 с фактической площадью 14,899 см2
.
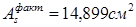
Подбор сечения арматуры на средней опоре.
Максимальный положительный момент на участке второго пролета: 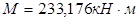
Вычисляем: 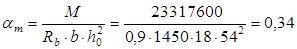
При 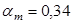 , ,
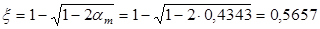 ; ;
тогда 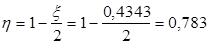
Требуемый диаметр арматуры:
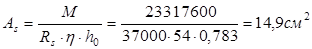
Принимаем 2 стержня ø25 и 2 стержня ø18 с фактической площадью 14,899 см2
.
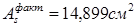
Расчет прочности ригеля по сечениям нормальным к продольной оси.
На средней опоре поперечная сила 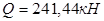
Определим величину поперечного усилия воспринимаемого бетоном, помноженную на длину проекции наклонного сечения по формуле:
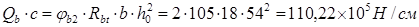
Т.к. 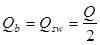 , отсюда можно получить максимальную длину проекции наклонного сечения на продольную ось изгибаемого элемента: , отсюда можно получить максимальную длину проекции наклонного сечения на продольную ось изгибаемого элемента:
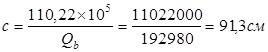
Условие 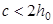 91,3см <108 см
удовлетворяется. 91,3см <108 см
удовлетворяется.
Вычисляем 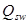 : :
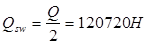 , тогда , тогда 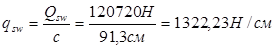
Диаметр поперечных стержней устанавливаем из условия сварки с продольной арматурой. Диаметр поперечных стержней принимаем 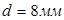 , с площадью поперечного сечения , с площадью поперечного сечения 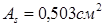 . При классе А-III . При классе А-III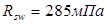 , но т.к , но т.к 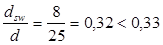 , вводится коэффициент условия работы , вводится коэффициент условия работы 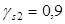 . Тогда . Тогда 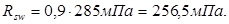 При числе каркасов =2, При числе каркасов =2,
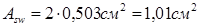 . .
Шаг поперечных стержней
Шаг поперечных стержней определяем по формуле:
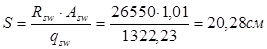
По конструктивным условиям:
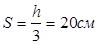 . .
Принимаем 20 см на всех приопорных участках.
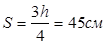 . .
Принимаем на средней части пролета 40 см.
Проверка прочности по сжатой полосе между наклонными трещинами:
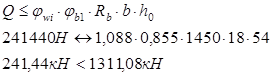
Условие удовлетворяется.
Коэффициенты:
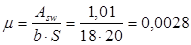
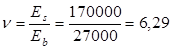
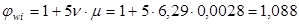
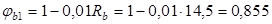 . .
Конструирование арматуры ригеля.
Армирование ригеля производится двумя сварными каркасами, часть продольных стержней каркасов обрывается в соответствии с эпюрой арматуры. Обрываемые стержни заводятся за место теоретиеского обрыва на длину зоны анкеровки.
Первый пролет.
Принятая из расчета на действие максимального изгибающего момента продольная рабочая арматура: 4 стержня ø22, 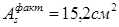 . В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете. Причем, до опор доводятся два стержня большего диаметра. . В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете. Причем, до опор доводятся два стержня большего диаметра.
Определим изгибающий момент, воспринимаемый ригелем с фактической арматурой:
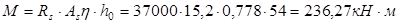
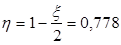
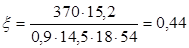
До опоры доводятся 2ø22 A-III.
Вычислим изгибающий момент, воспринимаемый сечением ригеля с арматурой 2ø22:
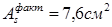
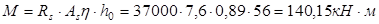
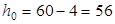 (т.к. арматура расположена в 1 ряд). (т.к. арматура расположена в 1 ряд).
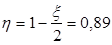
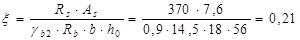
Определяем длину зоны анкеровки обрываемых стержней.
Поперечная сила определяется графически в месте теоретического обрыва стержней. 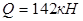 . .
Поперечные стержни ø8 A-III, в месте теоретического обрыва имеют шаг 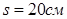 . .
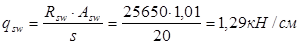
Длина зоны анкеровки определяется по формуле:
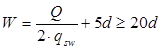
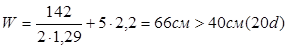
Средний пролет.
Принятая рабочая арматура: 2 стержня ø18, 2 стержня ø16 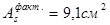
Определим изгибающий момент, воспринимаемый ригелем с фактической арматурой:
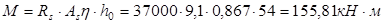
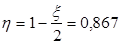
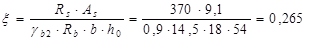
До опоры доводятся 2ø16 A-III.
Вычислим изгибающий момент, воспринимаемый сечением ригеля с арматурой 2ø16:
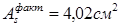
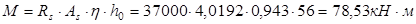
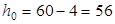 (т.к. арматура расположена в 1 ряд). (т.к. арматура расположена в 1 ряд).
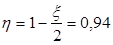
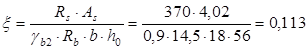
Длина зоны анкеровки 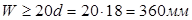 . .
Сечение на средней опоре слева.
Принятая рабочая арматура: 2 стержня ø25, 2 стержня ø18 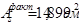
Определим изгибающий момент, воспринимаемый ригелем с фактической арматурой:
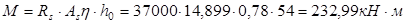
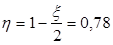
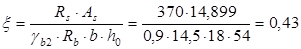
До опоры доводятся 2ø18 A-III.
Вычислим изгибающий момент, воспринимаемый сечением ригеля с арматурой 2ø18:
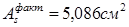
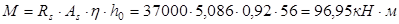
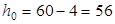 (т.к. арматура расположена в 1 ряд). (т.к. арматура расположена в 1 ряд).
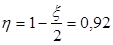
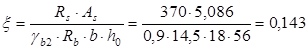
Длина зоны анкеровки 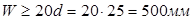 . .
Сечение на средней опоре справа.
Принятая рабочая арматура: 2 стержня ø25, 2 стержня ø18 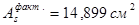
Так принятая рабочая арматура аналогична принятой арматуре в сечении средней опоры слева, расчет полностью аналогичен.
Армирование ригеля показано в Графическом приложении (лист №3)
.
5. Расчет колонны
Исходные данные для проектирования:
- здание с подвалом и 8-ю надземными этажами,
- сетка колонн 6,4 х 5,5,
- высота этажа 3м,
- высота подвала 2,8м..
- расстояние от уровня пола подвала до подошвы фундамента 0,15 м.
Назначаем размеры поперечного сечения колонны одинаковыми на всех этажах, равными 40 х 40см. Колонны будут иметь расчетный собственный вес с учетом коэффициента надежности 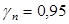 . .
Собственный вес колонны подвала:
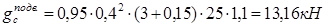
Собственный вес колонны надземных этажей:
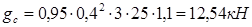
Подсчет нагрузок, определение продольных сил в колоннах.
Таблица 2. Подсчет нагрузок
| Наименование и вид нагрузки |
Нормативное значение, кН
/
м2
|
Коэффициент надежности |
Расчетное значение, кН
/
м2
|
| 1. Нагрузки на покрытие:
|
2,15
0,44
1,7
1,8
|
1,2
1,1
1,1
1,4
|
2,58
0,484
1,87
2,52
|
Постоянные нагрузки:
-
собственный вес кровли
- собственный вес ригеля
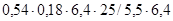
- собственный вес панели
Временная нагрузка:
- снеговая (кратковременная)
|
| 2. Нагрузки на перекрытие:
|
3,094
0,44
6,6
4,62
1,98
|
-
1,1
1,2
1,2
1,2
|
3,4934
0,484
7,92
5,544
2,376
|
Постоянные нагрузки:
- собственный вес панели и пола
- собственный вес ригеля
Временная нагрузка:
- полезная
-длительная (70% от полезной)
-кратковременная (30% от полезной)
|
Грузовая площадь - 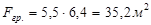 . .
Нагрузки, передаваемые на колонну в виде сосредоточенных сил:
От покрытия:
- длительная: 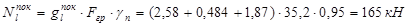
- кратковременная: 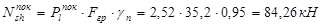
От перекрытия:
- длительная:
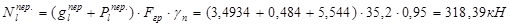
- кратковременная: 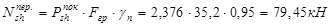
Вычисляем продольные сжимающие силы в колоннах на уровнях этажей:
8-й этаж:
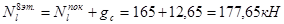
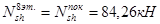
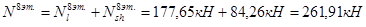
7-й этаж:
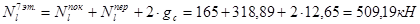
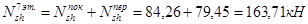
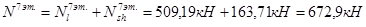
6-й этаж:
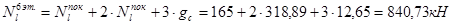
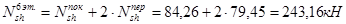
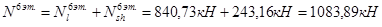
5-й этаж:
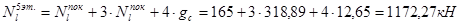
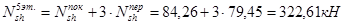
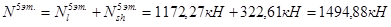
4-й этаж:
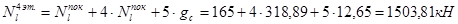
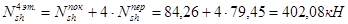
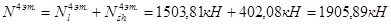
3-й этаж:
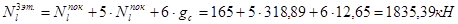
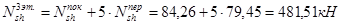
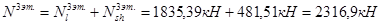
2-й этаж:
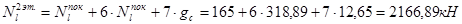
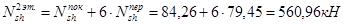
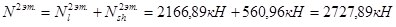
1-й этаж:

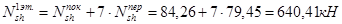
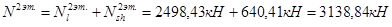
Подвал:
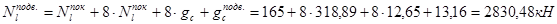
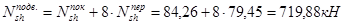
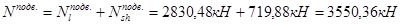
Расчетные схемы и длины колонн.
Колонну подвала рассчитывается как стойка, жестко защемленная в фундаменте и шарнирно-неподвижно опертую на уровне перекрытия.
Расчетная длина колонны подвала: 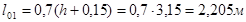
Расчетная длина колонны этажа: 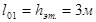
Для колонн подвала назначаем бетон класса В35 (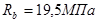 ) )
Для колонн 1-го, 2-го этажей назначаем бетон класса В30 (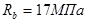 ) )
Для колонн остальных этажей назначаем бетон класса В25 (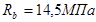 ) )
Арматура – класса А-Ш.
Расчет колонн по прочности.
Колонна подвала.
По таблицам 7, 8 (п.2 см. Литература
) в зависимости от отношений 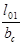 и и 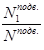 находим значения коэффициентов находим значения коэффициентов 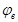 и и 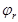 . .
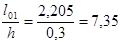 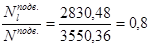
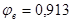 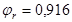
Принимаем коэффициент армирования 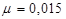
Вычисляем коэффициент 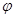 по формуле: по формуле:
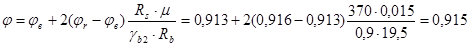
Определяем требуемую площадь продольной арматуры:
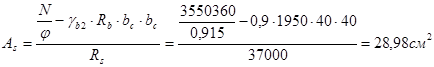
Принимаем арматуру 4ø32 A-III с 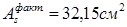 . .
При этом коэффициент армирования 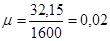 . Сечение считаем подобранным удовлетворительно, т.к. . Сечение считаем подобранным удовлетворительно, т.к. 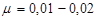 . .
Колонна 1-го этажа.
По таблицам 7, 8 (п.2 см. Литература
) в зависимости от отношений 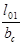 и и 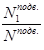 находим значения коэффициентов находим значения коэффициентов 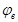 и и 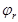 . .
 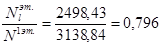
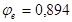 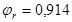
Принимаем коэффициент армирования 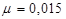
Вычисляем коэффициент 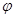 по формуле: по формуле:
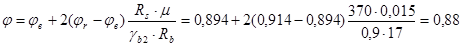
Определяем требуемую площадь продольной арматуры:
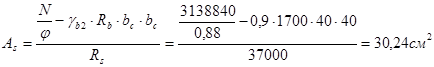
Принимаем арматуру 4ø32 A-III с 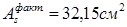 . .
При этом коэффициент армирования 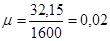 . Сечение считаем подобранным удовлетворительно, т.к. . Сечение считаем подобранным удовлетворительно, т.к. 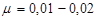 . .
Колонна 2-го этажа.
По таблицам 7, 8 (п.2 см. Литература
) в зависимости от отношений 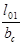 и и 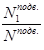 находим значения коэффициентов находим значения коэффициентов 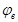 и и 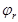 . .
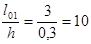 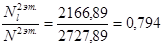
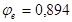 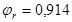
Принимаем коэффициент армирования 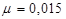
Вычисляем коэффициент 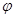 по формуле: по формуле:
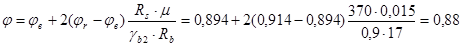
Определяем требуемую площадь продольной арматуры:
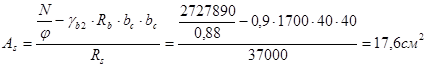
Принимаем арматуру 4ø25 A-III с 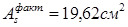 . .
При этом коэффициент армирования 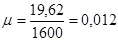 . Сечение считаем подобранным удовлетворительно, т.к. . Сечение считаем подобранным удовлетворительно, т.к. 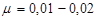 . .
Колонна 3-го этажа.
По таблицам 7, 8 (п.2 см. Литература
) в зависимости от отношений 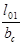 и и 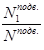 находим значения коэффициентов находим значения коэффициентов 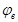 и и 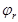 . .
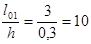 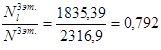
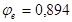 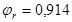
Принимаем коэффициент армирования 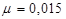
Вычисляем коэффициент 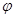 по формуле: по формуле:
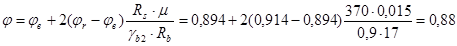
Определяем требуемую площадь продольной арматуры:
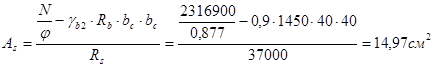
Принимаем арматуру 4ø25 A-III с 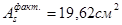 . .
При этом коэффициент армирования 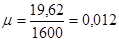 . Сечение считаем подобранным удовлетворительно, т.к. . Сечение считаем подобранным удовлетворительно, т.к. 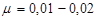 . При принятии арматуры меньшего диаметра рабочей арматуры, коэффициент поперечного армирования выходит из допусков, что говорит о недостаточном содержании арматуры в сечении. . При принятии арматуры меньшего диаметра рабочей арматуры, коэффициент поперечного армирования выходит из допусков, что говорит о недостаточном содержании арматуры в сечении.
Колонны остальных этажей армируем конструктивно, принимая арматуру 4ø25 A-III с 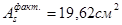 . .
Диаметры поперечной арматуры принимаем по условиям свариваемости с продольной арматурой, в зависимости от ее диаметра, по таблице 6. (п.2 см. Литература
).
Для колонн всех этажей принимаем поперечную арматуру ø8A-I,
с шагом S=500 мм. (по условию 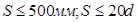 ). ).
Расчет консоли колонны.
Опорное давление ригеля, передаваемое на консоль 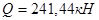 ; ;
Бетон класса В25; 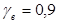 . .
Арматура класса А-Ш.
Сопряжение ригеля с консолью колонны обетонированы, зазор между торцом ригеля и гранью колонны – 5 см. Обетонирование производится до приложения нагрузки на смонтированный ригель.
Размеры опорной консоли зависят от опорного давления, создаваемого ригелем. Ригеля опирается на площадку консоли длинной, которая определяется из условия 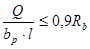 . .
Примем длинной опорной площадки ориентировочно 20 см. Проверяем условие:
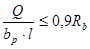 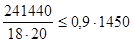 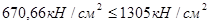 . .
Вылет консоли с учетом зазора составит: 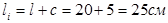 . .
Расстояние от грани колонны до точки приложения равнодействующей силы давления ригеля:
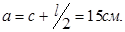
Высоту сечения консоли у грани колонны принимаем равной 0,7-0,8 от высоты ригеля.
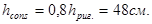
Высота консоли, со стороны свободного края равно 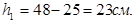 (для обеспечения угла наклона сжатой зоны 45о
). (для обеспечения угла наклона сжатой зоны 45о
).
Рабочая высота сечения консоли: 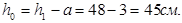
Т.к. 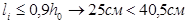 , консоль считается короткой. , консоль считается короткой.
Проверяем высоту сечения короткой консоли по условиям прочности:
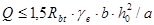 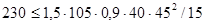 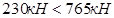
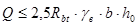 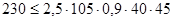 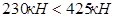
Условия удовлетворяются.
Изгибающий момент у грани колонны равен:
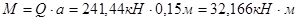
Площадь сечения арматуры подбирается по изгибающему момент, значение которого увеличено на 25%, с учетом 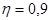 : :
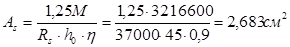
Принимаем 2ø14A-Ш, 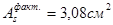 . .
Короткие консоли армируются горизонтальными хомутами и отогнутыми стержнями.
Суммарное сечение отгибов, пересекающих верхнюю половину отрезка
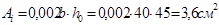 , принимаем 2ø16A-Ш, , принимаем 2ø16A-Ш, 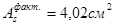 . .
Длина отгибов 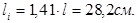
Горизонтальные хомуты принимаем ø6A-I, шаг 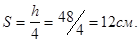
6. Расчет железобетонного фундамента
Исходные данные:
- расчетное усилие 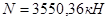 , усредненной значение коэффициента надежности по нагрузке , усредненной значение коэффициента надежности по нагрузке 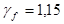 , нормативно усилие , нормативно усилие 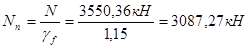 ; ;
- грунт основания под фундаментом – супесью, в пластичном состоянии, непросадочная.
расчетное сопротивление грунта – 0,325 МПа;
- сечение колонн – 40х40 см;
- вес единицы объема бетона фундамента и грунта на его обрезах 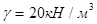 . .
- подготовка под фундамент – гравийная.
Назначением бетон класса В20.
Арматура А-II (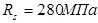 ). ).
В соответствии с конструктивными требованиями, определяем высоту фундамента. Высота фундамента в соответствии с этими требованиями должна быть:
- Достаточной для анкеровки продольной арматурой колонны:
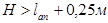 , ,
Длина зоны анкеровки (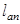 ) продольной арматуры колонны (А-Ш, ) продольной арматуры колонны (А-Ш, 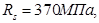 ø32) должна быть не менее, чем: ø32) должна быть не менее, чем:
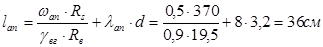
где 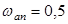 ; ; 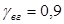 ; ; 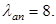
Следовательно, 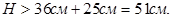
- Достаточной, для обеспечения жесткого защемления колонны сплошного сечения в фундаменте:
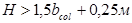
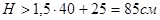
Принимаем высоту фундамента, кратную 30 см, 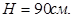 Глубина заложения составляет Глубина заложения составляет 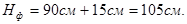
Определяем требуемую площадь подошвы (без поправок на ее ширину и заложение):
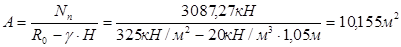
Размер стороны квадратной подошвы 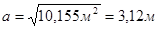
Принимаем размер подошвы 3,2м (кратно 0,3м).
Тогда давление на грунт от расчетной нагрузки:
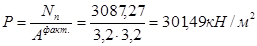 . .
Полезную (рабочую) высоту фундамента вычислим по приближенной формуле:
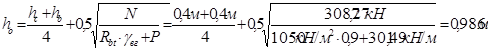
Полная высота фундамента равна:
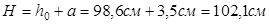
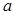 - величина, принимаемая равной 3,5 см, при подготовке под фундамент (7 см – фундаментов без подготовки). - величина, принимаемая равной 3,5 см, при подготовке под фундамент (7 см – фундаментов без подготовки).
Окончательно, с учетом конструктивных требований, принимаем высоту фундамента равную 105 см.
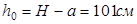
Глубина заложения окончательно: 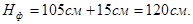
Проверяем величину требуемой площади, с учетом изменения глубины заложения:
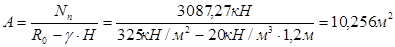
Размер стороны квадратной подошвы 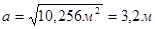 - удовлетворяется. - удовлетворяется.
По форме принимаем фундамент ступенчатым, с 3-мя ступенями т.к 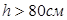 . Высоту ступеней принимаем кратной высоте фундамента, равной 35 см. Размеры ступеней в плане получаем геометрическим построением, соблюдая условие, что бы вертикальные грани ступеней не пересекали пирамиду продавливания. Исходя из этого ширина 2-й ступени принимается шириной 1,8; 3-ей ступени – 1,1м. . Высоту ступеней принимаем кратной высоте фундамента, равной 35 см. Размеры ступеней в плане получаем геометрическим построением, соблюдая условие, что бы вертикальные грани ступеней не пересекали пирамиду продавливания. Исходя из этого ширина 2-й ступени принимается шириной 1,8; 3-ей ступени – 1,1м.
Производим проверку рабочей высоты нижней ступени, на действие поперечной силы без поперечного армирования в наклонном сечении (ширина сечении 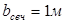 ). ).
Рабочая высота равна: 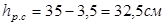 . .
Поперечная сила в наклонном сечении (начинающемся в сечении Ш-Ш):
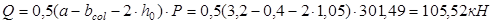
Проверяем условие:
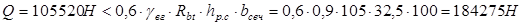
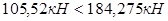 - условие прочности удовлетворяется, высота нижней ступени в 35 см, достаточна. - условие прочности удовлетворяется, высота нижней ступени в 35 см, достаточна.
Вычисляем величины изгибающих моментов в сечениях I-I, II-II, Ш-Ш по формулам:
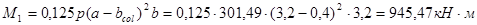
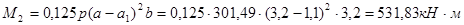
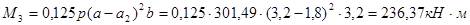
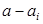 - плечо. - плечо.
Определяем требуемую площадь сечения арматуры в соответствующих сечениях, при 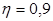 . .
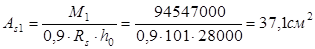
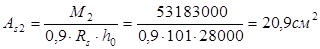
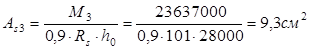
Принимаем нестандартную с одинаковой в обоих направлениях рабочей арматурой из стержней
15ø18 A-II (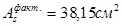 ) c шагом 225мм. ) c шагом 225мм.
Вычисляем процент армирования расчетных сечений:
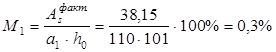
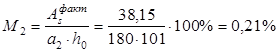
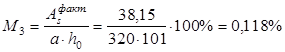
Все значения больше минимального значения 0,05%.
СПИСОК ЛИТЕРАТУРЫ
1.СНиП 2.03.01-84. Бетонные и железобетонные конструкции. М., ЦИТП Госстроя СССР, 1985.
2.Байков В.Н., Стронгин С.Г. Строительные конструкции. М, Стройиздат, 1980.
3.Байков В.Н. , Сигалов Э.Е. Железобетонные конструкции. М,Стройиздат, 1985.
4.Попов НЛ., Забегаев А.В. Проектирование и расчет железобетонных конструкций. М, Высшая школа, 1985.
5.К. Темикеев, Г.Д. Адыракаева, А.К. Стамалиев. “Проектирование железобетонных конструкций”. Бишкек 2005г.
|