Вариант 37
Задача 1
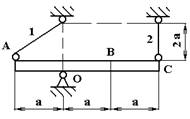
Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стержням с равным поперечным сечением. Площадь сечения стержней А = 2∙10-4
м2
. Модуль упругости материала стержней Е = 2×105
МПа, коэффициент линейного расширения a = 12×10–6
1/град.Размеры бруса: a = 0,5 м, b = 3 м, h = 1м, с = 2 м.
Требуется:
1. Вычислить допускаемую нагрузку [Q], приняв большее из напряжений за допускаемое [s] = 160 МПа.
2. Вычислить допускаемую нагрузку по предельному состоянию [Q]пр
.
3. Сравнить полученные результаты.
4. Вычислить монтажные напряжения в обоих стержнях, если длина второго стрежня короче номинальной на величину d2
= 2∙10-3
м
5. Вычислить напряжения в обоих стержнях, если температура первого стержня увеличится на величину Dt1
= -40°С.
6. Вычислить напряжения в обоих стержнях от совместного действия нагрузки, неточности изготовления второго стержня и изменение температуры первого стержня.

1. Вычислить допускаемую нагрузку [Q], приняв большее из напряжений в стержнях за допускаемое [s].
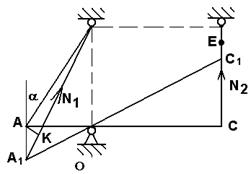
Составляем расчетную схему. Под действием силы Q стержни 1 и 2 будет растягиваться. Вследствие этого появятся внутренние силы N1
и N2
. Составим уравнение моментов относительно точки О:
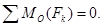
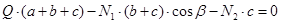
При неизвестных реактивных усилиях N1
, N2
, Rox
, Roy
и трех уравнений статики (плоская система сил) заданная стержневая система является статически неопределимой, и степень статической неопределимости (ССН) определяется:
ССН = m – n,
где m – количество неизвестных реакций, n – количество уравнений. Таким образом, ССН = 4 – 3 =1, то есть для решения данной задачи необходимо составить еще одно дополнительное уравнение, называемое уравнением совместности деформаций.
Составляем уравнение совместности деформаций. Из подобия треугольников АА1
О и СС1
О имеем:
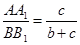 . .
Считаем, что угловые деформации малы, поэтому изменением угла b пренебрегаем.
АА1
=Dl2
, 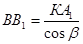 , KА1
=Dl1
. То есть: , KА1
=Dl1
. То есть: 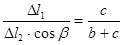
По закону Гука имеем:
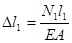 ; ; 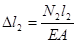 . .
Длину первого стержня определяем по теореме Пифагора:
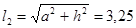 м м
Подставляем значения удлинений в уравнение совместности деформаций:
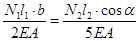 . .
Тогда, 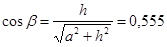 . Окончательно имеем: N2
= 1,3×N2 . Окончательно имеем: N2
= 1,3×N2
Реклама

Из этого выражения видно, что N1
<N2
. Соответственно, напряжения в первом стержне sI
меньше, чем напряжения во втором sII
. Поэтому, максимальные напряжения по абсолютному значению будут во втором стержне: sII
= [s] и 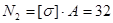 кН. Значение N1
= 24,62 кН. кН. Значение N1
= 24,62 кН.
Оба стержня сжаты.
Найдем напряжения в обоих стержнях: sII
= [s] = -160 МПа; sI
= -123,1 МПа. растянуты.
Подставим значения сил N1
и N2
в первое уравнение и определим значение [Q]:
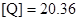 кН. кН.
2. Вычислить допускаемую нагрузку по предельному состоянию [Q]пр
.
Предельное состояние будет возникать, если напряжения в стержнях будут равны предельным, то есть пределу текучести sт
: sI
= sII
= sт
Составляем уравнение предельного равновесия:
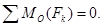 ; ;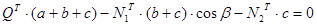 . .
Предельные усилия в каждом из стержней:
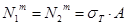 . .
Решаем относительно предельной нагрузки для системы:
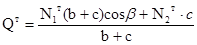 . .
Допускаемая нагрузка по предельному состоянию [Q]пр
определяется как:
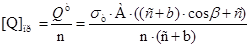 , ,
где n – коэффициент запаса прочности.
С учетом, что 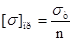 получим [Q]пр
= 23,51 кН. получим [Q]пр
= 23,51 кН.
3. Сравнить полученные результаты.
Определяем погрешность между расчетами:
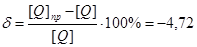 %. %.
По условию предельного состояния допускаемую нагрузку можно не менять (погрешность d < 5%).
4. Вычислить монтажные напряжения в обоих стержнях, если длина второго стержня короче номинальной на величину d2
=1,5 мм.
Составляем расчетную схему. С учетом удлинения стержня 2 точка А должна совпасть с точкой Е, если бы не было стержня 1. Сопротивление первого стержня приводит к тому, что точка А занимает положение А1
. В связи с этим, в стержнях появляются внутренние усилия N1
и N2
. Составим уравнение статики:
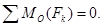 ; ; 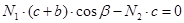
Из этого уравнения следует, что:
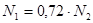
Составляем уравнение совместности деформаций. Из подобия треугольников АА1
О и ВВ1
О имеем:
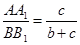 ; ; 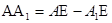
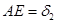 ; ; 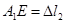 ; ; 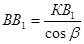
KВ1
=Dl1
.
По закону Гука:
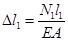 ; ; 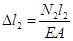 . .
Решая совместно уравнения получим:
N1
= 29,76 кН; N2
= 41,34 кН.
2 стержень сжат; 1 – растянут.
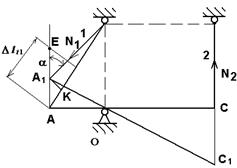
Определим напряжения:
sI
=148,8 МПа; sII
= -206,7 МПа.
5. Вычислить напряжения в обоих стержнях, если температура первого стержня уменьшится на величину Dt1
=40°.
Составим расчетную схему. С учетом удлинения стержня 1 точка В должна совпасть с точкой Е, если бы не было стержня 2. Сопротивление второго стержня приводит к тому, что точка В занимает положение В1
. В связи с этим, в стержнях появляются внутренние усилия N1
и N2
. Составим уравнение статики:
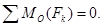 ; ; 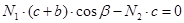
Из этого уравнения следует, что: 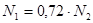
Составляем уравнение совместности деформаций. Из подобия треугольников АА1
О и ВВ1
О имеем:
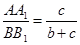 ; ; 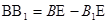 ; ; 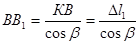 ; ; 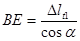 ; ; 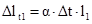 ; АА1
=Dl2
. ; АА1
=Dl2
.
Реклама

По закону Гука:
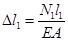 ; ; 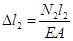 . .
Решая совместно получим:
N1
=5,15 кН; N2
=7,15 кН.
2 стержень сжат; 1 – растянут.
Определим напряжения:
sI
=25,75 МПа; sII
= -35,76 МПа.
5. Вычислить напряжения в обоих стержнях от совместного действия нагрузки, неточности изготовления второго стержня и изменение температуры первого стержня.
Сведем данные расчетов в Таблицу
Таблица 1.
| Фактор, вызывающий напряжения |
Напряжения, МПа |
| 1 стержень |
2 стержень |
| Нагрузка [Q] = 20,96 МПа |
-160 |
-123,1 |
| Неточность изготовления 2-го стержня |
148,8 |
-206,7 |
| Изменение температуры 1-го стержня |
25,75 |
-35,76 |
| ИТОГО |
14,55 |
-365,56 |
Из таблицы видно, что для заданной схемы для стержня 1 сочетания всех трех факторов является благоприятным фактором (напряжения значительно меньше допускаемых), а для стрежня 2 - неблагоприятным: стержень разрушится.
Задача 2
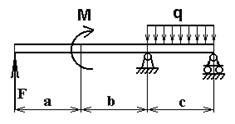
Дана двух опорная балка с приложенными к ней нагрузками М= -15кНм; F=-20 кН; q = 12 кН/м. Допускаемое напряжение [s] = 160 МПа. размеры балки a = 0,8 м; b = 0,7 м; c = 0,5 м.
Требуется:
1. Подобрать для схем (а) балку круглого, прямоугольного (отношение сторон h/b=2), кольцевого (отношение диаметров с=0,5), двутаврового сечений при заданном [s];
2. Сравнить площади поперечных сечений и сделать вывод о том, какая форма наиболее рациональна.
Решение
1. Определяем опорные реакции балки.
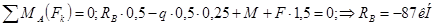
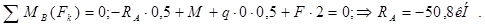
Проверяем правильность определения опорных реакций:
 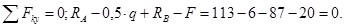
Реакции определены верно.
2. Запишем уравнения поперечных сил и изгибающих моментов для каждого участка балки.
Участок
I
. О ≤
Z
1
≤0,8
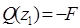 ; ; 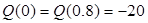 кН; кН;
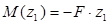 ; ; 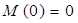 ; ; 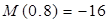 кНм. кНм.
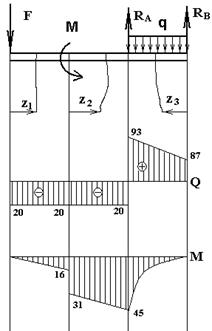
Строим эпюры по вычисленным значениям.
Участок
П. 0 <
Z
2
< 0,7
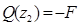 ; ; 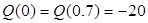 кН; кН;
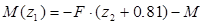 ; ; 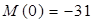 кН×м; кН×м; 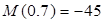 кН×м. кН×м.
Строим эпюры по вычисленным значениям.
Участок
I
П.
0 <
Z
3
< 0,5
Q(z3
) = -RВ
+ q×z3
; Q(0) = 87 кH; Q(0.5) = 93 кН
M(z3
)= RВ
z3
– q×z3
×z3
×0.5; M(0) = 0; M(0.5)= -45 кH×м
3. Опасным будет сечение, в котором изгибающий момент достигает максимального значения по абсолютной величине.
В данной задаче Mmax
= 45 кН×м.
Вычисляем необходимый момент сопротивления поперечного сечения балки
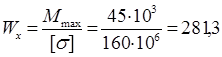 см3
. см3
.
3.1. Двутавровое поперечное сечение.
Этому моменту сопротивления соответствует двутавр №24, момент сопротивления и площадь поперечного сечения которого соответственно равны Wx
=289 cм3
; А= 34,8 см2
.
3.2. Прямоугольное сечение (h/b = 2).
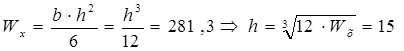 см см
h=15 см; b=7,5 см; А=112,5 см2
.
3.3. Круглое поперечное сечение:
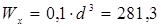 ,
,
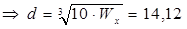 см см
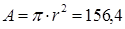 см2
. см2
.
3.4. Кольцевое сечение (с = 0,7).
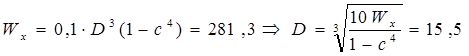 см см
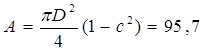 см2 см2
3. Сравниваем площади поперечных сечений А, подобранных профилей, сведя данные в Таблицу 2:
Таблица 2.
| Тип сечения |
Площадь сечения, см2
|
| Двутавровое |
38,4 |
| Прямоугольное |
112,5 |
| Круглое |
156,4 |
| Кольцевое |
95,7 |
Таким образом, при изгибе оптимальным является сечение двутавра.
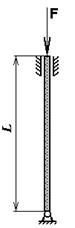
Задача 3
Дан стержень с опорами, закрепленными по указанной схеме, сжат силой F = 90 кН. Поперечное сечение – равносторонний треугольник. Длина стержня 1
= 0,85 м. Материал стержня - чугун. Модуль упругости Е = 1,3×105
МПа, допускаемое напряжение [σ] = 130 МПа. Коэффициент закрепления опор m = 0,7
Требуется определить:
- размеры поперечного сечения при допускаемом напряжении на сжатие [σ];
- величину критической силы Fk
;
- коэффициент запаса устойчивости nу
.
Решение.
Задача решается методом приближения. В первом приближении задаемся коэффициентом уменьшения основного допускаемого напряжения j1
= 0,5. Из условия устойчивости определяем площадь сечения:
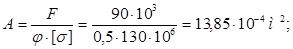
Из площади сечения находим сторону сечения b:
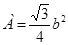 Þ Þ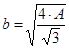 = 4,3 см. = 4,3 см.
Определяем минимальный радиус инерции по формуле:
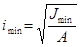 , где , где 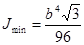 . .
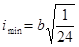 =0,88 см =0,88 см
Определяем гибкость стержня:
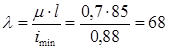
По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j' = 0,36. Производим проверку на устойчивость:
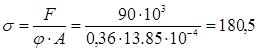 МПа > [s] МПа > [s]
Так как σ > [σ], то задаемся новым значением φ и повторяем весь расчет.
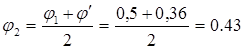
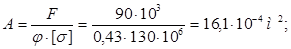
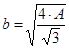 =6,1 см. =6,1 см. 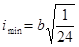 = 1,24 см. = 1,24 см.
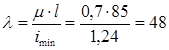
По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j' = 0,6. Производим проверку на устойчивость:
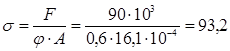 МПа МПа
Допускаемая погрешность не более 5%. Определяем погрешность
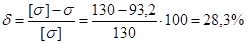
Погрешность больше допустимой, поэтому задаемся новым значением φ и повторяем весь расчет.
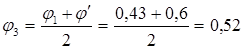
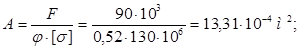
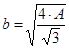 =5,54 см. =5,54 см. 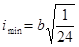 = 1,13 см. = 1,13 см.
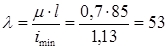
По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j' = 0,46. Производим проверку на устойчивость:
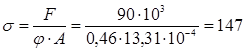 МПа МПа
Определяем погрешность
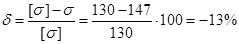
Погрешность не находится в допускаемых пределах.
Задаемся новым значением φ и повторяем весь расчет.
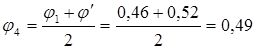
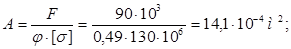
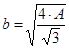 =5,71 см. =5,71 см. 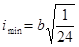 = 1,16 см. = 1,16 см.
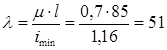
По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j' = 0,56. Производим проверку на устойчивость:
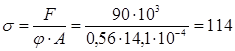 МПа МПа
Определяем погрешность
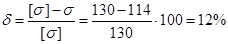
Погрешность не находится в допускаемых пределах.
Задаемся новым значением φ и повторяем весь расчет.
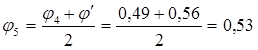
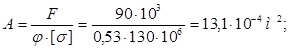
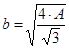 =5,5 см. =5,5 см. 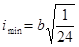 = 1,12 см. = 1,12 см.
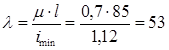
По таблице находим соответствующее значение коэффициента уменьшения основного допускаемого напряжения j' = 0,46. Производим проверку на устойчивость:
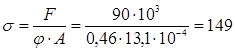 МПа МПа
Значения повторяются. Поэтому принимаем b = 5,71 см, А = 14,1 см2
.
Определяем критическую силу:
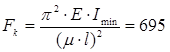 кН. кН.
Определяем коэффициент запаса устойчивости:
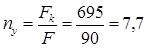
Ответ: FK
=695 кН; nу
= 7,7.
|