Донецкий национальный технический университет
Квалификационная работа
На тему:
Разработка динамической модели привода с фрикционным вариатором
Выполнил:
Студент гр. МС-03н: Касатка П.О.
Руководитель: Деркач О.В.
Консультант: Горобець I.О.
ДОНЕЦЬК 2007
РЕФЕРАТ
Бакалаврская работа: 38 страниц, 15 рисунков, 1 приложение, 1 таблица, 5 источников.
В данной бакалаврской работе необходимо разработать динамическую модель привода, содержащего фрикционный вариатор; составить дифференциальные уравнения, которые описывают динамические процессы в приводе.
Объект исследования: привод с фрикционным вариатором.
Цель работы: необходимо разработать динамическую модель привода, содержащего фрикционный вариатор, с помощью программного пакета MatLab Sіmulіnk, для обеспечения необходимых параметров переходного процесса.
ФРИКЦИОННЫЙ ВАРИАТОР, ПЕРЕХОДНЫЙ ПРОЦЕСС, ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ, ДИНАМИЧЕСКАЯ МОДЕЛЬ, ГЕОМЕТРИЧЕСКОЕ СКОЛЬЖЕНИЕ, МОМЕНТ ИНЕРЦИИ
Содержание
Введение
1 Общие сведения о фрикционных вариаторах
2 Исходные данные
3 Проектный расчет фрикционного вариатора по контактным напряжениям
4 Разработка динамической модели
4.1 Структурная схема объекта и процесса в нем
4.2 Анализ допущений и факторов, принимаемых при создании модели
4.3 Динамическая модель
4.4 Определение инерционных характеристик подвижных деталей и жесткости элементов привода
4.5 Реализация динамической модели в Simulink
5 Анализ динамических процессов в объекте
5.1 Анализ динамических процессов во временной области
5.2 Представление динамической модели в пространстве состояний
5.3 Проектирование модального регулятора
Заключение
Перечень ссылок
Приложение
Вступление
Большинство современных машин и установок создается по схеме: двигатель – передача – рабочий орган (исполнительный механизм). Необходимость введения передачи как промежуточного звена между двигателем и рабочими органами машины связано с решением задачи повышения производительности, т.е. увеличения их быстродействия.
Время срабатывания фрикционной передачи входит в общее время рабочего цикла машины, следовательно, влияет на производительность машины в целом. Проблема повышения производительности непосредственно связана с разработкой методов динамического исследования машин и выбора их оптимальных параметров и структуры.
Реклама

С помощью динамической модели производится анализ системы, без участия реального объекта и на ее основе можно построить систему управления объектом, и пронаблюдать поведение системы управления и объекта.
1 Общие сведения о фрикционных вариаторах
Фрикционной называют передачу, работа которой основана на использовании сил трения, возникающих в месте контакта двух тел вращения под действием сжимающей силы Q.
Фрикционные передачи вращательного движения можно разделить на две основные группы: передачи нерегулируемые, т.е. с условно постоянным передаточным отношением, и передачи регулируемые, позволяющие плавно изменять передаточное отношение (бесступенчатое регулирование) (рис. 1.1).
Одной из наиболее простых и во многих случаях достаточно надёжной является фрикционная передача, состоящая в простейшем случае из двух колёс (катков), закреплённых на ведущем и ведомом валах. Для передачи движения без скольжения необходимо приложить к одному из колёс силу Q, достаточную для возникновения трения в месте контакта, при этом касательная сила их сцепления равна по величине передаваемого окружному усилию [1].
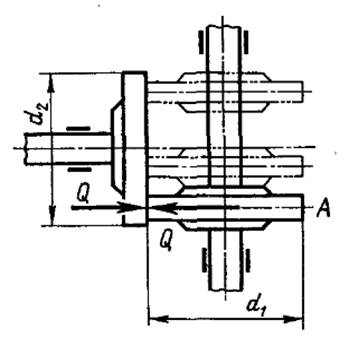
Рисунок 1.1 – Лобовой фрикционный вариатор
Достоинствами фрикционных передач являются: плавность и бесшумность в работе, простота конструкции, невозможность поломки при резком изменении крутящего момента на одном из валов благодаря возможности проскальзывания катков, возможность бесступенчатого регулирования скоростей на ходу, без остановки передачи.
Недостатками являются: необходимость прижимного устройства, большие давления на валы и опоры от действия внешней силы прижимного устройства, что увеличивает их размеры и делает передачу громоздкой, а также ограничивает величину передаваемой мощности; непостоянство передаточного отношения из-за проскальзывания катков; сравнительно высокий износ.
Фрикционные вариаторы применяют как в кинематических, так и силовых передачах в тех случаях, когда требуется бесступенчатое регулирование скорости (зубчатая передача не позволяет такого регулирования). Фрикционные вариаторы используются станкостроении, в литейных машинах, подъемных и транспортных машинах, приводах летательных аппаратов и металлорежущих станках, роботах и манипуляторах, цифровых следящих системах, механизмах для сельского хозяйства и других изделиях.
Значение фрикционных вариаторов как бесступенчатых регуляторов скорости возрастает в связи с широким фронтом работ по автоматизации управления производственными процессами.
Реклама

Один из катков фрикционного вариатора изготовляют из качественных сталей (40, 50, ШХ15 и т.д.), а другой – из серого чугуна, текстолита, фибры и других пластмасс.
Из всех типов фрикционных бесступенчатых передач с твердыми телами касания лобовые фрикционные вариаторы конструктивно наиболее просты. В таком вариаторе возможно перемещать колесо по валу в направлениях, указанных стрелками, при этом передаточное отношение будет плавно меняться в соответствии с изменением рабочего диаметра диска.
Геометрическое скольжение вариатора определяют по формуле:

знак «+» - для ведущего колеса, знак «-» - для ведущего диска (рис 1.2 а и б),
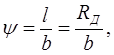
где 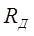 - радиус диска, при - радиус диска, при 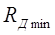 скольжение максимальное; скольжение максимальное;
b – ширина диска.
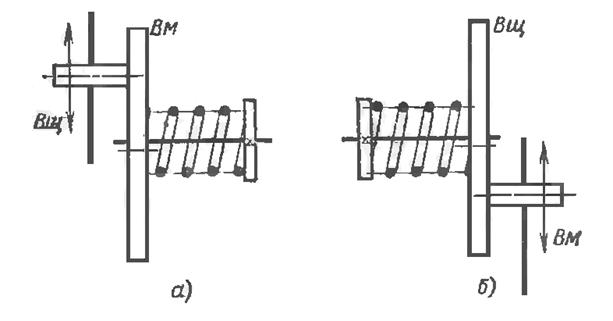
Рисунок 1.2 – Лобовой фрикционный вариатор:
а) с ведущим колесом; б) с ведущим диском
Основной недостаток лобовых вариаторов – большое геометрическое скольжение, поэтому в силовых передачах их диапазон регулирования передаточного отношения приходится ограничивать 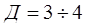 . .
При ведущем колесе его радиус определяют по формуле:
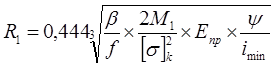 ;
;
где 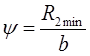 . .
При проектном расчете принимают:
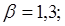 - коэффициент запаса сцепления; - коэффициент запаса сцепления;
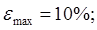
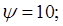
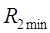 - минимальный рабочий радиус диска. - минимальный рабочий радиус диска.
Рабочие поверхности стальных фрикционных колес выполняются шлифованными с шероховатостью Ra 0,63 ... 0,32 мкм.
Соединение дисков с валами рекомендуется осуществлять шариковыми или винтовыми нажимными устройствами (рис. 1.3).
Во избежание чрезмерного скольжения центральную часть диска использовать не следует.
Расчет на контактные напряжения следует вести на минимальном диаметре диска, при котором требуется наибольшая сила нажатия и скольжение достигает наибольшей величины.
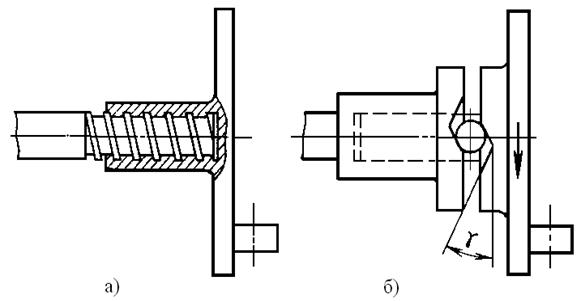
Рисунок 1.3 – Нажимные устройства: а) винтовое; б) шариковое
2
Исходные данные
Рассчитаем лобовую фрикционную передачу для привода ленточного конвейера при условии, что ведущее колесо передает мощность Р= 2 кВт при угловой скорости ω1
=90 рад/с ведомому колесу, вращающемуся с угловой скоростью ω2max
= 45 рад/с [2].
В качестве прижимного устройства выбираем винтовое прижимное устройство, обеспечивающее постоянную силу прижатия.
Назначаем материалы колес: меньшего — текстолит ПТК, а большего — сталь 45.
Принимаем диапазон регулирования передаточного отношения 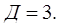
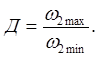
Тогда,
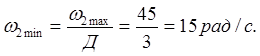
Передаточное отношение определяем по формуле:
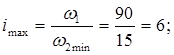
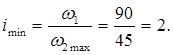
Крутящий момент Мn
, передаваемый ведущим колесом
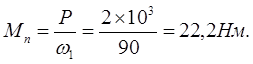
Для передачи заданной мощности, выраженной окружной силой 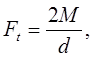 необходимо обеспечить условие необходимо обеспечить условие 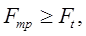 где где 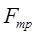 — сила трения между катками. — сила трения между катками.
Тогда
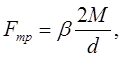
где β – коэффициент запаса сцепления колес, β=1,3.
Момент трения определяем по формуле:
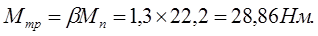
3 Проектный расчет фрикционного вариатора
по контактным напряжениям
Определим диаметр d1
меньшего колеса из условия контактной прочности. Принимаем коэффициент запаса сцепления колес β=1,3; коэффициент трения по длине контактной линии f=0,3; допускаемое контактное напряжение (текстолит по стали) [σ]k
= 70 Н/мм2
, модуль упругости для меньшего колеса (текстолит) Е1
=6х103
МПа, для большего колеса (сталь) Е2
= 2,15х105
МПа.
Приведенный модуль упругости Е по формуле:
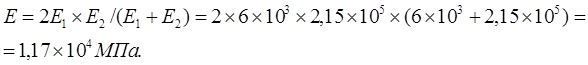
Диапазон регулирования:
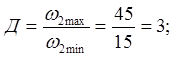
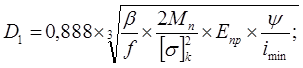
где 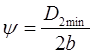 . .
При проектном расчете принимают 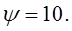
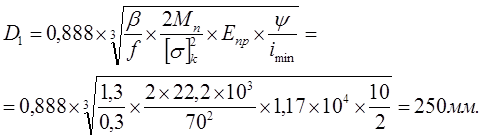
Конструктивно наибольший диаметр диска:
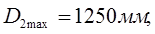
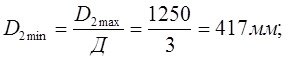
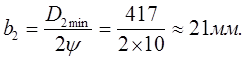
Геометрическое скольжение при ведущем колесе:
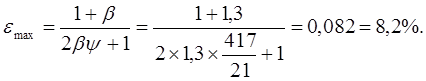
Остальные размеры колес принимают конструктивно.
4 Разработка динамической модели
4.1 Структурная схема объекта
Рассматриваемая система состоит из электродвигателя, который создает момент двигателя Мn
, муфты, ведущего колеса, ведомого диска, подшипников качения и рабочего органа. Двигатель создает крутящий момент с угловой скоростью ω, который передается через муфту на ведущее колесо, с него на ведомый диск, затем на рабочий орган (рис. 3.1). Винтовое прижимное устройство обеспечивает передачу крутящего момента.
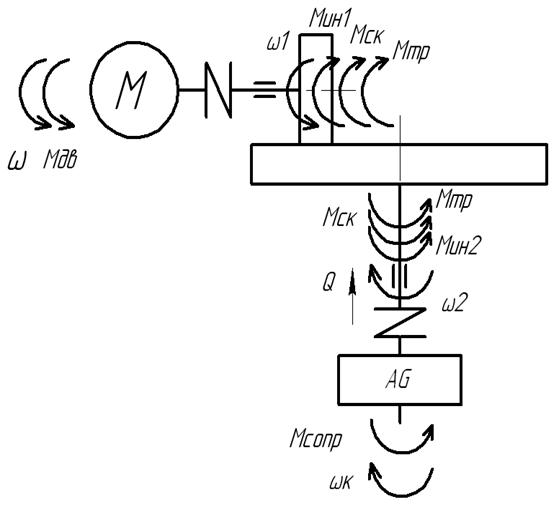
Рисунок 4.1 – Расчетная схема привода.
4.2 Анализ допущений, принимаемых при создании модели
Для создания модели принимаем электродвигатель, обеспечивающий постоянный крутящий момент, муфты с η =0,98, шариковые подшипники качения с η=0,99 и роликовые подшипники качения с η=0,97. Деформации колеса и диска не учитываются.
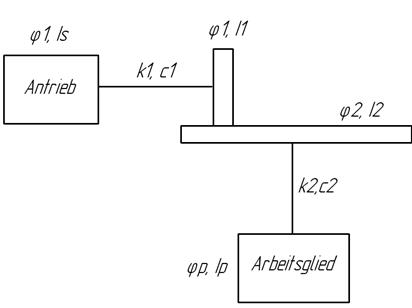
Рисунок 4.2 – Модель лобовой передачи
4.3 Динамическая модель
Модель имеет 4 степени свободы и движение тел, входящих в модель, описывается системой дифференциальных уравнений, на основании результатов решения которой получим динамические параметры привода. Система дифференциальных уравнений имеет вид [3]:
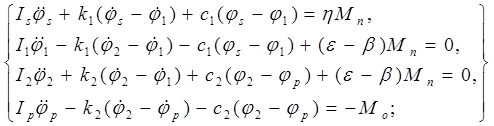
где Is
, Ip
– приведенные моменты инерции вращающихся деталей двигателя и рабочего органа;
I1
, I2
– приведенные моменты инерции колеса и диска соответственно;
φs
, φp
, φi
– угловые координаты вращающихся масс;
Мn
– момент движущих сил (двигателя);
Мо
– момент сил сопротивления (рабочего органа);
с1
, с2
– жесткости валов;
k1
, k2
– коэффициенты демпфирования;
ε – геометрическое скольжение.
На основании дифференциальных уравнений, которые описывают поведение привода в процессе работы, была составлена его динамическая модель. Далее выполняем исследование составленной модели. Нагружаем модель единичным ступенчатым воздействием, которое воздействует на вал двигателя.
4.4 Определение инерционных характеристик подвижных
деталей и жесткости элементов привода
Моменты инерции вращающихся звеньев определяются расчетным путем [4]. Приведенный момент инерции вращающихся деталей двигателя:
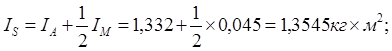
где
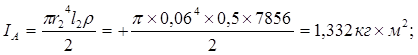
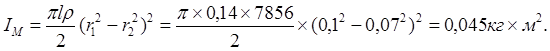
Приведенный момент инерции вращающихся деталей рабочего органа:
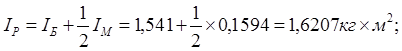
где
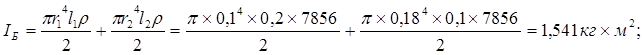 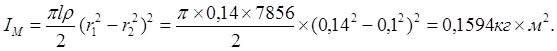
Приведенный момент инерции колеса:
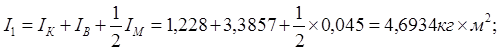
где
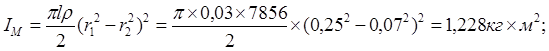
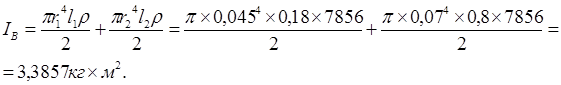
Приведенный момент инерции диска:
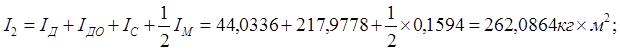
где
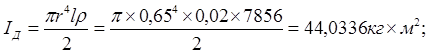
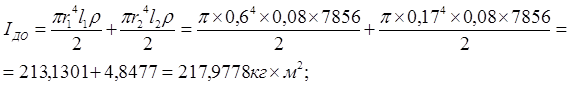
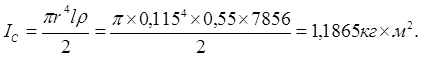
Рассчитаем жесткости валов:
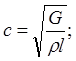
где 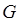 - модуль упругости 2-го рода (сдвига), - модуль упругости 2-го рода (сдвига),
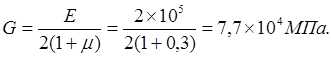
Жесткость шлицевого вала:
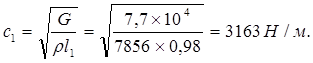
Жесткость винта:
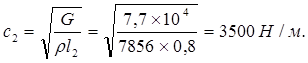
4.5 Реализация динамической модели в Simulink
На основе системы дифференциальных уравнений (п. 4.3) с помощью интерактивной системы Simulink для моделирования нелинейных динамических систем составим схему динамической модели привода с фрикционным вариатором (рис. 4.3). Обозначения переменных, используемых в схеме динамической модели приведены в таблице 4.1.
Таблица 4.1 - Обозначения переменных, используемых
в динамической модели
| Описание переменной |
Обозначение |
Схема |
Ед. |
| Приведенный момент инерции вращающихся деталей двигателя |
Is
|
Is |
кг*м2
|
| Приведенный момент инерции вращающихся деталей рабочего органа |
Ip
|
Ip |
кг*м2
|
| Приведенный момент инерции колеса |
I1
|
I1 |
кг*м2
|
| Приведенный момент инерции диска |
I2
|
I2 |
кг*м2
|
| Угловые координаты вращающихся масс |
φs
, φp
, φi
|
- |
рад |
| Момент движущих сил (двигателя) |
Мn
|
Mn |
Н*м |
| Момент сил сопротивления (рабочего органа); |
Мо
|
Мо |
Н*м |
| Жесткость шлицевого вала |
с1
|
с1 |
Н/м |
| Жесткость винта |
с2
|
с2 |
Н/м |
| Коэффициент демпфирования |
k1
|
k1 |
- |
| Коэффициент демпфирования |
k2
|
k2 |
- |
| Коэффициент запаса сцепления колес |
β |
b |
- |
| Геометрическое скольжение |
ε |
е |
- |
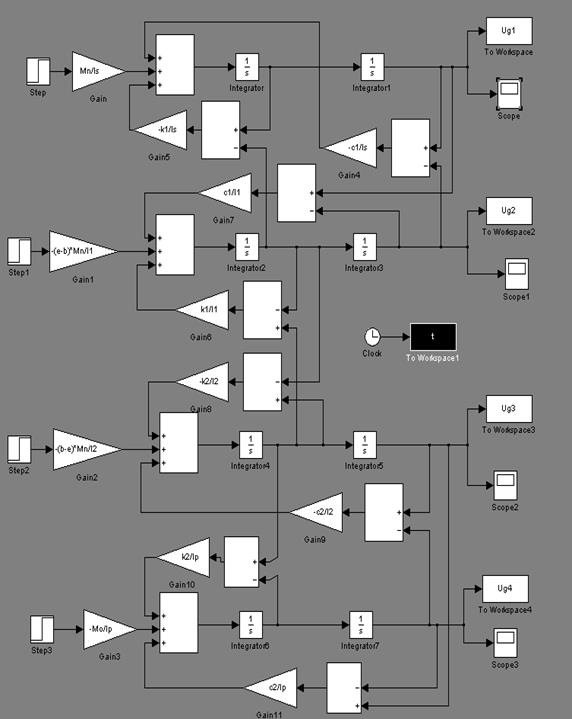
Рисунок 4.3 – Реализация динамической модели в Simulink
Исходные данные:
Is=1.3545;
Ip=1.6205;
I1=4.6934;
I2=262.0864;
c1=3163;
c2=3500;
Mn=22.2;
Mo=15;
e=0.08;
k1=0.7;
k2=0.7;
b=1,3.
5 Анализ динамических процессов в объекте
5.1 Анализ динамических процессов во временной области
Из анализа графиков видно, что из-за инерционных свойств объектов,
из-за упругих свойств, геометрического скольжения и силы трения разгон системы происходит замедленно. Перемещение диска в период первой секунды приложения крутящего момента вал двигателя, практически равно нулю (рис. 5.1–5.4).
Это обусловлено упругими свойствами вала и винта и инерционными свойствами колеса и диска, поэтому в момент пуска происходит задержка вращения, затем при преодолении крутящим моментом момента проскальзывания происходит вращение диска.
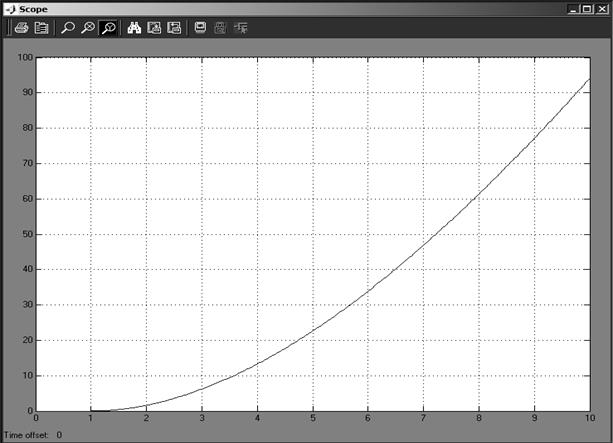
Рисунок 5.1 – Зависимость угла поворота вала двигателя (рад) от времени (с)

Рисунок 5.2 – Зависимость угла поворота колеса (рад) от времени (с)
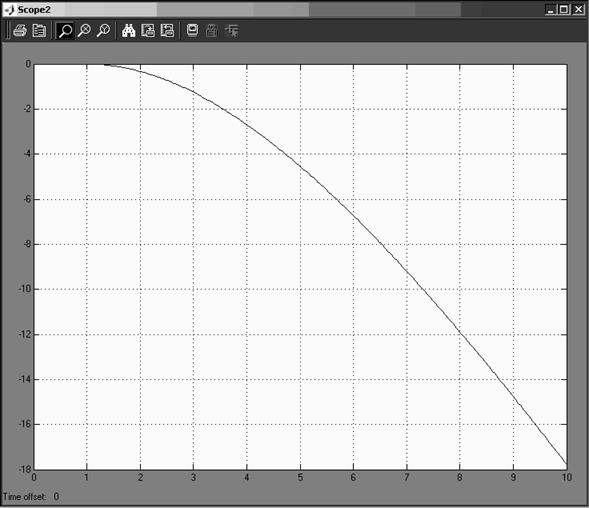
Рисунок 5.3 – Зависимость угла поворота диска (рад) от времени (с)

Рисунок 5.4 – Зависимость угла поворота рабочего органа (рад) от времени (с)
5.2 Представление динамической модели
в пространстве состояний
Динамическая модель, описанная дифференциальными уравнениями, может быть представлена в форме матричных уравнений (матрицы А, В, С, D) или представлена в виде передаточной функции. Так как модель имеет 4 степени свободы, то преобразование Лапласа необходимое для получения передаточной функции произвести достаточно трудно. Поэтому представим модель в форме матриц, используя для их расчета интерактивную систему MATLAB.
Дифференциальные уравнения динамической модели:
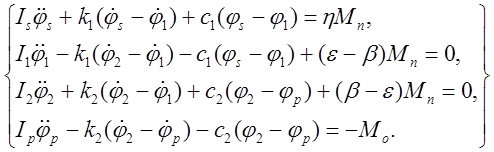
Преобразуем систему.
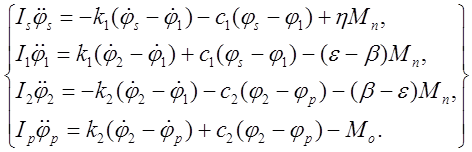
Представим модель в матричной форме:
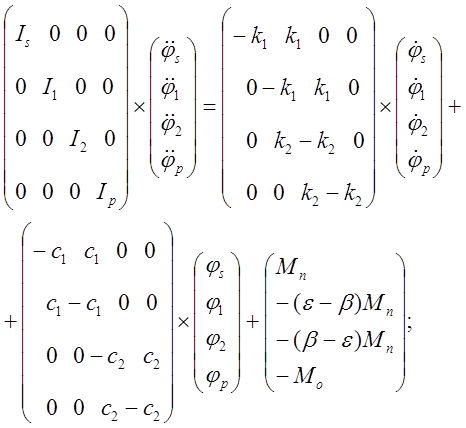
Введем следующие обозначения:
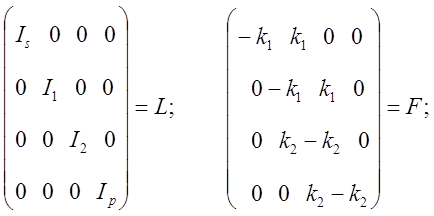
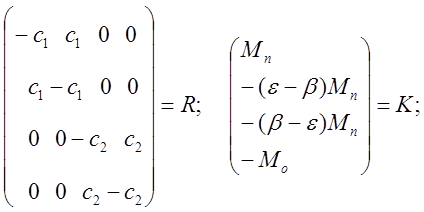
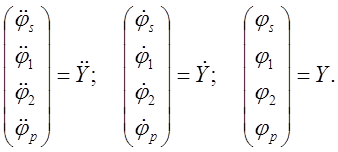
Динамическая модель принимает вид:
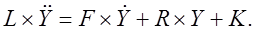
Умножим обе части уравнения на обратную матрицу 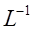 : :
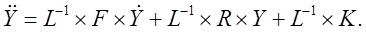
Обратную матрицу 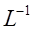 с помощью MATLAB: с помощью MATLAB:
L=[Is 0 0 0; 0 I1 0 0; 0 0 I2 0; 0 0 0 Ip];
inv(L)
ans =
0.7383 0 0 0
0 0.2131 0 0
0 0 0.0038 0
0 0 0 0.6171.
Умножим обратную матрицу 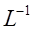 на матрицу на матрицу 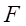 : :
F=[-k1 k1 0 0; 0 -k1 k1 0; 0 k2 -k2 0; 0 0 k2 -k2];
ans =
-0.7000 0.7000 0 0
0 -0.7000 0.7000 0
0 0.7000 -0.7000 0
0 0 0.7000 -0.7000
ans=inv(L)*F
ans =
-0.5168 0.5168 0 0
0 -0.1491 0.1491 0
0 0.0027 -0.0027 0
0 0 0.4320 -0.4320
Умножим обратную матрицу 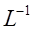 на матрицу на матрицу 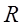 : :
R=[-c1 c1 0 0;c1 -c1 0 0; 0 0 -c2 c2; 0 0 c2 -c2];
ans=R
-3163 3163 0 0
3163 -3163 0 0
0 0 -3500 3500
0 0 3500 -3500
ans=inv(L)*R
ans =
1.0e+003 *
-2.3352 2.3352 0 0
0.6739 -0.6739 0 0
0 0 -0.0134 0.0134
0 0 2.1598 -2.1598
Умножим обратную матрицу 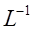 на матрицу на матрицу 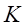 : :
К=[Mn; -(e-b)*Mn; -(b-e)*Mn; -Mo];
ans=K
22.2000
27.0840
-27.0840
-15.0000
ans=inv(L)*К
16.3898
5.7707
-0.1033
-9.2564
Матрицы А, В, С, D имеют вид:
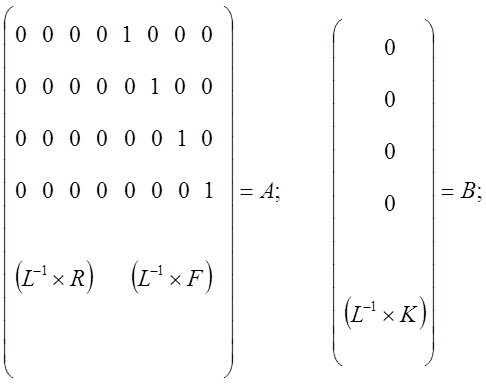
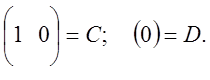
Введем полученные матрицы в M-file MATLAB и получим передаточную функцию динамической модели, которая описывает реакцию модели на скачкообразное задающее воздействие (рис. 5.5, 5.6).
A=[0 0 0 0 1 0 0 0;
0 0 0 0 0 1 0 0;
0 0 0 0 0 0 1 0;
0 0 0 0 0 0 0 1;
-2335.2 2335.2 0 0 -0.5168 0.5168 0 0;
673.9 -673.9 0 0 0 -0.1491 0.1491 0;
0 0 13.4 13.4 0 0.0027 -0.0027 0;
0 0 2159.8 -2159.8 0 0 0.4320 -0.4320];
B=[0; 0; 0; 0; 16.3898; 5.7707; -0.1033; -9.2564];
C=[1 0]; D=[0].
Передаточная функция имеет вид:
W(s) = (-2.132e-014 s^7 + 16.39 s^6 + 6.586 s^5 + 3.275e004 s^4 - 2343 s^3- 6.166e006s^2 - 7.573e004 s + 1.407e008)/(s^8 + 1.101 s^7 + 5156 s^6 + 3080 s^5 + 6.401e006 s^4 + 6.915e005 s^3 - 1.742e008 s^2 - 2.015e007 s + 2.25e-007).
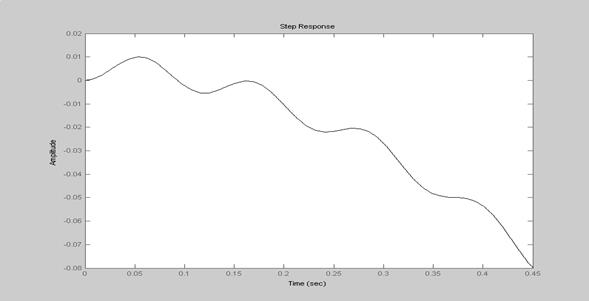
Рисунок 5.5 – Переходной процесс в динамической модели
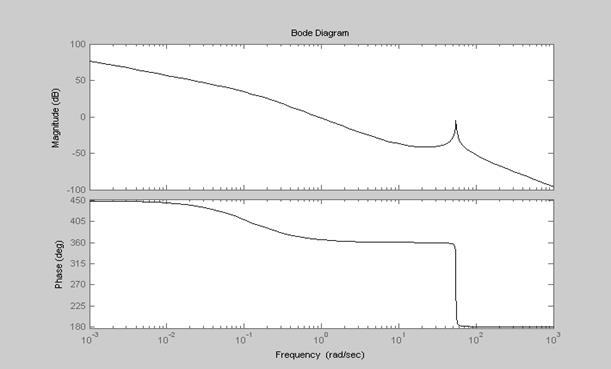
Рисунок 5.6 – Амплитудно-фазо-частотная и фазо-частотная характеристики
Из анализа графиков видно, что колебания в модели возрастают и она не устойчива. Поэтому необходимо спроектировать регулятор (корректирующее звено) (рис. 5.7), чтобы динамическая модель имела затухающие колебания при переходном процессе и малое время успокоения (1-5 секунд) с перерегулированием не более 10-15%.
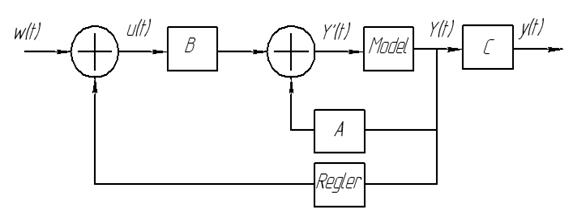
Рисунок 5.7 – Динамическая модель с модальным регулятором
5.4 Проектирование модального регулятора
Идея создания модального регулятора заключается в том, чтобы подобрать его коэффициенты так, чтобы полюса замкнутого контура регулирования оказались в заштрихованной области. Это обеспечит затухающие колебания при переходном процессе и малое время успокоения с перерегулированием не более 10-15% (рис. 5.7).
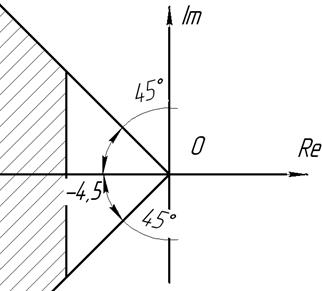
Рисунок 5.8 – Область расположения полюсов устойчивых систем
Для построения модального регулятора необходима проверка управляемости модели.
Проверку управляемости произведем с помощью критерия Калмана:
если ранг квадратной матрицы Ss(n,n)=[B A*B A2
*B … An-1
*B] равен порядку матрицы n, то модель, описываемая матрицами А, В, С, D, является управляемой. Порядок матрицы А динамической модели равен 8.
Ранг матрицы – максимальный размер квадратной матрицы, определитель которой не равен нулю.
Ранг матрицы можно определить с помощью функции rank
в MATLAB:
Ss=ctrb(A,B);
rank(Ss);
ans=8.
Ранг матрицы А динамической модели равен порядку, значит модель управляема.
Методом подбора назначаем полюса для новой передаточной функции замкнутого контура. С помощью MATLAB можно найти коэффициенты модального регулятора и получить переходной процесс в динамической модели с регулятором (рис. 5.9).
p=[-7-0.2i -7+0.2i -5-0.5i -5+0.5i -5 -6 -17 -10];
k=place(A,B,p);
sysE=ss(A-B*k,B,C,D);
step(sysE)
Коэффициенты модального регулятора:
k=[-237.0116 237.0565 173.5746 -185.8740 8.6474 -8.5860 16.0462 14.2642].
Из анализа графика на рисунке 5.7 видно, что переходной процесс в системе заканчивается через 2,5 секунды без перерегулирования.
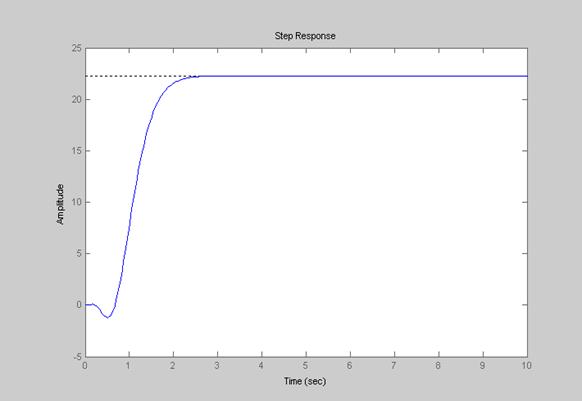
Рисунок 5.9 – Переходной процесс в динамической модели c регулятором
Заключение
В данной работе были изучены динамические процессы, возникающие в приводе с фрикционным вариатором. Выбраны исходные данные, приведен проектный расчет фрикционного вариатора, определены инерционные характеристики подвижных деталей и жесткости элементов привода.
Была составлена структурная схема объекта исследования, математическое описание и динамическая модель, позволяющие изучить возможное поведение системы при действии на неё единичной нагрузки.
Также приведен анализ динамических процессов в объекте во временной области и пространстве состояний. Спроектирован модальный регулятор, который обеспечивает завершение переходного процесса в динамической модели за 2,5 секунды.
Литература
1. Гузенков П.Г. Детали машин: Учеб. для вузов. – М.: Высш. шк., 1986. – 359 с.
2. Бакаев Н.А., Волошина О.Н. Основы проектирования фрикционных передач. – Издательство Ростовского университета, 1985. – 176 с.
3. Пронин Б.А., Ревков Г.А. Бесступенчатые клиноременные и фрикционные передачи. – М.: Машиностроение, 1980. – 320 с.
4. Комаров М.С. Динамика механизмов и машин. Машиностроение, М., 1969.
5. Иванов Е.А. Муфты приводов. Машгиз, М, 1959.
|