Статистические распределения и их основные характеристики
План
1. Вариация признаков в совокупности и значение её изучения
2. Основные характеристики и графическое изображение вариационного ряда
3. Показатели центра распределения
4. Показатели колеблемости признака
Составной частью сводной обработки данных статистического наблюдения является построение рядов распределения. Цель его - выявление основных свойств и закономерностей стат. совокупности.
Различают два типа рядов распределения:
атрибутивный;
вариационный.
Ряды распределения, построенные по качественным признакам, называют атрибутивными
. (Например, распределение население по полу, характеру труда, национальности и т.д.)
Ряды распределения, построенные по количественному признаку называются вариационными
. Числовые значения признака - вариантами.
Например, себестоимость 1 кВт/ч электроэнергии по различным тепловым станциям:
| Станции |
1 |
2 |
3 |
4 |
5 |
| с/с 1кВт/ч руб |
0,58 |
0,66 |
0,59 |
0,67 |
0,66
|
Здесь представлены четыре варианты признака в пределах от 0,58 до 0,67 руб. Колебания себестоимости 1 кВт/ч электроэнергии на различных ТЭЦ обусловлены различными факторами, часто действующими в противоположных направлениях (например, снижение уд. расхода топлива ведёт к снижению себестоимости 1 кВт/ч, а повышение цен на топливо - к увеличению себестоимости). В результате совместного действия многих факторов складывается величина собственности 1 кВт/ч на отдельных ТЭЦ.
Изучение характера и степени вариации признаков и отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Данные о стоимости 1 кВт. ч электроэнергии по 5 ТЭЦ образуют так называемый первичный ряд. При наличии достаточно большого количества вариантов значений признака первичный ряд становится труднообозримым и непосредственное рассмотрение его не дает представления о распределении единиц по величине признака в совокупности. Первым шагом в упорядочении первичного ряда является его ранжирование, т.е. расположение всех вариантов ряда в возрастающем (или убывающем) порядке x1
£x2
£…£xi
£…£ xn.
В нашем примере ранжированный ряд имеет вид:
| 1 |
3 |
2 |
5 |
4 |
| 0,58 |
0,59 |
0,66 |
0,66 |
0,67 |
Рассматривая первичный ряд можно видеть, что варианты признака у отдельных единиц совокупности повторяются.
Реклама

Число повторений отдельных вариантов называют частотой
(обозначим ƒ)
Сумма частот, равная объему изучаемой совокупности - n.
По характеру вариации
различают дискретные и непрерывные признаки.
Дискретные
признаки отличаются друг от друга на некоторую конечную величину, т.е. даны в виде конкретных чисел. (Например, число детей в семье).
Непрерывные
признаки могут отличаться друг от друга на сколь угодно малую величину и в определенных границах принимать любые значения. Например, зарплата рабочих, % выполнения.
Способы
построения вариационного ряда для этих видов признаков различны
. Для построения дискретного ряда с небольшим числом вариантов достаточно перечислить все встречающиеся варианты значений признака (xi
), а затем подсчитать частоту повторений каждого варианта ƒi. (
Например, распределение студентов по успеваемости и т.п.)
Ряд распределения принято оформлять в виде таблицы, например, распределение рабочих участка по квалификации.
Таблица 1.
| Тарифный разряд рабочего (xi
) |
Число рабочих, имеющих этот разряд (ƒi
) |
Частости
(vi
)
|
Накопление частоты (Si
) |
| 1 |
2 |
3 |
4 |
| 2 |
1 |
0,05 |
1 |
| 3 |
5 |
0,25 |
6 |
| 4 |
8 |
0,40 |
14 |
| 5 |
4 |
0, 20 |
18 |
| 6 |
2 |
0,10 |
20 |
| Итого |
20 |
1,00 |
Таким образом, ряд первичных данных, характеризующих квалификацию двадцати рабочих, заменен коротким рядом, состоящим из 5 групп. Вместо абсолютного числа рабочих, имеющих определенный разряд, можно установить долю рабочих этого разряда.
Частоты, представленные в относительном выражении, называют частостями
(выражаются в долях единиц или %, обозначаются vi
).
В случаях, когда число вариантов дискретного признака велика, а также при анализе вариации непрерывного признака строятся интервальные ряды распределения.
Интервал указывает пределы значений варьирующего признака и обозначаются нижней и верхней границами интервала. Такие распределения наиболее распространены в практике статистической работы.
При построении интервальных рядов необходимо прежде всего установить число групп (интервалов). Для этого нужно определить величину интервала (h). Для построения вариационного ряда с равными интервалами следует:
определить размах вариации (
R)
- разность между максимальным и минимальным значением признака:
R = xmax
- xmin
;
Размах вариации делится на число групп k, т.е. 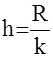 . Число групп приблизительно определяется по формуле Стерджесса . Число групп приблизительно определяется по формуле Стерджесса
k» 1+3,322 lgn,
где n- число изучаемых единиц совокупности. Это выражение, почти всегда дробное число, округляем до целого.
Величина интервала должна определяться в соответствии с точностью данных наблюдения: если исходные данные представлены целыми числами, то и величина интервала округляется до ближайшего целого числа.
Реклама

Далее можно определить границы всех интервалов ряда распределения. Нижнюю границу I-го интервала можно принять равной минимальному значению признака.
При построении интервальных рядов для непрерывных признаков имеет место совпадение верхних границ предшествующих интервалов и нижних границ следующих за ними интервалом. В какой интервал относить единицы совокупности.
Рассмотрим пример
построения ряда распределения по данным о среднегодовой стоимости основных фондов 20 предприятий главка одного министерства (млн. рублей): 3,7; 4,3; 6,7; 5,6; 5,1; 8,1; 4,6; 5,7; 6,4; 5,9; 5,2; 6,2; 6,3; 7,2; 7,9; 5,8; 4,9; 7,6; 7,0; 6,9.
Определяем количество групп вариационного ряда:
k» 1+3,322 lg20 = 1+3,322*1,301»5,32=5 (групп).
Величина интервала 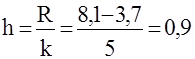 млн. руб. млн. руб.
В результате группировки получим ряд распределения предприятий по среднегодовой стоимости основных фондов.
Таблица 2.
| Среднегодовая стоимость ОФ, млн. руб. |
Число предприятий |
Накопление частоты |
| 3,7 - 4,6 |
2 |
2 |
| 4,6 + 5,5 |
4 |
6 |
| 5,5 + 6,4 |
6 |
12 |
| 6,4 + 7,3 |
5 |
17 |
| 7,3 + 8,2 |
3 |
20 |
Значения признака у отдельных единиц совпала с границами интервала (3,7; 4,6 и 6,4). Так как xmin
= 3,7 и совпадает с нижней границей I‑го интервала и включается в этот интервал, то и другие значения следует включать в интервал, нижняя граница которого совпадает с указанным значением (4,6 - включается во II‑й интервал, а 6,4 - в IV-ый).
Если приведенный вариационный ряд с неравными интервалами, то для правильного представления о характере распределения необходимо рассчитать абсолютную и относительную плотности распределения.
Абсолютная плотность:
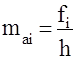 ; ;
Относительная плотность:
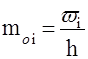
Эти показатели необходимы для преобразования интервалов изменения оценки данных, собранных по различным совокупностям и по разному обработанных.
Например, по двум предприятиям известно распределение рабочих по проценту выполнения норм выработки.
Таблица 3.
| Завод 1 |
Завод 2 |
| Группы рабочих |
Кол-во рабочих,
% к итогу
|
Группы рабочих |
Кол-во рабочих,
% к итогу
|
| До 90 |
2 |
До 100 |
8 |
| 90-100 |
3 |
100-120 |
40 |
| 100-110 |
50 |
120-150 |
20 |
| 110-120 |
30 |
150-180 |
15 |
| 120-140 |
8 |
180 и выше |
17 |
| 140-150 |
5 |
| 150-160 |
2 |
| ИТОГО |
100 |
100 |
Воспользуемся укрупнением интервалов для перегруппировки данных.
Таблица 4.
| Группы рабочих по проценту выполнения норм выработки |
Количество рабочих,% к итогу |
| Завод 1 |
Завод 2 |
| До 100 |
5 |
8 |
| 100-120 |
80 |
40 |
| 120-150 |
13 |
20 |
| 150 и выше |
2 |
32 |
| ИТОГО |
100 |
100 |
Можно воспользоваться и другой группировкой по проценту выполнения норм выработки, например, выделить такие интервалы:
| Группы рабочих |
1 |
2 |
3 |
4 |
5 |
| % выполнение нормы выработки |
До 100 |
100-110 |
110-120 |
120-140 |
140-160 |
Для такой группировки возникает необходимость расширения ряда распределения рабочих Завода 2.
Если известна относительная плотность распределения, то частости соответствующего интервала можно определить: произведение плотности на величину интервала.
vi
=m0
i
´h.
По данным таблицы 3 определяем плотности распределения группы рабочих по проценту выполнение норм выработки для интервалов:
ІІ - го: 100-120 m02
=2,0 (40/20)
ІІІ - го: 120-150 m03
=2/3 (20/30)
IV- го: 150-180 m04
=1/2 (15/30)
Тогда количество рабочих (% к итогу) Завода 2, выполняющих норму на 140‑160% определяются так:
2/3´10+1/2´10=12.
Результаты перегруппировки представлены в таблице 5.
Таблица 5.
| Группы рабочих по проценту выполнения норм выработки |
Количество рабочих,% к итогу |
| Завод 1 |
Завод 2 |
| До 100 |
5 |
8 |
| 100-110 |
50 |
20 |
| 110-120 |
30 |
20 |
| 120-140 |
8 |
13 |
| 140-160 |
7 |
12 |
| 160 и выше |
- |
27 |
| ИТОГО |
100 |
100 |
Для целей анализа и сравнительной характеристики различных рядов распределения применяются обобщающие показатели вариационного ряда. Систему показателей рассмотрим на примере.
Допустим, что по 5 производственным участкам известны данные о распределении 100 рабочих по квалификации (табл.6).
Таблица 6.
| Разряд рабочих |
Число рабочих участка |
| I |
II |
III |
IV |
V |
| 2 |
20 |
- |
10 |
1 |
5 |
| 3 |
60 |
20 |
20 |
9 |
10 |
| 4 |
20 |
60 |
40 |
80 |
6 |
| 5 |
- |
20 |
20 |
9 |
15 |
| 6 |
- |
- |
10 |
1 |
10 |
| Итого |
100 |
100 |
100 |
100 |
100 |
Распределения рабочих І-го и ІІ-го участков, имеют одинаковый размах вариации и характер распределения частично отличаются: величиной варьирующего признака, т.е. центром группирования.
Среднее квадратическое отклонение показывает также как расположена основная масса единиц совокупности относительно средней арифметической. В соответствии с теоремой Чебышева можно утверждать, что независимо от формы распределения 75% значений признака попадают в интервал 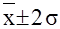 ; а по крайней мере 89% всех значений попадают в интервал ; а по крайней мере 89% всех значений попадают в интервал 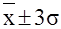
Необходимо отметить, что если при расчете арифметической для достаточно симметричного ряда распределения м/д 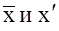 не оказывают существенного влияния на ее отклонение от средней арифметической, рассчитанной по первичным данным, то при расчете дисперсии этот факт приводит к появлению систематической ошибки. не оказывают существенного влияния на ее отклонение от средней арифметической, рассчитанной по первичным данным, то при расчете дисперсии этот факт приводит к появлению систематической ошибки.
В.Ф. Шеппард установил, что ошибка в дисперсии, вызванная применением сгруппированных данных при расчете составляет 1/12 квадрата величины интервала, т.е. скорректированная дисперсия равна
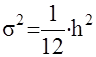
І группа обобщающих показателей - характеристика центра группирования
в качестве которых используют: среднюю арифметическую,
моду;
медиану.
Распределение рабочих ІІ-го и ІІІ-го участков имеют один и тот же центр группирования и симметричное расположение частот вокруг него, но отличаются пределами вариации.
ІІ группа- показатели степени вариации
- т.е. характеристика колеблемости признака.
Распределение рабочих ІІІ-го и IV-го участков имеют и тот же центр группирования, пределы варьирования признака, симметричный характер ƒ расположения частот, но имеют разную степень вытянутости вдоль оси ординат, которая характеризуется показателями эксцесса.
Распределение рабочих IV-го и V-го участков показывает, что они отличаются характером распределения частот относительно центра. Для IV-го участка оно симметрично, для V-го участка оно не симметрично.
Степень отклонения от симметричной формы характеризуется показателями асимметрии.
ІІІ группа показателей - показатели формы распределения.
Графическое изображение рядов расширения облегчает их анализ и позволяет судить о форме распределения. Для графического изображения дискретного ряда применяют полигон распределения.
На оси абсцисс отмечают точки, соответствующие величине варианты признака. Из них восстанавливаются перпендикуляры, высота которых - частости этих вариантов. Вершины перпендикуляров соединяются отрезками прямых. Крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление от xmax
и xmin
.
Для графического изображения интервальных вариационных рядов применяется гистограмма.
Она строится так, что на оси абсцисс откладываются равные отрезки, которые соответствуют величине интервалов вариационного ряда. На отрезках строят прямоугольники, площади которых пропорциональны частотам (частостям) интервала.
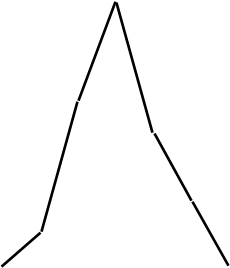
По данным табл.1 построим полигон распределения.
 f f
|
| 8 |
| 7 |
Распределение рабочих участка по квалификации:
X – тарифный разряд
f
– число рабочих
|
|
6 |
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
x |
По данным табл.2 построим гистограмму ряда распределения предприятий по стоимости основных фондов.
| f |
| 6 |
Распределение по размеру прибыли:
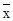 - средняя годовая стоимость ОФ - средняя годовая стоимость ОФ
f
– число предприятий
|
|
5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 3,7 |
4,6 |
5,5 |
6,4 |
7,3 |
8,2 |
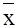 |
Гистограмма может быть преобразована в полигон распр еделения, для чего середины верхних сторон прямоугольников соединяют отрезками прямых. Две крайние точки прямоугольников замыкаются по оси абсцисс на середины интервалов, в которых частоты равны 0. еделения, для чего середины верхних сторон прямоугольников соединяют отрезками прямых. Две крайние точки прямоугольников замыкаются по оси абсцисс на середины интервалов, в которых частоты равны 0.
При увеличении числа наблюдений совокупности увеличивается число групп интервального ряда, что соответственно приводит к уменьшению величины интервала. При этом ломанная линия будет иметь тенденцию превращения в плавную кривую, которую называют кривой распределения.
Она характеризует в обобщенном виде вариацию признака и распределение частот внутри однокачественной совокупности.
В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулянта
). Построим кумулятивную кривую по данным табл.2 о распределении банков по размеру прибыли. Накопленные частоты рассчитаны в графе 3 табл.2.
При построении кумулянты интервального ряда распределения нижней границе первого интервала соответствует частота, равная 0, а верхней границе - вся частота данного интервала. Верхней границе второго интервала соответствует накопленная частота, равная сумме частот первых двух интервалов и т.д.
| S |
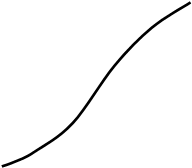 20 20 |
| 16 |
| 12 |
| 8 |
| 4 |
| 3,7 |
4,6 |
5,5 |
6,4 |
7,3 |
8,2 |
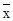 |
Изображение вариационного ряда в виде кумулянты особенно удобно при сравнении вариационных рядов, а так же в экономических исследованиях, в частности для анализа концентрации производства
Для характеристики среднего значения признака в вариационном ряду используются средняя арифметическая, мода и медиана.
Общие понятия о средних величинах и их свойствах рассматривались в предыдущей лекции. Здесь же мы рассмотрим расчет показателей центра распределения для вариационных рядов.
Напоминаю, что средняя арифметическая рассчитывается по формуле:
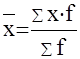
В интервальном ряду средняя арифметическая определяется по формуле:
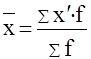 , ,
где x’ - средина соответствующего интервала;
f- частота повторений варианты признака.
В отличие от алгебраических средних, которые в значительной мере являются абстрактной характеристикой статистического ряда, мода и медиана выступают как конкретные величины, совпадающие с вполне определенными вариантами этого ряда.
Мода
- это наиболее часто встречающаяся величина признака в данной совокупности.
В вариационном ряду моду будет представлять варианта, которая обладает наибольшей частотой.
В дискретном ряду распределения мода определяется просто.
Пример 1. Распределение семей по числу совместно проживающих членов семьи.
Таблица.
| Число членов семьи |
Число семей,% к итогу |
Накопленные частоты, S |
| 2 |
10 |
10 |
| 3 |
37 |
47 |
| 4 |
28 |
75 |
| 5 |
15 |
90 |
| 6 |
9 |
99 |
| 7 |
1 |
100 |
| ИТОГО |
100 |
- |
Модой в данном примере являются 3 члена семьи, т.к этой величине соответствует наибольшая частность (37).
Мода интервального вариационного ряда определяется по формуле:
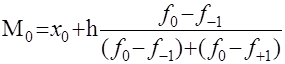 ; ;
где x0
- начало модального интервала,
h- величина интервала (модального),
f
0
- частота модального интервала,
f
-1
- частота предмодальная,
f
+1
- послемодальная частота.
Используя данные табл.2 определим моду:
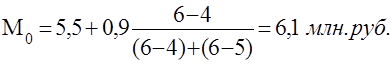
При неравных интервалах для расчета моды применяется эта же формула, но вместо частот в ней следует использовать плотность распределения.
Медианой
в статистике
называется численное значение признака у той единицы совокупности, которая находится в середине ранжированного ряда.
Порядковый номер медианы определяется следующим образом: численность (дискретного) ряда увеличивается на единицу и делится пополам, т.е. (n+1) /2.
Если вариантов - четное число, то медиана определяется как среднее из двух центральных вариантов, порядковые номера которых n/2 и (n/2) +1. Так, если в ряду распределения 100 единиц, то в центре стоят единицы с порядковыми номерами 100: 2=5 и 100: 2+1=51 и медиана должна быть получена как средняя из величин этих вариантов. Однако, если единиц в совокупности достаточно много и различия между величинами рядом стоящи вариантов небольшие, то можно считать медианой один из центральных вариантов с порядковым номером n/2. Так обычно делают, определяя медиану при четном числе членов ряда.
При определении медианы для интервальных рядов, вначале определяется медианный интервал, т.е. интервал, в котором лежит медиана. Он определяется также как и при определении медианы дискретного ряда, т.е. подсчитывают суммы накопленных частот.
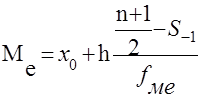 , ,
Где x0
- нижняя граница медианного интервала,
h- величина интервала,
S-1
- накопленная частота интервала, предшествующего медианному,
f
ме
- частота медианного интервала.
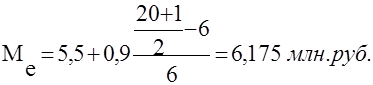
Моду и медиану можно определить графически. Медиана определяется по кумулянте. Моду - по гистограмме распределения.
В ходе анализа средних величин возникает вопрос степени колеблемости, степени вариации, скрывающейся за средней величиной. Для характеристики колеблемости варьирующего признака в изучаемой совокупности явлений применяются следующие показатели:
Размах вариации;
Среднее линейное отклонение;
Дисперсия;
Среднее квадратическое отклонение;
Коэффициент.
Размах вариации
или размах колеблемости
является наиболее простым измерителем вариации признака. Он равен разности между наибольшим (максимальным) и наименьшим (минимальным) значением варьирующего признака в данном ряду.
R = xmax
- xmin
.
При определении величины размаха вариации учитываются только два крайних значения признака, колеблемость же и распространенность (частота) его в этом показателе не находят отражения.
Среднее линейное
отклонение является несколько более совершенной мерой вариации и характеризует колеблемость значений признака по всей совокупности явлений.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных отклонений варьирующего признака от его среднего значения. Так как алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической всегда равна 0, то для расчета среднего линейного отклонения используется арифметическая сумма отклонений, т.е. суммируются абсолютные значения индивидуальных отклонений независимо от знака.
Среднее линейное отклонение 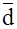 вычисляется по следующим формулам: вычисляется по следующим формулам:
Для первичного ряда: 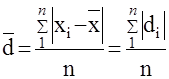
Для вариационного ряда: 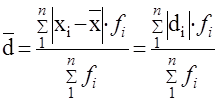
Дисперсия
s2
- средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
Для первичного ряда:
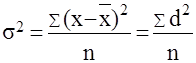
для вариационного ряда:
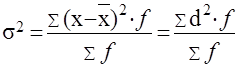
Формулу для расчета дисперсии можно преобразовать:
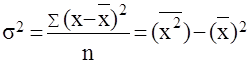 , ,
т.е. дисперсия равна разности средней из квадратов и квадрата средней. Этой формулой пользуются машинной обработке исходных данных.
Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления:
дисперсия постоянной величины равна 0;
если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится;
если все варианты значений признака уменьшить в одно и то же число раз (kраз), то дисперсия уменьшится в k2
раз.
Среднее квадратическое отклонение
представляет собой среднюю, исчисленную на основе квадратов отклонений отдельных значений варьирующего признака от их среднего значения.
Среднее квадратическое отклонение s представляет собой корень квадратный из дисперсии:
Для первичного ряда:
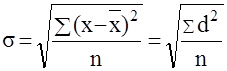
Для вариационного ряда:
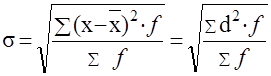
Размах вариации, среднее линейное и среднее квадратическое отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.
Дисперсия и среднее квадратическое отклонение - наиболее широко применяемые показатели вариации. Объясняется это тем, что они входят в большинство теорем теории вероятности, служащих фундаментом математической статистики.
Расчет показателей вариации для предприятий, сгруппированных по среднегодовой стоимости основных фондов, показан в таблице.
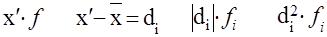 Средняя годовая стоимость ОФ, млн. руб. Средняя годовая стоимость ОФ, млн. руб. |
Число предприятий
f
|
Средина интервала
X’
|
| 3,7-4,6 |
2 |
4,15 |
8,30 |
-1,935 |
3,870 |
7,489 |
| 4,6-5,5 |
4 |
5,05 |
20, 20 |
-1,035 |
4,140 |
4,285 |
| 5,5-6,4 |
6 |
5,95 |
35,70 |
-0,135 |
0,810 |
0,109 |
| 6,4-7,3 |
5 |
6,85 |
34,25 |
+0,765 |
3,825 |
2,926 |
| 7,3-8,2 |
3 |
7,75 |
23,35 |
+1,665 |
4,995 |
8,317 |
| ИТОГО |
20 |
121,70 |
17,640 |
23,126 |
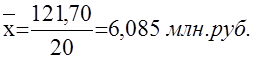
Среднее линейное отклонение:
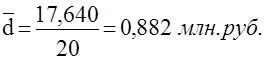
Среднее квадратическое отклонение:
Дисперсия: 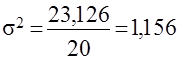
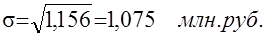
Так как средняя величина колеблемости средней годовой стоимости основных фондов составляет:
По среднему линейному отклонению - 0,822 млн. руб.
По среднему квадратическому - 1,075 млн. руб.
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Эти показатели вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах, среднее линейное отклонение, среднее квадратическое отклонение, относительные показатели колеблемости:
Коэффициент осцилляции
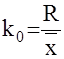 - -
отражает относительную колеблемость значений признака вокруг средней, крайних.
Относительное линейное отклонение
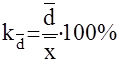
- характеризует долю усредненного значения абсолютных отклонений от средней величины.
Коэффициент вариации 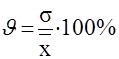
Наиболее часто применяется показатель колеблемости - коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Для рассмотренного примера:
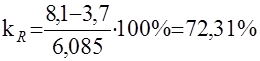
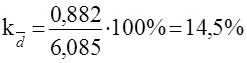
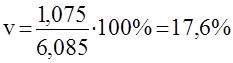
Оставалась на коэффициенте вариации, можно сделать вывод, что по размеру прибыли совокупность является однородной.
Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, можно воспользоваться разложением дисперсии на составляющие: на межгрупповую и внутригрупповую дисперсии.
Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности и вычисляется:
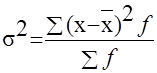
где - общая средняя для всей изучаемой совокупности.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних около общей средней.
Межгрупповая дисперсия вычисляется по формуле:
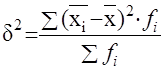 , ,
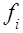 где - средняя по отдельным группам, где - средняя по отдельным группам,
- частота отдельных групп.
Средняя из внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов и не зависит от условия, положенного в основу группировки.
Она определяется по формуле:
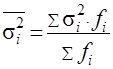
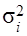 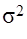 Между общей дисперсией, средней из внутригрупповых дисперсий и межгрупповой d2
дисперсиями существует соотношение, определяемое правилом сложения дисперсий: Между общей дисперсией, средней из внутригрупповых дисперсий и межгрупповой d2
дисперсиями существует соотношение, определяемое правилом сложения дисперсий:
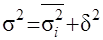 . .
Рассмотрим правило сложение дисперсий на следующем примере.
По результатам маркетингового обследования туристических фирм, организующих недельные туры в Испанию в различные курортные города, получены следующие данные о вариации стоимости туров в сентябре 1997 г.
| Месторасположение курорта |
Число турист. фирм, f
i |
Средняя цена недельного тура, дол. |
Дисперсия цен тура в группе |
| Коста - Брава |
7 |
528,57 |
2728,04 |
| Коста-дель-Соль |
6 |
588,33 |
8851,14 |
| ИТОГО: |
13 |
556,16 |
5554,08 |
Вариация цен в обследованной группе туристических фирм, обусловленная различием в месторасположении курорта будет характеризоваться величиной межгрупповой дисперсии.
Средняя цена тура по всем фирмам составила:
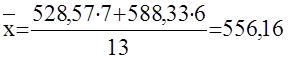 $ $
Тогда межгрупповая будет равна:
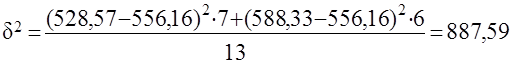
Вариация цен под влиянием всех прочих факторов, кроме месторасположения курорта, будет характеризоваться величиной средней из внутригрупповых дисперсий:
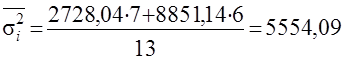
Вариация цен на недельные туры в Испанию, обусловленная влиянием всех факторов, формирующих уровень цен в заданной группе:
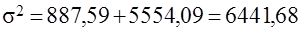
Правило сложения дисперсий имеет большую практическую значимость, т.к. позволяет выявить зависимость результатов от определяющих факторов соотношением межгрупповой и общей дисперсии - коэффициент детерминации.
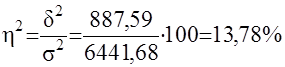
Отсюда можно сделать вывод, что на 13,78% дисперсия цен на недельные туры объясняется различиями в месторасположении курорта, а на 86,22% - влиянием прочих факторов.
Таким образом, преобладающее влияние на вариацию цен недельных туров в Испанию оказывают прочие факторы.
В статистике наряду с показателем вариации количественного признака определяются показатели вариации альтернативного признака. Альтернативными являются признаками, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Например: при, изучении качества изготовленной продукции можно разделить её на две группы годную и бракованную, т.е. в данном случае это два взаимно исключающих вариантов.
При статистическом выражении колеблемости альтернативных признаков наличие изучаемого признака обозначается 1, а его отсутствие - 0. Доля вариантов, обладающих изучаемым признаком обозначается р, а доля вариантов, не обладающих - q, следует
p + q = 1
Допустим, общее число единиц совокупности равно n. Число единиц обладающих признаком - f, тогда число единиц не обладающих дополнительными признаком будет равно n- f.
Учитывая изложенное
Значение переменнойЧастота повтора
f
n- f
Отсюда 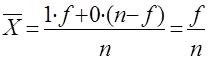
Дисперсия
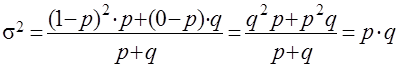
Средняя квадратичная равна
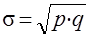 . .
Например в результате контроля из 1000 готовых изделий 20 - бракованных.
Отсюда
1 - соответствует бракованным изделиям
0 - годной продукции
Процент барка равен 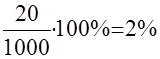 . .
Тогда величина дисперсии
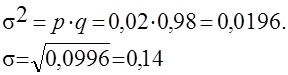
Если признак принимает больше двух значений, то оценка вариации равна
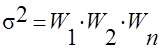 , ,
где W- доля каждого признака.
Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). Число наблюдений, по которому строится эмпирическое распределение, обычно невелико. С увеличением числа наблюдений и одновременным уменьшением величины интервала зигзаги полигона начинают сглаживаться и в результате чего получается плавная кривая, которая называется кривой распределения.
Если кривая построена по данным наблюдения, то она называется эмпирической кривой, а если она отражает закономерность соотношения вариант и частот, то она называется теоретической кривой. Исследование закономерности (формы) распределения включает решение трёх последовательных задач:
выяснение общего характера распределения
выравнивание эмпирического распределения, которое состоит в том, что на основании эмпирического распределения строится кривая y=f (x)
проверка соответствия найденного теоретического распределения эмпирическому.
В практике статистического исследования встречаются различные распределения.
Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности. Появление двух вершинной или асимметричной кривой означает, нарушение при изменении условий получения и обработки сведений в этом случае необходима перегруппировка данных.
Выявление общего характера распределения предполагает не только степень его однородности, а также вычисление показателей асимметрии и эксцесса.
Симметричным является распределение в котором частота любых двух вариантов равноотстоящих в обе стороны от центра распределения, равны между собой. Для симметричного распределения
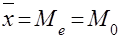 . .
Поэтому показатель асимметрии, основан на соотношении показателей центра распределения: чем больше разница между средними (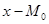 ) тем больше асимметрия ряда. ) тем больше асимметрия ряда.
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывают относительный показатель AS
.
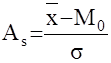
AS
может быть положительным и отрицательным.
Положительная величина указывает на наличие правосторонней асимметрии
(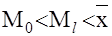 ) )Отрицательный знак свидетельствует о наличии левосторонней асимметрии
( ) )
Другим показателем асимметрии, предложенный шведским математиком Линбергом, рассчитывают по формуле:
AS
= П - 50,
где П - процент тех значений признака, которые превосходят по величине среднюю арифметическую.
Наиболее точным и распространенным является показатель, основанный на определении центрального момента третьего порядка (в симметричном распределении его величина равна 0).
Моментом распределения
называется средняя арифметическая тех или иных степеней отношения индивидуальных значений признака от определенной исходной величины.
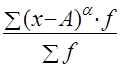 , ,
где А - величина, от которой определяется отклонение
a - степень отклонения (порядок момента)
В зависимости от того, что принимают за величину А, различают три вида моментов:
Начальные моменты
получают при А=0
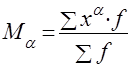
Центральные моменты
получают при А=
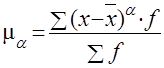
Условные моменты ma
получают при А, не равной средней арифметической и отличной от нуля:
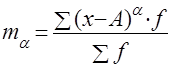
В статистической практике пользуются моментами превого, второго, третьего и четвертого порядков.
| Моменты распределения порядка |
Начальные |
Центральные |
Условные |
| I |
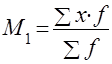 |
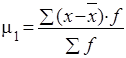 |
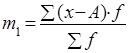 |
| II |
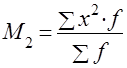 |
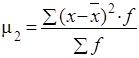 |
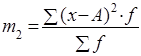 |
Начальные моменты второго, третьего и четвертого порядков так же, как и условные моменты самостоятельного значения не имеют, а используют для упрощенного вычисления центральных моментов.
Например,
используя начальные моменты первого и второго порядка можно вычислить дисперсию по формуле:
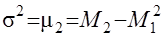 . .
Таким образом, показатель асимметрии может быть вычислен по формуле:
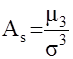
Применение этого показателя дает возможность не только определить степень асимметрии, но и ответить на вопрос о наличии или отсутствии асимметрии в распределении признака в генеральной совокупности.
Эта оценка делается при полюции след. показателя (сред. квадр. отклон)
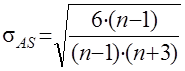
Если отношение
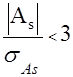 , ,
а асимметрия несущественна и наличие может быть объяснено влиянием различных случайных обстоятельств.
Для симметричных распределений рассчитывается показатель эксцесса (островершинности).
Наиболее точным является показатель оснований на использовании центрального момента четвертого порядка.
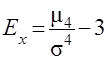
На рисунке:
островершинное распределение (величина эксцесса положительная)
плосковершинное (величина эксцесса отрицательная)
кривая нормального распределения.
Эксцесс
- выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. В нормальном распределении:
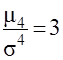 . .
Оценка показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения, которое имеет следующие особенности:
кривая симметрична относительно максимальной ординаты, которая равна x=M0
=Ml
и величина
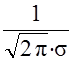
кривая приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Следовательно, чем больше значения отклоняются от 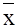 , тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку, отклонения значений переменной х от , тем реже они встречаются. Одинаковые по абсолютному значению, но противоположные по знаку, отклонения значений переменной х от 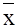 - равновероятны. - равновероятны.
При 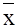 =const и при увеличении s кривая становится более пологой. При s=constс изменением =const и при увеличении s кривая становится более пологой. При s=constс изменением  кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс. кривая не меняет свою форму, а лишь сдвигается вправо или влево по оси абсцисс.
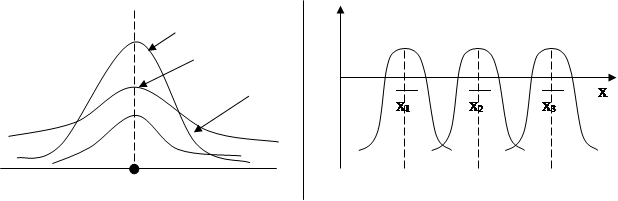
s1<
s2<
s3
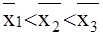
В промежутке 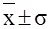 находится 68,3% всех значений признака. находится 68,3% всех значений признака.
В промежутке 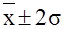 находится 95,4% всех значений признака. находится 95,4% всех значений признака.
В промежутке  находится 99,7% всех значений признака. находится 99,7% всех значений признака.
Нормальное распределение возможно в том случае, когда на величину признака влияет большое число случайных причин. Действие этих причин независимо, и ни одна из причин не имеет преобладающего влияния над другим. |