КОНТРОЛЬНА РОБОТА
з дисципліни
"Теорія ймовірностей та математична статистика”
Завдання 1
Два стрільці незалежно один від одного роблять по одному пострілу по мішені. Ймовірність влучення першого – 0,8, а другого – 0,4. Відомо, що є одне влучення. Знайти ймовірність того, що влучив другий стрілець.
Розв’язання
Позначимо випадкові події:
Х1
:”влучив перший стрілець”,
Х2
:”влучив другий стрілець”,
Y
: “є одне влучення у мішень”,
Z
: “влучив другий, а перший не влучив”
Апріорна ймовірність того, що при одному пострілі влучить другий стрілець і не влучить перший, (подія Z
) визначаємо як ймовірність перерізу (добутку) подій 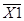 :”перший не влучив” і Х2
:”другий влучив”. :”перший не влучив” і Х2
:”другий влучив”.
За умовою
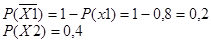
Ймовірність події Y дорівнює (згідно з теоремами множення і додавання):
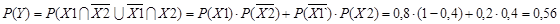
В силу незалежності подій Х1
та Х2
, і враховуючи, що ймовірність події Z
– це умовна ймовірність події Х2
при умові події 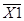 , знаходимо , знаходимо
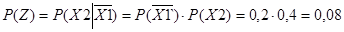
З іншого боку, подію Z
можна подати як переріз події Y
та події Х2
при умові, що подія Y здійснилася. Згідно з теоремою множення
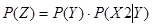 , ,
де 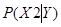 – апостеріорна ймовірність того, що наявне одне влучення у мішень зроблено другим стрільцем. – апостеріорна ймовірність того, що наявне одне влучення у мішень зроблено другим стрільцем.
Звідси знаходимо шукану ймовірність того, що влучив другий стрілець при умові, що є одне попадання:
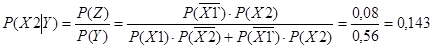
Завдання 2
Ймовірність настання події А
у кожному з 18 незалежних випробуваннях дорівнює 0,2. Знайти ймовірність настання цієї події принаймні двічі.
Розв’язання
Задані в задачі випробування є випробуваннями Бернуллі. Ймовірність появи події А
у кожному окремому випробуванні становить
р=Р(А)=0,2,
а ймовірністьїї непояви
q=P(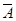 )=1-
P(A)=1-0,2=0,8. )=1-
P(A)=1-0,2=0,8.
Ймовірність того, що подія А
відбудеться К разів у серії з N випробувань визначається за формулою Бернуллі:
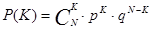 , ,
де 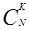 – число сполучень з N елементів по K. – число сполучень з N елементів по K.
Ймовірність того, що подія А
відбудеться принаймні 2 рази (тобто 2 або більше) дорівнює
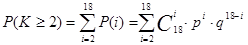
Для спрощення розрахунків перейдемо до протилежної події (поява події А
менше 2 разів, тобто 0 або 1 раз):
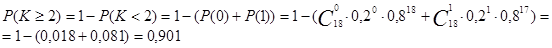
Завдання 3
Випадкова величина Х
задана рядом розподілу
| Х |
х1 |
х2 |
х3 |
х4 |
| Р |
р1 |
р2 |
р3 |
р4 |
Визначити невідому р
і
. Знайти функцію розподілу випадкової величини
F(Х)
та побудувати її графік. Обчислити математичне сподівання М(Х),
дисперсію D(Х)
та середнє квадратичне відхилення випадкової величини Х
.
| Х |
11 |
13 |
15 |
19 |
| Р |
0,18 |
0,32 |
0,4 |
? |
Розв’язання
Згідно з умовою нормування розподілу ймовірностей випадкової величини
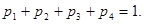
Звідси знаходимо 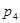 : :
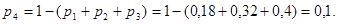
Функцію розподілу знаходимо на основі означення функції розподілу:
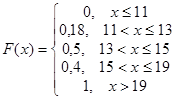
Графік функції розподілу зображено на рис.1.
Математичне сподівання:
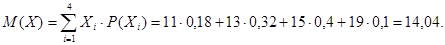
Дисперсія:
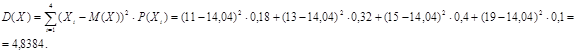
Середнє квадратичне відхилення
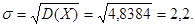
Завдання 4
1. Записати вибірку у вигляді:
- варіаційного ряду;
Реклама

- статистичного ряду частот;
- статистичного ряду відносних частот.
2. Побудувати полігон, гістограму та кумуляту для вибірки, поданої у вигляді таблиці частот.
3. Обчислити числові характеристики варіаційного ряду розподілу:
- середнє арифметичне значення;
- моду;
- медіану;
- дисперсію;
- середнє квадратичне відхилення;
- коефіцієнт варіації.
4. Пояснити зміст обчислених числових характеристик.
Вибірка:
7 8 4 0 4 6 5 4 3 2 4 8 6 2 2 5 3 6 6 5 5 3 5 6 7 8 9 5 2 5 4 5
6 6 3 6 5 3 4 5 10 3 7 5 3 3 3 7 5 3 4 9 2 1 4 4 4 2 4 3 4 4 5 5
3 7 5 3 2 6 2 4 4 4 0 6 1 3 4 4 5 4 8 3 5 4 11 9 9
Розв’язання
1:
a) Варіаційний ряд – це послідовність варіант (спостережуваних значень), розташованих у зростаючому порядку.
Задана вибірка у вигляді варіаційного ряду:
0 0 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 7 7 7 7 7 8 8 8 8 9 9 9 9 10 11.
б) Статистичний ряд частот – це перелік значень варіант вибірки, розташованих у порядку зростання, з відповідними їх частотами (тобто числом повторень кожного значення у вибірці).
Задана вибірка у вигляді статистичного ряду частот (Хі
– значення варіанти, ns
– частота):
| Хі
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| ni
|
2 |
2 |
8 |
15 |
20 |
17 |
10 |
5 |
4 |
4 |
1 |
1 |
в) Статистичний ряд відносних частот – це перелік значень варіант вибірки, розташованих у порядку зростання, з відповідними їх відносними частотами. Відносна частота – це відношення частоти даного значення до об’єму вибірки.
Об’єм вибірки становить 89 (вибірка містить 89 варіант).
Задана вибірка у вигляді статистичного ряду відносних частот (Хі
– значення варіанти, Ps
– відносна частота):
| Хі
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| Pi
|
2/89 |
2/89 |
8/89 |
15/89 |
20/89 |
17/89 |
10/89 |
5/89 |
4/89 |
4/89 |
1/89 |
1/89 |
2:
а) Полігон частот – це ламана, відрізки якої з’єднують точки (Хі
, Рі
) що відповідають елементам статистичного ряду частот. Полігон частот зображено на рис.1. Полігон побудовано за допомогою процесора електронних таблиць MS Excel (інструмент майстер діаграм).
б) Побудуємо для заданої вибірки гістограму частот.
Гістограма частот – це ступінчаста фігура, яка складається з прямокутників, основами яких є часткові інтервали шириною h, на які розбито інтервал зміни спостережуваної величини Х, а висота дорівнює відношенню частоти інтервалу ni
до ширини інтервалу h (ni
/h). Висота прямокутника має зміст густини частоти.
Для побудови гістограми візьмемо ширину часткових інтервалів рівною 1 (тоді висоти прямокутників будуть рівними частоті значень варіант).
Полігон частот зображено на рис.2. Полігон побудовано за допомогою процесора електронних таблиць MS Excel.
Реклама

в) Побудуємо кумуляту частот для заданої вибірки.
Кумулята являє собою графік статистичного ряду нагромадженої (кумулятивної) частоти. Кумулятивна частота для кожного значення варіанти дорівнює сумі частот усіх попередніх (менших) значень варіант.
Для побудови кумуляти побудуємо статистичний ряд нагромадженої частоти даної вибірки:
| Хі
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
>11 |
| ni
|
0 |
2 |
4 |
12 |
27 |
47 |
64 |
74 |
79 |
83 |
87 |
88 |
89 |
Кумуляту зображено на рис. 3.
3:
Обчислення числових характеристик варіаційного ряду розподілу.
Середнє арифметичне значення (вибіркове середнє)
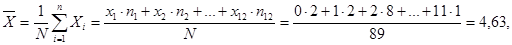
де xі
– і-те значення варіанти, ni
– частота цього значення, N – об’єм вибірки.
Мода – це значення, яке має найбільшу частоту у вибірці. З статистичного ряду частот вибираємо варіанту, яка має найбільшу частоту. Це варіанта х=4, яка має частоту 20. Мода Мod(X) дорівнює
Mod(X)=4
Медіана – це варіанта, яка ділить варіаційний ряд на дві частини, рівні за числом варіант. Оскільки число елементів вибірки непарне (N=89), то медіаною є варіанта, яка має номер
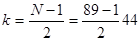
З варіаційного ряду знаходимо медіану
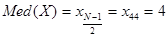
Дисперсія визначається за формулою
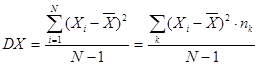
і дорівнює
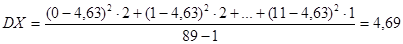
Cереднє квадратичне відхилення σ дорівнює
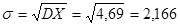
Коефіцієнт варіації R
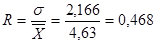
4:
Середнє арифметичне (вибіркове середнє) є найкращою оцінкою математичного очікування величини Х (її середнього значення).
Мода і медіана також є оцінками істиного значення величини. Вони характеризуються меншою, ніж середнє арифметичне чутливістю до брутальних промахів.
Дисперсія є мірою мінливості спостережуваної величини. Чим більша дисперсія, тим більша мінливість величини, її розсіювання навколо середнього значення. Одиниця вимірювання дисперсії – квадрат одиниці вимірювання самої величини.
Середнє квадратичне відхилення також є характеристикою мінливості величини, її відхилення від математичного очікування. Одиниці вимірювання – ті ж, що самої величини.
Коефіцієнт варіації служить для порівняння величин розсіювання відносно вибіркового середнього двох варіаційних рядів.
Список використаної літератури
1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. – М.: Высшая школа, 2001. – 479 с.
2. Горбань С.Ф., Снижко Н.В. Теория вероятностей и математическая статистика: Учеб. пособие. – К.: МАУП, 1999. – 168 с.
3. Горкавий В.К., Ярова В.В. Математична статистика: Навчальний посібник. – К.: ВД «Професіонал», 2004. – 384 с.
4. Жлуктечко В.І., Наконечний С.І., Савіна С.С. Теорія ймовірностей і математична статистика: Навч.-метод. посібник: У 2-х ч. – Ч.П. Математична статистика. – К.: КНЕУ, 2001. – 336 с.
5. Іванюта І.Д., Рибалка В.І., Рудоміно-Дусятська І.А. Елементи теорії ймовірностей та математичної статистики. – К.: Слово, 2003. – 272 с.
6. Савчук М.В. Програма з навчальної дисципліни «Теорія ймовірностей та математична статистика» для спеціальності 6.050200 «Менеджмент організацій» - К.: ІПК ДСЗУ, 2006. – 16 с.
7. Шефтель З.Г. Теорія ймовірностей: Підручник. – К. Вища школа, 1994. – 192 с.
|