Розрахунково-пояснювальна записка
До курсової роботи з основ теорії систем та системного аналізу:
Дослідження властивостей технологічного агрегата як многомірної системи
Одеса - 2010
1. Еквівалентні та апроксимаційні перетворення моделі
1.1 Нелінійна модель агрегату
На прикладі розглянемо конкретну технічну систему - змішувальний бак:
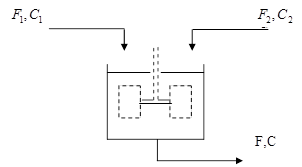
Рисунок 1. Модель бака.
F1
,F2
,F - витрати рідини на притоці і витоці системи, м3
/с;
C1
,C2
,C - концентрація на витоці і притоці системи, кмоль/м3
;
h - рівень рідини в бакові, м; S - площа бака, м2
;
V - об'єм рідини в бакові, м3
;
Запишемо рівняння системи в стаціонарному (встановленому) стані, коли притік дорівнює витоку (рівняння матеріального балансу):
F10
+F20
-F0
=0; C1
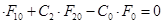 , ,
де індекс 0 означає встановлений стан.
Записавши умови балансу кінетичної і потенціальної енергії на виході із бака
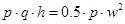 , ,
де
p - густина рідини, кг/м3
;
w - швидкість витоку, м/с;
q - прискорення вільного падіння,q=9.81 м/с2
;
і припускаючи, що
d - діаметр вихідного трубопроводу, м.
Одержимо:
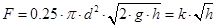 чи, відповідно, чи, відповідно,
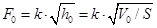 , де , де
k - коефіцієнт.
При зміні витрат у системі відбувається накопичення речовини і перехід до нового встановленого стану. Цей перехідний процес описується диференціальними рівняннями
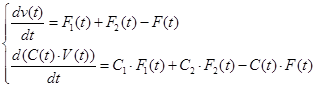
де dv/dt - приріст об'єму рідини, 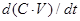 - приріст маси рідини. - приріст маси рідини.
Наведемо цю систему у стандартному вигляді:
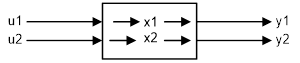
Позначимо:
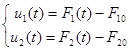
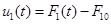 − зміна у часі відхилення витрати від номінального щодо першого каналу − зміна у часі відхилення витрати від номінального щодо першого каналу
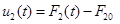 − теж щодо другого каналу − теж щодо другого каналу
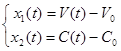
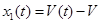 − зміна у часі відхилення об'єму від номінального у бакові; − зміна у часі відхилення об'єму від номінального у бакові;
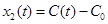 − відхилення концентрації від номінальної; − відхилення концентрації від номінальної;
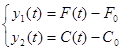
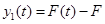 - зміна втрати на виході; - зміна втрати на виході;
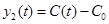 - зміна концентрації на виході. - зміна концентрації на виході.
1.2 Нелінійна модель в стандартній формі
Розглянемо поповнення бака від 0 до номінального значення витрати з урахуванням приросту поданого лінеаризованій моделі. Таким чином, розглянемо стрибок u1
=0,03; u2
=0.
Позначивши 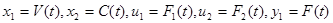 , рівняння бака запишемо у вигляді системи: , рівняння бака запишемо у вигляді системи:
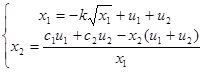 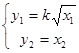 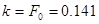
Перше рівняння є нелінійним зі змінними що розділяються
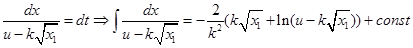
З урахуванням того, що 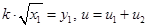 запишемо: запишемо:
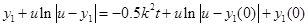 , ,
чи підставляючи
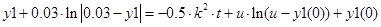
Виразимо 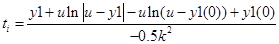
Підставляємо 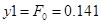 та та 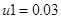
Таблиця 1.
| y1 |
0.141 |
0.142 |
0.143 |
0.144 |
0.145 |
0.146 |
0.147 |
0.148 |
0.149 |
0.150 |
0.151 |
| t, с |
0 |
1.5 |
3.188 |
5.116 |
7.357 |
10.026 |
13.315 |
17.585 |
23.643 |
34.072 |
68.958 |
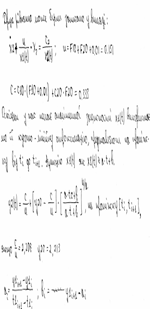

1.3 Отримання квадратичної моделі
Рівняння квадратичної моделі має вигляд:
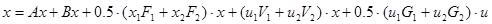
Матриці з підстановкою номінального режиму:


1.4 Запис білінійної моделі
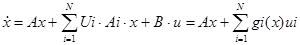
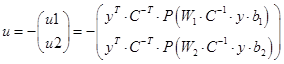
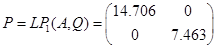
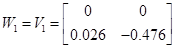 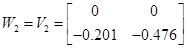
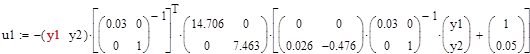
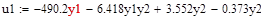
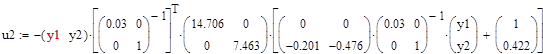
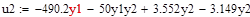
1.5 Лінеаризована модель
Лінеаризуємо залежність 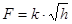 , розклавши її на ряд Тейлора. , розклавши її на ряд Тейлора.
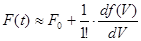  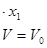
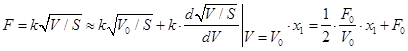
З урахуванням раніше викладеного запишемо:
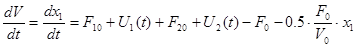
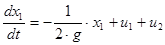 ; (т.к ; (т.к 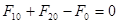 ), где ), где 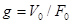 ; ;
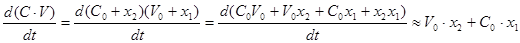
Припустивши у випадку остатку 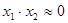 . Тоді підставивши похідну . Тоді підставивши похідну 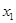 , отримаємо , отримаємо
 ; ;
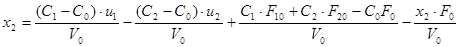
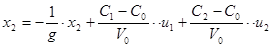
В результаті маємо
Реклама

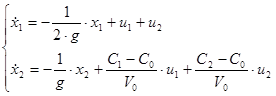
Представивши цю систему в матричній формі:
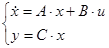
Тоді матриці А і В запишуться в вигляді
 , , 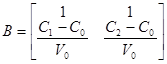
Для визначення матриці С необхідно встановити зв'язок між векторами x и y. Оскільки 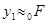 , , 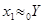 , то , то
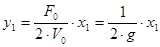 ; ; 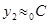  , то , то 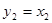
Тоді
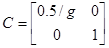
Система буде мати вигляд
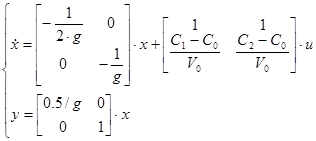
Коефіцієнти моделі системи:
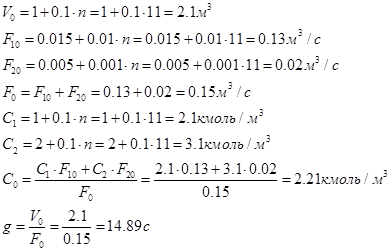
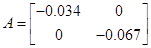 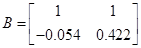 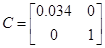
1.6 Модель в дискретному часі
система в дискретному часі має вид:
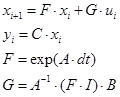
dt=14,89 c.
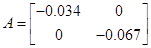
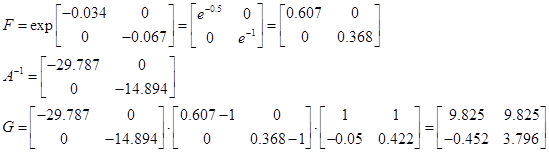
Таким чином
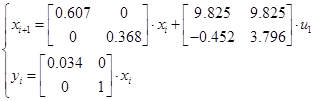
Задавшись  , ,  , тоді , тоді
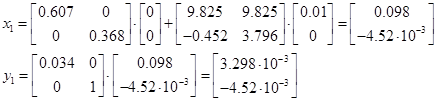
Результати подальших ітерацій представлено в таблиці:
Таблиця 3.
| Збурення |
Реакція виходу системи y (t) |
u1=0
u2=0,01
|
y1
y2
|
0
0
|
0,003298
0,00452
|
0,005299
0,00469
|
0,00773
0,006183
|
0,006512
0,006795
|
0,00725
0,00702
|
0,00769
0,00713
|
| час t, с |
0 |
14,894 |
29,787 |
44,681 |
59,574 |
74,468 |
89,362 |
1.7 Перетворення моделі у форму Ассео
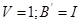
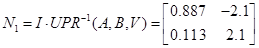
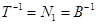
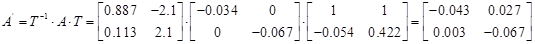
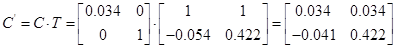
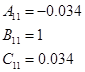 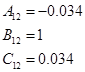 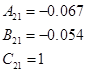 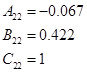
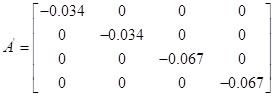 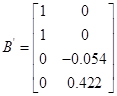
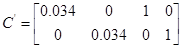
1.8 Обчислення МПФ системи
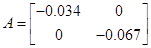
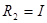 ; ; 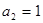 ; ; 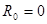 ; n=2; i=1; ; n=2; i=1; 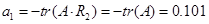
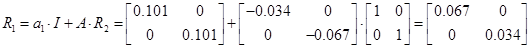
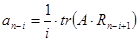
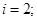
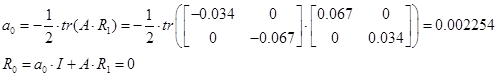
Таким чином
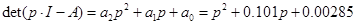
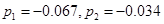
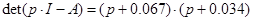
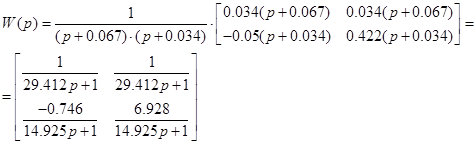
1.9 Структурні схеми системи в початковій формі, формі Ассео, ЗЗП
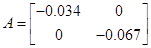  
Рисунок 2. Структурна схема системи в початковій формі.
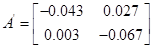 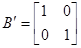 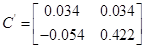
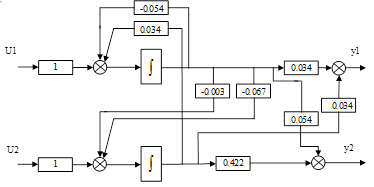
Рисунок 3. Структурна схема системи в формі Ассео.
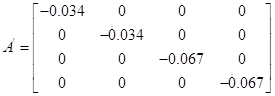 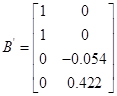
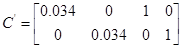

Рисунок 4. Структурна схема системи у зовнішньозв'язанному поданні.
1.10 Лінеаризована модель в непереривному і дискретному часі з датчиками і ВМ
a) в непереривному часі
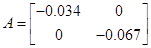 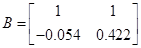 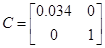
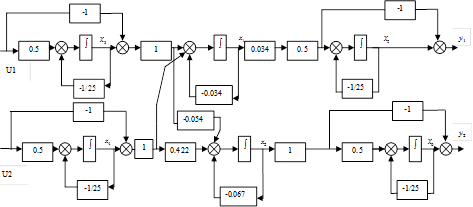
Рисунок 5. Структурна схема системи в неперервному часі з датчиками і ВМ.
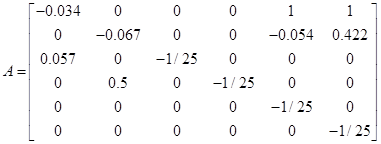 
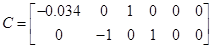
б) в дискретному часі
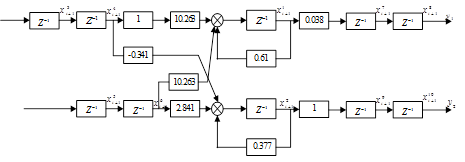
Рисунок 6. Структурна схема системи в дискретному часі з датчиками і ВМ.
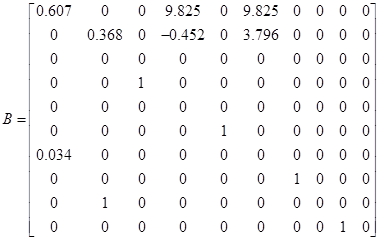 
 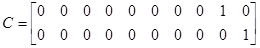
1.11 Умова правомірності децентралізації
Система в формі Ассео:
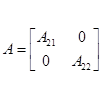 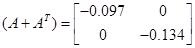
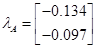 , , 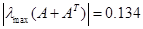 , ,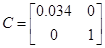 , ,
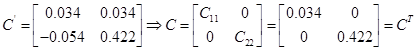
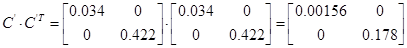
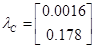
Спектральна норма матриці 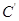 , тобто максимальне сингулярне число матриці: , тобто максимальне сингулярне число матриці:
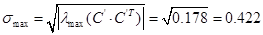 , ,  . .
Спектральна норма матриці F:
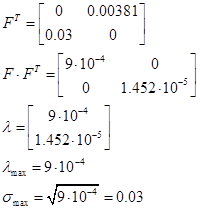
Тоді:
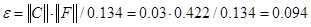
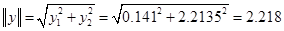
Похибка складає:
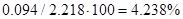
Можна допустити, що децентралізація є допустимою.
2. Аналіз якісних властивостей системи
А) 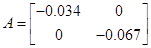 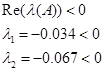
Матриця являється гурвіцевою.
Б)  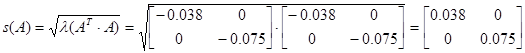
max s1 (A) =||A||2=0.067<1
Відповідно, матриця А є нільпотентною.
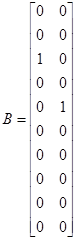
Перевірити, чи є система (А, В, С) сталою, керованою, спостережною, ідентифікованою з вектором-стовпцем х = (1; 1.25), параметрично інваріантною, мінімально фазовою, розчеплюваною, мінімально.
А) сталість:
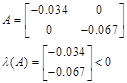
Відповідно система являється сталою.
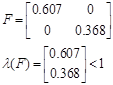
Відповідно система являється сталою.
Б) керованість:
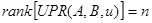
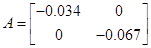 ; ; 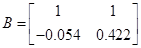 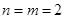
По першому входу:
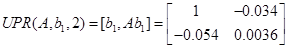
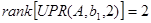
Система керована по першому входу.
По другому входу:
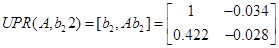
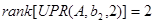
Система керована по другому входу.
В) спостережність:
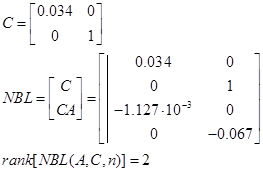
Система спостережна.
Г) ідентифікованість:
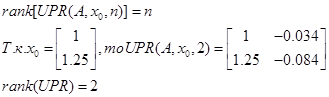
Система є ідентифікована.
Д) параметрична інваріантність:
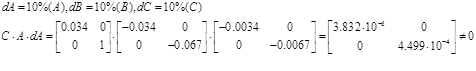
Система не інваріантна відносно відхилення dA.

Система не інваріантна відносно відхилення dB.
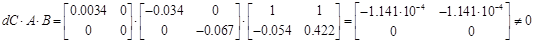
Система не інваріантна відносно відхилення dС.
Е) мінімальнофазовість і астатичність:
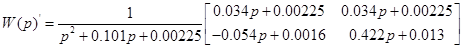
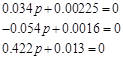 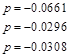 
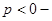 система являється мінімально фазовою і статичною. система являється мінімально фазовою і статичною.
Ж) розчеплюваність:
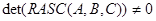
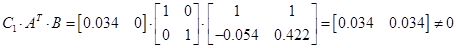
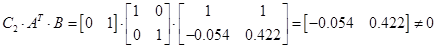
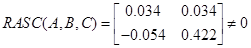 det=0.016 det=0.016
Система є розчеплюваною.
3. Дослідження процесів в системі і аналіз кількісних властивостей системи
3.1 Побудова графіків розгінних кривих непереривної системи
Побудова графіку розв'язання у (t) для системыи {А, В, С}, якщо
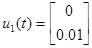 и и 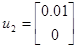
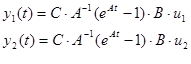
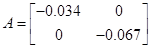 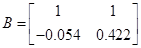 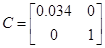
Таблиця 4.
| Збурення |
Реакція виходу системи y (t) |
u1=0,01
u2=0
|
y1
y2
|
0
0
|
0,00435
0,00445
|
0,00681
0,00609
|
0,00820
0,0067
|
0,00898
0,00692
|
0,00942
0,00700
|
0,00967
0,00703
|
u1=0
u2=0,01
|
y1
y2
|
0
0
|
0,00435
0,037
|
0,00681
0,051
|
0,00820
0,056
|
0,00898
0,058
|
0,00942
0,059
|
0,00967
0,059
|
| час t, с |
0 |
14,3 |
28,6 |
42,9 |
57,2 |
71,5 |
85,8 |
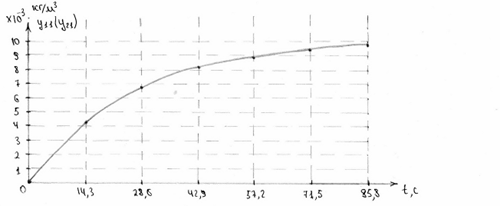
Рисунок 7. Розгінна крива витрати рідини для неперервної системи при збуренні 0 і 0,01.
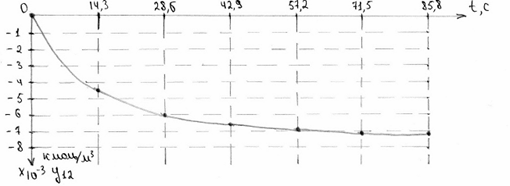
Рисунок 8. Розгінна крива концентрації для неперервної системи при збуренні 0.
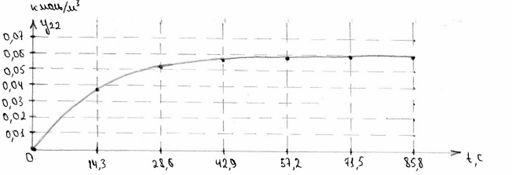
Рисунок 9. Розгінна крива концентрації для неперервної системи при збуренні 0,01.
Реклама

3.2 Побудова графіків кривих разгону дискретної системи
Система в дискретному часі має вид:
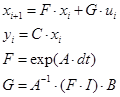
dt=14,89 c.
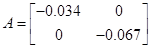
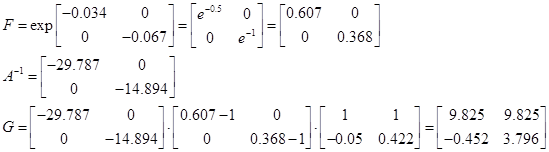
Таким чином
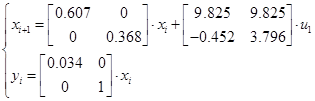
Задавшись 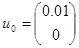 , , 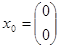 , тоді , тоді
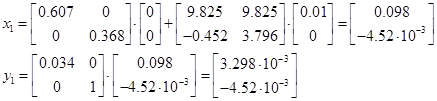
Результати подальших ітерацій представлено в таблиці:
Таблиця 5.
| Збурення |
Реакція виходу системи y (t) |
u1=0
u2=0,01
|
y1
y2
|
0
0
|
0,003298
0,00452
|
0,005299
0,00469
|
0,00773
0,006183
|
0,006512
0,006795
|
0,00725
0,00702
|
0,00769
0,00713
|
| час t, с |
0 |
14,894 |
29,787 |
44,681 |
59,574 |
74,468 |
89,362 |
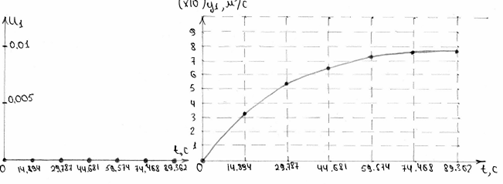
Рисунок 10. Характеристика витрати рідини в дискретному часі.
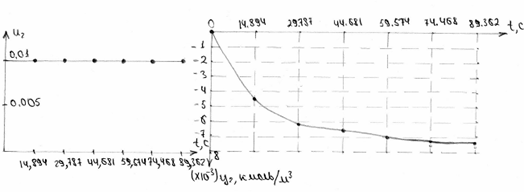
Рисунок 11. Характеристика концентрації в дискретному часі.
3.3 Побудова графіків кривих разгону нелінійної системи
Розглянемо поповнення бака від 0 до номінального значення витрати з урахуванням приросту поданого лінеаризованій моделі. Таким чином, розглянемо стрибок u1
=0,03; u2
=0.
Позначивши 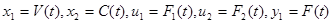 ,рівняння бака запишемо у вигляді системи: ,рівняння бака запишемо у вигляді системи:
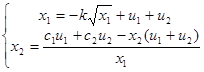 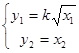 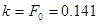
Перше рівняння є нелінійним зі змінними що розділяються
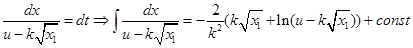
З урахуванням того, що 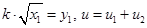 запишемо: запишемо:
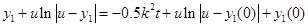 , чи підставляючи , чи підставляючи
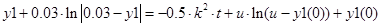
Виразимо 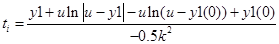
Підставляємо  та та 
Таблиця 6.
| y1 |
0.141 |
0.142 |
0.143 |
0.144 |
0.145 |
0.146 |
0.147 |
0.148 |
0.149 |
0.150 |
0.151 |
| t, с |
0 |
1.5 |
3.188 |
5.116 |
7.357 |
10.026 |
13.315 |
17.585 |
23.643 |
34.072 |
68.958 |
По отриманим даним побудуємо графік:

Рисунок 12. Лінійна та нелінійна характеристика витрати води.
Так як немає аналітичної залежності 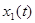 , використаємо її кус очно-лінійну апроксимацію, представляючи на проміжкові від , використаємо її кус очно-лінійну апроксимацію, представляючи на проміжкові від 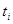 до до 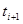 функцію функцію 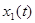 как как  . Тоді, . Тоді,
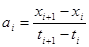 ; ; 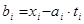
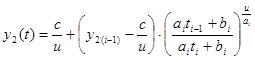
Отримані дані занесемо в таблицю:
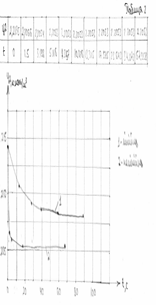
Рисунок 13. Лінійна та нелінійна характеристика концентрації.
3.4 Сталий стан системи
Вичислимо постійне значення системи при умовах
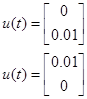
І порівняємо його з результатом розрахунку.
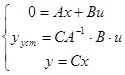
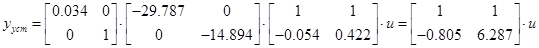
4. Ідентифікація багатомірної математичної моделі по даним експеремента
4.1 Активна ідентифікація
Для дискретної форми системи (F, G, C) провести реалізацію системи.
Запишемо систему у вигляді:
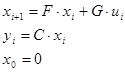
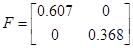 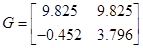 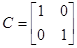
Подавши імпульс по першому входу, розрахуємо:
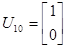 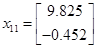 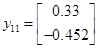
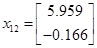 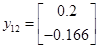
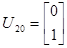 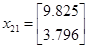 
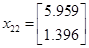 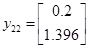
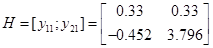
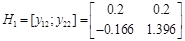
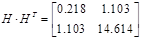
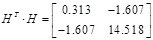
Із власних векторів від ( ) і ( ) і (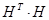 ) побудуємо: ) побудуємо:
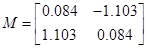 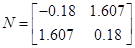
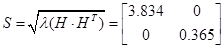 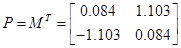 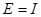
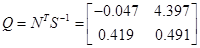
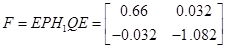
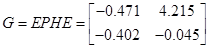
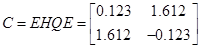
При 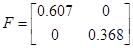 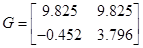 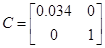
Знайдемо передаточну функцію системи:
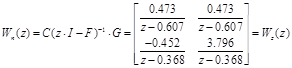 . .
4.2 Пасивна ідентифікація
Для дискретної форми системи (F, G, C) провести пасивну ідентифікацію системи:
Таблиця 7.
| Такт, n |
0 |
1 |
2 |
3 |
4 |
5 |
| U (n) |
0.01 |
0 |
0 |
0.04 |
0 |
0 |
| 0 |
0.01 |
0.02 |
0 |
0.03 |
0 |
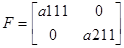 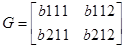 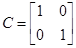
Використовуючи матриці системи в дискретній формі для заданих значень вектора входу, розрахуємо значення вектора виходу
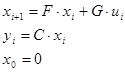
Результати розрахунку занесемо до таблиці:
Таблиця 8.
| Такт, n |
1 |
2 |
3 |
4 |
5 |
6 |
| y (n) |
0.117 |
0.188 |
0,349 |
0.68 |
0.765 |
0.464 |
| -0.00509 |
0.03787 |
0.09342 |
0.01402 |
0.12438 |
0.04577 |
Тогда
 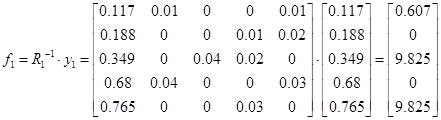
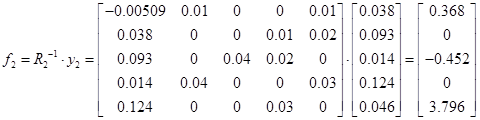
Следовательно, 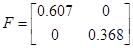 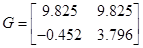 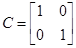
5. Конструювання багатомірних регуляторів, оптимізуючи динамічні властивості агрегату
5.1 Конструювання П-регулятора, оптимізую чого систему по інтегральному квадратичному критерію
Регулятор стану який оптимізує систему по критерію:
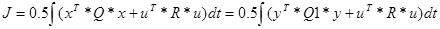 
Визначається по співвідношенню: P=LR1 (A,B,Q,R);
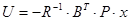
 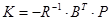
Притом Q=R=I
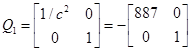
Так як матриця С є інвертованою, для створення регулятора виходу немає
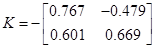
Необхідно конструювати спостерігач стану -недосяжний стан вичислюється по формулі 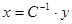 . Відповідно регулятор виходу має вид . Відповідно регулятор виходу має вид 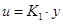
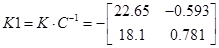
Позначивши через z задане значення виходу у і припускаючи, що 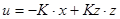 , отримаємо , отримаємо
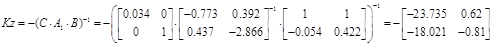
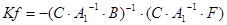
5.2 Конструювання компенсаторів завдань і вимірюваних збурень
Прийнявши до уваги, що А=В
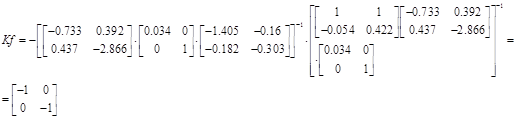
Якщо при компенсації збурень і завдань зчитувати "вартість" управління, записавши критерій в виді
 , ,
то компенсатори визначаються залежностями
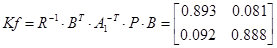
Значення виходу при дії збурення f в системі без компенсаторів при z=0
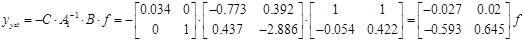
З оптимальною компенсацією
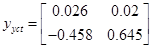 f f
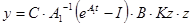
5.3 Конструювання регулятора з компенсатором взаємозв'язків
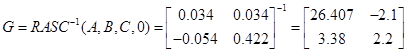
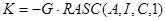
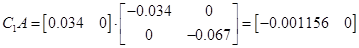
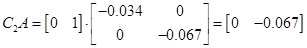
Следовательно,
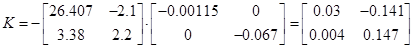
Перевіримо чи регулятор дійсно розчіплює систему, тобто матриця передаточних функцій являється діагональною
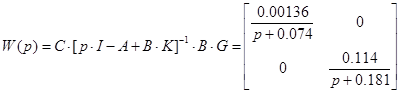
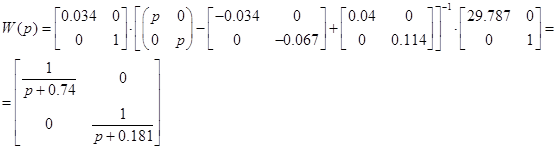
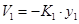 , , 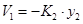 , де , де 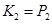 , , 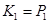 . .
Знайдемо
1. 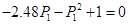 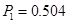
2. 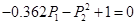 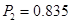 . .
5.4 Конструювання аперіодичного
Аперіодичний регулятор для дискретної системи може бути отриманий із умови 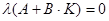 . Запишем . Запишем 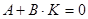
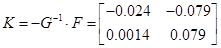
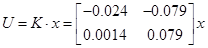
5.5 Конструювання децентралізованого регулятора
Використовуючи форму Ассео, запишем:
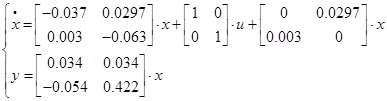
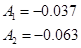 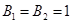
Відповідно, отримаємо 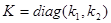
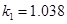 , , 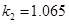
Розв'яжим рівняння Ляпунова.
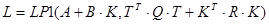 T=B T=B
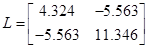
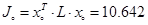
5.6 Конструювання надійного регулятора
Якщо матриця G моделяє відмови каналів вимірювання, то регулятор знаходиться в виді 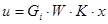

нехай s=0.041
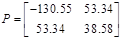
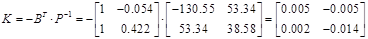
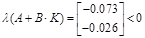
Відповідно, система являеться постійною при любих відхиленнях.
5.7 Конструювання блочно-ієрархічного регулятора
Використаємо регулятор стану і перевіримо чи можна створити послідовність регуляторів стану.
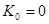 ; ;  ; ; 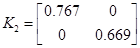 ; ; 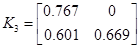 ; ; 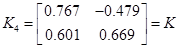
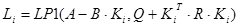
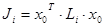
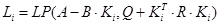
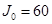
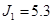
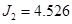
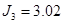
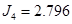
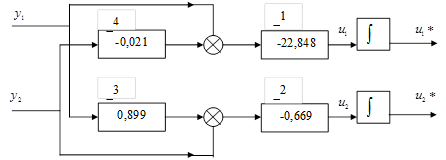
Рисунок 14. Схема блочно-ієрархічного регулятора.
5.8 Конструювання регулятора для білінійної моделі
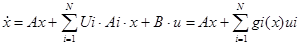
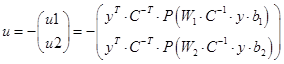
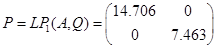
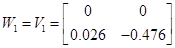 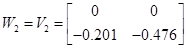
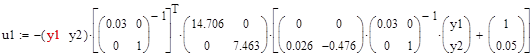
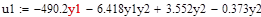
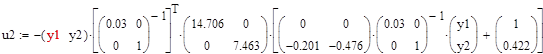
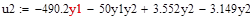
5.9 Конструювання регулятора для нелінійної системи
Сконструювати нелінійний регулятор, використовуючи початкову не спрощену модель бака.
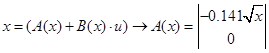 , , 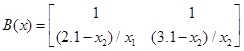
Розрахункове співвідношення для регулятора - 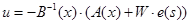 , де , де 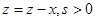
При s=4, W=1 запишемо
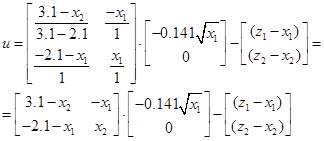
Підставивши  запишемо запишемо
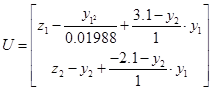
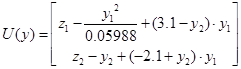
5.10 Конструювання програмного регулятора
Використовуючи лінеаризовану модель в дискретному часі, запишемо програму переходу системи із стану 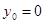 в стан в стан
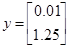 . .
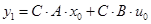
При 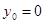 ; ; 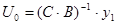
Отримаємо
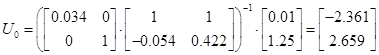
6. Аналіз властивостей зконструйованої системи з оптимальним П-регулятором
6.1 Побудова процесу в системі з П-регулятором
Стале значення виходу при дії збурення f у системі без компенсаторів при z=0
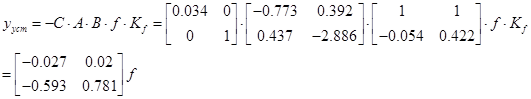
З оптимальною компенсацією
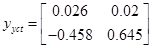 f f
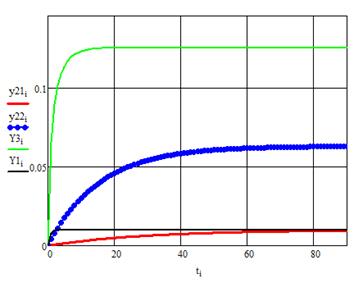
Рисунок 15. Графіки перехідних процесів та кривих розгону по першому та другому виходах з оптимальним П-регулятором з компенсатором і без.
6.2 Обчислення критерію оптимальності в системі
Величина критерію оптимальності обчислюється за залежністю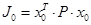 . Для обчислення величини критерію з довільним регулятором слід використовувати формулу . Для обчислення величини критерію з довільним регулятором слід використовувати формулу
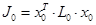 , де , де 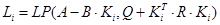 . .
розв'язавши рівняння Ляпунова отримаємо
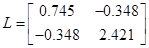
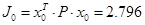
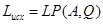
розв'язавши рівняння Ляпунова отримаємо
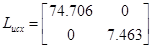
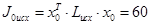
При 10% та 5%
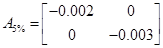 , ,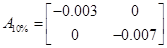
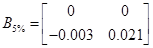 , ,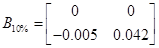
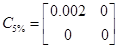 , , 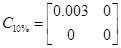
Розв'яжемо  для всіх матриць при нових значеннях для всіх матриць при нових значеннях
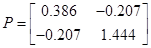 , , 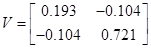
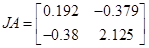 , , 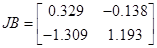 , , 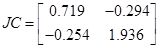 , , 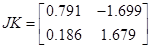
При 10% та 5%
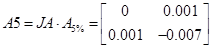 , , 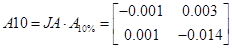
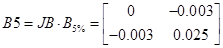 , ,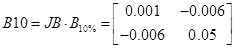
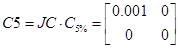 , ,  . .
6.3 Обчислити чуйність системи
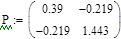
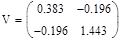
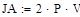
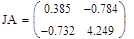
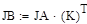
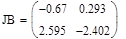
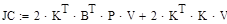
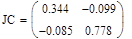
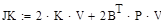
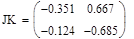
6.4 Проаналізувати робастність системи
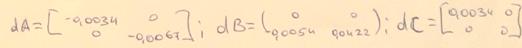

6.5 Розв'язати зворотну задачу конструювання
Знайти за яким критерієм є оптимальний регулятор з компенсаторів взаємозв'язків.
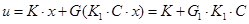
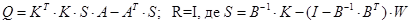
де W - довільна матриця яка задовольняє умові S>0
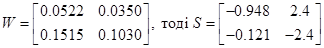
розв'язавши отримаємо
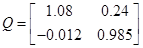
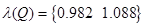
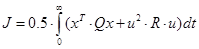
Висновок
Таким чином, в ході виконання курсової роботи на прикладі моделі змішувального бака була розгляне на технологічна послідовність конструювання систем: побудова та перетворення моделей системи, аналіз властивостей початкової системи, конструювання регуляторів, аналіз властивостей і порівняння сконструйованих систем. Також при виконанні були отримані ряд кривих розгону та перехідних процесів для моделі бака, були побудовані структурні схеми моделі в початковій формі, Ассео, зовнішньо зв’язаній формі. Отримали навики конструювання систем з використанням регулятора з компенсатором взаємозв”язків, аперіодичного, децентралізованого, надійного, блочно-ієерархічного регуляторів, програмного регулятора, регулятора для нелінійної моделі, регулятора для білінійної моделі.
Література
1. Методические указания к практическим занятиям по курсу "Основы системного анализа и теория систем", А.А. Стопакевич
2. "Сложные системы: анализ, синтез, управление", А.А. Стопакевич
Додаток
Розв'язання рівняння Рікарті
Розв'язання рівняння Рікарті 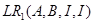 визначення матриці Р. визначення матриці Р.
Сформуємо матрицю
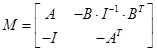
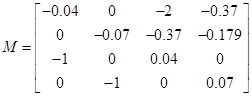
Для обчислення власних значень розкриємо визначник 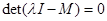

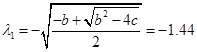 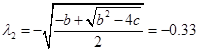
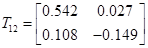 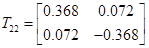
 . .
Розв'язання рівняння Ляпунова 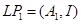
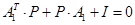
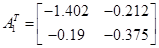
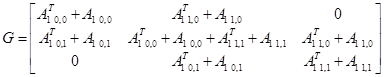
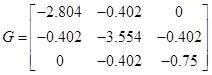 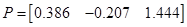 . .
Обчислення матричної експоненти
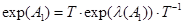
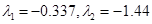
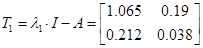 , ,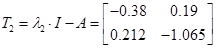
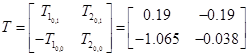 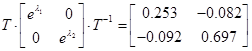 . .
Фробеніусові матриці
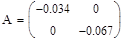
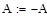
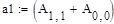
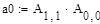
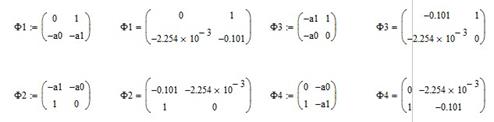
Вандермордова матриця
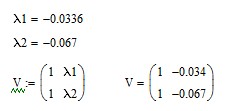
|