Содержание
1. Цель и задачи ККР
2. Назначение, особенности конструкции пули
3. Оценка массоинерцеонных характеристик
4.Расчет аэродинамических характеристик
5. Оценка начальных условий полета пуль
6. Оценка кучности стрельбы по детерменированой модели
Список использованной литературы
1. Цель и задачи ККР
Получение практических навыков, требующихся при разработке конструкции пуль стрелкового и спортивного оружия, при контроле или прогнозировании в процессе производства и самостоятельной проверке выполнения поставленных техническим заданием требований. Основной задачей является определить аэродинамические и массоинерционные характеристики, предложенной для разработки конструкции пули и оценить точность стрельбы комплекса "Пуля-патрон-оружие" при заданных условиях.
2. Назначение, особенности конструкции пули
Дано:
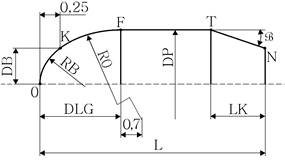
L=24.8мм.; DLG=17,1мм.; RO=70,0 мм.;
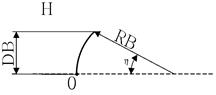
RB=1,18 мм.; DB=1,2мм.; DP= 5,55 мм.;
LK=4,0мм; 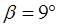 ; V=910 м/с. ; V=910 м/с.
Данная пуля предназначена для поражения живой силы противника и небронированной техники из стрелкового оружия. Состоит из двух частей: корпуса и внутренней части.
3. Оценка массоинерцеонных характеристик
При проектировании различных машин и механизмов возникают задачи, для решения которых необходимо иметь точные сведения о распределении массы в конструируемой механической системе. Для изделий отрасли к таким задачам относятся: прогнозирование элементов траекторий полета, оценка устойчивости движения на траектории, обеспечение требуемой эффективности функционирования и др.
Оценка массоинерционных характеристик – массы [m], моментов инерции 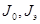 , осевой координаты центра масс - , осевой координаты центра масс - 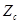 . Массоинерционные характеристики определяются по существующим и методикам расчета на компьютере программы «Масса». . Массоинерционные характеристики определяются по существующим и методикам расчета на компьютере программы «Масса».
В определенном масштабе вычерчивают сечение (по оси симметрии) конкретного изделия. Главную прямоугольную систему координат AXYZ располагают у левого края изделия, направив по оси симметрии главную ось АХ, а ось AZ перпендикулярно плоскости чертежа. В выбранном масштабе вычерчивают отдельно сечения всех деталей изделия, сохранив их положение относительно осей системы координат AXYZ. Всем деталям присваивается порядковый номер.
Реклама

Координаты и параметры для 1-ой детали.
Точка 1.
x =0;
D=0;
R=1.18;
Точка 2.
x =0.25;
D=1.2;
R=70;
Точка 3.
x =20.8;
D=5.55;
R=0;
Точка 4.
x =20.8;
D=5.55;
R=0;
Точка 5.
x =24.8;
D=4.92;
R=0;
Точка 6.
x =24.8;
D=3.92;
R=0;
Точка 7.
x =20.8;
D=4.55;
R=0;
Точка 8.
x =17.1;
D=4.55;
R=69.5;
Точка 9.
x =1;
D=1;
R=0;
Точка 10.
x =1;
D=0;
R=0;
Координаты и параметры для 2-ой детали.
Точка 1.
x =1;
D=1;
R=69,5;
Точка 2.
x =17,1;
D=4,55;
R=0;
Точка 3.
x =17,1;
D=4,55;
R=0;
Точка 4.
x =24,8;
D=3,92;
R=0;
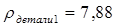 
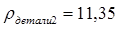 
После введения исходных данных получили значение характеристик корпуса и внутренней части и общее значение.
Деталь 1
Масса детали 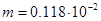 кг. кг.
Координаты центра масс относительно базовой плоскости х=14,55мм
Момент инерции
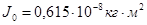 , ,
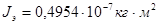 . .
Деталь 2
Масса детали 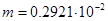 кг. кг.
Координаты центра масс относительно базовой плоскости х=15,53мм
Момент инерции
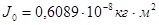 , ,
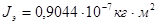 . .
Изделие.
Масса детали 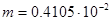 кг. кг.
Координаты центра масс относительно базовой плоскости х=15,24
Момент инерции
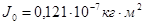 , ,
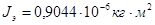 . .
4. Расчет аэродинамических характеристик
Оценки аэродинамических характеристик пули – аэродинамических коэффициентов пули, силы лобового сопротивления – Сл, подъемной силы Су, 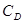 и J. и J.
Синтез летательного аппарата связан с анализом аэродинамических свойств, проектируемой конструкции.
Высокие тактико-технические данные аппарата во многом обусловлены удачным выбором аэродинамической схемы. Поэтому при общем проектировании возникает необходимость хотя бы приближенно оценить аэродинамические свойства изделия.
При выборе аэродинамической схемы обычно используют разнообразные методы приближенного аэродинамического расчета, либо корректируют аэродинамические данные прототипа.
Расчет коэффициентов аэродинамических сил
Аэродинамические силы, действующие на изделие в полете, можно представить в виде компонентов, ориентированных параллельно осям скоростей системы координат.
Аэродинамические силы на основании теории аэродинамического подобия выражают формулами экспериментальной аэродинамики:
(1) 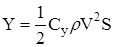 — подъемная сила; — подъемная сила;
(2) 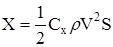 — сила лобового сопротивления; — сила лобового сопротивления;
(3) 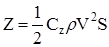 — боковая сила; — боковая сила;
Здесь 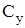 — коэффициент подъемной силы; — коэффициент подъемной силы;
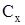 — коэффициент силы лобового сопротивления; — коэффициент силы лобового сопротивления;
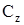 — коэффициент боковой силы; — коэффициент боковой силы;
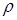 — плотность воздуха — плотность воздуха
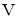 — скорость полета — скорость полета
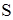 — характерная площадь — характерная площадь
Для изделий осесимметричных схем обычно принимают 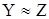 , поэтому расчет аэродинамических сил сводится к определению , поэтому расчет аэродинамических сил сводится к определению 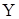 и и 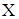 . .
Продольную (осевую) силу тела вращения, имеющего донный срез, обычно представляют в виде суммы составляющих от давления 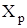 на боковую поверхность и давления на донный срез (донная осевая сила) на боковую поверхность и давления на донный срез (донная осевая сила) 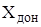 , а также осевой силы , а также осевой силы 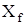 , зависящей от поверхностного трения. В соответствии с этим полный коэффициент осевой силы , зависящей от поверхностного трения. В соответствии с этим полный коэффициент осевой силы
Реклама

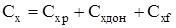
Составляющие осевой силы и их коэффициенты можно определить, если известно распределение давления и касательного напряжения по поверхности корпуса.
Рассмотрим корпус в виде тела вращения и оценим полный коэффициент осевой силы используя комбинированные методы расчета, согласно которым 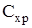 и и 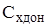 определяют по результатам экспериментов, а определяют по результатам экспериментов, а 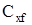 по теоретическим зависимостям. по теоретическим зависимостям.
Найдем необходимые данные к расчету
1) Критерий аэродинамического подобия 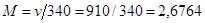
2) Коэффициент давления в точке торможения потока (точка О)
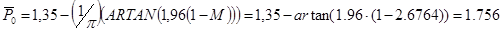
3) 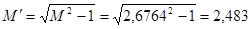
4) Вспомогательная величина (параметр)
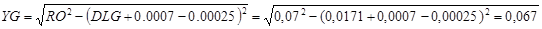 ; ;
5) 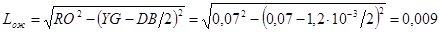 ; ;
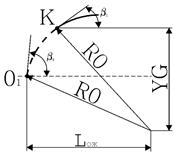
6) Относительная длина оживала
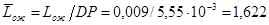 ; ;
7) Угол при вершине заостренного оживала
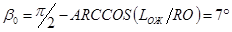 ; ;
8) Угол при вершине притупленного оживала
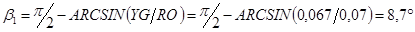 ; ;
9) 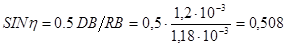
Найдем Сх
1. Оценка волнового сопротивления 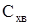 корпуса корпуса
(*) 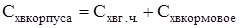
(**)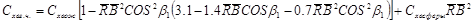 , ,
где 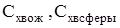 — коэффициенты волнового сопротивления заостренной параболической головки и сферического носка. — коэффициенты волнового сопротивления заостренной параболической головки и сферического носка.
В случае затупления в виде плоского торца
(***) 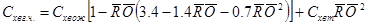
Оценим составляющие (**)
1) 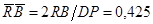
2) 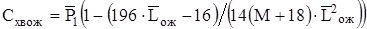 , ,
где 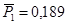 — коэффициент давления в вершине конуса с — коэффициент давления в вершине конуса с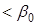 ; ;
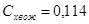
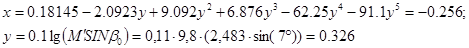
3) Волновое сопротивление изолированной сферической части с углом h
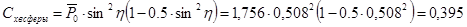
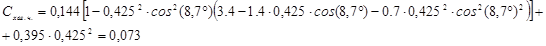
4) По (**) оценим 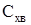 головной части. головной части.
Примечание. Если торец плоский, то 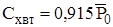
Оценка 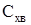 кормового кормового
(****) 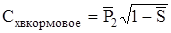 , где , где
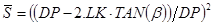 — относительное донное сужение — относительное донное сужение
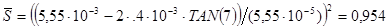
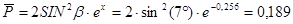
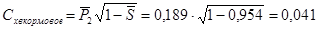
1. Оценка волнового сопротивления 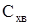 корпуса корпуса
(*) 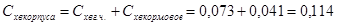
Суммарное волновое 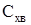 корпус по (*) корпус по (*)
2.Оценка донного сопротивления — 
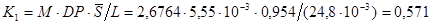 ; ;
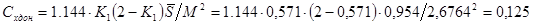
3. Оценка сопротивления трения
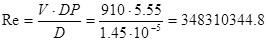
При V=910, к=1,18
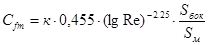
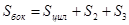

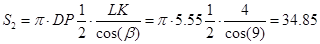
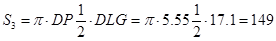
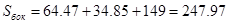
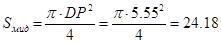
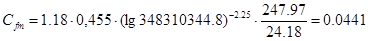
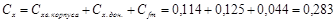
На компьютере с помощью программы «Аэро 0» определяем параметры:
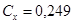 , , 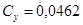 , , 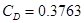 , , 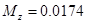 , , 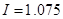
5. Оценка начальных условий полета пуль
Формализованные модели, формирования элементов траекторий полета, характерны для современных методов проектирования. Они учитывают влияние конструктивных характеристик пуль при выстреле. В данном разделе определяются начальные условия полета пуль: угол нутации δ0 и начальная боковая скорость.
Расчетами установлено, что в процессе периода последействия угол нутации меняется по величине и фазе примерно на 5 – 7 % по отношению к углу нутации в конце переходного периода, а боковая скорость меняется незначительно. Поэтому можно считать, что начальные условия движения пули в воздухе равны параметрам движения пули в конце переходного периода.
Для оценки δ0 и Vδ воспользуемся известными формулами, полученными на кафедре ГД.
Начальный угол нутации δ0 оцениваем по зависимости
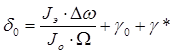
Где,
g0 - моментная неуравновешенность пули, обусловленная погрешностью изготовления;
величина g* принимается в пределах 10 ¸ 15% от первого слагаемого;
Ω – угловая скорость собственного вращения пули при потере контакта со стволом оружия.
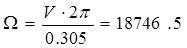
Боковую скорость в конце переходного периода Vб определяем по зависимости
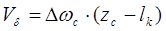 , ,
где
lk – длина хвостового конуса пули;
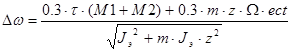 ; ;
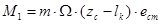
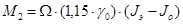
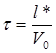 [с], [с],
где l* - путь пули за время переходного периода
Величины средних значений эксцентриситета центра масс - eст и моментной неуравновешенности пули - g принимаем в следующих пределах:
eст=3*10-6 [м];
g0=0,036 [градус].
Cd=0.3763
Z=cd*L=0.3761*24.8=9.3272
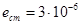
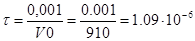
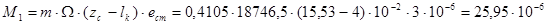
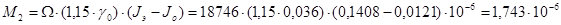
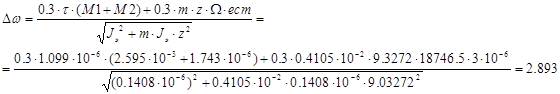
Начальный угол нутации δ0 оцениваем по зависимости
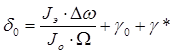
Где, величина g* принимается в пределах 10 ¸ 15% от первого слагаемого;
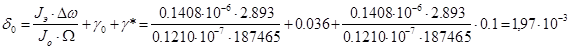
Боковую скорость в конце переходного периода Vб определяем по зависимости
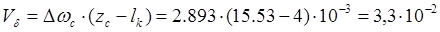 . .
6. Оценка кучности стрельбы по детерменированой модели
На основании известных и рассчитанных геометрических, аэродинамических, массоинерционных и кинематических параметров пули и выстрела приближенную оценку кучности стрельбы проводим по детерминированной модели. Предварительно с помощью основных функций Сиаччи рассчитываем Tпол.
Радиус отклонения пули от СТП оценивается по зависимости:
R100= [P12+(Vб *Tпол)2]0.5,
где P1=f(A,n,Tпол). Этот радиус прямо пропорционален ускорению А от суммарной боковой силы FбS и полетному времени Tпол и обратно пропорционален скорости прецессии ωпр (числу оборотов прецессионного вращения пули - n)
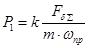 , ,
где
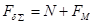 ; ; 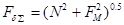 ; ;
k – коэффициент согласования, определяемый как функция времени полёта Tпол и скорости прецессии ωпр; k=1
N – подъемная сила;
Fм - сила Магнуса.
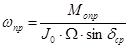 ; ; 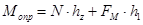 . .
Или, так как N и FM векторные величины и всегда взаимно перпендикулярны, то
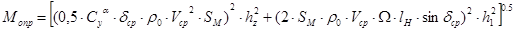 ; ;
hz – расстояние между центром масс и центром давления;
h1 - расстояние между центром масс и серединой следа нарезов.
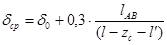 ; ;
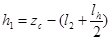 , ,
где – lAB несоосность вершины пули относительно ГЦОИ
l2 - расстояние от донного среза пули до следа нарезов на ведущей части пули;
lH --длина следа нарезов на ведущей части пули.
l/ =0,25 мм. --расстояние от вершины пули до плоскости замера диаметра вершины пули (длина головной части пули).
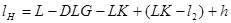
где
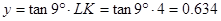
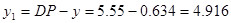
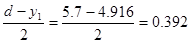
где d-диаметр по дну нареза = 5,7
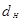 -диаметр по полям нареза = 5,4 -диаметр по полям нареза = 5,4
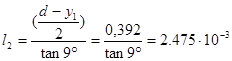 м. м.
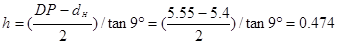
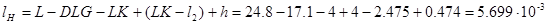 м. м.
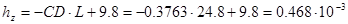 м. м.
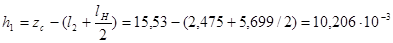 м. м.
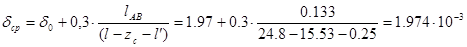 м. м.
где 
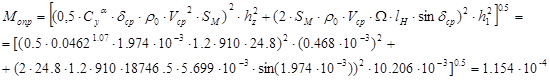
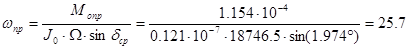
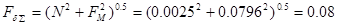
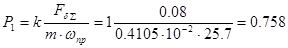
Вывод: По найденным значениям FбS, ωnp и алгоритму программы расчета элементов траектории полета –«Полёт» при выстреле рассчитываем средний и макс. Радиус кучности стрельбы на дистанции 100м - 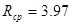 мм, мм, 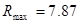 мм. мм.
Список использованной литературы
1.Кириллов В.М. "Основания устройства и проектирования стрелкового оружия".- Пенза:ПВАИУ, 1968 г.
2.Кириллов В.М., - Сабельников В.М. "Патроны стрелкового оружия". – М.:ЦНИТИ, 1980 г.
3.Прохоров Б.А "Боеприпасы артиллерии". – М.:Машиностроение, 1973 г.
4.Шапиро Я.М. "Внешняя баллистика". – М.:Оборонгиз – 1946 г.
5.Краснов Н.Ф. "Основы аэродинамического расчета". – М.:Высшая школа, 1981 г.
6."Расчет коэффициентов аэродинамических сил" (методические указания) инв.№ 110.
|