Кафедра «Гидравлика»
Курсовая работа
«Гидравлический расчет узла гидротехнических сооружений»
Минск 2009
Содержание..................................................................................................... 2
Задание............................................................................................................ 3
1. Расчет магистрального канала................................................................... 5
1.1Определение размеров поперечного сечения......................................... 5
1.2 Расчет канала гидравлически наивыгоднейшего сечения....................... 9
1.3 Определение нормальных глубин для заданных расходов Qmin
, Q, Qmax
и построение кривой Q=f
(h)............................................................................... 9
1.4 Определение типа и построение кривой свободной поверхности........ 11
2. Расчет сбросного канала........................................................................... 14
3. Расчет водозаборного регулятора........................................................... 16
4. Расчет многоступенчатого перепада........................................................ 18
4.1 Расчет входной части (щелевой водослив)............................................ 18
4.2 Расчет ступеней....................................................................................... 20
Литература.................................................................................................... 23
Магистральный канал подает воду на орошение и обводнение подкомандной ему территории. От магистрального канала отходит сбросной канал, в головной части которого устраивается регулятор. На сбросном канале предусматривается сооружение многоступенчатого перепада.
Требуется выполнить гидравлические расчеты следующих гидротехнических сооружений.
1. Расчет магистрального канала
— Определение размеров канала из условия его неразмываемости (Qmax
=1,8Q) и незаиляемости (Qmin
=0,75Q).
— Определение нормальных глубин для заданных расходов Qmax
, Qmin
, Qн
и построение кривой Q=f
(
h
)
.
— Определение типа и построение кривой свободной поверхности.
2. Расчет сбросного канала
Реклама

Определение размеров трапециидального сбросного канала при заданном β=
b
/
h
3. Расчет водозаборного регулятора
Определение рабочей ширины регулятора при глубинах равномерного движения в магистральном и сбросном каналах при пропуске максимального расхода.
4. Расчет многоступенчатого перепада
— Расчет входной части
— Расчет ступеней
— Расчет выходной части
| 1. Магистральный канал |
| Расход Qн
м3
/с |
7 |
| Уклон дна канала i
|
0,0004 |
| Грунты |
Плотный лесс |
| Условия содержания |
Среднее |
| Глубина воды в конце канала |
1,2h0
|
| 2. Сбросной канал |
| Q |
Qmax
|
| β
=b/h
|
4 |
| Уклон дна канала i
|
0,0006 |
| 3. Водозаборный регулятор |
| Сопряжение при входе по типу |
Конусов |
| Ширина одного пролета, м. |
3,0÷5,0 |
| 4. Перепад |
| Разность отметок дна верхнего и нижнего бьефов |
6 |
| Число ступеней |
3 |
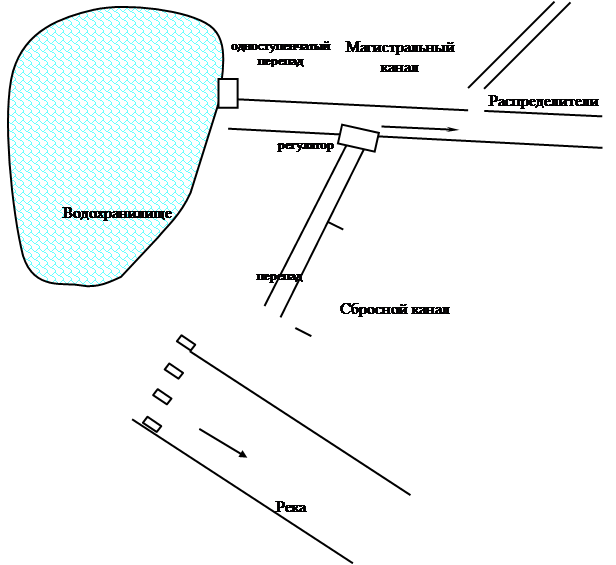
Схема гидротехнических сооружений
Равномерное движение жидкости, т.е. движение, при котором средние скорости v
, площади живых сечений ω и глубины h по длине потока остаются неизменными, наблюдается в искусственных призматических руслах (каналах), имеющих большую протяженность.
Основная расчетная формула для равномерного движения жидкости – формула Шези:
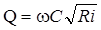
C– коэффициент Шези: 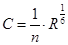
n– коэффициент шероховатости. Для плотного лесса n = 0,02
Наиболее распространенной формой сечения канала является трапецеидальная.
   m =1,5 m =1,5
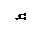 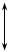    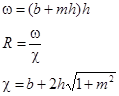
1.1
Определение размеров поперечного сечения
Определение размеров поперечного сечения сводится к определению ширины по дну и глубины наполнения по заданным параметрам (расход Q, уклон i
, коэффициенты шероховатости n и заложения откосов m). При расчетах используется рациональное соотношение β между шириной канала по дну и глубиной наполнения.
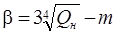
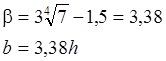 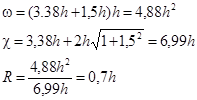
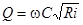 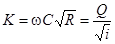
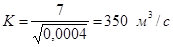 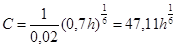
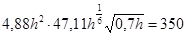
Решив это уравнение найдем:
h=1,25 м b=3,38h=4,23 м.
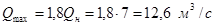 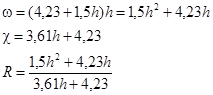
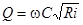 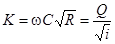
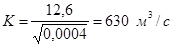 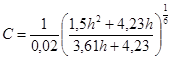
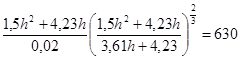
Решив это уравнение найдем:
h=1,72 м ω=1,5h2
+4,23h=11,68м2
.
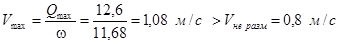
Изменяем уклон дна, для этого в начале канала сделаем одноступенчатый перепад.
i
=0,00015
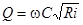 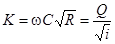
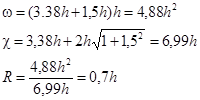
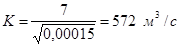 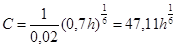
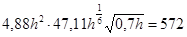
Решив это уравнение найдем:
h=1,5 м b=3,38h=5,1 м.
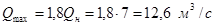 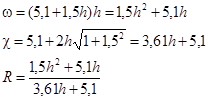
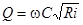 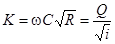
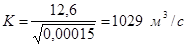 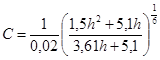
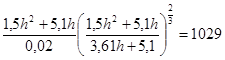
Решив это уравнение найдем:
h=2,06 м ω=1,5h2
+5,1h=16,81м2
.
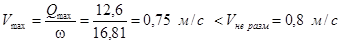
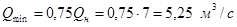 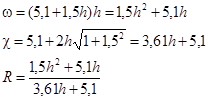
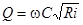 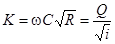
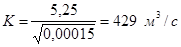 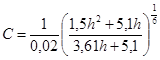
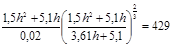
Решив это уравнение найдем:
h=1,29 м ω=1,5h2
+5,1h=9,04 м2
R=0,93 м.
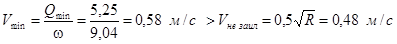
1.2 Расчет канала гидравлически наивыгоднейшего сечения
Гидравлически наивыгоднейшее сечение – такое, у которого при заданных ω, i
расход Q оказывается максимальным.
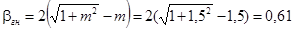
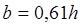 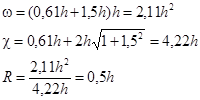
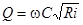 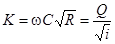
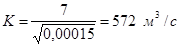 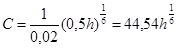
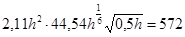
Решив это уравнение найдем:
h=3,01 м b=0,61h=1,84 м.
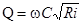
i
=0,00015
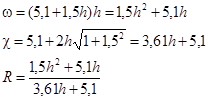 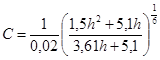
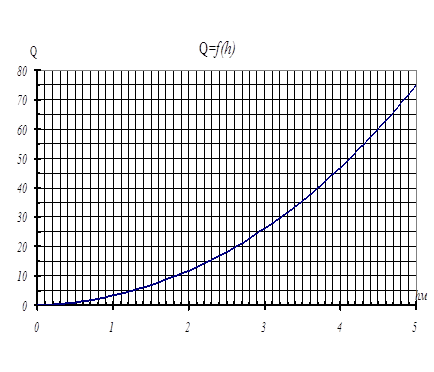
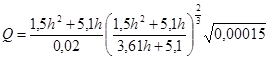
Вычисления удобно свести в таблицу:
|
h, м |
Q, м3
/с |
| 0 |
0 |
| 0,5 |
1,0037 |
| 1 |
3,3392 |
| 1,5 |
6,9297 |
| 2 |
11,847 |
| 2,5 |
18,188 |
| 3 |
26,059 |
| 3,5 |
35,566 |
| 4 |
46,814 |
| 4,5 |
59,907 |
| 5 |
74,946 |
По графику можно определить нормальные глубины для заданных расходов.
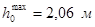 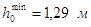 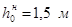
При проведении гидравлических расчетов неравномерного движения, например, при расчете кривых свободной поверхности, сопряжении бьефов, необходимо знать критическую глубину hкр
. Критическая глубина соответствует минимуму удельной энергии сечения и в общем случае определяется из уравнения:
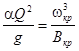
α ≈1
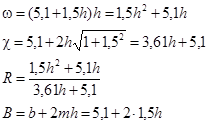 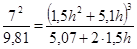
Решив это уравнение найдем:
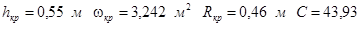
Критический уклон найдем по формуле:
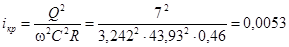 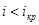 – обычный канал. – обычный канал.
Тип кривой а
I
, кривая подпора.
Построение кривой свободной поверхности:
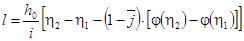 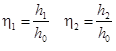 – относительные глубины – относительные глубины 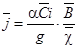 – средняя кинетичность потока – средняя кинетичность потока
Реклама

φ(η) – определяется в зависимости от гидравлического показателя русла X и относительной глубины.
Определение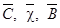 : :
h1
=1,5 м h2
=2,06 м С1
=50,4 C2
=52,3 B1
=9,57 м B2
=11,25 м χ1
=10,5 м χ2
=12,5 м
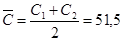 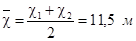 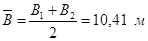
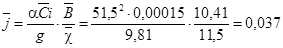
Гидравлический показатель русла:
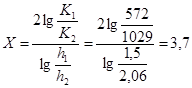
Задаемся: h1
=1,79 м h2
=1,2 h0
=1,8 м, тогда 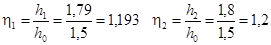 , φ(η1
)=0,312 φ(η2
)=0,301 , φ(η1
)=0,312 φ(η2
)=0,301
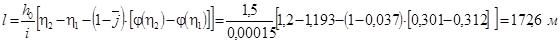
Вычисления удобно свести в таблицу:
| №
|
h1
|
h2
|
η
1
|
η2
|
X
|

|
φ(η1
)
|
φ(η2
)
|
l
|
| 0 |
1,8 |
1,8 |
1,2 |
1,2 |
3,7 |
0,037 |
0,301 |
0,301 |
0 |
| 1 |
1,79 |
1,8 |
1,193 |
1,2 |
3,7 |
0,037 |
0,312 |
0,301 |
172,6 |
| 2 |
1,78 |
1,8 |
1,187 |
1,2 |
3,7 |
0,037 |
0,315 |
0,301 |
268,2 |
| 3 |
1,77 |
1,8 |
1,18 |
1,2 |
3,7 |
0,037 |
0,323 |
0,301 |
411,9 |
| 4 |
1,76 |
1,8 |
1,173 |
1,2 |
3,7 |
0,037 |
0,331 |
0,301 |
555,6 |
| 5 |
1,75 |
1,8 |
1,167 |
1,2 |
3,7 |
0,037 |
0,339 |
0,301 |
699,3 |
| 6 |
1,73 |
1,8 |
1,153 |
1,2 |
3,7 |
0,037 |
0,357 |
0,301 |
1006 |
| 7 |
1,7 |
1,8 |
1,133 |
1,2 |
3,7 |
0,037 |
0,389 |
0,301 |
1514 |
| 8 |
1,67 |
1,8 |
1,113 |
1,2 |
3,7 |
0,037 |
0,427 |
0,301 |
2080 |
| 9 |
1,65 |
1,8 |
1,1 |
1,2 |
3,7 |
0,037 |
0,456 |
0,301 |
2493 |
| 10 |
1,6 |
1,8 |
1,067 |
1,2 |
3,7 |
0,037 |
0,553 |
0,301 |
3760 |
| 11 |
1,55 |
1,8 |
1,033 |
1,2 |
3,7 |
0,037 |
0,732 |
0,301 |
5817 |
| 12 |
1,507 |
1,8 |
1,005 |
1,2 |
3,7 |
0,037 |
1,231 |
0,301 |
10909 |
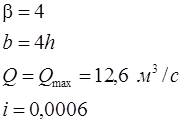 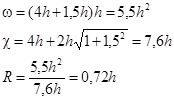
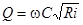 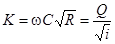
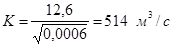 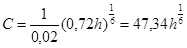
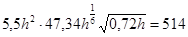
Решив это уравнение найдем:
h=1,37 м b=4h=5,48 м ω=5,5h2
=10,32 м2
.
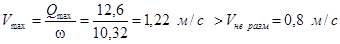
Так как скорость в канале больше размывающей, то необходимо сделать «одежду» для канала, т.е. выполнить укрепление дна и откосов. В качестве «одежды» примем гравийно-галечную обсыпку. При этом коэффициент шероховатости n=0,02 т.е. остается таким же как и до обсыпки, следовательно, скорость течения и глубина воды в канале не изменятся.
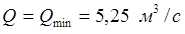 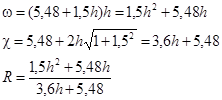
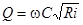 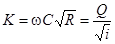
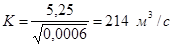 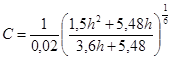
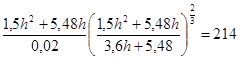
Решив это уравнение найдем:
h=0,84 м ω=1,5h2
+5,48h=5,66м2
R=0,67 м.
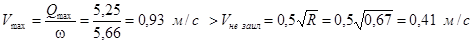
В качестве водозаборного регулятора используется водослив с широким порогом. Сопряжение водослива с широким порогом осуществляется по типу конусов. Высота водослива со стороны верхнего бьефа P назначается конструктивно в пределах P=0,25÷1 м, а толщина δ=(3÷5) H.
Коэффициент расхода m определяется в зависимости от вида сопряжения водослива с подводящим каналом и отношения P/H.
Расчет водослива с широким порогом заключается в определении его ширины, при которой перед сооружением сохраняется нормальная глубина.
Основное расчетное уравнение:
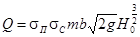
hмаг. канала
=2,06 м hсбр. канала
=1,37 м
bмаг. канала
=5,1 м bсбр. канала
=5,48 м
Вмаг. канала
=11,28 м bсбр. канала
=9,59 м
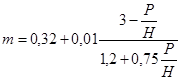 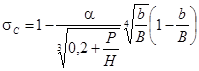
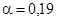 – при прямоугольном очертании быков и береговых устоев. – при прямоугольном очертании быков и береговых устоев.
Задаемся P=0,4 м, тогда Н= hмаг. канала
-Р=2,06–0,4=1,66 м.
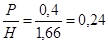 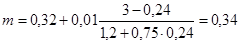
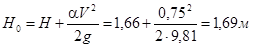
Проверка подтопления:
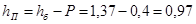 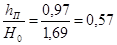
Водослив считается подтопленным если 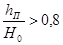 , следовательно водослив не подтоплен , следовательно водослив не подтоплен 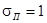
I приближение:
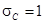
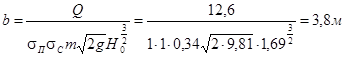
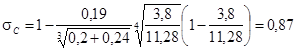
II приближение:
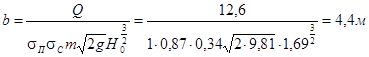
Окончательно принимаем: Р=0,4 м., b=4,4 м., δ=3Н≈5 м.
Если входная часть проектируется как щелевой водослив, то для предельных значений расходов Qmax
и Qmin
можно так подобрать размеры водослива, что бы равномерное движение в подводящем канале сохранялось бы при различных расходах в интервале Qmax
и Qmin
.
Необходимо определить среднюю ширину щели по низу «bср
» при пропуске Q1
и Q2
через щель. Эти расходы определяют при нормальных глубинах:
h01
=h0
max
-0,25 (h0
max
-h0
min
)=1,37–0,25 (1,37–0,84)=1,24 м
h02
=h0min
+0,25 (h0max
-h0min
)=0,84+0,25 (1,37–0,84)=0,97 м
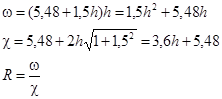 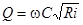
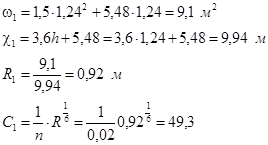
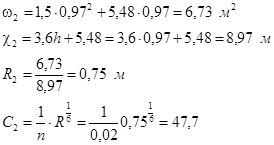
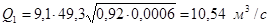 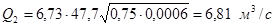
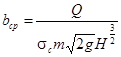
Для щелевых водосливов коэффициент расхода m≈0,48, коэффициент сжатия σс
=0,95
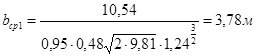 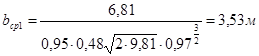
Окончательная ширина щели по низу определяется по формуле:
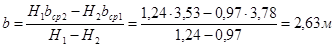
Коэффициент заложения откосов щели: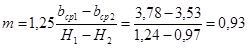 δ=(0,5÷2) Н=2 м. δ=(0,5÷2) Н=2 м.
Число ступеней – 3, ширина перепада b=5,5 м, удельный расход q=Q/b=12,6/5,5=2,3 м2
/с.
Первая ступень.
Высота стенки падения Р1
=2 м.
Высота водобойной стенки: 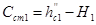
Геометрический напор перед водобойной стенкой:
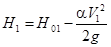 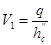
Полный напор перед водобойной стенкой: 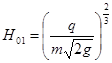
Критическая глубина: 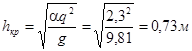
Глубина в сжатом сечении: 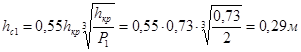
Вторая сопряженная глубина:
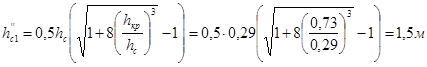
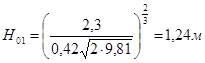 
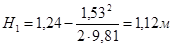
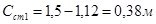
Длина колодца: 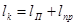
Длина прыжка: 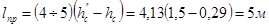
Полный напор на щелевом водосливе: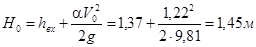
Дальность полета струи: 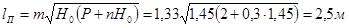
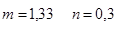
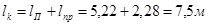
Вторая ступень.
Высота стенки падения Р2
=2 м.
Высота водобойной стенки: 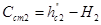
Геометрический напор перед водобойной стенкой:
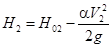 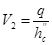
Полный напор перед водобойной стенкой: 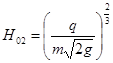
Критическая глубина: 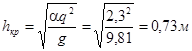
Глубина в сжатом сечении: 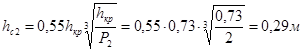
Вторая сопряженная глубина:
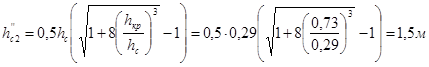
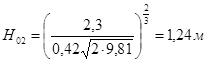 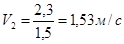
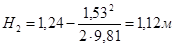
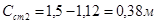
Длина колодца: 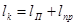
Длина прыжка: 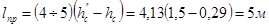
Дальность полета струи: 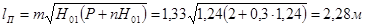
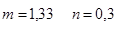
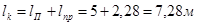
Третья ступень.
Высота стенки падения Р3
=2,5 м.
Бытовая глубина: hб
=hсброного канала
Глубина колодца: 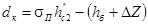
Величина перепада: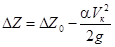 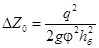 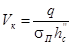
Критическая глубина: 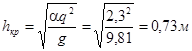
Глубина в сжатом сечении: 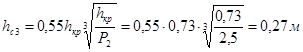
Вторая сопряженная глубина:
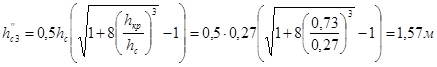
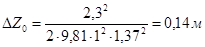 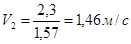
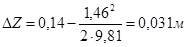
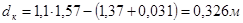
Длина колодца: 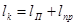
Длина прыжка: 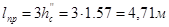
Дальность полета струи: 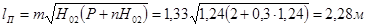
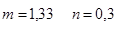
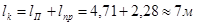
1. Справочник по гидравлическим расчетам. Под ред. П.Г. Киселева. М.; Энергия, 1972.
2. Примеры гидравлических расчетов. Под ред. А.И. Богомолова. М.; Транспорт, 1977.
3. Чугаев Р.Р. Гидравлика. Л.; Энергоиздат, 1982.
4. Методические указания к курсовой работе «Гидравлический расчет узла гидротехнических сооружений» по курсу «Гидравлика» для студентов дневного обучения специальности 1203 – «Гидротехническое строительство речных сооружений и ГЭС». И.П. Вопнярский, Н.Е. Бонч-Осмоловская. Минск 1984.
|