Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Красноярский государственный торгово-экономический институт»
М. С. Шемякина
ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ
Учебное пособие
для студентов экономических специальностей
всех форм обучения
Красноярск 2007
УДК 336.6 : 51 (075.8)
ББК 65.26Я73
Ш46
Рецензенты
кандидат экономических наук, доцент М. А. Конищева;
зам. директора КФ «Банк Москвы» Н. М. Еременко
Шемякина М. С.
Ш46 Основы финансовых вычислений : учеб. пособие / М. С. Шемякина; Краснояр. гос. торг.-экон. ин-т. – Красноярск, 2007. – 68 с.
В учебном пособии представлены методы начисления простых и сложных процентов, операции дисконтирования, производимых при обслуживании клиентов банка, способы учета векселей, методы расчета валютных операций, определение доходности вложений в ценные бумаги и т. д. Приведены примеры из практической деятельности и предложены задачи для самостоятельного решения.
Для студентов, аспирантов, преподавателей и практических работников, специализирующихся в области управления финансами.
УДК 336.6 : 51 (075.8)
ББК 65.26Я73
© ГОУ ВПО «Красноярский государственный торгово-экономический институт», 2007
© Шемякина М. С., 2007
ОГЛАВЛЕНИЕ
Введение
1. Общая методика финансовых вычислений
1.1 Начисление процентов. Расчет наращенной стоимости
Задачи для самостоятельного решения
1.2 Дисконтирование. Расчет первоначальной стоимости
Задачи для самостоятельного решения
2. Практическое применение финансовых расчетов
2.1 Учет инфляции
2.2 Операции с векселями
2.3 Операции с ценными бумагами
2.4. Валютные расчеты
2.5 Кредитные отношения
Задачи для самостоятельного решения
Глоссарий
ЗАКЛЮЧЕНИЕ
Библиографический список
Приложения
ВВЕДЕНИЕ
В настоящее время в условиях рыночных отношений в экономике России появилась потребность в использовании количественных методов оценки финансовых операций. Причины этого очевидны: появились самостоятельные предприятия, функционирующие на условиях самофинансирования и самоокупаемости, произошло становление рынка капитала, изменилась роль банковской системы в экономике и т. д.
Многие решения финансового характера целесообразно принимать, используя формализованные методы оценки, которые называются методы финансовых вычислений или методы финансовой математики.
Реклама

Владение методами финансовых вычислений необходимо студентам, обучающимся по специальности «Финансы и Кредит», «Экономика и управление на предприятии (в торговле)», «Бухгалтерский учет, анализ и аудит», для рационального выбора привлечения или вложения средств с учетом инвестиционного риска.
Данное учебное пособие содержит две главы (общую и прикладную), задачи для самостоятельного решения, словарь использованных терминов (глоссарий), приложения (порядковые номера дней в году, множитель наращения для сложных процентов, кредитный договор, договор о залоге (ипотеке), динамику ставки рефинансирования Центрального банка Российской Федерации, динамику курсов валют, динамику денежной массы и динамику уровня цен), а также библиографический список, включающий нормативные документы, учебные пособия, практикумы, тренинги и методические указания по курсу финансовых вычислений.
В главе 1 основное внимание сосредоточено на изучении методов финансовых вычислений, которые позволяют принимать финансовые решения в стандартных ситуациях; рассматриваются общие процентные расчеты, расчеты эффективных ставок, способы начисления процентов, методы корректировки процентных ставок на конкретный период, методы дисконтных оценок и исчисления первоначальной стоимости. Глава содержит основные понятия и формулы, после которых представлены примеры решения типовых задач.
Во второй главе учебного пособия приведено практическое применение финансовых вычислений. Глава разделена на пять пунктов, характеризующих отдельные финансовые операции. Здесь представлены теоретические основы и особенности проведения данных операций, рассмотрены на примерах типовые задачи, которые решают субъекты экономических отношений.
Учебное пособие может быть использовано при проведении лекционных и практических занятий по дисциплинам: «Финансы», «Финансы и кредит», «Финансы, денежное обращение, кредит», «Банковское дело», «Деньги, кредит, банки» и т. д., а также рекомендовано студентам для самостоятельной работы.
Настоящее пособие разработано для студентов экономических специальностей всех форм обучения.
1. ОБЩАЯ МЕТОДИКА ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ
1.1 Начисление процентов. Расчет наращенной стоимости
В условиях рыночной экономики любое взаимодействие лиц, фирм и предприятий с целью получения прибыли называется сделкой. При кредитных сделках прибыль представляет собой величину дохода от предоставления денежных средств в долг, что на практике реализуется за счет начисления процентов (процентной ставки – i). Проценты зависят от величины предоставляемой суммы, срока ссуды, условий начисления и т. д.
Реклама

Важнейшее место в финансовых сделках занимает фактор времени (t). С временным фактором связан принцип неравноценности и неэквивалентности вложений. Для того чтобы определить изменения, происходящие с исходной суммой денежных средств (P), необходимо рассчитать величину дохода от предоставления денег в ссуду, вложения их в виде вклада (депозита), инвестированием их в ценные бумаги и т. д.
Процесс увеличения суммы денег в связи с начислением процентов (i) называют наращением, или ростом первоначальной суммы (P). Таким образом, изменение первоначальной стоимости под влиянием двух факторов: процентной ставки и времени называется наращенной стоимостью (S).
Наращенная стоимость может определяться по схеме простых и сложных процентов. Простые проценты используются в случае, когда наращенная сумма определяется по отношению к неизменной базе, то есть начисленные проценты погашаются (выплачиваются) сразу после начисления (таким образом, первоначальная сумма не меняется); в случае, когда исходная сумма (первоначальная) меняется во временном интервале, имеют дело со сложными процентами.
При начислении простых процентов наращенная сумма определяется по формуле
S= P(1 + it), (1)
где S– наращенная сумма (стоимость), руб.; P– первоначальная сумма (стоимость), руб.; i– процентная ставка, выраженная в коэффициенте; t– период начисления процентов.
Пример 1
Рассчитать сумму начисленных процентов и сумму погашения кредита, если выдана ссуда в размере 10 000 руб., на срок 1 год при начислении простых процентов по ставке 13 % годовых.
Решение
S= 10 000 (1+ 0,13 · 1) = 11 300, руб. (сумма погашения кредита);
ΔР = 11 300 – 10 000 = 1 300, руб. (сумма начисленных процентов).
Пример 2
Определить сумму погашения долга при условии ежегодной выплаты процентов, если банком выдана ссуда в сумме 50 000 руб. на 2 года, при ставке – 16 % годовых.
Решение
S= 50 000 (1+ 0,16 · 2) = 66 000, руб.
Таким образом, начисление простых процентов осуществляется в случае, когда начисленные проценты не накапливаются на сумму основного долга, а периодически выплачиваются, например, раз в год, полугодие, в квартал, в месяц и т. д., что определяется условиями кредитного договора. Также на практике встречаются случаи, когда расчеты производятся за более короткие периоды, в частности на однодневной основе.
В случае, когда срок ссуды (вклада и т. д.) менее одного года, в расчетах необходимо скорректировать заданную процентную ставку в зависимости от временного интервала. Например, можно представить период начисления процентов (t) в виде отношения 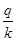 , где q– число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k– число дней (месяцев, кварталов, полугодий и т. д.) в году. , где q– число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k– число дней (месяцев, кварталов, полугодий и т. д.) в году.
Таким образом, формула (1) изменяется и имеет следующий вид:
S= P(1 + i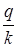 ). (2) ). (2)
Пример 3
Банк принимает вклады на срочный депозит на срок 3 месяца под 11 % годовых. Рассчитать доход клиента при вложении 100 000 руб. на указанный срок.
Решение
S= 100 000 (1+ 0,11 · 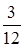 ) = 102 749,9, руб.; ) = 102 749,9, руб.;
ΔР = 102 749,9 – 100 000 = 2 749,9, руб.
В зависимости от количества дней в году возможны различные варианты расчетов. В случае, когда за базу измерения времени берут год, условно состоящий из 360 дней (12 месяцев по 30 дней), исчисляют обыкновенные, или коммерческие проценты. Когда за базу берут действительное число дней в году (365 или 366 – в високосном году), говорят о точных процентах.
При определении числа дней пользования ссудой также применяется два подхода: точный и обыкновенный. В первом случае подсчитывается фактическое число дней между двумя датами, во втором – месяц принимается равным 30 дням. Как в первом, так и во втором случае, день выдачи и день погашения считаются за один день. Также существуют случаи, когда в исчислении применяется количество расчетных или рабочих банковских дней, число которых в месяц составляет 24 дня.
Таким образом, выделяют четыре варианта расчета:
1) обыкновенные проценты с точным числом дней ссуды;
2) обыкновенные проценты с приближенным числом дней ссуды;
3) точные проценты с приближенным числом дней ссуды;
4) точные проценты с банковским числом рабочих дней.
При этом необходимо учесть, что на практике день выдачи и день погашения ссуды (депозита) принимают за один день.
Пример 4
Ссуда выдана в размере 20 000 руб. на срок с 10.01.06 до 15.06.06 под 14 % годовых. Определить сумму погашения ссуды.
Решение
1. Обыкновенные проценты с точным числом дней ссуды:
156=21+28+31+30+31+15;
S= 20 000 (1+0,14 · 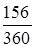 ) =21 213,3, руб. ) =21 213,3, руб.
2. Обыкновенные проценты с приближенным числом дней ссуды:
155= (30·5)+5
S= 20 000 (1+0,14 · 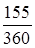 ) =21 205,6, руб. ) =21 205,6, руб.
3. Точные проценты с приближенным числом дней ссуды:
S= 20 000 (1+0,14 · 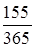 ) =21 189,0, руб. ) =21 189,0, руб.
4. Точные проценты с банковским числом рабочих дней:
S= 20 000 (1+0,14 · 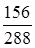 ) =21 516,7, руб. ) =21 516,7, руб.
Данные для расчета количества дней в периоде представлены в прил. 1, 2.
Как сказано выше, кроме начисления простых процентов применяется сложное начисление, при котором проценты начисляются несколько раз за период и не выплачиваются, а накапливаются на сумму основного долга. Этот механизм особенно эффективен при среднесрочных и долгосрочных кредитах.
После первого года (периода) наращенная сумма определяется по формуле (1), где iбудет являться годовой ставкой сложных процентов. После двух лет (периодов) наращенная сумма S2
составит:
S2
= S1
(1 + it) = P(1 + it) · (1 + it) = P(1 + it)2
.
Таким образом, при начислении сложных процентов (после nлет (периодов) наращения) наращенная сумма определяется по формуле
S= P(1 + it)n
, (3)
где i– ставка сложных процентов, выраженная в коэффициенте; n– число начислений сложных процентов за весь период.
Коэффициент наращения в данном случае рассчитывается по формуле
Кн = (1 + it)n
, (4)
где Кн – коэффициент наращения первоначальной стоимости, ед.
Пример 5
Вкладчик имеет возможность поместить денежные средства в размере 75 000 руб. на депозит в коммерческий банк на 3 года под 10 % годовых.
Определить сумму начисленных процентов к концу срока вклада, при начислении сложных процентов.
Решение
S= 75 000 (1+ 0,1 · 1)3
= 99 825, руб.
ΔР = 24 825, руб.
Таким образом, коэффициент наращения составит:
Кн = (1+ 0,1 · 1)3
= 1,331
Следовательно, коэффициент наращения показывает, во сколько раз увеличилась первоначальная сумма при заданных условиях.
Доля расчетов с использованием сложных процентов в финансовой практике достаточно велика. Расчеты по правилу сложных процентов часто называют начисление процентов на проценты, а процедуру присоединения начисленных процентов – их реинвестированием или капитализацией.
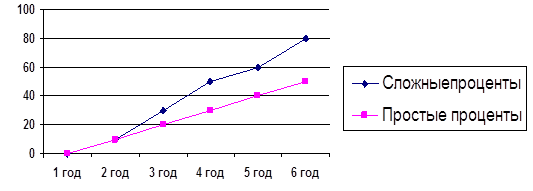
Рис. 1. Динамика увеличения денежных средств при начислении простых и сложных процентов
Из-за постоянного роста базы вследствие реинвестирования процентов рост первоначальной суммы денег осуществляется с ускорением, что наглядно представлено на рис. 1.
В финансовой практике обычно проценты начисляются несколько раз в году. Если проценты начисляются и присоединяются чаще (mраз в год), то имеет место m-кратное начисление процентов. В такой ситуации в условиях финансовой сделки не оговаривают ставку за период, поэтому в финансовых договорах фиксируется годовая ставка процентов i, на основе которой исчисляют процентную ставку за период (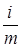 ). При этом годовую ставку называют номинальной, она служит основой для определения той ставки, по которой начисляются проценты в каждом периоде, а фактически применяемую в этом случае ставку (( ). При этом годовую ставку называют номинальной, она служит основой для определения той ставки, по которой начисляются проценты в каждом периоде, а фактически применяемую в этом случае ставку ((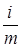 )mn
) – эффективной, которая характеризует полный эффект (доход) операции с учетом внутригодовой капитализации. )mn
) – эффективной, которая характеризует полный эффект (доход) операции с учетом внутригодовой капитализации.
Наращенная сумма по схеме эффективных сложных процентов определяется по формуле
S= P(1+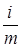 )mn
, (5) )mn
, (5)
где i– годовая номинальная ставка, %; (1+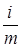 )mn
– коэффициент наращения эффективной ставки; m– число случаев начисления процентов за год; mn– число случаев начисления процентов за период. )mn
– коэффициент наращения эффективной ставки; m– число случаев начисления процентов за год; mn– число случаев начисления процентов за период.
Пример 6
Рассчитать сумму выплаты по депозиту в размере 20 000 руб., помещенному на 1 год под 14 % годовых с ежеквартальным начислением процентов.
Решение
S= 20 000 (1+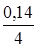 )4·1
= 22 950, руб. )4·1
= 22 950, руб.
Следует отметить, что при периоде, равным 1 году, число случаев начисления процентов за год будет соответствовать числу случаев начисления процентов за весь период. Если, период составляет более 1 года, тогда n(см. формулу (3)) – будет соответствовать этому значению.
Пример 7
Рассчитать сумму погасительного платежа, если выдан кредит в размере 20 000 руб. на 3 года под 14 % годовых с ежеквартальным начислением процентов.
Решение
S= 20 000 (1+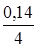 )4·3
= 31 279, 1 , руб. )4·3
= 31 279, 1 , руб.
Начисление сложных процентов также применяется не только в случаях исчисления возросшей на проценты суммы задолженности, но и при неоднократном учете ценных бумаг, определении арендной платы при лизинговом обслуживании, определении изменения стоимости денег под влиянием инфляции и т. д.
Как говорилось выше, ставку, которая измеряет относительный доход, полученный в целом за период, называют эффективной. Вычисление эффективной процентной ставки применяется для определения реальной доходности финансовых операций. Эта доходность определяется соответствующей эффективной процентной ставкой.
Эффективную процентную ставку можно рассчитать по формуле
Iэф
= (1+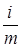 )mn
– 1 . (6) )mn
– 1 . (6)
Пример 8
Кредитная организация начисляет проценты на срочный вклад, исходя из номинальной ставки 10 % годовых. Определить эффективную ставку при ежедневном начислении сложных процентов.
Решение
i= (1+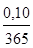 )365
– 1 = 0,115156, т. е. 11 %. )365
– 1 = 0,115156, т. е. 11 %.
Реальный доход вкладчикана1руб. вложенных средствсоставитне10коп. (из условия), а 11 коп. Таким образом, эффективная процентная ставка по депозиту выше номинальной.
Пример 9
Банк в конце года выплачивает по вкладам 10% годовых. Какова реальная доходность вкладов при начислении процентов: а) ежеквартально; б) по полугодиям.
Решение
а) i= (1+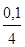 )4
– 1 = 0,1038, т. е. 10,38 %; )4
– 1 = 0,1038, т. е. 10,38 %;
б) i= (1+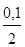 )2
– 1 = 0,1025, т. е. 10,25 %. )2
– 1 = 0,1025, т. е. 10,25 %.
Расчет показывает, что разница между ставками незначительна, однако начисление 10 % годовых ежеквартально выгодней для вкладчика.
Расчет эффективной процентной ставки в финансовой практике позволяет субъектам финансовых отношений ориентироваться в предложениях различных банков и выбрать наиболее приемлемый вариант вложения средств.
В кредитных соглашениях иногда предусматривается изменение во времени процентной ставки. Это вызвано изменением контрактных условий, предоставлением льгот, предъявлением штрафных санкций, атакжеизменением общих условий совершаемых сделок, в частности, изменение процентной ставки во времени (как правило, в сторону увеличения) связано с предотвращением банковских рисков, возможных в результате изменения экономической ситуации в стране, роста цен, обесценения национальной валюты и т. д.
Расчет наращенной суммы при изменении процентной ставки во времени может осуществляться как начислением простых процентов, так и сложных. Схема начисления процентов указывается в финансовом соглашении и зависит от срока, суммы и условий операции.
Пусть процентная ставка меняется по годам. Первые n1
лет она будет равна i1
, n2
– i2
и т. д. При начислении на первоначальную сумму простых процентов необходимо сложить процентные ставки i1
, i2
, in
, а при сложных – найти их произведение.
При начислении простых процентов применяется формула
S = P (1+i1
t1
+ i2
t2
+ i3
t3
+ in
tn
) , (7)
где in
– ставка простых процентов; tn
– продолжительность периода начисления.
Пример 10
В первый год на сумму 10 000 руб. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты выплачиваются ежегодно.
Решение
S= 10 000 (1+0,10 · 1 +0,105 · 1 + 0,11 · 1)=13 150, руб.;
ΔР = 3 150, руб.
При начислении сложных процентов применяется формула
S = P(1+i1
t1
)·(1+ i2
t2
)·(1+ i3
t3
)·(1+ in
tn
) (8)
где in
– ставка сложных процентов; tn
– продолжительность периода ее начисления.
Пример 11
В первый год на сумму 10 000 руб. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты капитализируются.
Решение
S= 10 000 (1+0,10 · 1)·(1 +0,105 · 1)·(1 + 0,11 · 1)= 13 492, 05, руб.
Приведенные примеры подтверждают тот факт, что начисление простых процентов связано с определением наращенной суммы по отношению к неизменной базе, т. е. каждый год (период) проценты начисляются на одну и ту же первоначальную стоимость. Если рассмотреть пример 10, то в этом случае наращенная стоимость составит:
– за первый год: S1
= 10 000 (1+0,10 · 1) = 11 000, руб.;
ΔР1
= 1 000, руб.;
– за второй год: S2
= 10 000 (1+0,105 · 1) = 11 050, руб.;
ΔР 2
= 1 050, руб.;
– за третий год: S3
= 10 000 (1+0,11 · 1) = 11 100, руб.;
ΔР 3
= 1 100, руб.
Таким образом, сумма процентов за 3 года составит:
ΔР = 1 000+1 050+1 100 = 3 150, руб. (см. пример 10).
В случае начисления сложных процентов, исходная сумма меняется после каждого начисления, так как проценты не выплачиваются, а накапливаются на основную сумму, т. е. происходит начисление процентов на проценты. Рассмотрим пример 11:
– в первом году: S1
= 10 000 (1+0,10 · 1) = 11 000, руб.;
– во втором году: S2
= 11000 (1+0,105 · 1) = 12 100, руб.;
– в третьем году: S3
= 12100 (1+0,11 · 1) = 13 431, руб.
Таким образом, сумма процентов за 3 года составит: i3
= 3 431, руб. (см. пример 10).
При разработке условий контрактов или их анализе иногда возникает необходимость в решении обратных задач – определение срока операции или уровня процентной ставки.
Формулы для расчета продолжительности ссуды в годах, днях и т. д. можно рассчитать, преобразуя формулы (1) и (5).
Срок ссуды (вклада):
t= 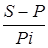 · 365 . (9) · 365 . (9)
Пример 12
Определить на какой срок вкладчику поместить 10 000 руб. на депозит при начислении простых процентов по ставке 10 % годовых, чтобы получить 12 000 руб.
Решение
t= (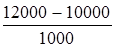 ) · 365 = 730 дней (2 года). ) · 365 = 730 дней (2 года).
Процентную ставку можно рассчитать по формуле
i= (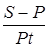 ). (10) ). (10)
Пример 13
Клиент имеет возможность вложить в банк 50 000 руб. на полгода. Определить процентную ставку, обеспечивающую доход клиента в сумме 2 000 руб.
Решение
t= (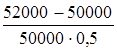 ) = 0,08 = 8 % годовых ) = 0,08 = 8 % годовых
Аналогично определяется необходимый срок окончания финансовой операции и ее протяженность, либо размер требуемой процентной ставки при начислении сложных процентов.
Для упрощения расчетов значения коэффициента (множитель) наращения представлены в прил. 3.
Задачи для самостоятельного решения
1. Предприятие получило кредит на 1 год в размере 7 000 000 руб. с условием возврата 8 000 000 руб. Рассчитать простую процентную ставку.
2. Какую сумму нужно положить в банк, выплачивающий 4 % годовых по простой процентной ставке, чтобы получить 50 000 руб.: а) через 4 месяца; б) через 1 год; в) через 2 года 9 месяцев.
3. Организации предоставлен кредит в размере 100 000 000 руб. под 17 % годовых с1 января по1 июля текущегогода. Определитьподлежащую возвратусумму, применяя разные способы начисления процентов(точные иобыкновенные).
4. Г-н Семенов имеет возможность поместить на депозит в коммерческий банк «Енисей» 60 000 руб. под 12 % годовых. При простом начислении процентов на счете г-на Семенова накопится 75 000 руб. через:
а) _______ лет;
б) _______ месяцев;
в) _______ дней.
5. Для финансирования оборотного капитала предприятие взяло кредит в банке в размере 100 000 000 руб. сроком на 2 года с ежегодным погашением процентов. Ставка процента за пользование заемными средствами 15 % годовых. Определить сумму погашения кредита и сумму начисленных процентов.
6. Молодая семья получила в банке ипотечный кредит на приобретение квартиры в размере 600 000 руб., сроком на 5 лет под простую процентную ставку 15 % годовых. Определить сумму основного долга и процентов по кредиту.
7. Банк принимает вклады на срочный депозит на следующих условиях: процентная ставка при сроке 35 дней – 3 % годовых; при сроке – 65 дней – 5 % годовых; при сроке 90 дней – 6 % годовых. Определить доход клиента при вкладе 70 000 руб. на указанные сроки.
8. Клиент вложил в банк на депозит 2 000 долл. на срок с 12 апреля по 26 июня под простую процентную ставку 9 % годовых. Рассчитать доход клиента разными способами начисления процентов (точные и обыкновенные). Год не високосный.
9. Коммерческий банк привлекает средства населения под простые проценты 10 % годовых. Клиент внес 20 000 руб. на депозит с 10 мая по 15 октября. Определить величину коэффициента наращения и наращенную сумму:
а) при начислении точных процентов с точным числом дней в году;
б) при начислении точных процентов с банковским числом рабочих дней. Год не високосный.
10. Вкладчик положил в банк выплачивающий 6 % годовых 100 000 руб. Какая сумма будет на счете вкладчика через:
а) 2 месяца;
б) полгода;
в) 1 год.
11. Клиент поместил в банк 120 000 руб. 1 февраля. Процентная ставка банка с 1 февраля по 18 февраля – 8 % годовых; с 19 февраля по 7 марта – 9 % годовых; с 8 марта по 23 марта – 10 % годовых; с 24 марта по 19 апреля, когда был изъят вклад – 11 % годовых. Определить доход клиента и эффективную процентную ставку, используя методику расчета обыкновенных процентах с приближенных числом дней.
12. Производственное объединение «Русь» 1 сентября имеет на расчетном счете обслуживающего банка среднедневные остатки денежных средств в размере 612 000 руб. На вклады «до востребования» банк начисляет проценты – 3 % годовых. Определить сумму начисленных процентов на 16 декабря этого же года, применяя различные способы начисления процентов (точные и обыкновенные).
13. Коммерческая фирма получила в банке ссуду на 1,5 года на следующих условиях: за первое полугодие начисляется 17 % годовых, за второе и третье полугодие – 15 % годовых. Определить размер ссуды, полученной в банке, если сумма погашения ссуды составит 300 000 руб.
14. Условия кредитного договора между коммерческим банком «Югра» и промышленным предприятием «Ника» предусматривают следующий порядок начисления процентов: в первый квартал 20 % годовых; во второй 19 % годовых; в третий 18 % годовых; в четвертый 16 % годовых. Рассчитать сумму погашения кредита в размере 500 000 руб., если предприятию представляется возможность погашения суммы долга в конце срока и право ежеквартального погашения процентов.
15. Банк принимает валютные вклады на депозит под 12 % годовых при ежемесячном начислении процентов и их погашением в конце срока. Рассчитать доход клиента при вкладе 2 500 долл. на 6 месяцев.
16. Кредитная организация принимает вклады юридических лиц под 13 % годовых с ежеквартальным начислением процентов и их погашением в конце срока. Рассчитать сумму возврата денежных средств, если вложено:
а) 250 000 на 2 года;
б) 150 000 на 3 года;
в) 170 000 на 3,5 года.
17. Кредитная организация начисляет сложные проценты на срочный вклад, исходя из номинальной ставки 11 % годовых. Определить эффективную ставку:
а) при ежемесячном начислении процентов;
б) при ежеквартальном начислении процентов.
18. АО «Вектор» заключило контракт с финансовой корпорацией по займу денежных средств в размере 10 000 000 руб. сроком на 3 года и следующими условиями начисления процентов: в первый год 20 %, а каждое последующее полугодие ставка процента снижается на 0,5 %. Определить сумму, которую должно вернуть АО «Вектор» финансовой корпорации по истечении срока действия контракта, если проценты погашаются в конце срока.
19. По дебетовой платежной карте ежеквартально начисляются и присоединяются проценты по ставке 2 % годовых. Рассчитать сумму, которой будет располагать владелец платежной карты через 8 месяцев, если она оформлена на 500 долл.
20. Вкладчик имеет возможность поместить в коммерческий банк 200 000 руб. на 2 года. Первый банк предлагает 13 % годовых с ежемесячным начислением процентов; второй банк – 15 % годовых с ежеквартальным начислением процентов; третий банк – 16 % годовых с полугодовым начислением процентов. Определить наиболее эффективный вариант вложения средств при условии погашения процентов в конце установленного срока.
21. КФ «Банк Москвы» принимает вклады физических лиц на рублевый депозит под 10 % годовых и на валютный по 7 % годовых. Рассчитать эффективность вложения 1 000 евро на 1 год при ежемесячном начислении процентов в валютном и рублевом эквиваленте, если курс евро на начало года составил 35,14 руб., а к концу года ожидается его повышение к рублю на 70 пунктов:
а) при начислении простых процентов;
б) при начислении сложных процентов.
22. КФ «Банк Москвы» принимает вклады юридических лиц на рублевый депозит под 11 % годовых и на валютный по 9 % годовых. Выбрать оптимальный вариант вложения 10 000 евро на 1,5 года при ежеквартальном начислении процентов в валютном и рублевом эквиваленте, если курс евро на начало года составил 35,34 руб., а на конец периода – 35,91 руб.:
а) при начислении простых процентов;
б) при начислении сложных процентов;
23. Банк в конце периода выплачивает по вкладам 9 % годовых (по сложной ставке). Какова реальная доходность вкладов при начислении процентов:
а) ежемесячно;
б) ежеквартально;
в) по полугодиям.
25. Клиент имеет возможность вложить в банк 10 000 руб. на 2 года. Определитьсложнуюпроцентную ставку приежегодномначислениипроцентов, обеспечивающую совокупный доход клиента в конце срока в сумме 5 000 руб.
26. Кредитная организация принимает срочные вклады на 1 год с условием начисления сложных процентов по ставке 12 % годовых и минимальной суммой вклада 100 000 руб. Разработать график начисления процентов, при котором сумма средств на депозите клиента на конец срока составит не менее:
а) 112 500 руб.;
б) 120 000 руб.
27. На срочные «накопительные» вклады населения коммерческий банк начисляет в первый год 4 % годовых, а в последующие 4 года ставка увеличивается на1,5%. Определитьэффективную процентную ставку наконецпериода, если проценты по вкладу капитализируются.
28. Рассчитать период времени, в течение которого вложенные средства в банке под 14 % годовых при ежемесячном, поквартальном и полугодовом начислении процентов удвоятся (использовать сложные проценты).
29. Реклама одного коммерческого банка предлагает 8 % годовых при ежемесячном начислении процентов; другого 9 % годовых при поквартальном начислении. Срок хранения вклада – 12 месяцев. Какому банку отдать предпочтение, если начисляются сложные проценты?
30. Появилась возможность получить кредит либо на условиях 12 % годовых с квартальным начислением процентов, либо на условиях 12,4 % годовых с годовым начислением процентов. Какой вариант предпочтительней, если выплата процентов будет сделана единовременно с погашением кредита?
1.2 Дисконтирование. Расчет первоначальной стоимости
В практике финансовых расчетов может возникнуть и обратная по отношению к наращению задача: по известной наращенной сумме (S) определить размер размещенных средств (P), что наглядно представлено на рис. 2
 P = ? P = ? |
d |
 S время S время
|
Рис. 2. Дисконтирование с течением времени
Вычисление Sна основе Pназывается дисконтированием. Таким образом, исчисление первоначальной стоимости связано с дисконтированием наращенной стоимости (ее уменьшением).
Дисконт (d) – это скидка (в процентах), определяемая по отношению к наращенной (будущей) стоимости для получения исходной величины, называемой первоначальной суммой.
Дисконтирование – действие, противоположное начислению процентов.
К дисконтированию обращаются, прежде всего, в практике торговой, инвестиционной и банковской деятельности.
Сумму дисконта (D) можно рассчитать по формуле
D= S– P. (11)
В финансовой практике используются два метода дисконтирования: метод математического дисконтирования и метод банковского (коммерческого) учета.
К математическому дисконтированию прибегают в тех случаях, когда по известной наращенной сумме (S), процентной ставке (i) и времени обращения (t) необходимо найти первоначальную стоимость (P). При этом предполагается, что проценты начисляются на первоначальную, а не наращенную сумму денег.
Дисконт, как и саму первоначальную сумму, можно находить по схеме простых и сложных процентов.
Первоначальную сумму при простом математическом дисконтировании можно рассчитать по формуле
P= 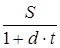 , (12) , (12)
где 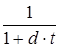 – дисконтный множитель. – дисконтный множитель.
Пример 14
Через 6 месяцев с момента выдачи ссуды заемщик уплатил кредитору 21 400 руб. Кредит предоставлялся под 14 % годовых. Определить сумму кредита и сумму дисконта.
Решение
P= 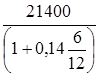 = 20 000, руб.; = 20 000, руб.;
D= 21 400 – 20 000 = 1 400, руб.
Для математического дисконтирования по сложным процентам используется формула
P= 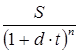 , (13) , (13)
где d– ставка дисконта, выраженная в коэффициенте.
Пример 15
Определить первоначальную величину банковского вклада, если ее будущая стоимость через 2 года составит 23 328 руб. Сложная процентная ставка – 8 % годовых.
Решение
Р = 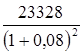 = 20 000, руб.; = 20 000, руб.;
D= 23 328 – 20 000 = 3 328, руб.
На практике математическое дисконтирование используется для определения суммы капитала, необходимого для инвестирования под определенные проценты для получения требуемой величины денежных средств, а также в случаях начисления процентов, удерживаемых вперед при выдаче ссуды.
Наиболее распространенным методом дисконтирования является банковское дисконтирование (коммерческий учет).
Эта процедура представляет собой действие, обратное математическому дисконтированию. Отличие банковского дисконтирования от математического состоит в том, что в случае коммерческого учета ставкой выступает дисконт (d), а при математическом дисконтировании ставкой является обычная процентная ставка (i).
Таким образом, в случаях операций банковского дисконтирования целесообразно воспользоваться следующими формулами:
S= P· (1 – d·t) (14)
или
P= 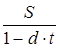 . (15) . (15)
Соответственно, при инвестировании денежных средств соблюдается неравенство S> P, а в случаях дисконтирования, соответственно P> Sили S< P, что раскрывает сущность вычисления наращенной, в первом примере, и первоначальной стоимости во втором.
На практике операции, связанные с дисконтированием денежных средств используются при финансовых операциях по учету векселей, выдачи дисконтных ссуд или перепродажи контрактов, в процессе уменьшения балансовой стоимости имущества (амортизации средств), первичного и вторичного размещения ценных бумаг и т. д.
Пример 16
Финансовая компания выдала ссуду 10 000 руб. на 2 года под простой дисконт, равный 9 % в год. Какую сумму получит клиент в момент получения ссуды?
Решение
S= 10 000 (1 – 0,09 · 2) = 8 200, руб.
Также как и в случае начисления процентов, срок обращения актива при дисконтировании может составлять менее года. В связи с этим, можно скорректировать ставку дисконта под заданный временной интервал в виде отношения 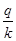 , где q– число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k– число дней (месяцев, кварталов, полугодий и т. д.) в году. , где q– число дней (месяцев, кварталов, полугодий и т. д.) ссуды; k– число дней (месяцев, кварталов, полугодий и т. д.) в году.
В связи с этим, формула (14) изменяется и имеет следующий вид:
S= P(1 – d· 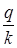 ). (16) ). (16)
Пример 17
Финансовая компания выдала ссуду 10 000 руб. на 180 дней под простой дисконт, равный 10 % в год. Какую сумму получит клиент в момент получения ссуды?
Решение
S= 10 000 (1 – 0,1·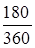 ) = 9 500, руб. ) = 9 500, руб.
В случаях непрерывного дисконтирования или неоднократного учета векселей, ценных бумаг на одинаковых условиях в финансовых расчетах применяется сложная ставка дисконта:
S= P(1 – 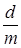 )mn
. (17) )mn
. (17)
Задачи для самостоятельного решения
31. Финансовая корпорация выдает ссуды физическим лицам под простой дисконт 13 % годовых. Рассчитать срок, на который выдана ссуда в размере 10 000 руб., если сумма к погашению составит:
а) 10 335 руб.;
б) 11 500 руб.;
в) 13 513 руб.
32. Финансовая корпорация выдает ссуды юридическим лицам под простой дисконт 15 % годовых. Рассчитать срок, на который выдана ссуда в размере 250 000 руб., если сумма к погашению составит: а) 454 545 руб.; б) 285 714 руб.; в) 266 667 руб.
33. Рассчитать простую учетную ставку (ставку дисконта) по которой долговое обязательство номинальной стоимостью 1 000 руб. и сроком обращения 180 дней реализуется в первый день за 945 руб.
34. Специализированное финансовое учреждение выдало заемщику кредит в сумме 20 000 руб., под простой дисконт равный 7 % годовых: а) на 1,5 года; б) на 280 дней; в) на 3 года. Какую сумму получит клиент в момент получения кредита?
35. Простая ставка размещения краткосрочных денежных ресурсов для банков на 3 месяца составляет 6 % годовых. Какой объем средств необходимо разместить для получения 250 000 руб.?
36. Определить текущую стоимость денег при простой ставке дисконтирования 3 % годовых, если через 10 лет она обратится в 20 000 долл.
37. Ломбард выдает кредиты населению сроком от 1 месяца до года под залог драгоценных металлов по учетной ставке 24 % годовых. Сумма кредита не может превышать 60 % стоимости залога. Определить минимальную стоимость внесенного залога, если заемщику необходимы 10 000 руб. на 3 месяца.
38. Найти величину дисконта, если долговое обязательство на выплату 40 000 руб. учтено за 3 года до срока погашения по сложной учетной ставке: а) 7 % годовых; б) 10 % годовых.
39. Через 1 год с момента выдачи ссуды заемщик уплатил кредитору 30 000 руб. Кредит предоставлялся под 15 % годовых. Определить сумму кредита и сумму дисконта.
40. Определить первоначальную величину банковского вклада, если ее будущая стоимость через 5 лет составит 50 000 руб. Сложная процентная ставка – 9 % годовых.
2. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ФИНАНСОВЫХ РАСЧЕТОВ
2.1. Учет инфляции
В современной России возникла необходимость учитывать влияние инфляционных процессов на результаты деятельности предприятий, финансово-кредитных организаций, доходы населения и т. д. С помощью финансовых расчетов можно оценить степень обесценения денег.
Инфляция представляет собой процесс обесценивания денег, обусловленный чрезмерным увеличением выпущенной в обращение массы бумажных денег и безналичных выплат по сравнению с реальным предложением товаров и услуг в стране.
Инфляция проявляется в росте цен на товары и услуги. Изменение цен на товары и услуги определяется при помощи индекса потребительских цен J. Численно индекс цен равен отношению цен на товары, работы, услуги в один период времени tк ценам этих товаров, работ, услуг в другой период времени и показывает, во сколько раз увеличились цены на определенные товары или услуги за конкретный период времени.
Процентное изменение индекса потребительских цен называется уровнем инфляции.
В зависимости от уровня инфляции в год, ее подразделяют:
– на ползучую (умеренную) – 3-10 % в год;
– галопирующую – 10-100 % в год;
– гиперинфляцию – свыше 30 % в месяц.
От изменения уровня инфляции зависит реальная стоимость денежных средств или финансовый результат от вложения или предоставления денежных средств на временной основе.
Инфляция способствует перераспределению доходов: под влиянием инфляции потери несет кредитор (если процентная ставка или ставка дисконта не скорректирована с учетом сложившегося уровня инфляции), а заемщик или плательщик, наоборот, получает дополнительную финансовую выгоду.
В любом случае, инфляционные процессы увеличивают номинальную стоимость денег по сравнению с их реальной величиной. Таким образом, можно представить уровень инфляции как r, текущую (или реальную) стоимость как P, и номинальную (наращенную) стоимость S.
Следовательно, изменение стоимости под влиянием инфляции можно рассчитать:
S= P(1 + r· t), (18)
где (1 + r· t) – средний уровень цен за конкретный период; r– уровень инфляции, выраженный в коэффициенте.
Пример 18
Определить, как изменится сумма денежных средств в размере 5 000 руб. через год, если среднегодовой уровень инфляции составит 13 %?
Решение
S= 5 000 (1 + 0,13 · 1) = 5 650, руб.
Иначе говоря, через год на сумму 5 650 руб. можно будет приобрести тот же набор товаров и услуг, что и в начале периода, только на сумму 5 000 руб.
Если требуется определить, как изменится первоначальная сумма денежных средств под влиянием инфляции за период, составляющий менее 1 года, тогда следует скорректировать период времени t(формула (2)).
Следует обратить внимание, что формулы подсчета Sс учетом инфляции выбираются в зависимости от применяемого процента (простой и сложный).
С экономической точки зрения, правильнее рассчитывать инфляционные изменения методом сложного начисления, так как инфляция – процесс непрерывный, то есть обесцениваются уже обесцененные деньги или, начисление процентов осуществляется не на первоначальную стоимость, а на стоимость с учетом ранее начисленных процентов (формулы (1), (3)).
S= P(1 + r)t
, (19)
где t– число лет.
Пример 19
Определить, как изменится сумма денежных средств в размере 5 000 руб. через 5 лет, если среднегодовой уровень инфляции составит 13 %?
Решение
S= 5 000 (1 + 0,13)5
= 9 212, руб.
Если стоит обратная задача, т. е. необходимо определить средний уровень инфляции за конкретный временной интервал (внутри периода), исходя из данных об уровне цен за год или более, то решение осуществляется с помощью вычисления математического корня (квадратного, кубического и т. д.).
Пример 20
Годовой уровень инфляции составил 10 %. Рассчитать среднеквартальный уровень цен.
Решение
r= 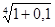 4 = 1, 033 = 3,3 , %. 4 = 1, 033 = 3,3 , %.
2.2 Операции с векселями
Вексельные расчеты широко применяются на практике между хозяйствующими субъектами.
Учет векселей является обычной банковской операцией, при которой банки или финансовые компании покупают векселя с дисконтом по цене, меньшей, чем номинальная стоимость векселя.
В соответствии с Гражданским кодексом Российской Федерации вексель является ценной бумагой. С 1997 г. действует Федеральный закон «О переводном и простом» [5].
Вексель – составленное по установленной законом форме безусловной письменное долговое обязательство, выданное одной стороной (векселедателем) другой стороне (векселедержателю).
Вексель – это абстрактное, ничем не обусловленное обязательство векселедателя или приказ векселедателя третьему лицу выплатить указанному лицу (или по его приказу) определенную сумму денег в определенный срок.
Основными чертами векселя являются следующие:
1) абстрактный характер обязательства, выраженного векселем;
2) безусловный характер обязательства, выраженного векселем;
3) бесспорный характер обязательства, выраженного векселем.
Вексель – краткосрочная ценная бумага сроком погашения до 1 года.
Продается с дисконтом (по цене ниже, чем номинальная стоимость), а погашается по номинальной стоимости.
В вексельных расчетах участвуют:
– векселедатель – заемщик;
– векселедержатель – кредитор;
– плательщик (или третье лицо) – коммерческий банк или финансовая компания.
Для расчета суммы денежных средств, полученных векселедержателем при учете векселя в банке, используется формула простого дисконта. Введем следующие обозначения:
S= P(1 – d· t), (20)
где P– номинальная стоимость векселя, руб.; d– учетная ставка (ставка дисконта), выраженная в коэффициенте; t– период времени.
Сумма дохода банка по учету векселя рассчитывается по формуле
D= P– S= P– 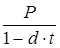 , (21) , (21)
где D– сумма дисконта по векселю, руб.
Пример 21
Вексель на сумму 20 000 руб. и сроком погашения 10 октября учтен в банке 10 сентября текущего года по учетной ставке 10 % годовых. Рассчитать сколько получит владелец векселя (S) и сумму дохода банка (D).
Решение
S= 20 000 (1 – 0,1 · 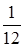 ) = 19 840, руб. ) = 19 840, руб.
D= 20 000 – 19 840 = 160, руб.
На практике вексель часто применяется как инструмент вложения временно свободных денежных средств, обеспечивающий держателю доход в виде дисконта. В таких случаях, цена приобретения векселя рассчитывается по формуле (20), а доход от покупки данной ценной бумаги может быть рассчитан по формуле (21). При расчете дохода от приобретения векселя можно учитывать влияние инфляционных факторов. В этой ситуации инфляция будет увеличивать затраты кредитора (векселедержателя) по приобретению векселя и влиять на изменение доходности осуществляемой операции (п. 2.1).
Пример 22
Вексель на сумму 50 000 руб. и сроком обращения 1 год реализуется с дисконтом 12 % годовых. Определить целесообразность покупки векселя, если среднегодовой уровень инфляции составит 13 %.
Решение
S= 50 000 (1 – 0,12 · 1) = 44 000, руб.
S1
= 44 000 (1 + 0,13 · 1) = 49 720, руб.
D= 50 000 – 49 720 = 280, руб.
Таким образом, покупку векселя можно считать целесообразной, так как доход по операции является положительным и составит 280 руб.
Операции банковского учета иногда проводятся по сложной учетной ставке. В этом случае сумма денег, выплачиваемая банком вычисляется по формулам (13) (п. 1.2).
2.3 Операции с ценными бумагами
С юридической точки зрения, ценная бумага представляет собой денежный документ, удостоверяющий имущественные права, осуществление или передача которых возможны только при его предъявлении или если доказано закрепление этих прав в специальном реестре (в случаях, определенных законом).
С экономической точки зрения, ценная бумага – это совокупность имущественных прав на те или иные материальные объекты, которые обособились от своей материальной основы и получили собственную материальную форму. Ценные бумаги могут предоставлять и неимущественные права (например, акция предоставляет право голоса на общем собрании акционеров, а также право получать информацию о деятельности акционерного общества и т. д.).
Фундаментальные свойства ценных бумаг:
– обращаемость;
– доступность для гражданского оборота;
– стандартность и серийность;
– документальность;
– признание государством и регулируемость;
– рыночность;
– ликвидность;
– рискованность;
– обязательность исполнения обязательства.
Гражданский кодекс Российской Федерации выделяет следующие ценные бумаги: государственные, муниципальные, корпоративные облигации, вексель, акции, депозитный и сберегательный сертификат и другие.
Характеристика основных видов ценных бумаг представлена в табл. 1.
Таблица 1
Характеристика основных видов ценных бумаг
Ценная
бумага
|
Характеристика |
| Акция |
Долевая, эмиссионная ценная бумага, дающая право ее владельцу на участие в управлении акционерным обществом, получение части прибыли в форме дивидендов и части имущества при ликвидации акционерного общества. Цель выпуска – формирование и увеличение уставного капитала.
Различают привилегированные и обыкновенные акции.
Привилегированные акции не дают права на участие в управлении акционерным обществом, но дают первоочередное право на получение дивиденда по фиксированной ставке, независимо от результатов финансово-хозяйственной деятельности предприятия, и на первоочередное погашение при ликвидации общества по отношению к обыкновенным акциям.
Бессрочная ценная бумага.
По акции выплачивается доход в виде дивиденда.
Дивиденд – это часть чистой прибыли акционерного общества, выплачиваемая каждому акционеру пропорционально количеству акций, находящихся в его собственности.
|
| Облигация |
Долговая эмиссионная ценная бумага, закрепляющая право ее держателя на получение от эмитента облигации в предусмотренный срок ее номинальной стоимости и зафиксированного в ней процента от этой стоимости или иного имущественного эквивалента.
Доходом по облигации называется процент или купонный доход.
Существуют бескупонные облигации, доход по которым определяется в виде дисконта.
В зависимости от эмитента выделяют:
– государственные облигации;
– муниципальные;
– корпоративные.
|
Сертификат
|
Письменное свидетельство кредитного учреждения о депонировании в нем денежных средств, удостоверяющее право вкладчика на получение по истечении установленного срока депозита (вклада) и процентов по нему.
Эмитентами депозитных и сберегательных сертификатов являются банки.
Сертификаты выпускаются как именные, так и на предъявителя. Не предусмотрено ограничений на сумму номинала, который может быть выражен как в российских рублях, так и в иностранной валюте. Минимальные сроки обращения сертификатов не установлены, максимальный срок для депозитных сертификатов – 1 год, для сберегательных – 3 года.
Деление на депозитные и сберегательные сертификаты связано с их владельцами, которыми могут быть юридические лица (депозитные) и физические лица (сберегательные).
Выпускаются в документарной форме.
Доход определяется в виде процента, который зависит от срока обращения сертификата и его номинальной стоимости.
|
Размер дохода по данным ценным бумагам можно рассчитать по следующей формуле
D=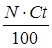 , (22) , (22)
где N– номинальная стоимость ценной бумаги, руб.; Ct– ставка дивиденда, процента, купона, %.
Как правило, срочные ценные бумаги (вексель, облигация, сертификат) имеют определенный срок обращения. В результате воздействия факторов времени и инфляции реальный доход от приобретения ценных бумаг меняется, что следует учитывать при инвестировании денежных средств.
Увеличение и обесценение капитала можно рассчитать на основе формул простого и сложного процентов, рассмотренных выше.
Пример 23
Облигация номинальной стоимостью 1 000 руб. и фиксированной ставкой дохода 14 % годовых выпускается сроком на 3 года с ежегодной выплатой дохода. Определить целесообразность покупки данной облигации, если среднегодовой уровень инфляции составит 11 %.
Решение
S= 1 000 (1 + 0,14 · 3) = 1 420, руб.
Sинфл
= 1 000 (1 + 0,11 · 1) 3 = 1 367, руб.
D= 1 420 – 1 367 = 53, руб.
Таким образом, покупка облигации выгодна для инвестора, так обеспечит доход в размере 53 руб.
Начисляемый процентный доход по ценным бумагам может изменяться в течение времени, тогда увеличение капитала следует определять по формулам (7) и (8) (также как и инфляция, только применяется формула (8)).
Пример 24
На депозитный сертификат номиналом 1 000 руб. и сроком обращения 1 год начисляются проценты исходя из следующих данных: Iквартал – 6 % годовых, IIквартал – 8 % годовых. Каждый последующий квартал ставка процента увеличивается на 1 %. Рассчитать общую сумму погашения по сертификату, если проценты погашаются в конце срока.
Решение
S= 1 000(1 + 0,06·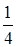 )·(1 + 0,08· )·(1 + 0,08·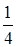 )·(1 + 0,09· )·(1 + 0,09·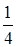 )·(1 + 0,1· )·(1 + 0,1·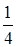 ) = 1 085, руб. ) = 1 085, руб.
Характерной особенностью облигации, также как и векселя, является существование ситуаций размещения данной ценной бумаги с дисконтом, т. е. по цене, ниже номинальной.
В таком случае, цену приобретения облигации можно рассчитать по формуле
C= P(1 – dt), (23)
где C– цена приобретения облигации, тыс. руб.; P– первоначальная (номинальная) стоимость облигации, тыс. руб.; d– ставка дисконта, выраженная в коэффициенте; t– срок обращения облигации, дни, годы и т. д.
Таким образом, влияние всех факторов, а именно процентного дисконтированного дохода, инфляции при обращении ценных бумаг, можно объединить в примере 25.
Пример 25
Целевая муниципальная облигация номинальной стоимостью 10 000 руб. имеет процентный доход в размере 8 % годовых, реализуется с дисконтом 4 % годовых. Рассчитать финансовый результат от приобретения облигации, если срок ее обращения составляет 1 год и среднегодовой уровень инфляции 12 %.
Решение
Сумма погашения облигации:
S= 10 000 (1 + 0,08 · 1) = 10 800, руб.
Цена приобретения облигации:
С = 10 000 (1-0,04 · 1) = 9 600, руб.
Увеличение затрат по покупке облигации под влиянием инфляции:
Sинфл
= 9 600 (1 + 0,12 · 1) = 10 752, руб.
Финансовый результат от покупки облигации:
10 800 – 10 752 = 48, руб.
Приобретение ценной бумаги целесообразно.
2.4 Валютные расчеты
Валютные расчеты (операции) можно определить как соглашения (контракты) участников валютного рынка по купле-продаже, платежам, предоставления в ссуду иностранной валюты на конкретных условиях (наименование валют, сумма, курс обмена, процентная ставка и т. д.).
Под иностранной валютой понимаются денежные знаки иностранных государств, а также кредитные средства обращения и платежа, выраженные в иностранных денежных единицах и используемые в международных денежных расчетах.
Валютный курс – «цена» (отношение) денежной единицы одной страны, выраженная (выраженное) в денежных единицах других стран.
Котировка валют – установление курса иностранной валюты в национальной (или наоборот).
Способы определения валютного курса: прямая котировка, косвенная котировка, кросс-курс, курсы наличных и срочных сделок.
При прямой котировке стоимость единицы иностранной валюты выражается в национальной денежной единице:
Кп
= 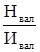 , (24) , (24)
где Кп
– прямая котировка; Нвал
– национальная валюта, руб.; Ивал
– иностранная валюта, у.е.
К примеру, 1 USD= 28 руб.
При косвенной котировке за единицу принята национальная денежная единица, курс которой выражается в определенном количестве иностранной валюты:
Кк = 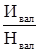 (25) (25)
или
Кк = 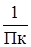 1 , (26) 1 , (26)
где Кк – косвенная котировка.
К примеру, 1 руб. = 0,028 USD.
Кросс–курс представляет соотношение между двумя валютами по отношению к третьей валюте.
Кросс-к =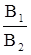 , (27) , (27)
где Кросс-к – кросс-курс покупки валюты, у. е.; В1
– валютный курс денежной единицы одной страны, выраженный в денежной единице страны А, у. е.; В2
– валютный курс денежной единицы другой страны, выраженный в денежной единице страны А, у. е.
Пример 26
На 26 января 2006 г. ЦБ РФ установил для целей учета и таможенных платежей следующие курсы:
– 1 евро = 35,21 руб.;
– 1 долл.США = 28,54 руб.
Кпок.евро
= 1 евро · 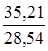 = 1,2337 долл. США. = 1,2337 долл. США.
Изменение курса в течение определенного времени образует курсовую прибыль (или убыток). Операции по покупке-продаже валюты с последующим совершением контрсделки (обратной сделки) для получения курсовой прибыли есть валютный арбитраж.
К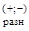 = В = В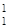 – В – В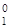 , (28) , (28)
где К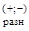 – курсовая прибыль (убыток) от операций с валютой, у. е.; В – курсовая прибыль (убыток) от операций с валютой, у. е.; В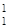 –валютныйкурс надату продажи, у.е.; В –валютныйкурс надату продажи, у.е.; В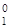 – валютный курс надату покупки, у.е. – валютный курс надату покупки, у.е.
Пример 27
Приобретено 100 долл. США по курсу 31,24 руб. за 1 долл. Рассчитать курсовую разницу от продажи валюты по курсу 31,04 руб. за 1 долл.
Решение
К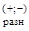 = (31,04 – 31,24) · 100 = –20, долл. – отрицательная курсовая разница. = (31,04 – 31,24) · 100 = –20, долл. – отрицательная курсовая разница.
Кроме конверсионных операций, банки осуществляют депозитные операции с валютой, представляющие собой операции по размещению или привлечению средств в иностранной валюте на счетах в банках.
К существенным условиям любой операции относится дата ее заключения и дата исполнения. Если дата заключения и исполнения контракта совпадает, значит имеют место операции «спот». В мировой практике к операциям «спот» относятся сделки, исполнение которых осуществляется на второй рабочий день после их заключения.
Другая группа сделок – это сделки с датой исполнения контракта не ранее третьего рабочего дня с момента заключения договора. К таким сделкам относятся: биржевой опцион или форвардные операции и фьючерсные операции.
При форвардных сделках поставка и платеж за валюту производятся через определенный срок по курсу, зафиксированному в момент заключения сделки. Форвардные сделки обеспечивают экспортно-импортные операции, хеджирование – страхование от неблагоприятных изменений валютного курса, спекуляций на продаже валюты.
Обычно форвардные сделки заключаются на срок от одной недели до 12 месяцев на стандартные периоды: 1, 2, 3, 6, 9, 12 месяцев
Определение дохода от форвардной сделки осуществляется с помощью формул простейших финансовых вычислений.
Пример 28
Курс валют доллара США и евро 1,112/1,186, банковские процентные ставки в Германии – 8,5 %, в Англии – 14% годовых. Если фирма поместит 10 000 долл. на месяц в банк Германии, то получит следующий доход:
S= 10 000·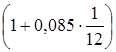 = 10 070,83 , долл. США. = 10 070,83 , долл. США.
Д1 = 10 070,83 – 10 000 = 70,83, долл. США
Если фирма конвертирует доллары в евро, поместит их в английский банк и через месяц вновь конвертирует в доллары, то получит доход:
S= 8 992,8 (1+0,14·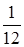 ) = 9 097,7 , долл. США. ) = 9 097,7 , долл. США.
или 9 097,7 · 1,186 = 10 789,9 , евро.
Д = 10 789,9 – 10 000 = 789,9 , долл. США.
На валютном рынке различие в процентных ставках учитывается в форвардном курсе посредством форвардной премии или дисконта. Если процентная ставка для конкретной валюты более высока, то она должна продаваться по более низкому валютному курсу. Размер форвардной премии (дисконта) рассчитывается по формуле
F= Кспот
· (i1
– i2
) · t, (29)
где F– форвардная премия, у. е.; Кспот
– текущий курс валюты («спот»), у. е.; (i1
– i2
) – разница в относительных процентных ставках для имеющейся валюты и валюты, в которую конвертируют; t– период времени, скорректированный на общее число дней в году, дни.
Пример 29
Фирма намерена продать в Англии товар на сумму 10 000 евро и купить в Германии партию компьютеров. Для этого фирма заключает форвардную сделку на срок 3 месяца. Текущий курс доллара/евро – 1,112; годовые процентные ставки в Англии – 14 %, в Германии – 8,5 %.
Решение
При текущей сделке фирма получит:
1,112 · 10 000 = 11 120, долл. США.
Сумма процентов за 3 месяца:
11 120(1+0,085·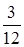 ) = 11 356,3, долл. США. ) = 11 356,3, долл. США.
Форвардная премия составит:
1,112 (0,14 – 0,085) · 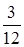 = 0,015. = 0,015.
Сумма процентоввАнглии за3месяца:
10 000(1+ 0,14·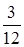 )=10 349,9, евро. )=10 349,9, евро.
Так как процентная ставка в Германии ниже, то евро должен продаваться по более низкому курсу.
Курс евро/доллар будет:
1,112 – 0,015 = 1,097 , долл. США.
При форвардной сделке фирма получит:
1,097·10000 = 10970, долл.США.
Таким образом, наращенная сумма за три месяца составит:
10 349,9 · 1,097 = 11 353,8 , долл. США.
Кроме форвардных расчетов на валютном рынке могут совершаться сделки, основанные на разнице курсов валют в разных странах, или в одной и той же стране, но через некоторое время. Это фьючерсные сделки – стандартный биржевой договор купли-продажи биржевого актива в определенный момент времени в будущем по цене, установленной сделкой в момент ее заключения.
Пример типичного фьючерсного контракта, заключенного 10.01.2006 г. Клиент соглашается принять поставку 10 т кофе по цене 1 500 долл. 25.04.2007 г. Суть фьючерсного контракта – зафиксировать в данный момент цену, по которой состоится сделка в будущем. Фьючерсные контракты легко перепродаются, что удобно для расчетов фирм.
Одним из инструментов финансового рынка являются опционы – договорные обязательства, позволяющие владельцу опциона за предварительную плату (премию) купить у банка или продать ему валюту или ценные бумаги по оговоренной в момент сделки цене. Если цена валюты повысится, то владельцу опциона выплачивается разница. При понижении цены владелец опциона может отказаться от покупки, но при этом он теряет премию.
2.5 Кредитные отношения
Кредит – предоставление денежных средств во временное пользование на условиях возвратности в определенный срок и уплатой процентов.
Если кредит выдается банком или финансовой компанией, то это банковский кредит. К разновидностям банковского кредита относятся: ипотечный, потребительский, кредит на неотложные нужды, на производственные цели и т. д. Обычно это краткосрочные или среднесрочные кредиты (за исключением ипотечного, средний срок которого составляет до 30 лет) с целью увеличить оборотный капитал предприятия или кредит на удовлетворение личных потребностей для физических лиц.
Перед заключением кредитного договора банк проверяет дееспособность, правоспособность и платежеспособность клиента. Для этого проводится анализ бухгалтерской отчетности предприятия, отчеты о состоянии дел, структура капитала, экономическая эффективность и т. д. Если в качестве клиента выступает физическое лицо, тогда необходимы документы, подтверждающие личность, справки о доходах, индивидуальный идентификационный номер налогоплательщика и т. д. В кредитном договоре указываются сумма и срок кредита, проценты и прочие расходы, обеспечение кредита, форма выдачи кредита.
Если фирма хорошо известна и надежна, обеспечением служит само имя и репутация фирма. В других случаях обеспечением является имущество предприятия – здание, оборудование, ценные бумаги, запасы и т. д.
Физическим лицам кредит может выдаваться под залог имеющегося в собственности заемщика имущества (квартиры, дачного участка, автомобиля и т.д.) и поручительства третьих лиц.
В кредитном соглашении оговариваются условия погашения и возврата кредита. Напрактике, всясумма ипроценты покредиту могутбытьвозвращены:
а) в конце срока или единым платежом;
б) по частям в течение срока погашения кредита:
– равными платежами;
– уменьшающимися платежами.
Для определения суммы возврата кредита и процентов по нему, на условии его погашения в конце срока, используется методика финансовых вычислений, рассмотренная в гл. 1. Другие случаи имеют следующие особенности в расчетах.
Если сумма кредита погашается равными частями в течение срока погашения кредита после определения наращенной стоимости, тогда величина равного платежа определяется по формуле
R1
= 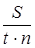 , (30) , (30)
где R1
– сумма погасительного платежа, руб.; S– наращенная сумма, руб.; t– срок обращения кредита, годы, дни и т. д.; n– число погасительных платежей за весь срок обращения кредита.
Если же сумма кредита погашается равными частями в течение срока погашения кредита и окончательная сумма наращенной стоимости неизвестна (что чаще встречается на практике банковского кредитования при составлении графика платежей по кредиту), тогда величина равного платежа определяется по формуле
R2
= 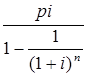 , (31) , (31)
где р – первоначальная стоимость кредита, руб.
Пример 30
Составить план погашения кредита в размере 900 млн руб. серией из 6 равных платежей, которые должны выплачиваться в конце каждого года. Процентная ставка – 10 % годовых.
Решение
Ежегодный платеж составит:
R= 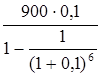 = 206,647 , млн. руб. = 206,647 , млн. руб.
Таблица 2
План погашения кредита (график платежей)
| Годы |
Остаток кредита, млн. руб. |
Годовые взносы, млн.руб. |
| Кредит |
Проценты |
Всего |
| 4-3 |
iна остаток кредита |
R2
|
| А |
1 |
2 |
3 |
4 |
| 1 |
900,000 |
116,647 |
90,000 |
206,647 |
| 2 |
783,353 |
128,312 |
78,335 |
206,647 |
| 3 |
655,042 |
141,143 |
65,504 |
206,647 |
| 4 |
513,899 |
155,257 |
51,390 |
206,647 |
| 5 |
358,642 |
170,783 |
35,864 |
206,647 |
| 6 |
187,860 |
187,860 |
18,786 |
206,647 |
| Итого |
0 |
0 |
- |
1 239,882 |
Общие расходы по погашению кредита составят 1 239,882 млн руб.
В случае погашения кредита уменьшающимися платежами, проценты начисляются на оставшуюся сумму долга, и в результате сумма погасительного платежа будет уменьшаться к концу срока погашения кредита. Пример погашения кредита уменьшающимися платежами представлен в примере 31.
Пример 31
Господин Иванов получил кредит на потребительские цели в размере 60 000 руб. на 1 год под 19 % годовых. Рассчитать сумму погашения кредита и начисленных процентов уменьшающимися платежами, при условии ежемесячного погашения кредита.
Решение
Таблица 3
План погашения кредита (график платежей)
| Период |
Остаток
кредита, тыс.руб.
|
Сумма взноса, тыс.руб. |
| Сумма кредита |
Сумма процентов |
Всего |
| R1
|
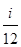 на остаток кредита на остаток кредита |
2+3 |
| А |
1 |
2 |
3 |
4 |
| 1 |
60 |
5 |
0,948 |
5,948 |
| 2 |
55 |
5 |
0,869 |
5,869 |
| 3 |
50 |
5 |
0,790 |
5,790 |
| А |
1 |
2 |
3 |
4 |
| 4 |
45 |
5 |
0,711 |
5,711 |
| 5 |
40 |
5 |
0,632 |
5,632 |
| 6 |
35 |
5 |
0,553 |
5,553 |
| 7 |
30 |
5 |
0,474 |
5,474 |
| 8 |
25 |
5 |
0,395 |
5,395 |
| 9 |
20 |
5 |
0,250 |
5,250 |
| 10 |
15 |
5 |
0,237 |
5,237 |
| 11 |
10 |
5 |
0,158 |
5,158 |
| 12 |
5 |
5 |
0,079 |
5,079 |
| Итого |
0 |
0 |
– |
66,096 |
В данном примере на остаток долга начисляются проценты исходя из ставки 19 % годовых. Таким образом, реальная ежемесячная ставка составила 1,58 % (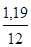 ). Однако в различных ситуациях на остаток долга может начисляться процент, исходя из установленной процентной ставки, то есть без корректировки на конкретный период начисления. ). Однако в различных ситуациях на остаток долга может начисляться процент, исходя из установленной процентной ставки, то есть без корректировки на конкретный период начисления.
Иногда банк или финансовая компания, выдавшие кредит, требуют внести обеспечение (залог) в виде процентной ставки от номинальной стоимости кредита. Если залог и проценты за выданный кредит выплачиваются при выдаче кредита, то это увеличивает реальную процентную ставку за пользование кредитом (о которой говорилось в гл. 1). Таким образом, в этой ситуации реальная процентная ставка рассчитывается по формуле
ip
= 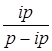 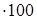 , (32) , (32)
где p– первоначальная сумма кредита, руб.; i– процентная ставка за пользование кредитом, выраженная в коэффициенте, ед.
Если банк требует залог (процент от суммы кредита), то реальная процентная ставка в этом случае рассчитывается по формуле
ip
= 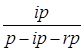 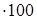 , (33) , (33)
где r –залог,ввидепроцентаотсуммыкредита,выраженныйвкоэффициенте,ед.
Одной из форм кредита является ломбардный кредит, выдаваемый под залог ценных бумаг. На практике срок ломбардного кредита не превышает 3 месяцев, а величина кредита – 90 % курсовой стоимости ценных бумаг.
Пример 32
Предприятие получило кредит на два месяца под залог 100 акций, курсовая стоимость которых составила 100 000 руб. Номинальная величина кредита – 70 % от курсовой стоимости акций. Процентная ставка за кредит – 16 %. Банк за обслуживание кредита взимает 0,3 %. Рассчитать сумму кредита и реальную процентную ставку.
Решение
Сумма кредита:
100 · 100 · 0,7 = 7 , млн. руб.
Проценты за кредит:
7 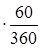 · 0,16 = 0,19 , млн. руб. · 0,16 = 0,19 , млн. руб.
За обслуживание кредита:
7 · 0,003 = 0,021 , млн. руб.
Сумма полученного кредита:
7 – 0,19 – 0,021 = 6,789 , млн. руб.
Реальная процентная ставка за кредит:
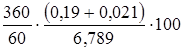 = 18,6 , %. = 18,6 , %.
Особенностями коммерческого кредита является то, что кредит предоставляется одной фирмой другой. На практике, это поставка товара. Оплата производится после реализации товаров или выполнения услуг. Оформляется коммерческий кредит векселем или счет-фактурой, и отражается как дебиторская задолженность покупателя и кредиторская задолженность для продавца. Процентная ставка по коммерческому кредиту ниже, чем по банковскому.
Для покупки дорогостоящих товаров физическим лицам предоставляется потребительский кредит. Обычно его предоставляет банк, торговая организация или финансовая компания. Одна из форм такого кредита – продажа товаров в рассрочку.
В настоящее время банки начинают выдавать ипотечные кредиты. Под ипотекой понимается денежная ссуда, предоставляемая под залог недвижимого имущества. На период ипотеки заложенное имущество находится в собственности кредитора, но во владении заемщика. В случае нарушения заемщиком условий сделки по решению суда заложенное имущество продается для удовлетворения требований кредитора или объявляется его собственностью.
Существуют следующие варианты ипотеки:
- традиционная ипотека, при которой сумма кредита погашается равными частями через определенные периоды;
- ипотека, с изменяющейся процентной ставкой (в некоторых случаях процентную ставку привязывают к коэффициенту инфляции и (или) курсу доллара.
Расчет суммы погашения ипотечного кредита и размера равного периодического платежа осуществляется с помощью следующих формул:
S= 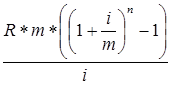 ; (34) ; (34)
R= 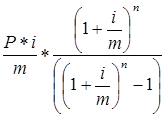 . (35) . (35)
Пример 33
Размер ипотечного кредита 500 000 руб. Срок – 20 лет. Процентная ставка – 12 % годовых. Рассчитать сумму погашения кредита и размер ежемесячного равного платежа.
Решение
R= 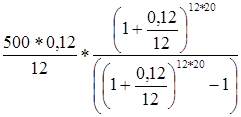 = 5,5054 , руб. = 5,5054 , руб.
S= 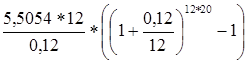 = 5 446,276 , руб. = 5 446,276 , руб.
Задачи для самостоятельного решения
41. Объем денежной массы, находящейся в обращении на начало года, составляет 4 566 млрд. руб. Определить, как изменится объем денежной массы за год под влиянием инфляции, если среднемесячный уровень инфляции составит 0,6 %?
42. Инвестор имеет возможность вложить 100 000 руб. на 2 года. Рассчитать минимальную процентную ставку, чтобы окупить затраты инвестора, если известно, что среднегодовой уровень инфляции составит 7,5%.
43. Определить целесообразность вложения денежных средств на год под 14 % годовых, если ежеквартальный уровень инфляции составляет 2,5 %?
44. Рассчитать ежемесячный уровень инфляции, если годовой уровень составил 12 %?
45. Выбрать оптимальный вариант вложения 50 000 руб. на 5 лет, если среднегодовой уровень инфляции составляет 10 %, банковская ставка по депозиту составляет 9 % годовых при условии начисления сложных процентов.
46. Ежемесячный уровень инфляции составляет 1 %. Определить годовой индекс инфляции и годовой уровень цен.
47. Вклад в сумме 50 000 руб. помещен в банк на 3 месяца с ежемесячным начислением сложных процентов. Годовая ставка по вкладам 8 %. Уровень инфляции 1 % в месяц. Определить сумму погашения вклада, индекс инфляции за 3 месяца, реальный доход вкладчика с точки зрения покупательной способности.
48. Переводной вексель выдан на 30 000 руб. с уплатой 20 ноября. Владелец векселя учел его в банке 20 апреля того же года по учетной ставке 12 % годовых. Рассчитать сколько получил владелец векселя и доход банка.
49. Номинальная стоимость векселя со сроком погашения через 6 месяцев составляет 16 000 руб. Рассчитать цену покупки векселя, если он реализуется с дисконтом 10 % годовых.
50. Вексель номиналом 1 000 руб. продается с дисконтом по ставке 13 % годовых. Срок погашения через 120 дней. Определить величину дисконтированного дохода.
51. Казначейский вексель номинальной стоимостью 3 000 руб. реализуется с дисконтом 25 % годовых 15 февраля. Срок погашения векселя 15 мая. Определить сумму дохода по векселю.
52. Рассчитать учетную ставку, которая обеспечит держателю казначейского векселя получение 6 000 руб., если номинальная стоимость векселя 10 000 руб., срок погашения через 1 год и 1 месяц.
53. Какова сумма дисконта при продаже финансового векселя на сумму 5 000 руб., если срок его погашения равен 2,5 года, а покупатель применил сложную учетную ставку, равную 8 % годовых?
54. Тратта (переводной вексель) выдана на сумму 1 000 000 руб. с уплатой 25 декабря 2006 г. Владелец векселя учел его в банке 18 августа 2006 г. по учетной ставке 20 % годовых. Рассчитать полученную продавцом при учете сумму и дисконт в пользу банка.
55. Коммерческий вексель торговой компании реализуется по номинальной стоимости 40 000 руб. с дисконтированной ставкой дохода 16 % годовых и сроком погашения через 95 дней. Среднегодовой уровень инфляции 11 %. Целесообразна ли покупка данного векселя?
56. Казначейский вексель номинальной стоимостью 25 000 руб. реализуется юридическим и физическим лицам по учетной ставке 25 % годовых. Срок погашения векселя через 91 день. Среднегодовой уровень инфляции 12 %. Выгодно ли приобретение данного векселя?
57. Коммерческий вексель торговой корпорации продается с дисконтом по цене 9 050 руб. при номинальной стоимости 10 000 руб. Срок погашения векселя через 5 месяцев. Среднемесячный уровень инфляции 1 %. Стоит ли приобретать вексель?
58. Финансовый вексель номинальной стоимостью 50 000 руб. реализуется по цене 75 % от номинала по учетной ставке 13 % годовых. Срок погашения векселя через 180 дней. Среднеквартальный уровень инфляции 1,5 %. Определить целесообразность покупки векселя?
59. Банковский вексель эмиссионного синдиката номинальной стоимостью 25 000 руб. реализован дилерской фирме с дисконтом 15 % годовых. Срок погашения векселя через 100 дней. По истечении 30 дней вексель продан частному лицу по цене 24 300 руб. Среднегодовой уровень инфляции составил 10 %. Рассчитать финансовый результат от приобретения векселя для дилерской фирмы и индивидуального инвестора.
60. Три векселя финансовой корпорации номинальной стоимостью по 10 000 руб. реализуются по учетной ставке 13 % годовых и имеют сроки погашения: первый – через 90 дней, второй – через 95 дней, третий – через 120 дней. Определить совокупный чистый доход инвестора от приобретения векселей, если годовой уровень инфляции составит 11 %.
61. Минский маргариновый завод выпустил 6 000 акций (номинальная стоимость 1 000 руб.). В 2004 г. дивиденды на одну акцию были выплачены в размере 400 руб., в 2005 г. собрание акционеров постановило в связи с увеличением финансовых результатов выплатить дивиденды по ставке 16 % годовых. Определить величину дохода от покупки акций.
62. Предприниматель купил на свои сбережения акции трех компаний. Акций первой компании куплено на 50 % сбережений, второй – на 35 %, третьей – на 15%. Дивиденды по акциям каждой компании составляют 16, 20 и 24 %. Сравните выгодность покупки для трех вариантов.
63. Рассчитать размер дивиденда по обыкновенным акциям. Прибыль АО, направляемая на выплату дивидендов, составляет 2 000 000 руб. Общая сумма акций – 4 500 000 руб., в том числе привилегированных акций – 500 000 руб. с фиксированным размером дивиденда.
64. Определите ставку дивиденда по обыкновенным акциям АО «Янтарь», если величина уставного капитала общества 80 000 000 руб. и он разделен на 16 000 акций, 25 % которых являются привилегированными и имеют ставку дивиденда 22 % годовых. Сумма объявленных дивидендов составляет 22 400 000 руб.
65. Государственная краткосрочная бескупонная облигация номинальной стоимостью 1 000 руб. и сроком обращения 1 год, реализуется с дисконтом 10 % годовых. Определите доход по облигации.
66. Государственная краткосрочная бескупонная облигация номинальной стоимостью 1 000 руб. и сроком обращения 6 месяцев, реализуется с дисконтом 18 % годовых. Определить доход по облигации.
67. Государственная облигация федерального займа, номинальной стоимостью 1 000 руб. и сроком обращения 1 год имеет доход в размере 14 % годовых. Определить доход по данной облигации.
68. Определить срок обращения облигации, если ее номинальная стоимость равна 2 500 руб., наращенная стоимость – 3 000 руб., а доход начисляется по простой процентной ставке 9 % годовых.
69. Определите купонную ставку по облигации, если ее номинальная стоимость равна 5 400 руб., сумма к погашению 6 000 руб., срок обращения 150 дней.
70. Государственная облигация продается с дисконтом по цене 5 250 руб. при номинальной стоимости 10 000 руб. Ставка дохода 9 % годовых, срок погашения через 3 года. Проценты по облигации выплачиваются ежегодно. Среднегодовой уровень инфляции 10 %. Требуется определить финансовый результат от покупки облигации.
71. Беспроцентная целевая муниципальная облигация номинальной стоимостью 1 000 руб. продается с дисконтом 8 % годовых и имеет срок погашения 1 год. Доходна или убыточна будет покупка данной облигации, если среднегодовой уровень инфляции составит 10 %?
72. Облигация государственного федерального займа номинальной стоимостью 5 000 руб. имеет 4 купона со сроком погашения 1 апреля, 1 июля, 1 октября и 1 января. Проценты выплачиваются при погашении купона по ставке 5 % годовых. Определить доход по облигации.
73. Предприятие приобрело пакет облигаций финансовой корпорации, состоящий из 15 ценных бумаг, номинальной стоимостью 1 000 руб. и сроком обращения 1 год по цене 95 % от номинала. Определите сумму дохода по пакету облигаций, если по ним выплачивается 13 % годовых.
74. Муниципальная облигация с постоянно возрастающей ставкой дохода продается по номинальной стоимости 5 000 руб. Срок погашения облигации через 5 лет. Выплата процентов производится при погашении. В первый год начисляется доход в размере 6 % годовых, во второй – 8 %, в третий – 9 %, в четвертый и пятый – 12 % годовых. Определить целесообразность покупки облигации, если среднегодовой уровень инфляции составит 9 %?
75. Для размещения внутреннего долга правительство выпустило облигации номинальной стоимостью 2 000 руб. и сроком погашения через 3 года. Облигации реализуются с дисконтом 10 % годовых и имеют фиксированную процентную ставку 12 % годовых. Проценты по облигации выплачиваются ежегодно. Ожидаемый уровень инфляции составит 9, 10 и 11 % соответственно по годам. Определить целесообразность покупки облигации:
а) на дату размещения;
б) через год после даты размещения;
в) через два года от даты размещения.
76. Депозитный сертификат номинальной стоимостью 500 руб. выдан 14 марта с погашением 10 июня под 10 % годовых. Определить сумму начисленных процентов, применяя разные способы начисления процентов.
77. Государственный жилищный сертификат номинальной стоимостью 2 000 руб. и сроком погашения через 190 дней продается с дисконтом 13 % годовых. Определить доход от покупки сертификата.
78. Сберегательный сертификат коммерческого банка с фиксированной ставкой дохода 15 % годовых и сроком обращения 3 года имеет номинальную стоимость 1 000 руб. Рассчитать доход от покупки сертификата, если проценты выплачиваются в конце срока.
79. Депозитный сертификат номинальной стоимостью 5 000 руб. и сроком обращения 2 года имеет простую ставку дохода 9 % годовых. Стоит ли приобретать сертификат при условии, что среднегодовой уровень инфляции составит 7,5 %?
80. Одновременно в обращение выпущены облигация государственного внутреннего займа и сберегательный сертификат известного банка. Облигация имеет ставку дохода 12 % годовых и реализуется с дисконтом 30 % при номинальной стоимости 3 000 руб. Сберегательный сертификат имеет ту же номинальную стоимость и ставку дохода 16 % годовых. Срок обращения ценных бумаг 4 года. Проценты погашаются в конце срока. Определить оптимальный вариант вложения средств.
81. Инвестору предлагается покупка одной из следующих видов ценных бумаг.
1. Муниципальная облигация 7 %-го целевого займа местных органов власти, реализуемая с дисконтом по цене 900 руб. при номинальной стоимости 1 000 руб. и сроком погашения через три года.
2. Облигация промышленной корпорации с постоянно возрастающей ставкой дохода по номинальной стоимости 1 000 руб., сроком погашения через 3 года и начислением дохода 6 % в первый, 9 % во второй и 13 % в третий год.
3. Сберегательный сертификат коммерческого банка номинальной стоимостью 1 000 руб. с фиксированной ставкой дохода 12 % годовых и сроком погашения через 3 года.
Требуется определить, покупка какой из перечисленных ценных бумаг наиболее выгодна инвестору при условии, что доход по ним выплачивается при погашении, а среднегодовой уровень инфляции составит 9 %.
82. Выбрать наиболее приемлемый вариант увеличения капитала акционерного общества в размере 138 000 руб. на 1 год:
– выпустить акции номинальной стоимостью 500 руб. и ставкой дивиденда 5 % в год;
– эмитировать облигации номинальной стоимостью 10 000 руб., реализовать их с дисконтом 8 % годовых и ежеквартально выплачивать доход исходя из ставки 6 % простых годовых.
– разместить векселя номинальной стоимостью 1 000 руб., реализовать их с дисконтом по цене 950 руб.
83. Вкладчик имеет возможность вложить 40 000 руб. на 2 года на следующих условиях:
а) купить иностранную валюту по курсу 28,54 руб. за 1 долл. США, с учетом того, что через 2 года курс доллара возрастет на 204 пункта.
б) вложить денежные средства на депозит в финансовую компанию под 8 % годовых с ежеквартальной капитализацией процентов.
в) приобрести облигацию промышленной корпорации по цене 90 % от номинала с ежегодной выплатой процентов по ставке 6 % годовых.
Выбрать наиболее оптимальный вариант вложения средств, если среднегодовой уровень инфляции составит 7 %.
84. Определить кросс-курс американского доллара к евро, если:
– курс американского доллара к рублю составляет 28,13 руб.;
– курс евро к рублю составляет 34,10 руб.;
– имеется в наличии 1 350 евро.
85. Определить кросс-курс американского доллара к казахской тыньге, учитывая следующее:
– курс американского доллара к рублю составляет 28,76 руб.;
– курс тыньге к рублю: 1 руб. = 4,56 тыньге;
86. Рассчитать курсовую разницу от сделки и определить убыток (прибыль) хозяйствующего субъекта, если приобретено 10 000 долл. США по курсу 29,77 руб. за 1 долл. США. Курс Центрального Банка РФ на день покупки составил 29,61 руб. за 1 долл. США.
87. Арбитражер заключает следующие сделки: покупает на бирже 10 000 долл. США по курсу СПОТ 28,54 руб. за 1 долл. США и заключает форвардный контракт на продажу через три месяца по курсу 30,86 руб. за 1 долл. США. Размещает 10 000 долл. США на 3 месяца на международном денежном рынке по ставке, размер которой составляет 3,16 % годовых. Определить сумму прибыли от купли-продажи валюты.
88. Стоимость капитала 400 000 долл. США при продаже на евро по курсу СПОТ 1,015. Рассчитать шестимесячный форвардный курс доллара к евро и сумму арбитражной прибыли, если процентная ставка депозита по долларам США составляет 3 % годовых, по евро – 9 % годовых.
89. Стоимость капитала 294 400 долл. США, что эквивалентно 203 000 евро. Рассчитать сумму прибыли (убытка) арбитражера при текущем курсе доллара к евро 0,89 и 1,12.
90. Остаток на счете 52 равен 1 000 долл. США, приобретенный по курсу 28,56 руб. за 1 долл. США. На первый день отчетного квартала курс доллара равен 29,54 руб. Рассчитать курсовую разницу.
91. ООО «Морэкспорт» подало в банк заявку на добровольную продажу 20 000 долл. США. Банк продал валюту по курсу 29,64 руб. Официальный курс ЦБ РФ и на дату списания, и на дату зачисления выручки от ее продажи равен 29,81 руб. Согласно договору, комиссионное вознаграждение банка 2 000 руб. Определить сумму внереализационных расходов.
92. Курс рубля к доллару США составляет 0,035. Имеется в наличии 36 000 руб. Рассчитать эквивалент суммы в долларах и определить курс американского доллара к рублю.
93. Курс рубля к евро составляет 0,029. Имеется в наличии 45 600 руб. Рассчитать эквивалент суммы в евро и определить курс евро к рублю.
93. Предприниматель должен приобрести евро на 100 долл. США. Текущий курс доллар/евро – 0,848. Годовые процентные ставки для доллара – 8,3%, для евро – 9,96%. Сколько евро получит предприниматель при форвардной сделке через месяц?
94. Рассчитать размер форвардной премии или дисконта, если текущий курс евро к доллару составляет 1,171, а годовые процентные ставки на 3 месяца на международном валютном рынке для доллара – 8,5 %, для евро – 9 %.
95. Покупатель приобрел холодильник по цене 30 000 руб., уплатив сразу 18 000 руб. и обязавшись уплатить остальное в течение 6 месяцев, делая ежемесячные равные платежи. Определить сумму ежемесячного платежа, если продавец требует за кредит 10 % в год.
96. Автосалон продал автомобиль за 210 000 руб., получив в момент продажи 80 % стоимости. Остальная сумма и процент за кредит в размере 12 % годовых должны быть уплачены покупателем в течение 4 месяцев равными платежами. Рассчитать сумму равного платежа.
97. Магазин бытовой техники предлагает покупателям приобретение товаров в кредит на условиях 10-10-10: 10 % – первоначальный взнос, 10 % – ставка за кредит, 10 месяцев – срок кредита. Оплата кредита в любом филиале Сбербанка. Рассчитать реальную процентную ставку за пользование кредитом, если приобретен компьютер, стоимостью 20 000 руб., банк взимает комиссию за каждую операцию 1 %.
98. Г-жа Смирнова желает приобрести дубленку за 30 000 руб. за счет кредитных средств, предоставленных КБ «Русское правило». Банк предоставляет кредит посредством выдачи пластиковой карты на следующих условиях: стоимость оформления карты составляет 400 руб., за открытие счета взимается 900 руб., ежемесячная транзакция 1% от суммы выданного кредита, за обналичивание средств списывается 1,5 % от суммы кредита, процентная ставка банка 14 % годовых. Определить сумму погашения кредита и реальную процентную ставку за пользование кредитом, если Смирнова рассчитается за кредит в течение 3 месяцев.
99. Фирма взяла кредит в сумме 300 000 руб. сроком на 1 год по 16 % годовых. Проценты за кредит банк берет авансом. Рассчитать реальную процентную ставку за пользование кредитом.
100. Акционерное общество получило кредит с 13 апреля по 13 июня под залог 600 акций, курсовая стоимость которых составляла 100 000 руб. Номинальная величина кредита – 60 % от курсовой стоимости акций. Процентная ставка 20 % годовых. Банк взимает за обслуживание кредита 0,7 %. Определить сумму полученного кредита, сумму процентов за кредит и реальную процентную ставку, при условии, что банк взимает проценты авансом.
101. Производственное объединение получило на полгода банковский кредит в размере 800 000 руб. под 21 % годовых. Проценты за кредит банк берет авансом. Рассчитайте реальную процентную ставку за пользование кредитом в случае:
а) не требуется залога,
б)залог за предоставление кредита составляет 6 % от суммы кредита.
102. Организация для строительства цеха по производству медпрепаратов получила кредит на 3 месяца под залог недвижимости стоимостью 1 600 000 руб. Величина кредита составляет 80 % от стоимости недвижимости. Процентная ставка по кредиту 19 % годовых, комиссионное обслуживание кредита составляет 2 %. Определите сумму полученного кредита и реальную процентную ставку, если проценты за кредит банк берет авансом.
103. Предприятие для модернизации оборудования решило взять в банке кредит в 600 000 руб. Кредит выдается под 24 % годовых. Срок кредита – 9 месяцев. Кроме того, банк требует залог – 8 % от суммы кредита. Какую сумму получит заемщик, если проценты простые и оплачиваются при выдаче кредита? Какова реальная процентная ставка по кредиту?
104. Фирма получила кредит в 180 000 руб. на три года под 18 % годовых. Погашение кредита и процентов должно происходить в конце каждого года равными суммами. Проценты начисляются на непогашенную часть кредита. Определить платежи по кредиту и процентные платежи по годам. Расчеты оформить в таблице.
105. Предприятие получило кредит в 800 000 руб. сроком на 2 года под простую процентную ставку 20 % годовых. Рассмотреть план погашения кредита и начисленных на оставшуюся сумму кредита процентов серией из восьми равных платежей, которые выплачиваются в конце каждого квартала.
106. Физическое лицо получило кредит в Сбербанке на потребительские цели в сумме 120 000 руб. и сроком на 2 года. Кредит должен погашаться ежемесячно уменьшающимися платежами. Составить план погашения кредита, определить сумму погашения долга и сумму начисленных процентов.
107. Под залог недвижимости банк выделил ссуду в 300 000 руб. на 2 года под 15 % годовых. Оплата ипотечной ссуды и процентов должна происходить ежеквартально равными платежами. Определить сумму к возврату и размер ежеквартального платежа.
108. Для приобретения квартиры банк выделил денежную ссуду в размере 1 000 000 руб. на 10 лет под 13 % годовых. Залогом является выкупленная квартира. Согласно условиям сделки, оплата ипотечной ссуды и процентов происходит по полугодиям равными суммами. Определить общую сумму возврата ипотечного кредита и размер периодического платежа.
109. Для внедрения новой производственной линии и закупки современного оборудования промышленный концерн получил кредит в размере 900 000 руб. на 6 лет под 10 % годовых. Проценты выплачиваются кредитору ежегодно. Выберите наиболее экономный график погашения кредита для заемщика и наиболее доходный для банка.
110. Банк выдал фермерскому объединению кредит с 20 мая по 20 августа под залог 600 облигаций курсовой стоимости 50 000 руб. Номинальная величина кредита – 60 % от курсовой стоимости ценных бумаг. Процентная ставка – 20 % годовых. Рассчитать сумму выданного кредита и реальную процентную ставку за пользование кредитом если:
– удерживаются комиссионные в размере 0,7 % от суммы кредита;
– удерживаются комиссионные в размере 0,8 % от суммы кредита;
– удерживаются комиссионные в размере 0,5 % от суммы кредита.
ГЛОССАРИЙ
Активы – деньги, вклады, права и собственность, которыми располагает компания или отдельно взятое лицо.
Акция – ценная бумага, приобретение которой дает права ее покупателю на пропорциональное владение компанией, выпустившей данную ценную бумагу. Компании-эмитенты выпускают акции, чтобы основать (учредить) или увеличить свой капитал.
Арбитраж – третейский суд для разрешения споров по поводу сделок с ценными бумагами; положительная разница в ставках процентов, валютных курсах или ценах на товары, получаемая за счет переоформления сделки (рефинансирование денежных средств).
Вексель – составленное по установленной законом форме безусловное письменное долговое денежное обязательство, выданное векселедателем векселедержателю
Вторичный рынок – рынок, на котором перепродаются ценные бумаги. Операторами рынка являются посредники.
Государственные облигации – облигации, выпускаемые органами власти от имени и по поручению правительства соответствующих стран. В обеспечение государственных облигаций привлекаются золотовалютные резервы и другие активы, принадлежащие государству. Государственные облигации – один из самых надежных и, вместе с тем, наименее доходных видов ценных бумаг.
Депозитный сертификат – соглашение с банком, обязывающее вкладчика внести свои деньги на депозит на определенный период, по истечении которого вкладчик получит их с определенным процентом.
Дивиденд – доход, причитающийся к выплате владельцу акции.
Дисконт – разность между будущей и текущей суммами денег. На практике – скидка с номинала дисконтной ценной бумаги.
Дисконтирование – принятое в финансовой математике название процедуры определения стоимости денег в более ранний момент времени в соответствии с принятой ставкой дисконтирования.
Дисконтирование коммерческое (банковский учет) – дисконтирование, при котором его ставкой выступает ставка дисконта.
Дисконтирование математическое – дисконтирование, при котором его ставкой является обычная процентная ставка (ставка процентов).
Дисконтирующий множитель – прошлая стоимость 1 д.е. несколько процентных периодов назад. Дисконтный множитель показывает, во сколько раз уменьшается стоимость денег при ее дисконтировании.
Заем – полученный кредит частным лицом или фирмой в банке на определенный срок с условием возврата и выплаты определенного процента.
Инвестиции – вложение денег в бизнес с целью получения прибыли и последующего их перевложения (реинвестиции). В узком смысле – капитальные вложения, в т. ч. производственные (инвестиции в производство или реальный сектор производства) и непроизводственные (инвестиции в сектор нематериального производства, в том числе в услуги, включая финансовые услуги).
Инвестор, инвестиционная компания – посредник между корпорацией, выпускающей новые ценные бумаги, и потенциальным владельцем этих бумаг, покупающим новую эмиссию ценных бумаг и распродающим их частным лицам и организациям. Выступает также в роли агента по продаже крупных пакетов ценных бумаг.
Индекс потребительских цен – сводный индекс цен фиксированного состава; характеризует динамику затрат на постоянный потребительский набор товаров и услуг за счет ценового фактора.
Инфляция – изменение баланса между денежной массой и объемом созданных в стране благ и услуг в сторону увеличения денег. Проявляется в росте цен и обесценении денег.
Капитализация процентов – процедура систематического присоединения их к сумме денег, относительно которой они определялись.
Корпорация – объединение капиталов двух или более владельцев, принадлежащих одному отдельно взятому.
Корпоративная облигация – облигация, эмитируемая корпорацией.
Купон – процентная ставка, оплачивающаяся по фиксированному или плавающему курсу облигаций.
Либор – лондонская межбанковская процентная ставка; устанавливается ежедневно по состоянию на 11 часов утра пятью ведущими лондонскими банками.
Множитель наращения – будущая стоимость 1 д.е. через несколько процентных периодов из ставки наращения за период. Множитель наращения показывает, во сколько раз увеличивается стоимость денег при ее наращивании.
Муниципальная облигация – облигация, выпущенная муниципалитетом или другими приравненными органами местной власти.
Наращение – процесс увеличения капитала за счет присоединения процентов. Так же в финансовой математике называют процедуры вычисления суммы денег с начислением процентов.
Наращенная (будущая) стоимость денег – сумма денег, увеличенная за единицу времени к величине капитала.
Нераспределенная прибыль – прибыль после выплаты дивидендов и налогов, которую компании резервируют для совершения финансовых операций.
Номинальная доходность – номинальная годовая процентная ставка, базовая ставка по договору, из расчета которой определяется и начисляются проценты.
Опцион – сделка с условием; продажа (опцион «пут») товара или услуги, валюты, ценных бумаг или прав с условием последующего обязательного выкупа или покупка (опцион «колл») на тех же заранее оговоренных условиях (покупная цена опциона, опцион с нулевой «внутренней» стоимостью или опцион аннулирования) или на любых иных, обычно текущих условиях.
Облигация – документарное обязательство погасить заем (долг) в определенный срок с выплатой процента.
Объект финансовых вычислений – финансовые операции и сделки (шире – финансовые проекты и программы) и их технико-экономическое обоснование, осуществляемые с целью извлечения прибыли.
Предмет финансовых вычислений – охватывает финансовый учет, бюджет, баланс, отчет, контроль и аудит; определение финансового состояния и финансового обеспечения всех категорий и видов заимствующих организаций; обоснование предпочтительных финансовых решений.
Процентная ставка – отношение процентных денег, уплаченных (полученных) за единицу времени к величине капитала; плата, выраженная в процентах, которую взимают банки с заемщика за пользование кредитными деньгами.
Процентный период – период времени между двумя последовательными процедурами вычисления процентов.
Проценты – сумма, уплаченная за пользование заемными денежными средствами.
Проценты авансовые – проценты, уплачиваемые в момент выдачи денежных средств. Вычисляются относительно суммы денег с процентами.
Проценты обычные – проценты, начисляемые по истечении определенного периода после вложения средств. Вычисляются относительно первоначальной суммы денег.
Проценты простые – проценты, определяемые на весь срок финансовой операции относительно первоначальной суммы.
Проценты сложные – проценты, база для определения которых постоянно меняется за счет присоединения (снятия) начисленных ранее процентов.
Рыночная котировка – цена актива, устанавливаемая на бирже исходя из спроса и предложения.
Реинвестиции – перевложение полученных доходов с целью увеличения объемов деятельности и прибыли.
Ставка дисконтирования – ставка, по которой осуществляется операция дисконтирования.
Уровень инфляции – темп прироста денежной массы; темп прироста индекса потребительских цен.
Финансовый учет – процесс сбора, обработки, анализа и передачи данных о финансовых результатах деятельности отдельно взятых финансовых компаний или их отдельно взятых сделок и операций, равно как и всех взятых вместе компаний, операций и сделок.
Финансовое состояние – состояние любого финансового агента (государства, региона, компании, предпринимателя, семьи, отдельного лица), характеризующее баланс его финансовых обязательств и ресурсов, их достаточность, нехватку (дефицит) или превышение (профицит), необходимых для поддержания нормального режима работы и жизни, осуществления денежных расчетов с другими агентами финансовой системы.
Финансовая компания – любая кредитная или иная заимствующая организация, осуществляющая операции с финансовыми ресурсами и вступающая в финансовые связи и отношения (банки, биржи, инвестиционные фонды, страховые компании, государственные финансовые учреждения).
Финансово-кредитные институты – лицензируемые государственные и частные кредитные организации, уполномоченные осуществлять банковские операции – операции по кредитованию клиентов, ведению расчетных счетов, купле и продаже валюты и ценных бумаг, оказанию финансовых услуг и др. Наряду с банковскими различают и небанковские кредитные организации, функционирующие на правах осуществления отдельных видов банковских операций.
Эквивалентные процентные ставки – ставки доходности, соответствующие различным способам начисления процентов, но обеспечивающие одинаковый относительный доход по операции за одинаковый промежуток времени.
Эффективная доходность – годовая процентная ставка, характеризующая полный относительный годовой доход по операции с учетом внутригодовой капитализации.
ЗАКЛЮЧЕНИЕ
Предлагаемое учебное пособие рассматривает финансовые вычисления, предметом которых является результат деятельности инвестиционных, биржевых, кредитных, страховых, валютных и иных заимствующих организаций.
Эти финансовые вычисления называют также эффективными, или высшими, так как они выступают инструментом не только фиксирования, но и оценки рыночных ожиданий различных финансовых исходов (учетных и кредитных ставок, курсов валют, аннуитетов и т. д.), выполняемых, как правило, в условиях неопределенности и риска с учетом будущих доходов (или убытков).
Различают простые и сложные виды финансовых вычислений, соответствующие простым и сложным схемам финансовых сделок. Финансовые вычисления используются в практике начисления банковского процента, депозитных и заемных ставок, дохода по ценным бумагам и другим вложениям денежных средств.
В данном учебном пособии освещены вопросы практического применения финансовых расчетов при учете инфляции, в операциях с векселями и другими ценными бумагами, операций с валютой и в кредитных отношениях.
В качестве отдельного раздела в учебном пособии представлены задачи для самостоятельного решения и комплект приложений, включающий таблицы и диаграммы, характеризующие современную ситуацию и изменения важных экономических показателей.
Автор надеется, что данное учебное пособие послужит для студентов значимым источником информации при изучении тем «Деньги», «Кредит», «Ценные бумаги», «Валютные операции», а также окажет помощь при самостоятельном изучении курса.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Российская Федерация. Законы. Гражданский кодекс Российской Федерации от 14.12.2002 г. № 138-ФЗ; ред. от 29.12.2004 г. // www.duma.gov.ru
2. Российская Федерация. Законы. О валютном регулировании и валютном контроле в РФ : федер. закон от 10.12.2003 г. № 186-ФЗ // Рос. газета. – 2003. – 17 дек. – № 253.
3. Российская Федерация. Законы. Об ипотечных ценных бумагах : федер. закон от11.11.2003 г. № 152-ФЗ // Парламент. газета. – 2003. – 19 ноябр. – № 215-216.
4. Российская Федерация. Законы. О Центральном банке (Банке России) : федер. закон от 10.07.2002 г. № 86-ФЗ // Рос. газета. – 2002. – 13 июля. – № 127.
5. Российская Федерация. Законы. О переводном и простом векселе : федер. закон от 11.03.1997 г. № 48-ФЗ // Рос. газета. – 1997. – 18 марта. – № 53.
6. Российская Федерация. Законы. О рынке ценных бумаг : федер. закон от 22.04.1996 № 39-ФЗ // Рос. газета. – 1996. – 25 апр.– № 79.
7. Российская Федерация. Законы. Об акционерных обществах : федер. закон от 26.02.1995 г. № 208-ФЗ // Рос. газета. – 1995. – 29 дек. – № 248.
8. Владимирова О. Н. Фондовый рынок и ценные бумаги: тренинг по курсу для студентов всех специальностей и всех форм обучения / О. Н. Владимирова. – Красноярск, 2002. – 74 с.
9. Гусева И. А. Практикум по рынку ценных бумаг : учеб. пособие / И. А. Гусева. – М. : Юристъ, 2000. – 320 с.
10. Деньги. Кредит. Банки. Ценные бумаги. Практикум : учеб. пособие для вузов / под ред. Е. Ф. Жукова. – М. : Юнити-Дана, 2001. – 310 с.
11. Капельян С. Н. Основы коммерческих и финансовых расчетов / С. Н. Капельян, О. А. Левкович. – Минск : НТЦ «АПИ»,1999. – 224 с.
12. Раковская С. А. Сборник задач по финансовой математике : метод. пособие / С. А. Раковская. – Красноярск, 2001. – 92 с.
13. Салин В. Н. Техника финансово-экономических расчетов : учеб. пособие / В. Н. Салин, О. Ю. Ситникова. – М. : Финансы и статистика, 2000. – 80 с.
14. Симчера В. М. Введение в финансовые и актуарные вычисления / В. М. Симчера. – М. : Финансы и статистика, 2003. – 352 с.
15. Статистика финансов / под ред. проф. В. Н. Салина. – М. : Финансы и статистика, 2000. – 816 с.
16. Уланов В. А. Сборник задач по курсу финансовых вычислений / под ред. проф. В. В. Ковалева. – М. : Финансы и статистика, 2000. – 400 с.
17. Финансы и кредит : учеб. пособие / под ред. А. Ковалева. – М. : Финансы и статистика, 2003. – 511 с.
ПРИЛОЖЕНИЯ
Приложение 1
Порядковые номера дней в обычном году (365 дней)
| День месяца |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
| 1 |
1 |
32 |
60 |
91 |
121 |
152 |
182 |
213 |
244 |
274 |
305 |
335 |
| 2 |
2 |
33 |
61 |
92 |
122 |
153 |
183 |
214 |
245 |
275 |
306 |
336 |
| 3 |
3 |
34 |
62 |
93 |
123 |
154 |
184 |
215 |
246 |
276 |
307 |
337 |
| 4 |
4 |
35 |
63 |
94 |
124 |
155 |
185 |
216 |
247 |
277 |
308 |
338 |
| 5 |
5 |
36 |
63 |
95 |
125 |
156 |
186 |
217 |
248 |
278 |
309 |
339 |
| 6 |
6 |
37 |
65 |
96 |
126 |
157 |
187 |
218 |
249 |
279 |
310 |
340 |
| 7 |
7 |
38 |
66 |
97 |
127 |
158 |
188 |
219 |
250 |
280 |
311 |
341 |
| 8 |
8 |
39 |
67 |
98 |
128 |
159 |
189 |
220 |
251 |
281 |
312 |
342 |
| 9 |
9 |
40 |
68 |
99 |
129 |
160 |
190 |
221 |
252 |
282 |
313 |
343 |
| 10 |
10 |
41 |
69 |
100 |
130 |
161 |
191 |
222 |
253 |
283 |
314 |
344 |
| 11 |
11 |
42 |
70 |
101 |
131 |
162 |
192 |
223 |
254 |
284 |
315 |
345 |
| 12 |
12 |
43 |
71 |
102 |
132 |
163 |
193 |
224 |
255 |
285 |
316 |
346 |
| 13 |
13 |
44 |
72 |
103 |
133 |
164 |
194 |
225 |
256 |
286 |
317 |
347 |
| 14 |
14 |
45 |
73 |
104 |
134 |
165 |
195 |
226 |
257 |
287 |
318 |
348 |
| 15 |
15 |
46 |
74 |
105 |
135 |
166 |
196 |
227 |
258 |
288 |
319 |
349 |
| 16 |
16 |
47 |
75 |
106 |
136 |
167 |
197 |
228 |
259 |
289 |
320 |
350 |
| 17 |
17 |
48 |
76 |
107 |
137 |
168 |
198 |
229 |
260 |
290 |
321 |
351 |
| 18 |
18 |
49 |
77 |
108 |
138 |
169 |
209 |
230 |
261 |
291 |
322 |
352 |
| 19 |
19 |
50 |
78 |
109 |
139 |
170 |
200 |
231 |
262 |
292 |
323 |
353 |
| 20 |
20 |
51 |
79 |
110 |
140 |
171 |
201 |
232 |
263 |
293 |
324 |
354 |
| 21 |
21 |
52 |
80 |
111 |
141 |
172 |
202 |
233 |
264 |
294 |
325 |
355 |
| 22 |
22 |
53 |
81 |
112 |
142 |
173 |
203 |
234 |
265 |
295 |
326 |
356 |
| 23 |
23 |
54 |
82 |
113 |
143 |
174 |
204 |
235 |
266 |
296 |
327 |
357 |
| 24 |
24 |
55 |
83 |
114 |
144 |
175 |
205 |
236 |
267 |
297 |
328 |
358 |
| 25 |
25 |
56 |
84 |
115 |
145 |
176 |
206 |
237 |
268 |
298 |
329 |
359 |
| 26 |
26 |
57 |
85 |
116 |
146 |
177 |
207 |
238 |
269 |
299 |
330 |
360 |
| 27 |
27 |
58 |
86 |
117 |
147 |
178 |
208 |
239 |
270 |
300 |
331 |
361 |
| 28 |
28 |
59 |
87 |
118 |
148 |
179 |
209 |
240 |
271 |
301 |
332 |
362 |
| 29 |
29 |
– |
88 |
119 |
149 |
180 |
210 |
241 |
272 |
302 |
333 |
363 |
| 30 |
30 |
– |
89 |
120 |
150 |
181 |
211 |
242 |
273 |
303 |
334 |
364 |
| 31 |
31 |
– |
90 |
– |
151 |
– |
212 |
243 |
– |
304 |
– |
365 |
Приложение 2
Порядковые номера дней в високосном году (366 дней)
| День месяца |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
| 1 |
1 |
32 |
61 |
92 |
122 |
153 |
183 |
214 |
245 |
275 |
306 |
336 |
| 2 |
2 |
33 |
62 |
93 |
123 |
154 |
184 |
215 |
246 |
276 |
307 |
337 |
| 3 |
3 |
34 |
63 |
94 |
124 |
155 |
185 |
216 |
247 |
277 |
308 |
338 |
| 4 |
4 |
35 |
63 |
95 |
125 |
156 |
186 |
217 |
248 |
278 |
309 |
339 |
| 5 |
5 |
36 |
65 |
96 |
126 |
157 |
187 |
218 |
249 |
279 |
310 |
340 |
| 6 |
6 |
37 |
66 |
97 |
127 |
158 |
188 |
219 |
250 |
280 |
311 |
341 |
| 7 |
7 |
38 |
67 |
98 |
128 |
159 |
189 |
220 |
251 |
281 |
312 |
342 |
| 8 |
8 |
39 |
68 |
99 |
129 |
160 |
190 |
221 |
252 |
282 |
313 |
343 |
| 9 |
9 |
40 |
69 |
100 |
130 |
161 |
191 |
222 |
253 |
283 |
314 |
344 |
| 10 |
10 |
41 |
70 |
101 |
131 |
162 |
192 |
223 |
254 |
284 |
315 |
345 |
| 11 |
11 |
42 |
71 |
102 |
132 |
163 |
193 |
224 |
255 |
285 |
316 |
346 |
| 12 |
12 |
43 |
72 |
103 |
133 |
164 |
194 |
225 |
256 |
286 |
317 |
347 |
| 13 |
13 |
44 |
73 |
104 |
134 |
165 |
195 |
226 |
257 |
287 |
318 |
348 |
| 14 |
14 |
45 |
74 |
105 |
135 |
166 |
196 |
227 |
258 |
288 |
319 |
349 |
| 15 |
15 |
46 |
75 |
106 |
136 |
167 |
197 |
228 |
259 |
289 |
320 |
350 |
| 16 |
16 |
47 |
76 |
107 |
137 |
168 |
198 |
229 |
260 |
290 |
321 |
351 |
| 17 |
17 |
48 |
77 |
108 |
138 |
169 |
209 |
230 |
261 |
291 |
322 |
352 |
| 18 |
18 |
49 |
78 |
109 |
139 |
170 |
200 |
231 |
262 |
292 |
323 |
353 |
| 19 |
19 |
50 |
79 |
110 |
140 |
171 |
201 |
232 |
263 |
293 |
324 |
354 |
| 20 |
20 |
51 |
80 |
111 |
141 |
172 |
202 |
233 |
264 |
294 |
325 |
355 |
| 21 |
21 |
52 |
81 |
112 |
142 |
173 |
203 |
234 |
265 |
295 |
326 |
356 |
| 22 |
22 |
53 |
82 |
113 |
143 |
174 |
204 |
235 |
266 |
296 |
327 |
357 |
| 23 |
23 |
54 |
83 |
114 |
144 |
175 |
205 |
236 |
267 |
297 |
328 |
358 |
| 24 |
24 |
55 |
84 |
115 |
145 |
176 |
206 |
237 |
268 |
298 |
329 |
359 |
| 25 |
25 |
56 |
85 |
116 |
146 |
177 |
207 |
238 |
269 |
299 |
330 |
360 |
| 26 |
26 |
57 |
86 |
117 |
147 |
178 |
208 |
239 |
270 |
300 |
331 |
361 |
| 27 |
27 |
58 |
87 |
118 |
148 |
179 |
209 |
240 |
271 |
301 |
332 |
362 |
| 28 |
28 |
59 |
88 |
119 |
149 |
180 |
210 |
241 |
272 |
302 |
333 |
363 |
| 29 |
29 |
60 |
89 |
120 |
150 |
181 |
211 |
242 |
273 |
303 |
334 |
364 |
| 30 |
30 |
– |
90 |
121 |
151 |
182 |
212 |
243 |
274 |
304 |
335 |
365 |
| 31 |
31 |
– |
91 |
– |
152 |
– |
213 |
244 |
– |
305 |
– |
366 |
Приложение 3
Множитель наращения FM1(r,n) = 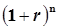
Число
периодов
|
Процентная ставка |
| 9% |
10 % |
11 % |
12 % |
13 % |
14 % |
15 % |
16 % |
| 1 |
1.0900 |
1.1000 |
1.1100 |
1.1200 |
1.1300 |
1.1400 |
1.1500 |
1.1600 |
| 2 |
1,1881 |
1.2100 |
1.2321 |
1.2544 |
1.2769 |
1.2996 |
1.3225 |
1.3456 |
| 3 |
1.2950 |
1.3310 |
1.3676 |
1.4049 |
1.4429 |
1.4815 |
1.5209 |
15609 |
| 4 |
1.4116 |
1.4641 |
1.5181 |
1.5735 |
1.6305 |
1.6890 |
1.7490 |
1.8106 |
| 5 |
1.5386 |
1.6105 |
1.6851 |
1.7623 |
1.8424 |
1.9254 |
2.0114 |
2.1003 |
| 6 |
1.6771 |
1.7716 |
1.8704 |
1.9738 |
2.0820 |
2.1950 |
2.3131 |
2.4364 |
| 7 |
1.8280 |
1.9487 |
2.0762 |
2.2107 |
2.3526 |
2.5023 |
2.6600 |
2.8262 |
| 8 |
1.9926 |
2.1436 |
2.3045 |
14760 |
2.6584 |
2.8526 |
3.0590 |
3.2784 |
| 9 |
2.1719 |
2.3579 |
2.5580 |
2.7731 |
3.0040 |
3.2519 |
3.5179 |
3.8030 |
| 10 |
2.3674 |
2.5937 |
2.8394 |
3.1058 |
3.3946 |
3.7072 |
4.0456 |
4.4114 |
| 11 |
2.5804 |
2.8531 |
3.1518 |
3.4785 |
3.8359 |
4.2262 |
4.6524 |
5.1173 |
| 12 |
2.8127 |
3.1384 |
3.4985 |
3.8960 |
4.3345 |
4.8179 |
5.3503 |
5.9360 |
| 13 |
3.0658 |
3.4523 |
3.8833 |
4.3635 |
4.8980 |
5.4924 |
6.1528 |
6.8858 |
| 14 |
3.3417 |
3.7975 |
4.3104 |
4.8871 |
5.5348 |
6.2613 |
7.0757 |
7.9875 |
| 15 |
3.6425 |
4.1772 |
4.7846 |
5.4736 |
6.2543 |
7.1379 |
8.1371 |
9.2655 |
| 16 |
3.9703 |
4.5950 |
5.3109 |
6.1304 |
7.0673 |
8.1372 |
9.3576 |
10.7480 |
| 17 |
4.3276 |
5.0545 |
5.8951 |
6.8660 |
7.9861 |
9.2765 |
10.7613 |
12.4677 |
| 18 |
4.7171 |
5.5599 |
6.5436 |
7.6900 |
9.0243 |
10.5752 |
12.3755 |
14.4625 |
| 19 |
5.1417 |
6.1159 |
7.2633 |
8.6128 |
10.1974 |
12.0557 |
14.2318 |
16.7765 |
| 20 |
5.6044 |
6.7275 |
8.0623 |
9.6463 |
11.5231 |
13.7435 |
16.3665 |
19.4608 |
| 21 |
6.1088 |
7.4002 |
8.9492 |
10.8038 |
13.0211 |
15.6676 |
18.8215 |
22.5745 |
| 22 |
6.6586 |
8.1403 |
9.9336 |
12.1003 |
14.7138 |
17.8610 |
21.6447 |
26.1864 |
| 23 |
7.2579 |
8.9543 |
11.0263 |
13.5523 |
16.6266 |
20.3616 |
24.8915 |
30.3762 |
| 24 |
7.9111 |
9.8497 |
12.2392 |
15.1786 |
18.7881 |
23.2122 |
28.6252 |
35.2364 |
| 25 |
8.6231 |
10.8347 |
13.5855 |
17.0001 |
21.2305 |
26.4619 |
32.9190 |
40.8742 |
| 26 |
9.3992 |
11.9182 |
15.0799 |
19.0401 |
23.9905 |
30.1666 |
37.8568 |
47.4141 |
| 27 |
10.2451 |
13.1100 |
16.7386 |
21.3249 |
27.1093 |
34.3899 |
43.5353 |
55.0004 |
| 28 |
11.1671 |
14.4210 |
18.5799 |
23.8839 |
30.6335 |
39.2045 |
50.0656 |
63.8004 |
| 29 |
12.1722 |
15.8631 |
20.6237 |
26.7499 |
34.6158 |
44.6931 |
57.5755 |
74.0085 |
| 30 |
13.2677 |
17.4494 |
22.8923 |
29.9599 |
39.1159 |
50.9502 |
66.2118 |
85.8499 |
| 31 |
14.4618 |
19.1943 |
25.4104 |
33.5551 |
44.2010 |
58.0832 |
76.1435 |
99.5859 |
| 32 |
15.7633 |
21.1138 |
28.2056 |
37.5817 |
49.9471 |
66.2148 |
87.5651 |
115.5196 |
| 33 |
17.1820 |
23.2252 |
31.3082 |
42.0915 |
56.4402 |
75.4849 |
100.6998 |
134.0027 |
| 34 |
18.7284 |
25.5477 |
34.7521 |
47.1425 |
63.7774 |
86.0528 |
115.8048 |
155.4432 |
| 35 |
20.4140 |
28.1024 |
38.5749 |
52.7996 |
72.0685 |
98.1002 |
133.1755 |
180.3141 |
| 36 |
22.2512 |
30.9127 |
42.8181 |
59.1356 |
81.4374 |
111.8342 |
153.1519 |
209.1643 |
| 37 |
24.2538 |
34.0039 |
47.5281 |
66.2318 |
92.0243 |
127.4910 |
176.1246 |
242.6306 |
| 38 |
26.4367 |
37.4043 |
52.7562 |
74.1797 |
103.9874 |
145.3397 |
202.5433 |
281.4515 |
| 39 |
28.8160 |
41.1448 |
58.5593 |
83.0812 |
117.5058 |
165.6873 |
232.9248 |
326.4838 |
| 40 |
31.4094 |
45.2593 |
65.0009 |
93.0510 |
132.7816 |
188.8835 |
267.8635 |
378.7212 |
| 41 |
34.2363 |
49.7852 |
72.1510 |
104.2171 |
150.0432 |
215.3272 |
308.0431 |
439.3165 |
| 42 |
37.Я75 |
54.7637 |
80.0876 |
116.7231 |
169.5488 |
245.4730 |
354.2495 |
509.6072 |
| 43 |
40.6761 |
60.2401 |
88.8972 |
130.7299 |
191.5901 |
279.8392 |
407.3870 |
591.1443 |
| 44 |
44.3370 |
66.2641 |
98.6759 |
146.4175 |
216.4968 |
319.0167 |
468.4950 |
685.7274 |
| 45 |
48.3273 |
72.8905 |
109.5302 |
163.9876 |
244.6414 |
363.6791 |
538.7693 |
795.4438 |
| 46 |
52.6767 |
80.1795 |
121.5786 |
183.6661 |
276.4448 |
414.5941 |
619.5847 |
922.7148 |
| 47 |
57.4176 |
88.1975 |
134.9522 |
205.7061 |
312.3826 |
472.6373 |
712.5224 |
1070.3492 |
| 48 |
62.5852 |
97.0172 |
149.7970 |
230.3908 |
352.9923 |
538.8065 |
819.4007 |
1241.6051 |
| 49 |
68.2179 |
106.7190 |
166.2746 |
258.0377 |
398.8813 |
614.2395 |
942.3108 |
1440.2619 |
| 50 |
74.3575 |
117.3909 |
184.5648 |
289.0022 |
450.7359 |
700.2330 |
1083.6574 |
1670.7038 |
Продолжение прил. 3
Множитель наращения FM1(r,n) = 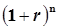
Число
периодов
|
Процентная ставка |
| 17 % |
18 % |
19 % |
20 % |
21 % |
22 % |
| 1 |
1.1700 |
1.1800 |
1.1900 |
1.2000 |
1.2100 |
12200 |
| 2 |
1.3689 |
1.3924 |
1.4161 |
1.4400 |
1.4641 |
14884 |
| 3 |
1.6016 |
1.6430 |
1.6852 |
1.7280 |
1.7716 |
18158 |
| 4 |
1.8739 |
1.9388 |
2.0053 |
2.0736 |
2.1436 |
2.2153 |
| 5 |
2.1924 |
2.2878 |
2.3864 |
2.4883 |
2.5937 |
2.7027 |
| 6 |
2.5652 |
2.6996 |
2.8398 |
2.9860 |
3.1384 |
3.2973 |
| 7 |
3.0012 |
3.1855 |
3.3793 |
3.5832 |
3.7975 |
4.0227 |
| 8 |
3.5115 |
3.7589 |
4.0214 |
4.2998 |
4.5950 |
4.9077 |
| 9 |
4.1084 |
4.4355 |
4.7854 |
5.1598 |
5.5599 |
5.9874 |
| 10 |
4.8068 |
5.2338 |
5.6947 |
6.1917 |
6.7275 |
7.3046 |
| 11 |
5.6240 |
6.1759 |
6.7767 |
7.4301 |
8.1403 |
8.9117 |
| 12 |
6.5801 |
7.2876 |
8.0642 |
8.9161 |
9.8497 |
10.8722 |
| 13 |
7.6987 |
8.5994 |
9.5964 |
10.6993 |
11.9182 |
13.2641 |
| 14 |
9.0075 |
10.1472 |
11.4198 |
12.8392 |
14.4210 |
16.1822 |
| 15 |
10.5387 |
11.9737 |
13.5895 |
15.4070 |
17.4494 |
19.7423 |
| 16 |
12.3303 |
14.1290 |
16.1715 |
18.4884 |
21.1138 |
24.0856 |
| 17 |
14.4265 |
16.6722 |
19.2441 |
22.1861 |
25.5477 |
29.3844 |
| 18 |
16.8790 |
19.6733 |
22.9005 |
26.6233 |
30.9127 |
35.8490 |
| 19 |
19.7484 |
23.2144 |
27.2516 |
31.9480 |
37.4043 |
43.7358 |
| 20 |
23.1056 |
27.3930 |
32.4294 |
38.3376 |
45.2593 |
53.3576 |
| 21 |
27.0336 |
32.3238 |
38.5910 |
46.0051 |
54.7637 |
65.0963 |
| 22 |
31.6293 |
38.1421 |
45.9233 |
55.2061 |
66.2641 |
79.4175 |
| 23 |
37.0062 |
45.0076 |
54.6487 |
66.2474 |
80.1795 |
96.8894 |
| 24 |
43.2973 |
53.1090 |
65.0320 |
79.4968 |
97.0172 |
118.2050 |
| 25 |
50.6578 |
62.6686 |
77.3881 |
95.3962 |
117.3909 |
144.2101 |
| 26 |
59.2697 |
73.9490 |
92.0918 |
114.4755 |
142.0429 |
175.9364 |
| 27 |
69.3455 |
87.2598 |
109.5893 |
137.3706 |
171.8719 |
214.6424 |
| 28 |
81.1342 |
102.9666 |
130.4112 |
164.8447 |
207.9651 |
261.8637 |
| 29 |
94.9271 |
121.5005 |
155.1893 |
197.8136 |
251.6377 |
319.4737 |
| 30 |
111.0647 |
143.3706 |
184.6753 |
237.3763 |
304.4816 |
389.7579 |
| 31 |
129.9456 |
169.1774 |
219.7636 |
284.8516 |
368.4228 |
475.5046 |
| 32 |
152.0364 |
199.6293 |
261.5187 |
341.8219 |
445.7916 |
580.1156 |
| 33 |
177.8826 |
235.5625 |
311.2073 |
410.1863 |
539.4078 |
707.7411 |
| 34 |
208.1226 |
277.9638 |
370.3366 |
492.2235 |
652.6834 |
863.4441 |
| 35 |
243.5035 |
327.9973 |
440.7006 |
590.6682 |
789.7470 |
1053.4018 |
| 36 |
284.8991 |
387.0368 |
524.4337 |
708.8019 |
955.5938 |
1285.1502 |
| 37 |
333.3319 |
456.7034 |
624.0761 |
850.5623 |
1156.2685 |
1567.8833 |
| 38 |
389.9983 |
538.9100 |
742.6506 |
1020.6747 |
1399.0849 |
1912.8176 |
| 39 |
456.2980 |
635.9139 |
883.7542 |
1224.8096 |
1692.8927 |
2333.6375 |
| 40 |
533.8687 |
750.3783 |
1051.6675 |
1469.7716 |
2048.4002 |
2847.0378 |
| 41 |
624.6264 |
885.4464 |
1251.4843 |
1763.7259 |
2478.5643 |
3473.3861 |
| 42 |
730.8129 |
1044.8268 |
1489.2664 |
2116.4711 |
2999.0628 |
4237.5310 |
| 43 |
855.0511 |
1232.8956 |
1772.2270 |
2539.7653 |
3628.8659 |
5169.7878 |
| 44 |
1000.4098 |
1454.8168 |
2108.9501 |
3047.7183 |
4390.9278 |
6307.1411 |
| 45 |
1170.4794 |
1716.6839 |
2509.6506 |
3657.2620 |
5313.0226 |
7694.7122 |
| 46 |
1369.4609 |
2025.6870 |
2986.4842 |
4388.7144 |
6428.7574 |
9387.5489 |
| 47 |
1602.2693 |
2390.3106 |
3553.9162 |
5266.4573 |
7778.7964 |
11452.8096 |
| 48 |
1874.6550 |
2820.5665 |
4229.1603 |
6319.7487 |
9412.3437 |
13972.4277 |
| 49 |
2193.3464 |
3328.2685 |
5032.7008 |
7583.6985 |
11388.9358 |
17046.3618 |
| 50 |
2566.2153 |
3927.3569 |
5988.9139 |
9100.4382 |
13780.6123 |
20796.5615 |
Окончание прил. 3
Множитель наращения FM1(r,n) = 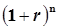
| Число периодов |
Процентная ставка |
| 23 % |
24 % |
25 % |
30 % |
40 % |
| 1 |
1.2300 |
1.2400 |
1.2500 |
1.3000 |
1.4000 |
| 2 |
1.5129 |
1.5376 |
1.5625 |
1.6900 |
1.9600 |
| 3 |
1.8609 |
1.9066 |
1.9531 |
2.1970 |
2.7440 |
| 4 |
2.2889 |
2.3642 |
2.4414 |
2.8561 |
3.8416 |
| 5 |
2.8153 |
2.9316 |
3.0518 |
3.7129 |
5.3782 |
| 6 |
3.4628 |
3.6352 |
3.8147 |
4.8268 |
7.5295 |
| 7 |
4.2593 |
4.5077 |
4.7684 |
6.2749 |
10.5414 |
| 8 |
5.2389 |
5.5895 |
5.9605 |
8.1573 |
14.7579 |
| 9 |
6.4439 |
6.9310 |
7.4506 |
10.6045 |
20.6610 |
| 10 |
7.9259 |
8.5944 |
9.3132 |
13.7858 |
28.9255 |
| 11 |
9.7489 |
10.6571 |
11.6415 |
17.9216 |
40.4957 |
| 12 |
11.9912 |
13.2148 |
14.5519 |
23.2981 |
56.6939 |
| 13 |
14.7491 |
16.3863 |
18.1899 |
30.2875 |
79.3715 |
| 14 |
18.1414 |
20.3191 |
22.7374 |
39.3738 |
111.1201 |
| 15 |
22.3140 |
25.1956 |
28.4217 |
51.1859 |
155.5681 |
| 16 |
27.4462 |
31.2426 |
35.5271 |
66.5417 |
217.7953 |
| 17 |
33.7588 |
38.7408 |
44.4089 |
86.5042 |
304.9135 |
| 18 |
41.5233 |
48.0386 |
55.5112 |
112.4554 |
426.8789 |
| 19 |
51.0737 |
59.5679 |
69.3889 |
146.1920 |
597.6304 |
| 20 |
62.8206 |
73.8641 |
86.7362 |
190.0496 |
836.6826 |
| 21 |
77.2694 |
91.5915 |
108.4202 |
247.0645 |
11713556 |
| 22 |
95.0413 |
113.5735 |
135.5253 |
321.1839 |
1639.8978 |
| 23 |
116.9008 |
140.8312 |
169.4066 |
417.5391 |
2295.8569 |
| 24 |
143.7880 |
174.6306 |
211.7582 |
542.8008 |
3214.1997 |
| 25 |
176.8593 |
216.5420 |
264.6978 |
705.6410 |
4499.8796 |
| 26 |
217.5369 |
268.5121 |
330.8722 |
917.3333 |
6299.8314 |
| 27 |
267.5704 |
332.9550 |
413.5903 |
1192.5333 |
8819.7640 |
| 28 |
329.1115 |
412.8642 |
516.9879 |
1550.2933 |
12347.6696 |
| 29 |
404.8072 |
511.9516 |
646.2349 |
2015.3813 |
17286.7374 |
| 30 |
497.9129 |
634.8199 |
807.7936 |
2619.9956 |
24201.4324 |
| 31 |
612.4328 |
787.1767 |
1009.7420 |
3405.9943 |
33882.0053 |
| 32 |
753.2924 |
976.0991 |
1262.1774 |
4427.7926 |
47434.8074 |
| 33 |
926.5496 |
1210.3629 |
1577.7218 |
5756.1304 |
66408.7304 |
| 34 |
1139.6560 |
1500.8500 |
1972.1523 |
7482.9696 |
92972.2225 |
| 35 |
1401.7769 |
1861.0540 |
2465.1903 |
9727.8604 |
130161.1116 |
| 36 |
1724.1856 |
2307.7070 |
3081.4879 |
12646.2186 |
182225.5562 |
| 37 |
2120.7483 |
2861.5567 |
3851.8599 |
16440.0841 |
2S5115.7786 |
| 38 |
2608.5204 |
3548.3303 |
4814.8249 |
21372.1094 |
357162.0901 |
| 39 |
3208.4801 |
4399.9295 |
6018.5311 |
27783.7422 |
500026.9261 |
| 40 |
3946.4305 |
5455.9126 |
7523.1638 |
36118.8648 |
700037.6966 |
| 41 |
4854.1095 |
6765.3317 |
9403.9548 |
46954.5243 |
980052.7752 |
| 42 |
5970.5547 |
8389.0113 |
11754.9435 |
61040.8815 |
1372073.8853 |
| 43 |
7343.7823 |
10402.3740 |
14693.6794 |
79353.1460 |
1920903.4394 |
| 44 |
9032.8522 |
12898.9437 |
18367.0992 |
103159.0898 |
2689264.8152 |
| 45 |
11110.4082 |
15994.6902 |
22958.8740 |
134106.8167 |
3764970.7413 |
| 46 |
13665.8021 |
19833.4158 |
28698.5925 |
174338.8617 |
5270959.0378 |
| 47 |
16808.9365 |
24593.4356 |
35873.2407 |
226640.5203 |
7379342.6529 |
| 48 |
20674.9919 |
30495.8602 |
44841.5509 |
294632.6763 |
10331079.7140 |
| 49 |
25430.2401 |
37814.8666 |
56051.9386 |
383022.4792 |
14463511.6000 |
| 50 |
31279.1953 |
46890.4346 |
70064.9232 |
497929.2230 |
20248916.2390 |
Приложение 4
Кредитный договор
г. _________ «_____»____________200...г.
Коммерческий банк «____________________» (далее именуемиый – Банк) в лице ______________________________, действующего на основании Устава, с одной стороны, и ______________________________ с другой стороны (далее именуемый – Клиент) в лице ______________________________ действующего на основании _______________________ с другой стороны, заключили настоящий договор о нижеследующем.
1. Предмет договора
1. Банк предоставляет Клиенту краткосрочный кредит в сумме __________________________________________________________________
(сумма прописью)
2. Объектами кредитования являются ____________________________
3. Цель кредитования состоит в финансировании затрат Клиента, указанных в п. 2 настоящего договора.
4. Для учета полученного Клиентом кредита Банк открывает ему ссудный счет №____
5. Клиент обязуется принять сумму, указанную в п.1 настоящего договора. Клиент не имеет права передавать третьим лицам свое право на получение кредита, возникшее после подписания настоящего договора, без письменного согласия Банка, включая передачу его в залог или по договору об уступке права требования (цессии).
6. В процессе пользования кредитом Клиент обязуется соблюдать принципы кредитования:__________________________________
2. Срок договора
7. Срок действия договора составляет с ________ по _______
8. Банк обязуется предоставить кредит в следующие сроки:
| Сумма (прописью цифрами) |
Дата выдачи кредита |
9.Клиент обязуется возвратить полученный кредит в следующие сроки:
| Сумма (прописью цифрами) |
Дата возврата кредита |
3. Цель договора
10. Клиент обязуется уплатить Банку следующее вознаграждение за пользованием кредитом:
10.1. В пределах срока пользования кредитом (до наступления обусловленного настоящим договором срока погашения кредита) – _______ % годовых.
10.2. При нарушении срока возврата кредита – ________% годовых за весь период просрочки от обусловленного настоящим договором срока погашения кредита до его фактического возврата.
11. Проценты за пользование кредитом начисляются Банком, который предоставляет Клиенту соответствующий расчет.
12. Банк имеет право в одностороннем порядке повысить размер процентов за пользование кредитом (включая повышенные) в случае увеличения процентной ставки Центрального Банка РФ за пользование централизованными кредитными ресурсами (учетная ставка ЦБ РФ) – пропорционально этому увеличению.
4. Порядок расчетов
13. Банк предоставляет Клиенту кредит на условиях, предусмотренных настоящим договором. Путем перечисления соответствующей суммы на расчетный счет Клиента в сроки. Указанные в п. 8 настоящего договора.
14. Клиент обязуется погасить выданный ему кредит в сроки, указанные в п. 9 настоящего договора, с помощью ______________ платежных поручений, наличный расчет).
15. Клиент выплачивает Банку обусловленные настоящим договором проценты за пользование кредитом платежным поручением на основании расчета Банка ежеквартально не позднее 15 числа первого месяца квартала. Следующего за расчетным. При просрочке уплаты процентов свыше десяти дней Банк вправе списать причитающиеся ему суммы в безакцептном порядке.
16. В случае образования просроченной задолженности по возврату полученного Клиентом кредита и процентам за пользование им (включая повышенные) суммы, выплачиваемые Клиентом в погашение указанной задолженности. Направляются вначале на погашение долга по процентам. А затем засчитываются в счет возврата предоставленного кредита.
5. Контроль Банка
17. В процессе кредитования Банк имеет право проверять финансово-хозяйственное положение Клиента, целевое использование кредита и его обеспеченность.
18. Для реализации контрольных прав Банка, указанных в п. 18 настоящего договора, Клиент обязуется предоставить Банку следующие документы: __________________________
19. Клиент также обязуется предоставлять по требованию Банка другие документы, отвечать на вопросы работников Банка, предоставлять справки и совершать другие действия, необходимые для выяснения Банком обстоятельств, указанных в п. 18 настоящего договора.
20. Клиент обязуется допускать работников Банка в служебные, производственные, складские помещения для проведения целевых проверок.
6. Обеспечение кредита
21. Кредит, предоставленный по настоящему договору, обеспечивается ___________________________________ (залогом, поручительством и гарантией)
22. Документ, устанавливающий обеспечение, является Приложением к настоящему договору и предоставляется Клиентом Банку не позднее одной недели с момента подписания настоящего договора.
7. Ответственность сторон
23. В случае ухудшения финансово-хозяйственного положения Клиента. использования кредита не по целевому назначению, уклонения от банковского контроля, несвоевременного возврата ранее полученного кредита, а также в случаях, если выданный кредит окажется по различным причинам необеспеченным, Банк имеет право приостанавливать дальнейшую выдачу кредита и/или досрочно взыскать выданную сумму, в том числе путем обращения взыскания на обеспечение.
24. В случае нарушения обязательств, предусмотренного п. 22 Банк имеет право отказать в выдаче кредита.
25. За нарушение срока возврата полученного кредита Клиент уплачивает банку пеню в размере __% от несвоевременно уплаченной суммы за каждый календарный день просрочки.
8. Юридические адреса и подписи сторон
Приложение 5
Договор об ипотеке №______
г._________________ «______»________________г.
____________________________________, именуемый в дальнейшем «Залогодатель», в лице __________________________, действующего на основании _____________, с одной стороны и ______________________________________________________________, именуем в дальнейшем «Залогодержатель», в лице _________________________________________, действующего на основании ____________________, с другой стороны, а вместе именуемые «Стороны», заключили настоящий договор о нижеследующем:
1. Обязательство, обеспеченное ипотекой
1.1. Настоящий договор заключен с целью обеспечения исполнения обязательств Залогодателя перед Залогодержателем по договору_____________ (долевого инвестирования строительства, купли-продажи, аренды, подряда и пр.) №___, заключенному Сторонами «____»______________г. в г.________________(далее основной договор).
1.2. По основному договору Залогодатель выступает______________ (Застройщиком, Заказчиком и пр., Должником), а Залогодержатель _____________________ (Инвестором, Подрядчиком и пр., Кредитором).
Кредитор в соответствии с основным договором принимает на себя обязательства _________________________________________________(суть обязательства) на условиях, предусмотренных основным договором, а Должник обязуется _____________________________________________(суть обязательства).
1.3. В соответствии с основным договором срок исполнения Должником своих обязательств наступает «_____»__________________________г.
1.4. В силу п.___ основного договора в случае нарушения Должником сроков исполнения обязательств он выплачивает Кредитору неустойку (штраф) в рублях в размере ___________________________ руб. 00 коп. В случае если просрочка составляет более ________________, Кредитор вправе отказаться от исполнения обязательств по основному договору в одностороннем порядке, предварительно письменно уведомив об этом Должника за _______дней.
При наступлении обязательств, указанных в настоящем пункте, Должник возвращает Кредитору денежные средства в размере _____________________________ в течение _______________ дней с момента получения уведомления о расторжении договора.
1.5. Основной договор вступил в силу с момента его подписания сторонами «____»_________________г. и действует до момента ___________________ или расторжения договора в случае одностороннего отказа Кредитора от исполнения договора в соответствии с п._______ основного договора.
1.6. Залогодержатель имеет право получить удовлетворение своих денежных требований к Залогодателю, вытекающих из основного договора, из стоимости заложенного по настоящему договору имущества Залогодателя преимущественно перед другими кредиторами Залогодателя.
2. Требования, обеспеченные ипотекой
2.1. Ипотека, установленная в соответствии с настоящим договором, обеспечивает уплату Залогодержателю следующих сумм, причитающихся ему в случае нарушения Залогодателем своих обязательств по основному договору:
– в уплату основной суммы долга полностью;
– в счет оплаты неустойки (штрафа) при ненадлежащем исполнении Залогодателем своих обязательств по основному договору;
– в виде процентов за пользование чужими денежными средствами в соответствии со ст. 395 Гражданского Кодекса РФ;
– в возмещение судебных издержек и иных расходов, вызванных обращением взыскания на заложенное имущество;
-в возмещение расходов по реализации заложенного имущества.
2.2. Настоящим договором обеспечиваются требования Залогодержателя в том объеме, какой они будут иметь к моменту их удовлетворения за счет заложенного имущества.
3. Предмет ипотеки
3.1. В обеспечение исполнения своих обязательств по основному договору Залогодатель заложил Залогодержателю следующее недвижимое имущество:
3.1.1. _____________________________общей площадью______ кв.м., расположенной по адресу:_____ _____________________________________(далее «имущество»).
3.2 Указанное в пп. 3.1.1 договора имущество принадлежит Залогодателю на праве собственности, что подтверждается Свидетельством о государственной регистрации права собственности от «____»___________________________ г. серии №______, выданным _________________________(запись в ЕГРП №_____________).
4. Оценка предмета ипотеки
4.1. Балансовая стоимость имущества, указанного в пп. 3.1.1 договора, оценивается в размере____________________________________________________.
5. Права и обязанности залогодателя
5.1. Залогодатель вправе:
5.1.1. Владеть и пользоваться заложенным имуществом в соответствии с его назначением.
5.2. Залогодатель обязан:
5.2.1. Нести расходы по содержанию заложенного имущества.
5.2.2. Обеспечивать сохранность заложенного имущества, в том числе для защиты его от посягательств третьих лиц, огня, стихийных бедствий.
5.2.3. В случае реальной угрозы, утраты или повреждения заложенного имущества уведомить об этом Залогодержателя.
5.2.4. Не совершать действий, влекущих уменьшение стоимости заложенного имущества.
5.2.5. Не препятствовать Залогодержателю производить осмотр заложенного имущества в период действия настоящего договора.
5.2.6. Гарантировать Залогодержателю, что передаваемое ему в залог имущество не будет перезаложено до момента исполнения обеспеченного залогом обязательства в полном объеме.
5.2.7. Немедленно сообщать Залогодержателю сведения об изменениях, происшедших с предметом залога, о посягательствах третьих лиц на предмет залога.
5.2.8. Не отчуждать заложенное имущество третьим лицам без письменного согласия Залогодержателя.
5.3. Залогодатель несет риск случайной гибели и случайного повреждения имущества, заложенного по настоящему договору.
6. Права залогодержателя
6.1. Залогодержатель вправе:
6.1.1. Проверять по документам и фактически наличие, состояние и условия содержания заложенного по настоящему договору имущества.
6.1.2. Требовать от залогодателя принятия мер, необходимых для сохранения заложенного имущества.
6.1.3. Требовать досрочного исполнения обеспеченного ипотекой обязательства, если заложенное имущество утрачено или повреждено настолько, что вследствие этого обеспечение ипотекой обязательства существенно ухудшилось.
7. Гарантии прав залогодержателя
7.1. Залогодатель гарантирует, что до момента государственной регистрации настоящего договора указанное в п. 3.1 имущество никому не заложено, не продано, не сдано в аренду, не обременено сервитутами, в споре и под запрещением (арестом) не состоит, свободно от любых прав третьих лиц.
8. Страхование заложенного имущества
8.1. Залогодатель обязан застраховать за свой счет указанное в п. 1.1 настоящего договора имущество в полной его стоимости от рисков утраты и повреждения.
8.2. Выбор страховой компании осуществляется Залогодателем самостоятельно.
8.3. Нотариально заверенная копия заключенного договора страхования и копия правил страхования предоставляются Залогодержателю.
8.4. Залогодержатель имеет право на удовлетворение своего требования по обязательству, обеспеченному ипотекой, непосредственно из страхового возмещения за утрату или повреждение заложенного имущества независимого от того, в чью пользу оно застраховано, и преимущественно перед требованиями других кредиторов Залогодателя и лиц, в чью пользу осуществлено страхование, за изъятиями, установленными федеральным законом.
9. Обращение взыскания на предмет ипотеки
9.1 Залогодержатель приобретает право обратить взыскание на имущество, заложенное по настоящему договору, для удовлетворения за счет этого имущества указанных в п. 2.1 настоящего договора требований, вызванных неисполнением или ненадлежащим исполнением обеспеченного ипотекой обязательства.
9.2 Взыскание по требованию Залогодержателя обращает на предмет ипотеки по решению суда. Иск об обращении взыскания на имущество, заложенное по настоящему договору, предъявляется Залогодержателем в _________________ суд г.________________.
10. Государственная регистрация договора об ипотеке
10.1. Настоящий договор должен быть нотариально удостоверен.
10.2. Настоящий договор считается заключенным и вступает в силу с момента его государственной регистрации в установленном законодательством порядке в ______________________________________ (наименование регистрирующего органа).
10.3. Расходы, связанные с нотариальным удостоверением, государственной регистрации настоящего договора и вытекающих из него прав, внесением изменений и дополнений в регистрационную запись об ипотеке, оплачиваются за счет ___________________________ (Залогодателя/Залогодержателя).
10.4. Настоящий договор действует до полного исполнения Залогодателем своих обязательств по основному договору. После полного исполнения обязательств Залогодателя по основному договору стороны подают совместное заявление в ________________________ (наименование регистрирующего органа) для погашения регистрационной записи об ипотеке.
11. Разрешение споров
11.1. Все споры и разногласия, которые могут возникнуть между сторонами в результате исполнения настоящего договора, будут разрешаться путем переговоров.
11.2. В случае невозможности разрешения споров путем переговоров стороны передают их на рассмотрение в ________________суд г.__________________.
11.3. По вопросам, не урегулированными настоящим договором и дополнительными соглашениями к нему, стороны руководствуются действующим законодательством Российской Федерации.
12. Заключительные положения
12.1. Настоящий договор может быть изменен или прекращен по письменному соглашению сторон.
12.2. Любые изменения и дополнения к настоящему договору оформляются дополнительными соглашениями сторон в письменной форме, которые должны быть подписаны надлежаще уполномоченными на то представителями сторон, скреплены печатями, нотариально удостоверены и зарегистрированы в установленном законодательством РФ порядке. Такие изменения вступают в силу с момента их государственной регистрации.
12.3. Все приложения к договору, согласованные обеими сторонами, являются его неотъемлемой частью.
12.4. Настоящий договор составлен на _____страницах, в четырех экземплярах, имеющих одинаковую юридическую силу, по одному экземпляру для каждой их сторон, один экземпляр хранится в делах нотариуса ___________ по адресу: г. __________ наименование регистрирующего органа).
12.5. Последующая ипотека заложенного имущества по настоящему договору имущества запрещена.
13. Адреса и реквизиты сторон
Залогодатель: _______________________________________________
_____________________________________________________________
Залогодержатель:______________________________________________ _________________________________________________________________
ПОДПИСИ СТОРОН:
От Залогодателя___________________
От Залогодержателя________________
Приложение 6
Динамика ставки рефинансирования
Центрального Банка Российской Федерации
| Период действия |
% |
Нормативный документ |
| 23 октября 2006 г. – |
11 |
Телеграмма ЦБ РФ от 20.10.2006 № 1734-У |
| 26 июня 2006 г. – 22 октября 2006 г. |
11,5 |
Телеграмма ЦБ РФ от 23.06.2006 № 1696-У |
| 26 декабря 2005 г. – 25 июня 2006 г. |
12 |
Телеграмма ЦБ РФ от 23.12.2005 № 1643-У |
| 15 июня 2004 г. – 25 декабря 2005 г. |
13 |
Телеграмма ЦБ РФ от 11.06.2004 № 1443-У |
| 15 января 2004 г. – 14 июня 2004 г. |
14 |
Телеграмма ЦБ РФ от 14.01.2004 № 1372-У |
| 21 июня 2003 г. – 14 января 2004 г. |
16 |
Телеграмма ЦБ РФ от 20.06.2003 № 1296-У |
| 17 февраля 2003 г. – 20 июня 2003 г. |
18 |
Телеграмма ЦБ РФ от 14.02.2003 № 1250-У |
| 7 августа 2002 г. – 16 февраля 2003 г. |
21 |
Телеграмма ЦБ РФ от 06.08.2002 № 1185-У |
| 09 апреля 2002 г. – 06 августа 2002 г. |
23 |
Телеграмма ЦБ РФ от 08.04.2002 № 1133-У |
| 04 ноября 2000 г. – 08 апреля 2002 г. |
25 |
Телеграмма ЦБР от 03.11.2000 № 855-У |
| 10 июля 2000 г. – 03 ноября 2000 г. |
28 |
Телеграмма ЦБР от 07.07.2000 № 818-У |
| 21 марта 2000 г. – 09 июля 2000 г. |
33 |
Телеграмма ЦБР от 20.03.2000 № 757-У |
| 07 марта 2000 г. – 20 марта 2000 г. |
38 |
Телеграмма ЦБР от 06.03.2000 № 753-У |
| 24 января 2000 г. – 06 марта 2000 г. |
45 |
Телеграмма ЦБР от 21.01.2000 № 734-У |
| 10 июня 1999 г. – 23 января 2000 г. |
55 |
Телеграмма ЦБР от 09.06.99 № 574-У |
| 24 июля 1998 г. – 09 июня 1999 г. |
60 |
Телеграмма ЦБР от 24.07.98 № 298-У |
| 29 июня 1998 г. – 23 июля 1998 г. |
80 |
Телеграмма ЦБР от 26.06.98 № 268-У |
| 05 июня 1998 г. – 28 июня 1998 г. |
60 |
Телеграмма ЦБР от 04.06.98 № 252-У |
| 27 мая 1998 г. – 04 июня 1998 г. |
150 |
Телеграмма ЦБР от 27.05.98 № 241-У |
| 19 мая 1998 г. – 26 мая 1998 г. |
50 |
Телеграмма ЦБР от 18.05.98 № 234-У |
| 16 марта 1998 г. – 18 мая 1998 г. |
30 |
Телеграмма ЦБР от 13.03.98 № 185-У |
| 2 марта 1998 г. – 15 марта 1998 г. |
36 |
Телеграмма ЦБР от 27.02.98 № 181-У |
| 17 февраля 1998 г. – 01 марта 1998 г. |
39 |
Телеграмма ЦБР от 16.02.98 № 170-У |
| 02 февраля 1998 г. – 16 февраля 1998 г. |
42 |
Телеграмма ЦБР от 30.01.98 № 154-У |
| 11 ноября 1997 г. – 01 февраля 1998 г. |
28 |
Телеграмма ЦБР от 10.11.97 № 13-У |
| 06 октября 1997 г. – 10 ноября 1997 г. |
21 |
Телеграмма ЦБР от 01.10.97 № 83-97 |
| 16 июня 1997 г. – 05 октября 1997 г. |
24 |
Телеграмма ЦБР от 13.06.97 № 55-97 |
| 28 апреля 1997 г. – 15 июня 1997 г. |
36 |
Телеграмма ЦБР от 24.04.97 № 38-97 |
| 10 февраля 1997 г. – 27 апреля 1997 г. |
42 |
Телеграмма ЦБР от 07.02.97 № 9-97 |
| 02 декабря 1996 г. – 09 февраля 1997 г. |
48 |
Телеграмма ЦБР от 29.11.96 № 142-96 |
| 21 октября 1996 г. – 01 декабря 1996 г. |
60 |
Телеграмма ЦБР от 18.10.96 № 129-96 |
| 19 августа 1996 г. – 20 октября 1996 г. |
80 |
Телеграмма ЦБР от 16.08.96 № 109-96 |
| 24 июля 1996 г. – 18 августа 1996 г. |
110 |
Телеграмма ЦБР от 23.07.96 № 107-96 |
| 10 февраля 1996 г. – 23 июля 1996 г. |
120 |
Телеграмма ЦБР от 09.02.96 № 18-96 |
| 01 декабря 1995 г. – 09 февраля 1996 г. |
160 |
Телеграмма ЦБР от 29.11.95 № 131-95 |
| 24 октября 1995 г. – 30 ноября 1995 г. |
170 |
Телеграмма ЦБР от 23.10.95 № 111-95 |
| 19 июня 1995 г. – 23 октября 1995 г. |
180 |
Телеграмма ЦБР от 16.06.95 № 75-95 |
| 16 мая 1995 г. – 18 июня 1995 г. |
195 |
Телеграмма ЦБР от 15.05.95 № 64-95 |
| 06 января 1995 г. – 15 мая 1995 г. |
200 |
Телеграмма ЦБР от 05.01.95 № 3-95 |
| 17 ноября 1994 г. – 05 января 1995 г. |
180 |
Телеграмма ЦБР от 16.11.94 № 199-94 |
| 12 октября 1994 г. – 16 ноября 1994 г. |
170 |
Телеграмма ЦБР от 11.10.94 № 192-94 |
| 23 августа 1994 г. – 11 октября 1994 г. |
130 |
Телеграмма ЦБР от 22.08.94 № 165-94 |
| 01 августа 1994 г. – 22 августа 1994 г. |
150 |
Телеграмма ЦБР от 29.07.94 № 156-94 |
| 30 июня 1994 г. – 31 июля 1994 г. |
155 |
Телеграмма ЦБР от 29.06.94 № 144-94 |
| 22 июня 1994 г. – 29 июня 1994 г. |
170 |
Телеграмма ЦБР от 21.06.94 № 137-94 |
| 02 июня 1994 г. – 21 июня 1994 г. |
185 |
Телеграмма ЦБР от 01.06.94 № 128-94 |
| 17 мая 1994 г. – 01 июня 1994 г. |
200 |
Телеграмма ЦБР от 16.05.94 № 121-94 |
| 29 апреля 1994 г. – 16 мая 1994 г. |
205 |
Телеграмма ЦБР от 28.04.94 № 115-94 |
| 15 октября 1993 г. – 28 апреля 1994 г. |
210 |
Телеграмма ЦБР от 14.10.93 № 213-93 |
| 23 сентября 1993 г. – 14 октября 1993 г. |
180 |
Телеграмма ЦБР от 22.09.93 № 200-93 |
| 15 июля 1993 г. – 22 сентября 1993 г. |
170 |
Телеграмма ЦБР от 14.07.93 № 123-93 |
| 29 июня 1993 г. – 14 июля 1993 г. |
140 |
Телеграмма ЦБР от 28.06.93 № 111-93 |
| 22 июня 1993 г. – 28 июня 1993 г. |
120 |
Телеграмма ЦБР от 21.06.93 № 106-93 |
| 02 июня 1993 г. – 21 июня 1993 г. |
110 |
Телеграмма ЦБР от 01.06.93 № 91-93 |
| 30 марта 1993 г. – 01 июня 1993 г. |
100 |
Телеграмма ЦБР от 29.03.93 № 52-93 |
| 23 мая 1992 г. – 29 марта 1993 г. |
80 |
Телеграмма ЦБР от 22.05.92 № 01-156 |
| 10 апреля 1992 г. – 22 мая 1992 г. |
50 |
Телеграмма ЦБР от 10.04.92 № 84-92 |
| 01 января 1992 г. – 09 апреля 1992 г. |
20 |
Телеграмма ЦБР от 29.12.91 № 216-91 |
Приложение 7
Курсы иностранных валют к рублю РФ, установленные Центральным Банком Российской Федерации на 01.12.2006 г. для целей учета и таможенных платежей
| Цифр. Код |
Букв. Код |
Валюта |
Единиц |
Курс |
| 036 |
AUD |
Австралийский доллар |
1 |
20,6703 |
| 974 |
BYR |
Белорусский рублей |
1 000 |
12,2874 |
| 208 |
DKK |
Датская крона |
10 |
46,5243 |
| 840 |
USD |
Доллар США |
1 |
26,3081 |
| 978 |
EUR |
Евро |
1 |
34,6899 |
| 352 |
ISK |
Исландская крона |
100 |
38,3780 |
| 398 |
KZT |
Казахская тенге |
100 |
20,5628 |
| 124 |
CAD |
Канадский доллар |
1 |
23,1178 |
| 156 |
CNY |
Китайский юань Ренминби |
10 |
33,5242 |
| 949 |
TRY |
Новая турецкая лира |
1 |
17,9577 |
| 578 |
NOK |
Норвежская крона |
10 |
42,2349 |
| 960 |
XDR |
СДР |
1 |
39,6195 |
| 702 |
SGD |
Сингапурский доллар |
1 |
17,0500 |
| 980 |
UAH |
Украинская гривна |
10 |
52,0303 |
| 826 |
GBP |
Фунт стерлингов Соединенного королевства |
1 |
51,3876 |
| 752 |
SEK |
Шведская крона |
10 |
38,1913 |
| 756 |
CHF |
Швейцарский франк |
1 |
21,7981 |
Динамика курсов иностранных валют к рублю РФ, установленные Центральном Банком Российской Федерации на 01.12.1992-2006 гг.
| Период |
Доллар США |
Евро |
| 01.01.1992 |
– |
– |
| 01.01.1993 |
414,5000 |
– |
| 01.01.1994 |
1 247,0000 |
– |
| 01.01.1995 |
3 550,0000 |
– |
| 01.01.1996 |
4 640,0000 |
– |
| 01.01.1997 |
5 560,0000 |
– |
| 01.01.1998 |
5,9600 |
– |
| 01.01.1999 |
20,6500 |
24,0900 |
| 01.01.2000 |
27,0000 |
27,2000 |
| 01.01.2001 |
28,1600 |
26,1400 |
| 01.01.2002 |
30,1372 |
26,6172 |
| 01.01.2003 |
31,7844 |
33,2719 |
| 01.01.2004 |
28,4545 |
37,0979 |
| 01.01.2005 |
27,7487 |
37,8409 |
| 01.01.2006 |
28,7825 |
34,1850 |
Приложение 8
Динамика ежемесячных курсов доллара США и евро к рублю РФ,
установленных Центральным Банком Российской Федерации за 2005-2006 гг.
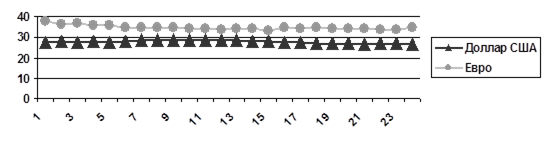
Динамика ежемесячных курсов доллара США и евро к рублю РФ, установленных Центральным Банком Российской Федерации за 2004-2006 гг.
| Период |
Доллар США |
Евро |
| 01.01.04 |
29,4545 |
37,0979 |
| 01.02.04 |
28,4937 |
35,3635 |
| 01.03.04 |
28,5156 |
35,5076 |
| 01.04.04 |
28,5151 |
34,9082 |
| 01.05.04 |
28,9612 |
34,6289 |
| 01.06.04 |
28,9993 |
35,3907 |
| 01.07.04 |
29,0471 |
35,0889 |
| 01.08.04 |
29,1019 |
35,0532 |
| 01.09.04 |
29,2591 |
35,3713 |
| 01.10.04 |
29,2224 |
36,0312 |
| 01.11.04 |
28,7655 |
36,6472 |
| 01.12.04 |
28,1496 |
37,3264 |
| 01.01.05 |
27,7487 |
37,8409 |
| 01.02.05 |
28,1136 |
36,5899 |
| 01.03.05 |
27,7007 |
36,7200 |
| 01.04.05 |
27,8548 |
36,0274 |
| 01.05.05 |
27,7726 |
36,0072 |
| 01.06.05 |
28,1946 |
34,9134 |
| 01.07.05 |
28,6282 |
34,6258 |
| 01.08.05 |
28,6341 |
34,7160 |
| 01.09.05 |
28,5566 |
34,8790 |
| 01.10.05 |
28,5348 |
34,3074 |
| 01.11.05 |
28,5030 |
34,3946 |
| 01.12.05 |
28,7792 |
33,9393 |
| 01.01.06 |
28,7825 |
34,1850 |
| 01.02.06 |
28,1305 |
34,0492 |
| 01.03.06 |
28,1211 |
33,3291 |
| 01.04.06 |
27,6996 |
33,6273 |
| 01.05.06 |
27,2739 |
34,1906 |
| 01.06.06 |
26,9355 |
34,7064 |
| 01.07.06 |
26,9423 |
34,2383 |
| 01.08.06 |
26,8197 |
34,2112 |
| 01.09.06 |
26,7295 |
34,3180 |
| 01.10.06 |
26,7799 |
33,9783 |
| 01.11.06 |
26,7811 |
33,9852 |
| 01.12.06 |
26,3081 |
34,6899 |
Приложение 9
| Денежная масса М2
(национальное определение) на 01.12.1997-2006 гг., млрд. руб. |
| Период |
Денежная масса |
Цепные темпы прироста денежной массы, % |
| Всего |
В том числе |
| наличные деньги М0
|
безналичные
средства М1
|
| 01.01.1997 |
289,9 |
96,4 |
193,5 |
– |
| 01.01.1998 |
374,1 |
130,3 |
243,7 |
129,0 |
| 01.01.1999 |
453,7 |
187,7 |
266,0 |
121,3 |
| 01.01.2000 |
714,6 |
266,1 |
448,4 |
157,5 |
| 01.01.2001 |
1 154,4 |
418,9 |
735,5 |
161,5 |
| 01.01.2002 |
1 612,6 |
583,8 |
1 028,8 |
139,7 |
| 01.01.2003 |
2 134,5 |
763,2 |
1 71,2 |
132,4 |
| 01.01.2004 |
3 212,7 |
1 147,0 |
2 065,6 |
150,5 |
| 01.01.2005 |
4 363,3 |
1 534,8 |
2 828,5 |
135,8 |
| 01.01.2006 |
6 045,6 |
2 009,2 |
4 036,3 |
138,6 |
| 01.11.2006 |
7 769,6 |
2 402,2 |
5 367,4 |
128,5 |
|