Мы говорили об информационных моделях и об одном из видов программного обеспечения для работы с ними. Вы помните, что СУБД позволяет хранить большое количество информации и находить среди нее нужную. Однако, зачастую требуется не просто хранить некоторую информацию (знания об объектах), но и динамической39. Чаще всего правилами, описывающими функционирование системы являются математические формулы. В этом случае модель называют математической. Одним из средств для построения компьютерных математических моделей являются электронные таблицы (или табличные процессоры). Как ясно из названия, электронная таблица предназначена для табличных расчетов. Представление информации в ней похоже на реляционную базу данных. Но, в отличие от таблицы в базе данных, здесь строки совсем не обязательно должны быть однотипными (на рисунке 1-я и 151-я строки отличаются от остальных содержащих информацию строк).

Для того чтобы можно было записать правила, связывающие различные данные, все элементы таблицы имеют обозначения -- имена. Строки обозначаются числами, столбцы -- латинскими буквами. Если в таблице больше 26 столбцов, то после "Z" будет "AA", "AB" и т. д. Имя ячейки (клетки) таблицы образуется из имени столбца и номера строки, на пересечении которых она находится, например, "R37". Если же мы хотим указать, что действия выполняются с прямоугольной областью таблицы, нужно записать имена левой верхней и правой нижней клеток этой области, разделив их двумя точками (или, в зависимости от конкретной программы, двоеточием). Например, "F5..L27".
В каждую клетку таблицы можно занести число или текст (вспомните про типы данных!), а можно -- формулу. В этом случае компьютер выполнит заданные формулой действия, а на экране покажет результат.
Запись формул в компьютере несколько отличается от той, к которой вы привыкли. Например, в физике пишут "s=vt". Посмотрим, как такая формула будет выглядеть в электронной таблице? Пусть значение скорости находится в клетке B2, значение времени -- в клетке C2, а результат -- путь -- должен находиться в D2. В этом случае в ячейку D2 нужно вписать "=B2*C2". Какие же мы видим особенности записи?
Во-первых, формула начинается со знака "=", а обозначение искомой величины (в данном примере, пути) вообще отсутствует. Во-вторых, вместо переменных мы указываем имена ячеек таблицы, в которых содержатся их значения. В-третьих, используется специальный значок для обозначения умножения -- "*" (звездочка). Знаком деления является наклонная черта -- "/", для сложения и вычитания применяют обычные знаки -- "плюс" и "минус". Кроме того, формулы могут содержать функции. Причем не только математические (например, квадратный корень), но и функции, позволяющие упростить запись часто использующихся действий. К примеру, когда нужно найти общую стоимость полутора сотен товаров, то есть сложить значения ячеек, скажем, с D3 до D149, вместо длинной цепочки сложений достаточно написать "=SUM(D3..D149)". Существуют также функции (их называют условными), позволяющие выбирать те или иные действия в зависимости от значений каких-либо величин.
Реклама

Обычно в электронной таблице одинаковые действия нужно выполнять с большим числом (нередко, с сотнями) строк таблицы. Неужели приходится по многу раз набирать почти одинаковые формулы? Конечно нет. В табличных процессорах предусмотрено автоматическое заполнение ячеек.
Поскольку чаще всего формула связывает между собой данные одной и той же строки (или одного и того же столбца) таблицы, при заполнении все входящие в формулу имена изменяются одновременно. Если в клетке D5 была формула "=B5*C5", то в клетку D6 будет вписано "=B6*C6", в D7 -- "=B7*C7" и так далее. Компьютер ориентируется на расположение клеток друг относительно друга. Такая адресация называется относительной. Но бывает нужна и абсолютная адресация -- когда значение какой-либо величины для всех формул находится в одной ячейке, и следовательно, ее имя при заполнении меняться не должно. В большинстве электронных таблиц, чтобы "закрепить" имя столбца или номер строки, перед ним ставится знак "$", например, "A$4", "$N87", "$W$52".
Но вот мы создали математическую модель, занесли данные в таблицу, выполнили расчеты -- и получили большое количество чисел. Хорошо бы представить результаты вычислений понагляднее. Тут нам тоже поможет табличный процессор. Оказывается, он умеет строить диаграммы.
Диаграмма40 -- условное графическое изображение числовых величин или их соотношений. Рассмотрим три их разновидности: столбчатую, линейную и круговую диаграммы.
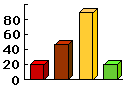 |
На столбчатой диаграмме каждая величина изображается в виде столбика. Его высота показывает в соответствующем масштабе (он наносится на вертикальной оси) числовое значение этой величины. Что обозначает каждый столбик может быть написано либо непосредственно около него, либо в так называемой "легенде" -- табличке, где указано чему соответствует каждый цвет. На практике одинаково часто встречаются диаграммы как с вертикальным, так и с горизонтальным расположением столбиков. |
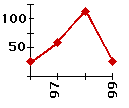 |
Линейная диаграмма наиболее часто используется, когда хотят показать изменение какой-либо величины, например, с течением времени. При ее построении отмечаются точки, расстояние которых от горизонтальной оси соответствует (в заданном масштабе) значениям величины, а затем эти точки соединяются отрезками. На горизонтальной оси указывают, чему соответствует каждое значение. |
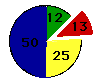 |
По круговой диаграмме , в отличие от двух предыдущих, нельзя определить значения величин. Это круг, разделенный на сектора, размеры которых соотносятся также как изображаемые ими числовые величины. |
Табличные процессоры позволяют строить не только несколько разновидностей диаграмм, но и графики (график, в отличие от диаграммы, изображает зависимость одной величины от другой).
Примечания
Statike (греч.) -- равновесие, неподвижность; dynamikos (греч.) -- сильный, действующий, движущийся.
Diagramma (греч.) -- рисунок.
|