| Аннотация
Данная выпускная работа бакалавра посвящена изучению релаксации напряжений и влияния термомеханической обработки на релаксационную стойкость металлов и сплавов. Выпускная работа состоит из пояснительной записки, выполненной на 87 листах формата А4, в том числе 21 иллюстраций, 16 источников литературы и графической части, выполненной на 4 листах формата А1.
Введение
1 Физическая природа и механизмы релаксации напряжений в металлах и сплавах
1.1 Явление релаксации напряжений
1.2 Особенности релаксации напряжений и ползучести
1.3 Релаксация напряжений и температура
1.4 Основы релаксационной стойкости металлических материалов
1.5 Связь релаксации напряжений и ползучести
2 Методы изучения релаксации напряжений
2.1 Релаксация при растяжении и сжатии
2.2 Релаксация при изгибе и кручении
2.3 Релаксация в винтовых пружинах
3 Влияние различных факторов на процесс релаксации напряжений и ее критерии
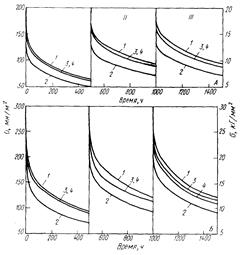
3.1 Влияние начального напряжения на протекание процесса релаксации
3.2 Влияние времени на протекание процесса релаксации напряжений
3.3 Влияние температуры на процесс релаксации напряжений
3.4 Масштабный фактор
3.5 Основные критерии релаксации напряжений
4 Влияние термомеханической обработки на релаксационную стойкость сталей и сплавов
4.1 Положительное влияние ТМО на релаксационную стойкость
4.2 Структурные превращения в процессе релаксации напряжений
Заключение
Список использованных источников
Введение
Среди конструкционных и жаропрочных материалов, применяемых во многих отраслях промышленности, немаловажное место занимают стали и сплавы (реже чистые металлы), работающие в условиях релаксации напряжений при различных температурах.
Для получения материалов с высокой релаксационной стойкостью необходимо знать механизм и основные закономерности процесса релаксации напряжений, а также факторы, влияющие на него.
Проведенные за последние годы теоретические и экспериментальные исследования в области релаксации напряжений в металлических материалах значительно расширили наши познания об этом процессе.
Большой вклад в изучение явления релаксации напряжений внесли русские ученые Н.С. Курнаков, Н.Н. Давидеиков, Я.И. Френкель, С.И. Губкин, С.Т. Копобеевский, И.А. Одинг, Б.М. Ровинский, Ю.Н. Работнов, Л.М. Качанов, Б.П. Финкельштейн и др.
Реклама

Под термином релаксация напряжений обычно понимают самопроизвольное снижение механических напряжений в металле (при постоянных линейных размерах). Такие напряжения либо специально создают при сборке узлов машин и установок для обеспечения нормальной работы последних (например, крепежные соединения, пружинящие элементы), либо они неизбежно возникают в процессе изготовления деталей (технологические напряжения).
В частности, релаксация напряжения может наблюдаться при вылеживании детали после термической обработки, при низкотемпературном отпуске, при переменном нагружении в условиях заданной амплитуды деформации и т. д. Исследования, проведенные в последние годы, показали, что релаксация напряжений может происходить в различных металлах и сплавах при нормальной, высоких, а в ряде случаев и при отрицательных температурах. Установлена возможность разрушения деталей, работающих в условиях релаксации напряжений.
Можно считать установленным, что релаксация напряжений (подобно ползучести) является результатом как сдвиговодислокационных, так и диффузионных процессов. Процессы первого типа связаны с кооперативным передвижением группы атомов (например, по плоскостям сдвигов и т. д.). Процессы второго типа — с индивидуальным перемещением отдельных атомов как у границ зерен основной структуры, так и по всему объему поликристалла. Преобладающая роль того или иного явления, контролирующего процесс релаксации, зависит от рабочей температуры и от уровня действующих напряжений.
Целесообразно различать макрорелаксацию напряжений (в материале, деталях), реализуемую путем макро-ползучести в условиях, затрудняющих изменение линейных размеров детали, и микрорелаксацию напряжений, вызванную процессами микроползучести как между элементами микроструктуры (релаксация 2-го рода), так и внутри их (релаксация 3-го рода). Макрорелаксация напряжений в детали может быть обусловлена процессами микрорелаксации в элементах структуры.
Сопротивление материала релаксации напряжений можно повысить посредством: термической обработки, обеспечивающей оптимальную для релаксационной стойкости структуру; стабилизации, увеличивающей сопротивление релаксации (и ползучести) на первой стадии процесса; термомеханической обработки; повторными нагружениями.
Можно полагать, что получение необходимой информации о характеристиках релаксационной стойкости различных конструкционных материалов в ближайшие годы будет идти двумя путями.
Реклама

Во-первых, непосредственным испытанием таких материалов на релаксацию напряжений по существующим методикам (включая наиболее распространенный в наших лабораториях метод испытания колец равного сопротивления изгибу) при длительностях, отвечающих заданным срокам службы или приближающихся к ним.
Во-вторых, применением расчетных методов оценки сопротивления релаксации (характеризуемой ползучестью при переменном напряжении) по данным испытаний на ползучесть (при постоянном напряжении). Например, характеристики релаксации для условий однократного нагружения можно с достаточной точностью рассчитывать по теориям упрочнения или течения. Распространение электронных вычислительных машин позволит широко использовать для определения характеристик релаксации первичные кривые ползучести материалов. Оба эти направления являются правомерными и отнюдь не исключают друг друга.
Так, если сплав разрабатывается или исследуется для деталей, работающих в условиях жесткого нагружения (возможной релаксации напряжений), то целесообразно проводить испытание не на ползучесть, а на релаксацию, поскольку последнее значительно менее трудоемко, особенно если испытывать кольца равного сопротивления изгибу (по И.А. Одингу) или винтовые пружины (по А.А. Чижику). В последнем случае результаты испытаний па релаксацию используют даже для расчетного определения характеристик ползучести. Кроме того, поскольку предложенные расчетные методы определения сопротивления повторной релаксации не нашли еще достаточно широкого применения, проведение соответствующих испытаний для оценки этой характеристики является совершенно необходимым.
1 Физическая природа и механизмы релаксации напряжений в металлах и сплавах
Кристаллическое тело, переведенное воздействием внешних сил в неравновесное состояние, всегда стремится возвратиться обратно в равновесное состояние. Процесс перехода кристаллического тела из неравновесного состояния в равновесное называют релаксационным.
В идеальном (бездефектном) монокристаллическом теле все процессы, вызванные воздействием внешних сил, обратимы. Но без освобождения тела от действия внешних сил стремление к возвращению в равновесное состояние в идеальных кристаллах может реализоваться только в условиях, при которых атомы под влиянием флуктуации тепловой энергии преодолевают энергетический барьер, или в том случае, если монокристалл дробится на субзерна. В реальных кристаллах релаксационные процессы обусловливаются наличием дефектов кристаллической решетки.
При упругом деформировании кристаллических тел с любой конечной скоростью уровень свободной энергии повышается и они переходят в термодинамически неравновесное состояние. Только в идеально упругом теле при бесконечно медленном (квазистатическом) деформировании в условиях низких напряжений не будет происходить рассеяние упругой энергии и упругое деформирование будет полностью обратимым процессом, для которого справедлив приближенный закон Гука: 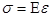 . .
Для реальных кристаллических тел, нагруженных в упругой области, эта зависимость, строго говоря, неприемлема, так как благодаря наличию дефектов в них почти всегда наблюдается переход из термодинамически неравновесного в более равновесное состояние. Такие отклонения от упругого поведения обычно называют общим термином «упругие несовершенства» или «явления неупругости». Процессы неупругости, развивающиеся во времени в направлении к равновесному состоянию, являются релаксационными.
Релаксационные процессы развиваются по-разному в зависимости от свойств тела, вида деформации и условий, в которых они протекают, и проявляются в виде упругого последействия, внутреннего трения, релаксации напряжений.
1.1 Явление релаксации напряжений
Еще в первой половине прошлого столетия были отмечены факты самопроизвольного уменьшения внутренних напряжений. По мнению Пуассона, в жидкостях в течение некоторого времени непрерывно выравниваются или ослабляются напряжения от внешнего давления. Распространив эту мысль на твердые тела, К.Максвелл сделал предположение, что спадание (или релаксация) напряжений в функции времени пропорционально величине напряжения. Он рассматривал твердое тело как упруго-вязкую систему, сочетающую в себе идеально упругое тело Гука и идеально вязкое тело Ньютона. Следовательно, по Максвеллу изменение (релаксация) напряжения во времени должно следовать закону:
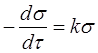 (1) (1)
где 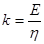 константа, характеризующая скорость релаксации; константа, характеризующая скорость релаксации;
Е— модуль упругости;
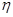 —коэффициент вязкости. —коэффициент вязкости.
После интегрирования в пределах от 0 до τ при начальных условиях τ=0; 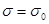 получаем получаем
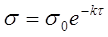 (2) (2)
Величину, обратную k, Максвелл назвал «временем релаксации» 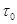 . Тогда уравнение (2) можно представить в виде . Тогда уравнение (2) можно представить в виде
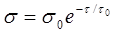 (3) (3)
Здесь 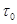 — время, в течение которого начальное напряжение убывает в e=2,71828 раз. — время, в течение которого начальное напряжение убывает в e=2,71828 раз.
Помимо модели Максвелла (рисунок 1,а), состоящей из последовательно соединенных элементов: упругого Е и вязкого η, для описания процессов ползучести используют модель Кельвина-Фойгта (рисунок 1,б), состоящую из параллельно соединенных элементов Е и η, а также комбинации моделей Кельвина-Фойгта, Максвелла и упругих элементов. Так, при описании ползучести и релаксации, согласно комбинированной гипотезе ползучести, предложенной Е. А. Хейном, использована модель рисунок 1,в. Она состоит из звена Максвелла, описывающего необратимую ползучесть, и совокупности звеньев Кельвина-Фойгта, моделирующих упругое последействие.
Н. С. Курнаков рассматривал явление релаксации напряжений в тесной связи с природой и свойствами испытуемого материала и его состоянием. Наблюдая во время опытов по изучению давления истечения пластических тел за процессом изменения напряжения во времени, он пришел к выводу, что скорость релаксации k (а следовательно, и время релаксации 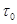 ) зависят не только от внешних условий (температуры, давления и др.), но и от природы металла и его предварительной обработки. ) зависят не только от внешних условий (температуры, давления и др.), но и от природы металла и его предварительной обработки.
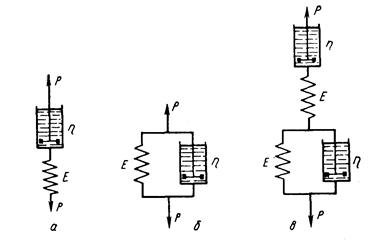
Рисунок 1 – Модели твердого тела
Н.С. Курнаков придавал большое значение явлению релаксации напряжений и даже включил «время релаксации» в число свойств, определяемых при физико-химическом анализе металлов и сплавов.
Основные идеи Н.С. Курнакова впоследствии были развиты при изучении физической природы релаксации напряжений С. И. Губкиным, Л. В. Шведовым и другими исследователями.
В частности, С.И. Губкин [2] высказал мысль, что в поликристаллическом металле скорость релаксации напряжений зависит от скорости межзеренных скольжений и внутрикристаллических сдвигов. Это положение было позднее развито и значительно дополнено И. А. Одингом. Далее, скорость процессов релаксации обусловлена не только скоростью деформации, но прежде всего является функцией состояния самого вещества.
Как уже упоминалось, релаксация напряжений — процесс самопроизвольного снижения напряжения в теле, поставленном в условия неизменности начальной деформации в направлении действия силы. Эти напряжения могут быть специально созданы при сборке узлов машин или приборов, например болтовые соединения, цилиндрические и ленточные пружины, сохраняющие свои размеры в процессе работы, различные тугие посадки и т.д., а также находящий все более широкое применение напряженный бетон, армированный предварительно напряженной проволокой. Во всех этих случаях желательно возможно дольше сохранить близкий к начальному уровень напряжений и поэтому их релаксация нежелательна.
В процессе изготовления (обработки) деталей в них могут возникать остаточные напряжения. В качестве примера можно привести сварные соединения, пленочные покрытия, детали, получаемые холодной штамповкой, и др. Такие «технологические» напряжения во многих случаях являются нежелательными, поскольку они могут вызнать во время службы недопустимое формоизменение детали или даже привести к ее разрушению. Поэтому следует создавать такие условия, чтобы релаксация технологических напряжений проходила с возможно большой интенсивностью.
Релаксация напряжений в чистом виде проявляется при постоянной начальной суммарной деформации. Основное условие релаксации (в упругой области) можно выразить соотношением
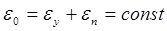 (4) (4)
где 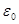 — начальная суммарная деформация; — начальная суммарная деформация;
εу
-— упругая деформация;
εп
— остаточная (пластическая) деформация, накапливающаяся в процессе релаксации.
Если тело было нагружено в упругой области, то в начальный момент времени (τ) 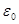 =εу
и εп
= 0. =εу
и εп
= 0.
Условие постоянства начальной суммарной деформации справедливо только в случае мгновенного первичного нагружения тела в упругой области с последующей релаксацией напряжений. Если нагружение производить замедленно, то при этом в результате релаксации напряжений может возникнуть пластическая деформация. Пластическая деформация происходит и в случае нагружения тела выше предела упругости. Таким образом, более строго условие постоянства начальной суммарной деформации следует записать
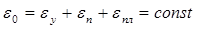 (4’) (4’)
где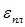 — пластическая деформация, возникающая при нагружении детали. — пластическая деформация, возникающая при нагружении детали.
С течением времени в нагруженном теле, поставленном в условии неизменности начальной суммарной деформации, упругая деформация снижается и соответственно этому растет пластическая деформация. Уменьшение упругой деформации (упругих искажений кристаллической решетки) влечет за собой снижение (релаксацию) напряжений. Это наглядно показано на рисунке 2,а, на котором дана схема уменьшения упругой деформации и соответственного роста пластической, а на рисунке 2,6 — кривая релаксации напряжений.
Ряд закономерностей процесса релаксации напряжений был установлен на монокристаллах. Протекание процессов релаксации напряжений в поликристаллическом металле вследствие наличия границ зерен осуществляется более сложным образом. Например, в поликристаллических металлах при определенных силовых и температурных условиях возникает напряженное состояние за счет упругих смещений по границам зерен. Поэтому возможно также и снятие напряжений путем релаксации по границам зерен. Оно может происходить двумя путями — либо путем направленного смещения атомов через границы (диффузионная пластичность), либо в результате скольжения по границам зерен.
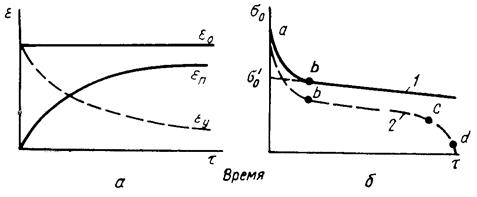
1-типичная зависимость σ-τ; 2-возможная форма кривой для сплава со структурными превращениями (а — b — I период; b — с — II период; с — d — III период релаксации)
Рисунок 2 – Схема изменения пластической и упругой деформаций. а) и начального напряжения б) в процессе релаксации.
Б.М. Ровинский [3] полагает, что в поликристаллическом теле возможны три разновидности процесса релаксации напряжений:
а) упруго-пластическая релаксация, описываемая уравнением
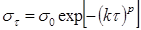 (5) (5)
где 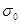 —начальное напряжение; —начальное напряжение;
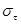 — напряжение в момент времени τ; — напряжение в момент времени τ;
p — показатель релаксационной стойкости;
k — относительная скорость релаксации напряжений.
Этот вид релаксации происходит преимущественно в области относительно невысоких температур, не превышающих температуру отдыха (ниже~0,25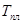 ); );
б) упруго-вязкая деформация по границам зерен (блоков)
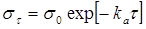 (6) (6)
характерная главным образом для области средних температур (0,25—0,5) 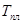 ; ;
в) упруго-вязкая деформация, обусловленная диффузионным током атомов (вакансий)-для области высоких температур (>0,5 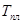 ): ):
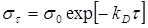 (7) (7)
Все эти уравнения можно рассматривать как частные случаи уравнения Одинга - Надаи:
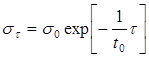 (8) (8)
в котором член 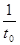 — обозначен через k, kа
, — обозначен через k, kа
, 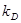 , а в уравнении введен степенной показатель , а в уравнении введен степенной показатель 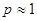
1.2 Особенности релаксации напряжений и ползучести
Необратимый рост пластической деформации во времени при релаксации напряжений делает этот процесс внешне тождественным с процессом ползучести, при которой пластическая деформация также непрерывно нарастает (но при σ=const). Однако условия, при которых происходит накопление пластической деформации, при релаксации и ползучести существенно различаются.
Прежде всего, при ползучести в условиях постоянного напряжения непрерывное увеличение общей (суммарной) деформации детали (образца) происходит за счет соответственного роста пластической деформации. При релаксации напряжений общая (суммарная) деформация остается неизменной, равной начальной деформации 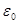 , а пластическая деформация растет только за счет соответственного уменьшения упругой. , а пластическая деформация растет только за счет соответственного уменьшения упругой.
При релаксации напряжений процесс роста пластической деформации происходит внутри первоначально напряженного объема металла. Предел, к которому стремится в этом случае накапливаемая в процессе релаксации пластическая деформация, — это очень небольшая упругая начальная деформация:
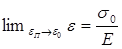 (9) (9) 
При ползучести рост пластической деформации продолжается непрерывно, иногда достигая значительной величины. Кроме того, рост пластической деформации происходит при постоянной нагрузке и приблизительно постоянном (не считая третьего периода) напряжении. Поэтому при всех прочих неизменных условиях пластическая деформация есть функция только времени:
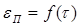 при при 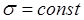 (10) (10)
При релаксации действующее напряжение постоянно только в момент нагружения, т. е. при τ=0, в последующее время оно непрерывно снижается. Так, как при релаксации пластическая деформация вызывается напряжением, являющимся переменной величиной, то пластическая деформация при постоянстве температуры и прочих условий — функция двух параметров (напряжения и времени)
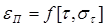 (11) (11)
Различие силовых и деформационных условий, при которых протекает пластическая деформация при ползучести и релаксации, обусловливает особенности этих процессов.
В области средних температур (0,25—0,5) 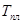 пластическая деформация реализуется главным образом за счет перемещения дислокаций (скольжения по плоскостям сдвига и переползания). пластическая деформация реализуется главным образом за счет перемещения дислокаций (скольжения по плоскостям сдвига и переползания).
При ползучести пластическая деформация накапливается вследствие взаимодействия двух процессов: упрочнения металла и его разупрочнения (возврат). Упрочнение происходит благодаря действию источников генерирования дислокаций с образованием дислокационных скоплений и иных препятствий. Возврат обусловливается рассасыванием дислокационных скоплений путем переползания краевых дислокаций (при более высоких температурах) и двойного поперечного скольжения винтовых дислокаций.
Участок установившейся ползучести обусловливается достигнутым равенством скорости упрочнения и скорости разупрочнения. Источники генерирования дислокаций действуют с приблизительно постоянной интенсивностью, так как действующее в данный момент напряжение а всегда больше критического напряжения генерирования дислокаций 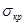 : :
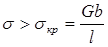 (12) (12)
где G — модуль сдвига;
b— вектор Бюргерса.
При релаксации же происходит исчерпывание (или «истощение») легко подвижных дислокаций. В каждый последующий момент напряжение меньше, чем в предыдущий, и поэтому интенсивность действия источников непрерывно уменьшается во времени. Уменьшение плотности легкоподвижных дислокаций и их связывание в устойчивые системы ведут к упрочнению. Но при высоких температурах интенсивность разупрочнения путем переползания и двойного поперечного скольжения дислокаций (при неизменной температуре) оказывается повышенной. В результате в условиях релаксации упрочнение незначительно и зависит от интенсивности снижения напряжения.
Ряд исследователей (И. А. Одинг и др.) отождествляют интенсивность разупрочнения при ползучести lс
со скоростью релаксации напряжений 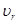 : :
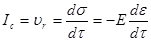 (13) (13)
По мере приближения напряжения и обусловленной им упругой деформации к нулю (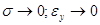 ) термодинамическое равновесие тела восстанавливается и уровень внутренней энергии снижается. При ползучести этого не наблюдается. ) термодинамическое равновесие тела восстанавливается и уровень внутренней энергии снижается. При ползучести этого не наблюдается.
Таковы основные различия в процессах релаксации напряжений и ползучести (в средней температурной области).
Металл, работающий в условиях, вызывающих релаксацию напряжений, находится в менее выгодных условиях, чем металл, испытывающий ползучесть, так как при релаксации напряжений упрочнение от пластической деформации ввиду ее ограниченности крайне невелико.
1.3 Релаксация напряжений и температура
Характер возрастания пластической деформации во времени при ползучести в различных температурных интервалах имеет определенные особенности. В зависимости от температуры различают три разновидности этого процесса. Такой подход, по-видимому, можно распространить и на явление релаксации.
1. Низкотемпературная релаксация — при температурах ниже температуры возврата (для чистых металлов ниже 0,25 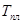 ). ).
В этой температурной области деформация растет во времени, подчиняясь приблизительно логарифмическому закону:
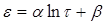 (14) (14)
где α и β — постоянные. Поэтому сам процесс роста деформации можно назвать логарифмическим. Пластическая деформация в этом случае обусловливается скольжением дислокаций по плоскостям сдвига. Упрочнение, согласно Мотту-Набарро и Коттреллу [4], происходит в результате непрерывного исчерпывания дислокаций, находящихся в условиях наиболее легкого скольжения. Исходя из этого, пластическая деформация зависит от времени следующим образом:
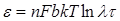 (15) (15)
где п — число дислокаций на единицу энергии активации;
F — средняя площадь, освобождаемая дислокациями;
b — вектор Бюргерса;
λ — частота колебания дислокаций в момент времени τ.
Релаксация, соответствующая логарифмической области, слабо зависит от температуры и совершенно не зависит от напряжения. Деформация находится в линейной зависимости от энергии активации.
Фелтам для этой температурной области дает следующее уравнение релаксации напряжений:
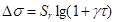 (16) (16)
где γ— коэффициент, не зависящий от времени τ и 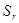 ; ;
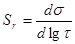 (17) (17)
Величина 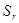 снижается приблизительно линейно с повышением температуры. снижается приблизительно линейно с повышением температуры.
Энергию активации релаксации определяют из зависимостей:
при напряжении сдвига
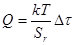 (18) (18)
при растягивающем напряжении
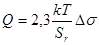 (18’) (18’)
2. Среднетемпературная релаксация наблюдается в области температур [(0,25-0,5)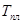 ], при которых активно развиваются процессы возврата, а ближе к верхнему уровню температур — рекристаллизации. Основные процессы, контролирующие ход релаксации напряжений,— переползание краевых дислокаций и двойное поперечное скольжение, благодаря которым происходит разупрочнение металла; последнее все в меньшей степени может компенсировать ослабевающее действие источников дислокаций. Диффузионные процессы вызывают переползание дислокаций из одной (заблокированной) плоскости скольжения в другую (незаблокированную). Скорость релаксации в этой температурной области находится в экспоненциальной зависимости от энергии активации: ], при которых активно развиваются процессы возврата, а ближе к верхнему уровню температур — рекристаллизации. Основные процессы, контролирующие ход релаксации напряжений,— переползание краевых дислокаций и двойное поперечное скольжение, благодаря которым происходит разупрочнение металла; последнее все в меньшей степени может компенсировать ослабевающее действие источников дислокаций. Диффузионные процессы вызывают переползание дислокаций из одной (заблокированной) плоскости скольжения в другую (незаблокированную). Скорость релаксации в этой температурной области находится в экспоненциальной зависимости от энергии активации:
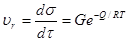 (19) (19)
Однако пока еще нет единого мнения, как правильнее определять энергию активации релаксации, Л.П. Никитина подсчитывает энергию активации, пользуясь зависимостью
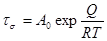 (20) (20)
где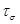 - время, через которое напряжение станет равным σ; - время, через которое напряжение станет равным σ;
А0
— коэффициент. Ф. И.
Ф. И. Алешкин для этой цели использует аналогичную зависимость [5]
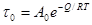 (20’) (20’)
3. Высокотемпературная релаксация наблюдается при температурах (выше~0,5 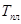 ), при которых активизируются процессы диффузии. В этой области преобладает вакансионный механизм диффузии, что приводит к ускорению переползания дислокаций. ), при которых активизируются процессы диффузии. В этой области преобладает вакансионный механизм диффузии, что приводит к ускорению переползания дислокаций.
При малых напряжениях энергия активации миграции вакансий определяет интенсивность процесса деформации. При больших напряжениях и в этом интервале температур деформация обусловлена движением дислокаций. Однако это не сопровождается заметным упрочнением, поскольку большинство дислокаций выходит на поверхность кристалла.
Для очень высоких температур (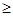 0,5 0,5 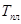 ) характерна совокупность диффузионных процессов (которые как бы создают предпосылки движения дислокаций) и процессов переползания дислокаций. ) характерна совокупность диффузионных процессов (которые как бы создают предпосылки движения дислокаций) и процессов переползания дислокаций.
Сопротивление металлических материалов релаксации напряжений зависит, прежде всего, от прочности связей в кристаллической решетке основного металла. Б.М. Ровинский и В.Г. Лютцау [6] показали, например, что чем «жестче» кристаллическая решетка, тем больше релаксационная стойкость металлов. В качестве критерия релаксационной стойкости используется величина
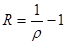 (21) (21)
Здесь 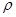 — параметр, характеризующий интенсивность релаксационного процесса, зависящий от состава и структурного состояния металла. — параметр, характеризующий интенсивность релаксационного процесса, зависящий от состава и структурного состояния металла.
Этот параметр находят из уравнения
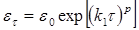 (22) (22)
где 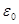 — начальная упругая деформация; — начальная упругая деформация;
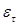 —упругая деформация в момент времени τ; —упругая деформация в момент времени τ;
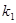 — параметр, определяемый уровнем напряжений. — параметр, определяемый уровнем напряжений.
С повышением температуры интенсивность тепловых колебаний атомов (ионов) в кристаллической решетке увеличивается. Б.М. Ровинский и В. Г. Лютцау [6] именно с этим связывают уменьшение с температурой релаксационной стойкости чистого никеля и некоторых его сплавов. По мнению этих авторов, уменьшение релаксационной стойкости этих материалов с повышением температуры обусловлено только изменением энергии тепловых колебаний атомов в решетке. Однако, как видно из более поздних работ, основное влияние оказывает интенсификация диффузионных процессов, облегчающих перемещение дислокаций.
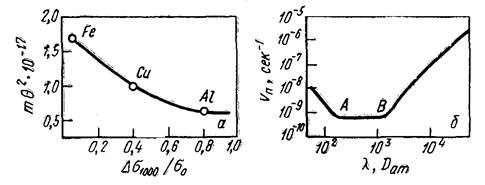
Рисунок 3 - Зависимость интенсивности релаксации от величины 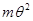 (а) и интенсивности ползучести от расстояния λ между частицами дисперсной фаз (б) (а) и интенсивности ползучести от расстояния λ между частицами дисперсной фаз (б)
Важное значение для релаксационной стойкости чистых металлов имеют дефекты упаковки. В объемно-центрированной кристаллической (о. ц. к.) решетке α-железа нет оснований ожидать большого количества расщепленных дислокаций, но в γ-железе и никеле и особенно в твердых растворах на основе этих металлов, обладающих гранецентрированной (г. ц. к.) решеткой, дислокации, как правило, являются расщепленными. Поэтому все процессы, связанные с развитием пластической деформации, в α-железе интенсифицируются с повышением температуры в значительно большей степени. В связи с этим для α-железа и его сплавов соотношение между максимальной рабочей температурой и температурой плавления (°К) приблизительно равно 0,48; для γ-железа и его сплавов 0,59; для никеля и его сплавов 0,68.
Прочность связей кристаллической решетки чистых металлов может быть изменена легированием элементами, образующими твердые растворы замещения, как было показано В.А. Ильиной и В.К. Крицкой. Большинство таких элементов, например кобальт, молибден, марганец, ниобий, увеличивает в возрастающем порядке силы связи феррита, и только ванадий уменьшает их. Хром в количестве 2—8% также значительно усиливает межатомные связи.
Имеющиеся экспериментальные данные подтверждают [7], что сопротивление феррита релаксации и ползучести повышают хром, молибден, кобальт и вольфрам. При этом наибольший эффект достигается при многокомпонентном легировании. Легирование железа никелем в количестве, необходимом для образования устойчивой при комнатной температуре аустенитной структуры, в значительной степени повышает релаксационную стойкость железа. Легирование сплавов Fe — Ni элементами, повышающими прочность связей (хромом, вольфрамом, молибденом и др.), способствует дальнейшему увеличению релаксационной стойкости.
Г.В. Курдюмов и Н.Т. Травина [16], рентгенографическим исследованием установили, что в твердых растворах на основе никеля введение добавок хрома, титана и алюминия приводит к повышению сил межатомных связей в тем большей степени, чем выше концентрация этих элементов (в исследованных пределах, не превышающих предельную растворимость их в никеле при комнатной температуре).
Однако роль легирующих элементов (находящихся в растворенном виде в основном металле) в повышении релаксационной стойкости заключается не только в увеличении сил межатомной связи. Растворенные элементы также влияют на скорость возврата, прежде всего потому, что они блокируют пороги и затрудняют переползание дислокаций. Кроме того, атомы растворенных элементов создают «облака» (атмосферы Коттрелла) на дефектах упаковки, изменяя их энергию. При уменьшении энергии дефекта упаковки переползание или поперечное скольжение дислокаций становится затрудненным. Это явление известно как сегрегационный механизм Сузуки. Влияние растворенных элементов может сохраняться до относительно высоких температур.
Легирующие элементы, растворенные в металле, влияют на скорость диффузии и самодиффузии в твердом растворе и с этой стороны также оказывают воздействие на развитие пластической деформации при высокой температуре.
Большая жаропрочность и релаксационная стойкость аустенитных сталей и сплавов по сравнению с ферритными обусловлена значительно (на несколько порядков) меньшей скоростью диффузии большинства легирующих элементов в γ-железе, чем в α-железе.
Способность растворенных элементов увеличивать силы межатомной связи и уменьшать скорость диффузии приобретает большую роль при весьма высоких температурах, превышающих 0,7 Тпл, когда пластическая деформация происходит главным образом за счет ориентированной диффузии атомов и вакансий. Легирующие элементы, растворенные в металле, изменяют условия его рекристаллизации. Уже малые количества (сотые и десятые доли процента) некоторых примесей повышают температуру начала рекристаллизации 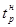 при больших степенях деформации (50—60%) и длительных отжигах. Такое влияние малых добавок объясняется тем, что облака растворенных атомов вокруг дислокаций препятствуют их перемещению. при больших степенях деформации (50—60%) и длительных отжигах. Такое влияние малых добавок объясняется тем, что облака растворенных атомов вокруг дислокаций препятствуют их перемещению.
Повышение концентрации растворенного элемента до нескольких процентов и больше по-разному влияет на величину 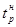 . Если легирующий элемент, введенный в металл, повышает прочность межатомных связей, то . Если легирующий элемент, введенный в металл, повышает прочность межатомных связей, то 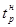 увеличивается. Однако интенсивность влияния примесных атомов при больших концентрациях намного слабее, чем при малых, и приращение величины увеличивается. Однако интенсивность влияния примесных атомов при больших концентрациях намного слабее, чем при малых, и приращение величины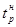 , приходящейся на 1% (ат.) добавляемого элемента, постепенно уменьшается. Для однофазных твердых растворов на основе никеля, железа и других металлов величина отношения , приходящейся на 1% (ат.) добавляемого элемента, постепенно уменьшается. Для однофазных твердых растворов на основе никеля, железа и других металлов величина отношения 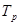 : :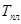 может быть повышена за счет увеличения межатомных связей только до 0,5—0,55. Более высокие температуры начала рекристаллизации могут быть получены в гетерофазных сплавах. может быть повышена за счет увеличения межатомных связей только до 0,5—0,55. Более высокие температуры начала рекристаллизации могут быть получены в гетерофазных сплавах.
Повышение температуры рекристаллизации сплава расширяет температурный интервал, в котором возможно эффективное сопротивление релаксации напряжений. Поэтому твердые растворы, образованные легирующими элементами, повышающими температуру начала рекристаллизации, сохраняют релаксационную стойкость до более высоких температур.
Однако наибольшее сопротивление релаксации напряжений (так же, как и ползучести) может быть достигнуто только в случае, если концентрация легирующих элементов превышает предельную растворимость их в металле основе при рабочих температурах и избыточные количества этих элементов выделяются с образованием частиц, задерживающих перемещения дислокаций.
Дислокации могут тормозиться зонами предвыделений, образующимися в кристаллической решетке выделяющимися фазами, еще когерентными с матричным твердым раствором и обособившимися частицами избыточных фаз разной степени дисперсности. При этом важное значение имеет расстояние между такими препятствиями. Если расстояние между препятствиями L мало по сравнению с предельным радиусом кривизны дислокации 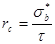 в поле напряжения σ, то дислокация с вектором Бюргерса b при перемещении по плоскости скольжения почти не искривляется. Это, например, происходит, когда препятствиями служат изолированные атомы элементов в твердом растворе. в поле напряжения σ, то дислокация с вектором Бюргерса b при перемещении по плоскости скольжения почти не искривляется. Это, например, происходит, когда препятствиями служат изолированные атомы элементов в твердом растворе.
Если же выделения находятся в виде крупных частиц, далеко отстоящих одна от другой (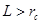 ), как в перестаренном сплаве при большой степени коагуляции частиц, то дислокация проходит между частицами. ), как в перестаренном сплаве при большой степени коагуляции частиц, то дислокация проходит между частицами.
Наибольшее торможение движению дислокаций наблюдается в промежуточном случае, когда 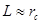 (весьма дисперсные выделения; частицы, когерентные с основным твердым раствором; зоны Гинье — Престона). (весьма дисперсные выделения; частицы, когерентные с основным твердым раствором; зоны Гинье — Престона).
Движущиеся с какой-то скоростью дислокации останавливаются частицами выделений; они могут преодолеть эти препятствия либо путем переползания, либо путем поперечного скольжения, чтобы пройти мимо препятствий или же между ними. Но частицы выделений, если они достаточно тверды и устойчивы, могут закрепить движущиеся дислокации, препятствуя их скольжению и переползанию.
Мак Лин [8] расчетным путем установил количественные соотношения между скоростью ползучести и расстоянием между центрами частиц упрочняющей фазы. При этом предполагалось, что плотность дислокаций и скорость их переползания таковы, что приводят к наблюдаемым в технике скоростям ползучести. При малых расстояниях между частицами (левая ветвь кривой) дислокации не смогут преодолеть частицы, а, вероятно, будут перерезать их или же «проталкивать» сквозь матрицу. При очень больших расстояниях между частицами (правая ветвь кривой), когда в интервале между ними может вместиться несколько дислокации, переползание их происходит одновременно, что и вызывает увеличение скорости ползучести. На горизонтальном участке АВ скорость ползучести не зависит от расстояния между частицами, так как при его увеличении пропорционально возрастает и размер частиц, вследствие него относительная величина свободного пути для движения дислокаций не меняется.
Высокая степень дисперсности частиц уменьшает скорость ползучести вследствие того, что она сильно уменьшает скорость возврата. Наличие дисперсных выделений оказывает заметное влияние и на протекание рекристаллизации в сплаве. По данным С. С. Горелика, большое число дисперсных частиц карбидных и других выделений может значительно повысить температуру начала рекристаллизации и увеличить 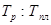 до ≈0,8. до ≈0,8.
Частицы избыточных фаз, находясь в мелкодисперсном состоянии, блокируют зародыши рекристаллизации, препятствуя их росту. Процессы рекристаллизации затрудняются и вследствие того, что частицы фаз выделения, удельный объем которых отличается от объема матрицы, могут находиться в состоянии фазового наклепа. И гетерофазных сплавах процесс рекристаллизации разбивается как бы на два раздельных процесса: зарождения и роста зародышей рекристаллизации. Температура 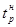 в пересыщенных твердых растворах является по существу температурой интенсивного роста зародышей рекристаллизации. Именно с этой температурой связано заметное разупрочнение таких сплавов. в пересыщенных твердых растворах является по существу температурой интенсивного роста зародышей рекристаллизации. Именно с этой температурой связано заметное разупрочнение таких сплавов.
Чем более термически устойчивыми являются частицы выделений, тем выше температурный порог рекристаллизации 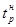 и тем выше релаксационная стойкость сплава. и тем выше релаксационная стойкость сплава.
Для того чтобы затормозить релаксацию напряжений, частицы выделений не только должны быть высокодисперсными, но и длительно сохранять высокую степень дисперсности. Перепутанные сетки дислокаций, образующиеся вследствие перемещения дислокаций в различных направлениях, малоподвижны и, кроме того, будут эффективно задерживаться мелкодисперсными частицами. Металл с такой структурой устойчиво сопротивляется возврату, ползучести и релаксации напряжений.
Коттрелл [4] указывает, что скорость деформации при ползучести может быть оценена отношением скорости возврата r к коэффициенту упрочнения h:(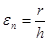 ). Стабильные дисперсные частицы оказывают сильное влияние на скорость возврата r. ). Стабильные дисперсные частицы оказывают сильное влияние на скорость возврата r.
При релаксации напряжений в температурной области, в которой активно развиваются процессы возврата, это имеет большое значение, так как деформационное упрочнение, а следовательно, и коэффициент упрочнения h, как было показано раньше, значительно меньше, чем при ползучести.
Стабильность размеров частиц избыточных фаз, определяющая интенсивность разупрочнения сплавов, в значительной степени зависит от природы этих фаз. Чем термически стабильнее избыточные фазы, тем менее активно идут обменные процессы между фазами выделений и матричным твердым раствором.
Особо следует остановиться на роли тонкой (блочной) структуры металла. Такие параметры тонкой структуры, как размер субзерен, угол их разориентировки и степень блокирования дислокационных границ, оказывают определенное влияние на сопротивление ползучести и релаксации напряжений. Образование специфичной дислокационной структуры с большим числом равномерно распределенных внутренних дислокационных барьеров является существенным фактором, тормозящим релаксацию микро- и макронапряжений (такие процессы в дальнейшем изложении мы будет называть соответственно микро- и макрорелаксацией).
Установлено, что более длительным сопротивлением релаксации напряжений и ползучести при повышенных температурах обладают металлы и сплавы с полигональной структурой. Объясняется это тем, что при полигонизации в структуре металла образуются устойчивые дислокационные стенки, в особенности если дислокации заблокированы инородными атомами. При этом важное значение имеет степень однородности полигональной структуры в данном объеме металла. В связи с изложенным практические методы создания оптимальных дислокационных структур применительно к релаксационностойким сплавам заслуживают пристального внимания.
Таким образом, релаксационная стойкость сплавов, предназначенных для работы в «среднем» интервале температур (от 0,25 до 0,5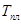 ), определяется: ), определяется:
1) атомнокристаллическим строением и типом кристаллической решетки основного металла. Например, сплавы на основе α-железа с о. ц. к. решеткой обладают эффективной релаксационной стойкостью до 600° С, сплавы на основе γ-железа с г. ц. к. решеткой — до 700° С, а сплавы на основе никеля — до 800° С;
2) содержанием легирующих элементов, образующих с основным металлом стабильные твердые растворы и способствующих повышению сил межатомного взаимодействия и температуры начала рекристаллизации;
3) гетерофазностью сплавов. В состав сплава должны входить элементы, образующие термически стабильные соединения, способные длительное время сохранять когерентность с основным твердым раствором и возможно медленнее коагулировать;
4) тонкой (блочной) структурой металла, образующей внутренние дислокационные барьеры, препятствующие движению дислокаций, и, в частности, наличием полигональных структур.
1.5 Связь релаксации напряжений и ползучести
Описанные выше теории ползучести позволяют на основе экспериментальных данных по ползучести при постоянных напряжениях рассчитывать кривые релаксации. Такие расчеты можно производить графически и аналитически.
В дальнейшем будут рассматриваться условия идеальной релаксации, когда во время нагружения перед испытанием на релаксацию ползучести не наблюдается.
Уравнение чистой релаксации может быть получено из дифференциального уравнения
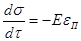 (23) (23)
Полагая, что 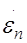 не зависит от времени [стационарная ползучесть не зависит от времени [стационарная ползучесть 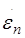 = =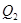 (σ)], и, проинтегрировав выражение при начальных условиях τ = 0, (σ)], и, проинтегрировав выражение при начальных условиях τ = 0, 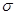 = =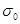 , получим , получим
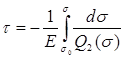 (24)
(24)
Примем вид зависимостей 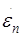 от напряжения в виде формул, предложенных Нортоном, Людвиком и Надаи, соответственно от напряжения в виде формул, предложенных Нортоном, Людвиком и Надаи, соответственно
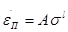 (25) (25)
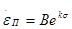 (26) (26)
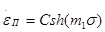 (27) (27)
где А, В, С, l, k, 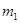 — константы. — константы.
Тогда из соотношения получим формулы для определения времени релаксации соответственно для уравнений:
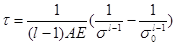 (28) (28)
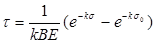 (29) (29)
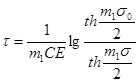 (30) (30)
При больших значениях времени τ и достаточно высоких температурах, когда оставшееся напряжение (σ) намного меньше начального (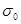 ), соотношения упрощаются: ), соотношения упрощаются:
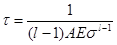 (31) (31)
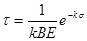 (32) (32)
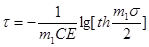 (33) (33)
Формулы справедливы при 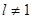 . При l = 1 решение уравнения преобразуется в известное уравнение Максвелла: . При l = 1 решение уравнения преобразуется в известное уравнение Максвелла:
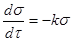 (34) (34)
имеющее решение
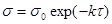 (35) (35)
Согласно уравнению, кривая релаксации может быть представлена в виде прямой линии в двойных логарифмических координатах lg σ—lg τ. В соответствии с уравнениями при некоторых ограничениях относительно констант 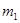 и С кривая релаксации может быть представлена в виде прямой линии в полулогарифмических координатах σ—lgτ. И, наконец, согласно уравнению, должна наблюдаться линейная зависимость в координатах lg σ—τ. и С кривая релаксации может быть представлена в виде прямой линии в полулогарифмических координатах σ—lgτ. И, наконец, согласно уравнению, должна наблюдаться линейная зависимость в координатах lg σ—τ.
Однако отсутствие неустановившейся стадии ползучести наблюдается лишь в условиях кратковременной ползучести и только при весьма высоких температурах.
Выражения, описывающие релаксационные процессы, были уточнены рядом авторов. Формула была видоизменена Б.М. Ровинским и В.Г. Лютцау введением показателя степени р, названного показателем пластичности или показателем релаксационной податливости:
 (35’) (35’)
Сопоставление результатов испытаний с значениями σ (τ), полученными расчетом по формуле, показано, что р изменяется от 0 до 1 в зависимости от концентрации легирующих элементов сплава, величины остаточной деформации, температуры, твердости.
Другая попытка уточнить формулу, описывающую кривые релаксации, была сделана Баушисом. Представив формулу в виде
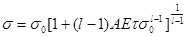 (36) (36)
и заменив АЕ предложенным выражением
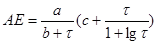 (37) (37)
получили следующую эмпирическую зависимость:
 (38) (38)
где а, b, с и l — константы.
Для нахождения уравнений релаксации в общем виде необходимо принять ту или иную гипотезу ползучести.
Из сказанного видны принципиальные отличия сопротивления релаксации и ползучести в условиях длительных сроков службы. Деформация ползучести, накопленная за срок службы материала, как правило, в основном определяется деформацией, накопленной на установившейся стадии, поскольку ползучесть на неустановившейся стадии сравнительно мала. Релаксационная же стойкость в значительной мере определяется скоростью ползучести на неустановившейся стадии.
Наиболее характерно это проявляется на титановых сплавах, у которых установившаяся скорость ползучести в диапазоне температур деформационного старения (300—350° С) близка к нулю.
В связи с изложенным при разработке релаксационностойких материалов и выборе режима их термической обработки большое внимание следует уделять повышению сопротивления ползучести не только на установившейся, но и на неустановившейся стадии.
2 Методы изучения релаксации напряжений
Процесс релаксации состоит из уменьшения упругих напряжений (деформаций) и накопления пластической деформации. Однако в отличие от пластического деформирования или ползучести пластическая деформация при релаксации незначительная и в объеме кристаллического тела она создается за счет весьма малых сдвигов (тонкое скольжение) по большому числу плоскостей скольжения, распределенных неравномерно, что затрудняет их микроскопическое изучение. Поэтому при исследовании релаксации напряжений в основном базируются на определении изменений упругой деформации.
2.1 Релаксация при растяжении и сжатии
Известны различные методы изучения релаксации напряжений в условиях одноосного растяжения, которые отличаются, в частности, тем, является ли разгружение образца в процессе испытаний необходимым для периодического измерения остаточного напряжения или нет.
Еще в 1953 г. Б.М. Ровинским и В.Г. Лютцау [12] был разработан метод испытаний, при котором периодически измеряют поперечное сечение образца, начальная продольная деформация которого остается постоянной.
Поперечную деформацию в испытаниях при комнатной температуре измеряют с помощью специальных чувствительных датчиков, а при повышенных температурах — методом обратных рентгеносъемок поперечной упругой деформации решетки.
Испытания проводят следующим образом: ненапряженный образец вместе с устройством для нагружения перед испытанием устанавливают в рентгеновской камере для определения периода решетки. Затем образец нагружают, и блок с образцом устанавливают в камере, где периодически измеряют упругую деформацию решетки.
В работе был предложен другой рентгеновский метод изучения релаксации напряжений. После определения периода решетки в исходном ненапряженном состоянии образец быстро растягивают до заданной величины пластической деформации, разгружают, а затем в нем периодически определяют период решетки прецизионной рентгеновской съемкой. Этот метод основан на том, что в деформированном металлическом образце при разгрузке возникают остаточная деформация решетки обратного знака и сжимающие ориентированные микронапряжения, которые релаксируют подобно напряжениям первого рода.
Для исследования релаксации напряжений при растяжении проводят испытания шпилек и болтов в обоймах и образцов на специальных релаксационных машинах.
Методики испытания в обоймах различной конструкции различаются степенью равномерности нагрева обоймы и образца, точностью измерения остаточных деформаций, точностью поддержания постоянной длины образца вовремя испытания, производительностью, используемыми приспособлениями для создания начального натяжения. Неравномерность нагрева обоймы и болта может вызывать местные перенапряжения болта. Недостаточное различие сечений обоймы и образца приводит к снижению жесткости напряженного состояния.
Кроме того, почти для всех методов испытаний в обоймах характерно нагружение при комнатной температуре и развитие процессов релаксации на первом этапе при переменной (повышающейся) температуре.
Одну из первых конструкций приспособлений для испытаний шпилек и болтов на релаксацию предложил Мохель. При каждом последующем нагружении напряжение в испытуемой шпильке доводили до первоначальной величины. Таким образом, условия испытания в этих опытах отличались от условий чистой релаксации. Методика Т.И. Волковой свободна от этого недостатка и позволяет проводить измерение оставшихся напряжений с точностью до ~ 46 МН/м2
(0,4 кг/мм2
). Измерение длины образца производят обычно на универсальном микроскопе. Для растяжения образца до заданной величины деформации используют специальное приспособление (ИР-4Р), представляющее собой комбинацию двух гаечных ключей, соединенных винтом, на котором находится рычаг с рукояткой. Полный оборот рукоятки создает натяжение 40 МН/м2
(4 кг/мм2
). Нагревательное устройство (ИР-3) рассчитано для работы в интервале 400—700° С. Однако при использовании этого метода возможны перенапряжения образца за счет неравномерного нагрева образца и обоймы.
Более производительный метод испытаний моделей болтовых соединений описан Б. М. Рахманом, предложившим конструкцию многоместной оправки. В этом случае образцы прогреваются несколько быстрее обоймы, в связи, с чем исключается возможность их перенапряжений.
Для изучения чистой релаксации напряжений на испытательной машине необходимо задавать и поддерживать заданную полную деформацию образца, фиксировать напряжение или изменение напряжений в образце, поддерживать с определенной точностью заданную температуру образца.
Поддержание полной деформации образца постоянной представляет значительные трудности в связи с податливостью системы и трудностями создания соответствующей системы разгрузки. Практически же условия чистой релаксации при испытаниях на машинах не реализуются. Для обеспечения указанных требований машины имеют нагружающее устройство, систему для поддержания деформации, систему для измерения напряжений и термостат (нагревательное устройство).
Основные параметры машин следующие:
1) диапазон изменения напряжений и деформаций;
2) диапазон температуры и точность ее поддержания;
3) точность измерений и поддержания нагрузки;
4) скорость нагружения и разгружения;
5) плавность изменения нагрузки;
6) надежность при длительной работе.
Известны различные виды нагружения: с помощью пружины, подвижного груза, груза, величина которого изменяется в процессе испытания (шары, вода), гидравлического пресса и др. Каждый из указанных видов обладает специфическими достоинствами и недостатками.
Так, например, машины с грузом, перемещающимся по одному рычагу, не позволяют проводить испытания при больших начальных пластических деформациях образца, закрепленного с одной стороны. Машины с нагрузкой, уменьшающейся во время испытания, могут производить лишь разгружение образца. Нагружение пружиной требует серьезного внимания к стабильности упругих свойств самой пружины.
Помимо нагружающей системы, релаксационные машины различаются системами, обеспечивающими поддержание заданной деформации образца. Эти системы, как правило, состоят из устройства, воспринимающего и увеличивающего деформацию образца (увеличитель деформации); устройства, вырабатывающего электрические импульсы при отклонении размеров образца, и, наконец, релейной системы, управляющей электродвигателем нагружающей системы.
Шевенар предложил рассматривать установку для измерения релаксации напряжений как замкнутую автоколебательную систему с обратной связью. В связи с этим требования, предъявляемые к релаксационным машинам, направлены на уменьшение амплитуды автоколебаний, что достигается увеличением жесткости частей увеличителя деформаций, повышением чувствительности системы датчика импульсов, увеличением жесткости нагружающей системы, уменьшением инерции движущихся частей машины и уменьшением трения в сочленениях нагружающей системы. На амплитуду автоколебаний влияют и такие параметры машины, как скорость нагружения и разгружения, время установления заданной скорости нагружения или разгружения после приема нагружающей системой импульса переключения.
Кинематическая схема модернизированной машины УИМ-5 представлена на рисунке 4.
Изменение длины образца О вызывает замыкание управляющих контактов контактного устройства К, связанного с экстензометром, и включение при помощи реле реверсивного электродвигателя М, который вращает червячное колесо 7. Вращение оси 6 червячного колеса передается на большой фрикционный ролик 5. На ось 4 ролика 5 намотан тросик 3, при помощи которого перемещается конец рычага 2. Конец малого плеча рычага 2 через тягу со встроенным динамометром Д соединен с концом нагружающего рычага 1. Таким образом, в зависимости от направления вращения электродвигателя конец нагружающего рычага перемещается вверх или вниз, соответственно уменьшая или увеличивая нагрузку на образец. Величина усилия регистрируется динамометром, соединенным с диаграммным механизмом, осуществляющим запись кривой релаксации напряжения.
Контактное устройство К, управляющее изменением нагрузки, имеет подвижный и два неподвижных контакта. Подвижный контакт, представляющий собой кусочек расплющенной серебряной проволоки, припаян к стрелке индикатора. Оба неподвижных контакта (небольшие серебряные пластинки) укреплены на плексигласовом стекле, заменяющем покрывающее стекло циферблата. Использование в качестве контактного устройства индикаторной головки с ценой деления 0,002 мм позволяет обеспечить постоянство замеряемой длины образца в пределах ±1 мкм при суммарном зазоре между контактами около 1 мм. Замыкание подвижного контакта с одним из неподвижных контактов вызывает вращение двигателя в ту или другую сторону.
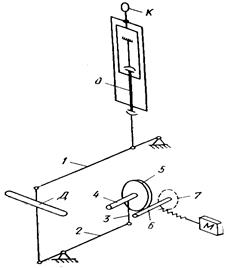
Рисунок 4 – Кинематическая схема модернизированной машины УИМ-5
При модернизации нагружающего устройства были использованы двигатель и червячная передача, которые в машине УИМ-5 служат для вращения бункера. Асинхронный двигатель типа МШ мощностью 75 Вт снабжен переменным сопротивлением, позволяющим регулировать число оборотов. Возможность реверсирования достигается изменением схемы питания щеток двигателя. Для реверсирования нагрузки введено дополнительное реле, срабатывающее от замыкания второго неподвижного контакта. Передаточное число червячной передачи равно 100. Большой фрикционный ролик 5 представляет собой текстолитовый диск с насаженным стальным кольцом. Диаметр валика 4, на который наматывается тросик 3, равен 4,3 мм, диаметр гибкого тросика 1,5 — 2 мм. Для обеспечения фрикционного сцепления один из подшипников, в которых вращается вал 4, движется свободно в вертикальном направлении. При натяжении тросика 3 создается контактное давление между фрикционными роликами, пропорциональное натяжению.
Это давление минимум в 95 раз больше, чем окружное усилие во фрикционном сцеплении, что гарантирует отсутствие проскальзывания при любом натяжении тросика.
Для того чтобы тросик наматывался на валик 4 по одной окружности независимо от угла подъема рычага 2 (это требуется для исключения возможности аксиального скольжения тросика по валику 4), соединение тросика с рычагом сделано подвижным. К концу тросика прикреплена горизонтальная ось с сидящими на ней двумя подшипниками, на которые опирается рычаг 2. Для устранения бокового давления на подшипники при отклонении рычага от горизонтали опорная поверхность рычага выполнена в виде эвольвенты. Эвольвентная поверхность пересекает плоскость намотки тросика под прямым углом при любом положении рычага, поэтому направление усилия, действующего на подшипники со стороны рычага, совпадает с осью тросика. В связи с заметной кривизной эвольвентной поверхности подшипники с достаточной точностью «находят» нужное положение, обеспечивая правильность намотки тросика.
Соотношение плеч рычага 2 равно в среднем 1:5. Опора рычага укреплена на плите (из листа толщиной 10—15 мм), подведенной под станину машины и жестко связанной с ней посредством анкерных болтов. Второй конец рычага 2 при помощи серьги соединен с резьбовой головкой динамометра Д. Другая резьбовая головка соединяется с концом нагружающего рычага 1.
Устройство для автоматической записи нагрузки состоит из барабанного часового механизма с недельным заводом и диаграммного пера. Перо укреплено на тонкой нити, которая наматывается на плексигласовый шкив, укрепленный на оси индикатора динамометра. Таким образом, изменение нагрузки, вызывающее поворот стрелки индикатора, приводит и к вертикальному перемещению пера. Так как характеристика динамометра линейна, смещение пера строго пропорционально нагрузке. Вся система уравновешена так, что ось индикатора не испытывает изгибающих нагрузок. Барабан помещен над нагружающим рычагом 1 и укреплен на траверсе, соединенной с тягой динамометра. Такое крепление необходимо для того, чтобы изменение наклона нагружающего рычага 1 не сказывалось на положении барабана.
Динамометр и диаграммное устройство тарируются на машине при помощи образцового динамометра, укрепляемого вместо образца и захватах машины. По данным тарировки строят тарировочные графики, которые позволяют по показаниям динамометра и по диаграмме рассчитать нагрузку на образец в процессе испытания.
Для нормальной работы нагружающего устройства угол наклона рычага 2 должен находиться в пределах 0—55° от горизонтали; соответственно максимально допустимый ход тросика составляет ~150 мм. Этого хода недостаточно для обеспечения нужной степени разгрузки образца в процессе испытания. Кроме того, колебания температуры помещения вызывают деформацию станины и наружных частей захватов. Происходящее при этом изменение натяжения образца автоматически компенсируется соответствующим перемещением рычага. Эти обстоятельства могут вывести рычаг 2 из нормального положения и нарушить правильный ритм работы машины. Чтобы этого избежать, на рычаге установлено реле, при помощи которого подается сигнал (звонок), указывающий на приближение рычага к крайнему верхнему или нижнему положению. С включением звонка останавливается двигатель. Перевод рычага 2 в нормальное положение (угол подъема 35—45°) осуществляется плавным подтягиванием или ослаблением цепочки при помощи рукоятки редуктора нижнего захвата. Так как длина образца автоматически поддерживается постоянной, то при помощи двигателя соответственно опускается, или поднимается рычаг.
Обслуживание машины с указанным выше нагружающим устройством состоит в наблюдении за температурой образца, периодической регистрации показаний индикатора динамометра и в редких случаях в подтягивании или ослаблении цепочки с образцом. Начальное натяжение образцу задается следующим образом. Рычаг 2 переводится в крайнее верхнее положение. С индикатора К снимается неподвижный контакт, управляющий увеличением нагрузки. Поворотом шкалы индикатора стрелка совмещается с делением, соответствующим заданной деформации образца (неподвижный контакт, управляющий разгружением, установлен на индикаторе так, что при соприкосновении с ним подвижного контакта стрелка совмещается с нулевым делением). Затем с помощью редукторного механизма подтягивают цепочку. При этом стрелка индикатора К движется до соприкосновения контакта, укрепленного на ней, с неподвижным контактом. В этот момент достигается заданная деформация, и двигатель начинает работать, разгружая образец. Второй неподвижный контакт установлен на индикаторе так, чтобы суммарный зазор составил 1 мм. После этого нагружающее устройство работает автоматически.
Кинематическая схема релаксационной машины 5ИМ, также сконструированной Н.Д. Зайцевым, приведена на рисунке 5. Она характеризуется большой скоростью нагружения и разгружения, позволяющей изучать кратковременную релаксацию напряжений при высоких температурах. Испытание на машине производят следующим образом.
Нагрев образца 8 производится в электропечи 9. После достижения необходимой температуры груз 1 устанавливают на рычаге 2 на расстоянии, соответствующем заданному начальному напряжению; электрический контакт 3 рычажка тензометра занимает нейтральное положение в узком зазоре между неподвижными контактами 4 и 5. Нагружение осуществляется снятием рычага с арретира 6. Одновременно вращением микрометрического винта 7 поддерживается установленное положение контакта 3. В момент отрыва рычага от арретира включают питание двигателя и диаграммного механизма. Барабан диаграммного аппарата вращается от сельсина 15 коробки скоростей 18 (υ =500 мм/ч). В дальнейшем процесс релаксации и регистрация изменений остаточного напряжения во времени происходят автоматически.
При накоплении пластической деформации определенной величины положение экстензометра 19 изменяется, что приводит к замыканию контактов 3 и 5 и срабатыванию электромагнитного реле. Под действием ртутного контакта 14 реле замыкается, цепь электродвигателя 13 и груз перемещаются в сторону уменьшения нагрузки, в результате чего напряжение снижается, образец сокращается до первоначальной длины, контакт тензометра приходит в исходное положение и снова начинается процесс релаксации в образце, но уже при меньшем растягивающем усилии и т. д. Одновременно с перемещением груза при вращении электродвигателя вращается ротор сельсина, закрепленного на стрелке рычага. Сельсин рычага электрически соединен с сельсином перемещения пера 16 диаграммного механизма, вследствие чего на барабане 17 регистрируется изменение нагрузки в процессе испытания.
Нагружение образца в машинах типа Рел-5 производят с помощью двуплечего рычага. Грузовое плечо рычага связано с парой пружин, которые можно заменять в зависимости от требуемого диапазона нагрузок [2500—12500, 5000—2500, 10000—50000 Н (250—1250, 500—2500, 1000—5000 кг)].
Пружины через винт, червячную пару и ременную передачу связаны с двигателем, вращение винта приводит к натягиванию или ослаблению пружин и соответственно нагружению или разгрузке образца. Система нагружения сопряжена с самопишущим диаграммным прибором, записывающим изменение нагрузки во времени. Измерение и передачи деформации производят с помощью трех кварцевых стержней тензометра. Величину деформации определяют измерительным микроскопом с винтовым окулярным микрометром. Для автоматического управления нагрузкой, действующей на образец, измеряемая деформация превращается в электрический сигнал с помощью датчика фотоэлемента. Луч света, направленный проекционной лампой через объектив к фотоэлементу, диафрагмируется в фокусе объектива специальной шторкой, прикрепленной к концу рычажной системы экстензометра. В условиях компенсации шторка диафрагмирует фотоэлемент примерно наполовину.
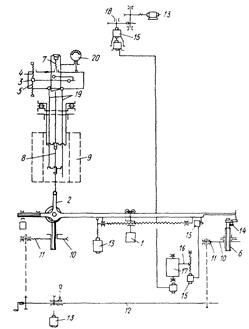
Рисунок 5 – Кинематическая схема машины 5ИМ для испытаний на релаксацию
Датчик фотоэлемента питается стабилизированным напряжением. Изменения тока фотоэлемента переносятся на ламповый мостик, который в свою очередь при разбалансировке передает соответствующий сигнал реле и блок контактам системы управления нагрузкой, действующей на образец.
Нагружение образца до заданной начальной деформации происходит с помощью измерительного микроскопа.
Для высокотемпературных испытаний на релаксацию в вакууме были приспособлены машины типа ПВ-152 и ПВ-3012 для испытаний на длительную прочность.
Указанные машины имеют вакуумную камеру для радиационного нагрева образцов вольфрамовыми стержневыми нагревателями до температуры 2000°С. Нагружающее устройство рычажное (передаточное отношение 1:60). Постоянная температура поддерживается стабилизацией напряжения с помощью специальных блоков регулирования, не допускающих колебаний температуры во время испытания не более ±2°С.
Машины снабжены устройством для автоматического перемещения верхнего захвата со скоростью 2 мм/мин во время нагрева и охлаждения образца без нарушения вакуумной плотности системы.
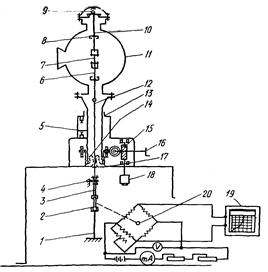
1— тяга нижняя; 2— упругий элемент; 3— тяга верхняя; 4— упор; 5— указатель положения подъемного винта; 6— захват нижний, 7— образец; 8— захват верхний; 5— шарнир специальный; 10— переходник; 11—электропечь; 12— тяга нижнего захвата; 13— винт подъемный; 14— сильфон; 15— редуктор; 16— рукоятка ручного перемещения винта; 17— диафрагма; 18— электродвигатель; 19—электронный потенциометр; 20— тензометрический мост
Рисунок 6 – Кинематическая схема машины ПВ-152М для испытаний на релаксацию
Видоизменение кинематической схемы машин ПВ-152М и ПВ-3012 для проведение испытаний на релаксацию состояло в демонтаже Системы нагружения, установке упругого элемента с тензодатчиками и жестком прикреплении цепочки с упругим элементом к станине.
Образец 1 (рисунок 6) закреплен в верхнем 2 и нижнем 3 захватах из молибденового сплава и может свободно расширяться при нагреве. Верхний захват через переходник 4 связан с опорным шарниром 5, а нижний — тягой 6 через упругий элемент 7 с корпусом машины. Тяга уплотнена с помощью резиновой диафрагмы. Нагружение образца производится автоматически путем подъема корпуса печи от электродвигателя 8 или вручную рукояткой 9 через редуктор 10.
Тензодатчики сопротивлением 100 Ом с базой 15 мм были изготовлены из константана и имели коэффициент тензочувствительности 2—2,2. Температурная компенсация (для исключения влияния колебаний температуры помещения) достигалась включением в симметричные плечи моста 11 константановых сопротивлений. Питание моста осуществлялось постоянным током 4—8 В от батарей. Рабочий ток составлял 15—90 МА в зависимости от диапазона тарировки.
Тарировку упругого элемента до 2000 Н (200 кг) производили методом непосредственного нагружения грузом определенной массы, при этом устанавливали зависимости показаний электронного потенциометра 12 (ЭПП-09) от величины нагрузки. Тарировку тензодатчика на 5000 и 10 000 Н (500 и 1000 кг) производили по образцовому динамометру, встроенному в цепочку нагружения. Цепочку с протарированным упругим элементом собирали таким образом, чтобы при откачке камеры не было подъема нижней тяги 13 под действием атмосферного давления; возникающее усилие воспринималось упругим элементом и электронный потенциометр фиксировал величину вакуумного груза.
Испытание на релаксацию осуществляется следующим образом. После достижения заданной температуры и установления силы тока заданной величины включаются электромеханический привод подъема печи 14 (скорость подъема 2 мм/мин) и привод диаграммы потенциометра ЭПП-09. По достижении нагрузки заданной величины привод подъема печи отключается и на диаграмме автоматически записывается кривая релаксации.
Для испытаний на релаксацию в условиях сжатия была предложена конструкция установки УМИР-10 мощностью 10 т.
Образец лежит на роликовых опорах и он может перемещаться по плоскостям соприкосновения с опорой. Чем больше напряжения в образце, тем больше сил необходимо для преодоления сил трения. Падение напряжений во время испытания измеряется по изменению сил трения.
Машина для испытании чугуна на релаксацию в условиях сжатия, была создана на основе установки для испытаний на ползучесть. Образец, представляющий собой цилиндр диаметром 6,35 и высотой 25,4 мм, сжимается между двумя стержнями, торцы которых имеют шлифованную притертую поверхность. Нагрузка прилагается с помощью системы рычагов. Деформацию измеряют специальным экстензометром, увеличивающим в 5 раз перемещение с помощью системы рычагов. Поддержание деформации на заданном уровне достигается перемещением груза вдоль нагружающего рычага, осуществляемым с помощью сервомотора и винта.
Указанная система характеризуется следующими параметрами: скорость двигателя 1,5 об/мин, шаг винта 25 мм, перемещение конца рычага экстензометра на 0 0075 мм приводит к изменению напряжения в образце на 0,84 МН/м (0,084 кг/мм2
). Начальное нагружение осуществляется отвинчиванием нажимного винта под концом рычага, на котором устанавливают на подвеске необходимые для создания заданного начального напряжения грузы. Одновременно с отвинчиванием винта ввинчивается микрометр до появления контакта с рычагом экстензометра. При этом срабатывает реле и начинается процесс испытания.
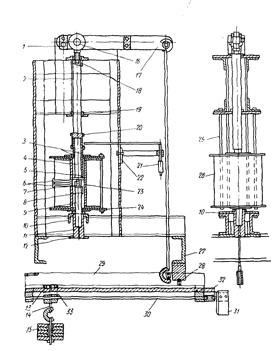
1 — опорная призма; 2— верхний толкатель; 3— стержень из кремнезема; 4 — участок верхнего толкателя из кремнезема; 5 и 8 — верхний и нижний вкладыши из жаропрочного сплава; 6 — термопарпые вводы; 7— образец; 9— участок верхнего толкателя из кремнезема; 10, 12— установочные детали; 13 — тележка; 14 — подвеска; 15 — груз; 16 — кольцо шарикоподшипника; 17 — верхний рычаг; 18 — втулка; 19 — втулка; 20 — экстензометр со скользящими полувтулками; 21 — головка микрометра; 22 —регулируемые направляющие; 23 — направляющая деталь; 24 — конец печи, 25 — направляющие стержни печи; 26— печь; 27— швеллер; 28 — опорная призма; 29 — нижний рычаг; 30 — шпиндель с прямоугольной резьбой; 31—электродвигатель; 32 — рельс; 33 — движущаяся пластина
Рисунок 7 – Схема машины для испытаний на релаксацию в условиях сжатия
2.2 Релаксация при изгибе и кручении
Наибольшее применение нашли два метода испытаний на релаксацию при изгибе: кольцевых образцов и плоских пружин. Метод И. А. Одинга, являющийся в наших лабораториях практически основным для получения характеристик сопротивления релаксации материалов, состоит в следующем: кольцевой образец, сконструированный в виде бруса равного сопротивления изгибу (рисунок 8), нагружают с помощью клина определенной толщины, вставленного в прорезь. Образец с клином помещают в нагревательное устройство (печь или жидкую ванну), где во времени происходят процессы релаксации первоначальных напряжений. Заданное начальное напряжение создается выбором толщины клина. Величину релаксированного напряжения определяют по изменению первоначальной ширины прорези. Напряжения определяют по формулам
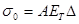 (39) (39)
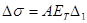 (39’) (39’)
где А — константа, полученная из условия линейного распределения напряжений по среднему сечению образца (А = 0,000583 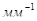 ); );
 —модуль упругости при температуре испытания; —модуль упругости при температуре испытания;
 — изменение ширины прорези за счет установки клина; — изменение ширины прорези за счет установки клина;
 — изменение первоначальной ширины прорези за счет ползучести. — изменение первоначальной ширины прорези за счет ползучести.
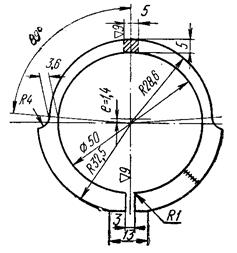
Рисунок 8 – Кольцо для испытаний на релаксацию по методу Одинга
Метод имеет следующее ограничение: если начальное напряжение 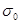 равно или превышает предел упругости (пропорциональности) материала при температуре испытания, то мгновенная пластическая деформация резко изменяет фактическое значение равно или превышает предел упругости (пропорциональности) материала при температуре испытания, то мгновенная пластическая деформация резко изменяет фактическое значение 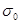 [так, пластическая деформация 0,05% приводит к уменьшению [так, пластическая деформация 0,05% приводит к уменьшению 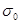 на 85 МН/м2
(8,5кг/мм2
). В связи с этим испытания кольцевых образцов возможны при на 85 МН/м2
(8,5кг/мм2
). В связи с этим испытания кольцевых образцов возможны при 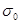 , равном , равном 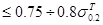 . Но и при . Но и при 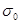 = =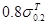 в ряде случаев возможны ошибки в связи с пластической деформацией при комнатной температуре, это наблюдается при условии в ряде случаев возможны ошибки в связи с пластической деформацией при комнатной температуре, это наблюдается при условии
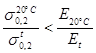 (40) (40)
Это условие выполняется, например, для сталей ЭИ612 и ЭИ787 при 650—700° С.
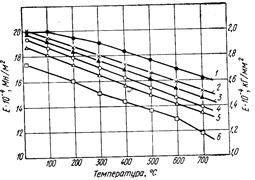
1,3,4 — в ЦНИИТМАШ; 2—в ЦКТИ; 5 — в институте им. Баранова; 6 — в ВИАМ
Рисунок 9 - Изменение модуля упругости сталей ЭИ612 и ЭИ481 в зависимости от температуры, определенного динамическим (1—5) и статическим методами (6), полученные в разных лабораториях.
При испытаниях кольцевых образцов точность расчета падения напряжений, согласно формуле, зависит от достоверности определения значений модуля упругости. В настоящее время широко используются два метода определения модуля упругости: статический и динамический.
Время замера и диапазон используемых напряжений практически исключают возможность протекания процессов ползучести при динамическом (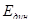 ) и статическом ( ) и статическом (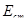 ) методах определения модуля упругости. Однако разница между значениями ) методах определения модуля упругости. Однако разница между значениями 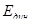 и и 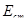 достигает иногда 20%. Кроме того, определенные различия значений модуля упругости наблюдаются при его определении на образцах разных размеров, на металле разных плавок, с разным уковом и т. п. достигает иногда 20%. Кроме того, определенные различия значений модуля упругости наблюдаются при его определении на образцах разных размеров, на металле разных плавок, с разным уковом и т. п.
На рисунке 9 в качестве примера приведены кривые зависимости модуля упругости сталей ЭИ481 и ЭИ612, полученные различными методами, в разных лабораториях.
Известны методы пересчета результатов испытаний кольцевых образцов на случай одноосного напряженного состояния. В.И. Розенблюм предложил решение задачи о перераспределении напряжений в изогнутом брусе, использовав гипотезу течения. И.А. Одинг и Г.Ф. Лепин провели соответствующие расчеты на основе предположения о превращении в процессе релаксации треугольной эпюры в трапецеидальную.
Оригинальный метод расчета изменений напряжений в кольцевом образце был предложен Е. А. Хейном, который рассматривает задачу релаксации напряжений в прямоугольном брусе при чистом изгибе. В этом случае все элементы объема находятся в линейном напряженном состоянии.
В любой момент времени τ распределение напряжений в образце σ(y) однозначно зависит от начального напряжения. При первом нагружении 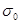 (у)= (у)=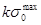
Обозначив 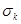 (y) — напряжение треугольной эпюры, равномоментной истинной эпюре напряжений, получим (y) — напряжение треугольной эпюры, равномоментной истинной эпюре напряжений, получим
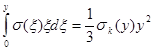 (41) (41)
Продифференцировав обе части уравнения по у
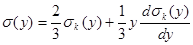 (42) (42)
и проведя элементарные преобразования, получим
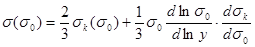 (43) (43)
Для первого нагружения 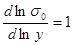 и и
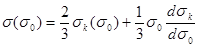 (44) (44)
Для расчетов n-ного нагружения по формуле необходимо знать величину начального напряжения 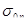 , которую определяют последовательно из формулы , которую определяют последовательно из формулы
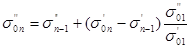 (45) (45)
выведенной из предположения трансформирования поперечного размера образца 2h:
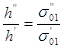 (46) (46)
где 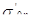 и и 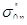 — начальное напряжение при п-м нагружении для образцов с начальными напряжениями при первом нагружении — начальное напряжение при п-м нагружении для образцов с начальными напряжениями при первом нагружении 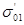 и и 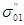 ; ; 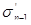 и и 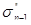 — конечные напряжения при (п—1)-м нагружении для образцов с начальными напряжениями при первом нагружении — конечные напряжения при (п—1)-м нагружении для образцов с начальными напряжениями при первом нагружении 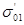 и и 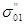 . .
На рисунке 10 приведены схема расчета начальных напряжений по уравнению для второго нагружения и графический метод расчета истинного напряжения. Проведенные расчеты показали, что кривые релаксации 1, рассчитанные по формулам 42-45 для первого нагружения близки к кривым 4, полученным по формуле. После повторных нагружений указанные кривые резко различаются: истинная кривая одноосной релаксации оказывается ниже найденной по формулам, рисунок 11. Кривые 2, рассчитанные по гипотезе трапеции, оказываются ниже истинных для первого и повторных нагружений. Кривые релаксации 3, подсчитанные по теории течения, оказались также близкими к истинной.
Значительно меньшее распространение получил другой способ испытания на релаксацию при изгибе, разработанный в ЦНИИТМАШе. Испытанию подвергают плоскую пластину, которой задается определенный прогиб. Принцип действия специального приспособления ИР-4Н, созданного для таких испытаний, следующий.
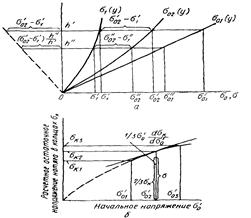
Рисунок 10 - Схема расчета начальных напряжений по уравнению для второго нагружения (а) и графический метод расчета истинного напряжения (б)
Кулачки приспособления, создающие необходимый прогиб пластины, выбирают в зависимости от величины заданного начального напряжения. Поворот кулачка на 90° обеспечивает создание прогиба двух одновременно испытываемых пружин. Кулачки после прогрева приспособления поворачивают с помощью специального ключа. Разгрузку образца производят тем же ключом.
А, Б —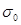 =2ОО и 300 МН/м2
(20 и 30 кг/мм =2ОО и 300 МН/м2
(20 и 30 кг/мм ) соответственно: I, II, III — первое, второе и третье погружение соответственно ) соответственно: I, II, III — первое, второе и третье погружение соответственно
Рисунок 11 - Кривые релаксации напряжений, рассчитанные по данным испытаний кольцевых образцов.
Напряжения рассчитывают по формулам:
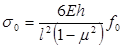 (47) (47)
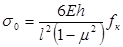 (48) (48)
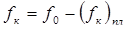 (49) (49)
где 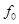 — начальный упругий прогиб; — начальный упругий прогиб;
(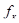 )) )) — остаточный прогиб; — остаточный прогиб;
l — длина пластины;
h — толщина;
μ— коэффициент Пуассона.
Для измерения (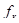 ) ) используют специальный электромикрометр. используют специальный электромикрометр.
Недостатком метода является трудность в изготовлении пластин, особенно в случае немагнитного материала.
Ограниченное применение получили также методы испытания на изгиб образцов в виде металлической ленты, предложенные применительно к пружинным лентам. Сущность метода состоит в следующем.
Пружинную ленту вводят в стальные кольца, внутренний диаметр которых выбирают в соответствии с начальным напряжением. Размеры колец должны обеспечивать получение только упругой деформации. «Заряженные» кольца выдерживают при температуре испытания в течение времени, необходимого для построения кривой релаксации. Метод нагрева колец с лентой, так же как и метод нагрева кольцевых образцов Одинга, выбирают в зависимости от тех требований, которые ставит перед собой исследователь в отношении тщательности изучения первого участка релаксации. В случае необходимости определения остаточного напряжения через несколько минут после нагружения применяют нагрев в расплаве солей, состав которых выбирают применительно к температуре испытания. Для углеродистых сталей и сталей с ограниченным количеством никеля возможен более интенсивный нагрев — в расплаве чистого свинца или его эвтектик. Испытания при температурах, не вызывающих интенсивного развития процессов ползучести, проводят с нагревом в печи. Остаточное напряжение определяют по замерам радиуса кривизны ленты, извлеченной из кольца, с помощью формулы
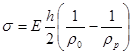 (50) (50)
где h — толщина ленты;
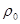 — радиус кольца; — радиус кольца;
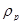 —радиус кривизны ленты, деформированный при релаксации. —радиус кривизны ленты, деформированный при релаксации.
Расчеты по формуле, так же как и по формуле для кольцевых образцов Одинга, предполагают треугольную эпюру распределения напряжений по сечению.
Для исследования релаксации напряжений в процессе быстрого нагрева металла (до 2000 град\сек) была разработана методика, позволяющая испытывать в условиях изгиба плоские пластины, нагреваемые пропусканием тока.
При этих испытаниях уменьшаются "напряжения в процессе нагрева за счет релаксации напряжений при переменной температуре и уменьшения модуля упругости при увеличении температуры:
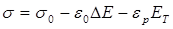 (51) (51)
где
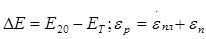 (52) (52)
причем  — начальное упругое напряжение при 20° С; — начальное упругое напряжение при 20° С; 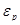 — пластическая деформация при температуре Т, слагающаяся из деформации ползучести — пластическая деформация при температуре Т, слагающаяся из деформации ползучести 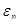 и мгновенной пластической деформации и мгновенной пластической деформации 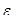 . .
Изучение релаксации напряжений при кручении проводят на образцах различного типа. Так, например, для испытания на релаксацию напряжений в стальной проволоке сконструирована установка, представленная схематически на рисунке 12. Начальное напряжение в образце на этой установке задается поворотом груза 6, связанного с одним из захватов. Величина остаточного напряжения регистрируется автоматически с помощью механизма 18, а также может контролироваться с помощью стрелки 10. Угол закручивания образца поддерживается постоянным с помощью следящей системы, которая отводит замыкающий контакт 13 системы, укрепленной на захвате без груза. Установка снабжена печью, позволяющей проводить испытания образцов при температуре до 600° С.
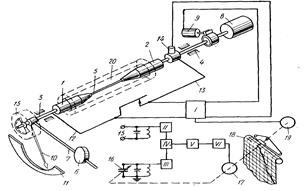
1, 2 —захваты; 3, 4 — опоры; 5 — образец; б — груз; 7 — рычаг с переменным плечом; 8, 9 и 17—электродвигатели; 10 — стрелка; 11 — шкала; 12 и 13 — замыкаемый контакт системы; 14 —электромагнитный фиксатор, 15 — емкостный датчик; 16 — конденсатор; 18 — механизм записи диаграмм; 19— ограничитель нагрузки; 20 — нагревательная печь;
I — релейное устройство нагрузки; II —III—высокочастотные генераторы; IV — смеситель; V — детектор; VI — выходное релейное устройство
Рисунок 12 - Схема установки для измерения релаксации напряжений в проволоке при кручении.
2.3 Релаксация в винтовых пружинах
Испытания на релаксацию натурных винтовых пружин обычно являются технологическими испытаниями, которые проводят для определения стабильности пружин во времени. Такая методика предусматривает испытание цилиндрической пружины, надетой на оправку и сжатой на определенную величину. Начальное напряжение рассчитывают по формуле:
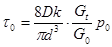 (53) (53)
где D — диаметр пружины;
d — диаметр проволоки;
G0
и 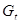 ; — модули сдвига при 20° С и температуре испытания t соответственно; ; — модули сдвига при 20° С и температуре испытания t соответственно;
k — коэффициент неравномерности навивок пружины;
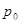 — нагрузка, приложенная при комнатной температуре для осуществления сжатия пружины до заданной величины — нагрузка, приложенная при комнатной температуре для осуществления сжатия пружины до заданной величины 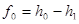 ( ( и и 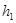 ) — высота пружины в свободном состоянии и в момент нагружения при 20° С соответственно). Остаточное напряжение ) — высота пружины в свободном состоянии и в момент нагружения при 20° С соответственно). Остаточное напряжение
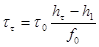 (54) (54)
где 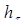 — высота пружины, разгруженной в момент времени τ, в свободном состоянии. — высота пружины, разгруженной в момент времени τ, в свободном состоянии.
Для измерения упругой осадки пружины применяют специальные приспособления с электрощупом, позволяющие производить замеры с точностью до ±0,01 мм.
Следует отметить, что при испытании пружин, так же как и при испытаниях на изгиб, нагружение производят лишь в упругой области.
Для уменьшения интенсивно развивающихся процессов релаксации напряжений непосредственно при их нагружении в ряде случаев применяют технологическую операцию, называемую «заневоливанием», состоящую в следующем. Изготовленную пружину сжимают до соприкосновения витков и длительно выдерживают в таком состоянии. Процесс заневоливания пружин считается законченным, когда скорость течения релаксационных процессов становится постоянной.
Для изучения закономерностей релаксации напряжений в пружинах сжатия при их заневоливании сконструирована специальная установка (рисунок 13), позволяющая проводить испытания при комнатной и повышенных температурах с автоматической записью кривых релаксации.
Установка состоит из нагружающего устройства, печи, весов и фотореле. Пружину 3 устанавливают на подставку, затем через нее продевают тягу 4. Домкрат 9 служит для подъема и опускания подвески 16, на которой устанавливают гири 5 и гидрогирю 6, при нагружении и разгружении пружины. Когда подвеска освобождается от домкрата 9 и вся нагрузка сосредоточивается на пружине 3, щель фотоэлемента устанавливается в тени флажка 15, и включается фотореле 19. При падении несущей способности пружины она сжимается и флажок, прикрепленный к стрелке индикаторной головки 1, открывает щель фотоэлемента, вследствие чего включается реле, замыкающее цепь электромагнитного пережима 8, открывается сифон 7 для откачки воды из гидрогири 6. Откачиваемая вода попадает в ведро 10 весоизмерителя 13 и ее масса, соответствующая падению нагрузки пружины во времени, регистрируется записывающим устройством 18.
В последние годы Чижиком А.А. разработан метод испытания на релаксацию металла натурных пароперегревательных труб. Испытания проводят в условиях сжатия на специальных пружинных образцах с прямоугольным сечением витка рисунок 14. Применительно к условиям получения достаточной точности испытаний и предупреждения потери устойчивости для труб диаметрами 25—75 мм установлены оптимальные размеры пружинного образца: длина 40, шаг спирали 8 мм. Образцы обычно изготовляют фрезерованием и каждый образец подвергают тарировке, состоящей в определении усилия, необходимого для осадки образца до высоты, соответствующей длине калибра. В результате тарировки определяют жесткость образца 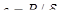 , где Р — приложенное усилие; δ— соответствующая этому усилию линейная деформация образца. , где Р — приложенное усилие; δ— соответствующая этому усилию линейная деформация образца.
Начальную осадку образца 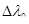 определяют по формуле определяют по формуле
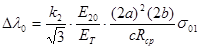 (55) (55)
где 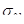 — условное начальное напряжение; — условное начальное напряжение; 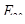 и и 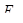 — модули упругости при 20° С и температуре испытания t; 2а — ширина сечения витка; 2b — высота; k2
— константа, зависящая от отношения b/a. — модули упругости при 20° С и температуре испытания t; 2а — ширина сечения витка; 2b — высота; k2
— константа, зависящая от отношения b/a.
Пружины испытывают в специальных приспособлениях (рисунок 14). Величина 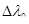 создается затягом двумя опорными гайками и фиксируется фиксирующими втулками высотой создается затягом двумя опорными гайками и фиксируется фиксирующими втулками высотой 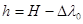 , где H — высота образца. Этот метод испытаний, так же как и испытания с кольцевыми образцами Одинга, является массовым: испытывается по 15—20 образцом. , где H — высота образца. Этот метод испытаний, так же как и испытания с кольцевыми образцами Одинга, является массовым: испытывается по 15—20 образцом.
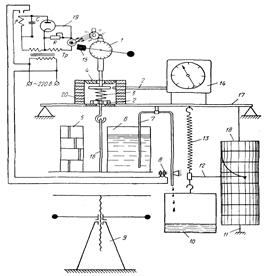
1— индикаторная головка; 2— термопара; 3 — испытуемая пружина; 4 — тяга; 5 —гиря; 6 — гидрогиря; 7 — резиновая трубка; 8 — электромагнитный пережим; 9 — домкрат; 10 —ведро; 11 — ось электрочасов; 12 — указывающая и записывающая стрелки; 13 — весоизмерительная пружина; 14 — потенциометр ЭМД-237; 15—стрелка-флажок; 16 — грузовая подвеска; 17 — стол установки; 18 — записывающие барабанные электрочасы; 19— фотореле; 20 — электропечь
Рисунок 13 - Схема автоматической установки для измерения релаксации напряжения в пружинах сжатия.
1 — опорные гайки; 2 — фиксирующие втулки; 3 — стержень; 4 — образец
Рисунок 14 - Образец (а) и приспособление (б) для массовых испытаний пароперегревательных труб на ползучесть и релаксацию напряжений.
Факторы, влияющие на протекание процесса релаксации напряжений, можно разделить на внутренние — зависящие от испытуемого материала и внешние — от него не зависящие.
К числу внутренних факторов относятся: химический состава сплава; структура: макро- и микроструктура, тонкая (мозаичная и дислокационная) структура; технологические особенности: способ выплавки, обработка давлением, наклеп, термическая обработка.
К главным внешним факторам относятся: условия нагружения и разгружения; начальное напряжение; время (срок службы детали); температура; масштабный фактор.
3.1 Влияние начального напряжения на протекание процесса релаксации
Начальное напряжение  оказывает существенное влияние на протекание процесса релаксации, а следовательно, и на величину напряжений оказывает существенное влияние на протекание процесса релаксации, а следовательно, и на величину напряжений 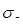 , «оставшихся» через различные промежутки времени. При этом влияние , «оставшихся» через различные промежутки времени. При этом влияние  в I и II периодах релаксации имеет свои особенности. в I и II периодах релаксации имеет свои особенности.
1 — 200(20); 2 —250(25); 3 — 300(30); 4 — 400(40)
Рисунок 15 — Первичные кривые релаксации жаропрочного никельхромового сплава при 750° С и различных значениях , МН/м2
. , МН/м2
.
Принято считать, что с повышением величины σ0
процесс релаксации напряжений в начальном периоде интенсифицируется и тем заметнее, чем выше гомологическая температура. Анализ начальных участков большого числа первичных кривых релаксации показывает, что влияние начального напряжения сказывается не столько на абсолютной величине падения напряжения  , сколько на скорости снижения напряжения, что видно, например, из рисунка 15. Однако взаимное расположение кривых σ—τ, получаемое при различных значениях , сколько на скорости снижения напряжения, что видно, например, из рисунка 15. Однако взаимное расположение кривых σ—τ, получаемое при различных значениях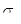 , на первом этапе процесса релаксации не всегда соответствует начальным напряжениям, при которых они получены. , на первом этапе процесса релаксации не всегда соответствует начальным напряжениям, при которых они получены.
Если задаться некоторой величиной , то при различных значениях , то при различных значениях 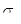 она будет достигнута через различные промежутки времени τ. Чем выше она будет достигнута через различные промежутки времени τ. Чем выше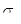 , тем короче время, необходимое для достижения заданной величины , тем короче время, необходимое для достижения заданной величины 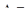 , и наоборот, хотя здесь нельзя установить строгой пропорциональности. , и наоборот, хотя здесь нельзя установить строгой пропорциональности.
Иная картина наблюдается во II периоде, когда процесс релаксации идет с более или менее установившейся скоростью. Здесь влияние 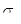 на интенсивность релаксации напряжения практически отсутствует, во всяком случае, при температурах ниже 0,5 Тпл
. Скорости релаксации при разных значениях на интенсивность релаксации напряжения практически отсутствует, во всяком случае, при температурах ниже 0,5 Тпл
. Скорости релаксации при разных значениях 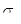 , как правило, весьма близки. Кривые σ—τ на втором участке подобны и эквидистантны, отличаясь лишь по взаимоположению относительно оси ординат, т. е. по уровню оставшихся в данный момент времени напряжений. Это хорошо иллюстрируется приведенным на рисунке 15 семейством первичных кривых релаксации жаропрочного никельхромового сплава при четырех значениях , как правило, весьма близки. Кривые σ—τ на втором участке подобны и эквидистантны, отличаясь лишь по взаимоположению относительно оси ординат, т. е. по уровню оставшихся в данный момент времени напряжений. Это хорошо иллюстрируется приведенным на рисунке 15 семейством первичных кривых релаксации жаропрочного никельхромового сплава при четырех значениях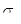 . .
При более высоких температурах (>0,5 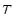 ) первичные кривые σ—τ часто утрачивают подобие, и скорости релаксации при разных значениях сто становятся непостоянными. ) первичные кривые σ—τ часто утрачивают подобие, и скорости релаксации при разных значениях сто становятся непостоянными.
Зависимость оставшегося (конечного) напряжения 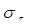 от начального определяется влиянием последнего на протекание процесса релаксации в обоих периодах. При температурах, не превышающих 0,5 от начального определяется влиянием последнего на протекание процесса релаксации в обоих периодах. При температурах, не превышающих 0,5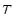 , степень увеличения интенсивности процесса релаксации в I периоде за счет повышения величины , степень увеличения интенсивности процесса релаксации в I периоде за счет повышения величины 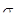 (в пределах до 0,8 (в пределах до 0,8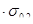 ) обычно такова, что в конечном счете более высокое начальное напряжение приводит к более высокому оставшемуся напряжению. ) обычно такова, что в конечном счете более высокое начальное напряжение приводит к более высокому оставшемуся напряжению.
Взаимосвязь начального и оставшегося (конечного) напряжений (или начального напряжения и падения напряжения  ) наиболее наглядно представлена графиками ) наиболее наглядно представлена графиками 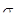 — —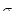 и и 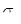 — —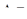 рисунок16. Такие кривые строят для переменных значений времени релаксации τ (либо температуры t). При t=const, рисунок16. Такие кривые строят для переменных значений времени релаксации τ (либо температуры t). При t=const, 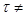 const эта зависимость изображается пучком расходящихся прямых для разных значений τ, проходящих через нулевую точку осей координат рисунка 16. const эта зависимость изображается пучком расходящихся прямых для разных значений τ, проходящих через нулевую точку осей координат рисунка 16.
Следует отметить, что начало пучка прямых в нулевой точке исключает понятие «условного предела релаксации» и возможность его графического определения. Более правильны схемы рисунок 16,в,г, где пучок прямых пересекается с осью начального напряжения в некоторой точке, отвечающей пределу релаксации.
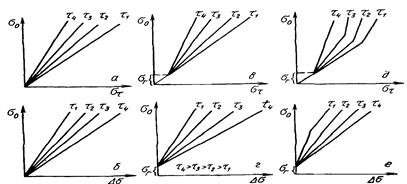
Рисунок 16 - Схематические зависимости 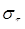 = f ( = f (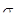 ) (а, в, д) и ) (а, в, д) и 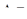 = f ( = f (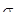 ) (б,г,е) ) (б,г,е)
Не получило подтверждения и высказанное в свое время Я. С. Гинцбургом [15] положение, что зависимость 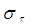 = f( = f(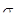 ) подчиняется степенному закону и может быть описана уравнением ) подчиняется степенному закону и может быть описана уравнением 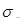 = a( = a(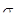 )р
. В действительности при построении графиков )р
. В действительности при построении графиков 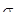 — —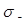 в двойной логарифмической системе координат в большинстве случаев не наблюдается прямолинейности кривых. в двойной логарифмической системе координат в большинстве случаев не наблюдается прямолинейности кривых.
Приведенные выше экспериментальные данные и основные закономерности следует учитывать при выборе начальных напряжений для деталей, предназначенных для работы в условиях релаксации напряжений. Очевидно, что более высокие начальные напряжения, как правило, обеспечивают и более высокие значения оставшихся (конечных) напряжений.
Однако при этом величина 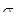 не должна превышать величину предела упругости материала при данной температуре. При назначении начальных напряжений в практике обычно ориентируются не на предел упругости, а на предел текучести не должна превышать величину предела упругости материала при данной температуре. При назначении начальных напряжений в практике обычно ориентируются не на предел упругости, а на предел текучести 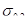 , допуская, как правило, , допуская, как правило, 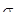 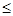 0.8 0.8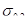 (за исключением особых случаев, о которых будет сказано ниже). (за исключением особых случаев, о которых будет сказано ниже).
Таким образом, начальное напряжение релаксации зависит от уровня упругих свойств материала. Исходя из этого, некоторые авторы выражают  в долях от величин в долях от величин  или или  , считая, что в случае необходимости сопоставить релаксационную стойкость ряда материалов целесообразно проводить сравнительные испытания не при одинаковых абсолютных значениях , считая, что в случае необходимости сопоставить релаксационную стойкость ряда материалов целесообразно проводить сравнительные испытания не при одинаковых абсолютных значениях  , а при одинаковой величине отношения , а при одинаковой величине отношения 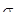 / /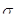 (или (или 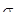 / /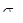 ). ).
Такой подход, без сомнения, является правильным, так как позволяет более строго сопоставлять релаксационную стойкость серии материалов, сильно различающихся по своим механическим свойствам (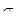 , ,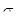 , ,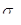 ) в определенном диапазоне температур. ) в определенном диапазоне температур.
Л.П. Никитиной [13] предложена методика выбора начальных напряжений, основанная на изложенном принципе и дающая широкие возможности сравнительной оценки разнообразных материалов по их сопротивляемости релаксации напряжения при разных температурах, притом с затратой минимального числа образцов, а следовательно, и общего времени испытаний.
До сих пор мы рассматривали влияние начальных напряжений на зависимости 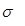 =f( =f( ) либо ) либо  = f ( = f ( ) при начальных напряжениях, не превышающих ) при начальных напряжениях, не превышающих  ( ( ), как это наблюдается в крепежных деталях. ), как это наблюдается в крепежных деталях.
В определенных условиях нередко отмечается релаксация при   , которая может реализоваться при растягивающих нагрузках (но не при испытаниях кольцевых образцов). Релаксация напряжений при , которая может реализоваться при растягивающих нагрузках (но не при испытаниях кольцевых образцов). Релаксация напряжений при   , например, наблюдалась в испытаниях на термическую усталость с выдержками при максимальной температуре цикла, а также в специальных опытах. , например, наблюдалась в испытаниях на термическую усталость с выдержками при максимальной температуре цикла, а также в специальных опытах.
В этих условиях процесс релаксации напряжений при   характеризуется следующими особенностями. характеризуется следующими особенностями.
При высоких температурах  снижается до снижается до 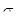 за короткое время, исчисляемое минутами; при нормальной и умеренно повышенных температурах действующее напряжение даже в течение весьма длительного времени может оставаться значительно больше за короткое время, исчисляемое минутами; при нормальной и умеренно повышенных температурах действующее напряжение даже в течение весьма длительного времени может оставаться значительно больше  . Кроме того, наблюдается немонотонный характер зависимости . Кроме того, наблюдается немонотонный характер зависимости 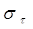 =f( =f(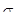 ) при τ = const. Действительно, как было показано выше, кривые релаксации для разных ) при τ = const. Действительно, как было показано выше, кривые релаксации для разных 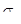 (больших (больших  ) могут пересекаться. Однако с увеличением времени эти кривые при сравнительно высоких температурах обычно сливаются в одну, мало отличающуюся от кривой, получаемой при ) могут пересекаться. Однако с увеличением времени эти кривые при сравнительно высоких температурах обычно сливаются в одну, мало отличающуюся от кривой, получаемой при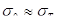 . .
Следует иметь в виду, что при нормальной и умеренно высоких температурах, но при очень высоких  , существенно превосходящих , существенно превосходящих 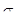 , может наблюдаться заметное упрочнение металла и повышение сопротивления релаксации за счет наклепа. В тех случаях, когда ненаклепанный металл обладает меньшим сопротивлением ползучести (релаксации), величина , может наблюдаться заметное упрочнение металла и повышение сопротивления релаксации за счет наклепа. В тех случаях, когда ненаклепанный металл обладает меньшим сопротивлением ползучести (релаксации), величина  при при 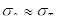 может оказаться больше, чем при может оказаться больше, чем при 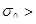 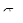 . .
3.2 Влияние времени на протекание процесса релаксации напряжений
Влияние времени на протекание процесса релаксации напряжений находится
в тесной зависимости от других факторов — начального напряжения и температуры, а также от структурной стабильности исследуемого сплава. Например, с повышением температуры влияние фактора времени усиливается.
Кривая релаксации в координатах напряжение — время (рисунок 15) отчетливо разбивается на два участка, отвечающих двум периодам релаксации. Первый период, продолжающийся в большинстве случаев весьма короткое время, характеризуется резким падением напряжения, чему отвечает ниспадающий участок аb.
Второй период релаксации, длительность которого намного больше первого, напротив, характеризуется весьма умеренной скоростью падения напряжения: релаксационная кривая на участке bс при большой длительности испытания приближается к оси абсцисс и в некоторых случаях она вообще затухает, т. е. выходит на горизонтальный участок.
Известно, немало попыток математического обобщения функциональной зависимости напряжения от времени. Например, И.А. Одингом были предложены следующие уравнения первого и второго периодов релаксации:
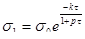 (56) (56)
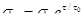 (57) (57)
где k и р — постоянные коэффициенты, зависящие от свойств металла;
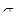 и и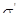 — начальные напряжения I и II периодов. — начальные напряжения I и II периодов.
Аналитические уравнения этого типа имеют общий недостаток: они не отражают возможного влияния структурных превращений, происходящих у дисперсионно твердеющих сплавов при определенных температурах. Между тем развивающиеся во времени структурные превращения часто существенно влияют на характер процесса релаксации. Так, если у сильно дисперсионно твердеющих сплавов постоянство скорости релаксации устанавливается сравнительно быстро, то у слабо твердеющих сплавов стадия затухания скорости релаксации иногда длится тысячи часов. Структурная нестабильность испытуемых материалов проявляется и при изучении влияния времени на зависимости 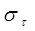 =f( =f(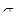 ) и ) и  = f( = f( ). ).
Продолжительность неустановившегося периода релаксации представляет существенный интерес, поскольку с этим связан практически важный вопрос о минимальной длительности опыта, достаточной для последующих экстраполяции. Изучение многочисленных первичных кривых релаксации показывает, что для стабильных при рабочей температуре материалов длительность начального периода обычно колеблется от 200 до 1000 ч. Однако для сплавов, у которых в процессе службы структурные превращения протекают медленно, неустановившийся период может продолжаться значительно большие сроки.
В связи с этим время испытаний на релаксацию материалов, предназначенных для длительной службы, в наших лабораториях составляет 1000—3000 ч. Значительно реже испытания на релаксацию при повышенных температурах доводят до 10—20 тыс. ч (т. е. До фактического срока службы крепежных деталей), а при нормальной температуре — до 50 тыс. ч. Результаты опытов столь большой длительности представляют большую ценность для проверки правильности экстраполяции по результатам менее длительных испытаний.
3.3 Влияние температуры на процесс релаксации напряжений
Влияние температуры на процесс релаксации напряжений в металлах и сплавах весьма велико. Аналогично ползучести различают релаксацию напряжений при низких (меньше 0,25 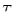 ), средних (0,25 ), средних (0,25 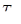 — 0,5 — 0,5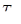 ) и высоких (более 0,5 ) и высоких (более 0,5  ) температурах. ) температурах.
Механизмы релаксации напряжений (и ползучести) в указанных диапазонах температур различны. Так, доминирующим механизмом низкотемпературной релаксации является скольжение и пересечение дислокаций. Релаксации напряжений в среднетемпературной зоне определяется пересечением дислокаций, преодолением дислокациями барьеров Пайерса и, главное, поперечным скольжением. Спецификой высокотемпературной релаксации являются диффузионные механизмы перемещения дислокаций, переползание дислокаций, движение винтовых дислокаций, вязкое перемещение атмосфер Коттрелла.
Следует отметить, что перечисленные механизмы по-разному проявляются при кратковременной и длительной релаксации, а также в металлах с различной решеткой и в сплавах с различной степенью легирования. Именно в связи с этим для некоторых сплавов характерны немонотонные кривые зависимости сопротивления релаксации от температуры (в пределах до 0,25 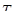 ). Согласно кривой 1 рисунка 17, наблюдаются температурные области, в которых процессы релаксации и ползучести заторможены вследствие деформационного старения, образования предвыделений (зоны Гинье-Престона) и т.д. Иллюстрацией может служить реальная температурная кривая релаксации 4 для аустенитной стали типа Х18Н10Т при (τ0
= 350 МН/м2
(35 кг/мм2
) и τ=24 ч (по данным Л.Б. Гецова). ). Согласно кривой 1 рисунка 17, наблюдаются температурные области, в которых процессы релаксации и ползучести заторможены вследствие деформационного старения, образования предвыделений (зоны Гинье-Престона) и т.д. Иллюстрацией может служить реальная температурная кривая релаксации 4 для аустенитной стали типа Х18Н10Т при (τ0
= 350 МН/м2
(35 кг/мм2
) и τ=24 ч (по данным Л.Б. Гецова).
Рисунок 17 - Зависимость  = f(T) = f(T)
В других случаях температурная зависимость сопротивления релаксации (ползучести) выражается монотонными кривыми 2 и 3, рисунок 17. Подобный вид кривых характерен для сплавов, у которых процессы деформационного старения либо вообще не наблюдаются (кривая 2), либо они протекают настолько интенсивно, что низкотемпературная релаксация (ползучесть) практически отсутствует (кривая 3).
Незначительная интенсивность релаксации напряжений в металлах при температурах ниже 0°С долгое время служила поводом для сомнений в ее существовании. Однако процессы релаксации напряжений действительно происходят при температурах ниже 0° С. Так, Фелтам изучил релаксацию в железе Армко, кобальте, меди, α-латуни и магниевом сплаве при температурах вплоть до -196°, С. В. Я. Зубов и С. В. Грачев в высокопрочной стали марок 70ХС и 70СЗХМВА при температуре -96° С, Б. А. Потехин и И. И. Богачев в аустенитной стали типа ЗХ10ГЮ также при -96° С.
Говоря о среднетемпературной области (0,25— 0,5) 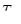 , следует отметить, что повышение температуры испытания сказывается на первичных кривых релаксации следующим образом: удлиняется I период релаксации и увеличивается угол наклона II (прямолинейного) участка. При дальнейшем повышении температуры (выше 0,5 , следует отметить, что повышение температуры испытания сказывается на первичных кривых релаксации следующим образом: удлиняется I период релаксации и увеличивается угол наклона II (прямолинейного) участка. При дальнейшем повышении температуры (выше 0,5 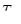 ) процесс релаксации вообще может ограничиться I периодом, что свидетельствует о полном релаксационном разупрочнении металла. Температура, вызывающая эту фазу релаксации, представляет известный интерес. Но с инженерной точки зрения большее значение имеет температура, отвечающая начальной стадии разупрочнения, когда начинается существенное спадание ах
, но еще наблюдается вполне устойчивый II период релаксации. ) процесс релаксации вообще может ограничиться I периодом, что свидетельствует о полном релаксационном разупрочнении металла. Температура, вызывающая эту фазу релаксации, представляет известный интерес. Но с инженерной точки зрения большее значение имеет температура, отвечающая начальной стадии разупрочнения, когда начинается существенное спадание ах
, но еще наблюдается вполне устойчивый II период релаксации.
Имеющиеся экспериментальные данные показывают, что разупрочнение чистых металлов, сталей и сплавов под воздействием температуры в условиях релаксации напряжений протекает значительно интенсивнее, чем в условиях ползучести.
Хотя температура начала релаксационного разупрочнения для сталей с интерметаллидной фазой примерно та же, что и при ползучести (~700°С), интенсивность протекания процесса релаксации напряжений с дальнейшим повышением температуры намного выше. В связи с этим возможность использования таких сталей при 750°С в качестве релаксационностойкого материала С длительным сроком службы практически отпадает.
Если считать, что ползучесть есть чередование двух противоположных процессов — разупрочнения под воздействием температуры и упрочнения от пластической деформации (наклеп), то отмеченное выше обстоятельство вполне объяснимо. В условиях релаксации напряжений (при неизменности начальной суммарной деформации) разупрочняющему действию температуры почти не противостоит упрочняющее влияние пластической деформации.
Я.С. Гинцбург [15] вводит понятие о критической температуре релаксации напряжений 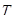 . По определению автора, это есть температура, при которой величина коэффициента . По определению автора, это есть температура, при которой величина коэффициента  , характеризующего сопротивляемость релаксации в I периоде, остается постоянной при любом значении , характеризующего сопротивляемость релаксации в I периоде, остается постоянной при любом значении  . Такая формулировка достаточно неопределенна, тем более что при умеренно высоких температурах, как известно, начальное напряжение . Такая формулировка достаточно неопределенна, тем более что при умеренно высоких температурах, как известно, начальное напряжение  вообще не влияет на величину вообще не влияет на величину . .
Температурная зависимость различных характеристик релаксации изучалась многими исследователями. Так, Ф.И. Алешкин приводит температурную зависимость относительного напряжения релаксации  =( =(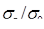 )100 («ресурс напряжений») в виде )100 («ресурс напряжений») в виде
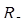 = 100[ = 100[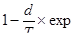 ( (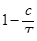 )] (58) )] (58)
где с и d— коэффициенты.
Л.П. Никитина исследовала температурную зависимость времени релаксации  , необходимого для достижения определенного уровня относительного напряжения , необходимого для достижения определенного уровня относительного напряжения  . Влияние на процесс релаксации трех основных параметров: напряжения, температуры и времени тесно связано между собой. . Влияние на процесс релаксации трех основных параметров: напряжения, температуры и времени тесно связано между собой.
Поэтому естественно стремление исследователей представить зависимость экспериментальных данных одновременно от всех перечисленных параметров, например  = f(t, = f(t,  , τ). , τ).
Кривые для различной длительности испытаний, полученные при каждом значении  , образуют пучок, расходящийся в направлении высоких температур. Последнее обстоятельство подтверждает, что с повышением температуры влияние времени на релаксационную стойкость усиливается. Пучки кривых для различных , образуют пучок, расходящийся в направлении высоких температур. Последнее обстоятельство подтверждает, что с повышением температуры влияние времени на релаксационную стойкость усиливается. Пучки кривых для различных  в области высоких температур, наоборот, сближаются, что говорит об уменьшении влияния в области высоких температур, наоборот, сближаются, что говорит об уменьшении влияния  с температурой. с температурой.
3.4 Масштабный фактор
Исследование влияния размеров образца (детали) на интенсивность процессов релаксации напряжений отражено в весьма ограниченном числе работ. Опыты Одинга и Бурдукского приводились при 600° С в условиях растяжения образцов различной длины (50 и 100 мм) и диаметра (5 и 10 мм), изготовленных из сталей Х18Н12МЗТ, Х18Н10Т и 4Х15Н7Г7ФМ (ЭИ388).
Результаты испытаний усредняли методом наименьших квадратов. При этом обнаружилось некоторое снижение релаксационной стойкости образцов меньших размеров. Было сделано предположение, что различная релаксационная стойкость образцов разных размеров связана с локальным характером протекания малых пластических деформаций при высоких температурах.
Для подтверждения этого проводили специальные опыты с образцами, на поверхности рабочей части которых через каждые 10 мм наносили отпечатки прибором Виккерса. Расстояние между отпечатками измеряли с большой точностью до и после испытания на релаксацию.
На рисунке 18 приведен график распределения пластической деформации по длине образца из стали Х18Н12МЗТ, испытывавшегося при 600° С в течение 500 ч. Из рисунка 18 следует, что в условиях релаксации наблюдается значительный разброс слабых и прочных объемов по длине и, по-видимому, по сечению образца. Отсюда следует, что в образцах сравнительно большого диаметра (длины) сопротивляемость релаксации должна быть усреднена по отдельным объемам. Вместе с тем в тонких и особенно в коротких образцах усреднение распределения слабых и прочных объемов затруднено. Поэтому в первом случае кривые релаксации устойчивы, во втором наблюдается их значительный разброс. Кроме того, локальность пластической деформации может привести в ряде случаев к некоторому снижению релаксационной стойкости образцов малых размеров, так как вероятность скопления слабых объемов по сечению образца в количестве, достаточном для его разупрочнения, у тонких образцов значительно больше, чем у образцов большого диаметра. В то же время у образцов малого диаметра эта вероятность тем больше, чем больше длина образца.
Было установлено также, что форма поперечного сечения, в том числе и наличие резьбы на поверхности, не оказывают заметного влияния на релаксационную стойкость.
Таким образом, проведенные исследования не позволяют сделать однозначных выводов о влиянии масштабного фактора на релаксационную стойкость различных материалов. По-видимому, аналогично ползучести, масштабный фактор может проявиться в результате:
а) неоднородного распределения сопротивления ползучести в разных микрообъемах, по-разному проявляющегося в образцах разных размеров;
б) различного влияния состояния поверхности образцов разных размеров (влияние наклепа, окисления);
в) облегчения выхода дислокаций на поверхность при увеличении отношения поверхности к объему.
Различные выводы исследователей объясняются не только проявлением масштабного фактора при релаксации в условиях сжатия и растяжения, но и особенностями поведения в этих условиях испытанных материалов (медь, перлитная и аустенитная стали).
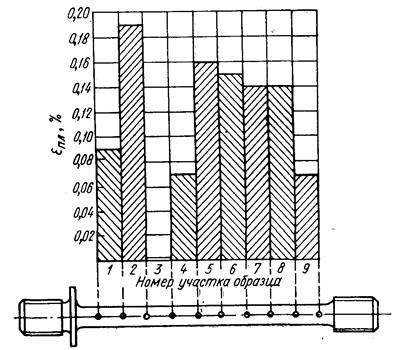
Рисунок 18 — График распределения пластической деформации при релаксации напряжений
3.5 Основные критерии релаксации напряжений
Для оценки релаксационной стойкости материалов служат следующие критерии: оставшееся напряжение; падение напряжения; ресурс напряжений; скорость релаксации; предел релаксации; условные коэффициенты релаксации.
Оставшееся напряжение. Напряжение  “оставшееся” в детали или испытуемом образце по истечении некоторого промежутка времени от момента нагружения детали (образца) начальным напряжением “оставшееся” в детали или испытуемом образце по истечении некоторого промежутка времени от момента нагружения детали (образца) начальным напряжением  , наиболее часто используется в качестве численной характеристики релаксационной стойкости металлов и сплавов. Несмотря на это, до сих пор нет единого термина для обозначения , наиболее часто используется в качестве численной характеристики релаксационной стойкости металлов и сплавов. Несмотря на это, до сих пор нет единого термина для обозначения  . Помимо оставшегося напряжения, величину . Помимо оставшегося напряжения, величину  называют остаточным, текущим и конечным напряжениями или же просто напряжением релаксации. называют остаточным, текущим и конечным напряжениями или же просто напряжением релаксации.
Термин остаточное напряжение неизбежно приведет к путанице с укоренившимися понятиями остаточных напряжений 1-го и 2-го рода. Термин текущее напряжение неудачен в смысловом отношении и, кроме того, вызывает ассоциации с пределом текучести. Наконец, напряжение бывает конечным не всегда, а лишь в том случае, когда оно совпадает с окончанием испытания или срока эксплуатации. По этим соображениям, мы придерживаемся термина оставшееся напряжение, который представляется наиболее удачным. бывает конечным не всегда, а лишь в том случае, когда оно совпадает с окончанием испытания или срока эксплуатации. По этим соображениям, мы придерживаемся термина оставшееся напряжение, который представляется наиболее удачным.
Величина  за данный период времени τ зависит от начального напряжения: за данный период времени τ зависит от начального напряжения:  =f( =f( ). Приводя численные значения ). Приводя численные значения  , необходимо указывать, при каком именно , необходимо указывать, при каком именно  они были получены, что, к сожалению, не всегда выполняется. они были получены, что, к сожалению, не всегда выполняется.
Основное преимущество оставшегося напряжения как критерия релаксации заключается в том, что величина  получается непосредственно из эксперимента и не требует дополнительной математической обработки. получается непосредственно из эксперимента и не требует дополнительной математической обработки.
Падение напряжения за обусловленный промежуток времени τ (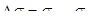 ) наряду с оставшимся напряжением ) наряду с оставшимся напряжением  можно считать основным критерием релаксационной стойкости, применявшимся еще в ранний период изучения процесса релаксации. Так же как и можно считать основным критерием релаксационной стойкости, применявшимся еще в ранний период изучения процесса релаксации. Так же как и  , величина , величина  является функцией начального напряжения: является функцией начального напряжения:  = f( = f( ). ).
Косвенной характеристикой релаксации, в принципе аналогичной  , можно считать величину осадки цилиндрической спиральной пружины под воздействием сжимающего усилия. Как известно, такая методика испытания широко применяется для оценки релаксационной стойкости пружинных сталей и сплавов. , можно считать величину осадки цилиндрической спиральной пружины под воздействием сжимающего усилия. Как известно, такая методика испытания широко применяется для оценки релаксационной стойкости пружинных сталей и сплавов.
Вместе с тем величина  и и  для данного времени τ недостаточно полно характеризуют сравнительную сопротивляемость релаксации исследуемых материалов, поскольку они не отражают ни предыдущего, ни дальнейшего протекания процесса релаксации. Для суждения о кинетике спадания напряжений необходимо знать для данного времени τ недостаточно полно характеризуют сравнительную сопротивляемость релаксации исследуемых материалов, поскольку они не отражают ни предыдущего, ни дальнейшего протекания процесса релаксации. Для суждения о кинетике спадания напряжений необходимо знать  или или 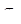 за различные промежутки времени, составляющие 0,05; 0,1; 0,2; 0,5 от полного времени испытания или заданного срока службы. за различные промежутки времени, составляющие 0,05; 0,1; 0,2; 0,5 от полного времени испытания или заданного срока службы.
Ресурс напряжений. В ряде случаев снижение напряжения в процессе релаксации удобно представлять в относительных значениях от начального напряжения. Относительная величина оставшихся напряжений, выраженная в процентах, получила название «ресурса напряжений»:
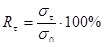 (59) (59)
Скорость релаксации. Различают «истинную», «среднюю» и «логарифмическую» скорости релаксации.
Истинную (или «мгновенную») скорость релаксации в любой точке кривой напряжение — время
 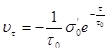 (60) (60)
практически не определяют. Обычно подсчитывают среднюю скорость релаксации ( ) за некоторый промежуток времени, ограниченный двумя точками ( ) за некоторый промежуток времени, ограниченный двумя точками ( и и 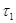 ) на первичной кривой релаксации; ) на первичной кривой релаксации;
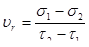 (61) (61)
Величину  измеряют в единицах напряжения, отнесенных к единице времени, или в процентах в час. измеряют в единицах напряжения, отнесенных к единице времени, или в процентах в час.
Логарифмическая скорость релаксации определяется уравнением
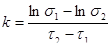 (62) (62)
и выражается в величинах  или или  Величина, обратная k: Величина, обратная k:
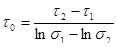 (63) (63)
под названием «время релаксации» ранее также применялась в качестве характеристики релаксации.
И.А. Одинг и Ф.И. Алешкин установили на железе Армко прямолинейную (в логарифмической системе координат) зависимость скорости релаксации  от времени испытания. Температурная зависимость от времени испытания. Температурная зависимость  выражена на логарифмическом графике ломаной линией. выражена на логарифмическом графике ломаной линией.
Предел релаксации. Этот термин применяют, по крайней мере, в трех вариантах: истинный (физический) предел релаксации напряжений; условное напряжение для заданной скорости релаксации; условный (технический) предел релаксации (по напряжению).
Под истинным (физическим, теоретическим) пределом релаксации напряжений по аналогии с физическим пределом ползучести понимают максимальное начальное напряжение, еще не вызывающее релаксации. Эта характеристика практически не применяется, и существование физического предела релаксации пока не имеет достаточного экспериментального подтверждения.
Релаксационная стойкость сплавов зависит не только от химического состава, но и от их структуры. Можно отметить общие для всех типов сплавов особенности структурного состояния, которые (прямо или косвенно) влияют на процесс релаксации напряжений при обычной и повышенной температурах. Сюда относятся: величина зерна твердого раствора, его стабильность, количество и размеры частиц избыточных фаз, их взаиморасположение и взаимодействие. Перечисленные структурные факторы регулируются термической обработкой.
Вместе с тем следует учитывать, что длительное пребывание сплава при повышенных температурах может существенно изменить исходное структурное состояние, созданное термической обработкой.
Термомеханическая обработка металлов и сплавов, представляющая собой сочетание пластического деформирования (наклепа) и термической обработки, является прогрессивным технологическим процессом, позволяющим повышать уровень механических свойств стали и других сплавов, в том числе и жаропрочных.
Возможность упрочнения металлических сплавов сочетанием механического и фазового наклепа отмечалась еще в 1943 г. в теоретических работах С.Т. Конобеевского. Реальная возможность применения термомеханической обработки для повышения жаропрочных свойств впервые показана В.Д. Садовским с сотрудниками. В дальнейшем было проведено значительное число экспериментальных исследований, исчерпывающий обзор которых можно найти в труде М. Л. Бернштейна [14].
Многочисленные способы такой обработки могут быть отнесены к трем основным видам: НТМО (низкотемпературная термомеханическая обработка), ВТМО (высокотемпературная термомеханическая обработка) и МТО (механико-термическая обработка).
Различные варианты этих обработок включают операции пластического деформирования, которые проводят при самых разнообразных степенях деформации и различных температурах, и собственно термическую обработку основные параметры которой (температура, время, скорости нагрева и охлаждения) могут колебаться в широких пределах. В результате получаются самые различные сочетания механического наклепа, рекристаллизации, возврата и старения, суммарное влияние которых на процесс релаксации напряжений может быть различно и зависит, кроме того, от конкретных рабочих условий — длительности и температуры.
При комнатной, пониженной и умеренно повышенной температурах любая термомеханическая обработка (так же, как и холодный наклеп), как правило, повышает релаксационную стойкость металлов и сплавов. Это объясняют тем, что ТМО приводит к созданию в структуре поликристаллических металлов равномерно распределенных внутренних дислокационных барьеров, препятствующих движению дислокаций. Одновременно увеличивается плотность дислокаций, причем последняя после НМТО (при одинаковой степени деформации) почти на порядок выше, чем после ВТМО.
Положительное влияние ТМО может быть показана на примере низколегированной стали 35ГС, исследованной в работе. ВТМО заключалась в деформировании на 30% при 900°С с последующими закалкой и отпуском;
Испытание на релаксацию проводилось при комнатной температуре кольцевым методом, при достаточно высоких значениях начального напряжения: 950, 1200, 1400 и 1600 МН/м2
(95, 120, 140, 160 кг/мм2
). Как видно из рисунка 19, падение напряжения у образцов, подвергнутых ВТМО, меньше, чем у закаленных и отпущенных образцов. Эта закономерность справедлива как для начального периода релаксации, так и по истечении 200—400 ч.
Кроме того, из полученных данных следует, что ВТМО приводит к более стабильной структуре стали: аномальные пики (на начальном участке) кривых для закаленных образцов, которые авторы объясняют распадом остаточного аустенита и выделением углерода из твердого раствора, на кривых, отвечающих ВТМО, отсутствуют.
Благоприятное влияние предварительной пластической деформации на сопротивление релаксации у перлитных сталей при комнатной и умеренно повышенных температурах не вызывает сомнений. Так, например, холодное деформирование углеродистой стали при значительных обжатиях (до 80%), но низком начальном напряжении [ = 400 МН/м2
(40 кг/мм2
)] повышает релаксационную стойкость при 20 и 150°С, тем в большей степени, чем выше содержание в стали углерода (в пределах 0,3—0,9%). При этом многие авторы указывают, что существует оптимальная степень наклепа. Как показал А. А. Красильников [11], эта оптимальная величина деформации для высокоуглеродистой стали У8А изменяется с температурой, составляя 80% при 20° С; 50% при 150° С и лишь 20% при 450° С. Болеее подробные данные по этому вопросу можно найти в книге В.Я. Зубова и С.В. Грачева. = 400 МН/м2
(40 кг/мм2
)] повышает релаксационную стойкость при 20 и 150°С, тем в большей степени, чем выше содержание в стали углерода (в пределах 0,3—0,9%). При этом многие авторы указывают, что существует оптимальная степень наклепа. Как показал А. А. Красильников [11], эта оптимальная величина деформации для высокоуглеродистой стали У8А изменяется с температурой, составляя 80% при 20° С; 50% при 150° С и лишь 20% при 450° С. Болеее подробные данные по этому вопросу можно найти в книге В.Я. Зубова и С.В. Грачева.
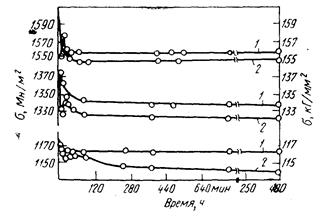
1 — после ВТМО; 2 — после закалки и отпуска при 200° С
Рисунок 19 - Кривые релаксации стали 35ГС при 20°С и различных начальных напряжениях.
При повышении температуры на процесс релаксации напряжений оказывают влияние такие явления, как рекристаллизация, возврат, старение. В этих условиях решающее значение приобретает временной фактор. По истечении некоторого промежутка времени, зависящего) от температуры, упрочняющее действие ТМО утрачивается и преимущество получает материал, не подвергавшийся ТМО.
Если требуется увеличить время эффективного воздействия ТМО на релаксационную стойкость данного материала, не следует стремиться к чрезмерно высокой плотности дислокаций в металле, так как такое структурное состояние, получаемое, например, путем НТМО, является при длительном температурном влиянии нестабильным. Лучшие результаты дает ВТМО, приводящая к несколько меньшей плотности дислокаций.
Для длительной высокотемпературной службы предпочтительна полигональная структура. Полигонизация может создаваться в определенных условиях и при ВТМО, и при НТМО, с применением относительно малых степеней пластической деформации. В случае НТМО для образования полигональной структуры необходим дополнительный нагрев в дорекристаллизационном интервале температур, называемой некоторыми авторами рекристаллизационным отжигом.
Стабильная полигональная структура получается с помощью механикотермической обработки (МТО), предложенной и разработанной И. А. Одингом и его школой. Этот вид обработки заключается в деформировании металла на 1—10% при определенной температуре и последующей выдержке в дорекристаллизационном интервале температур. Обе эти температуры Деформирования и тепловой выдержки — в некоторых случаях совпадают. Например, при обработке аустенитной стали 1Х18Н9 для обеих операций рекомендуется 600° С.
М.Л. Берншейн и Н.Б. Либман [14] изучали влияние ТМО (по схеме закалка — деформация — старение) на релаксацию напряжений элинварных сплавов марок Н41ХТА и Н35ХМВА при 550°С и начальных напряжениях 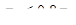 . При испытании образцов из сплава Н41ХТА после закалки с 1000° С, деформации на 8% и отпуска в течение 0,5 и 5 ч было установлено лишь незначительное повышение релаксационной стойкости по сравнению с недеформированными образцами (рисунок 20,а,б). Влияние температуры отпуска сказалось лишь в самый начальный момент процесса релаксации. . При испытании образцов из сплава Н41ХТА после закалки с 1000° С, деформации на 8% и отпуска в течение 0,5 и 5 ч было установлено лишь незначительное повышение релаксационной стойкости по сравнению с недеформированными образцами (рисунок 20,а,б). Влияние температуры отпуска сказалось лишь в самый начальный момент процесса релаксации.
Иная картина наблюдалась для сплава, деформированного после закалки с 1000°С на 14%, когда при последующем отпуске образовалась полигональная структура. В связи с заметным повышением при указанной обработке предела упругости величина  в испытаниях на релаксацию была доведена до 930 МН/м2
(93 кг/мм2
). Как видно из рисунка 20,в, релаксационная стойкость сплава также существенно повысилась, в особенности после отпуска при 800°С, которое создало в сплаве настолько устойчивую дислокационную структуру, что при 550°С релаксация напряжений при данной длительности испытаний вообще не наблюдалась. в испытаниях на релаксацию была доведена до 930 МН/м2
(93 кг/мм2
). Как видно из рисунка 20,в, релаксационная стойкость сплава также существенно повысилась, в особенности после отпуска при 800°С, которое создало в сплаве настолько устойчивую дислокационную структуру, что при 550°С релаксация напряжений при данной длительности испытаний вообще не наблюдалась.
а — закалка с 1050° С + отпуск; б — то же с 1003°С. + деформация 8% + отпуск; в — то же + деформация 11% + отпуск при t, °С:
1 - 600; 2 - 700; 3 - 800
Рисунок 20 — Кривые релаксации сплава Н41ХТА при 550°С.
Аустенитные стали и сплавы на никелевой основе, как известно, обладают большой способностью к пластической деформации, поэтому влияние ТМО на их свойства наиболее заметно. Например, путем ВТМО можно повысить 100-ч длительную прочность аустенитных сталей при 550—650°С на 15—25%. Примерно такое же приращение  (на 20%) при 600° С дает МТО стали 1Х18Н9Т. (на 20%) при 600° С дает МТО стали 1Х18Н9Т.
Эффективность ТМО жаропрочных аустенитных сталей и сплавов подтверждается многочисленными исследованиями. Однако в технической литературе почти отсутствуют сведения о влиянии ТМО и МТО аустенитных сталей и сплавов на их релаксационную стойкость. Имеются лишь отдельные данные о применении к ним холодной пластической деформации (наклепа), которая должна влиять на их сопротивляемость релаксации в том же направлении, как и различные варианты НТМО.
В частности, установлено, что холодное деформирование (с небольшими степенями обжатия) хромоникелевой аустенитной стали типа 18-9 и 18-10 марок Х18Н19, Х18Н9Т, Х18Н10, Х18Н10Т улучшает сопротивление релаксации при умеренно повышенных температурах (до 400°С).
На холоднодеформированной проволоке диаметром 3,8; 1, 9 и 1,5 мм из стали 1Х18Н9Т В.Я. Зубовым и Л.А. Красильниковым было изучено влияние более высоких обжатий (30, 60 и 90%). Отмечены заметное уменьшение сопротивления релаксации (в интервале от 150 до 450° С) с увеличением степени обжатия, а также положительная роль отпуска при температурах до 400° С. Следует отметить, что продолжительность испытаний на релаксацию в противоположность предыдущему исследованию здесь была невелика (15ч).
При более высоких температурах (600—850°С) отрицательное влияние предварительной пластической деформации отмечается уже при меньших степенях наклепа (15—30%). Влияние ТМО на релаксационную стойкость сплава ХН67ВМТЮ на никелевой основе исследовано М. Л. Бернштейном и Э. Л. Ситниковой. Эти авторы изучали влияние степени деформации и режимов старения на величину осадки (при сжатии) винтовых пружин диаметром 12,7 мм, изготовленных из волоченой проволоки указанного сплава с различными степенями обжатия. При 500° С и  = 600 = 600 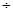 800 МН/м2
наименьшая осадка (12% за 25 ч) наблюдалась после 50%-ного обжатия с последующим старением в течение 6 ч при 600—650° С, а при 600° С (20% за 25 ч)—после 25%-ного обжатия и старения 6 ч при 750° С 800 МН/м2
наименьшая осадка (12% за 25 ч) наблюдалась после 50%-ного обжатия с последующим старением в течение 6 ч при 600—650° С, а при 600° С (20% за 25 ч)—после 25%-ного обжатия и старения 6 ч при 750° С
Практически же применение ТМО для жаропрочных сплавов в условиях релаксации связано с дальнейшим накоплением экспериментальных данных, которые позволят построить реальные графики.
4.2 Структурные превращения в процессе релаксации напряжений
Роль структурных превращений, происходящих в процессе релаксации напряжений при высоких температурах, удобнее всего рассмотреть на аустенитовых сталях и никельхромовых сплавах, поскольку в этих материалах, обычно относящихся к числу дисперсионно твердеющих, возможны различные варианты структурных превращений. Так, при длительном нагреве в определенном температурном интервале предварительно закаленной, а в большинстве случаев и отпущенной стали выделяются избыточные фазы из твердого раствора (карбидные либо интерметаллидные), а ранее выделившиеся метастабильные фазы переходят в более устойчивое структурное состояние. В некоторых аустенитных сталях, как уже отмечалось выше, под воздействием температуры возможен частичный распад твердого раствора, связанный с аллотропическим превращением 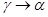 , , 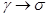 , ,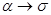 . .
Эти превращения в аустенитных сталях могут происходить и в процессе ползучести или релаксации напряжений при Высоких температурах (несмотря на предварительный стабилизирующий отпуск).
Поскольку перечисленные явления сопровождаются изменением объема, это может отразиться на процессе релаксации, когда длина детали или образца должна оставаться постоянной. Особый интерес представляет влияние на релаксацию напряжений структурных превращений, связанных с уменьшением объема. В этом случае прирост напряжения за счет сокращения длины стержня (вследствие уменьшения объема) может превысить падение напряжения в процессе релаксации. В результате действующее напряжение с течением времени возрастает (отрицательная релаксация или аккумуляция напряжений).
Структурные превращения при повышенных температурах в цветных сплавах в некоторых случаях также приводят к отрицательной релаксации.
Однако далеко не во всех случаях отрицательный объемный эффект скажется подобным образом на первичных кривых напряжение — время. Необходимо также принимать во внимание относительную жаропрочность основной структуры твердого раствора и выделяющейся фазы, а также ее количество, форму и размеры выделившихся частиц. Например, мелкодисперсные карбиды, повышая сопротивление релаксации, будут действовать в том же направлении, что и уменьшение объема металла, а скоагулированные выделения, разупрочняющие сталь, — аналогично увеличению объема.
Далее, если принять, что фазы α и σ в условиях релаксации (так же, как и при ползучести) имеют меньшую жаропрочность, чем γ-твердый раствор, то при достаточно большом содержании этих фаз в структуре сплава падение напряжения в результате релаксации может превысить прирост напряжения, связанный с уменьшением объема.
Конкретным примером может служить серия хромоникельмарганцевых сталей, склонных к образованию σ-фазы в процессе длительного нагрева при 650°С, исследованных Я.С. Гинцбургом [10]. Превращение происходит с уменьшением объема. Тем не менее, первичные кривые релаксации этих сталей изгибаются не кверху, а книзу, что свидетельствует о резком релаксационном разупрочнении стали в результате образования в структуре значительных количеств σ-фазы. Подобные явления могут наблюдаться, когда во время релаксационного процесса при соответствующей температуре начинается интенсивное выпадение избыточных фаз, обладающих пониженной жаропрочностью.
Рассмотренные случаи могут быть квалифицированы как аномальные. Практически применяемые для горячего крепежа аустенитные стали, как правило, имеют достаточно устойчивый твердый раствор и аллотропические превращения обычно отсутствуют. В условиях высокотемпературной релаксации структурные изменения в таких сталях ограничиваются выделением из твердого раствора вторичных фаз — карбидных или интерметаллидных. При невозможности полностью устранить внутренние превращения в сплавах в ряде случаев можно их использовать для повышения длительной релаксационной стойкости и жаропрочности.
Для примера приведем аустенитную жаропрочную сталь Х15Н25В4Т (ЭИ164). В процессе испытания на релаксацию при 680—700°С в структуре предварительно закаленной и отпущенной при 750° С стали непрерывно происходит дополнительное образование вторичных фаз (в основном Ni3
Тi). Поскольку частицы этого интерметаллида при указанной температуре выделяются из твердого раствора в достаточно дисперсном виде, они тормозят процесс релаксации и первичные кривые (рисунок 21,а) отражают монотонный спад напряжения.
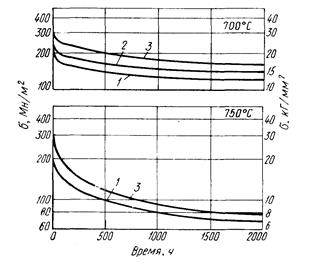
1 — 200(20); 2 — 250(25); 3 — 300(30)
Рисунок 21 — Первичные кривые релаксации стали Х15Н25В4Т при 700°С. 750° С и  , МН/м2
. , МН/м2
.
При повышении температуры до 750°С структурные превращения стали Х15Н25В4Т при длительном нагреве имеют более сложный характер. Как было показано Ю.В. Латышевым, фаза  (с кубической решеткой) частично перерождается в фазу (с кубической решеткой) частично перерождается в фазу 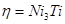 (с гексагональной решеткой). После 5000 ч начинается процесс обратного растворения фазы Ni3
Тi, количество которой по истечении 10000 ч уменьшается почти до исходного. Одновременно в структуре непрерывно образуется интерметаллическое соединение Fe2
W (типа фаз Лавеса), которое компенсирует «недостачу» в фазе Ni3
Тi. Таким образом, суммарное содержание интерметаллидных фаз в стали за 5000—10000 ч не только не уменьшается, но даже незначительно возрастает (с 4,9 до 5,35%). Количество фазы Ni3
Тi за то же время уменьшилось с ~4 до 2%, а количество фазы Fe2
W, наоборот, возросло до 3,3%. (с гексагональной решеткой). После 5000 ч начинается процесс обратного растворения фазы Ni3
Тi, количество которой по истечении 10000 ч уменьшается почти до исходного. Одновременно в структуре непрерывно образуется интерметаллическое соединение Fe2
W (типа фаз Лавеса), которое компенсирует «недостачу» в фазе Ni3
Тi. Таким образом, суммарное содержание интерметаллидных фаз в стали за 5000—10000 ч не только не уменьшается, но даже незначительно возрастает (с 4,9 до 5,35%). Количество фазы Ni3
Тi за то же время уменьшилось с ~4 до 2%, а количество фазы Fe2
W, наоборот, возросло до 3,3%.
Описанные превращения способствуют сохранению сопротивления ползучести на достаточном уровне даже при столь высокой для стали этого класса температуре, как 750°С. Однако в условиях релаксации напряжений замена фазы Ni3
Тi фазой Fe2
W лишь несколько затормаживает разупрочнение стали при температуре 750°С. По истечении 1000 ч оставшееся напряжение составляет всего 35—40% от начального (рисунок 21, б). Можно полагать, что структурная нестабильность данной стали при 750°С является в условиях релаксации отрицательным фактором.
Интересные результаты дало уникальное по длительности испытание на релаксацию жаропрочного сплава Х15Н65ВМТЮ на никельхромовой основе. Сплав был испытан на релаксацию при 750°С в течение 20000 ч при начальных напряжениях, составляющих 33, 40, 50 и 60% от среднего значения предела текучести сплава при той же температуре 600 МН/м2
. Термическая обработка состояла из закалки с 1180°С на воздухе и отпуска в течение 16 ч при 800°С.
Специально проведенные исследования показали, что длительный нагрев ХН65ВМТЮ при 750°С, несмотря на предшествовавший стабилизирующий отпуск, вызывает дополнительное выделение избыточной фазы типа Niз(Тi,Аl), сопровождающееся частичным перераспределением некоторых легирующих элементов между твердым раствором и избыточной фазой. Если в исходном состоянии количество последней составляет  10%, то за 5000 ч (при750°С) оно возрастает до 15,4%. В дальнейшем интенсивность выделения фазы Niз(Тi,Аl) заметно ослабевает; 77% дополнительно выделившегося количества этой фазы приходится на первые 5000 ч старения при 750°С и лишь 23% — на последующие 15000 ч. Непрерывное затухание процесса релаксации напряжений исследованного сплава связано с постепенной стабилизацией структуры и, в частности, с прекращением обеднения твердого раствора никелем и алюминием. По-видимому, стабилизация структуры сплавов с сильно легированным твердым раствором оказывает положительное влияние на длительную релаксационную стойкость. О том, что упрочнение твердого раствора в ряде случаев более эффективно, чем создание в структуре чрезмерного количества частиц избыточной фазы, говорят результаты сравнительного испытания на релаксацию при 800°С двух никельхромовых сплавов, из которых одни имел сильно легированный твердый раствор и умеренное количество вторичной (упрочняющей) фазы, а второй — менее легированный твердый раствор, но значительно большее количество той же упрочняющей фазы. В течение первых сотен часов оба сплава имели практически одинаковую релаксационную стойкость, но по истечении 1000 ч уровень оставшихся напряжений у второго сплава был ниже. 10%, то за 5000 ч (при750°С) оно возрастает до 15,4%. В дальнейшем интенсивность выделения фазы Niз(Тi,Аl) заметно ослабевает; 77% дополнительно выделившегося количества этой фазы приходится на первые 5000 ч старения при 750°С и лишь 23% — на последующие 15000 ч. Непрерывное затухание процесса релаксации напряжений исследованного сплава связано с постепенной стабилизацией структуры и, в частности, с прекращением обеднения твердого раствора никелем и алюминием. По-видимому, стабилизация структуры сплавов с сильно легированным твердым раствором оказывает положительное влияние на длительную релаксационную стойкость. О том, что упрочнение твердого раствора в ряде случаев более эффективно, чем создание в структуре чрезмерного количества частиц избыточной фазы, говорят результаты сравнительного испытания на релаксацию при 800°С двух никельхромовых сплавов, из которых одни имел сильно легированный твердый раствор и умеренное количество вторичной (упрочняющей) фазы, а второй — менее легированный твердый раствор, но значительно большее количество той же упрочняющей фазы. В течение первых сотен часов оба сплава имели практически одинаковую релаксационную стойкость, но по истечении 1000 ч уровень оставшихся напряжений у второго сплава был ниже.
На основании изложенного можно заключить, что структурные превращения, происходящие в сплавах при температурном режиме релаксации напряжений, оказывают определенное влияние на ход процесса релаксации. Эффект дисперсионного твердения или аллотропических превращений накладывается на чисто релаксационные явления, поэтому общая картина процесса заметно усложняется.
В связи с этим естественно возникает «обратный» вопрос: может ли процесс высокотемпературной релаксации напряжений (не приводящий к разрушению) оказывать в свою очередь определенное влияние на структуру испытуемой стали (или сплава).
Аустенитные стали марок 1Х18Н9Т, 1Х14Н18В2БР и Х20Н25ВМЗМ, а также сплав ХН77ТЮ были испытаны на релаксацию напряжений при температуре 650°С, примерно отвечающей температуре 0,5  Выбранные начальные напряжения во всех случаях были ниже предела текучести, составляя Выбранные начальные напряжения во всех случаях были ниже предела текучести, составляя  = (0,4 = (0,4  0,8) 0,8)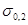 . .
Образцы, испытанные на релаксацию напряжений в течение 2000 ч, подвергали микроскопическому, электронномикроскопическому, фазовому, химическому и рентгеноструктурному анализам. Параллельно исследовали образцы в исходном состоянии, а также после нагрева той же длительности и температуре (при  = 0), что позволило отделить влияние температуры испытания от влияния самого процесса релаксации. = 0), что позволило отделить влияние температуры испытания от влияния самого процесса релаксации.
Так как различные исходные микроструктуры аустенитной стали могут обладать неодинаковой восприимчивостью к возможному влиянию процесса релаксации напряжений, кольцевые образцы перед испытаниями были подвергнуты шести вариантам термической обработки, что позволило исследовать каждую сталь в шести структурных состояниях. Последние отличались величиной зерна твердого раствора, количеством избыточной фазы и степенью ее дисперсности.
Заключение
Положительное влияние на релаксационную стойкость сплавов оказывают все факторы, повышающие сопротивление разупрочнению, уменьшающие скорость возврата и способствующие торможению диффузионных процессов, а также создающие стабильные препятствия движению дислокаций.
Таким образом, любое нарушение структурной однородности твердого раствора способствует развитию процессов релаксации. Это объясняется термодинамической неустойчивостью сплава, в котором образовались локальные участки структуры, несвойственной данным внешним (температура, давление) и внутренним (химсостав) условиям.
Можно ожидать понижения релаксационной стойкости сплава и в том случае, если в основном твердом растворе имеются концентрационные неоднородности. Последние могут возникать, например, при недостаточной выдержке стали во время термической обработки. В никельхромовых и некоторых других сплавах концентрационная неоднородность наблюдается в связи с возникновением, так называемого K-состояния.
Большое влияние на релаксационную стойкость металлов и сплавов (как и вообще на жаропрочность) оказывает величина зерна основного твердого раствора.
Для повышения релаксационной стойкости сплавов при относительно высоких температурах, в особенности при ограниченном сроке их службы, целесообразно увеличение размера зерна основной структуры; в связи с этим все виды термической обработки, приводящие к укрупнению зерна, являются предпочтительными. Однако наиболее крупное зерно почти неизбежно приводит к значительному уменьшению длительной пластичности и в ряде случаев способствует чувствительности к концентраторам напряжений. Поэтому, например, чрезмерно крупное зерно в металле крепежных деталей недопустимо.
Список
использованной литературы
1. Борздыка, А.М. Релаксация напряжений в металле и сплавах / А.М. Борздыка, Л.Б. Гецов. – М.: Металлургия, 1972. – 304 с.
2. Губкин, С. И. Теория течения металлического вещества / С.И. Губкин.– М.: ОНТИ, 1935.
– 234с.
3. Ровинский, Б.М. Влияние термомеханической обработки на релаксационную стойкость сталей и сплавов / Б.М. Ровинский // Известия ОТН АН СССР. – 1954. – №2. – С. 67.
4. Коттрелл, А. X. Дислокации и пластическое течение в кристаллах / А. Х. Коттрелл. – М.: Металлургиздат, 1958. – 390с.
5. Одинг, И. А. Исследования жаропрочных сталей и сплавов / И.А. Одинг, Ф. И. Алешкин // Наука. – 1964. – № 9 – С. 63.
6. Ровинский, Б.М. Релаксация напряжений / Б.М. Ровинский, В.Г. Лютцау // Известия ОТН АН СССР. – 1956. – № 11. – С. 96.
7. Петропавловская, 3. И. Релаксационная стойкость в металлах и сплавах / З.И. Петропавловская, В. А. Щенкова // Труды ЦНИИТМАШ. – 1964. –№45. – С. 29.
8. Мак Лин. Механические свойства металлов / Лин Мак. – М.: Металлургия, 1965. – 426с.
9. Одинг, И. А. Изучение явления релаксации напряжений / И. А. Одинг, А. В. Зубарев, З. Г. Фридман // Металловедение и термическая обработка металлов – 1961. – № 1. – С. 2.
10. Гинцбург, Я. С. Ограниченная ползучесть деталей машин / Я. С. Гинцбург. – М.: Машиностроение, 1968. – 249с.
11. Релаксационные явления в металлах и сплавах. – М.: Металлургиздат, 1963. – 354с.
12. Лютцау, В. Г. Методы изучения релаксационной стойкости / В. Г. Лютцау, Б. М. Ровинский // Заводская лаборатория. – 1957. – №9. – С. 61.
13. Никитина, Л. П. Новый метод изучения релаксационной стойкости / Л. П. Никитина // Заводская лаборатория. – 1963. – №11. – С. 148.
14. Бернштейн, М. Л. Термомеханическая обработка стали / М. Л. Бернштейн. – М.: Металлургия, 1968. – 568с.
15. Гинцбург Я. С. Релаксация напряжений в металлах / Я. С. Гинцбург. – М.: Машгиз, 1957. – 361с.
16. Проблемы металловедения и физики металлов (ЦНИИЧМ). – М.: Металлургиздат, 1955. – вып. IV. – 412с.
|