Курсовая работа: Основы подготовки детей к обучению математике в школе

Оглавление

Введение

Глава 1. Теоретические основы подготовки детей к обучению математике в школе

1.1. Вопросы подготовки детей к школе в психолого-педагогической и методической литературе

1.2. Понятие, сущность и значение математической готовности к обучению в школе

1.3. Проблема подготовки детей к обучению математике в школе

Выводы по главе

Глава 2. Организация подготовки будущих первоклассников к школьному обучению математике

2.1. Программа исследования

2.2. Выявление уровня готовности будущих первоклассников к обучению математике в школе. Анализ результатов

Выводы по главе

Практические рекомендации

Заключение

Список литературы

Приложение 1

Приложение 2

Приложение 3

Приложение 4

Введение

Пожалуй, не будет преувеличением то, что всех сознательных родителей и педагогов волнуют вопросы подготовки будущих первоклассников к обучению в школе. По всем ли параметрам готов ребенок стать школьником? Есть ли какие-то пробелы, недоработки в плане этой подготовки? Каков потенциал развития ребенка? В чем заключаются важнейшие источники развития? Только находя верные ответы на эти вопросы (и предпринимая соответствующие действия) можно не беспокоится за достойное вступление первоклассника в стены школы.

Среди наиглавнейших критериев готовности детей к обучению в школе по праву находится математическая готовность. Особенно сегодня, в век новейших технологий, нет смысла спорить о важности этого критерия. Поэтому и проблема изучения математической готовности будущих первоклассников к обучению в школе является на сегодняшний день неоспоримо актуальной и достаточно интересной для проработки как на теоретическом, так и на практическом уровне.

В целом, если говорить о психолого-педагогической литературе, вышеуказанные проблемы освещаются специалистами достаточно широко, что и неудивительно, учитывая сказанное выше. Вопросов готовности детей к школьному обучению в целом, и математической готовности в частности прямо и косвенно касались в своих трудах такие известные авторы, как Ш.А.Амонашвили, Л.А.Венгер, Ю.Н.Карандашев, Я.Л.Коломинский, Е.Е.Кравцова, Е.А.Панько, Н.Г.Салмина, У.В.Ульенкова и др. (общие вопросы), В.А.Антонов, Л.П.Князева, Л.И.Кузьминых, В.М.Назарова, Е.М.Фадеева, С.А. Яличев и др. (вопросы математической готовности).

Цель данной работы – теоретико-практический анализ проблемы математической готовности будущих первоклассников к обучению в школе.

Задачи:

- проанализировать научную литературу на предмет математической готовности будущих первоклассников к обучению в школе, а именно: выявить основы и нюансы подготовки детей к школе, раскрыть понятие, сущность и значение математической готовности к обучению в школе, осветить проблему подготовки детей к обучению математике в школе;

- сформировать и мотивировать к участию в исследовании две выборки будущих первоклассников (см. ниже);

- выявить и сравнить уровень развитости элементарных математических представлений у детей из разных выборок;

- сформулировать выводы;

- дать практические рекомендации родителям и педагогам детей, давших в исследовании отрицательный результат - по совершенствованию математических представлений.

Предмет исследования – математическая готовность как важный критерий общей готовности будущих первоклассников к школе.

Объект исследования – старшие дошкольники, готовящиеся к поступлению в первый класс школы; первая выборка – дошкольники, участвовавшие в реализации специальной программы по развитию элементарных математических представлений, вторая – дошкольники, в реализации этой и подобных программ участия не принимавшие (педагоги и родители на протяжении дошкольного возраста занимались с ними математикой, но неструктурированно, время от времени).

Гипотеза: реализация целенаправленных занятий, образующих в своей совокупности программу математической подготовки, обеспечивает лучшее развитие элементарных математических представлений дошкольников, по сравнению с реализацией неструктурированных, периодических занятий.

Структура работы включила теоретическую главу, практическую главу, практические рекомендации, заключение, список литературы и приложения.

Глава 1. Теоретические основы подготовки детей к обучению математике в школе

1.1. Вопросы подготовки детей к школе в психолого-педагогической и методической литературе

Поступление ребенка в школу ставит целый ряд задач перед психологами и педагогами в период работы с будущим первоклассником:

· выявить уровень его готовности к школьному обучению и индивидуальные особенности его деятельности, общения, поведения, психических процессов, которые необходимо будет учесть в ходе обучения;

· по возможности компенсировать возможные пробелы и повысить школьную готовность, тем самым провести профилактику школьной дезадаптации;

· спланировать стратегию и тактику обучения будущего первоклассника с учетом его индивидуальных возможностей.

Решение этих задач требует глубокой проработки психологических особенностей современных первоклассников, которые приходят в школу в 6-7 лет с разным «багажом», представляющим совокупность психологических новообразований предыдущего возрастного этапа — дошкольного детства.

Понимая психологическую готовность ребенка к школе как многокомпонентное образование, складывающееся из определенного уровня развития мыслительной деятельности, познавательных интересов, готовности к произвольной регуляции своей познавательной деятельности и к социальной позиции школьника, необходимо согласиться с тем, что нет и не может быть единственного теста, измеряющего готовность ребенка к школе, необходим комплекс методик [3],[5],[9].

Выбор методов диагностики психологической готовности ребенка к школе зависит от подхода к организации диагностического обследования, выбираемого тем или иным психологом.

Одним из вариантов организации может быть первоначальная общая диагностика, обнаруживающая при массовых обследованиях детей в общих чертах уровень интеллектуального развития, развития тонкой моторики руки, координации движения рук и зрения, умения ребенка подражать образцу. Далее, оценивая уровень готовности к школе, психолог продолжает работу с детьми с низким и особо низким уровнем сформированности компонентов психологической готовности к школе, которые нуждаются в дополнительном индивидуальном психологическом обследовании [1]. Благодаря последнему должна быть дана подробная качественная характеристика особенностей психического развития ребенка, необходимая как для уточнения выводов, сделанных на основе фронтального обследования, так и для выбора направлений коррекционной работы.

Для реализации первоначальной диагностики, составления общего представления об уровне готовности ребенка к школьному обучению можно использовать ориентационные тесты, например, тест школьной зрелости Керна—Йирасека. Подобные тесты обладает рядом существенных достоинств для первоначального обследования старших дошкольников:

· не требуют продолжительного времени для проведения;

· могут быть использованы как для индивидуальных, так и для групповых обследований;

· имеют нормативы, разработанные на больших выборках;

· не требуют специальных средств и условий для проведения

Коррекционная работа в начальной школе должна вестись по нескольким направлениям и быть связанна: с развитием мышления и эмоционально-волевой сферы, с развитием мотивации обучения и «комплекса произвольности», с формированием навыков письма, чтения, счета и интеллектуальных способностей, с развитием сферы межличностных отношений ребенка.

Важно подчеркнуть, что при проведении специфической коррекционной работы с младшими школьниками (коррекция учебных навыков, формирование произвольности, развитие психических процессов и т.п.), особое внимание должно уделяться коррекции личностного развития. Специальные проблемы коррекции составляют такие личностные особенности, как неадекватность самооценки, тревожность, неуверенность в своих силах, отражающие повышенную эмоциональную напряженность ребенка, а также конформизм, пассивность, безынициативность [1],[10],[19].

Основные методы развивающего и психокоррекционного характера используемые в начальных классах школ — это игровые методы. В форме игровых методов должно проводится и предметное обучение и психотерапевтическая тренинговая работа. Это требование продиктовано необходимостью создания постоянного поддерживающего психологического «фона» для детей, создания оптимальных психологических условий для успешного развития их личности.

Главное условие при этом — проводимые игры, занятия, упражнения, предъявляемый материал должны создавать благоприятный эмоциональный фон, стимулировать положительные эмоции. Коррекционное занятие обязательно должно завершаться позитивным эмоциональным настроем.

Личностная готовность к школе выражается в отношении ребенка к школе, к учебной деятельности, к учителям, к самому себе [14].

Как правило, дети выражают желание идти в школу. Всегда необходимо учитывать, что привлекает ребенка в школе. «Мне форму купят красивую», «У меня будет новенький ранец и пенал», «В школе Боря учится, он мой друг» - примерно такие высказывания характерны для старших дошкольников. Внешние аксессуары школьной жизни, желание сменить обстановку действительно кажутся заманчивыми. Но оказывается, это еще не самые главные мотивы. Важно, чтобы школа привлекала ребенка и своей главной деятельностью — учением («Хочу учиться, чтобы быть, как папа», «Люблю писать», «Научусь считать », «У меня братик есть маленький, ему тоже буду читать», «В школе буду задачи решать»). И это стремление естественно, оно связано с новыми моментами в развитии старшего дошкольника. Ему уже недостаточно лишь в игре приобщаться к жизни взрослых. А вот быть школьником — совсем другое дело. Это уже осознаваемая ребенком ступенька вверх, к взрослости, да и учеба в школе воспринимается им как ответственное дело. Не проходит мимо внимания 6-летнего ребенка и уважительное отношение взрослых к учебе как к серьезной деятельности.

Если ребенок не готов к социальной позиции школьника, то даже при наличии у него необходимого запаса умений и навыков, уровня интеллектуального развития ему трудно в школе. Ведь не всегда высокий уровень интеллектуального развития (например, рано проявившиеся способности к математике ) совпадает с личностной готовностью ребенка к школе.

Такие первоклассники ведут себя в школе, как говорится, по-детски, учатся очень неровно. Их успехи налицо, если занятия вызывают у них непосредственный интерес. Но если его нет и дети должны выполнять учебное задание из чувства долга и ответственности, то такой первоклассник делает его небрежно, наспех, ему трудно достичь нужного результата.

Еще хуже, если дети не хотят идти в школу. И хотя число таких детей невелико, они вызывают особую тревогу. «Нет, не хочу в школу, там двойки ставят, дома ругать будут», «Хочу, но боюсь!», «Не хочу в школу — там программа трудная и играть будет некогда». Причина подобного отношения к школе, как правило, результат ошибок воспитания детей [17]. Нередко к нему приводит запугивание детей школой, что очень опасно, вредно, особенно по отношению к робким, не уверенным в себе детям («Ты же двух слов связать не умеешь, как ты в школу пойдешь?», «Вот пойдешь в школу, там тебе покажут!»). Можно понять боязнь и тревогу этих детей, связанную с предстоящим обучением. И сколько же терпения, внимания, времени придется уделить потом этим детям, чтобы изменить их отношение к школе, вселить веру в собственные силы! А чего будут стоить первые шаги в школе самому ребенку? Намного разумнее — сразу сформировать верное представление о школе, положительное отношение к ней, к учителю, книге. При формировании такого отношения нужно учесть, что оно связано не только с расширением и углублением представлений ребенка об окружающем, оно определяется воспитательной ценностью, доступностью, достоверностью сообщаемой информации и, что следует отметить особо, способом ее подачи школьнику [10].

Создание эмоционального опыта, последовательное углубление эмоционального отношения к учению в процессе деятельности ребенка — необходимое условие формирования его положительного отношения к школе. Поэтому важно, чтобы сообщаемый детям материал о школе был не только понят, но и прочувствован, пережит ими, непременным условием чего является включение детей в деятельность, активизирующую как сознание, так и чувства. Разнообразны конкретные методы, средства, используемые для этого: совместное (семейное) чтение художественной литературы, организация книжного или математического уголка в семье для ребенка, обращение при детях к семейной библиотеке в поисках решения возникшей проблемы, просмотр диафильмов, фильмов о школе, телепередач о школьной жизни с последующим обсуждением, привлечение младших детей к школьным праздникам старших сыновей и дочерей, рассказы родителей о своих любимых учителях, показ фотографий, грамот, связанных со школьными годами родителей, знакомство с пословицами, поговорками, в которых славится ум, подчеркивается значение книги, учения, создание условий для игры в школу и непосредственное участие в ней, например, в роли учителя и др.

Родители и воспитатели в ДОУ должны способствовать и формированию у детей таких личностных качеств, которые помогли бы им войти в контакт с одноклассниками в школе, с учителем. Ведь даже те дети, которые посещали детский сад и привыкли обходиться какое-то время без родителей, быть в окружении сверстников (что, кстати, тоже очень важно), оказываются в школе среди не знакомых им людей. Умение ребенка войти в детское общество, действовать совместно с другими, уступать, починяться при необходимости, чувство товарищества — качества, которые обеспечивают ему безболезненную адаптацию к новым социальным условиям, способствуют созданию благоприятных условий для его дальнейшего развития. Конечно, общение ребенка с воспитателями и со сверстниками в детском саду, позиция педагогов в вопросах формирования взаимоотношений играют при этом важную роль. Но не менее значимо и то, какое внимание этой проблеме уделяют родители, какова семейная микросреда, какое место занимает ребенок среди братьев и сестер, успела ли душа ребенка потрудиться в семейных условиях, изолируют или приветствуют родители контакты своего ребенка со сверстниками во дворе, как оценивают его поведение, взаимоотношения. В дошкольном детстве развитие ребёнка фактически полностью определяется внешними воспитательными воздействиями. Это необходимо учитывать.

Серьезного внимания требует формирование и волевой готовности будущего первоклассника. Ведь его ждет напряженный труд, от него понадобится умение делать не только то, что ему хочется, но то, что от него потребует учитель, школьный режим, программа [7]. А это не так-то просто, когда в портфеле у тебя новенький значок и хочется поделиться с товарищами по парте последними важными новостями. Но чтобы делать не только приятное, но и необходимое, нужно волевое усилие, способность управлять своим поведением, своей умственной деятельностью — вниманием, мышлением, памятью.

К концу дошкольного возраста происходит оформление основных структурных элементов волевого действия — ребенок способен поставить цель, принять решение, наметить план действия, исполнить, реализовать его, проявить определенное усилие в процессе преодоления препятствия, оценить результат своего волевого действия. Правда, выделяемые цели еще не всегда достаточно устойчивы и осознанны; удержание цели в значительной степени определяется трудностью задания, длительностью его выполнения.

Все исследователи развития воли у детей отмечают, что в дошкольном возрасте цель успешнее достигается в игровой ситуации (касается это и математических занятий ).

Переход детей, переключение их от одного вида деятельности к другому происходит в игре легче [10].

Значительно изменяется к 6 годам степень произвольности движений ребенка. Так, если в 3 года ребенок осознает результат и способ действий с предметом, но не способен еще осознать отдельные этапы движения, то в 6—7 лет движения становятся объектом сознательной волевой деятельности. Возрастающее умение анализировать собственные движения и внимание к точности рисунка движений говорят о психологической готовности ребенка к обучению в условиях школы, о возможности сознательно приобретать двигательные умения уже трудового порядка, сложные формы умений и навыков типа письма, рисования, игры на инструментах, танца.

Произвольность в поведении 6-летнего ребенка проявляется не только в этом. Она и в преднамеренном заучивании стихотворения, в способности побороть непосредственное желание, отказаться от привлекательного занятия, игры ради выполнения поручения взрослого, общественного поручения (дежурство по столовой и т.д.), оказания помощи маме. Она и в умении побороть боязнь (войти в темную комнату, в кабинет зубного врача), преодолеть боль, не заплакать при ушибе.

Шестилетний ребенок оказывается способным соподчинить мотивы своего поведения — это очень важно. Важно в плане развития его личности, важно для создания предпосылок развития воли. Поэтому так необходимо в этом возрасте развить способность действовать по моральным мотивам, отказываться, руководствуясь этими мотивами, от того, что непосредственно привлекает.

Сложнее дело обстоит с познавательной деятельностью. Требуется время, прежде чем требования к ребенку со стороны взрослого, его программа (дать знания впрок, для будущего) превратятся в собственную программу ребенка. Зачатки этой способности уже формируются в старшем дошкольном возрасте. Но это только зачатки; в 6—7 лет они еще не достигают полного развития. Взрослым следует не забывать об этой особенности 6-летних, соблюдать постепенность в предъявлении требовательности, учитывать возможности, интересы, потребности детей этого возраста [4].

Следует иметь в виду, что отличительной чертой волевой регуляции поведения дошкольников является единство мотивационной и операционной сторон, т.е. характерного для ребенка отношения к трудностям и типичных для него способов их преодоления. Поэтому, как показывают специальные психологические исследования, первостепенное значение в формировании воли имеет воспитание мотивов достижения цели. Формирование у детей небоязни трудностей (принятие их), стремления не пасовать перед ними, а разрешать их, не отказываться от намеченной цели при столкновении с препятствиями поможет ребенку самостоятельно или лишь при незначительной помощи преодолеть трудности, которые возникнут у него в первом классе [3].

Развитие дисциплинированности, организованности и других качеств, помогающих 6-летнему ребенку овладеть, управлять своим поведением, в большей мере зависит от степени его восприимчивости к требованиям, от характера взаимоотношений ребенка и взрослого.

Важно, чтобы ребенок был умственно развит (интеллектуальная готовность ). Долгое время об умственном уровне развития судили по количеству умений, знаний, по объему «умственного инвентаря», который выявляется в словарном запасе. Еще и теперь некоторые взрослые думают, что чем больше слов знает ребенок, тем он больше развит. Это не совсем так. Следует учесть, что изменились условия жизни. В каждом доме теперь есть радио, телевизор. Дети буквально купаются в потоке информации, как губка, впитывают новые слова и новые выражения. Словарь их резко увеличивается, но это не значит, что такими же темпами развивается и мышление. Тут нет прямой зависимости.

Конечно же, интеллектуальная готовность предполагает наличие у ребёнка кругозора, запаса конкретных знаний.

Однако ошибочно думать, что словарный запас, специальные умения и навыки — это определяющее и единственное мерило интеллектуальной готовности ребенка к школе [4].

Существующие программы, их усвоение потребуют от ребенка умения сравнивать, анализировать, обобщать, делать самостоятельные выводы, потребуют достаточно развитых познавательных процессов. Готов ли дошкольник к этому?

Исследования обнаружили, например, что к старшему дошкольному возрасту дети овладевают некоторыми рациональными способами обследования внешних свойств предметов, пользуясь усвоенной системой общественно выработанных эталонов. Применение их дает возможность ребенку дифференцированно воспринимать, анализировать сложные предметы.

Оказалось, что дошкольникам доступно понимание общих закономерностей, лежащих в основе научного знания. Так, например, в 6—7 лет ребенок способен усвоить не только отдельные факты о природе, но и знания о взаимодействии организма со средой, зависимость между формой предмета и его функцией, стремлением и поведением. Однако достаточно высокого уровня познавательной деятельности дошкольники достигают, только если обучение в этот период направлено на активное развитие мыслительных процессов, является развивающим, ориентированным на «зону ближайшего развития».

Шестилетний ребенок может многое. Но не следует и переоценивать его умственные возможности. Логическая форма мышления хотя и доступна, но еще не типична, не характерна для него. Тип его мышления специфичен. Высшие формы образного мышления являются итогом интеллектуального развития дошкольника.

Опираясь на высшие схематизированные формы образного мышления, ребенок получает возможность вычленить наиболее существенные свойства, отношения между предметами окружающей действительности. С помощью наглядно-схематического мышления дошкольники без особого труда не только понимают схематические изображения, но и успешно пользуются ими (например, планом помещения для нахождения спрятанного предмета — «секрета», схемой типа географической карты для выбора верной дороги, графическими моделями при конструктивной деятельности). Однако, даже приобретая черты обобщенности, мышление ребенка остается образным, опирающимся на реальные действия с предметами и их «заместителями».

Не только педагогам, но и родителям полезно знать положение психологов о ведущей роли практической деятельности в развитии детей, о важной роли наглядно-действенного и наглядно-образного мышления — специфически дошкольных форм мышления. Кстати, исследования, проведенные в последние годы, убеждают, что данные формы мышления таят в себе не менее мощные резервы, чем словесно-логическое мышление. Они выполняют специфические функции в общем процессе умственного развития детей не только дошкольного, но и школьного возраста [14].

В дошкольные годы ребенок должен быть подготовлен к ведущей в младшем школьном возрасте деятельности — учебной. Важное значение при этом будет иметь формирование у ребенка умений, требуемых в этой деятельности. Обладание такими умениями обеспечивает высокий уровень обучаемости, характерной особенностью которого является умение выделить учебную задачу и превратить ее в самостоятельную цель деятельности. Это не просто для детей, не всем и не сразу удается. Такая операция требует от поступающего в школу ребенка не только определенного уровня интеллектуального развития, но и познавательного отношения к действительности, способности удивляться и искать причины замеченной перемены, новизны. Тут педагог может опереться на острую любознательность подрастающего человека, на его неисчерпаемую потребность в новых впечатлениях.

Познавательная потребность ярко выражена у большинства детей в 6—7-летнем возрасте. У многих она связана с бескорыстным интересом ко всему окружающему; у многих, но не у всех. Есть, наверное, в каждом классе дети, чья интеллектуальная пассивность приводит их в число отстающих, слабоуспевающих учеников. Причины такого рода пассивности часто лежат в ограниченности интеллектуальных впечатлений, интересов ребенка. Будучи не в состоянии справиться с самым простым учебным заданием, он быстро выполняет его, если оно переводится в практическую плоскость или в игру.

Неуспевающие дети требуют особого внимания: развития у них любознательности, познавательного отношения к окружающему, кругозора, поисков особых форм и методов работы с ними. Внимания требуют не только дети с практическим умом, но и те, чья познавательная активность имеет теоретическую направленность [2].

Но если познавательные интересы сформированы недостаточно, то не помогут никакие нотации и поучения. Бессмысленно объяснять ребенку, что без знаний нельзя стать ни матросом, ни поваром, что все должны учиться и т.п. Стремление к знаниям от этого не появится. Другое дело — интересные и содержательные занятия (в том числе математические ), беседы, наблюдения.

Нужно всегда отвечать на вопросы, которые задает ребенок. Общение с родителями — огромная ценность для ребенка в дошкольном возрасте. Если своим вниманием взрослый поддерживает интерес к познанию, то растущий человек будет развиваться, крепнуть. К сожалению, иногда родители, вместо того чтобы поддержать детскую любознательность, отмахиваются от надоевших вопросов.

Сын, например, пытается выяснить у папы, можно ли пересчитать все облака на небе. «Смотри под ноги, а не на небо», — раздраженно может ответить взрослый, занятый своими размышлениями, забывший о способности взрослого «слушать и слышать ребёнка». После нескольких подобных ответов желание спрашивать у дошкольника пропадает.

Взрослым надо включить ребенка в осмысленную деятельность, в процессе которой он бы сам смог обнаружить все новые и новые свойства предметов, замечать их сходство и различие. Можно выделить особо: «сам обнаружить...» Не отмахиваться от детских вопросов, не пичкать сразу готовыми знаниями, а дать возможность приобрести их самостоятельно — крайне важно в умственном воспитании [4].

Взрослые, заботясь об интеллектуальной готовности детей к школе, должны развить у них познавательную потребность, обеспечить достаточный уровень мыслительной деятельности, дать необходимую систему знаний об окружающем.

Далее, коммуникативная готовность как компонент психологической готовности к школе, предполагает развитие у детей потребности общения с другими, умение подчиняться интересам и обычаям детской группы, развивающиеся способности справляться с ролью школьника в ситуации школьного обучения.

По мнению ряда исследователей [4],[10],[20], в структуре социально-психологического компонента школьной готовности можно выделить следующие подструктуры:

· коммуникативную компетентность

· социальную компетентность

· языковую компетентность.

Использование понятия компетентности связывается с тем, что оно не так часто употребляется в детской психологии и, следовательно, таким образом можно избежать различий в его интерпретации. Само слово «компетентность» означает осведомленность в чем-либо. Исходя из этого, социальная компетентность — это знание норм и правил поведения, принятых в определенной социально-культурной среде, отношение к ним; реализация этих знаний на практике. Под языковой компетентностью понимается такой уровень речевого развития, который позволяет человеку в процессе общения свободно использовать свои знания о языке. Эти два вида компетентности можно рассматривать как элементы коммуникативной компетентности, или более широко — компетентность в общении, которая включает в себя еще знание и понимание невербального языка общения, умение вступать в контакт как со своими сверстниками, так и со взрослыми. Коммуникативная, социальная и речевая компетентности, формирующиеся в процессе социализации и воспитания ребенка, к окончанию дошкольного детства имеют определенный уровень развития, который и отражает уровень социально-психологической готовности ребенка к школьному обучению.

Все перечисленные аспекты готовности к обучению к школе естественным образом пересекаются с понятием математической готовности (математические возможности относятся к интеллектуальной готовности, интеллектуальные ресурсы могут остаться невостребованными без должного уровня коммуникативной готовности и так далее).

1.2. Понятие, сущность и значение математической готовности к обучению в школе

Математика – это одна из представленных в программе сфер культуры, взаимодействие с которой способствует органичному вхождению ребенка в современный мир.

Математическая готовность к обучению в школе - показатель освоения математического содержания окружающей действительности, которое направлено, прежде всего, на развитие познавательных и творческих способностей детей, умение обобщать, сравнивать, выявлять и устанавливать закономерности, связи и отношения, решать проблемы, выдвигать их, предвидеть результат и ход решения творческой задачи. В более конкретной трактовке математическая готовность – показатель возможностей выполнения арифметических действий с числами, владения знаковыми системами, основами моделирования, самостоятельность в решении творческих задач и оценке результата [1].

В содержании математического обучения дошкольников преобладают логические задачи, ведущие к познанию закономерностей, простых алгоритмов.

Освоение математического содержания направлено, прежде всего, на развитие познавательных и творческих способностей детей, таких как умение, обобщать, сравнивать, выявлять и устанавливать закономерности, связи и отношения, решать проблемы, выдвигать их, предвидеть результат и ход решения творческой задачи.

Учебно-игровые задачи представлены как образовательные: освоение детьми умений найти пару, сгруппировать предметы, осуществить поиск недостающего, определить направление движения и так далее.

Только должным образом подготовленные в дошкольном возрасте ученики школы могут быстро учиться делать правильные умозаключения, усваивать основные правила логического вывода, полностью «впитывать» сведения, относящиеся к математической логике — науке, содержащей концентрированное выражение законов дедуктивного мышления.

Только школьники, с которыми взрослые работали целенаправленно математически, способны в обучении на беспроблемное обобщение понятия числа, решение уравнений, изучение элементарных функций и др.

Гораздо легче дается правильно подготовленному дошкольнику и первичная геометрия в школе, правильно состыкуется она в дальнейшем с началами алгебры – через понятие множества, например (у неподготовленных в дошкольном возрасте детей с такими состыковками нередко бывают

1.3. Проблема подготовки детей к обучению математике в школе

Далеко не все дошкольники подходят к обучению в школе с необходимым багажом математических знаний или близких к ним. Нередко дефицит соответствующей работы со стороны родителей и педагогов приводит к тому, что будущий первоклассник не умеет выделять и сравнивать признаки различных предметов и явлений с помощью разнообразных способов обследования, а также (по принципу и/или) [14]:

- не определяет простейшие изменения, связи, зависимости между объектами по форме, величине составу (часть – целое), количеству, пространственному расположению (на предметном и числовом уровне);

– не знает последовательность первых десяти чисел и место каждого числа в порядке натурального ряда;

– не различает количественный и порядковый счет в пределах десяти;

– не умеет для каждого числа называть предыдущее и следующее за ним число, продолжать счет, как в прямом, так и в обратном порядке от любого заданного числа;

– не умеет сравнивать стоящие рядом в числовом ряду числа (в пределах десяти);

– не знает состав чисел первого десятка из двух меньших чисел и отдельных единиц;

– не умеет различать и читать печатные цифры, соотносить их с соответствующим множеством предметов, заданных с помощью числовых фигур и предметных картинок или количеством звуков;

– не составляет и не решает задачи в одно действие на сложение и вычитание, пользуясь арифметическими знаками действий;

– не знает простейшие монеты - достоинством 1, 2, 3, 5, 10 копеек;

– не умеет измерять и сравнивать предметы по величине (длине, ширине, высоте) с помощью условной мерки;

– не имеет представление о разнообразии общепринятых способов измерения;

- не осуществляет сериацию предметов по величине;

- неправильно называет элементарные геометрические фигуры (вершина, сторона, угол);

– не умеет распознавать круг, треугольник, четырехугольник (квадрат, прямоугольник).

- не имеет представления о многоугольнике, не понимает геометрические понятия: линия, точка, прямая, луч, отрезок, ломаная линия, угол (прямой, острый, тупой);

– не знает горизонтальные, вертикальные линии, не умеет пользоваться линейкой, трафаретами;

– не определяет свое местонахождение среди окружающих объектов;

– не умеет ориентироваться в пространстве (вверху, внизу, впереди, сзади, перед, за, между, рядом, слева, справа) и на листе бумаги;

– не понимает относительность пространственных ориентировок (выше чем, ниже чем, слева от, справа от, над, под);

– не воспроизводит предлагаемые графические образцы;

– не понимает словесные инструкции взрослого и действует в соответствии с ними;

– не знает последовательность дней недели, месяцев года;

– не имеет представления об определении времени по часам, не понимает отношения во времени: минута – час, неделя – месяц, месяц – год;

– не использует полученные знания в быту, игре, при конструировании и в других видах деятельности;

– не проявляет интерес к математическим играм.

Для того, чтобы этих «не» было поменьше или они вообще стали неактуальны, нужно, во-первых, заниматься с детьми математикой, а во-вторых, заниматься ею организованно, продуманно.

Дети по своей природе интересуются различными видами умственной деятельности, по не всегда в желаемом направлении. Изучение опыта работы дошкольников и экспериментальная проверка ряда видов практических работ показали, что при правильной методике организации руководства практической деятельностью детей можно управлять их интересами. Это может быть использовано и при организации математических занятий.

Если дошкольникам понятны методика и значение выполняемой работы, то они к ней относятся с определенным интересом. В этом большую роль играет тематика занятий, их продолжительность, практическая значимость и сложность выполняемого задания [4].

Укреплению возникшего интереса к математике способствует результативность выполняемой будущими первоклассниками работы. Сообщение или показ результатов математической деятельности дошкольников, поощрения их работы значительно укрепляют интерес к изучению мира математики.

Наблюдение за будущими школьниками в процессе выполнения математических заданий в каждом отдельном случае позволяет выявить, что радость открытия, даже незначительного, вселяет уверенность в познавательном поиске. Выполнив определенный вид математического действия, дошкольник становится более знающим, умеющим, и эти успехи выступают движущей силой интереса к математике, рожденного не из внешней заинтересованности, а путем определенных усилий в преодолении трудностей.

Выводы по главе

Подготовка будущего первоклассника к школе – проблема многогранная, включающая несколько определяющих аспектов – личностный, волевой, интеллектуальный и коммуникативный. Не «затерялась» среди них и математическая готовность к обучению в школе, так как математика, как было отмечено выше, способствует органичному вхождению ребенка в современный мир. Освоение «дошкольных начал» математики позволяет уже школьникам делать гораздо более важные открытия легко и непринужденно. И помочь осуществлению этой связи возрастных периодов должны взрослые – родители и педагоги будущих первоклассников.

Глава 2. Организация подготовки будущих первоклассников к школьному обучению математике

2.1. Программа исследования

Цель данного исследования – выявление уровня математической готовности к обучению в школе у современных старших дошкольников двух групп – целенаправленно занимавшихся до этого элементарной математикой и не принимавшие участия в подобных программах.

Задачи:

- сформировать и мотивировать к участию в эксперименте две выборки будущих первоклассников;

- выявить и сравнить уровень развитости элементарных математических представлений у детей из разных выборок;

- сформулировать выводы;

- дать практические рекомендации родителям и педагогам детей, давших в исследовании отрицательный результат - по совершенствованию математических представлений.

Предмет исследования – математическая готовность как важный критерий общей готовности будущих первоклассников к школе.

Объект исследования – старшие дошкольники, готовящиеся к поступлению в первый класс школы; первая выборка – дошкольники, на протяжении старшего дошкольного возраста участвовавшие в реализации специальной программы по развитию элементарных математических представлений (программа Л.И.Кляузер [14], см. приложение 2), вторая – дошкольники, в реализации этой и подобных программ участия не принимавшие (педагоги и родители на протяжении старшего дошкольного возраста занимались с ними математикой, но неструктурированно, время от времени).

Гипотеза: реализация целенаправленных занятий, образующих в своей совокупности программу дошкольной математической подготовки, обеспечивает лучшее развитие элементарных математических представлений дошкольников, по сравнению с реализацией неструктурированных, периодических занятий.

В качестве диагностического метода работы были выбраны индивидуальные креативные занятия с каждым ребенком. То есть, сущность этих занятий не была задана каким-то диагностическим шаблоном. Главное было – зафиксировать (в том числе документально), насколько развиты у детей математические представления. «Шаблонной» точкой был лишь список таких представлений, а именно:

(Согласно Л.И.Кляузер, готовый к обучению в школе ребенок):

– Умеет выделять и сравнивать признаки различных предметов и явлений с помощью разнообразных способов обследования.

– Определяет простейшие изменения, связи, зависимости между объектами по форме, величине составу (часть – целое), количеству, пространственному расположению (на предметном и числовом уровне).

– Знает последовательность первых десяти чисел и место каждого числа в порядке натурального ряда.

– Различает количественный и порядковый счет в пределах десяти.
– Умеет для каждого числа называть предыдущее и следующее за ним число, продолжать счет, как в прямом, так и в обратном порядке от любого заданного числа.

– Умеет сравнивать стоящие рядом в числовом ряду числа (в пределах десяти).
– Знает состав чисел первого десятка из двух меньших чисел и отдельных единиц.
– Умеет различать и читать печатные цифры, соотносить их с соответствующим множеством предметов, заданных с помощью числовых фигур и предметных картинок или количеством звуков.

– Составляет и решает задачи в одно действие на сложение и вычитание, пользуясь арифметическими знаками действий.

– Знает монеты достоинством 1, 2, 3, 5, 10 копеек.

– Умеет измерять и сравнивать предметы по величине (длине, ширине, высоте) с помощью условной мерки.

– Имеет представление о разнообразии общепринятых способов измерения. Осуществляет сериацию предметов по величине. Правильно называет элементарные геометрические фигуры (вершина, сторона, угол).
– Умеет распознавать круг, треугольник, четырехугольник (квадрат, прямоугольник).
– Имеет представление о многоугольнике. Понимает геометрические понятия: линия, точка, прямая, луч, отрезок, ломаная линия, угол (прямой, острый, тупой).

– Знает горизонтальные, вертикальные линии. Умеет пользоваться линейкой, трафаретами.

– Определяет свое местонахождение среди окружающих объектов. Умеет ориентироваться в пространстве (вверху, внизу, впереди, сзади, перед, за, между, рядом, слева, справа) и на листе бумаги.

– Понимает относительность пространственных ориентировок (выше чем, ниже чем, слева от, справа от, над, под).

– Воспроизводит предлагаемые графические образцы.

– Понимает словесные инструкции взрослого и действует в соответствии с ними.

– Знает последовательность дней недели, месяцев года.

– Имеет представление об определении времени по часам. Понимает отношение во времени: минута – час, неделя – месяц, месяц – год.

– Использует полученные знания в быту, игре, при конструировании и в других видах деятельности.

– Проявляет интерес к математическим играм.

(таким образом, всего двадцать три элемента)

В соответствии с этим списком (полностью), детям в ходе занятий поочередно демонстрировались монеты разного номинала, предъявлялись геометрические фигуры, рисунки с вертикальными и горизонтальными линиями, «тайно» указывались предметы, находящиеся сзади, справа, слева, спереди и так далее. Задавались уточняющие вопросы, позволявшие установить, владеет ли дошкольник элементарными математическими знаниями. Фиксировалось, сколько элементов из списка «доступно» дошкольнику (владение тем или иным элементом условно оценивалось в один балл; всего испытуемый мог набрать двадцать три балла).

После проведения занятия с последним дошкольником (всего в исследовании приняли участи сорок испытуемых, по двадцать в каждой выборке) было проведено сравнение между выборками, в том числе с использованием t – критерия Стьюдента (помимо этого статистического метода, в работе использовались и другие – нахождение среднего арифметического и дисперсии, формулы, см. ниже).

2.2. Выявление уровня готовности будущих первоклассников к обучению математике в школе. Анализ результатов

В период с 02.04.08 по 25.06.08. на базе ДОУ «Солнышко» (г.Ветлуга Нижегородской обл.) было проведено исследование развития элементарных математических представлений у испытуемых двух выборок (первая – из тех, кто принимал участие в реализации вышеуказанной программы – группа А, вторая – из тех, кто в реализации подобных программ не участвовал – группа Б, здесь и далее).

Зафиксированные в ходе исследования результаты представлены в приложении 3.

Как видно из этого приложения, средний балл в группе А оказался выше среднего балла в группе Б (рис. 1):

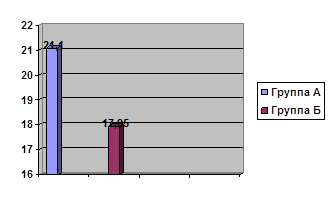
Рис. 1. Результаты исследования уровня развитости математических представлений у дошкольников (средние баллы)

Кроме того, в группе А оказался выше процент испытуемых, показавших максимально возможный результат (пять испытуемых против одного в группе Б, см. также рис. 2).

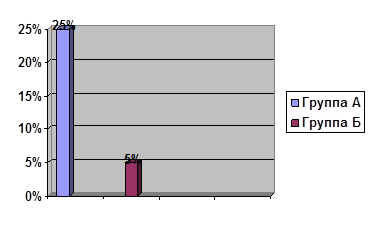
Рис. 2. Процент испытуемых, набравших максимальное количество баллов

Для того, чтобы гипотезу можно было считать полностью доказанной, целесообразно использовать, возвращаясь к сравнению средних баллов по группам, специальный метод статистической обработки – t – критерий Стьюдента:

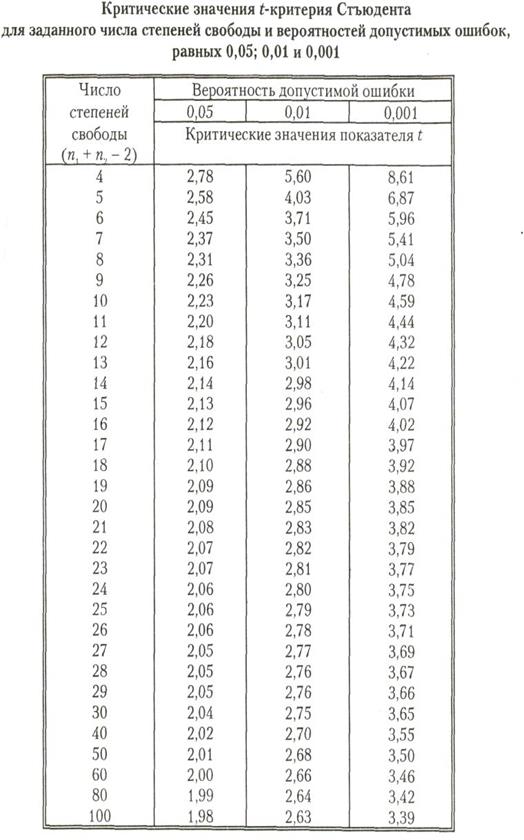
t = 5,24

Полученное значение больше табличного (приложение 4), поэтому значения по выборкам достоверно отличаются друг от друга. Гипотеза доказана.

Выводы по главе

Специально для проведения исследования были сформированы две выборки испытуемых - из тех, кто принимал участие в реализации программы дошкольной математической подготовки Л.И. Кляузер, и из тех, кто в реализации подобных программ не участвовал.

С испытуемыми были проведены индивидуальные занятия, в ходе которых фиксировался уровень владения дошкольниками элементарными математическими представлениями.

На основе анализа полученных результатов была доказана (с применением статистических результатов) гипотеза о том, что реализация целенаправленных занятий, образующих в своей совокупности программу дошкольной математической подготовки, обеспечивает лучшее развитие элементарных математических представлений дошкольников, по сравнению с реализацией неструктурированных, периодических занятий.

Практические рекомендации

Первая и главная рекомендация родителям испытуемых группы Б –задействовать дошкольников в специальных программах дошкольной математической подготовки (хотя бы ускоренных, благо, сегодня есть и такие).

Далее, в неструктурированной работе родителей и педагогов с детьми по совершенствованию элементарных математических представлений рекомендуются следующие приемы, которые побуждают дошкольников участвовать в соответствующих занятиях с интересом (проверено в ходе диагностической работы). Интерес к математике можно вызвать:

а) логикой мероприятий, направленных на возбуждение у дошкольников стремления изучать новое;

б) раскрытием значения предмета изучения, что придает занятиям сознательный характер;

в) занимательностью, характеризующейся привлечением в педагогический процесс второстепенных или даже побочных элементов для временного возбуждения дошкольников и привлечения их внимания к действиям и словам педагога или родителя;

г) поощрением дошкольников, выражающимся в умелом подчеркивании педагогом или родителем их успехов с целью повышения активности в дальнейшей работе;

е) простым указанием выполнить очередное задание и показом способа его выполнения.

Приемы побуждения, применяемые родителями и педагогами, вызывают познавательную деятельность дошкольников тогда, когда они раскрывают перед ними смысл учения, заостряют противоречие между трудной по меркам возраста математической задачей и имеющимися у них знаниями и навыками, а также между новым знанием и имеющимися у них представлениями, в силу чего и возникает стремление знать новое, приобрести недостающие навыки, научиться применять математические знания к решению посильных практических и теоретических задач.

Заключение

Целью данной работы был теоретико-практический анализ проблемы математической готовности будущих первоклассников к обучению в школе.

В ходе написания работы были решены следующие задачи:

- анализ научной литературы на предмет математической готовности будущих первоклассников к обучению в школе, а именно: выявление основ и нюансов подготовки детей к школе, раскрытие понятия, сущности и значения математической готовности к обучению в школе, освещение проблемы подготовки детей к обучению математике в школе;

- формирование и мотивирование к участию в исследовании двух выборок будущих первоклассников;

- выявление и сравнение уровня развитости элементарных математических представлений у детей из разных выборок;

- формулирование выводов;

- формулирование практических рекомендаций родителям и педагогам детей, давших в исследовании отрицательный результат - по совершенствованию математических представлений.

В ходе исследования была доказана гипотеза: реализация целенаправленных занятий, образующих в своей совокупности программу математической подготовки, обеспечивает лучшее развитие элементарных математических представлений дошкольников, по сравнению с реализацией неструктурированных, периодических занятий. Вывод о правомерности гипотезы был подтвержден статистически.

Проблема математической готовности будущих первоклассников к обучению в школе, несомненно, будет оставаться одной из наиболее актуальных в сфере гуманитарной науки. Это и понятно - общество требует от молодых людей хорошего знания математики, и основные знания закладываются в школе и вузе, но этот процесс, как показал проделанный анализ литературы во многом обусловлен дошкольным «фундаментом».

Список литературы

1. Детство: Программа развития и воспитания детей в детском саду. Под редакцией Т.И.Бабаевой, З.А.Михайловой, Л.М.Гурович. Изд. 2-е, переработанное – СПб: Акцидент, 1996 г.

2. Программа воспитания и обучения в детском саду. Под ред. М.А.Васильевой. М. 1987 г.

3. Школа 2100. Программа подготовки дошкольников по математике. Л.Г.Петерсон.

4. Раз – ступенька, два – ступенька… Часть 1 и 2. Л.Г.Петерсон, Н.П.Холина. Баласс. – 1998 г.

5. Математика до школы. А.А.Смоленцова, О.В.Пустовайт. СПб: Акцидент – 1998 г.

6. Логическая азбука для детей 4 – 5 лет. В.Г.Гоголева. СПб: Детство – Пресс – 1998 г.

7. Математика для малышей. Тетрадь №1, тетрадь №2, тетрадь №3. Е.П.Бененсон, Е.В.Вольнова. М: 1994 г.

8. Математика для малышей. А.Н.Харченко. Краснодар: 1995 г.

9. Праздник числа. В.В.Волина. М: 1993 г.

10. Веселая арифметика. В.В.Волина. Екатеринбург: 1999 г.

11. И учеба, и игра: математика. Т.И.Тарабанина, Н.В.Елкина. Ярославль: 1997 г.

12. Детям о времени. Т.И.Тарабанина. Ярославль: 1996 г.

13. Путешествие Бима и Бома в страну Математику. Т. Ахутина, Н. Пылаева, Н. Монелис, Т. Хотылева. М: 1999 г.

14. Адаптивная программа "Занимательная математика". Развитие элементарных математических представлений у детей старшего дошкольного возраста 5–7 лет. Л.И.Кляузер. М. 2008.

15. Математика – это интересно. Рабочая тетрадь 5 – 6 лет. Рабочая тетрадь 6 – 7 лет. И. Н. Чеплашкина, Л. Ю. Зуева. Акцидент: 1998 г.

16. Учимся считать. А. Дорофеева. М: 1997 г.

17. Логическое мышление. А. Дорофеева. М: 1997 г.

18. Математическая тетрадь для дошкольников. Т.И.Ерофеева, Л.Н.Павлова, В.П.Новикова. М: 1992 г.

19. Игры, задания и упражнения математического содержания. Л.И.Ермолаева. Иркутск: 2000 г.

20. Игровые занимательные задачи для дошкольников. З.А.Михайлова. М: 1990 г.

Приложение 1

Сведения об испытуемых

Группа А

Группа Б

Приложение 2

Л.И. Кляузер. Адаптивная программа "Занимательная математика". Развитие элементарных математических представлений у детей старшего дошкольного возраста 5–7 лет

Базисный учебный план

I год обучения 36 занятия

II год обучения 72 занятия.

Приложение 3

Результаты исследования

Группа А

Приложение 4