| ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Математический факультет
Кафедра математического анализа и методики преподавания математики
Курсовая работа
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Выполнила студентка IV курса
математического факультета группы М-41
Бузмакова И.С.
Научный руководитель Старостина О.В.
Киров 2006
Содержание
Наиболее важные примы преобразования уравнений
Методика решения иррациональных уравнений
Тождественные преобразования при решении иррациональных уравнений
Применение общих методов для решения иррациональных уравнений
Методика решения иррациональных неравенств
Заключение
Список библиографии
Введение
Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики.
В школе иррациональным уравнениям и неравенствам уделяется достаточно мало внимания.
Однако задачи по теме "Иррациональные уравнения и неравенства" встречаются на вступительных экзаменах, и они довольно часто становятся "камнем преткновения".
Так как при решении иррациональных уравнений и неравенств в школе применяются тождественные преобразования, то чаще всего возникают ошибки, которые обычно связаны с потерей или приобретением посторонних корней в процессе решения. Поэтому необходимо рассмотреть такие ситуации, показать, как их распознавать и как с ними можно бороться.
Цель данной курсовой работы: разработать методику обучения решению иррациональных уравнений и неравенств в школе, а также выявить возможности использования общих методов решения уравнений при решении иррациональных уравнений и неравенств.
Для достижения поставленной цели необходимо решить следующие задачи:
Проанализировать действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств;
Изучить стандарты образования по данной теме;
Изучить статьи и учебно-методическую литературу по данной теме;
Подобрать теоретический материал, связанный с равносильностью уравнений и неравенств, равносильностью преобразований, методами решения иррациональных уравнений и неравенств;
Показать, как общие методы решения уравнений применимы для решения иррациональных уравнений и неравенств;
Реклама

Подобрать примеры решения иррациональных уравнений и неравенств для демонстрации излагаемой теории.
Гипотеза исследования: применение разработанной методики решения иррациональных уравнений и неравенств позволит учащимся решать иррациональные уравнения и неравенства на сознательной основе, выбирать наиболее рациональный метод, применять разные методы решения, в том числе те, которые не рассмотрены в школьных учебниках.
Анализ школьных учебников по алгебре и началам анализа
При изучении любой новой темы в основном курсе школы встает проблема изложения данной темы в школьных учебниках. Поэтому сначала проанализируем действующие учебники по алгебре и началам математического анализа для 10-11 классов, чтобы выяснить, как в них представлены методы решения иррациональных уравнений и неравенств.
"Алгебра и начала анализа, 10-11", авт.А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницин и др. [
13].
Материал по данной теме изложен в IV главе "Показательная и логарифмическая функции", как пункт "Иррациональные уравнения" параграфа "Обобщение понятия степени". Автор рекомендует рассматривать решение иррациональных уравнений в теме "Уравнения, неравенства, системы", где систематизируются сведения об уравнениях.
В пункте "Иррациональные уравнения" дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида   , которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения удобно решать, используя равносильный переход от уравнения к системе, состоящей из уравнения и неравенства. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы "избавиться от радикала", обе части такого уравнения возводятся в куб. , которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения удобно решать, используя равносильный переход от уравнения к системе, состоящей из уравнения и неравенства. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы "избавиться от радикала", обе части такого уравнения возводятся в куб.
После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№417-420 предложены простейшие уравнения, решить которые можно с помощью возведения обеих частей уравнения либо в квадрат, либо в куб, а также используя равносильные переходы. Такие задачи, по мнению авторов учебника необходимо уметь решать для получения удовлетворительной оценки. Задачи же в №№422-425 чуть сложнее. Здесь уже уравнения содержат корни выше третьей степени.
Реклама

Иррациональным неравенствам в данном пункте внимания не уделено.
В заключительной главе учебника "Задачи на повторение" помещены практические упражнения для повторения курса. Здесь в параграфе "Уравнения, неравенства, системы уравнений и неравенств" иррациональным уравнениям и неравенствам посвящен пункт "Иррациональные уравнения и неравенства".
"Алгебра и начала анализа, 10-11", авт. Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.
[1].
В данном учебнике нет материала, посвященного иррациональным уравнениям и неравенствам. Лишь в конце ученика помещены упражнения для итогового повторения курса алгебры. Здесь есть только один номер для решения простейших иррациональных уравнений (№801). Упражнений для решения иррациональных неравенств нет.
Это можно объяснить тем, что, по мнению автора, умение решать иррациональные неравенства не является обязательным для учащихся и соответствующая тема может быть предложена для изучения самостоятельно или на факультативных занятиях. [14] Поэтому в учебнике предложены задачи для внеклассной работы, где встречаются иррациональные уравнения (№№934, 947) и неравенства (№942).
"Алгебра и начала анализа, 10-11", авт.М.И. Башмаков
[2].
В данном учебном пособии иррациональные уравнения и неравенства рассматриваются в заключительной VI главе "Уравнения и неравенства". Глава предназначена для систематизации и обобщения сведений об уравнениях, неравенствах и системах уравнений. В начале главы помещена вводная беседа, которая состоит из трех пунктов.
В пункте "Уравнение" вводятся такие понятия как уравнение, неизвестные, корень уравнения, подробно рассказывается, что значит решить уравнение с одним или двумя неизвестными, что означает найти корни уравнения, приведены некоторые рекомендации о форме записи ответа при решении уравнений с одним или двумя неизвестными.
В пункте "Равносильность" выясняется, когда одно уравнение является следствием другого, вводится понятие равносильных уравнений. Автор подробно останавливается на некоторых полезных преобразованиях уравнений:
Тождественное преобразование одной из частей уравнения и перенос членов из одной части уравнения в другую с противоположным знаком.
Переход к совокупности уравнений.
Переход к системе уравнений.
Все равносильные переходы представлены в виде схем и рассмотрены на примерах.
В следующем пункте "Неравенство" приведены примеры верных и неверных числовых неравенств, основные правила преобразования неравенств, при этом используются знаки следствия и равносильности. Вводятся такие понятия как ОДЗ неравенства, решение неравенства, равносильные неравенства, выясняется, когда одно неравенство является следствием другого.
§1 "Уравнения с одним неизвестным" состоит из трех пунктов: "Общие приемы", "Примеры решения уравнений" и "Приближенные методы вычисления корней". В первом пункте перечислены стандартные уравнения, которые были изучены ранее. Основным шагом в решении уравнения является преобразование уравнения к одному из стандартных. Приведены некоторые наиболее употребительные приемы, общие для всех типов уравнений:
Разложение на множители.
Введение нового неизвестного.
Графический метод.
Во втором пункте на ряду со стандартными уравнениями рассматривается решения одного простейшего иррационального уравнения с помощью равносильного перехода к системе.
В третьем пункте кратко рассказывается о таких методах приближенного вычисления корней как метод половинного деления, метод хорд и касательных.
§ 2 "Неравенства с одним неизвестным" состоит из двух пунктов: "Общие приемы" и "Примеры решения неравенств". В первом пункте демонстрируется два приема решения неравенств: разложение на множители и метод замены неизвестного.
Во втором пункте на примерах показана техника решения неравенств с помощью переходов, сохраняющих равносильность. На ряду со стандартными неравенствами рассматривается решение одного простейшего иррационального неравенства.
Глава заканчивается заданиями. К заголовку "Иррациональные уравнения" относится №17, к заголовку "Иррациональные неравенства" - №21, в котором есть задание со звездочкой, то есть относящееся к разделу "трудные задачи".
Иррациональным уравнениям и неравенствам в главе уделено мало внимания: решение одного простейшего иррационального уравнения и одного неравенства.
Цель данной главы - обобщить имеющиеся у учащихся знаний об уравнениях, неравенствах и системах уравнений, поэтому здесь подробно не рассматриваются конкретные виды уравнений, а лишь повторяются сведения об изученных видах уравнений и методах их решения. [14]
"Алгебра и начала анализа, 10-11", авт.А.Г. Мордкович
[10], [11].
Данное учебное пособие состоит из двух частей: учебника и задачника.
В первой части данного учебного пособия материал, касающийся иррациональных уравнений и неравенств, изучается в последней VIII главе "Уравнения и неравенства. Системы уравнений и неравенств", завершающей изучение школьного курса алгебры и начал математического анализа. Здесь уравнения и неравенства рассматриваются с самых общих позиций. Это, с одной стороны, своеобразное подведение итогов и, с другой стороны, некоторое расширение и углубление знаний.
В первых трех параграфах этой главы подведены итоги изучения в школе уравнений, неравенств. Использованы следующие термины
:
равносильность уравнений, равносильность неравенств;
следствие уравнения, следствие неравенства;
равносильное преобразование уравнения, неравенства;
посторонние корни (для уравнений);
проверка корней (для уравнений).
Сформулированы теоремы
:
о равносильности уравнений;
о равносильности неравенств.
Даны ответы на четыре главных вопроса
, связанных с решением уравнений:
как узнать, является ли переход от одного уравнения к другому равносильным преобразованием;
какие преобразования переводят данное уравнение в уравнение-следствие;
как сделать проверку, если она сопряжена со значительными трудностями в вычислениях;
в каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?
Перечислены возможные причины расширения области определения уравнения, одна из которых - освобождение в процессе решения уравнения от знаков корней четной степени; указаны причины, по которым может произойти потеря корней при решении уравнений.
Выделены четыре общих метода
решения уравнений:
замена уравнения h
(f
(x
)) =h
(g
(x
)) уравнением f
(x
) =g
(x
);
метод разложения на множители;
метод введения новых переменных;
функционально-графический метод.
Что касается иррациональных уравнений, то им в данном учебном пособии уделено достаточно большое внимание.
На примере иррационального уравнения показано как в три этапа осуществляется решение любого уравнения:
Первый этап - технический
;
Второй этап - анализ решения
;
Третий этап - проверка.
Также на примере иррационального уравнения показано, как сделать проверку, если проверка корней с помощью их подстановки в исходное уравнение сопряжена со значительными вычислительными трудностями.
Метод замены уравнения h
(f
(x
)) =h
(g
(x
)) уравнением f
(x
) =g
(x
) применятся при решении иррациональных уравнений для перехода от уравнения  к уравнению к уравнению  . .
Метод введения новой переменной также разобран и на примере решения иррационального уравнения.
Отдельный пункт посвящен иррациональным неравенствам. Здесь с теоретическим обоснованием рассматривается решение неравенств вида  , ,  . В первом случае иррациональное неравенство заменяется равносильной системой неравенств . В первом случае иррациональное неравенство заменяется равносильной системой неравенств  во втором - равносильной совокупностью систем неравенств во втором - равносильной совокупностью систем неравенств  
Система задач изложена в той же последовательности, что и соответствующий материал в I части. В § 55 "Равносильность уравнений" изложены различные типы заданий на равносильность и следствие уравнений, в том числе и иррациональных. В § 56 "Общие методы решения уравнений" помещены задания для использования четырех методов, изложенных в I части данного учебного пособия, для решения уравнений. Все задачи в соответствии с ними разбиты на четыре блока, в каждом из которых встречаются иррациональные уравнения. В § 57 "Решение неравенств с одной переменной" изложены различные типы заданий на равносильность и следствие неравенств, в том числе и иррациональных.
В № 1673 нужно решить простейшие иррациональные уравнения. №№1674, 1675, 1712-1719 - упражнения выше среднего уровня для решения иррациональных уравнений, №№1790, 1791 - неравенств. № 1792 - упражнение повышенной трудности для решения иррациональных неравенств.
Много заданий, в которых требуется решить "смешанное" уравнение или неравенство, то есть логарифмическое, показательное или тригонометрическое уравнение или неравенство, в которое входят и иррациональные выражения. Среди этих заданий есть задания как базового, так и повышенного уровня.
В I части учебника много внимание уделено равносильности уравнений и неравенств, достаточно строго рассмотрены общие методы решения уравнений, с оговоркой о потере корней и приобретении посторонних. II часть учебника отличается обилием и разнообразием задач. Достаточно много задач на равносильность и следствие уравнений и неравенств.
"Сборник задач по алгебре, 8-9", авт. М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич
[
5]
Данная книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики.
В начале параграфа "Степень с рациональным показателем" помещен справочный материал теоретического характера, посвященный иррациональным уравнениям и неравенствам. Описаны такие пути решения иррациональных уравнений, как:
возведение обеих частей уравнения в натуральную степень с последующей проверкой найденных корней;
переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в четную степень.
При решении иррациональных неравенств либо используется метод интервалов, либо с помощью равносильных преобразований заменяется данное иррациональное неравенство системой (или совокупностью систем) рациональных неравенств.
В параграфе рассмотрено три способа решения иррационального уравнения вида  : :
переход к равносильной системе;
введение новой переменной;
использование свойства монотонности функций.
Среди упражнений, помещенных в данном параграфе, есть упражнения для закрепления умений и навыков решать иррациональные уравнения и неравенства. В №№115-117 необходимо доказать, что уравнение не имеет решения, в №№118-119 - ответить на вопрос: равносильны ли уравнения. №№120-144 предлагаются для решения иррациональных уравнений, №№145-155 - для решения неравенств описанными выше способами.
"Алгебра и математический анализ, 11", авт.Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд
[4].
Данное учебное пособие представляет собой продолжение книги "Алгебра и начала анализа" для 10 класса и предназначено как для общеобразовательной школы, так и классов и школ с углубленным изучением курса математики.
Иррациональные уравнения и неравенства изучаются в параграфе "Степенная функция. Иррациональные выражения, уравнения и неравенства" VIII главы "Показательная, логарифмическая и степенные функции".
Пункт "Иррациональные уравнения" начинается с определения иррационального уравнения и примеров таких уравнений. Далее сформулирована и доказана теорема о равносильных уравнениях, на которой основано решение иррациональных уравнений. Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могут появиться посторонние корни. Поэтому, чтобы не было необходимости подставлять найденные корни в данное уравнение, сформулировано еще два утверждения о равносильном переходе от уравнений вида  и и  к системам, состоящим из уравнения и неравенства. Далее на примерах решения иррациональных уравнений демонстрируются данные равносильные переходы. Также автор рекомендует перед возведением обеих частей уравнения в некоторую степень "уединить радикал", то есть представить уравнение в виде к системам, состоящим из уравнения и неравенства. Далее на примерах решения иррациональных уравнений демонстрируются данные равносильные переходы. Также автор рекомендует перед возведением обеих частей уравнения в некоторую степень "уединить радикал", то есть представить уравнение в виде  . Далее данный метод применяется для решения иррациональных уравнений . Далее данный метод применяется для решения иррациональных уравнений
После данного пункта помещены упражнения для закрепления умений решать иррациональные уравнения описанными выше методами - №216. В №215 необходимо доказать, что данные иррациональные уравнения не имеют решений.
В следующем пункте "Иррациональные неравенства" сформулированы приемы решения иррациональных неравенств вида  и и  с помощью равносильного перехода к системе неравенств в первом случае и совокупности систем неравенств - во втором. Рассматривается решение иррационального неравенства вида с помощью равносильного перехода к системе неравенств в первом случае и совокупности систем неравенств - во втором. Рассматривается решение иррационального неравенства вида  с помощью равносильного перехода к неравенству с помощью равносильного перехода к неравенству  . Решение каждого из видов неравенств демонстрируется на примерах. . Решение каждого из видов неравенств демонстрируется на примерах.
После данного пункта помещены упражнения для закрепления умения решать иррациональные неравенства с помощью равносильных переходов, описанных выше - №217.
Все утверждения, сформулированные в данном учебном пособии, изложены со строгим обоснованием. Описан полезный метод при решении иррациональных уравнений - метод "уединения радикала". Не смотря на то, что учебник не отличается обилием упражнений, предлагаемые задания разнообразны, различной степени сложности
Проведенный анализ позволяет сделать следующие выводы:
В учебнике [1] материала по методам решения иррациональных уравнений нет. В учебниках [13] и [4] материал по теории методов решения скудный, но довольно строгий. В большом объеме теория по общим методам решения рассмотрена учебниках [2] и [10].
В каждом учебнике рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных переходов к системе, состоящей из уравнения и неравенства. В учебниках [2] и [10] рассмотрены такие общие методы решения уравнений как метод разложения на множители, метод введения новых переменных, функционально-графический метод
В учебниках [1] и [13] не рассмотрено решение иррациональных неравенств. В учебнике [2] материал по решению иррациональных неравенств скудный, изложение не достаточно строгое. В учебниках [4] и [10] теория по способам решения иррациональных неравенств вида  , ,  рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида  . .
Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны.
Основные понятия, относящиеся к уравнениям
Равенство вида
 , (1) , (1)
где  и и  - некоторые функции, называют уравнением с одним неизвестным
x
(с одной переменной x
). Это равенство может оказаться верным при одних значениях x
и неверным при других значениях x
. - некоторые функции, называют уравнением с одним неизвестным
x
(с одной переменной x
). Это равенство может оказаться верным при одних значениях x
и неверным при других значениях x
.
Число a
называется корнем (
или решением
) уравнения (1), если обе части уравнения (1) определены при  и равенство и равенство  является верным. Следовательно, каждый корень уравнения (1) принадлежит множеству, которое является пересечением (общей частью) областей определения функций является верным. Следовательно, каждый корень уравнения (1) принадлежит множеству, которое является пересечением (общей частью) областей определения функций  и и  и называется областью допустимых значений
(ОДЗ) уравнения (1). и называется областью допустимых значений
(ОДЗ) уравнения (1).
Решить уравнение
- значит найти все
его корни или доказать, что корней нет.
Если в условиях задачи не указано, на каком множестве нужно решить уравнение, то решение следует искать на ОДЗ этого уравнения.
В процессе решения часто приходится преобразовывать уравнение, заменяя его более простым (с точки зрения нахождения корней).
Есть одно правило, которое не следует забывать при преобразовании уравнений: нельзя выполнять преобразования, которые могут привести к потере корней
.
Назовем преобразование уравнения (1) допустимым
, если при этом преобразовании не происходит потери корней, то есть получается уравнение
 , (2) , (2)
которое либо имеет те же корни, что и уравнение (1), либо, кроме всех корней уравнения (1), имеет хотя бы один корень, не являющийся корнем уравнения (1), посторонний для уравнения (1) корень. В связи с этим используют следующие понятия.
Уравнение (2) называется следствием
уравнения (1), если каждый корень уравнения (1) является корнем уравнения (2).
Уравнения (1) и (2) называются равносильными (
эквивалентными), если каждое из этих уравнений является следствием другого. Иными словами, уравнения (1) и (2) равносильны, если каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Уравнения, не имеющие корней, считаются равносильными.
Если уравнения (1) и (2) равносильны, то пишут    или (1) или (1)  (2), а если уравнение (2) является следствием уравнения (1), то пишут (2), а если уравнение (2) является следствием уравнения (1), то пишут    или (1) или (1)  (2). (2).
Отметим, что если исходное уравнение с помощью допустимых преобразований заменено другим, причем в процессе преобразования хотя бы один раз уравнение заменялось неравносильным ему следствием, то проверка найденных корней путем подстановки в исходное уравнение является обязательной
.
Если же при каждом преобразовании уравнение заменялось равносильным, то проверка не нужна (не следует путать проверку с контролем вычислений).
Рассмотрим еще одно понятие, связанное с решением уравнений. Будем говорить, что уравнение (1) равносильно совокупности уравнений
 , (3) если выполнены следующие условия: каждый корень уравнения (1) является корнем, по крайней мере, одного из уравнений (3); любой корень каждого из уравнений (3) является корнем уравнении я (1). , (3) если выполнены следующие условия: каждый корень уравнения (1) является корнем, по крайней мере, одного из уравнений (3); любой корень каждого из уравнений (3) является корнем уравнении я (1).
Если указанные условия выполнены, то множество корней уравнения (1) является объединением множеств корней уравнений (3).
Если уравнение записано в виде
 , (4) , (4)
то каждое решение этого уравнения является решением, по крайней мере, одного из уравнений
 (5) (5)
Однако нельзя утверждать, что любой корень каждого из уравнений (5) есть корень уравнения (4).
Например, если  , то , то  - корень уравнения - корень уравнения  , но число 3 не является корнем уравнения (4), так как функция , но число 3 не является корнем уравнения (4), так как функция  не определена при не определена при  . .
Таким образом, в общем случае нельзя утверждать, что уравнение (4) равносильно совокупности уравнений (5).
Чтобы решить уравнение (4), достаточно найти корни уравнений  и и  , а затем отбросить те, которые не входят в ОДЗ уравнения (4), то есть не принадлежат множеству, на котором определены функции , а затем отбросить те, которые не входят в ОДЗ уравнения (4), то есть не принадлежат множеству, на котором определены функции  и и  . .
В ОДЗ уравнения (4) это уравнение равносильно совокупности уравнений (5).
Справедливо более общее утверждение: если функция  определена при всех x
таких, что определена при всех x
таких, что  , а функция , а функция  определена при всех x
таких, что определена при всех x
таких, что  , то уравнение (4) равносильно совокупности уравнений (5). [18] , то уравнение (4) равносильно совокупности уравнений (5). [18]
Все преобразования уравнений можно разделить на два типа:
равносильные, то есть преобразования, после применения любых из которых получится уравнение, равносильное исходному.
Неравносильные, то есть преобразования, после применения которых может произойти потеря или приобретение посторонних корней. [15]
Рассмотрим некоторые преобразования уравнений и выясним, к каким типам они относятся.
Перенос членов уравнения из одной части в другую
, то есть переход от уравнения
 (1) (1)
к уравнению
 . (2) . (2)
Указанное преобразование приводит к равносильному уравнению, то есть (1)  (2). (2).
В частности,  . .
Заметим, что здесь речь идет только о переносе членов уравнения из одной его части в другую без последующего приведения подобных членов (если таковые имеются). [18]
Приведение подобных членов
, то есть переход от уравнения
 (3) (3)
к уравнению
 . (4) . (4)
Справедливо следующее утверждение: для любых функций  , , , ,  уравнение (4) является следствием уравнения (3), то есть (3) уравнение (4) является следствием уравнения (3), то есть (3)  (4). (4).
Переход от уравнения (3) к уравнению (4) является допустимым преобразованием, при котором потеря корней не возможна, но могут появиться посторонние корни.
Таким образом, при приведении подобных членов, а также при отбрасывании одинаковых слагаемых в левой и правой частях уравнения получается уравнение, являющееся следствием исходного уравнения. [18]
Например, если в уравнении

вычеркнуть в левой и правой его частях слагаемое  , то получится уравнение , то получится уравнение
 , ,
являющееся следствием исходного: второе уравнение имеет корни  , ,  , а первое - единственный корень , а первое - единственный корень  . .
Отметим еще, что если ОДЗ уравнения (4) содержится в области определения функции  , то уравнения (3) и (4) равносильны. , то уравнения (3) и (4) равносильны.
Умножение обеих частей уравнения на одну и ту же функцию
, то есть переход от уравнения (4) к уравнению
 . (5) . (5)
Справедливы следующие утверждения:
если ОДЗ уравнения (4), то есть пересечение областей определения функций  и и  , содержится в области определения функции , содержится в области определения функции  , то уравнение (5) является следствием уравнения (4); , то уравнение (5) является следствием уравнения (4);
если функция  определена и отлична от нуля в ОДЗ уравнения (4), то уравнения (4) и (5) равносильны. [18] определена и отлична от нуля в ОДЗ уравнения (4), то уравнения (4) и (5) равносильны. [18]
Заметим, что в общем случае переход от уравнения (5) к уравнению (4) недопустим: это может привести к потере корней.
При решении уравнений вида (5) обычно заменяют его равносильным уравнением
 , ,
затем находят все корни уравнений
 и и 
и, наконец, проверяют, какие из этих корней удовлетворяют уравнению (5).]
Возведение обеих частей уравнения в натуральную степень
, то есть переход от уравнения
 (6) (6)
к уравнению
 . (7) . (7)
Справедливы следующие утверждения:
при любом  уравнение (7) является следствием уравнения (6); уравнение (7) является следствием уравнения (6);
если  (n
- нечетное число), то уравнения (6) и (7) равносильны; (n
- нечетное число), то уравнения (6) и (7) равносильны;
если  (n
- четное число), то уравнение (7) равносильно уравнению (n
- четное число), то уравнение (7) равносильно уравнению
 , (8) , (8)
а уравнение (8) равносильно совокупности уравнений
 . (9) . (9)
В частности, уравнение
 (10) (10)
равносильно совокупности уравнений (9). [18]
Следовательно, исходя из утверждений 1 и 2, возведение обеих частей уравнения в нечетную степень и извлечение из обеих частей уравнения корня нечетной степени является равносильным преобразованием.
Исходя из утверждения 1 и 3, возведение обеих частей уравнения в четную степень и извлечение из обеих частей уравнения корня четной степени является неравносильным преобразованием, при этом получается уравнение, являющееся следствием исходного.
Применение формулы
 при при  является равносильным преобразованием, при является равносильным преобразованием, при  - неравносильным. [15], [18] - неравносильным. [15], [18]
Преобразования уравнений, рассмотренные в пунктах 3, 4 и 5 будут продемонстрированы на примерах ниже.
В работе будем придерживаться следующего определения иррационального уравнения:
Иррациональным
уравнением
называется уравнение, содержащее неизвестное под знаком корня.
Прежде чем приступить к решению сложных уравнений учащиеся должны научиться решать простейшие иррациональные уравнения. К простейшим иррациональным уравнениям относятся уравнения вида:

Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Главный способ избавиться от корня и получить рациональное уравнение - возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее "освобождение" от радикалов по формуле  . [6] . [6]
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному. [6]
При возведении уравнения в четную степень получается уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения, но не возможна потеря корней. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение, а не в какие-то промежуточные.
Рассмотрим применение данного метода решения иррациональных уравнений. [7]
Пример 1
. Решите уравнение  . .
Решение.
Возведем обе части этого уравнения в квадрат  и получим и получим      , откуда следует, что , откуда следует, что  или или  . .
Проверка.
 : :   . Это неверное числовое равенство, значит, число . Это неверное числовое равенство, значит, число  не является корнем данного уравнения. не является корнем данного уравнения.
 : :  . Это верное числовое равенство, значит, число . Это верное числовое равенство, значит, число  является корнем данного уравнения. является корнем данного уравнения.
Ответ.
 . .
Проверка, осуществляемая подстановкой найденного решения в исходное уравнение, может быть легко реализована, если проверяемые корни - "хорошие" числа, а для "громоздких" корней проверка может быть сопряжена со значительными вычислительными трудностями. Поэтому каждый образованный школьник должен уметь решать иррациональные уравнения с помощью равносильных преобразований, так как, выполняя равносильные преобразования, можно не опасаться ни потери корней, ни приобретения посторонних решений. [17] Аккуратное возведение в четную степень уравнения вида  состоит в переходе к равносильной ему системе состоит в переходе к равносильной ему системе

Неравенство  в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки. [17] в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки. [17]
Школьники довольно часто добавляют к этой системе неравенство  . Однако этого делать не нужно и даже опасно, поскольку условие . Однако этого делать не нужно и даже опасно, поскольку условие  автоматически выполняется для корней уравнения автоматически выполняется для корней уравнения  , в правой части которого стоит неотрицательное выражение. [9] , в правой части которого стоит неотрицательное выражение. [9]
Пример 2
. Решить уравнение  . .
Решение.
Это уравнение равносильно системе

Решая первое уравнение этой системы, равносильное уравнению  , получим корни , получим корни  и и  . .
Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ.
 . .
При решении иррациональных уравнений полезно перед возведением обеих частей уравнения в некоторую степень "уединить радикал", то есть представить уравнение в виде  . .
Тогда после возведения обеих частей уравнения в n-
ую степень радикал справа исчезнет. [4]
Пример 3
. Решить уравнение 
Решение
. Метод уединения радикала приводит к уравнению  . Это уравнение равносильно системе . Это уравнение равносильно системе

Решая первое уравнение этой системы, получим корни  и и  , но условие , но условие  выполняется только для выполняется только для  . .
Ответ.  . .
Полезно запомнить схему решения еще одного вида иррациональных уравнений  . Такое уравнение равносильно каждой из двух систем . Такое уравнение равносильно каждой из двух систем


Поскольку после возведения в четную степень получаем уравнение-следствие  . Мы должны, решив его, выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство . Мы должны, решив его, выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство  (или (или  ). На практике из этих систем выбирают для решения ту, в которой неравенство проще. [9] ). На практике из этих систем выбирают для решения ту, в которой неравенство проще. [9]
Пример 4
. Решить уравнение
 . .
Решение.
Это уравнение равносильно системе

Решая первое уравнение этой системы, равносильное уравнению  , получим корни , получим корни  и и  . .
Однако при этих значениях x
не выполняется неравенство  , и потому данное уравнение не имеет корней. , и потому данное уравнение не имеет корней.
Ответ
. Корней нет.
Теперь можно перейти к решению иррациональных уравнений, не относящихся к простейшим.
Пример 5
. Решить уравнение  . .
Решение
. Возведем обе части уравнения в квадрат и произведем приведение подобных членов, перенос слагаемых из одной части равенства в другую и умножение обеих частей на  . .
В результате получим уравнение
 , (1) , (1)
являющееся следствием исходного.
Снова возведем обе части уравнения в квадрат. Получим уравнение
 , ,
которое приводится к виду
 . .
Это уравнение (также являющееся следствием исходного) имеет корни  , ,  . Оба корня, как показывает проверка, удовлетворяют исходному уравнению. . Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ
.  , ,  . .
При решении иррациональных уравнений и неравенств часто приходится применять тождественные преобразования, связанные с использованием известных формул. К сожалению, эти действия иногда столь же небезопасны, как уже рассмотренное возведение в четную степень, - могут приобретаться или теряться решения. [17]
Обсудим несколько ситуаций, в которых эти проблемы наступают, и посмотрим, как их распознать и как можно с ними бороться.
I
. Пример 6
. Решить уравнение  . .
Решение.
При первом же взгляде на это уравнение возникает мысль избавиться от корня с помощью "преобразования"  . .
Но это неверно, так как при отрицательных значениях x
оказывалось бы, что  . .
Необходимо запомнить формулу  . Уравнение теперь легко решается . Уравнение теперь легко решается
   . .
Ответ
.  . .
Теперь посмотрим "обратное" преобразование.
Пример 7
. Решить уравнение  . .
Решение.
Сейчас настало время задуматься о безопасности формулы
 . .
Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии  . Поэтому исходное уравнение равносильно системе . Поэтому исходное уравнение равносильно системе

Ответ.
 . .
II
. Следующее преобразование, которое должно явиться предметом заботы для каждого, кто решает иррациональные уравнения, определяется формулой
 . .
Если пользоваться этой формулой слева направо, расширяется ОДЗ и можно приобрести посторонние решения. Действительно, в левой части обе функции  и и  должны быть неотрицательны; а в правой неотрицательным должно быть их произведение. [17] должны быть неотрицательны; а в правой неотрицательным должно быть их произведение. [17]
Замечание. При возведении уравнения в квадрат учащиеся нередко в уравнении типа (1) из Примера 5
производят перемножение подкоренных выражений, т.е. вместо такого уравнения пишут уравнение
 . .
Такое "склеивание" не приводит к ошибкам, поскольку такое уравнение является следствием уравнения (1). Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения. Поэтому в рассмотренном выше примере можно было сначала перенести один из радикалов в правую часть уравнения, т.е. уединить один радикал. Тогда в левой части уравнения останется один радикал, и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональное выражение. [3]
Пример 8
. Решить уравнение
 . .
Решение
. Уединив первый радикал, получаем уравнение
 , ,
равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
 , ,
равносильное уравнению
 . (2) . (2)
Уравнение (2) является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат, приходим к уравнению
 , или , или  . .
Это уравнение является следствием уравнения (2) (а значит, и исходного уравнения) и имеет корни  , ,  . .
Первый корень удовлетворяет исходному уравнения, а второй - не удовлетворяет.
Ответ
.  . .
Рассмотрим пример, где реализуется проблема с "расклеиванием" корней, то есть использование формулы  . [13] . [13]
Пример 9
. Решить уравнение  . .
Решение.
Попробуем решить это уравнение разложением на множители
 . .
Заметим, что при этом действии оказалось потерянным решение  . Посмотрите, оно подходит к исходному уравнению и уже не подходит к полученному: . Посмотрите, оно подходит к исходному уравнению и уже не подходит к полученному:  не имеет смысла при не имеет смысла при  . Поэтому это уравнение лучше решать обычным возведением в квадрат . Поэтому это уравнение лучше решать обычным возведением в квадрат
  
Ответ.
 , ,  . .
Вывод. Есть два пути. Или аккуратно возводить уравнение в квадрат, или безошибочно определять, какие решения могли быть потеряны, и проверить, не случилось ли этого на самом деле.
III
. Существует еще более опасное действие - сокращение на общий множитель. [17]
Пример 10
. Решить уравнение  . .
"Решение".
Сократим обе части уравнения на  , получим , получим
 . .
Нет ничего более опасного и неправильного, чем это действие. Во-первых, подходящее решение исходного уравнения  было потеряно; во-вторых, было приобретено два посторонних решения было потеряно; во-вторых, было приобретено два посторонних решения  . Получается, что новое уравнение не имеет ничего общего с исходным! Вот правильное решение. . Получается, что новое уравнение не имеет ничего общего с исходным! Вот правильное решение.
Решение
. Перенесем все члены в левую часть уравнения и разложим ее на множители
    . .
Это уравнение равносильно системе

которая имеет единственное решение  . .
Ответ.
 . .
1. Метод разложения на множители.
Суть этого метода заключается в следующем: уравнение  можно заменить совокупностью уравнений: можно заменить совокупностью уравнений:
 ; ;  ; ;  . .
Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние. Приведем пример применения метода разложения на множители при решении иррациональных уравнений. [10]
Пример 11
. Решите уравнение  . .
Решение
. Для решения таких уравнений следует пользоваться правилом расщепления:
Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл. [
17]
Первый множитель равен нулю при  , но тогда второй множитель потеряет смысл, так как при , но тогда второй множитель потеряет смысл, так как при  он равен он равен  . Значит, . Значит,  решением данного уравнения быть не может. решением данного уравнения быть не может.
Второй множитель равен нулю при  или или  . Первый множитель определен для всех действительных чисел, значит, . Первый множитель определен для всех действительных чисел, значит,  и и  могут быть решениями данного уравнения. Ответ. могут быть решениями данного уравнения. Ответ.  , , 
2. Метод введения новой переменной
.
Мощным средством решения иррациональных уравнений является метод введения новой переменной, или "метод замены". Метод обычно применяется в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Тогда имеет смысл обозначить это выражение какой-нибудь новой буквой и попытаться решить уравнение сначала относительно введенной неизвестной, а потом уже найти исходную неизвестную. В ряде случаев удачно введенные новые неизвестные иногда позволяют получить решение быстрее и проще; иногда же без замены решить задачу вообще невозможно. [6], [17]
Пример 12
. Решить уравнение  . .
Решение
. Положив  , получим существенно более простое иррациональное уравнение , получим существенно более простое иррациональное уравнение   . Возведем обе части уравнения в квадрат: . Возведем обе части уравнения в квадрат:
 . .
Далее последовательно получаем:
 ; ;
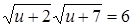 ; ;
 ; ;
 ; ;
 , ,  . .
Проверка найденных значений их подстановкой в уравнение  показывает, что показывает, что  - корень уравнения, а - корень уравнения, а  - посторонний корень. - посторонний корень.
Возвращаясь к исходной переменной x
, получаем уравнение  , т.е. квадратное уравнение , т.е. квадратное уравнение  , решив которое находим два корня: , решив которое находим два корня:  , ,  . .
Ответ
:  , ,  . .
Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение превращается в квадратное.
Пример 13
. Решить уравнение  . .
Решение.
Перепишем уравнение так:  . .
Видно, что если ввести новую переменную  , то уравнение примет вид , то уравнение примет вид  , откуда , откуда  , ,  . .
Теперь задача сводится к решению уравнения  и уравнения и уравнения  . Первое из этих решений не имеет, а из второго получаем . Первое из этих решений не имеет, а из второго получаем  , ,  . .
Ответ
.  , ,  . .
Отметим, что "бездумное" применение в Примере 11
метода "уединения радикала" и возведение в квадрат привело бы к уравнению четвертой степени, решение которого представляет собой в общем случае чрезвычайно сложную задачу.
Пример 14
. Решить уравнение
 . .
Введем новую переменную
 , ,  . .
Исходное уравнение принимает вид
 , ,
откуда учитывая ограничение  , получаем , получаем  . Тогда . Тогда  . .
Ответ
.  . .
Уравнения вида  (здесь a,
b,
c,
d -
некоторые числа, m,
n -
натуральные числа, обычно не превосходящие 4) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных и последующего перехода к рациональной системе. [17]. Пример 15
. Решить уравнение (здесь a,
b,
c,
d -
некоторые числа, m,
n -
натуральные числа, обычно не превосходящие 4) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных и последующего перехода к рациональной системе. [17]. Пример 15
. Решить уравнение  . .
Решение
. Введем новые переменные
 и и  . .
Тогда исходное уравнение принимает вид:  . Полученное уравнение обладает одним существенным недостатком: в нем две неизвестных. Но заметим, что величины a
и b
не являются независимыми переменными - они зависят одна от другой посредством старой переменной x
. Выразим x
через a
и b . Полученное уравнение обладает одним существенным недостатком: в нем две неизвестных. Но заметим, что величины a
и b
не являются независимыми переменными - они зависят одна от другой посредством старой переменной x
. Выразим x
через a
и b
 и и  . .
Теперь, можно заметить, что если первое уравнение умножить на два и затем вычесть из него второе, то переменная x
исключается, и остается связь только между a
и b
 . .
В результате получаем систему двух уравнений относительно двух неизвестных a
и b

Решая эту систему методом подстановки, приходим к уравнению  , корнями которого являются числа , корнями которого являются числа  и и  . Корень . Корень  посторонний, поскольку посторонний, поскольку  . Осталось решить уравнение . Осталось решить уравнение  , откуда находим , откуда находим  . .
Ответ
.  . .
Пример 16
. Решить уравнение
 . [6] . [6]
Решение
. Возведение обеих частей этого уравнения в четвертую степень не обещает ничего хорошего. Если же положить  , ,  , то исходное уравнение переписывается так: , то исходное уравнение переписывается так:  . Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y
и z
. . Поскольку мы ввели две новые неизвестные, надо найти еще одно уравнение, связывающее y
и z
.
Для этого возведем равенства  , , в четвертую степень и заметим, что в четвертую степень и заметим, что  . .
Итак, надо решить систему уравнений

она имеет два (действительных) решения:  , ,  ; ;  , ,  . Остается решить систему двух уравнений с одним неизвестным . Остается решить систему двух уравнений с одним неизвестным
 и систему и систему 
первая из них дает  , вторая дает , вторая дает  . .
Ответ
.  , ,  . .
Не всегда после введения новых переменных удается исключить неизвестную x
, как это было в рассмотренных Примерах 15, 16
. Однако, как можно убедиться из следующего примера, переход от уравнения к системе может помочь и в таком случае. [17]
Пример 17
. Решить уравнение
 . .
Решение.
Введем новые переменные
 и и  . .
По стандартной схеме получим следующую систему уравнений:

откуда следует, что
 . .
Так как  , то u
и v
должны удовлетворять системе , то u
и v
должны удовлетворять системе

из которой после несложных преобразований получаем уравнение
 . .
Заметим, что это уравнение имеет корень  . Тогда, разделив многочлен на . Тогда, разделив многочлен на  , получаем разложение левой части уравнения на множители , получаем разложение левой части уравнения на множители
 . .
Отсюда следует, что  - единственное решение этого уравнения. После проверки записываем это решение в ответ. - единственное решение этого уравнения. После проверки записываем это решение в ответ.
Ответ. 
3. Тригонометрическая замена.
Иногда подходящей заменой неизвестной иррациональное уравнение можно свести к тригонометрическому уравнению. При этом полезными могут оказаться следующие замены переменной. [17]
Если в уравнение входит радикал  , то можно сделать замену , то можно сделать замену  , ,  или или  , ,  . .
Если в уравнение входит радикал  , то можно сделать замену , то можно сделать замену  tg t
, tg t
,  или или  ctg t
, ctg t
,  . .
Если в уравнение входит радикал  , то можно сделать замену , то можно сделать замену  , ,  или или  , ,  . .
Проиллюстрируем использование этих замен на следующих примерах.
Пример 18
. Решить уравнение  . .
Решение
. В данное уравнение входит выражение  , поэтому в соответствии с пунктом 2, сделаем замену , поэтому в соответствии с пунктом 2, сделаем замену
 tg t
, где tg t
, где  . .
Тогда выражение  , входящее в уравнение, можно преобразовать , входящее в уравнение, можно преобразовать

и исходное уравнение можно записать в виде
 . .
Поскольку 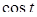 не равен нулю при рассматриваемых значениях t
, то полученное уравнение равносильно уравнению не равен нулю при рассматриваемых значениях t
, то полученное уравнение равносильно уравнению
 . .
Решая это уравнение, находим два возможных значения
 и и  . .
Из всех корней этих уравнений промежутку  принадлежит единственное значение принадлежит единственное значение  . .
Поэтому соответствующее значение x
равно
 . .
Ответ.  . .
Пример 19.
Решить уравнение  . .
Решение
. В этом уравнении x
по ОДЗ может принимать только значения из отрезка  , что приводит к мысли совершить замену , что приводит к мысли совершить замену
 , где , где  . .
В результате такой замены приходим к уравнению
 . .
Учтем, что  и и  , получим уравнение , получим уравнение  . .
В силу ограничения  выполнено выполнено  , поэтому приходим к уравнению , поэтому приходим к уравнению  , которое, пользуясь формулой приведения, сведем к стандартному виду , которое, пользуясь формулой приведения, сведем к стандартному виду
 . .
Решая последнее уравнение, находим
 или или  , ,  . .
Условию  удовлетворяют лишь три значения удовлетворяют лишь три значения
 , ,  , ,  . Поэтому . Поэтому
 , ,  , ,  . .
Ответ
.  , ,  , ,  . .
4. Умножение обеих частей уравнения на функцию
.
Иногда иррациональное уравнение удается решить довольно быстро, если обе его части умножить на удачно подобранную функцию. Конечно, при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули самой этой функции. Поэтому предлагаемый метод требует обязательного исследования получающихся значений. [6]
Пример 20.
Решить уравнение  . .
Решение
. Умножим обе части уравнения на одну и ту же функцию  . Выражение . Выражение  называется сопряженным
для выражения называется сопряженным
для выражения  . Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов. . Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.
В результате этого умножения и очевидных преобразований приходим к уравнению
 . .
Оно имеет единственный корень  , так как уравнение , так как уравнение  решений не имеет. решений не имеет.
Подстановка в исходное уравнение показывает, что  - корень. - корень.
Ответ
.  . .
Впрочем, здесь можно было обойтись и без подстановки: функция  нигде в нуль не обращается, и поэтому умножение обеих частей уравнения нигде в нуль не обращается, и поэтому умножение обеих частей уравнения  на эту функцию не приводит к появлению посторонних решений. на эту функцию не приводит к появлению посторонних решений.
Пример 21.
Решить уравнение  . [9] . [9]
Решение.
Умножим обе части уравнения на функцию  . После преобразований получим уравнение . После преобразований получим уравнение
 . .
Оно имеет два корня:  . Проверка показывает, что . Проверка показывает, что  - посторонний корень (нетрудно видеть, - посторонний корень (нетрудно видеть,  - корень функции - корень функции  ). Таким образом, уравнение имеет единственный корень ). Таким образом, уравнение имеет единственный корень  . .
Ответ
.  . .
Если в любом иррациональном уравнении заменить знак равенства на один из знаков неравенства: >, 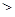 , <, , <, 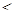 , то получим иррациональное неравенство. [19] Поэтому под иррациональным неравенством
будем понимать неравенство, в котором неизвестные величины находятся под знаком корня. [16] , то получим иррациональное неравенство. [19] Поэтому под иррациональным неравенством
будем понимать неравенство, в котором неизвестные величины находятся под знаком корня. [16]
Способ решения таких неравенств состоит в преобразовании их к рациональным неравенствам путем возведения обеих частей неравенства в степень.
Решение иррациональных неравенств осложняется тем обстоятельством, что здесь, как правило, исключена возможность проверки, поэтому надо стараться делать все преобразования равносильными.
При решении иррациональных неравенств следует запомнить правило: при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству.
[16]
Но если при решении уравнений в результате возведения четную степень мы могли получить посторонние корни (которые, как правило легко проверить) и не могли потерять корни, то корни неравенства при бездумном возведении в четную степень могут одновременно и теряться, и приобретаться. [8]
Например, возведя в квадрат:
верное
неравенство 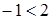 , мы получим верное
неравенство , мы получим верное
неравенство 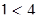 ; ;
верное
неравенство 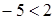 , мы получим неверное
неравенство , мы получим неверное
неравенство 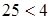 ; ;
неверное
неравенство 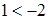 , мы получим верное
неравенство , мы получим верное
неравенство 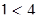 ; ;
неверное
неравенство 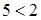 , мы получим неверное
неравенство , мы получим неверное
неравенство 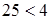 . .
Вы видите, что возможны все комбинации верных и неверных неравенств. [8]
Однако верно основное используемое здесь утверждение: если обе части неравенства возводят в четную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
[16]
Поэтому основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств. [17]
Наиболее простые иррациональные неравенства имеют вид: [16], [17]
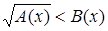 (или (или 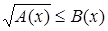 ); );
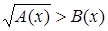 (или (или 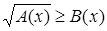 ); );
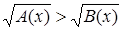 (или (или 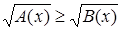 ). ).
Иррациональное неравенство 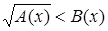 (или (или 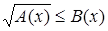 ) равносильно системе неравенств ) равносильно системе неравенств
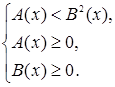 или или 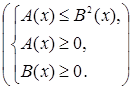 . {1} . {1}
Первое неравенство в системе {1} является результатом возведения исходного неравенства в степень, второе неравенство представляет собой условие существования корня в исходном неравенстве, а третье неравенство системы выражает условие, при котором это неравенство можно возводить в квадрат.
Иррациональное неравенство 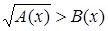 (или (или 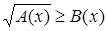 ) равносильно совокупности двух систем неравенств ) равносильно совокупности двух систем неравенств
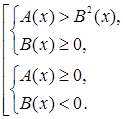 или или 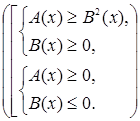 . {2} . {2}
Обратимся к первой системе схемы {2}. Первое неравенство этой системы является результатом возведения исходного неравенства в квадрат, второе - условие, при котором это можно делать.
Вторая система схемы {2} соответствует случаю, когда правая часть отрицательна, и возводить в квадрат нельзя. Но в этом и нет необходимости: левая часть исходного неравенства - арифметический корень - неотрицательна при всех x
, при которых она определена. Поэтому исходное неравенство выполняется при всех x
, при которых существует левая часть. Первое неравенство второй системы и есть условие существования левой части.
Иррациональное неравенство 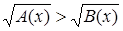 (или (или 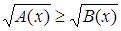 ) равносильно системе неравенств ) равносильно системе неравенств
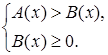 или или 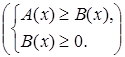 . {3} . {3}
Поскольку обе части исходного неравенства неотрицательны при всех x
, при которых они определены, поэтому его можно возвести в квадрат. Первое неравенство в системе {3} является результатом возведения исходного неравенства в степень. Второе неравенство представляет собой условие существования корня в исходном неравенстве, понятно, что неравенство 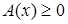 выполняется при этом автоматически. выполняется при этом автоматически.
Схемы {1}-{3} - наш основной инструмент при решении иррациональных неравенств, к ним сводится решение практически любой задачи. Разберем несколько примеров. [8]
Пример 1
. Решить неравенство 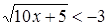 . .
Решение
. Заметим, что правая часто этого неравенства отрицательна, в то время как левая часть неотрицательна при всех значениях x
, при которых она определена. Поэтому неравенство решений не имеет.
Ответ
. Решений нет.
Пример 2
. Решить неравенство 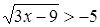 . .
Решение
. Как и в предыдущем примере, заметим, что правая часть данного неравенства отрицательна, следовательно, возводить это неравенство в квадрат нельзя. И не надо, поскольку левая часть исходного неравенства неотрицательна при всех значениях x
, при которых она определена. Это означает, что левая часть больше правой части при всех значениях x
, удовлетворяющих условию 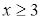 . .
Ответ.
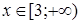 . .
Пример 3
. Решить неравенство 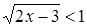 . .
Решение.
В соответствии со схемой {1} решения неравенств этого типа, запишем равносильную ему систему рациональных неравенств
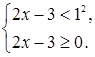
Условие 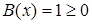 выполнено при всех x
, и нет необходимости добавлять его к выписанной системе. выполнено при всех x
, и нет необходимости добавлять его к выписанной системе.
Ответ. 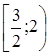 . .
Пример 4
. Решить неравенство 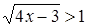 . .
Решение
. Это неравенство решается при помощи схемы {2}. В данном случае 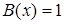 , поэтому можно сразу записать неравенство, равносильное исходному , поэтому можно сразу записать неравенство, равносильное исходному 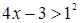 . Ответ. . Ответ. 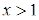 . .
Пример 5.
Решить неравенство 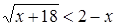 . .
Решение.
Это неравенство может быть решено при помощи схемы {1}. Система, равносильная исходному неравенству, имеет вид
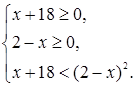
Ответ
. 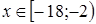 . .
Пример 6.
Решить неравенство 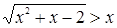 . .
Решение
. Данное неравенство можно решать с помощью схемы {2}. Оно равносильно совокупности двух систем
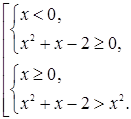
Ответ.
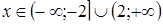 . .
Пример 7.
Решить неравенство 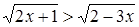 . .
Решение
. Согласно схеме {3}, данное неравенство равносильно системе
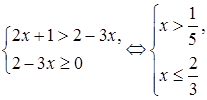 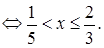
Ответ.
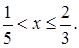
Более сложно решение иррациональных неравенств вида
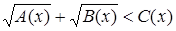 . .
Поскольку 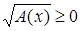 , , 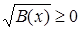 , то должны выполнятся условия , то должны выполнятся условия 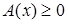 , , 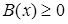 , , 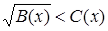 (соответственно (соответственно 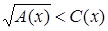 ). На множестве, где эти условия выполняются, данное неравенство равносильно неравенству ). На множестве, где эти условия выполняются, данное неравенство равносильно неравенству 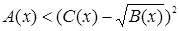 . .
(соответственно неравенству 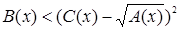 ), которое сводится к разобранным выше типам неравенств. [4] ), которое сводится к разобранным выше типам неравенств. [4]
Пример 8
. Решить неравенство 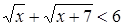 . .
Решение.
Данное неравенство равносильно следующей системе неравенств:
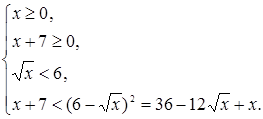
Последнее неравенство этой системы приводится к виду 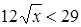 , откуда находим, что , откуда находим, что 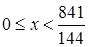 . Решение исходного неравенства является общей частью решений всех неравенств системы, т.е. имеет вид . Решение исходного неравенства является общей частью решений всех неравенств системы, т.е. имеет вид 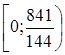 . .
Ответ.
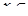 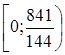 . .
Для решения иррациональных неравенств, так же как и для решения иррациональных уравнений, с успехом может применяться способ подстановки или введения новой переменной.
Весьма эффективны так называемые рационализирующие подстановки. Применение рационализирующих подстановок позволяет привести функцию, иррациональную относительно исходной переменной, к рациональной функции относительно новой переменной. [17]
Пример 9
. Решить неравенство 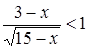 . .
Решение.
Введем новую переменную t
с помощью рационализирующей подстановки 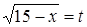 , , 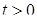 . .
Тогда 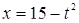 и для переменной t
получаем рациональное неравенство и для переменной t
получаем рациональное неравенство
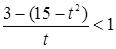 , где , где 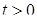 . .
Ответ.
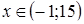 . .
В данной курсовой работе сделана попытка разработать методику обучения решению иррациональных уравнений и неравенств в школе.
В ходе работы были решены следующие задачи:
Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы:
теория методов изложена не достаточно строго;
в одном учебнике [1] материала по методам решения иррациональных уравнений нет. В остальных учебниках рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных преобразований;
очень мало материала по методам решения иррациональных неравенств;
среди предлагаемых заданий много однотипных;
Изучены стандарты образования по данной теме;
Изучена учебно-методическая литература по данной теме;
Рассмотрены ситуации, связанные с потерей или приобретением посторонних корней в процессе решения, показано, как их распознавать и как с ними можно бороться;
Подобраны примеры решения иррациональных уравнений и неравенств для демонстрации излагаемого теоретического материала;
Показано, что общие методы решения уравнений применимы для решения иррациональных уравнений и неравенств.
1. Алимов Ш.А. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1993. - 254 с.
2. Башмаков М.И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1992. - 351 с.
3. Болтянский В.Г. Математика: лекции, задачи, решения. - Литва: Альфа, 1996. - 637 с.
4. Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики. - М.: Просвещение, 1998. - 288 с.
5. Галицкий М.Л. Сборник задач по алгебре для 8-9 классов: Учеб. пособие для учащихся шк. и кл. с углубл. изуч. математики. - М.: Просвещение, 1999. - 271с.
6. Григорьев А.М. Иррациональные уравнения. // Квант, №1, 1972, с.46-49.
7. Денищева Л.О. Готовимся к единому государственному экзамену. Математика. - М.: Дрофа, 2004. - 120 с.
8. Егоров А. Иррациональные неравенства. // Математика. Первое сентября, №15, 2002. - с.13-14.
9. Егоров А. Иррациональные уравнения. // Математика. Первое сентября, №5, 2002. - с.9-13.
10. Мордкович А.Г. Алгебра и начала анализа.10-11 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. - М.: Мнемозина, 2004. - 315 с.
11. Мордкович А.Г. Алгебра и начала анализа.10-11 кл.: В двух частях. Ч.2: Задачник для общеобразоват. учреждений. - М.: Мнемозина, 2004. - 315 с.
12. Мордкович А.Г. Кто-то теряет, кто-то находит. // Квант, №5, 1970, с.48-51.
13. Колмогоров А.Н. Алгебра и начала анализа. Учеб. для 10-11 кл. сред. шк. - М.: Просвещение, 1991. - 320 с.
14. Кузнецова Г.М. Программа для общеобразоват. школ, гимназий, лицеев: Математика.5-11 кл. - М.: Дрофа, 2004, 320 с.
15. Потапов М. Как решать уравнения без ОДЗ. // Математика. Первое сентября, №21, 2003. - с.42-43.
16. Соболь Б.В. Пособие для подготовки к единому государственному экзамену и централизованному тестированию по математике. - Ростов на Дону: Феникс, 2003. - 352 с.
17. Черкасов О.Ю. Математика: Справочник для старшеклассников и поступающих в вузы. - М.: АСТ-ПРЕСС, 2001. - 576 с.
18. Шабунин М. Лекции для абитуриентов. Лекция 1. // Математика. Первое сентября, №24, 1996. - с.24.
19. Шувалова Э.З. Повторим математику. Учеб пособ. для поступающих в вузы. - М.: Высшая школа, 1974. - 519 с.
|