| Министерство науки и образования Украины
ЮГПУ им. К.Д. Ушинского
Институт физики и математики
Курсовая робота на тему:
„Интеграция математических и економ
и
ческих знаний”
Франкина А.В.
V МЭ
Одесса 2008
СОДЕРЖАНИЕ
Введение
Актуальность
Технология и уровни интеграции
Трудности использования математических моделей в экономике
Интеграция математики и экономики для высшего образования
Интеграция математики и экономики длясреднего образования
Интегрированый урок(план-конспект)
Использование новых информационных технологий обучения
Вывод
Список литературы
Введение
В новых социально-экономических условиях, связанных с вхождением Украины в международное информационное пространство, переходом экономики страны к рыночным методам регулирования, опосредующим увеличение скорости устаревания знаний и технологий их усвоения, перед школой остро стоит проблема совершенствования системы подготовки выпускников к будущей профессиональной деятельности.
Создание условий успешного овладения основами профессионального мастерства и формирование интереса учащихся к будущей деятельности является сегодня одной из важнейших задач организации образовательного процесса, призванного обеспечить профессиональное самоопределение личности. Результатом профессионального самоопределения выступает уровень сформированности готовности личности к выбору и овладению специальностью, проектированию вариантов профессионального жизненного пути.
Анализ особенностей профессиональной деятельности вне зависимости от объекта деятельности и условий ее реализации показал, что специалист должен быть готов к принятию решений в условиях неопределенности конкурентной среды. Это актуализирует проблему формирования у будущего специалиста таких элементов профессиональной культуры, как умение формулировать проблему; определять возможности, пути и средства ее разрешения; оптимизировать процесс принятия решений, выступающих ключевыми компетенциями, опосредующими успешность деятельности. Как показывает практика, данная проблема является достаточно актуальной для среднего образования, поскольку методически целесообразно совместить профессиональную подготовку с углубленным изучением отдельных дисциплин в рамках интегрированного курса.
Реклама

Актуальность
Сегодня и взрослые и ученики ставят перед обществом вопросы: «Чем (или кем) определяется сегодня уровень цен? Почему они только растут? Почему государство не может их установить на таком низком уровне, чтобы книг, игрушек, продуктов и других товаров хватало на всех? Почему "тают" наши сбережения и как их спасти? Что хорошего или плохого в изменении цены доллара, о которой нам сообщают по несколько раз в день? В чем смысл реструктуризации внешних долгов?» и т. д.
К сожалению, сегодня учитель школы находится в таком же «экономическом неведении», что и его ученики, и ответов на поставленные животрепещущие проблемные вопросы учитель дать не в состоянии. Такое положение учителя российской школы совсем не типично: как правило, он всегда умел, хотя бы в общих чертах, ответить ученику на поставленный вопрос, будь то устройство ядерной бомбы, структура ДНК, особенности космических полетов и т. д. и т. п.!
Именно в этом месте происходит взаимодействие двух процессов - перехода России к рыночным отношениям и преобразование системы среднего математического образования. Дело в том, что стремительная экономизация российского общества требует овладения школьниками некоторым набором экономических знаний уже на школьной скамье, а перестройка математического образования, усиление практической направленности школьного курса математики, позволит в его рамках рассмотреть новую содержательно-методическую линию - экономическую и сконструировать «экономическую составляющую школьного курса математики».
Под экономической составляющей школьного курса математики мы подразумеваем совокупность простейших экономических понятий, их свойства и специально сконструированный набор задач, имеющих реальное экономическое содержание, которые решаются на основании математического содержания программ соответствующих классов, начиная с 7 и до 11. Эти структуры обеспечат непрерывную экономическую линию в математике 7-11 классов общеобразовательной школы.
Такой подход позволит в рамках изучения математики модифицировать лишь объекты математической деятельности, оставляя без изменения методы и приемы их исследования. Это, в свою очередь, как отмечала И.А. Сасова в [184, с.69], позволяет осуществить переход к непрерывному экономическому образованию детей и учащейся молодежи, который «предполагает смену типа учения с информационно-репродуктивного на активно-творческий, продуктивный, от дидактических экономических игр для младших возрастов до деловых экономических игр, поисковой и производственно-экономической деятельности - для старших, от оправдавших себя классических форм и методов обучения до таких, которые воплощают в себе содержательную педагогическую интеграцию образования, науки, производства, компьютерную технологию обучения».
Реклама

Реализация описанных подходов требует перестройки методической системы обучения математике, в которой важнейшее место займет формирование умений применять полученные теоретические знания для анализа и решения конкретных практических задач, возникающих в окружающей всех нас действительности и экономических задач - в том числе. Именно это умение выступает сегодня как одна из важнейших целей современного математического образования.
Имплантация экономических знаний в содержание задач, решаемых математическими методами, преследует достижение двух целей. Первая из них состоит в том, чтобы продемонстрировать школьникам эффективность применения математических методов к решению реальных экономических задач и тем самым показать связь математики с окружающим миром и реальный смысл ее абстрактных конструкций. Вторая цель состоит в развитии экономического образа мышления - умения применять аппарат математики и экономики для анализа конкретных экономических явлений и процессов.
В последние десятилетия огромный набор работ был посвящен проблеме совершенствования математической и методической подготовки будущих преподавателей в высших педагогических учебных заведениях. Однако, при этом остались в стороне от обсуждения широчайшие возможности, которые предоставляет школьный курс математики для демонстрации разнообразных приложений математики к изучению реальных задач окружающего мира. Внимательный анализ показал, что экономике в этом вопросе принадлежит ведущая роль, ибо, как показано ниже, основные понятия курса алгебры 7-9 и алгебры и начал анализа 10-11 классов могут служить основой для решения важнейших экономических задач. (Мы не обсуждаем замечательных успехов математических методов в физике - их понимание выходит далеко за рамки школьных программ и по физике, и по математике.)
Однако, для того, чтобы учить школьников в процессе изучения математики еще и элементам экономики необходимо, чтобы к этой работе был готов учитель математики. Сегодня он к этой работе не готов.
Трудности решения проблемы подготовки преподавателей для работы по раскрытию связей математики с задачами окружающего мира отличаются тем, что до настоящего времени не было концепции такой ориентации обучения математике, отсутствовали учебно-методические пособия по проведению практикума по приложенческим вопросам математики, отсутствовали дидактические материалы для учителя и т. д.
Мы считаем, что выход из создавшейся ситуации может быть найден на следующем пути:
- выделение простых понятий экономики, с которыми учащихся можно знакомить в 7-11 классах на уроках математики;
- выделение содержательного экономического материала, математические модели которого не требуют знания математики в объеме, выходящем за рамки программ 7-11 классов;
- составление большого цикла примеров и задач с экономическим содержанием, его методическое и дидактическое обеспечение.
Вопросы подготовки учителя математики, способного обсуждать и экономические проблемы - это сложная задача, касающаяся педагогических вузов и она ждет еще своего решения. Мы обсуждать ее не будем.
Общее направление проведенных автором исследований связано с изучением возможностей, предоставляемых многочисленными и глубокими связями математики и экономики. Это способствует развитию у учащихся интереса к изучению математики, выяснению ее тесных связей с реальными задачами современной рыночной экономики, многими из которых должен владеть каждый человек независимо от сферы его интересов. Это поможет становлению экономической культуры, экономической грамотности и экономической этики наших учащихся, которым после окончания школы придется «функционировать» в обществе - новом, как для учеников, так и для большинства учителей и родителей.
Разработанный в данной работе принцип имплантации экономического содержания в круг решаемых в школе математических задач, рассмотрение вопросов интеграции экономических и математических знаний в процесс составления, анализа и решения задач, позволил обновить набор задач, решаемых в 7-11 классах. Это удалось сделать за счет замены части «безыдейных», устаревших или неинтересных задач на новые задачи, имеющие ярко выраженное экономическое содержание. Поскольку математический аппарат при этом не изменяется (меняется только объект, к которому он прилагается), то на математическую подготовку это не влияет, а экономическая составляющая школьного курса математики становится более содержательной и действенной. При этом ученик впервые сталкивается с триадой «экономика-математика - экономика» и начинает понимать, каким образом экономические задачи переводятся на математический язык, далее решаются всем известными, а если это необходимо, то и новыми методами математики и вычислительной техники, и как затем полученные с помощью математического инструментария результаты вновь истолковываются в экономических терминах, давая советы, рекомендации, перечисляя сценарии развития экономических процессов и т. д.
Все это способствует развитию активности и сознательности в обучении математике, которые, как утверждает П. И. Пидкасистый [161, с.181], реализуются, если:
1) опираться на интересы учащихся и одновременно формировать мотивы учения, среди которых на первом месте - познавательные интересы и профессиональные склонности;
2) включать учеников в решение проблемных ситуаций, «в процесс поиска и решения научных и практических проблем;
3) использовать такие методы обучения, как дидактические игры, дискуссии;
4) стимулировать коллективные формы работы, взаимодействие учеников в учении.
Предложенная автором исследования программа имплантации экономических знаний в курс алгебры 7-9 и курс алгебры и начал анализа в 10-11 классах, хорошо сопрягается с зарубежным опытом. Так, например, все рассматриваемые методами математики темы экономики, включенные в экономическую составляющую школьного курса математики, входят в программу экзамена по экономике в школах Великобритании (см. А. Бухвалов [34, с.204] и К.West [281, с.212]. Среди них:
- спрос и предложение (равновесие, эластичность);
- рынки;
- банковское дело;
- налоги и распределение налогового бремени;
- факторы производства;
- издержки;
- сбережения и инвестиции.
Автор исследования полагает, что введение в курс изучения математики новой содержательно-методической линии - экономической, в какой-то мере (далеко не полной) будет способствовать развитию у школьников экономической грамотности, что несомненно окажет им помощь в будущем.
В заключение приведем цитату из статьи А. Бухвалова [34, с.205]: «необычным для нас является то, что школьники в большинстве стран Запада имеют возможность в течение нескольких лет изучать экономику в качестве основной учебной дисциплины. Поэтому к моменту поступления в университет у них имеется значительный запас и полное представление о существе предмета. Даже те, кто не будет затем специализироваться в области экономики, используют в дальнейшем эти знания с пользой, т. к. в условиях рынка нельзя и рядовому члену общества жить без понимания котировки курсов акций и облигаций, знания теории и практики налогообложения... умения пользоваться банковским кредитом и т. д.».
Автор полагает, что внедрение в курс математики либо реальных экономических задач сегодняшнего дня, либо «логически» спроектированных экономических задач значительно расширит экономический кругозор и грамотность всех учащихся нашей школы безотносительно к тому, какой курс математики они изучают в старшей школе: гуманитарный, естественнонаучный или физико-математический.
В исследовании с целью реализации интеграционного подхода в построении содержания профессиональной подготовки учащихся в условиях среднеобразовательных школ разработан механизм многоуровневой интеграции образовательных областей "Математика", "Экономика". Предложенный механизм рассматривается в работе с позиций реализации нескольких уровней интеграции.
На первом уровне осуществляется выделение основных содержательных линий образовательных областей "Математика" и "Экономика" в соответствии с целевой установкой организации профессиональной подготовки учащихся. Их интеграция обеспечивает отбор содержательных линий на основе учета системы требований к уровню сформированности ключевых профессиональных компетенций.
Следующий уровень интеграции предполагает определение системы базовых понятий с учетом выделенных содержательных линий, что дает возможность провести согласование на основе определения роли и места математических понятий в процессе исследования экономических категорий.
Последующая интеграция предусматривает обоснование комплекса математических методов и средств решения задач, а также методов исследования экономических систем, процессов и явлений.
Данный комплекс позволяет сформировать систему математических методов и моделей исследования экономических систем и процессов, на основе которой определить структуру и содержание интегрированного курса.
Таким образом, в исследовании была выделена структура методологических знаний, определяющих содержание математической подготовки, и подходы к ее трансформации на изучение социально-экономических систем, что позволило определить специфику формирования математического аппарата решения экономических задач.
Технология организации профессиональной подготовки включает в себя следующие аспекты раскрытия содержания данного курса:
• наполнение математических задач экономическим содержанием;
• рассмотрение экономических задач, предполагающих использование математического аппарата.
Если в рамках первого аспекта предусмотрено освоение учащимися методов решения поставленных математических задач, то в рамках второго направления предполагается освоение методов исследования экономических систем и процессов посредством математического инструментария.
Учитывая тот факт, что интегрированный курс призван обеспечить формирование у обучающихся обобщенных способов решения экономических задач, в его содержании должны быть отражены все названные аспекты, при преобладающем значении второго направления, поскольку изучение социально-экономических систем предполагает представление аналитических данных не только как результата математической обработки, но и в качестве результата анализа функционирования системы (рис. 1).
Доступный уровень интеграции позволяет при выборе метода решения поставленной задачи в качестве результата рассматривать экономико-математическую модель. Таким образом, на основании предложенного подхода осуществлен отбор задач для реализации названных аспектов изучения данного курса.
Исследование практической деятельности в этом направлении позволили сделать заключение о целесообразности рассмотрения в рамках интегрированного курса наиболее характерных методов исследования экономических систем и выработки технологий решения поставленных задач. С этих позиций особое внимание уделено изучению качественных свойств экономических систем, формализации количественных взаимосвязей их элементов и закономерностей развития.
Исходя из данных положений, в качестве основных разделов курса выделены:
− развитие методологии экономико-математического моделирования;
− моделирование как метод научного познания;
− классификация моделей в экономике;
− формализация экономической задачи;
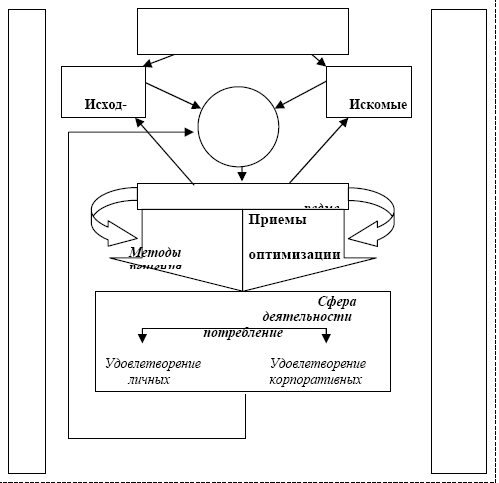
Рис. 1 Модель отбора и конструирования содержания интегрированного курса "Элементы экономико-математического моделирования" на основе интеграции образовательных областей "Математика" и "Экономика"
− методы математического программирования в построении и анализе экономических моделей:
применение линейного программирования для построения и анализа моделей производства; методы нелинейного программирования в моделировании экономических систем; целочисленное программирование; динамическое программирование; оптимальное управление (принцип максимума);
− моделирование сферы потребления;
− моделирование производственных процессов
− моделирование общего экономического равновесия.
Анализ психолого-педагогических особенностей организации профессиональной подготовки учащихся направленной на формирование готовности выпускника к овладению специальностью, позволил сделать вывод о том, что формирование элементов профессиональной культуры специалиста в процессе изучения образовательной области
"Математика", возможно при одновременной реализации двух направлений подготовки:
• организация профессиональной подготовки учащихся посредством реализации задачного подхода, т.е. осуществление прикладной направленности базового курса математики;
• использование элементов проблемного обучения с целью активизации учебно-познавательной деятельности обучающихся и развития их творческой самостоятельности.
Опыт показывает, что для современной практики подготовки учащихся характерно противоречие между индивидуальным творческим процессом становления и формирования будущего специалиста на этапе довузовской подготовки и массово-репродуктивным характером его подготовки. Однако общее и профессиональное саморазвитие обучающегося зависит от степени индивидуализации и творческой направленности учебного процесса.
Следовательно, организация учебно-познавательной деятельности обучаемых, обеспечивающей формирование готовности последних к восприятию и использованию специальной системы знаний должна быть ориентирована на реализацию индивидуально-творческого подхода, важным условием реализации которого является предоставление последним возможности реализации субъективной позиции в рамках учебно-информационной модели системы знаний (постановка, организация, реализация проекта).
С учетом данных положений, изучение каждой темы интегрированного курса "Элементы экономико-математического моделирования" строится в исследовании на основе реализации следующей технологии:
1) формулируется проблемная ситуация, требующая ввода нового понятия, определяется его актуальность и значимость;
2) раскрывается содержание нового понятия во взаимосвязи с ранее изученными категориями;
3) рассматриваются основные методы решения типовых задач на основе использования средств и методов с учетом нового понятия;
4) организуется коллективная, групповая или индивидуальная самостоятельная работа учащихся, ориентированная на разработку моделей и построение проектов исследуемых экономических процессов;
5) анализируются полученные результаты. Осуществляется проверка качества усвоения изучаемого понятия в процессе решения задач, предусматривающих:
• простое оперирование понятиями;
• построение математической модели изучаемого понятия;
• исследование экономических систем и процессов с использованием математического аппарата, включающее изученное понятие.
Нужно подчеркнуть особую значимость реализации условия состязательности и творческой самореализации обучающихся в процессе поиска знаний, определения путей и средств их совершенствования, которое обеспечивается в рамках изучения курса посредством организации конкурсов бизнес-идей, мини-олимпиад, работы творческих групп и пр.
С целью их проведения в исследовании разработан сборник экономических задач, основанный на предложенном подходе к интеграции математического и экономического содержания, рассмотрена технология организации такого типа мероприятий.
Трудности применения математических методов в экономике
Трудности применения математических методов в экономике, прежде всего, связаны с тем, что это наука, которая не имеет возможности проводить лабораторные эксперименты, не всегда возможно определить число факторов, влияющих на исследуемое экономическое явление. Экономическая наука, не дошла до такой степени своего развития, когда возможно выделить достаточно однородные и простые элементы, которые могут стать объектами счета. В 20-е годы нашего столетия сложилось новое направление в экономике - эконометрия. Основой этого направления послужили регрессионные методы. После второй мировой войны решающую роль широчайшему внедрению этих методов во все области научных исследований, экономического анализа и промышленного производства сыграла вычислительная техника, т.е. появление в 50-е годы массового производства ЭВМ привело к регрессионному буму. Одна из базовых (наряду с микро- и макроэкономикой) дисциплин экономического образования во всем мире - эконометрика, к сожалению, до начала 90-х годов по существу не была признана в СССР и в Украине, не включалась в учебные планы подготовки специалистов (студентов, аспирантов) экономического профиля. Объяснение этому найти нетрудно: из трех основных составляющих эконометрики - экономической теории, экономической статистики и математико-статистического инструментария две первые были представлены в нашей стране явно неудовлетворительно. Не было доброкачественной экономической теории, не было системы национальных счетов и необходимого информационного обеспечения эконометрического моделирования. Разумеется, такое положение имеет свои причины. Главная - ненужность для плановой экономики специалистов, обладающих знаниями математики. Действительно, центральная проблема экономики - это проблема рационального выбора. В плановой экономике отсутствует необходимость в специалистах, владеющих аппаратом анализа и выбора экономических вариантов. Названная причина обусловливала то, что экономическая система, близкая к замкнутой, не воспринимала идеи количественного анализа экономики.
Одной из характерных черт современного состояния социально-экономических исследований должно стать широкое применение в них методов математической статистики. При этом важен учет, как природы изучаемого явления, так и математико-статистических особенностей используемого метода. Недооценка той или иной стороны этого положения, как правило, приводит к неудачам. Логика статистического метода определяется спецификой объекта исследования, природой изучаемых связей, целями, задачами и гипотезами исследования.
Интеграция математики и экономики для высшего образования
В настоящее время в современной экономике необычайно большое число будущих экономистов, нуждается в серьезной математической подготовке, которая давала бы возможность математическими методами исследовать широкий круг новых проблем, применять современную вычислительную технику, использовать теоретические достижения в практике. Хорошее владение математическим аппаратом, в частности методами математической статистики, - должно стать стандартом экономического образования. Это требует базовой подготовки на основе, высокого уровня общего образования в области фундаментальных наук. Для этого, по меньшей мере, необходимо получение студентами отчетливого представления о том, что такое математика и математическая модель, в чем заключается математический подход к изучению явлений реального мира, как его можно применять и что они могут дать.
Следовательно, принципиальными моментами проблемы математического образования являются: выбор объема и содержания математических курсов, определение целей обучения, правильное сочетание широты и глубины изложения, строгости и наглядности, т. е. выбор наиболее эффективных и рациональных путей обучения, и все это с учетом ограниченного времени, отводимого на изучение математики.
Исходя из этого, можно утверждать, что в экономической науке не должно быть деления на «экономику» и «математическую экономику». Основная масса статей по экономике, так или иначе, использует математический аппарат. Либо это описание модели, либо эмпирическая проверка обсуждаемых гипотез или явлений средствами корреляционного или регрессионного анализа, либо удобная система обозначений, позволяющая в дальнейшем легко формулировать изучаемые отношения на количественном языке. Но количественное описание экономических законов средствами математики и статистики требует использования более сложного математического инструментария и в большинстве случаев оказывается более сложной задачей, чем описание законов природы.
Таким образом, уже на стадии формирования учебных планов, рабочих программ и логико-структурных схем нужно учитывать изменения, которые происходят, и будут происходить в ближайшее время в постановке математического образования в вузах в результате новых требований, предъявляемых в настоящее время к выпускникам. Необходимость усиления прикладной направленности курса математики для экономистов и повышение уровня фундаментальной математической подготовки очевидна, но невозможна без взаимопонимания тех, кто применяет в своей деятельности математические методы исследования для изучения реальных экономических явлений, и так называемых «чистых» математиков. Для достижения этого взаимопонимания специальным кафедрам нужно привлекать к сотрудничеству математиков, которые должны способствовать плодотворному содружеству математики и ее приложений. В случае, когда для рассматриваемых приложений уже имеются готовые математические понятия и основные математические модели, решения задачи указанного взаимопонимания просто и имеет учебный характер. Эта задача очень сложна в том случае, когда отсутствуют даже элементарные математические модели простейших явлений, когда их надо только еще создавать, примером могут послужить ряд вопросов экономики и социологии.
Для этого, прежде всего, необходимо исходить из того, что обучение решению прикладных задач математическими методами не является только задачей математически. При этом в фундаментальных понятиях математики нужны: простейшие конкретные примеры, иллюстрирующие применение математических понятий для изучения реальных явлений; обучение студентов решению прикладных задач математиками. Однако, необходимо предостеречь новаторов-математиков, которые смело выхолащивают внутреннюю логическую строгость математических курсов, подменяя доказательства основных утверждений примерами и задачами экономического содержания не отражающими их сути, теряя логическую строгость мышления.
Однако, приходится констатировать, что математическая экономика не занимает должного места в специальных экономических курсах. К сожалению, для многих преподавателей специальных экономических дисциплин в силу специфики используемого аппарата даже существующие математические методы и модели не доступны.
Только при наличии четких представлений об используемых математических методах может быть объективная уверенность в правильности сделанных выводов. Для того чтобы применять математику как метод исследования, весьма важно осознать и хорошо освоить сущность и взаимосвязь ее основных идей и понятий. В этом случае можно смело использовать правдоподобные рассуждения, ибо они надежны только, если базируются на истинном знании. Строить же все обучение математики на правдоподобных рассуждениях заведомо недопустимо, поскольку в этом случае невозможно четко (а значит, правильно) очертить границы допустимого применения рассматриваемого математического аппарата.
Использование математических и статистических методов в экономике само по себе не создает новый предмет исследований, а всегда основано на началах, той науки, в которой имеет место такое приложение. Поэтому многие проблемы на этом пути еще остаются нерешенными. К ним относится проблема модификации или адаптации существующих математико-статистических методов, методологии и методики их применения с учетом свойств социально-экономических данных. Это связано с тем, что условия и предположения, использованные математиками при разработке этих методов и выполняющиеся с разумной строгостью в других приложениях, для социально-экономических данных чаще нарушаются, чем выполняются. Отмеченная ограниченная возможность переноса математических приемов исследования порождает методологические ошибки двоякого рода: отрицание приложимости сложившегося математико-статистического аппарата в социально-экономических исследованиях и представление, будто один и тот же метод без каких-либо модификаций аппарата или методики применения способен равно удовлетворительно описывать явления различной природы. Поэтому наряду с модификацией существующих методов требуется разработка нового математического аппарата, методологии и методики анализа, ориентированных на социально-экономическую информацию, и прежде всего на нечисловые данные. К этим проблемам примыкают проблемы использования ЭВМ. Доступность ЭВМ и внешняя простота решения задач, анализа данных с помощью стандартных программных средств, привели к тому, что зачастую на практике многие из математических методов используются неправильно. Это в свою очередь порождает ошибочные решения и выводы научно-практического характера, а тем самым дискредитируется и сама идея активного применения современных методов прикладной статистики в комплексных системных исследованиях социально-экономических явлений.
Фетишизация эмпирических статистических закономерностей, полученных без достаточно тщательного предварительного теоретического обоснования, пренебрежение, а иногда и полный отказ от априорных экономических теорий, от абстрактно-логических решений фундаментальных теоретических проблем - нередкое явление при применении математических методов.
Возвратимся к вопросу о математических курсах еще раз. К математическим курсам нередко предъявляются претензии, что в них в недостаточном количестве выводятся математические, описывающие реальные явления. В этом вопросе следует четко отдать себе отчет в том, что математическое моделирование реальных явлений, т. е. составление математической модели такого явления, - это не задача математики.
Задача математики состоит в изучении математической структуры, ее свойств и особенностей. Большое удивление должно вызывать не то, что в математических курсах не строятся все математические модели, необходимые для данной экономической специальности, а то, что это не делается в специальных курсах. Так, например, трудно найти общий курс по экономике, в котором бы строилась математическая модель описания какого-либо процесса. Поскольку математика изучает математические модели, то ее задачей при изучении уравнений могут являться вопросы, например, следующего вида: как влияет изменение данного члена уравнения на существование решения, его единственность,на корректность постановки задачи, на устойчивость решения и т.д. и т. п.
Таким образом, владение математическим аппаратом, должно стать стандартом экономического образования. Для этого необходима разработка методики преподавания и осуществление самого процесса обучения студентов математике на основе систематического применения математических методов, изучаемых ими в курсе математики, к решению прикладных задач, а осуществляться это должно на профилирующих кафедрах. Усиление прикладной направленности курса математики для экономистов и повышение уровня фундаментальной математической подготовки очевидно, но это требует базовой подготовки на основе, высокого уровня общего образования в области фундаментальных наук.
Интеграция математики и экономики для среднего образования
Экономику принято считать гуманитарной дисциплиной лишь по недоразумению. На самом деле эта наука оперирует преимущественно количественно измеряемыми величинами – экономическими показателями – и функциональными или статистическими связями между ними – расчетными формулами и экономическими законами. Современная экономика – наука точная.
Из этого вытекает, что методика преподавания основ экономических знаний, прежде всего, в школе, вполне может (а скорее всего, должна) иметь общие черты с технологией обучения другим прикладным научным дисциплинам, скажем, физике или химии. В частности, такой общей чертой, по нашему мнению, является широкое применение в ходе обучения экономике и проверки усвоения материала учащимися математических задач.
Стоит заметить, что зарубежные методики преподавания начал экономики как школьникам, так и взрослым, обычно ориентированы не на задачи, а на метод тестирования. Действительно, с помощью тестов учащиеся могут вспомнить те положения, которые им преподносились учителем, а преподаватели – без особого труда оценить успехи своих учеников.
Опыт преподавания экономики в школе показал, что для словянских школьников тесты с наборами готовых ответов и с элементами игры в “Угадайку” – это слишком просто, если не сказать – примитивно. Средняя школа отличается хорошо известными крепкими математическими традициями, и наши дети с самых младших классов приучены самостоятельно решать небольшие научные проблемы – школьные задачи. Теоретический курс было решено дополнить широким набором практических упражнений с математическим уклоном.
Можно утверждать, что использование задач превращает обучение началам экономики в творческий процесс, способствуя более глубокому осмыслению и освоению материала. Попутно закрепляются и отдельные темы школьного курса математики.
Экономических задач нужно много. Они должны быть разнообразны по тематике и по необходимому для решения математическому аппарату, должны быть самого разного уровня сложности – от элементарных до головоломных олимпиадных.
Пока в качестве поля деятельности здесь можно предложить следующий набор тем курса основ экономических знаний и соответствующих разделов курса математики.
|  Темы курса экономики Темы курса экономики
|
Разделы курса математики
|
| Кривая производственных возможностей.
|
Составление и решение уравнений и систем уравнений.
Анализ функций.
|
| Спрос, предложение, равновесие.
Построение и анализ серии графиков в одной системе координат.
Составление и решение уравнений.
|
Определение наибольшего значения функции на отрезке.
Анализ функций.
|
| Эластичность спроса и предложения.
|
Составление и решение уравнений и систем уравнений.
Планиметрия с тригонометрией.
|
| Выручка, издержки, прибыль, рентабельность.
|
Составление и решение уравнений и систем уравнений.
Определение наибольшего значения функции на отрезке.
|
| Банки: проценты по вкладам и проценты за кредит.
|
Составление и решение уравнений.
Прогрессии.
|
| Показатели экономической динамики (приросты, темпы роста и прироста).
|
Составление и решение уравнений.
|
| Темп инфляции; расчеты в текущих и приведенных ценах.
|
Составление и решение уравнений.
|
| Сравнительное преимущество: обмен, внешняя торговля.
|
Составление и решение уравнений.
|
Конечно, приведенным списком возможности составителя задач не исчерпываются. Зачастую задачи не вписываются ни в предложенную выше, ни в какую-либо другую схему. Простор для творчества в области создания школьных экономико-математических задач огромен. Это творчество может оказаться полезным для тысяч учителей и для миллионов школьников.
Вернемся к вопросу о роли математики на уроках экономики. Экономика и математика связаны между собой уже тысячелетия. Само появление чисел, создание систем счисления и всего того, что ныне составляет основу математики, было вызвано к жизни задачами практики, производства, обмена и торговли. И по мере становления и развития математики укреплялись ее связи с экономикой. Поэтому неудивительно, что и современная экономика широко использует математические методы.
Взаимодействие математики и экономики приносит обоюдную пользу: математика получает широчайшее поле для многообразных приложений, а экономика – могучий инструмент для получения новых знаний.
Современная экономика с ее огромным количеством разнообразных взаимосвязей между основными ее структурами представляет широкую возможность для использования одного из основных понятий математики – понятие функции. Дело в том, что многочисленные величины, характеризующие экономические процессы, существуют не изолированно друг от друга, а, наоборот, очень тесно друг с другом связаны. Таковы цена товара и спрос на него, прибыль фирмы и объем ее производства, затраты ресурсов и объем выпуска продукции, размер кредита, выданного банком и плата за его использование, и т.д.
Во многих ситуациях, где возникают тесно связанные между собой переменные величины, как правило, найдется место для функции.
Удовлетворение неограниченно растущих потребностей людей происходит, в основном через производство, под которым мы понимаем процесс создания различных видов экономического продукта и материальных благ в том числе. Задача максимального удовлетворения потребностей человека приводит к тому, что все общество в целом, отдельное хозяйство и каждая семья должны выбирать наилучшие варианты хозяйствования, сопоставляя сегодняшние затраты труда с его результатами в экономической и социальной сферах.
Следует еще раз отметить одно очень важное обстоятельство: изучение элементов экономики, должно происходить в рамках стандартной программы по математике, соответствующей данному возрасту и не требовать привлечения нового математического материала.
Интегрированный урок
План урока.
Тема урока:
Ценовая эластичность.
Цели урока:
Обучающая
: изучение понятия эластичности спроса по цене, ценовые факторы, влияющие на изменение эластичности, вывод формул и практическое применение при решении задач.
Развивающая:
развитие внимания, памяти, речи, логического мышления при решении задач, умения анализировать поведение продавца в условиях изменения цен и получения выручки.
Воспитательная:
воспитание самостоятельности, коллективизма, ответственности, научного отношения к решению жизненных проблем в условиях рынка.
Оснащение урока:
1. Комплект формул.
2. Карточки-задания.
3. Информация на стендах.
4. Презентация (формулы, таблица соотношения цены и выручки, задачи).
Тип урока
: интегрированный.
Межпредметные связи:
математика, экономика.
Основные понятия для изучения:
понятие ценовой эластичности спроса и предложения, коэффициент эластичности, эластичный и неэластичный спрос, изменение эластичности при наличии заменителей, необходимых благ, соотношения расходов в семейном бюджете и времени.
Ход урока
1. Организационный момент. Сообщение темы и цели урока
.
2. Изучение нового материала:
Понятие эластичности спроса по цене.
Факторы, влияющие на изменение эластичности.
Решение задач.
3. Закрепление нового материала. Проверка усвоения основных понятий темы.
4. Домашнее задание.
5. Подведение итогов урока.
План-конспект урока.
1. Понятие эластичности спроса по цене
На предыдущем уроке мы установили, что величина спроса на товар находится в обратной зависимости от цены. Допустим, произошло повышение цен на молоко и “Пепси-колу” в 2 раза. Но величина спроса на эти товары снизится в разной степени: от “Пепси-колы” покупатель быстрей откажется, чем от молока. Поведение покупателей в условиях снижения или повышения цен характеризуется показателем “ценовая эластичность”.
Ценовая эластичность
– это степень изменения величины спроса на товар при изменении цены.
Количественное значение определяется коэффициентом эластичности, который показывает, на сколько изменится в процентном отношении величина спроса при изменении цены на 1%.
Ер =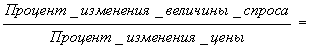 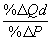
Ep=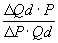 ; Ep= ; Ep=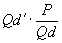
Значение коэффициента эластичности изменяется относительно единицы:
Если Ер > 1, то спрос на товар эластичный, т.е. изменение величины спроса происходит в большей степени, чем изменение цены. Покупатель быстро реагирует на незначительное снижение или повышение цен. Например, увеличение цены на ювелирные изделия заставит покупателей отказаться от предметов роскоши.
Если Ер < 1, то спрос на товар неэластичный, т.е. изменение цены на товар происходит в большей степени, чем величина спроса. Покупатель слабо реагирует на незначительное снижение или повышение цен. Например, увеличение цены на хлеб не заставит покупателей отказаться от этого жизненно важного продукта.
Если Ер = 1, то эластичность считается единичной, т.е. величина спроса и цена изменяются в равной степени.
Эластичность в различных точках кривой спроса проиллюстрирована на плакате.
2. Неценовые факторы, влияющие на изменение эластичности
Наличие заменителей у данного товара. Если есть заменители, то спрос эластичный (мыло-порошок, автобусы - троллейбусы). Если нет заменителей – спрос неэластичный (электроэнергия).
Степень необходимости товара для потребителей. Жизненно важные товары – спрос неэластичный (продукты питания, жильё). Предметы роскоши (украшения, автомобили) – спрос эластичный.
Доля расходов на товар в семейном бюджете. Дешёвые товары (соль, спички, мыло) – спрос неэластичный. Дорогие товары (мебель, телевизор) – спрос эластичный.
Фактор времени. Спрос в долгосрочном периоде эластичен, т.к. люди постепенно находят заменители подорожавшему товару. Спрос, ограниченный коротким промежутком времени, неэластичен (цветы к празднику 8-ое Марта).
Информация об эластичности или неэластичности спроса на товар очень важна для продавца, т.к. от этого зависит размер выручки или дохода от продаж. Выручка подсчитывается умножением цены за единицу товара на количество проданного товара. Поведение продавца можно проанализировать при решении практических задач.
3. Решение задач на определение коэффициента эластичности
Задание №1
. Соотношение цены и величины спроса задано таблицей. Определить коэффициент эластичности. Дать оценку действиям продавца.
| Варианты
|
Цена за единицу продукции P
|
Объём продаж Qd
|
Выручка
P·Qd
|
| Исходное положение
|
50 руб.
|
20 шт
|
1000 руб.
|
| Измененное положение
|
60 руб.
|
15 шт.
|
900 руб.
|
Решение:
Ер =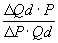 ; Ep === ; Ep ===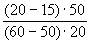 = =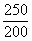 =1,25>1 =1,25>1
Вывод: Спрос эластичный. Действие продавца не верное, т.к. в условиях эластичного спроса выгоднее снижать цену, а не повышать.
Варианты
|
Цена за единицу продукции P
|
Объём продаж
Qd
|
Выручка
P·Qd
|
| Исходное положение
|
40 руб
|
20кг
|
800 руб
|
| Измененное положение
|
45руб.
|
18 кг
|
810 руб
|
Решение:
Ер =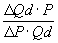 ; Ep ; Ep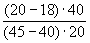 = =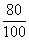 =0,8<1 =0,8<1
Вывод: Спрос неэластичный. Действие продавца верное, т.к. в условиях неэластичного спроса выгоднее осуществлять незначительное повышение цены.
Сведем выводы, сделанные нами после решения задач в таблицу.
Если цена и доход изменяются в противоположных направлениях, то мы имеем товар эластичного спроса. Если доход и цена изменяются в одном направлении, то товар неэластичного спроса.
| Тип эластичности
|
Изменение цены
|
Изменение дохода
|
Взаимное изменение цен и доходов
|
| Спрос эластичный
|
Рост
Снижение
|
Снижение
Рост
|
Противоположное
|
| Спрос неэластичный
|
Рост
Снижение
|
Рост
Снижение
|
Одинаковое
|
| Единичная эластичность спроса
|
Рост
Снижение
|
Без изменения
|
Изменение цены не влияет на доход
|
Задание №2.
Соотношение цены товара и величины спроса задано функцией Q= 38-3p. Определить коэффициент эластичности при цене 5 рублей и 7 рублей.
Дано: Решение:
Qd=38-3p Ep=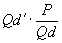
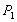 =5р. Ep= =5р. Ep= 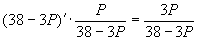
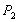 =7р. =7р. 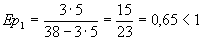
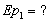 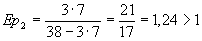
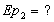
Вывод: При цене товара 5 рублей спрос неэластичный. При цене 7 рублей спрос эластичный.
Задание №3.
Соотношение цены товара и величины спроса задано функцией Qd=21-5P. При какой цене спрос на товар будет неэластичным (Ер = 0,9) или эластичным (Ер = 1,1).
Дано: Решение:
Qd=21-5P 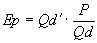
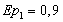 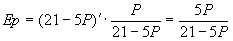
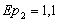 1) 0,9= 1) 0,9= 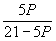 2) 1,1= 2) 1,1= 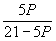
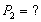 5P=0,9 (21-5P) 5P= 1,1(21-5P) 5P=0,9 (21-5P) 5P= 1,1(21-5P)
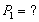
5P=18,9-4,5P 5P= 23,1 –5,5P
9,5P=18,9 10,5P=23,1
P=1,99 P=2,2
Вывод. Спрос эластичный при цене товара P=2,2 рубля, спрос неэластичный при цене P=1,99 рубля.
Вопросы для закрепления нового материала.
Зачем продавцу необходимо учитывать показатель эластичности?
В условиях эластичного спроса выгодно снижать или повышать цену?
В условиях неэластичного спроса выгодно снижать или повышать цену?
Что означает ценовая эластичность спроса?
Какой эластичностью обладают следующие виды товаров: бензин, легковые автомобили отечественного производства, грузовые автомобили, легковые автомобили зарубежного производства, компьютеры, сотовые телефоны.
Спрос на перевозки пассажиров в маршрутных автобусах неэластичный. Что нужно предпринять, чтобы спрос стал эластичным?
Приведите примеры товаров, спрос на которые ограничен коротким промежутком времени.
Продавец решает увеличить цену на мороженое на 20%, при этом предполагает, что объем продаж, снизится на 40%. Выиграет ли продавец в выручке?
Домашняя работа.
Каждому учащемуся выдается карточка с домашним заданием, где три задачи подобные тем, которые решали на уроке.
Рефлексия. Подведение итогов урока.
Нові інформаційні технології навчання (НІТН)
Проблема систематизації навчального матеріалу в старших класах сучасної школи є однією з найбільш актуальних як для вчителів так і для учнів, особливо в умовах характерної для останнього десятиліття кризи “інформаційного вибуху”, що стала вже звичним явищем і породжує цілий ряд проблем як загального психолого-педагогічного, так і дидактичного плану. Необхідність побудови єдиної системи знань на час закінчення дитиною середньої школи підкреслював ще К.Д. Ушинський, зазначаючи: “Тільки система…що виходить з самої суті предметів, дає нам повну владу над нашими знаннями”. Вітчизняні дослідники, зокрема С.Л. Рубінштейн, підкреслювали, що завдяки цілеспрямованому формуванню систематизації як цілісного мислительного процесу “…загальне перестає бути тільки збираною сукупністю часткових властивостей, окремих предметів, перетворюючись у сукупність однорідних, суттєво пов’язаних між собою властивостей”.
Нові інформаційні технології навчання (НІТН) надають широкі можливості щодо значної інтенсифікації формування систематизації як мислительної операції, особливо з предметів природничо-математичного циклу, таких як математика та основи економічних знань. Ми розглядаємо систематизацію як один з чинників, здатних суттєво впливати на формування інформаційної культури старшокласника, а засоби НІТН, залучені до виконання цієї задачі, можуть і повинні бути застосовані як при поурочному освоєнні нового навчального матеріалу, так і при заключному тематичному повторенні.
Наш досвід використання програмного засобу GRAN1 на уроках з основ економічних знань свідчить про принципову можливість ефективного застосування НІТН при формуванні системи знань з основ економіки, що має своїм підгрунтям доступні старшокласникам методи створення математичних моделей, поєднані з графічним аналізом необхідних при цьому функцій.
Наведемо декілька прикладів. Початкові етапи знайомства з основами економіки містять розгляд питання про найпростіші лінійні математичні моделі в бізнес-аналізі. Поняття про лінійну функцію, добре відоме нашим учням з попереднього курсу математики, дістає при цьому нової для них акцентуації в плані наповнення відомих символів стандартного запису Y=kx+b новим змістом, а потужні засоби візуалізації інформації, що їх надає GRAN1, сприяють формуванню початків системної якості знання. Розглянемо, зокрема, як розв’язання простих задач економічного змісту з побудовою їхніх математичних моделей та можливістю перекладення на комп’ютер чисто технічних операцій з побудови відповідних графіків здатне значно розширити і поглибити міжпредметні зв’язки і вести до дієвої інтеграції окремих навчальних предметів.
Приклад 1. Нехай видатки на перевезення вантажівками (Y) знаходяться в лінійній залежності від відстані, на яку необхідно доставити вантаж (X): Y=216+5,16 X, де Y подано в грн., X – в км. З точки зору економіки вантажних перевезень b=216 (в позначеннях стандартного подання лінійної функції Y=kx+b) означає видатки у 216 грн. на кожну вантажівку незалежно від того, відбуваються перевезення чи ні. Графік функції, побудований з допомогою GRAN1, перетинає вісь Y в точці (0;216), ординату якої можна розуміти як видатки на утримання бізнесу – витрати на ліцензування, страхування і т.п. Кутовий коефіцієнт прямої k=5,16 означає фактично збільшення видатків на транспортування (на 5,16 грн.) при збільшенні довжини пробігу вантажівки на 1 км. Аналогічно, зменшення шляху пробігу на 1 км кожного разу веде до економії 5,16 грн.
Аналізуючи з учнями наведений приклад, приходимо до нового подання змісту кутового коефіцієнту прямої в термінах основ бізнесу: тангенс кута нахилу прямої, що є графіком лінійної функції з однією незалежною змінною дорівнює відношенню зміни залежної змінної (наприклад, видатків на транспортування) до зміни незалежної змінної (наприклад, довжини пробігу вантажівки). Використавши GRAN1 для швидкісної і точної побудови графіків різних лінійних функцій, отримуємо додаткові можливості бізнес-аналізу ситуацій подібних вище описаній.
Приклад 2. Щорічні прибутки від податкових надходжень у міську управу залежать від рівня безробіття в даному регіоні, причому ця залежність виражається лінійною функцією Y=3,7-0,4 X, де Y (в млн. грн.) означає прибутки вказаної державної установи, а X – рівень безробіття (у відсотках). Виконуючи побудову графіка функції з допомогою GRAN1, учні спочатку передбачають, а потім переконуються самі, що збільшення видатків на подолання безробіття в даному регіоні веде до зменшення відсотку громадян, які не мають роботи (така взаємна залежність обумовлена k=-0,4). Отже, в процесі аналізу цього нескладного прикладу отримуємо не тільки швидку і точну геометричну інтерпретацію аналітичного виразу, але й можливість наповнення його новим змістом економічного характеру. Так, наприклад, точка перетину графіка функції з віссю ординат (0; 3,7) має той зміст, що навіть при нульовому рівні безробіття щорічні видатки мерії становитимуть 3,7 млн.грн. значення k=-0,4 означає, що кожний 1% збільшення безробіття (наприклад з 10 до 11 відсотків працездатного населення) призведе до зменшення доходної частини міського бюджету на 0,4 млн.грн. За графіком, побудованим в GRAN1, визначаємо, наприклад, видатки з прибуткової частини бюджету при різних значеннях відсотку незайнятого роботою працездатного населення.
В багатьох проблемних ситуаціях бізнес-аналізу виникає необхідність знаходження коефіцієнтів k і b для побудови рівняння лінійної функції. З’ясування рівняння прямої за відомими статистичними даними дозволяє, з одного боку, передбачити гіпотетичні значення змінних, які визначають певну економічну ситуацію, оцінити інтенсивність їхніх взаємних змін, а з іншого боку в учителя з’являється можливість розв’язання з учнями комплексу взаємно-обернених задач, що значно сприяє формуванню систематизації. Таким чином, ми фактично розв’язуємо з учнями задачу протиставлення вихідної форми знання видозміненій, адже перетворення знань шляхом перекодування інформації ще на ступені циркулювання її в оперативній пам’яті дитини створює підгрунтя як для ефективного засвоєння знань, так і для їхньої систематизації. Подальше об’єктивування отриманих закономірностей в графічних образах з допомогою GRAN1 створює інформаційну спільність між окремими елементами знання, адже кодування алгебраїчного через геометричне і навпаки повністю відповідає важливій фізіологічній закономірності функціональної асиметрії головного мозку.
Застосування GRAN1 в даному випадку дозволяє окрім усього вище зазначеного дати відповідь на питання, чому саме ця математична модель може бути використана для опису і пояснення даної проблемної ситуації з економіки, адже часто основою для аналізу тієї чи іншої моделі є лінійна залежність між двома змінними, яку можна уявити у вигляді “розсипної” діаграми, яка складається з окремих точок з відомими координатами. Візуальний аналіз подібної графічної побудови дозволить учням зробити прогноз стосовно кута нахилу прямої до додатного напрямку осі абсцис і оцінити ступінь майбутньої відповідності обраної математичної моделі попереднім дослідженням або статистичним даним.
Литература
1. С.И.Иванов, “Основы экономической теории”, Вита-Проф., Москва 2003г.
2. Б.И.Табачников, “Основы экономики”, Учебное пособие для студентов учреждений среднего профессионального образования, Вита-Пресс., Москва 2000г.
3. Л.Л.Любимов, Н.А.Ранева, “Основы экономических знаний”, Вита-Проф., Москва 1999г.
4. В.С.Автономов “Введение в экономику”, Вита-Пресс., Москва 2005г.
5. А.Г.Мордкович, “Алгебра и начала анализа”, Москва 2000г.
Вывод
Нарастающий поток общественной, научной и технической информации приводит к усложнению содержания образования, перегрузке обучающихся информацией, не имеющей прикладного значения. В то же время стратегия современного образования и социальный запрос общества определяют в качестве одного из основных направлений усиление практической направленности школьного преподавания. • математические знания часто оказываются формальными и невостребованными в жизни, а их усвоение требует от большинства школьников значительных усилий. • Становится очевидной необходимость формирования знаний о законах общества, в частности, основ экономических знаний, на уроках математики и во внеурочной деятельности, перехода от изолированного изучения дисциплин к комплексному, например, к интеграции математики и экономики.
Большое значение приобретает решение математических задач с экономическим содержанием, использование деловых игр, обсуждение ситуаций, типичных для экономики семейного хозяйства, предприятия и страны в целом.
В сфере интересов каждого человека, начиная со школьного возраста, оказываются вопросы, связанные с проблемой выбора наилучшего из предложенных вариантов, оценкой степени риска, прогнозирования возможных последствий того или иного решения. Поэтому актуальную значимость приобретает изучение вероятностно-статистического материала на уроках математики.
Школьникам, интересующимся компьютерными технологиями и прикладными вопросами, необходимо продемонстрировать возможность моделирования случайных экспериментов с помощью компьютера. При подготовке проектов у обучающихся формируется умение использовать информационно-коммуникационные технологии и мультимедийные ресурсы для обработки информации, создания баз данных, презентаций результатов познавательной и практической деятельности.
Необходимо не только включить в комплекс задач, предлагаемых учебником, задания прикладной направленности, но и продумать систему внеклассных занятий: факультативов и элективных курсов практического содержания, способствующих реализации деятельностного подхода, формированию навыков экономического обоснования при решении задач реальной жизни.
Независимо от того, какой жизненный путь и профессию выберут выпускники в дальнейшем, опыт решения жизненных задач, несомненно, пригодится им в жизни и поможет адаптироваться к изменениям, происходящим в российском обществе.
Экономика не развивается по шаблонам, хотя в хозяйственных процессах обнаруживается немало закономерностей, тенденций, существуют объективные экономические законы. Научные предпосылки анализа всегда в той или иной мере ограничивают объект исследования. Без подобных предпосылок не обходится ни одна модель, ни одна формула или функция. Важно осознавать эти ограничения математического подхода и не абсолютизировать его эффективность.
Изучение математических дисциплин организует мышление, способствует развитию четкости и лаконичности в изложении доводов и дисциплинирует научные исследования и создает необходимую базу для понимания и сопоставления исследовательских работ и учебных дисциплин разных стран. Язык математики – это, образно говоря, язык музыки, которые могут в большинстве случаев понимать все без переводчика. Проблема состоит в том, чтобы отобрать те математические дисциплины, которые более всего необходимы как экономистам-теоретикам, так и экономистам-практикам.
Литература
1. Евгений и Наталья Винокуровы. Экономика в задачах. 50 непростых задач о предложении денег и средних ценах, издержках и прибыли, спросе и предложении, производстве и инфляции, экспорте и импорте. – М.: Начала-пресс, 1995.
2. Е. и Н. Винокуровы. Экономика в задачах. – “Математика”. Еженедельное учебно-методическое приложение к газете “Первое сентября”. № 34, сентябрь 1998 г.
3. Евгений Винокуров. Поиграем в экономику. – “Ять”. №№ 1–7 за 2000 г.
4. Е.Ф. Винокуров. Бизнес в три вопроса: Издержки? Цена? Выручка? – "Математика в школе", № 8 за 2002 г.
5. А.А. Мицкевич. Сборник заданий по экономике. Издание второе. – М.: Вита-Пресс, 1998.
6. А.С. Симонов. Экономика на уроках математики. М.: “Школа-Пресс”, 1999.
7. Е. Ф. Винокуров, Н.А. Винокурова. Трудные задачи по экономике. – М.: Вита-Пресс, 2001.
8. Андрющенко Алла Рудольфовна (диссертация)
9. Жалдак М.І. Комп’ютер на уроках математики: Посібник для вчителів.-К.:Техніка, 1997.-303с.
10. Жалдак М.І. Яким бути шкільному курсу “Основи інформатики”//Комп’ютер у школі та сім’ї.- 1998.-№1.-с.3-7.
11. Основи нових інформаційних технологій навчання: Посібник для вчителів/Авт.кол.; За ред. Ю.І.Машбиця/Інститут психології ім.Г.С.Костюка АПН України.-К.: ІЗМН, 1997.-264с.
12. Бурда М.І. Структура і зміст профільного навчання математики. // Математика в школі. – 2007. – №7, с.3-6.
13. Кремень В.Г. Освіта і наука в Україні – інноваційні аспекти. Стратегія. Реалізація. Результати. – К.: Грамота, 2005. – 448 с.
14. Нічуговська Л.І. Науково-методичні основи математичної освіти студентів економічних спеціальностей вищих навчальних закладів: Дис. докт. пед. наук (13.00.04). – Полтава, 2004. – 464 с.
15. Раков С. Формування математичних компетентностей випускника школи як місія математичної освіти. // Математика в школі. – 2007. – №5, с.2-7.
16. Хуторской А. Ключевые компетенции как компонент личностно-ориентированного образования. // Народное образование. – 2003. – №2, с. 58-64.
|