| Государственный Университет Управления
Институт Финансового Менеджмента
Кафедра прикладной математики
Учебно-исследовательская работа
по дисциплине
Эконометрическая модель национальной экономики Германии
Москва
ФРГ – одна из крупнейших стран Западной Европы (после Франции и Испании). Берлин – столица и резиденция правительства; некоторые министерства расположены в Бонне. Форма правления – парламентская республика, форма государственного устройства – симметричная федерация. Государство состоит из 16 частично независимых земель.
Германия является членом Европейского союза, принимает активное участие в НАТО, а также входит в «Большую восьмёрку».
По уровню экономического развития, величине экономического потенциала, доле в мировом производстве, степени вовлеченности в международное разделение труда и другим важнейшим критериям она относится к числу наиболее высокоразвитых государств мира. По объему ВВП она занимает пятое место в мире. По уровню жизни – 18 место в мире, согласно Human Development Index. Она мало уступает США – крупнейшей торговой державе мира – по объему внешней торговли, хотя ее экономический потенциал почти втрое меньше. Она является также одним из крупнейших экспортеров и импортеров капитала. По качественным характеристикам национальной экономики (уровень производительности труда, капиталооснащенность и наукоемкость производства и др.) страна также занимает одно из первых мест в мировом хозяйстве.
С точки зрения обеспеченности природными ресурсами ФРГ нельзя отнести к числу богатых стран. Она располагает немногими видами топлива и сырья. К их числу относятся каменный и бурый уголь, калийная соль, небольшие запасы железной руды, легирующих и цветных металлов. Подавляющая часть топлива – нефти и газа, а также атомного сырья ввозится из-за рубежа.
Внешняя торговля – одна из наиболее динамичных отраслей экономики ФРГ, стимулятор ее экономического роста. В послевоенный период происходил постоянный рост доли экспорта в ВНП (1950 – 9,3%; 1980 – 26,7%; 1991 – 32,8%). К слабым сторонам экономического развития Германии можно отнести следующее: заниженная оценка затрат на модернизацию Восточной Германии, дефицит специалистов (необходимость их привлечения из-за рубежа); старение населения, стабильный уровень безработицы (11%), острая конкуренция со стороны быстро развивающихся стран Азии.
Реклама

Задачей исследования является идентификация двухшаговым методом наименьших квадратов упрощенной модели Клейна (т.е. нахождение оценок коэффициентов 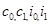 ): ):
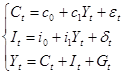 (1) (1)
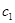 – склонность к потреблению, – склонность к потреблению,
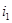 – склонность к инвестированию, – склонность к инвестированию,
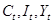 - эндогенные переменные модели, - эндогенные переменные модели, 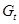 - экзогенная переменная модели, - экзогенная переменная модели, 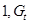 – предопределенные переменные. Лаговых эндогенных переменных в модели нет. – предопределенные переменные. Лаговых эндогенных переменных в модели нет.
Идентификация модели состоит в нахождении по исходным данным оценок коэффициентов модели 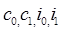 (а также дисперсий случайных составляющих (а также дисперсий случайных составляющих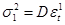 , , 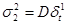 ) )
На первом шаге установим регрессионную зависимость эндогенных переменных (
C
,
I
)
от предопределенных переменных. Предварительно необходимо преобразовать модель от расширенной формы к структурной (2), а затем к приведенной (3):
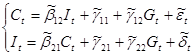 (2) (2)
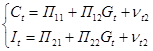 (3) (3)
Используя инструмент «Регрессия» пакета «Анализ данных» проведем парную регрессию потребления и инвестиций по государственным расходам (т.е. эндогенных переменных по предопределенным) и найдем МНК-оценки коэффициентов 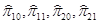 приведенной формы. приведенной формы.
| ВЫВОД ИТОГОВ
|
| Регрессионная статистика
|
| Множественный R
|
0,98
|
| R‑квадрат
|
0,96
|
| Нормированный R‑квадрат
|
0,96
|
| Стандартная ошибка
|
38,37
|
| Наблюдения
|
38
|
| Дисперсионный анализ
|
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
1
|
1 205 387,78
|
1 205 387,78
|
818,94
|
2,334E‑26
|
| Остаток
|
36
|
52 987,74
|
1 471,88
|
| Итого
|
37
|
1 258 375,52
|
| Коэффициенты
|
Стандартная ошибка
|
t‑статистика
|
P‑Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y‑пересечение
|
-161,88
|
33,83
|
-4,79
|
0,00
|
-230,49
|
-93,27
|
-230,49
|
-93,27
|
| G
|
3,46
|
0,12
|
28,62
|
0,00
|
3,22
|
3,71
|
3,22
|
3,71
|
Таким образом, имеем 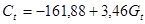
| Регрессионная статистика
|
| Множественный R
|
0,90
|
| R‑квадрат
|
0,81
|
| Нормированный R‑квадрат
|
0,80
|
| Стандартная ошибка
|
40,61
|
| Наблюдения
|
38
|
| Дисперсионный анализ
|
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
1
|
251965,2
|
251965,2
|
152,8
|
1,621E‑14
|
| Остаток
|
36
|
59366,3
|
1649,1
|
| Итого
|
37
|
311331,4
|
| Коэффициенты
|
Стандартная ошибка
|
t‑статистика
|
P‑Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y‑пересечение
|
-138,86
|
35,81
|
-3,88
|
0,000429971
|
-211,48
|
-66,23
|
-211,48
|
-66,23
|
| G
|
1,58
|
0,13
|
12,36
|
1,62091E‑14
|
1,32
|
1,84
|
1,32
|
1,84
|
 . .
Вычислим также выровненные значения Ĉ и Î. (Приложение 2)
На втором шаге запишем уравнения в стандартном виде, т.е. по одной эндогенной переменной в левой части с коэффициентом 1. Эндогенные же переменные в правых частях заменим на их выровненные значения.
Реклама

Рассмотрим второй шаг применительно к первому уравнению, для этого в него вместо 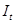 подставим подставим 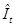 , тогда получим , тогда получим
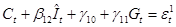
или
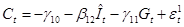
Т.к. согласно первоначальной модели 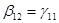 , последнее уравнение запишется как модель парной регрессии , последнее уравнение запишется как модель парной регрессии
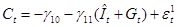 , ,
в которой зависимой переменной служит 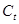 , а независимой – , а независимой – 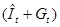 . .
МНК-оценки параметров этой модели имеют вид
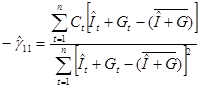
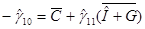 . .
Подставив в последние формулы значения временных рядов 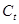 , , 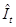 и и 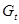 получим получим
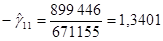 . .
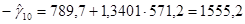 . .
Подставляя эти значения в формулы, имеем:
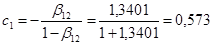 . .
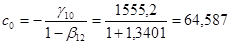 . .
Таким образом, применение двухшагового МНК к первому уравнению структурной формы позволило идентифицировать первое уравнение первоначальной формы: 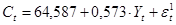 . .
Рассмотрим второй шаг для второго уравнения, для этого в него вместо 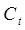 подставим подставим 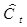 , тогда получим: , тогда получим:
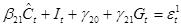
Или
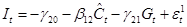 . .
Поскольку 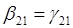 , то последнее уравнение запишется как модель парной регрессии: , то последнее уравнение запишется как модель парной регрессии:
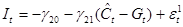 , ,
в которой зависимой переменной служит 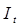 , а регрессором выступает – ( , а регрессором выступает – (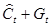 ), поэтому МНК – оценки параметров этой модели имеют вид: ), поэтому МНК – оценки параметров этой модели имеют вид:
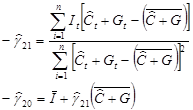
Подставив в последние формулы значения временных рядов 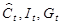 , получим: , получим:
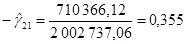
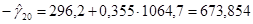
Подставляя эти значения в формулы:
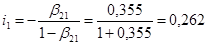 . .
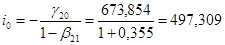 . .
Таким образом, применение двухшагового МНК ко второму уравнению структурной формы позволило идентифицировать второе уравнение первоначальной формы: 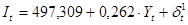 . .
Найдем оценки дисперсий случайных составляющих 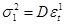 , , 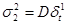 . .
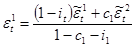
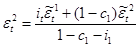
Для этого решим систему уравнений, подставив в левую часть квадрат стандартной ошибки для регрессий потребления по государственным расходам, а также чистых инвестиций по государственным расходам:
Таким образом, по итогам двухшагового МНК эконометрическая модель имеет вид:
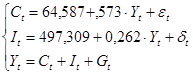
Для прогноза эндогенных переменных на 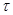 шагов вперед (в нашем случае на два шага) необходимо задать значения предопределенных переменных шагов вперед (в нашем случае на два шага) необходимо задать значения предопределенных переменных 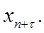 Предопределенная переменная в нашей работе (в нашем случае экзогенная) – Предопределенная переменная в нашей работе (в нашем случае экзогенная) – 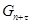 (государственные расходы в год (государственные расходы в год 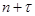 ). Поскольку у нас нет данных о будущих государственных расходах, то получим их путем прогноза по линейному тренду: ). Поскольку у нас нет данных о будущих государственных расходах, то получим их путем прогноза по линейному тренду: 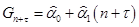 . .
Оценки параметров линейного тренда получаем как МНК-оценки параметров парной регрессии:
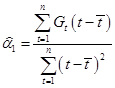 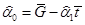
Используя пакет прикладных программ Excel, получим оценки коэффициентов линейного тренда:
| Регрессионная статистика
|
| Множественный R
|
0,98
|
| R‑квадрат
|
0,96
|
| Нормированный R‑квадрат
|
0,96
|
| Стандартная ошибка
|
10,18
|
| Наблюдения
|
38
|
| Дисперсионный анализ
|
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
1
|
96 938,13
|
96 938,13
|
936,08
|
2,309E‑27
|
| Остаток
|
36
|
3 728,08
|
103,56
|
| Итого
|
37
|
100 666,21
|
| Коэффициенты
|
Стандартная ошибка
|
t‑статистика
|
P‑Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y‑пересечение
|
185,18
|
3,37
|
54,98
|
2,48681E‑36
|
178,35
|
192,01
|
178,35
|
192,01
|
| Period
|
4,61
|
0,15
|
30,60
|
2,30864E‑27
|
4,30
|
4,91
|
4,30
|
4,91
|
 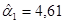 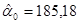
Осуществляем прогноз эндогенных переменных:
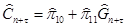 . .
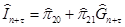 . .
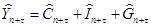 . .
Находим прогноз будущих значений государственных расходов на 2008 г. и 2009 г. (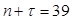 и и 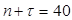 ). Прогнозные значения приведены в Приложении. ). Прогнозные значения приведены в Приложении.
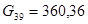
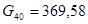
Подставив эти значения в формулы для выровненных значений эндогенных переменных, получим:
Прогноз на 2008 г.
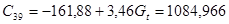
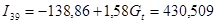
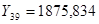
Прогноз на 2009 г.
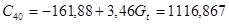
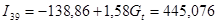
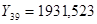
Приложение 1
Исходные данные
| Period
|
Y
|
C
|
I
|
G
|
| 1970
|
845,9
|
476,6
|
204,8
|
164,5
|
| 1971
|
872,4
|
502,6
|
194,8
|
174,9
|
| 1972
|
909,9
|
529,6
|
196,7
|
183,5
|
| 1973
|
953,3
|
544,4
|
214,2
|
194,7
|
| 1974
|
961,8
|
542,8
|
213,7
|
205,3
|
| 1975
|
953,5
|
563,0
|
176,0
|
214,5
|
| 1976
|
1 000,7
|
587,2
|
194,4
|
219,1
|
| 1977
|
1 034,2
|
612,4
|
198,0
|
223,8
|
| 1978
|
1 065,3
|
634,3
|
198,0
|
233,1
|
| 1979
|
1 109,5
|
654,8
|
212,4
|
242,3
|
| 1980
|
1 125,1
|
664,5
|
210,0
|
250,6
|
| 1981
|
1 131,1
|
661,6
|
207,6
|
261,9
|
| 1982
|
1 126,6
|
654,8
|
212,6
|
259,2
|
| 1983
|
1 144,3
|
664,4
|
221,8
|
258,1
|
| 1984
|
1 176,6
|
677,5
|
237,9
|
261,3
|
| 1985
|
1 204,0
|
690,2
|
250,3
|
263,5
|
| 1986
|
1 231,6
|
717,0
|
247,2
|
267,4
|
| 1987
|
1 248,8
|
742,8
|
237,0
|
269,1
|
| 1988
|
1 295,1
|
762,5
|
259,5
|
273,1
|
| 1989
|
1 345,6
|
785,8
|
292,5
|
267,3
|
| 1990
|
1 416,3
|
819,0
|
324,6
|
272,7
|
| 1991
|
1 488,7
|
854,7
|
352,2
|
281,8
|
| 1992
|
1 521,8
|
883,0
|
342,1
|
296,8
|
| 1993
|
1 509,6
|
890,0
|
322,5
|
297,1
|
| 1994
|
1 549,7
|
907,7
|
336,8
|
305,2
|
| 1995
|
1 579,0
|
927,4
|
340,7
|
310,9
|
| 1996
|
1 594,7
|
939,7
|
337,7
|
317,3
|
| 1997
|
1 623,5
|
947,5
|
357,0
|
318,9
|
| 1998
|
1 656,4
|
961,4
|
370,4
|
324,6
|
| 1999
|
1 689,8
|
990,0
|
371,4
|
328,4
|
| 2000
|
1 744,0
|
1 013,5
|
397,7
|
332,9
|
| 2001
|
1 765,6
|
1 032,4
|
398,6
|
334,6
|
| 2002
|
1 765,6
|
1 024,3
|
401,7
|
339,5
|
| 2003
|
1 761,8
|
1 025,7
|
395,2
|
340,9
|
| 2004
|
1 780,4
|
1 027,7
|
416,9
|
335,9
|
| 2005
|
1 794,4
|
1 027,0
|
430,0
|
337,4
|
| 2006
|
1 845,8
|
1 036,9
|
468,7
|
340,3
|
| 2007
|
1 891,7
|
1 032,0
|
512,3
|
347,4
|
Приложение 2
Выровненные значения Ĉ и Î
| Period
|
G
|
Ĉ
|
Î
|
| 1970
|
164,5
|
407,3
|
121,4
|
| 1971
|
174,9
|
443,5
|
137,9
|
| 1972
|
183,5
|
473,2
|
151,5
|
| 1973
|
194,7
|
511,9
|
169,2
|
| 1974
|
205,3
|
548,6
|
186,0
|
| 1975
|
214,5
|
580,4
|
200,5
|
| 1976
|
219,1
|
596,3
|
207,8
|
| 1977
|
223,8
|
612,5
|
215,2
|
| 1978
|
233,1
|
644,6
|
229,9
|
| 1979
|
242,3
|
676,5
|
244,5
|
| 1980
|
250,6
|
705,4
|
257,7
|
| 1981
|
261,9
|
744,5
|
275,5
|
| 1982
|
259,2
|
735,1
|
271,2
|
| 1983
|
258,1
|
731,3
|
269,5
|
| 1984
|
261,3
|
742,2
|
274,5
|
| 1985
|
263,5
|
749,9
|
278,0
|
| 1986
|
267,4
|
763,3
|
284,1
|
| 1987
|
269,1
|
769,4
|
286,9
|
| 1988
|
273,1
|
783,1
|
293,2
|
| 1989
|
267,3
|
763,2
|
284,1
|
| 1990
|
272,7
|
781,9
|
292,6
|
| 1991
|
281,8
|
813,1
|
306,9
|
| 1992
|
296,8
|
865,1
|
330,7
|
| 1993
|
297,1
|
866,1
|
331,2
|
| 1994
|
305,2
|
894,2
|
344,0
|
| 1995
|
310,9
|
913,8
|
353,0
|
| 1996
|
317,3
|
936,3
|
363,2
|
| 1997
|
318,9
|
941,7
|
365,7
|
| 1998
|
324,6
|
961,5
|
374,7
|
| 1999
|
328,4
|
974,5
|
380,7
|
| 2000
|
332,9
|
990,0
|
387,8
|
| 2001
|
334,6
|
996,0
|
390,5
|
| 2002
|
339,5
|
1 013,1
|
398,3
|
| 2003
|
340,9
|
1 017,6
|
400,4
|
| 2004
|
335,9
|
1 000,3
|
392,5
|
| 2005
|
337,4
|
1 005,6
|
394,9
|
| 2006
|
340,3
|
1 015,6
|
399,5
|
| 2007
|
347,4
|
1 040,2
|
410,7
|
|