1. Теоретическая часть
1.1 Характеристика предприятия
Товарищество с ограниченной ответственностью ТОО "Реверс" как юридическое лицо было зарегистрировано 11 ноября 1999 года и является крупнейшим поставщиком компьютерной техники в Экибастузе.
Основная производственная и коммерческая деятельность компании:
производство и поставка компьютеров, серверов, комплектующих и периферийных устройств;
поставка копировальной техники;
реализация лицензионного программного обеспечения;
реализация и обслуживание копировальной техники;
прокладка локальных сетей;
внедрение и поддержка информационных систем на базе программных продуктов "Фирмы 1С";
разработка и поддержка веб-сайтов;
техническое и сервисное обслуживание предприятий города Экибастуза на договорной основе.
Благодаря тесному сотрудничеству с производителями, в Техцентре Revers всегда низкие цены и широкий ассортимент товара. Имеется собственный авторизованный сервисный центр ТОО "Аверс-Сервис" специализирующийся на ремонте и обслуживании бытовой техники, электроники, кондиционеров.
В настоящий момент целью компании является дальнейшее глубокое освоение частного сектора рынка и закрепление своих лидирующих позиций. Для выполнения этой цели руководство компании постоянно ищет новые методы работы с клиентами, улучшая сервисное обслуживание.
Руководство компании делает основную ставку на снижение розничных цен, в сравнении с их уровнем у существующих на сегодняшний день конкурентов, а также на качество реализуемой продукции и сервисное обслуживание.
1.2 Экономическая постановка задачи
Техцентр "Реверс" в 2009 году в октябре месяце объявил скидки на весь месяц по следующим отделам: Отдел копировальной техники и заправки картриджей (B1) Отдел продажи компьютерной техники (B2) Отдел ремонта и обслуживание компьютерной техники (B3)
В Октябре месяце заявки в Техцентр "Реверс" сделали четыре организации: СОШ 24 (A1) СОШ 35 (A2) ЦТДЮ "Кайнар" (A3) Компьютерный клуб (A4).
Для СОШ 24 от техцентра "Реверс" в связи с акцией во всех отделах были сделаны скидки. В отделе копировальной техники и заправки картриджей скидка в 5%, в отделе продажи компьютерной техники 10%, в отделе ремонта и обслуживания компьютерной техники 10%.
Для СОШ 35 от техцентра "Реверс" в связи с акцией во всех отделах были сделаны скидки. В отделе копировальной техники и заправки картриджей скидка в 5%, в отделе продажи компьютерной техники как постоянному клиенту скидка 15%, в отделе ремонта и обслуживания компьютерной техники в 12%,
Реклама

Для ЦТДЮ "Кайнар" в связи с акцией во всех отделах были сделаны скидки. В отделе копировальной техники и заправки картриджей скидка в 3%, в отделе продажи компьютерной техники скидка в 5%, в отделе ремонта и обслуживания компьютерной техники 6%.
Для Компьютерного клуба "Бест" во всех отделах были сделаны скидки. В отделе копировальной техники и заправки картриджей скидка в 2%, в отделе продажи компьютерной техники скидка в 5%, в отделе ремонта и обслуживания компьютерной техники 6%.
Составить план обслуживания организаций с максимальной выгодой для техцентра, учитывая предоставленные скидки.
При обслуживании отделом продажи СОШ 24 должен быть не более 15 продаж, обслуживание отдела ремонта для СОШ 24 должен быть не менее 15 вызовов.
Таблица 2.1 - Исходная таблица
| ai/ bj
|
B1
|
B2
|
B3
|
B4
|
| 25
|
25
|
15
|
25
|
| A1
|
40
|
10
|
15
|
5
|
5
|
| A2
|
30
|
10
|
12
|
6
|
6
|
| A3
|
30
|
5
|
5
|
3
|
2
|
Х11<=15 x12>=15
1.3 Экономико-математическое моделирование
Содержанием любой экономико-математической модели является выраженная в формально-математических соотношениях экономическая сущность условий задачи и поставленной цели. В модели экономическая величина представляется математическим соотношением, но не всегда математическое соотношение является экономическим. Описание экономических условий математическими соотношениями - результат того, что модель устанавливает связи и зависимости между экономическими параметрами или величинами.
По содержанию различают экономико-математические и экономико-статистические модели. Различие между ними состоит в характере функциональных зависимостей, связывающих их величины. Так, экономико-статистические модели связаны с показателями, сгруппированными различными способами. Статистические модели устанавливают зависимость между показателями и определяющими их факторами в виде линейной и нелинейной функции. Экономико-математические модели включают в себя систему ограничений, целевую функцию.
Система ограничений состоит из отдельных математических уравнений или неравенств, называемых балансовыми уравнениями или неравенствами.
Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция - функция многих переменных величин и может иметь свободный член.
Реклама

Критерии оптимальности - экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.
Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.
Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремальные значения целевой функции. План, для которого целевая функция модели имеет экстремальное значение, называют экстремальным планом, или экстремальным решением.
Для нелинейных моделей иногда существуют экстремальные значения целевой функции, а для линейных моделей экстремальных планов и экстремальных значений целевой функции быть не может.
Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.
Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения. Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям.
1.4 Математическая постановка задачи
Математическая модель транспортной задачи в общем случае имеет вид
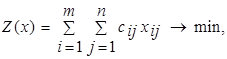 (1.1) (1.1)
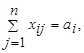 i=1,2,…,m, (1.2) i=1,2,…,m, (1.2)
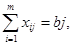 j=1,2,…,n, (1.3) j=1,2,…,n, (1.3)
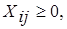 i=1,2,…,m; j=1,2,…,n. (1.4) i=1,2,…,m; j=1,2,…,n. (1.4)
Целевая функция задачи (1.1) выражает требования обеспечить минимум суммарных затрат на перевозку всех грузов. Первая группа из т
уравнений (1.2) описывает тот факт, что запасы всех т
поставщиков вывозятся полностью. Вторая группа из n уравнений (1.3) выражает требования полностью удовлетворить запросы всех n потребителей. Неравенства (1.4) являются условиями неотрицательности всех переменных задачи.
Таким образом, математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи
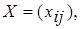 i=1,2,…,m; j=1,2,…,n, (1.5) i=1,2,…,m; j=1,2,…,n, (1.5)
удовлетворяющее системе ограничений (1.2), (1.3), условиям неотрицательности (1.4) и обеспечивающее минимум целевой функции (1.1).
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.
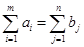 . (1.6) . (1.6)
1.5 Транспортная задача с ограниченными возможностями транспортных средств
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
В общей постановке транспортной задачи предполагается, что из любого пункта производства любой пункт потребления может быть перевезено любое количество груза.
В целом ряде случаев оптимизации планирования перевозок приходится учитывать ограниченные возможности транспортных путей и средств. Поэтому математическую модель транспортной задачи:
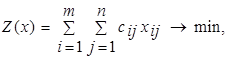 (1.7) (1.7)
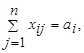 i=1,2,…,m, (1.8) i=1,2,…,m, (1.8)
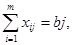 j=1,2,…,n, (1.9) j=1,2,…,n, (1.9)
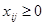 (1.10) (1.10)
должны быть введены дополнительные ограничительные условия, учитывающие возможность транспортных путей и средств.
Если обозначиться транспортные возможности между пунктами I и j через dij, то количество груза  , которое может быть перевезено по этому направлению за планируемый период времени, не должно превышать транспортных возможностей, т.е. , которое может быть перевезено по этому направлению за планируемый период времени, не должно превышать транспортных возможностей, т.е.
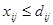 (1.11) (1.11)
Тогда ограничения 1.10, 1.11 объединяются, и модель задачи усложняется двусторонними ограничениями на переменные
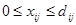 (1.12) (1.12)
При этом общая транспортная возможность дорог, соединяющих I -й пункт производства со всеми n пунктами потребления, должна быть ровна или больше количества продукции, предназначенной к постановке из этого i-го пункта всем n потребителя, т.е.
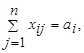 i=1,2,…,m, (1.13) i=1,2,…,m, (1.13)
Общая же транспортная возможность дорог, соединяющих j-й пункт потребления со всеми m пунктами производства, должна быть равна или больше количества продукции, которые надо поставить в этот j-й пункт от всех m поставщиков, т.е.
 i=1,2,…,n, (1.14) i=1,2,…,n, (1.14)
Существуют различные подходы к решению этой задачи. Рассмотрим наиболее простой из них.
Путей некоторых преобразований условий ее можно свести к типу обычной транспортной задачи. Для этого пункт производства или потребления, для которых условия ограничены транспортные возможности, разбивается на два условных пункта. При этом следует подчеркнуть непременно один пункт.
Мощность условного поставщика А’i -
принимается равный установленной возможности средств, соединяющих пункт и с потребителями j
A’i
=dij
(
1.15)
а мощность условного поставщика А’j
- равной разности между заданными в условии задачи мощностью поставщика в пункте I и возможностью средств между I-м и j-м пунктами, т.е.
a’’i
=ai
-dij
. (1.16)
При этом затраты на поставку грузов из пунктов I’ в пункт j-cij
принимаются равными действительным расходам cij
приведенным в условии задачи. В оптимальном решение переменные хij
могут иметь любое неотрицательное значение от нуля до a’i
, т.е.
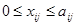 (1.17) (1.17)
В отличие от них переменные хij
в оптимальном решении непременно должны быть равны нулю, поскольку мощность А’j
характеризует количество в пункте и сверх установленной средств, соединяющих пункты i и j, следовательно это часть груза должна быть направлена не j-му а любому другому потребителю. Для того, чтобы в оптимальном решении обеспечить значение переменных хij
равно нулю, затраты на поставку груза из пункта i’’ в пункт j принимаются равными М, т. е cij
=М.
При минимизации целевой функции (1.7) и коэффициентах cij
=М, в оптимальном решении получим
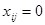
Отсюда следует, что
Xij
= Xi
’
j+
Xi
’
j
= Xij
(
1.18)
Тогда, исходя из условий (1.15), (1.17), получим
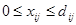
Таким образом, объем поставки груза из пункта i в пункт j не превысит установленной способности транспортных средств, обеспечивающих эти пункты.
Если для какой то пары пунктов производства i потребления s транспортные возможности не ограничены, объем поставки груза от поставщика Аi к потребителю Bs
определится как сумма значений пары соответствующих переменных:
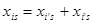
Дальнейший расчет будет выполнен с помощью венгерского метода решении транспортного алгоритма.
1.6 Решение транспортной задачи с ограниченными возможностями транспортных средств венгерским методом
Предварительный этап. По исходной матрице С выполняется построение матрицы С', а затем матрицы Co, по известным правилам.
Выполняется построение начального плана Xo. Построение плана выполняется, сверху-вниз по столбцам матрицы Co начиная с левого, для O матрицы Co, при этом учитывается пропускная возможность коммуникаций.
Разметка. На этапе разметки отмечают символом "+" столбцы с нулевыми невязками и существенные нули матрицы С. Точкой отмечают существенные неполные нули, а двумя точками - полные. Несущественные нули остаются без разметки. С точки зрения коммуникации они являются неполными.
Поисковый этап. Целью поиска является отыскать неполный нуль (без разницы существенный или несущественный), расположенный в строке с полной невязкой. Алгоритм поиска по колонкам известен.
Отыскание нуля на этапе поиска Элемент, который стоит на пересечении выделенной строки и выделенного столбца называется дважды выделенным.
Выбирается корректирующий элемент h. Корректирующий элемент получаем как минимальный положительный элемент среди невыделенной части матрицы, либо как минимальный модуль двух выделенных отрицательных элементов, если поисковый этап окончился неудачей в невыделенной части матрицы элементы неположительны, а все дважды выделенные элементы неотрицательны, то задача неразрешима при данных ограничениях на пропускную способность. Прибавляется h к выделенным элементам и вычитается из невыделенных. Если дважды выделенный элемент становится равным нулю, то его выделяют "*"Знак выделения над столбцом снимается.
Расчёт целевой функции.
2. Практическая часть
2.1 Описание алгоритма реализации модели
Определившись с методами, которые мы будем использовать в решении задачи, приступим к непосредственному получению результата. Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют различные способы. Например, способ “Метод ограничений”/ Условия транспортной задачи заданы транспортной таблицей (2.1).
Таблица 2.1 - Условие транспортной задачи
| ai/ bj
|
B1
|
B2
|
B3
|
B4
|
| 25
|
25
|
15
|
25
|
| A1
|
40
|
10
|
15
|
5
|
5
|
| A2
|
30
|
10
|
12
|
6
|
6
|
| A3
|
30
|
5
|
5
|
3
|
2
|
В данном случае Σai
=100 = Σbj
=100 имеем дело с закрытой моделью транспортной задачи.
Вводим количество поставщиков и потребителей, затем строим матрицу элементы которой отображают стоимость перевозки. Если задача по условию не является сбалансированной, то для этого добавляем фиктивный пункт производства и потребителя. В нашем случаи задача является сбалансированной, для ее решения строим матрицу Хij
- план перевозок.
Элементы этого типа характеризуют количество товаров, которое будет перемещаться от i-го поставщика к j-му потребителю. Выводим целевую функцию (см рисунок 2.1)
Рисунок 2.1 - блок-схема подпрограммы проверки на условие баланса.
Происходит начальное вычисление опорного плана.
Построение плана выполняется сверху-вниз по столбцам матрицы Co начиная с левого, для O матрицы Co, при этом учитывается пропускная возможность коммуникаций.
На этапе разметки отмечают символом "+" столбцы с нулевыми невязками и существенные нули матрицы С. Точкой отмечают существенные неполные нули, а двумя точками - полные. Несущественные нули остаются без разметки. С точки зрения коммуникации они являются неполными.
Целью поиска является отыскать неполный нуль (без разницы существенный или несущественный), расположенный в строке с полной невязкой. Алгоритм поиска по колонкам известен.
Элемент который стоит на пересечении выделенной строки и выделенного столбца называется дважды выделенным.
Выбирается корректирующий элемент h. Корректирующий элемент получаем как минимальный положительный элемент среди невыделенной части матрицы, либо как минимальный модуль двух выделенных отрицательных элементов
Если поисковый этап окончился неудачей в невыделенной части матрицы элементы неположительны, а все дважды выделенные элементы неотрицательны, то задача неразрешима при данных ограничениях на пропускную способность.
Прибавляется h к выделенным элементам и вычитается из невыделенных. Если дважды выделенный элемент становится равным нулю, то его выделяют "*"Знак выделения над столбцом снимается.
Рисунок 2.2 - Общий алгоритм вычисления опорного плана Вычисление невязки.
На основании матрицы С0
строится начальный план. Заполнение плана осуществляется по нулям матрицы С0
, двигаясь по столбцам сверху вниз, слева направо.
После заполнения элемента плана объемы производства и потребления корректируются. Коррекции предшествует построение цепочки. Цепочка содержит обязательно нечетное число нулей и в принципе может состоять из одного нуля. Построение цепочки начинается с последнего найденного нуля со штрихом. Затем по столбу к нулю со звездочкой, а уже от него по строке к нулю со штрихом. Для коррекции плана выбирается корректирующий элемент  .
Он выбирается из невязки строки сначала, из невязки конца цепочки и элементов конца Х, соответствующих нулям со звездочкой, которые вошли в цепочку. Элемент .
Он выбирается из невязки строки сначала, из невязки конца цепочки и элементов конца Х, соответствующих нулям со звездочкой, которые вошли в цепочку. Элемент 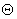 прибавляется к элементу Хij,
если ему в цепочку соответствовал элемент Сij
=0', и отнимается от элемента Хij
, если в цепочке ему соответствовал элемент Сij
=0*
. Для коррекции плана рассчитывается невязка по строкам и столбцам, а так же суммарная невязка.
прибавляется к элементу Хij,
если ему в цепочку соответствовал элемент Сij
=0', и отнимается от элемента Хij
, если в цепочке ему соответствовал элемент Сij
=0*
. Для коррекции плана рассчитывается невязка по строкам и столбцам, а так же суммарная невязка.
Рассчитываются невязки по столбцам и строкам.
Невязка по строке  , i=1,m, j=1,n (2.19)
, i=1,m, j=1,n (2.19)
Невязка по строке  , i=1,m, j=1,n (2.20)
, i=1,m, j=1,n (2.20)
Затем рассчитывается суммарная невязка плана
∆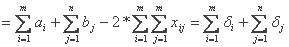 (2.21)
(2.21)
Если суммарная невязка плана = 0, то это говорит о получении оптимального решения. Если не равно 0, то переходим к этапу разметки. Выводим L - общая стоимость перевозок (см рисунок 2.3). Рисунок 2.3 - блок - схема подпрограммы вычисления невязки.
Описание программы.
Описание работы программы:
пользователь вводит количество поставщиков и потребителей;
пользователь вводит все данные о поставщиках и потребителях;
пользователь вводит ограничения;
строит матрицу Сij,
элементы которой отображают определенную скидку;
Все используемые в программе переменные и подпрограммы, кратко описаны в таблицах 2.1
Описание блок-схемы:
блок-схема проверка на условие баланса представлена на рисунке 2.1;
блок - схема общего алгоритма вычисления опорного плана представлена на рисунке 2.2;
блок схема вычисления невязки представлено на рисунке 2.3
Таблица 2.1 -Используемые переменные
| Имя
|
Тип
|
Описание
|
| Cont
|
TZLPTableContext
|
В каждой конкретной библиотеке будет свой тип контекста
|
| Значение функции
|
Integer
|
Код возврата:
ResultError = - 1 - ошибка в алгоритме;
ResultFinish = 0 - успешное окончание расчетов;
ResultNoSolution = 1 - нет решения;
|
| SourceF
|
TFunction
|
Целевая функция
|
| Limitations
|
TLimitations
|
Ограничения
|
| MinMax
|
TFunctionType
|
Функция на минимум или максимум.
ftMin - минимум;
ftMax - максимум.
|
|
|
Integer
|
Длина массива ограничений
|
| Factors
|
TDynIntegerArray
|
Массив ограничений: последовательность из Len целых чисел (Integer)
|
| Значение функции
|
TIntegerMatrix
|
матрица из целых чисел
|
|