| МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ ІМ. ВАДИМА ГЕТЬМАНА
Кафедра економіко-математичних моделювання
ЛАБОРАТОРНА РОБОТА З ЕКОНОМЕТРІЇ № 2
Виконав:
студент ІІ курсу
спец. 6504, гр. № 5
Нікіфоров Клим
Перевірила:
Кузубова В.В.
Київ — 2009
ВАРІАНТ 11
1.
Визначимо середні значення та стандартні відхилення
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| 1
|
48
|
200
|
25
|
3
|
| 2
|
49
|
205
|
25
|
3,5
|
| 3
|
50
|
210
|
23
|
4
|
| 4
|
46
|
180
|
27
|
2,5
|
| 5
|
43
|
160
|
29
|
2
|
| 6
|
53
|
215
|
23
|
4,5
|
| 7
|
55
|
220
|
20
|
5
|
| 8
|
56
|
222
|
20
|
5
|
| 9
|
54
|
220
|
21
|
4,5
|
| 10
|
55
|
221
|
19
|
5,5
|
| 11
|
57
|
225
|
18
|
5,5
|
| 12
|
58
|
228
|
16
|
6
|
| 13
|
46
|
178
|
26
|
2,8
|
| 14
|
47
|
181
|
24
|
2,8
|
| 15
|
50
|
208
|
22
|
4,2
|
| 16
|
54
|
222
|
19
|
5,8
|
| 17
|
56
|
230
|
17
|
6
|
| 18
|
59
|
230
|
15
|
6,2
|
| 19
|
58
|
229
|
15
|
6,1
|
| 20
|
61
|
235
|
13
|
6,3
|
| 21
|
60
|
231
|
13
|
6,3
|
| 22
|
63
|
240
|
11
|
6,5
|
| 23
|
62
|
238
|
12
|
6,4
|
| 24
|
66
|
245
|
8
|
7
|
| Середнє
|
54,41667
|
215,5417
|
19,20833
|
4,891667
|
| Станд.відх.
|
6,035523
|
21,84526
|
5,548044
|
1,480575
|
2.
Виконаємо нормалізацію змінних за допомогою формул:
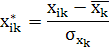
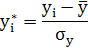
Функція нормалізації дозволяє перетворити інформацію в однакові одиниці виміру (стандартні відхилення)
В результаті нормалізації отримаємо:
| Y*
|
X1*
|
X2*
|
X3*
|
| -1,06315
|
-0,71144
|
1,043911
|
-1,27766
|
| -0,89746
|
-0,48256
|
1,043911
|
-0,93995
|
| -0,73178
|
-0,25368
|
0,683424
|
-0,60224
|
| -1,39452
|
-1,62697
|
1,404399
|
-1,61536
|
| -1,89158
|
-2,5425
|
1,764886
|
-1,95307
|
| -0,23472
|
-0,0248
|
0,683424
|
-0,26454
|
| 0,09665
|
0,204087
|
0,142693
|
0,07317
|
| 0,262336
|
0,29564
|
0,142693
|
0,07317
|
| -0,06904
|
0,204087
|
0,322937
|
-0,26454
|
| 0,09665
|
0,249863
|
-0,03755
|
0,410876
|
| 0,428021
|
0,43297
|
-0,21779
|
0,410876
|
| 0,593707
|
0,570299
|
-0,57828
|
0,748583
|
| -1,39452
|
-1,71853
|
1,224155
|
-1,41274
|
| -1,22884
|
-1,5812
|
0,863668
|
-1,41274
|
| -0,73178
|
-0,34523
|
0,50318
|
-0,46716
|
| -0,06904
|
0,29564
|
-0,03755
|
0,613501
|
| 0,262336
|
0,661852
|
-0,39804
|
0,748583
|
| 0,759393
|
0,661852
|
-0,75853
|
0,883666
|
| 0,593707
|
0,616076
|
-0,75853
|
0,816125
|
| 1,090764
|
0,890735
|
-1,11901
|
0,951207
|
| 0,925079
|
0,707629
|
-1,11901
|
0,951207
|
| 1,422136
|
1,119617
|
-1,4795
|
1,08629
|
| 1,25645
|
1,028064
|
-1,29926
|
1,018749
|
| 1,919193
|
1,3485
|
-2,02023
|
1,423997
|
3.
Розрахунок кореляційних матриць rxx
та rxy
Знаходимо кореляційні матриці за формулами:
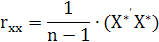
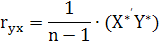
Транспонуємо матрицю Х*:
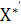 = =
| -0,71144
|
-0,48256
|
-0,25368
|
-1,62697
|
-2,5425
|
-0,0248
|
0,204087
|
0,29564
|
0,204087
|
0,249863
|
0,43297
|
0,570299
|
-1,71853
|
-1,5812
|
-0,34523
|
0,29564
|
0,661852
|
0,661852
|
0,616076
|
0,890735
|
0,707629
|
1,119617
|
1,028064
|
1,3485
|
| 1,043911
|
1,043911
|
0,683424
|
1,404399
|
1,764886
|
0,683424
|
0,142693
|
0,142693
|
0,322937
|
-0,03755
|
-0,21779
|
-0,57828
|
1,224155
|
0,863668
|
0,50318
|
-0,03755
|
-0,39804
|
-0,75853
|
-0,75853
|
-1,11901
|
-1,11901
Реклама

|
-1,4795
|
-1,29926
|
-2,02023
|
| -1,27766
|
-0,93995
|
-0,60224
|
-1,61536
|
-1,95307
|
-0,26454
|
0,07317
|
0,07317
|
-0,26454
|
0,410876
|
0,410876
|
0,748583
|
-1,41274
|
-1,41274
|
-0,46716
|
0,613501
|
0,748583
|
0,883666
|
0,816125
|
0,951207
|
0,951207
|
1,08629
|
1,018749
|
1,423997
|
Отримаємо:
| 1
|
-0,90857
|
0,960757
|
| -0,90857
|
1
|
-0,95464
|
| 0,960757
|
-0,95464
|
1
|
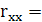
| 0,947927
|
| -0,98042
|
| 0,964746
|
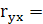
Кожен елемент матриці rxx
характеризує тісноту зв’язку однієї пояснювальної змінної з іншою. Парні коефіцієнти кореляції характеризують тісноту між двома змінними. Вони можуть змінюватись в межах від 1 до -1.
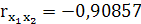
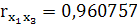
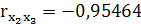
Тобто, вони є парними коефіцієнтами кореляції між пояснювальними змінними. Користуючись цими коефіцієнтами можна зробити висновок, що між змінними х1
, х2
, х3
існує зв’язок.
4.
Визначення детермінанту матриці r
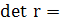 0,006749 0,006749
Детермінант матриці rxx
є точковою мірою мультиколінеарності, в нашому випадку наближається до нуля, а отже мультиколінеарність існує.
5.
Розрахунок критерію
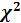
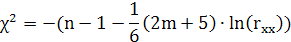
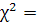 105,7992 105,7992
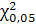 = 7,815 = 7,815
Розраховане значення 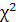 порівнюємо з табличним при вибраному рівні значущості порівнюємо з табличним при вибраному рівні значущості 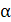 і ступені свободи і ступені свободи 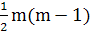 . Оскільки . Оскільки 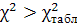 , то мультиколінеарність існує. , то мультиколінеарність існує.
6.
Розрахунок оберненої матриці
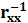
| 13,13842
|
-1,27429
|
-13,8393
|
| -1,27429
|
11,40152
|
12,10859
|
| -13,8393
|
12,10859
|
25,8555
|
C=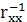 = =
7.
Визначення F-критерію
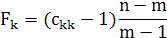
F1
= 127,4534
F2
= 109,2159
F3
= 260,9828
F0,05
=19,44
Оскільки значення критерію Фішера перевищують критичне значення, то пояснювальні змінні мультиколінеарні з рештою змінних.
8.
Визначення частинних коефіцієнтів кореляції
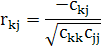
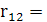 0,104115 0,104115
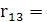 0,750872 0,750872
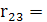 -0,70524 -0,70524
Частинні коефіцієнти кореляції характеризують рівень тісноти зв'язку між двома змінними, за умови, що решта змінних на цей зв'язок не впливає.
9.
Розрахунок t-критерію
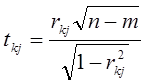
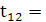 0,4797228 0,4797228
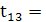 5,21 5,21
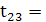 -4,558447 -4,558447
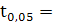 2,11 2,11
Оскільки t13
більше за tтабл
, то це означає що між змінними x1 та х3 існує мультиколінеарність.
10.
Способи звільнення від мультиколінеарності методом перетворення інформації
10.1
Відхилення від свого середнього
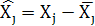
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| Y
|
X1
|
X2
|
X3
|
| 1
|
-6,41667
|
145,5833
|
-29,4167
|
-51,4167
|
| 2
|
-5,41667
|
150,5833
|
-29,4167
|
-50,9167
|
| 3
|
-4,41667
|
155,5833
|
-31,4167
|
-50,4167
|
| 4
|
-8,41667
|
125,5833
|
-27,4167
|
-51,9167
|
| 5
|
-11,4167
|
105,5833
|
-25,4167
|
-52,4167
|
| 6
|
-1,41667
|
160,5833
|
-31,4167
|
-49,9167
|
| 7
|
0,583333
|
165,5833
|
-34,4167
|
-49,4167
|
| 8
|
1,583333
|
167,5833
|
-34,4167
|
-49,4167
|
| 9
|
-0,41667
|
165,5833
|
-33,4167
|
-49,9167
|
| 10
|
0,583333
|
166,5833
|
-35,4167
|
-48,9167
|
| 11
|
2,583333
|
170,5833
|
-36,4167
|
-48,9167
|
| 12
|
3,583333
|
173,5833
|
-38,4167
|
-48,4167
|
| 13
|
-8,41667
|
123,5833
|
-28,4167
|
-51,6167
|
| 14
|
-7,41667
|
126,5833
|
-30,4167
|
-51,6167
|
| 15
|
-4,41667
|
153,5833
|
-32,4167
|
-50,2167
|
| 16
|
-0,41667
|
167,5833
|
-35,4167
Реклама

|
-48,6167
|
| 17
|
1,583333
|
175,5833
|
-37,4167
|
-48,4167
|
| 18
|
4,583333
|
175,5833
|
-39,4167
|
-48,2167
|
| 19
|
3,583333
|
174,5833
|
-39,4167
|
-48,3167
|
| 20
|
6,583333
|
180,5833
|
-41,4167
|
-48,1167
|
| 21
|
5,583333
|
176,5833
|
-41,4167
|
-48,1167
|
| 22
|
8,583333
|
185,5833
|
-43,4167
|
-47,9167
|
| 23
|
7,583333
|
183,5833
|
-42,4167
|
-48,0167
|
| 24
|
11,58333
|
190,5833
|
-46,4167
|
-47,4167
|
| Середнє
|
2,37E-15
|
161,125
|
-35,2083
|
-49,525
|
| Станд.відх.
|
6,035523
|
21,84526
|
5,548044
|
1,480575
|
| 1
|
-0,90857
|
0,960757
|
| -0,90857
|
1
|
-0,95464
|
| 0,960757
|
-0,95464
|
1
|
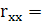
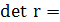 0,006749 0,006749
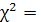 105,7992 105,7992
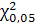 = 7,815 = 7,815
Оскільки 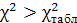 , то мультиколінеарність існує. , то мультиколінеарність існує.
10.2
Абсолютний приріст
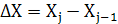
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| Y
|
X1
|
X2
|
X3
|
| 1
|
| 2
|
1
|
5
|
0
|
0,5
|
| 3
|
1
|
5
|
-2
|
0,5
|
| 4
|
-4
|
-30
|
4
|
-1,5
|
| 5
|
-3
|
-20
|
2
|
-0,5
|
| 6
|
10
|
55
|
-6
|
2,5
|
| 7
|
2
|
5
|
-3
|
0,5
|
| 8
|
1
|
2
|
0
|
0
|
| 9
|
-2
|
-2
|
1
|
-0,5
|
| 10
|
1
|
1
|
-2
|
1
|
| 11
|
2
|
4
|
-1
|
0
|
| 12
|
1
|
3
|
-2
|
0,5
|
| 13
|
-12
|
-50
|
10
|
-3,2
|
| 14
|
1
|
3
|
-2
|
0
|
| 15
|
3
|
27
|
-2
|
1,4
|
| 16
|
4
|
14
|
-3
|
1,6
|
| 17
|
2
|
8
|
-2
|
0,2
|
| 18
|
3
|
0
|
-2
|
0,2
|
| 19
|
-1
|
-1
|
0
|
-0,1
|
| 20
|
3
|
6
|
-2
|
0,2
|
| 21
|
-1
|
-4
|
0
|
0
|
| 22
|
3
|
9
|
-2
|
0,2
|
| 23
|
-1
|
-2
|
1
|
-0,1
|
| 24
|
4
|
7
|
-4
|
0,6
|
| Середнє
|
0,782609
|
1,956522
|
-0,73913
|
0,173913
|
| Станд.відх.
|
3,976711
|
19,10611
|
3,13655
|
1,078811
|
| 1
|
-0,89028
|
0,937177
|
| -0,89028
|
1
|
-0,92345
|
| 0,937177
|
-0,92345
|
1
|
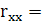
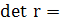 0,006749 0,006749
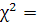 85,87077 85,87077
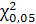 = 7,815 = 7,815
Оскільки 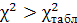 , то мультиколінеарність існує. , то мультиколінеарність існує.
10.3
Спосіб темпів зміни показників
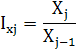
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| Y
|
X1
|
X2
|
X3
|
| 1
|
| 2
|
1,020833
|
1,025
|
1
|
1,166667
|
| 3
|
1,020408
|
1,02439
|
0,92
|
1,142857
|
| 4
|
0,92
|
0,857143
|
1,173913
|
0,625
|
| 5
|
0,934783
|
0,888889
|
1,074074
|
0,8
|
| 6
|
1,232558
|
1,34375
|
0,793103
|
2,25
|
| 7
|
1,037736
|
1,023256
|
0,869565
|
1,111111
|
| 8
|
1,018182
|
1,009091
|
1
|
1
|
| 9
|
0,964286
|
0,990991
|
1,05
|
0,9
|
| 10
|
1,018519
|
1,004545
|
0,904762
|
1,222222
|
| 11
|
1,036364
|
1,0181
|
0,947368
|
1
|
| 12
|
1,017544
|
1,013333
|
0,888889
|
1,090909
|
| 13
|
0,793103
|
0,780702
|
1,625
|
0,466667
|
| 14
|
1,021739
|
1,016854
|
0,923077
|
1
|
| 15
|
1,06383
|
1,149171
|
0,916667
|
1,5
|
| 16
|
1,08
|
1,067308
|
0,863636
|
1,380952
|
| 17
|
1,037037
|
1,036036
|
0,894737
|
1,034483
|
| 18
|
1,053571
|
1
|
0,882353
|
1,033333
|
| 19
|
0,983051
|
0,995652
|
1
|
0,983871
|
| 20
|
1,051724
|
1,026201
|
0,866667
|
1,032787
|
| 21
|
0,983607
|
0,982979
|
1
|
1
|
| 22
|
1,05
|
1,038961
|
0,846154
|
1,031746
|
| 23
|
0,984127
|
0,991667
|
1,090909
|
0,984615
|
| 24
|
1,064516
|
1,029412
|
0,666667
|
1,09375
|
| Середнє
|
1,016849
|
1,013627
|
0,96511
|
1,080477
|
| Станд.відх.
|
0,077519
|
0,102025
|
0,179452
|
0,33136
|
| 1
|
-0,70849
|
0,964155
|
| -0,70849
|
1
|
-0,62121
|
| 0,964155
|
-0,62121
|
1
|
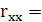
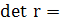 0,031236 0,031236
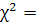 73,36757 73,36757
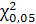 = 7,815 = 7,815
Оскільки 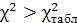 , то мультиколінеарність існує. , то мультиколінеарність існує.
10.4
Спосіб темпів приросту показників
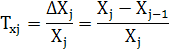
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| Y
|
X1
|
X2
|
X3
|
| 1
|
| 2
|
1,020833
|
1,025
|
1
|
1,166667
|
| 3
|
1,020408
|
1,02439
|
0,92
|
1,142857
|
| 4
|
0,92
|
0,857143
|
1,173913
|
0,625
|
| 5
|
0,934783
|
0,888889
|
1,074074
|
0,8
|
| 6
|
1,232558
|
1,34375
|
0,793103
|
2,25
|
| 7
|
1,037736
|
1,023256
|
0,869565
|
1,111111
|
| 8
|
1,018182
|
1,009091
|
1
|
1
|
| 9
|
0,964286
|
0,990991
|
1,05
|
0,9
|
| 10
|
1,018519
|
1,004545
|
0,904762
|
1,222222
|
| 11
|
1,036364
|
1,0181
|
0,947368
|
1
|
| 12
|
1,017544
|
1,013333
|
0,888889
|
1,090909
|
| 13
|
0,793103
|
0,780702
|
1,625
|
0,466667
|
| 14
|
1,021739
|
1,016854
|
0,923077
|
1
|
| 15
|
1,06383
|
1,149171
|
0,916667
|
1,5
|
| 16
|
1,08
|
1,067308
|
0,863636
|
1,380952
|
| 17
|
1,037037
|
1,036036
|
0,894737
|
1,034483
|
| 18
|
1,053571
|
1
|
0,882353
|
1,033333
|
| 19
|
0,983051
|
0,995652
|
1
|
0,983871
|
| 20
|
1,051724
|
1,026201
|
0,866667
|
1,032787
|
| 21
|
0,983607
|
0,982979
|
1
|
1
|
| 22
|
1,05
|
1,038961
|
0,846154
|
1,031746
|
| 23
|
0,984127
|
0,991667
|
1,090909
|
0,984615
|
| 24
|
1,064516
|
1,029412
|
0,666667
|
1,09375
|
| Середнє
|
1,016849
|
1,013627
|
0,96511
|
1,080477
|
| Станд.відх.
|
0,077519
|
0,102025
|
0,179452
|
0,33136
|
| 1
|
-0,70849
|
0,964155
|
| -0,70849
|
1
|
-0,62121
|
| 0,964155
|
-0,62121
|
1
|
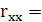
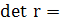 0,031236 0,031236
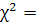 73,36757 73,36757
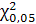 = 7,815 = 7,815
Оскільки 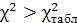 , то мультиколінеарність існує. , то мультиколінеарність існує.
10.5
Логарифмування вихідної інформації
| Місяць
|
Прибуток
|
Інвестиції
|
ОВФ
|
ФРЧ
|
| Y
|
X1
|
X2
|
X3
|
| 1
|
3,871201
|
5,298317
|
3,218876
|
1,098612
|
| 2
|
3,89182
|
5,32301
|
3,218876
|
1,252763
|
| 3
|
3,912023
|
5,347108
|
3,135494
|
1,386294
|
| 4
|
3,828641
|
5,192957
|
3,295837
|
0,916291
|
| 5
|
3,7612
|
5,075174
|
3,367296
|
0,693147
|
| 6
|
3,970292
|
5,370638
|
3,135494
|
1,504077
|
| 7
|
4,007333
|
5,393628
|
2,995732
|
1,609438
|
| 8
|
4,025352
|
5,402677
|
2,995732
|
1,609438
|
| 9
|
3,988984
|
5,393628
|
3,044522
|
1,504077
|
| 10
|
4,007333
|
5,398163
|
2,944439
|
1,704748
|
| 11
|
4,043051
|
5,4161
|
2,890372
|
1,704748
|
| 12
|
4,060443
|
5,429346
|
2,772589
|
1,791759
|
| 13
|
3,828641
|
5,181784
|
3,258097
|
1,029619
|
| 14
|
3,850148
|
5,198497
|
3,178054
|
1,029619
|
| 15
|
3,912023
|
5,337538
|
3,091042
|
1,435085
|
| 16
|
3,988984
|
5,402677
|
2,944439
|
1,757858
|
| 17
|
4,025352
|
5,438079
|
2,833213
|
1,791759
|
| 18
|
4,077537
|
5,438079
|
2,70805
|
1,824549
|
| 19
|
4,060443
|
5,433722
|
2,70805
|
1,808289
|
| 20
|
4,110874
|
5,459586
|
2,564949
|
1,84055
|
| 21
|
4,094345
|
5,442418
|
2,564949
|
1,84055
|
| 22
|
4,143135
|
5,480639
|
2,397895
|
1,871802
|
| 23
|
4,127134
|
5,472271
|
2,484907
|
1,856298
|
| 24
|
4,189655
|
5,501258
|
2,079442
|
1,94591
|
| Середнє
|
3,990664
|
5,367804
|
2,909514
|
1,533637
|
| Станд.відх.
|
0,112558
|
0,107973
|
0,322294
|
0,354314
|
| 0,106663
|
-0,10581
|
0,107762
|
| 0,107973
|
-0,08877
|
0,105211
|
| -0,26498
|
0,322294
|
-0,27325
|
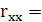
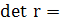 1,37E-05 1,37E-05
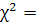 236,9638 236,9638
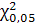 = 7,815 = 7,815
Оскільки 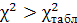 , то мультиколінеарність існує. , то мультиколінеарність існує.
11.
Побудова моделі на основі нормалізованих змінних і перехід до моделі в абсолютному виразі
Економетрична модель на основі нормалізованих данних записується так:
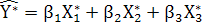
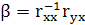
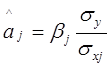
| a^1=
|
0,097302
|
| a^2=
|
-0,76639
|
| a^3=
|
-0,18812
|
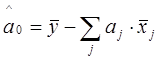
Таким чином модель має вигляд:
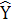 =49,08539+0,097X1
–0,766X2
–0,188X3 =49,08539+0,097X1
–0,766X2
–0,188X3
|