Основным в процессе программирования является разработка алгоритма. Это один из наиболее сложных этапов решения задачи с использованием ЭВМ. В начале обучения программированию, на наш взгляд, целесообразно не привязываться сразу к какому-либо языку, разрабатывать алгоритмы без записи на ЯПВУ, а, например, с помощью блок-схем или иным аналогичным способом. После такой "чистой" алгоритмизации учащимся или студентам проще перейти к записи того же алгоритма на определённом языке программирования. В настоящей публикации продемонстрирован именно такой подход.
Напомним, что основными алгоритмическими структурами (ОАС) являются следование, развилка и цикл. В более сложных случаях используются суперпозиции (вложения) ОАС.
Ниже приведены графические обозначения (обозначения на блок-схемах) ОАС.
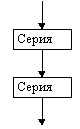
Структура “следование” |
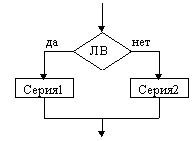
Полная развилка |
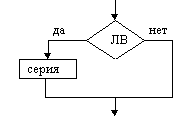
Неполная развилка |
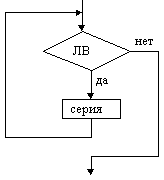
Цикл с предусловие (цикл ПОКА) |
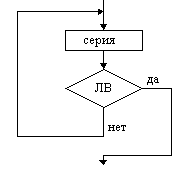
Цикл с постусловием (цикл ДО) |
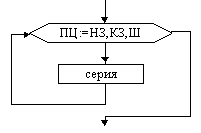
Цикл с параметром |
На схемах СЕРИЯ обозначает один или несколько любых операторов; УСЛОВИЕ есть логическое выражение (ЛВ) (если его значение ИСТИНА, переход происходит по ветви ДА, иначе — по НЕТ). На схеме цикла с параметром использованы обозначения: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.
Начало и конец алгоритма на блок-схемах обозначают овалом, вводимые и выводимые переменные записываются в параллелограмме.
В примерах мы будем использовать запись алгоритмов с помощью блок-схем и словесное описание.
Линейные алгоритмы
Простейшие задачи имеют линейный алгоритм решения. Это означает, что он не содержит проверок условий и повторений.
Пример 1. Пешеход шел по пересеченной местности. Его скорость движения по равнине v1 км/ч, в гору — v2 км/ч и под гору — v3 км/ч. Время движения соответственно t1, t2 и t3 ч. Какой путь прошел пешеход?
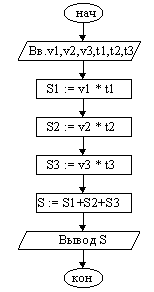 |
1. Ввести v1, v2, v3, t1, t2, t3.
2. S1 := v1 * t1.
3. S2 := v2 * t2.
4. S3 := v3 * t3.
5. S := S1 + S2 + S3.
6. Вывести значение S.
7. Конец.
|
Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.
Пример 2. Дано натуральное трехзначное число n, в записи которого нет нулей. Составить алгоритм, который возвращает значение ИСТИНА, если верно утверждение: "число n кратно каждой своей цифре", и ЛОЖЬ — в противном случае.
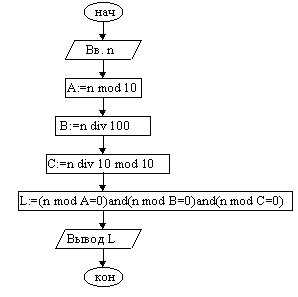 |
1. Ввести число n
2. A := n mod 10 {разряд единиц}
3. B := n div 100 {разряд сотен}
4. C := n div 10 mod 10 {десятки}
5. L := (n mod A=0) and (n mod B=0) and (n mod C=0)
6. Вывод L
7. Конец
|
На приведенной выше схеме DIV и MOD соответственно операции деления нацело и получения остатка от целочисленного деления. В фигурных скобках записаны пояснения (комментарии) к операторам.
Развилка
Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. В таких случаях используется развилка.
Реклама

Пример 1. Вычислить значение функции
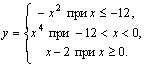
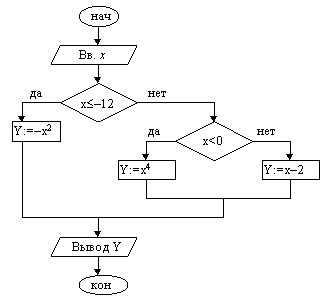 |
1. Ввести x.
2. Если x£–12, то y:=–x2
3. Если x<0, то y:=x4
4. y := x–2
5. Вывести y
6. Конец
|
При тестировании алгоритмов с развилкой необходимо подбирать такие исходные данные, чтобы можно было проверить все ветви. В приведенном выше примере должно быть по крайней мере три тестовых набора.
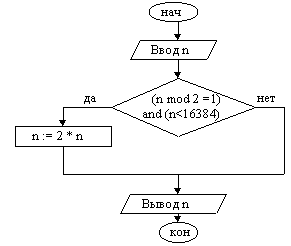
Пример 2. Дано натуральное число n. Если число нечётное и его удвоение не приведет к выходу за 32767 (двухбайтовое целое число со знаком), удвоить его, иначе — оставить без изменения.
Чтобы удовлетворить условию удвоения, число n должно быть нечетным и меньше 16384.
 |
1. Ввести число n
2. Если число n нечетное и меньше 16384, то n := n * 2
3. Вывод n
4. Конец
|
Рассмотренный пример иллюстрирует неполную развилку. Также следует отметить, здесь логическое выражение, являющееся условием, содержит 2 операнда.
Циклы
Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.
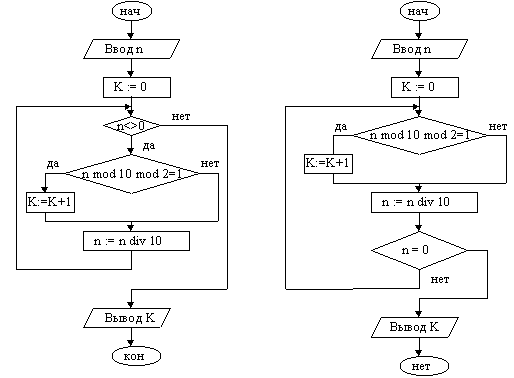
Пример 1. Подсчитать количество нечетных цифр в записи натурального числа n.
Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.
 |
1. Ввести число n
2. K := 0 {подготавливаем счётчик}
3. Если n = 0, переход к п. 7
4. Если n mod 10 mod 2 = 1, то K := K +1
5. n := n div 10
6. Переход к п. 3
7. Вывод K
8. Конец
|
Задача решена двумя способами. Слева решение оформлено с использованием цикла с предусловием, справа — с постусловием.
Пример 2. Дана последовательность, общий член которой определяется формулой
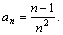
Вычислить при n>2 сумму тех ее членов, которые больше заданного числа e.
При решении задачи находится очередной член последовательно и, если он больше e, добавляется к сумме.
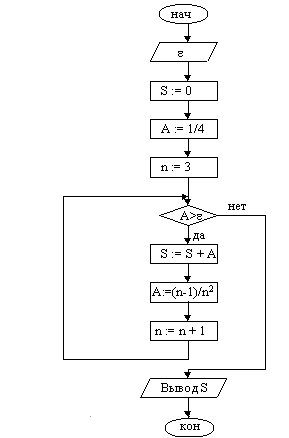 |
1. Ввестиe
2. S := 0
3. A := 1/4
4. n := 3
5. Сравнить А с e. Если A>=e, переход к п. 10
6. S := S + A
7. A := (n-1)/(n*n)
8. n := n + 1
9. Переход к п. 5
10. Вывод S
11. Конец
|
В рассмотренных выше примерах количество повторений заранее неизвестно. В первом оно зависит от количества цифр в записи натурального числа, во втором — от числа e.
В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.
Пример 3. Найти произведение первых k натуральных чисел, кратных трём.
Реклама

При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.
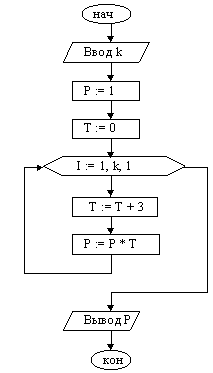 |
1. Ввод k
2. P := 1 {здесь накапливаем произведение}
3. T := 0 {здесь будут числа, кратные 3}
4. I := 1
5. Если I > k, переход к п. 10
6. T := T + 3
7. P := P * T
8. I := I + 1
9. Перейти к п. 5
10. Вывод P
11. Конец
|
Другие примеры будут записаны уже на ЯПВУ. В настоящей же публикации предпринята попытка продемонстрировать, что изучение программирования разумно начинать собственно с разработки алгоритмов, не акцентируя первоначально внимания на записи алгоритма на том или ином языке программирования. В то же время автор, являясь сторонником структурного подхода к программированию, предлагает придерживаться этого подхода и при программировании на уровне блок-схем.
|