| Контрольная работа №2
Задача №1
Для изучения связи между активами-нетто и объемом капитала по 30 коммерческим банкам (согласно Вашему варианту):
а) изобразите связь между изучаемыми признаками графически построением поля корреляции;
б) постройте уравнение регрессии. Параметры уравнения определите методом наименьших квадратов. Рассчитайте теоретические значения объема кредитных вложений и нанесите их на построенный график.
Решение:
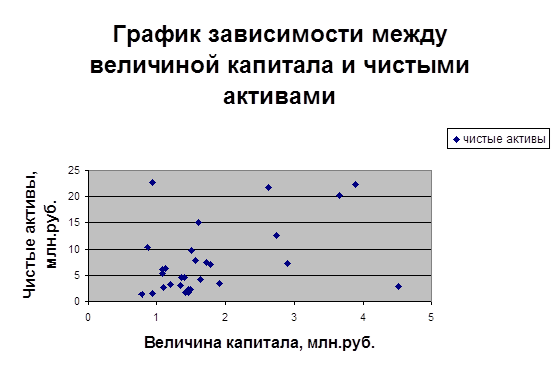
Рисунок 1
Расчетная таблица для определения параметров уравнения регрессии зависимости чистых активов и капитала коммерческих банков.
Таблица 1.1
| № банка
|
Капитал, млн.руб. (X)
|
Чистые активы, млн.руб. (Y)
|
X²
|
Y²
|
X*Y
|
Yx
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 1
|
1,46
|
1,68
|
2,13
|
2,82
|
2,45
|
232,1
|
| 2
|
1,51
|
2,81
|
2,28
|
7,9
|
4,24
|
240,4
|
| 3
|
2,63
|
21,84
|
6,92
|
476,9
|
57,44
|
422,0
|
| 4
|
1,72
|
7,38
|
2,96
|
54,46
|
12,7
|
264,8
|
| 5
|
1,50
|
9,82
|
2,25
|
96,43
|
14,73
|
240,1
|
| 6
|
1,64
|
4,26
|
2,69
|
18,15
|
6,99
|
258,2
|
| 7
|
1,36
|
4,61
|
1,85
|
21,25
|
6,27
|
228,4
|
| 8
|
1,21
|
3,32
|
1,46
|
11,02
|
4,02
|
219,6
|
| 9
|
1,49
|
2,33
|
2,22
|
5,43
|
3,47
|
234,9
|
| 10
|
1,35
|
3,08
|
1,82
|
9,49
|
4,16
|
227,6
|
| 11
|
1,61
|
15,14
|
2,59
|
229,2
|
24,37
|
254,8
|
| 12
|
1,78
|
7,12
|
3,17
|
50,7
|
12,67
|
266,1
|
| 13
|
1,42
|
1,68
|
2,01
|
2,82
|
2,38
|
229,7
|
| 14
|
1,41
|
4,60
|
1,99
|
21,16
|
6,49
|
229,2
|
| 15
|
1,46
|
2,20
|
2,13
|
4,84
|
3,21
|
232,1
|
| 16
|
3,65
|
20,21
|
13,32
|
408,4
|
73,77
|
587,4
|
| 17
|
1,57
|
7,74
|
2,46
|
59,9
|
12,15
|
252,1
|
| 18
|
1,10
|
2,72
|
1,21
|
7,4
|
2,99
|
173,8
|
| 19
|
0,94
|
1,59
|
0,88
|
2,53
|
1,49
|
151,9
|
| 20
|
3,89
|
22,37
|
15,13
|
500,42
|
87,02
|
598,4
|
| 21
|
0,78
|
1,42
|
0,61
|
2,02
|
1,11
|
121,9
|
| 22
|
2,74
|
12,61
|
7,51
|
159,01
|
34,55
|
439,8
|
| 23
|
0,87
|
10,26
|
0,76
|
105,27
|
8,93
|
136,6
|
| 24
|
1,08
|
6,12
|
1,17
|
37,45
|
6,61
|
169,9
|
| 25
|
1,08
|
5,27
|
1,17
|
27,8
|
5,69
|
169,9
|
| 26
|
2,90
|
7,33
|
8,41
|
53,73
|
21,26
|
465,8
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
| 27
|
1,13
|
6,30
|
1,28
|
39,69
|
7,12
|
178,7
|
| 28
|
0.94
|
22,67
|
0,88
|
513,93
|
21,31
|
151,9
|
| 29
|
1.92
|
3,42
|
3,69
|
11,7
|
6,57
|
306,8
|
| ИТОГО
|
48,14
|
221,9
|
96,95
|
2941,81
|
456,16
|
7684,9
|
Система нормальных уравнений для нахождения параметров парной регрессии методом наименьших квадратов имеет следующий вид:
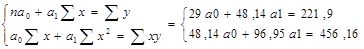
а0 = (221,9 – 48,14а1)/29
48,14*((221,9 – 48,14а1)/29)+ 96,95а1 = 456,16
368,354 – 79,912а1 + 96,95а1 = 456,16
17,037а1 = 87,806
а1 = 5,154
а0 = (221,9 – 48,14*5,154)/29 = -0,9
Yx = а0 + а1*х = 5,154х - 0,9
Задача №2
По данным задачи 1 вычислите показатели тесноты связи между изучаемыми признаками. В случае линейной связи для оценки тесноты связи необходимо применить формулу линейного коэффициента корреляции, при нелинейной связи – теоретического корреляционного отношения.
Сделайте выводы о тесноте и направлении связи между изучаемыми признаками.
Реклама

Решение
Линейный коэффициент корреляции рассчитывается по формуле:
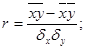
σх = √х² - (х)²
σу = √у² - (у)²
х² = ∑ х²/29 = 96,95/29 = 3,34
(х)² = (∑ х/29)² = (48,14/29)² = 2,756
у² = ∑ у²/29 = 2941,81/29 = 101,441
(у)² = (∑ у/29)² = (221,9/29) ² = 58,549
X = ∑ х/29 = 48,14/29 = 1,66
Y = ∑ у/29 = 221,9/29 = 7,65
XY = ∑х*у/29 = 456,16/29 = 15,73
σх =√3,34 – 2,756 = 0,764
σу = √101,441 – 58,549 = 6,55
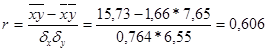
Задача №3
По данным любого статистического ежегодника или периодической печати выполните следующее:
1. Выберите интервальный ряд динамики, состоящий из 8-10 уровней.
2. Изобразите графически динамику ряда с помощью статистической кривой.
3. По данным выбранного ряда вычислите абсолютные и относительные показатели динамики. Результаты расчетов изложите в табличной форме.
4. Вычислите средние показатели динамики.
Решение
1. Выберем интервальный ряд динамики, состоящий из восьми уровней и отразим его в таблице 3.1
Таблица 3.1. Среднемесячное потребление горячей воды в течение 8-ми месяцев, куб.м.
| Месяц
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| куб.м.
|
10,5
|
9,8
|
7,4
|
9,6
|
10,9
|
9,2
|
13,7
|
11,3
|
Рассмотрим динамический ряд потребления горячей воды в таблице 3.2
Таблица 3.2. Динамика потребления горячей воды за 8 месяцев
| Месяц
|
Потребление, куб.м.(уi)
|
Абсолютные приросты, куб.м.
|
Темпы роста, %
|
Темпы прироста, %
|
Абсолютное значение 1% прироста, куб.м.
|
| цепные
|
базисные
|
цепные
|
базисные
|
цепные
|
базисные
|
| 1
|
10,5
|
-
|
-
|
-
|
100
|
-
|
-
|
-
|
| 2
|
9,8
|
-0,7
|
-0,7
|
93,3
|
93,3
|
-6,7
|
-6,7
|
0,105
|
| 3
|
7,4
|
-2,4
|
-3,1
|
75,5
|
70,5
|
-24,5
|
-29,5
|
0,098
|
| 4
|
9,6
|
2,2
|
-0,9
|
129,7
|
91,4
|
29,7
|
-8,6
|
0,074
|
| 5
|
10,9
|
1,3
|
0,4
|
113,5
|
103,8
|
13,5
|
3,8
|
0,096
|
| 6
|
9,2
|
-1,7
|
-1,3
|
84,4
|
87,6
|
-15,6
|
-12,4
|
0,109
|
| 7
|
13,7
|
4,5
|
3,2
|
148,9
|
130,5
|
48,9
|
30,5
|
0,092
|
| 8
|
11,3
|
-2,4
|
0,8
|
82,5
|
107,6
|
-17,5
|
7,6
|
0,137
|
| Итого
|
82,4
|
0,8
|
-
|
-
|
-
|
-
|
-
|
-
|
2. Изобразим графически динамику ряда с помощью статистической кривой.
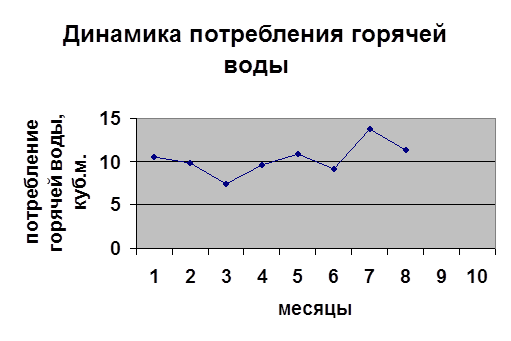
Рисунок 2. Динамика ряда в виде статистической кривой
3. По данным выбранного ряда вычислим абсолютные и относительные показатели динамики.
Средний абсолютный прирост:
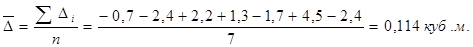 , ,
или 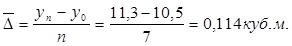
Средний темп роста:
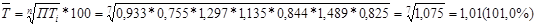 , ,
или 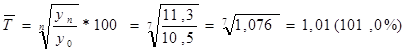
Средний темп прироста:
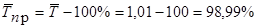
Средний уровень интервального ряда определяется по формуле средней арифметической:
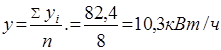
Средний уровень моментального ряда определяется по формуле:
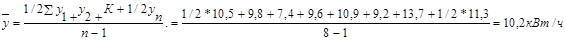
Согласно произведенным вычислениям можно сделать следующие выводы:
Наибольшее потребление горячей воды было в 7-ом месяце, а наименьшее в 3-ем месяце. Среднее потребление горячей воды 10,3 куб.м.
Реклама

Задача №4
По данным задачи 3 произведите сглаживание изучаемого ряда динамики с помощью скользящей средней и аналитического выравнивания. Расчетные уровни нанесите на построенный ранее график.
Сделайте выводы о характере тенденции рассмотренного ряда динамики.
Решение
1. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень от определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго и т.д.
Расчет скользящей средней по данным о потреблении горячей воды за восемь месяцев приведен в таблице 4.1.
Таблица 4.1. Сглаживание потребления горячей воды за восемь месяцев методом скользящей средней
| Месяцы
|
Потребление горячей воды, куб.м.
|
Скользящая
|
средняя
|
| трехмесячная
|
пятимесячная
|
| 1
|
10,5
|
|
|
| 2
|
9,8
|
(10,5+9,8+7,4)/3=9,2
|
|
| 3
|
7,4
|
(9,8+7,4+9,6)/3=8,9
|
(10,5+9,8+7,4+9,6+10,9)/5=9,6
|
| 4
|
9,6
|
(7,4+9,6+10,9)/3=9,3
|
(9,8+7,4+9,6+10,9+9,2)/5=9,4
|
| 5
|
10,9
|
(9,6+10,9+9,2)/3=9,9
|
(7,4+9,6+10,9+9,2+13,7)/5=10,2
|
| 6
|
9,2
|
(10,9+9,2+13,7)/3=11,3
|
(9,6+10,9+9,2+13,7+11,3)/5=10,9
|
| 7
|
13,7
|
(9,2+13,7+11,3)/3=11,4
|
|
| 8
|
11,3
|
|
|
2. Аналитическое выравнивание ряда динамики уровни ряда представляются как функции времени:
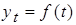
При использовании уравнения прямой
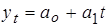
Параметры вычисляются по следующим формулам:
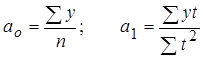
Таблица 4.2. Выравнивание по прямой ряда динамики потребления горячей воды отражено в таблице 4.2
| Месяцы
|
Потребление горячей воды, куб.м. (у
i
)
|
t
|
t
²
|
y
i
t
|
y
t
|
(
y
i
-
y
t
i
) ²
|
| 1
|
10,5
|
-4
|
16
|
-42,0
|
8,98
|
2,31
|
| 2
|
9,8
|
-3
|
9
|
-29,4
|
9,31
|
0,24
|
| 3
|
7,4
|
-2
|
4
|
-14,8
|
9,64
|
5,02
|
| 4
|
9,6
|
-1
|
1
|
-9,6
|
9,97
|
0,14
|
| 5
|
10,9
|
1
|
1
|
10,9
|
10,63
|
0,07
|
| 6
|
9,2
|
2
|
4
|
18,4
|
10,96
|
3,1
|
| 7
|
13,7
|
3
|
9
|
41,1
|
11,29
|
5,8
|
| 8
|
11,3
|
4
|
16
|
45,2
|
11,62
|
0,1
|
| Сумма
|
82,4
|
0
|
60
|
19,8
|
82,4
|
16,78
|
а0 = 82,4/8 = 10,3 куб.м.
а1 = 19,8/60 = 0,33 куб.м.
Уравнение прямой, представляющее собой трендовую модель искомой функции, будет иметь вид:
Yt
= 10,3 + 0,33t
Полученное уравнение показывает что, несмотря на колебания в отдельные месяцы, наблюдается тенденция увеличения потребления горячей воды.
Потребление горячей воды в среднем возрастало на 0,33 куб.м. в месяц.
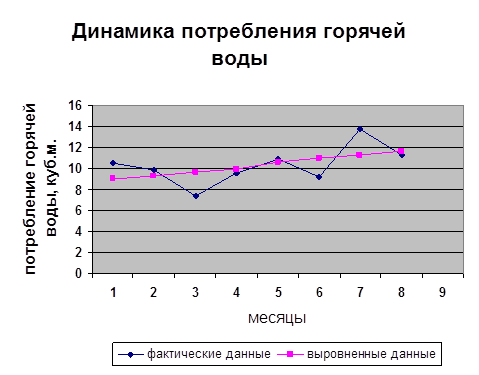
Рисунок 3. Динамика ряда потребления горячей воды с фактическими и выровненными данными
Задача №5.
По данным варианта следующее:
1) индивидуальные и общие (агрегатные) индексы цен;
2) индексы цен в среднегармонической форме;
3) сводные индексы физического объема проданных товаров;
4) сводные индексы товарооборота двумя способами;
а) по формуле индекса товарооборота в текущих ценах;
б) на основе ранее рассчитанных индексов цен и физического объема товарооборота.
Таблица 5.1
| № п/п
|
Продукт
|
Базисный период
|
Отчетный период
|
Расчетные графы
|
| Кол-во реализованных единиц, шт., q0
|
Цена за единицу,
Руб., P0
|
Q, шт., q1
|
P1,
руб,
P1
|
P1*q1
|
P0*q1
|
P
1
*
q
1
i
|
P0*q0
|
| 1
|
Б
|
175
|
120
|
180
|
135
|
24300
|
21600
|
21504
|
21000
|
| 2
|
В
|
400
|
50
|
360
|
42
|
15120
|
18000
|
18000
|
20000
|
| 3
|
Г
|
150
|
115
|
89
|
126
|
11214
|
10235
|
10195
|
17250
|
| ∑
|
3
|
-
|
-
|
-
|
-
|
50634
|
49835
|
49699
|
58250
|
1. Индивидуальные и общие индексы цен рассчитываются по формуле:
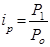 , ,
где 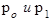 - соответственно цены отчетного и базисного периодов. - соответственно цены отчетного и базисного периодов.
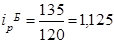 (+12,5%) (+12,5%)
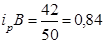 (-16%) (-16%)
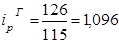 (+9,6%) (+9,6%)
Общий (сводный) индекс цен имеет следующий вид:
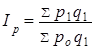 , ,
где q1
- количество проданных товаров в отчетном периоде.
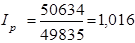
Цены в отчетном периоде по сравнению с базисным возросли на 1,6%.
2. Среднегармонический индекс тождествен агрегатному и вычисляется по следующей формуле:
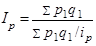
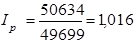
3. Сводные индексы физического объема проданных товаров:
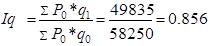
Физический объем проданных товаров в отчетном периоде по сравнению с базисным снизился на 14,4%.
4. Сводные индексы товарооборота:
а) по формуле индекса товарооборота в текущих ценах:
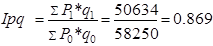
б) на основе ранее рассчитанных индексов цен и физического объема товарооборота:
Ipq
= Ip
Iq
= 1,016*0,856 = 0,869
Товарооборот в отчетном периоде по сравнению с базисным сократился на 13,1%.
|