| Государственное образовательное учреждение высшего профессионального образования
«Московский государственный институт электронной технки
(технический универститет)»
Курсовая работа
по дисциплине
«Теория вероятности и математическая статистика»
Тема работы
«Анализ данных в линейной регрессионной модели»
Выполнил:
Студент группы ЭКТ-21
Рыжов С.А.
Проверил:
Преподаватель
Бардушкина И. В.
Москва - 2010
Вариант 20.
Задание 1
Выполнить предварительную обработку результатов наблюдений, включающую:
1 построение диаграммы рассеивания (корреляционного поля);
2 группировку данных и построение корреляционной таблицы;
3 оценку числовых характеристик для негруппированных и группированных данных.
Оценка числовых характеристик для негруппированных данных:
| X
|
Y
|
X
|
Y
|
| 4,19
|
9,19
|
4,44
|
9,13
|
| 3,04
|
11,94
|
11,31
|
4,58
|
| 4,6
|
8,09
|
7,57
|
3,14
|
| 9,83
|
10,33
|
1,62
|
14,61
|
| 8,66
|
7,15
|
5,71
|
6,48
|
| 1,3
|
12,34
|
11,06
|
6,78
|
| 4,22
|
16,35
|
10,35
|
2,15
|
| 5,11
|
7,7
|
2,46
|
9,66
|
| 9,85
|
5,64
|
1,02
|
11,19
|
| 8,8
|
4,52
|
5,77
|
7,77
|
| 12,17
|
4,52
|
8,63
|
4,05
|
| 11,25
|
2,06
|
6,91
|
4,76
|
| 5,73
|
7,41
|
3,56
|
8,54
|
| 4,05
|
10,51
|
9,47
|
2,22
|
| 5,41
|
9,97
|
6,16
|
3,72
|
| 1,28
|
14,68
|
8,26
|
3,57
|
| 1,67
|
9,67
|
6,7
|
14,32
|
| 11,99
|
3,31
|
4,95
|
10,64
|
| 7,66
|
5,93
|
3,37
|
10,73
|
| 5,17
|
9,87
|
1,53
|
10,13
|
| 3,26
|
11,52
|
9,54
|
4,95
|
| 12,58
|
2,88
|
3,11
|
5,38
|
| 8,34
|
3,57
|
5,09
|
5,79
|
| 5,79
|
4,39
|
11,08
|
3,87
|
| 3,42
|
9,71
|
8,74
|
-2,23
|
| Сумма X
|
317.78
|
|
|
| Сумма Y
|
369,18
|
|
|
| MX
|
6,3556
|
|
|
| MY
|
7,3836
|
|
|
| s2
X
|
11,02005
|
|
|
| s2
Y
|
15,31479
|
|
|
| KXY
|
-9,1594
|
|
|
| ρXY
|
-0,7194
|
|
|
Числовые характеристики для негруппированной выборки находятся по следующим формулам:
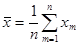 , , 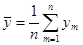 ; ;
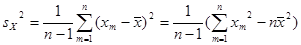 ; ;
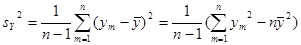 ; ;
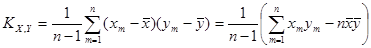 ; ;
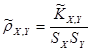 ; ;
Построение корреляционного поля:
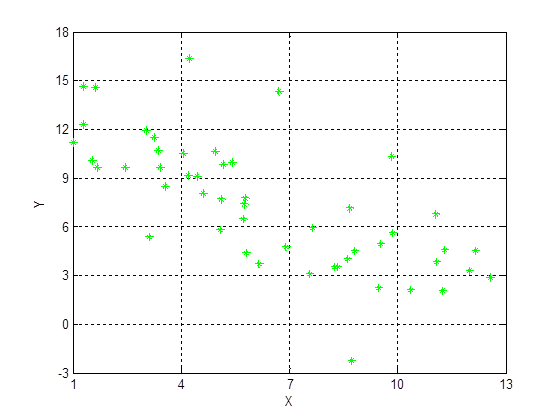
Построение корреляционной таблицы:
Таблица 1.1
| Y
X
|
-1.5
|
1.5
|
4.5
|
7.5
|
10.5
|
13.5
|
16.5
|
ni
.
|
| 2.5
|
0
|
0
|
1
|
1
|
8
|
3
|
0
|
13
|
| 5.5
|
0
|
0
|
4
|
5
|
6
|
1
|
1
|
17
|
| 8.5
|
1
|
1
|
8
|
1
|
1
|
0
|
0
|
12
|
| 11.5
|
0
|
3
|
4
|
1
|
0
|
0
|
0
|
8
|
| nj
.
|
1
|
4
|
17
|
8
|
15
|
4
|
1
|
50
|
Оценка числовых характеристик для группированных данных:
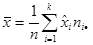 , , 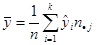 ; ;
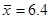 , , 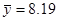 ; ;
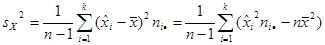 ; ;
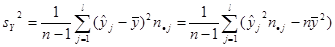 ; ;
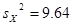 , ,
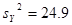 ; ;
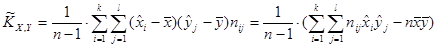 ; ;
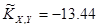
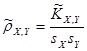 ; ;
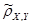 = - 0.87 = - 0.87
Задание 2
Для негруппированных данных проверить гипотезу 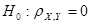 об отсуствии линейной статистической связи между компонентами X и Y при альтернативной гипотезе об отсуствии линейной статистической связи между компонентами X и Y при альтернативной гипотезе 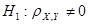 ( уровень значимости α = 0,05); ( уровень значимости α = 0,05);
Выборочное значение статистики равно
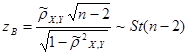 , ,
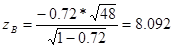
Используя средства Matlab, найдем
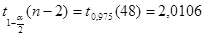
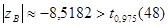
Так как выборочное значение статистики больше квантили распределения Стьюдента, гипотеза H
0
отклоняется в сторону гипотезы H
1
. Корреляция значима.
Задание 3
Для негруппированых данных получить интервальную оценку для истинного значения коэффициента корреляции ρX
,
Y
,
при уровне значимости α = 0,05.
Используя средства Matlab, найдем
Реклама

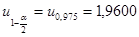
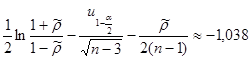 , , 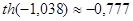
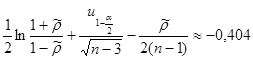 , , 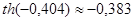
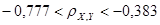
Задание 4
Для негруппированных и группированных данных составить уравнения регрессии Y на x и X на Y.
Рассмотрим вначале случай негруппированных данных.
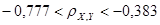
Этот интервал не содержит нуля, т.е. с доверительной вероятностью 1 – ЫВА = 0,95 существует корреляция между X и Y и имеет смысл построение уравнений регрессии.
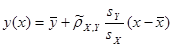 , , 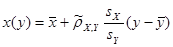
y
(
x
)
= 12,77 – 0,848*x
;
x
(
y
)
= 10,86 – 0,6*y
;
Проверка.
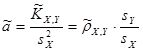 , , 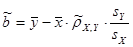 . .
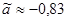 , , 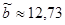 ; ;
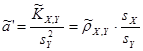 , , 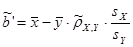
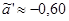 , , 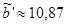 ; ;
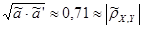
Случай группированных данных.
Подставим найденные значения 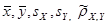 в уравнеиня линейной регрессии Y
на x
и X
на y
.
Получим: в уравнеиня линейной регрессии Y
на x
и X
на y
.
Получим:
y
(
x
)
= 17,14 – 1,4*x
;
x
(
y
)
= 10,83 – 0,54*y
;
Проверка: 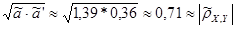
Задание 5
Для негруппированных данных нанести графики выборочных регрессионных прямых на диаграмму рассеивания.
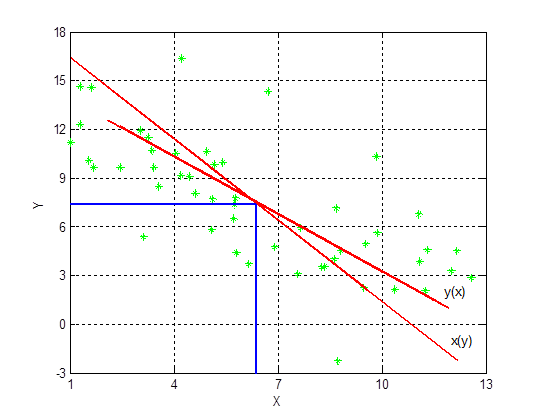
Задание 6
Для негруппированных данных по найденным оценкам параметров линейной регрессии Y
на x
получить оценку s
2
для дисперсии ошибок наблюдений σ
2
, найти коэффициент детерминации R
2
, построить доверительные интервалы для параметров регрессии a и b, дисперсии ошибок наблюдений σ
2
и среднего значения Y
при x
= x
0
.
Для негруппированных данных были получены следующие оценки числовых характеристик и коэффициентов регрессии: 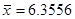 , , 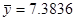 , , 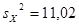 , , 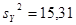 , , 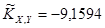 , , 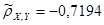 , , 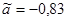 , , 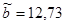 . .
Используя соотношение 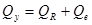 , вычислим остаточную сумму , вычислим остаточную сумму 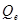
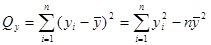 ; ;
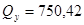 ; ;
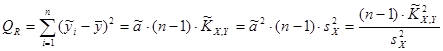 ; ;
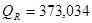 . .
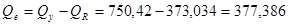 ;
;
Тогда оценка дисперсии ошибок наблюдений равна
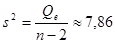 . .
Коэффициент детерминации равен
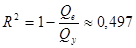 .
.
Поскольку 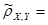 (знак (знак 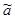 ) )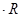 , то сделаем проверку правильности расчетов: , то сделаем проверку правильности расчетов:
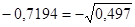 (верно).
(верно).
Полученный результат для коэффициента детерминации означает, что уравнение регрессии 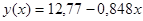 на 49,7% объясняет общий разброс результатов наблюдений относительно горизонтальной прямой на 49,7% объясняет общий разброс результатов наблюдений относительно горизонтальной прямой 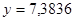 . .
Построим доверительные интервалы для параметров линейной регрессии и дисперсии ошибок наблюдений.
С помощью Matlab найдем квантили распределений Стьюдента и 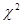 : :
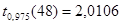 , , 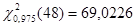 , , 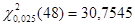 ; ;
– доверительный интервал для параметра 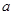 : :
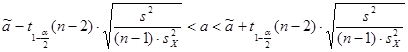 ;
;
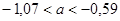 ;
;
– доверительный интервал для параметра 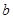 : :
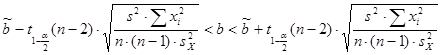 ;
;
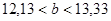 ;
;
– доверительный интервал для дисперсии ошибок наблюдений 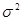 : :
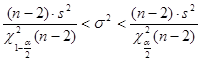 ; ;
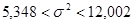 .
.
-Найдем границы доверительных интервалов для среднего значения 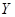 при при 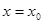 : :
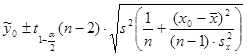 ;
;
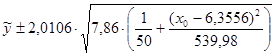 . .
Задание 7.
Для негруппированных данных проверить значимость линейной регрессии Y на x (уровень значимости α = 0,05).
Гипотеза 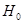 : : 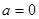 отклоняется на уровне значимости отклоняется на уровне значимости 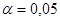 , так как доверительный интервал , так как доверительный интервал 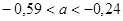 не накрывает нуль с доверительной вероятностью 0,95.
не накрывает нуль с доверительной вероятностью 0,95.
Этот же результат можно получить, используя для проверки гипотезу 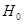 : : 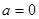 и статистику и статистику 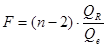 . .
С помощью Matlab найдем квантили распределения Фишера:
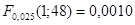 , , 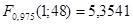 . .
Выборочное значение статистики 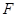 равно: равно:
Реклама

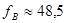 . .
Поскольку 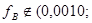 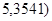 , то гипотеза , то гипотеза 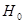 : : 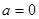 отклоняется на уровне значимости отклоняется на уровне значимости 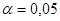 . Таким образом, линейная регрессия . Таким образом, линейная регрессия 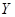 на на 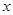 статистически значима. статистически значима.
Задание №8
Для данных, сгруппированных только по 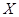 , проверить адекватность линейной регрессии , проверить адекватность линейной регрессии 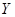 на на 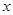 (уровень значимости (уровень значимости 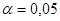 ). ).
Для проверки адекватности воспользуемся корреляционной таблицей. Будем считать, что середины интервалов группировки 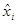 , , 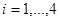 , являются значениями компоненты , являются значениями компоненты 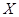 . Тогда число . Тогда число 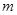 повторных наблюдений равно 4. Запишем результаты этих наблюдений в виде таблицы повторных наблюдений равно 4. Запишем результаты этих наблюдений в виде таблицы
Таблица 1.2
| 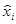
|
2,5
|
5,5
|
8,5
|
11,5
|
| 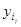
|
11,94
12,34
14,68
9,87
11,52
9,71
14,61
9,66
11,19
8,54
10,73
10,13
5,38
|
9,19
8,09
16,35
7,70
7,41
10,51
9,97
9,87
4,39
6,48
7,77
4,76
3,72
14,32
10,64
5,79
9,13
|
10,33
7,15
5,64
4,52
4,52
3,57
3,14
4,05
2,22
3,57
4,95
-2,23
|
4,52
2,06
3,11
2,88
4,58
6,78
2,15
3,87
|
| 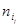
|
13
|
17
|
12
|
8
|
| 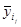
|
10,79
|
8,59
|
9,65
|
3,74
|
Для удобства расчетов в последней строке таблицы приведены средние значения 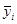 , , 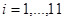 . .
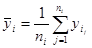 . .
Получим уравнение выборочной линейной регрессии 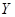 на на 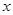 для данных, сгруппированных по для данных, сгруппированных по 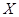 : :
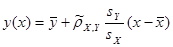 ; ;
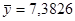 , , 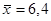 , , 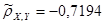 , , 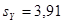 , , 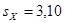 ; ;
y
(
x
)
= 8,29 – 0,9x
.
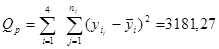 ; ;
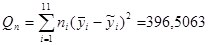 . .
Выборочное значение статистики 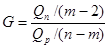 равно равно
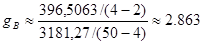 . .
Так как квантиль распределения Фишера, вычисленный с помощью Matlab, равен
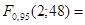 3,19, 3,19,
то 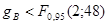 , а значит, линейная регрессия , а значит, линейная регрессия 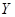 на на 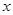 для данных, сгруппированных по для данных, сгруппированных по 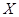 , адекватна результатам наблюдений. , адекватна результатам наблюдений.
Задание 9.
Для негруппированных данных проверить гипотезу 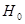 : :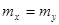 при альтернативной гипотезе при альтернативной гипотезе 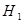 : :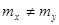 (уровень значимости (уровень значимости  ) )
Имеются следующие величины: 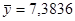 , , 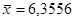 , , , , 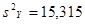 , , 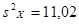 . .
Сначала проверяется гипотеза 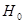 : :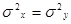 , альтернативная гипотеза , альтернативная гипотеза 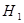 : :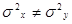 . .
Статистика равна
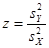 = 1,931 = 1,931
С помощью средств Matlab, найдем:
F0,975
(n
-1; n
-1)=F0,975
(49,49) = 1.7622
z > F0,975
(n
-1; n
-1),
следовательно 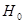 отклоняется, а значит что отклоняется, а значит что 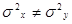
Теперь можно проверить гипотезу, 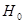 : :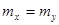 , при альтернативной гипотезе , при альтернативной гипотезе 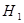 : :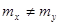 . .
Т.к. 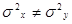 , статистика имеет вид , статистика имеет вид
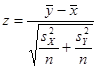 = 1,418 = 1,418
Найдем количество степеней свободы
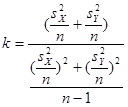 ≈3,625 ≈3,625
С помощью средств Matlab, найдем:
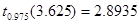
z < 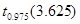 , значит нет оснований отклонять гипотезу , значит нет оснований отклонять гипотезу 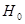 : :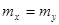 . .
Приложение
A = [ 4.19 3.04 4.60 9.83 8.66 1.30 4.22 5.11 9.85 8.80 12.17 11.25 5.73 4.05 5.41 1.28 1.67 11.99 7.66 5.17 3.26 12.58 8.34 5.79 3.42 4.44 11.31 7.57 1.62 5.71 11.06 10.35 2.46 1.02 5.77 8.63 6.91 3.56 9.47 6.16 8.26 6.70 4.95 3.37 1.53 9.54 3.11 5.09 11.08 8.74;
9.19 11.94 8.09 10.33 7.15 12.34 16.35 7.70 5.64 4.52 4.52 2.06 7.41 10.51 9.97 14.68 9.67 3.31 5.93 9.87 11.52 2.88 3.57 4.39 9.71 9.13 4.58 3.14 14.61 6.48 6.78 2.15 9.66 11.19 7.77 4.05 4.76 8.54 2.22 3.72 3.57 14.32 10.64 10.73 10.13 4.95 5.38 5.79 3.87 -2.23]
x = A(1,:);
y = A(2,:);
Mx = mean(x)
Dx = var(x,1)
My = mean(y)
Dy = var(y,1)
plot(x,y,'g*')
grid on
hold on
axis([1 13 -3 18]);
gca1 = gca;
set(gca1,'xtick',[1 4 7 10 13],'ytick',[-3 0 3 6 9 12 15 18]);
xlabel('X');
ylabel('Y');
z = 12.77 - 0.848*x; %построение регрессии Y на x
Zplot = plot(z,x);
set(Zplot,'Color','Red','LineWidth',[2])
hold on
text(12, -1,'x(y)');
text(11.8, 2,'y(x)');
t = 10.86 - 0.6*y; %построение регрессии X на y
Tplot = plot(t,y);
set(Tplot,'Color','Red','LineWidth',[2])
hp = line([1 6.36],[7.38 7.38]); %эти прямые показывают положение
set(hp,'Color','blue','LineWidth',[1.5]) %среднего выборочного
hp = line([6.36 6.36],[-3 7.38]);
set(hp,'Color','blue','LineWidth',[1.5])
K = cov(x,y) %находим ковариацию
DEtK = det(K)
M = corrcoef(x,y) %коэффициент корреляции
detM = det(M)
|