СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ
Контрольная работа №1
Дисциплина Экономико-математические методы
Применение математического моделирования в экономике
Студент
Качан Татьяна Юрьевна
2010 г.
Содержание
1. Задание 1
2. Задание 2
3. Задание 3
4. Задание 4
5. Задание 5
6. Задание 6
7. Задание 7
8. Задание 8
Список используемой литературы
Задание 1 Производственные функции
1. Дайте понятие производственной функции и изокванты. Что означает взаимозаменяемость ресурсов?
Производственной функцией называется зависимость количества продукта, которое может произвести фирма, от объемов затрат ресурсов. Производственная функция характеризует чисто техническую зависимость между количеством применяемых ресурсов и объемом выпускаемой продукции в единицу времени. Производственная функция описывает множество технически эффективных способов производства заданного объема продукции. Изокванта (в теории производственных функций) - это геометрическое место точек в пространстве ресурсов, в которых различные сочетания производственных ресурсов дают одно и то же количество выпускаемой продукции. Взаимозаменяемость ресурсов - это возможность использования разных видов ресурсов для достижения народно-хозяйственного оптимума. Различают взаимозаменяемость ресурсов техническую и экономическую. Разработаны экономико-математические модели расчетов эффективности взаимной замены ресурсов.
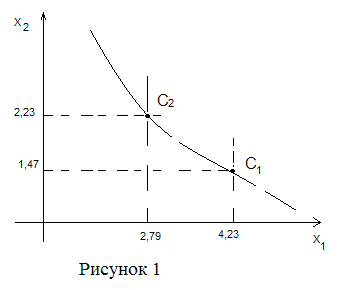
2. Производственная функция для райпо имеет вид f(x1,x2)=10√x1*√x2, где f – товарооборот, млн.руб.; x1 – производственная площадь, тыс.кв. м; x2 – численность работников, сотни чел. Рассмотрите изокванту уровня y0 =√100+β и найдите на ней точку С1 с координатами x1, x2, где x1=(β-100)/100, и точку С2 с координатами x1, x2, где х2=(β-300)/100. Сделайте вывод о возможности замены ресурсов (x1, x2) и (x1, x2). Полученные результаты изобразите графически.
Решение: число β=523, тогда уравнение изокванты 10√x *√x=√523, ( 100+523= 623).
Возводя обе части в квадрат и деля их на 100, получим: х1*х2=6,23.
Найдем координаты точки С1. Так как х1=(523-100)/100=4,23, то из уравнения изокванты находим х2=6,23/4,23=1,47. Аналогично находим координаты точки С2. Так как х2=(523-300)/100=2,23, то х1=6,23/2,23=2,79.
Реклама

Итак, 147 работников райпо, используя 4,23 тыс.кв.метров производственной площади, обеспечат товарооборот √623≈25,0 (млн.руб.), и такой же товарооборот могут обеспечить 223 работника райпо, используя площадь 2,79 тыс.кв. метров (рис.1).
Задание 2. Классификация товаров
1. Дайте понятие малоэластичных, среднеэластичных и высокоэластичных товаров. Какие товары называются взаимозаменяемыми?
Если ценовая эластичность больше единицы, то такой товар принято называть высокоэластичным; если меньше единицы — низкоэластичным; если равен единице — товар с единичной эластичностью.
Если небольшие изменения в цене на товар приводят к значительным изменениям в количестве покупаемой продукции, то такой спрос называют относительно высокоэластичным. Если существенное изменение в цене ведет к небольшому изменению в количестве покупок, то такой спрос - малоэластичный. Когда процентное изменение цены и последующее изменение количества спрашиваемой продукции равны по величине, то такой случай называют среднеэластичностью.
Взаимозаменяемые товары — по определению Закона РФ "О конкуренции и ограничении монополистической деятельности на товарных рынках" от 22 марта 1991 г. "группа товаров, которые могут быть сравнимы по их функциональному назначению, применению, качественным и техническим характеристикам, цене и другим параметрам таким образом, что покупатель действительно заменяет или готов заменить их друг другом в процессе потребления (в том числе производственного)".
При повышении цены на один из таких товаров растет спрос на другой, заменяющий его товар.
2. Произведите классификацию товаров по следующей таблице эластичностей:
| Товар |
Первый |
Второй |
Третий |
| Первый |
β-610/100 |
550,5-β/100 |
570,5-β/100 |
| Второй |
550,5-β/120 |
β-640/100 |
520-β/100 |
| Третий |
570,5-β/120 |
520-β/90 |
680-β/100 |
Пусть β=523. Тогда таблица эластичностей принимает вид:
| Товар |
Первый |
Второй |
Третий |
| Первый |
-0,87 |
0,28 |
0,48 |
| Второй |
0,23 |
-1,17 |
-0,03 |
| Третий |
0,40 |
-0,03 |
-1,57 |
Так как |Е11| =0,87 ‹ 1, то первый товар малоэластичный;
так как |Е22¦ = 1,17 › 1, то второй товар высокоэластичный;
так как |Е33| =1,57 › 1, то третий товар высокоэластичный.
Поскольку Е12 =0,028 › 0 и Е21=0,23 › 0, то первый и второй товары взаимозаменяемые.
Поскольку Е13 =0,48 › 0 и Е31=0,40 › 0, то первый и третий товары взаимозаменяемые.
Поскольку Е23 =-0,03 ‹ 0 и Е32=-0,03 ‹ 0, то второй и третий товары взаимодополняемые.
Задание 3. Межотраслевой баланс
1. Дайте определение коэффициентов прямых затрат. Где они могут быть использованы?
aij = xij / Xj,
где aij — коэффициент прямых затрат продукта i на производство единицы продукта j, xij — общий объём затрат продукта i на производство продукта j, Xj — весь объём производства продукта j. К. п. з. изменяются под влиянием технического прогресса, улучшения организации производства и т. п. и тем самым отражают рост эффективности общественного производства.
Реклама

Коэффициенты прямых затрат aij - это отношение объема продукта i-ой отрасли, используемого за отчетный период j-ой отраслью, к валовому выпуску продукции j-ой отрасли.
Коэффициенты прямых затрат могут использоваться для определения планового производства валовой продукции отраслей.
2. За отчетный период имел место следующий баланс продукции:
x1= x11+ x12+у1
x2= x21+ x22+у2
x11= 800- β;
x12= 700- β
x21= 750- β;
x22= 850- β
у1 =300;
у2 =220
а) Вычислите коэффициенты прямых затрат.
б) Вычислите плановый объем валовой продукции отраслей, если план выпуска конечной продукции y1= 350; y2=250 при условии неизменности технологии производства.
x11=800-523=277
x12=700-523=177
x21=750-523=227
x22=850-523=327
x1=277+177+300=754
x2=227+327+220=774
а) Вычислим коэффициенты прямых затрат:
а11=х11/х1=277/754=0,367
а12=х12/х2=177/774=0,229
а21=х21/х1=227/754=0,301
а22=х22/х2=327/774=0,422
б) Вычислим плановый объем валовой продукции отраслей:
(1-0,367)х1-0,229х2=350 0,633х1-0,229х2=350
-301х1+(1-0,422)х2=250 -0,301х1+0,578х2=250
Выразим из первого уравнения x1:
0,633х1=350+0,229х2
х1=350/0,633+0,229/0,633х2
х1=552,923+0,362х2 –и поставим во второе уравнение
-0,301(552,923+0,362х2)+0,578х2=250
-166,43-0,109х2+0,578х2=250
0,578х2-0,109х2=250+166,43
0,469х2=416,43
х2=416,43/0,469=887,91
х1=552,923+0,362*887,91=552,923+321,423=874,346.
Таким образом, х1=874,346 – плановый объем валовой продукции первой отрасли;
х2=887,91 – плановый объем валовой продукции второй отрасли.
Задание 4. Использование метода теории игр в торговле
1. Объясните смысл элементов платежной таблицы и способы выбора стратегий с позиций крайнего пессимизма, крайнего оптимизма и оптимизма-пессимизма. Рассмотрим проблему уценки неходового товара с целью получения возможно большей выручки от реализации. Предположим, что эластичность спроса в зависимости от цены неизвестна, т.е. неясно, как отреагирует рынок на то или иное снижение цены. Иными словами, нужно принять решение в условиях неопределенности. В таком случае можно использовать методы теории игр. Обозначим А1, А2, …, Аm – стратегии снижения цены на товар на α1%, α2%,…, αm% соответственно. Возьмем достаточно подробный перечень возможных значений эластичности ε1, ε2 ,…, εn. Если выбрать определенную стратегию Аi и знать эластичность товара εj, то, используя еще некоторые, обычно известные величины, можно подсчитать выручку от реализации товара аij. Проделав это для всех Аi и для всех εj, получим платежную таблицу. В таблице представлен подробный перечень различных ситуаций. Для принятия решения можно использовать следующие способы.
Подход с позиции крайнего пессимизма
Он заключается в том, чтобы считать, что при выборе любой стратегии Аi
эластичность товара будет самая неблагоприятная и выручка αi
будет минимально возможной, т.е.
αi
= min (αi1,
αi2,
…,αim
).
Вычислив все величины αi
(α1
, α2
,…,αm
), нужно взять наибольшую из них α: α = max (αi
).
Та стратегия, которая соответствует числу α, и есть стратегия крайнего пессимизма. Иначе говоря, такая стратегия есть наилучший выбор из плохих ситуаций, и эта стратегия гарантирует, что, как бы ни сложилась действительная ситуация, выручка будет не меньше, чем α.
Подход с позиции крайнего оптимизма
Он заключается в том, чтобы считать, что при выборе любой стратегии Аi
эластичность будет наиболее благоприятной и выручка βi
наибольшая, т.е.
βi
= max (αi1,
αi2,
…,αim
).
Вычислив все βi
, нужно взять наибольшую из них: β = max (βi
).
Та стратегия, которая соответствует величине β, и есть искомая.
Подход с позиции пессимизма-оптимизма
Рассмотрим величину H = max [(1-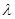 ) )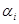 + + 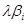 ], где ], где
λ – числовой параметр, 0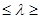 1 1
Предлагается выбирать стратегию, соответствующую величине H.
При λ = 0 Н = max αi
= α, и этот подход превращается в подход с позиции крайнего пессимизма. При λ = 1 Н = max βi
=β , и этот подход превращается в подход с позиции крайнего оптимизма. Вообще, величина Н при изменении λ от 0 до 1 непрерывно изменяется от α до β, и выбор некоторого промежуточного λ соответствует сочетанию пессимизма и оптимизма при выборе стратегии. Возьмем, например, λ=0,5 и вычислим
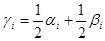 , ,
а затем выберем наибольшее из них
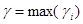
Стратегию, на которой достигается величина γ, будем называть соответствующей подходу с позиции пессимизма-оптимизма.
2. Выберите стратегии с позиций крайнего пессимизма, крайнего оптимизма и оптимизма-пессимизма для следующей платежной таблицы. Укажите соответствующие выигрыши.
| А Е |
Е1 |
Е2 |
Е3 |
| А1 |
β -490 |
β -480 |
620- β |
| А2 |
610- β |
620- β |
630- β |
| А3 |
Ι550-βΙ +10 |
Ι560- βΙ+10 |
640- β |
Для числа β=523 таблица приобретает вид:
| А Е |
Е1 |
Е2 |
Е3 |
| А1 |
33 |
43 |
97 |
| А2 |
87 |
97 |
107 |
| А3 |
37 |
47 |
117 |
Выберем по каждой строке таблицы минимальное из чисел αi, максимальное βi ,а затем вычислим их полусумму γi.
| А Е |
Е1 |
Е2 |
Е3 |
αi |
βi |
γi |
| А1 |
33 |
43 |
97 |
33 |
97 |
65 |
| А2 |
87 |
97 |
107 |
87 |
107 |
97 |
| А3 |
37 |
47 |
117 |
37 |
117 |
77 |
Получим:
α= max (α 1, α 2, α 3,)=(33,87,37)=87;
β= max (β1, β2, β3)=max (97;107;117)=117;
γ= max (γ1, γ2, γ3)=max (65,97,77)=97.
Так как α =87 и это число находится в строке, соответствующей А2, то А2 – стратегия крайнего пессимизма, ожидаемый выигрыш равен 87 единицам. Так как β =117 и это число находится в строке, соответствующей А3, то А3 стратегия крайнего оптимизма, ожидаемый выигрыш равен 117 единицам. Так как γ =97 и это число находится в строке, соответствующей А2, то А2 стратегия оптимизма-пессимизма, ожидаемый выигрыш равен 97 единицам.
Задание 5. Системы массового обслуживания
1. Дайте описание входящего потока требований и каналов обслуживания. Какие экономические показатели характеризуют работу СМО?
Системы массового обслуживания - это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если такое имеется в блоке ожидания. Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.
Обслуживание требований в СМО производится обслуживающими приборами. Классическая СМО содержит от одного до бесконечного числа приборов. Основными элементами СМО являются: входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований Входящий поток требований - совокупность требований, поступающих в СМО. В общем случае под требованием обычно понимают запрос на удовлетворение некоторой потребности. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания. В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также интервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными. Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований, и она показывает, сколько в среднем требований поступает в единицу времени.
Средства, обслуживающие требования, называются обслуживающими устройствами или каналами обслуживания. Одной из важнейших характеристик обслуживающих устройств, которая определяет пропускную способность всей системы, является время обслуживания. Время обслуживания одного требования - случайная величина, которая может изменяться в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований. Интенсивность обслуживания показывает, сколько в среднем требований обслуживается одним каналом в единицу времени.
Экономические показатели, характеризующие работу СМО:
Pk - доля времени работы k каналов, k=0,1,+,n;
L - средняя длина очереди
P0 - вероятность того, что система свободна
П - вероятность образования очереди
Pотк - вероятность отказа в обслуживании
g - относительная пропускная способность
А - абсолютная пропускная способность
nзан - среднее количество занятых каналов
tож - среднее время нахождения в очереди
2. В магазине самообслуживания работают две кассы с интенсивностью µ=(β+300)/100 (треб./мин.) каждая. Входящий поток требований имеет интенсивность λ=(β+400)/100 (треб./мин.). Рассчитай те долю времени простоя касс и среднюю длину очереди. Если интенсивность входящего потока станет равной λ =(700- β)/10 (треб./мин.), то будет ли выполнено условие стационарности? Если будет, то во сколько раз увеличится средняя длина очереди?
Пусть β =523. Тогда µ=8,23 (треб./мин.), а первоначальное значение λ равно 9,23 (треб./мин.)
α = 9,23/8,23=1,122
р0= (2-1,122)/(2+1,122) = 0,878/3,122 = 0,281 (р0 = 28,1%)
L1 = (1,122) /4- (1,122) = 1,412/2,741 = 0,515 (треб.)
Если интенсивность λ станет равной (700-523)/10 = 17,7 (треб./мин.), то в силу неравенства 17,7 › 2·8,23 условие стационарности СМО не будет выполнено.
Задание 6 Оптимальное управление запасами
1. Сформулируйте задачу оптимального управления запасами.
Задача: определить такой объем заказываемой партии товара, при котором затраты на складские операции в единицу времени будут минимальные и темп поступления заказанного товара будет, превышает норму спроса на этот товар.
2. Дайте экономическую интерпретацию предельной арендной платы.
Предельная арендная плата λ экономически интерпретируется как предельная (максимальная) арендная плата за использование дополнительных складских емкостей. Если фактическая арендная плата α 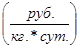 меньше либо равна предельной λ меньше либо равна предельной λ 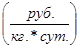 , т.е. α ≤ λ, то аренда выгодна, если же α › λ, то аренда не выгодна. , т.е. α ≤ λ, то аренда выгодна, если же α › λ, то аренда не выгодна.
3. Сделайте вывод о целесообразности аренды дополнительных складских емкостей или о необходимости сокращения объема заказываемой партии товара с учетом имеющихся складских емкостей при сравнении фактической α (руб/кг*сут) и предельной λ (руб/кг*сут) арендной платы за хранение единицы товара в единицу времени.
α = (700 – β) / 4000
λ = (β – 400) / 4000
Решение
α = (700 – 523) / 4000 = 0,044 (руб/кг*сут)
λ = (523– 400) / 4000 = 0,031 (руб/кг*сут)
α › λ
Вывод: фактическая арендная плата больше предельной арендной платы. Следовательно, аренда дополнительных складских емкостей невыгодна, и тогда объем заказываемой партии надо сократить до таких пределов, чтобы возникший товарный запас можно было разместить в имеющихся складских емкостях.
Задание 7. Выборочный метод
1. Дайте понятия генеральной и выборочной совокупностей.
Совокупность генеральная - множество результатов всех возможных наблюдений, которые могли бы быть получены при данном исследовании. При выборочном наблюдении совокупность генеральную называют совокупность (множество) объектов, из которых производится выборка.
Выборочная совокупность - часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение о всей генеральной совокупности.
2. Определите соотношения между доверительными интервалами:
а) при фиксированных значениях среднеквадратического отклонения σ, надежности Р и различных значениях объема выборки
n1=610- β, n2= β -490;
б) при фиксированных значениях среднеквадратического отклонения σ, объема выборки n и различных значениях надежности
р1=800- β /400
р2= β-300/400
в) при фиксированных значениях надежности Р, объема выборки n и различных значениях среднеквадратического отклонения
σ1= (700- β)/100
σ2 = (β – 400)/100
а) n1=610-523=87 ; n2=523-490=33.
Объемы выборок находятся в соотношении n1 >n2 . Тогда из формулы нахождения погрешности следует, что при возрастании объема выборки n значение Δ уменьшается и Δ1< Δ2, т.е. доверительный интервал, соответствующий объему выборки n1=87, будет меньше доверительного интервала, соответствующего объему выборки n2=33.
Задание 8. Корреляционные методы
1. Дайте понятия функциональной и корреляционной зависимостей.
Корреляционная зависимость - это такая связь между результативными и факторными признаками, когда значение результативного признака функции полностью определяется значениями факторных признаков.
Функциональная зависимость - форма устойчивой взаимосвязи между объективными явлениями или отражающими их величинами, при которой изменение одних явлений вызывает определенное количественное изменение (определенным значениям факторных признаков соответствует множество случайных значений результативного признака).
2. Коэффициент корреляции. Его смысл и свойства.
Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными.
Коэффициентом корреляции rхуслучайных величинX и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.
rxy= µxy/σxσy
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойства:
1. Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.
│µxy│≤ √DxDy
2. Абсолютная величина коэффициента корреляции не превышает единицы.
│rxy│≤ 1
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю. Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости. Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.
3. Оцените тесноту связи и направление связи между признаками x и y, если известны: b – коэффициент регрессии, 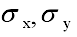 – среднеквадратические отклонения признаков x и y. – среднеквадратические отклонения признаков x и y.
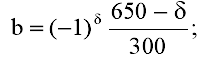 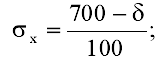 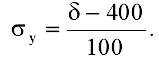
Направление и теснота связи между признаками x и y оцениваются на основе коэффициента корреляции, который рассчитывается по формуле
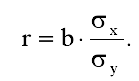
b = (-1) (650-523)/300 = -0,423;
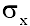 = (700-523)/100 = 1,77; = (700-523)/100 = 1,77;
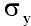 = (523-400)/100 = 1,23; = (523-400)/100 = 1,23;
r = -0,423* 1,77/1,23 = -0,423*1,439 = -0,609;
r = -0,609.
Полученный коэффициент корреляции показывает, что связь между признаками x и y умеренная и обратная, т.е. при возрастании факторного признака x значение результативного признака y уменьшается.
Список используемой литературы
1. Иванилов Ю.П., Лотов А.В. Математические методы в экономике – М.: Наука, 1979.
2. Лопатников Л.И. Экономико-математический словарь. – М.: Наука, 1987.
3. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева. - М.: ЮНИТИ, 2000.
4. Громенко В. В. Математическая экономика: Учебно-практическое пособие, руководство по изучению дисциплины, учебная программа по дисциплине / Московский государственный университет экономики, статистики и информатики. – М.:МЭСИ, 2004. – 100 с.
5. Щедрин И.И., Кархов А.Н. Экономико-математические методы в торговле. – М.: Экономика , 1980.
|