План лекції
з навчальної дисципліни
ФІЗИКА
Тема ЕЛЕКТРОЄМНІСТЬ. КОНДЕНСАТОРИ
ОРГАНІЗАЦІЙНО-МЕТОДИЧНІ ВКАЗІВКИ ДО ПРОВЕДЕННЯ ЛЕКЦІЇ
Звернути увагу, що електроємність провідника вимірюється зарядом, надання якого провіднику змінює його потенціал на одиницю; вказати, що ємність провідника залежить від його форми, лінійних розмірів та діелектричної проникності середовища. Пояснити, що для накопичення значних по величині зарядів на практиці використовуються конденсатори. В залежності від форми конденсатори поділяються на плоскі, циліндричні та сферичні, а по типу діелектриків паперові, слюдяні, керамічні та ін.
1. Вказати на широке застосування в техніці зв’язку. Показати різні типи конденсаторів.
2. Продемонструвати енергію зарядженого конденсатора дослідом з демонстраційним конденсатором, вивести формулу енергії конденсатора.
3. Вивести формулу для об’ємної густини енергії електричного поля конденсатора, пояснити її.
ВСТУП
Електроємністю (ємністю) провідника С називають величину, що дорівнює відношенню заряду Q, наданою провіднику, до його потенціалу j:
Ємність провідника залежить від його форми, лінійних розмірів і діелектричної проникності середовища і не залежить ні від заряду, ні від потенціалу. В СІ одиниця ємності називається фарад ( Ф ).
1мкФ=10-6 Ф (мікрофарад)
1 нФ =10-9Ф (нанофарад)
1 пФ=10-12 Ф (пікофарад)
Ємність кулі, радіус якої r,
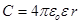
Ємність Землі: 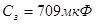 . .
На практиці необхідні пристрої, які при малих розмірах і невеликих відносно навколишніх тіл потенціалах можуть накопичувати значні по величині заряди (мати велику ємність).
Конденсатором називають системи двох або кількох провідників, розділених шаром діелектрика, товщина якого мала порівняно з розмірами провідників (обкладок).
Електроємність 1Ф має такий конденсатор, напруга (різниця потенціалів) між обкладками якого дорівнює 1В при наданні обкладками різнойменних зарядів по 1 Кл.
Конденсатори з’єднуються у батареї паралельно
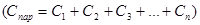 , ,
або послідовно
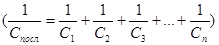 . .
По типу діелектрика, що використовується, конденсатори називаються паперовими, слюдяними, полістирольними, керамічними, повітряними). Паперовий конденсатор виготовляють із двох смуг металевої фольги, ізольованих одна від другої смугами парафінового паперу.
Реклама

Звернуті в рулон смуги фольги й паперу, вміщуються в металевий або фарфоровий корпус.
Через спеціальні ізолятори від смуг фольги двома проводами конденсатор підключається в електричне коло. Аналогічна будова і конденсаторів інших типів. Також використовуються конденсатори змінної ємності.
Конденсатори являються основним елементом коливального контуру, мають широке застосування в техніці зв’язку.
Вони використовуються для згладжування пульсацій в випрямлячах змінного струму для розділу сталої і змінної складової струму, в електричних коливальних контурах радіопередачах і радіоприймачів, для накопичення великих запасів електричної енергії під час проведення фізичних експериментів в галузі лазерної техніки та керованого термоядерного синтезу.
Як і кожен заряджений провідник конденсатор має енергію, яка виражається формулою
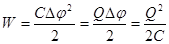 . .
Об’ємна густина енергії електричного поля з напруженістю Е:
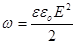 . .
Для однорідного ізотропного діелектрика
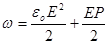 . .
ПРОВІДНИКИ В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ. ЕЛЕКТРОСТАТИЧНИЙ ЗАХИСТ ПРИЛАДІВ
В металевих провідниках існують вільні електрони, які можуть переміщатись під дією надзвичайно малої сили. Тому, якщо провідник внести в електричне поле 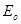 , то ці електрони зразу ж почнуть рухатись протилежно напрямку поля. В результаті на одній поверхні провідника зросте концентрація електронів і вона зарядиться від’ємно, а на протилежній поверхні концентрація електронів зменшиться, заряд додатних іонів буде не скомпенсованим, і вона зарядиться додатньо (Рис. 1 а). , то ці електрони зразу ж почнуть рухатись протилежно напрямку поля. В результаті на одній поверхні провідника зросте концентрація електронів і вона зарядиться від’ємно, а на протилежній поверхні концентрація електронів зменшиться, заряд додатних іонів буде не скомпенсованим, і вона зарядиться додатньо (Рис. 1 а).
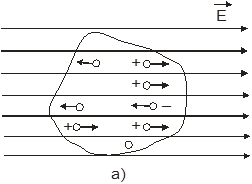 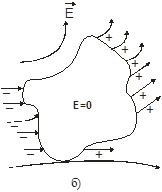
Рис. 1
Розділені заряди створять всередині провідника поле Е, напрямлене протилежно зовнішньому полю. Направлений рух електронів зупиниться тільки тоді, коли поле Е з компенсує в провіднику внутрішнє поле (рис. 1 б).
Таким чином, рівновага зарядів на провіднику може спостерігатись лише при виконанні наступних умов:
1. Напруженість поля всередині провідника повинна бути рівною нулю. Е=0. Це означає, що потенціал всередині провідника повинен бути постійним (j = const).
2. Напруженість поля на поверхні провідника повинна бути в кожній точці напрямлена перпендикулярно до поверхні (в протилежному випадку вільні заряди будуть рухатись в провіднику). Але напруженість поля перпендикулярна еквіпотенціальній поверхні. Значить, у випадку рівноваги зарядів поверхня провідника буде еквіпотенціальною. Наданий провіднику заряд, внаслідок взаємного відштовхування однойменних зарядів, повинен розподілятись по поверхні провідника таким чином, щоб всередині провідника поле задовольняло умови (рис. 2 а).
Реклама

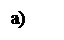 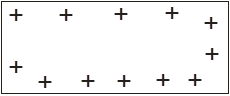 Рис. 2 Рис. 2
Заряди на протилежних кінцях провідника, розміщеного в полі, називають індуцірованим або наведеним. А саме явище розділення зарядів під дією зовнішнього поля називається електростатичною індукцією.
Після видалення провідника з електричного поля заряди знову рівномірно розподіляються по його об’єму. В момент появи і в момент зникнення індукованих зарядів в провіднику існують короткочасні струми.
Як видно з рис. 1 зовнішнє поле під дією індукованих в провіднику зарядів спотворюється. Частина силових ліній розривається провідником так, що воно закінчується на від’ємних зарядах і починаються на додатніх, а силові лінії поза провідником викривляються. Явище електростатичної індукції можна використати для одержання обох видів електрики. Для цього потрібно розрізати провідник в електричному полі по лінії АВ (рис. 2 б).
Заряди розміщаються по поверхні провідника незалежно від того, суцільний він, чи має порожнину.
Дійсно, якщо провести всередині провідника замкнену поверхню якомога ближче до поверхні тіла, то потік вектора зміщення через цю поверхню буде дорівнювати нулю, оскільки рівна нулю напруженість поля. Тоді з теореми Остроградського-Гауса випливає, що заряд всередині замкнутої поверхні (тобто всередині провідника) дорівнює нулю. А це означає, що вилучення частини речовини із внутрішнього об’єму провідника не впливає на рівноважний розподіл заряду в провіднику.
Таким чином, наданий заряд розподіляється по поверхні як в суцільному, так і в провіднику, що має порожнину. Тому всередині провідника, що має порожнину, поле теж дорівнює нулю. Отже провідник, що має порожнину, може бути використаний для захисту приладів від електричного поля. Для того, щоб чутливі прилади і частини різноманітних пристосувань захистити від електричного поля, їх поміщають в замкнений металевий екран, з’єднаний з землею. Потенціал екрана відносно землі буде дорівнювати нулю, а всередині нього поля не буде. Такий захист приладів називається екранізацією. Практично для екранізації достатньо густої металевої сітки, яка являється ефективною не лише для постійних, а й для змінних електричних полів.
ЕЛЕКТРОЄМНІСТЬ. КОНДЕНСАТОРИ
Для відокремленого провідника можна записати Q = Cj. Величину
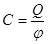
називають електроємністю (або просто ємністю) відокремленого провідника. Ємність відокремленого провідника визначається зарядом, надання якого провіднику підвищує його потенціал на одиницю
Для того, щоб провідник мав велику ємність, він повинен мати дуже великі розміри. На практиці, одначе, необхідні пристрої, які при малих розмірах і невеликих відносно навколишніх тіл потенціалах можуть накопичувати значні по величині заряди, другими словами можуть мати велику ємність. Ці пристрої одержали назву конденсаторів.
Конденсатор складається з двох провідників (обкладок), розділених діелектриком. В залежності від форми обкладок конденсатори поділяються на плоскі, циліндричні та сферичні.
Так як поле зосереджено всередині конденсатора, то лінії напруженості починаються на одній обкладці і закінчуються на другій, тому вільні заряди, які виникають на різних обкладках, являються рівними по модулю різнойменними зарядами. Під ємністю конденсатора розуміється фізична величина, рівна відношенню заряду Q, накопиченого на конденсаторі, до різниці потенціалів 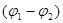 між його обкладинками: між його обкладинками:
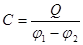 . .
Розрахуємо ємність плоского конденсатора, який складається з двох паралельних металевих пластин площею 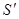 кожна, розміщених на відстані d одна від другої і несучих заряди +Q та -Q. Якщо відстань між пластинами мала в порівнянні з їх лінійними розмірами, то крайовими ефектами можна знехтувати і поле між обкладинками вважати однорідним. Його можна визначити, користуючись формулами: кожна, розміщених на відстані d одна від другої і несучих заряди +Q та -Q. Якщо відстань між пластинами мала в порівнянні з їх лінійними розмірами, то крайовими ефектами можна знехтувати і поле між обкладинками вважати однорідним. Його можна визначити, користуючись формулами:
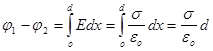 і і 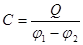
При наявності діелектрика між обкладинками різниця потенціалів між ними, згідно
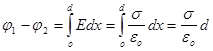
буде
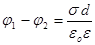 , ,
де e - діелектрична проникність середовища, яке знаходиться між обкладинками.
Тоді з формули
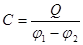
Заміняючи Q = s S, одержуємо, з урахуванням
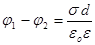
вираз для ємності плоского конденсатора
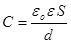 . .
Для визначення ємності циліндричного конденсатора, що складається з двох порожнистих коаксіальних циліндрів з радіусами 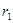 і і 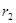 ( (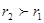 ), вставлених один в другий, знову нехтуючи крайовими ефектами, вважаємо поле радіально-симетричним і зосередженим між циліндричними обкладинками. ), вставлених один в другий, знову нехтуючи крайовими ефектами, вважаємо поле радіально-симетричним і зосередженим між циліндричними обкладинками.
Різницю потенціалів між обкладинками розраховуємо по формулі
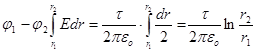
для поля рівномірно зарядженого нескінченого циліндра з лінійною густиною
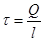
(l - довжина обкладок ).
З урахуванням наявності діелектрика між обкладинками:
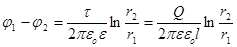
З урахуванням формули
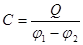 , ,
одержимо формулу для ємності циліндричного конденсатора:
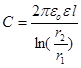 . .
Конденсатори характеризуються пробивною напругою – різницею потенціалів між обкладинками конденсатора, при якій відбувається пробій – електричний розряд через шар діелектрика в конденсаторі. Пробивна напруга залежить від форми обкладинок, властивостей діелектрика та його товщини.
ЕНЕРГІЯ ЗАРЯДЖЕНОГО КОНДЕНСАТОРА
Якщо підключити лампу до зарядженого конденсатора, то спостерігається короткочасний спалах світла. Це означає, що заряджений конденсатор має енергію.
Виведемо формулу потенціальної енергії конденсатора, користуючись такими міркуваннями.
Процес виникнення на обкладках конденсатора зарядів +Q і -Q можна уявити так, що від одної обкладинки послідовно віднімаються дуже малі порції заряду DQ і переміщуються на другу обкладинку. Робота переміщення чергової порції заряду дорівнює
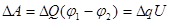
( U - напруга на конденсаторі).
Замінюючи U на 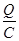 і, переходячи до диференціалів, маємо і, переходячи до диференціалів, маємо
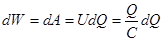 . .
Після інтегрування одержимо формулу зарядженого конденсатора:
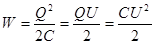 . .
Або для різниці потенціалів між обкладинками конденсатора:
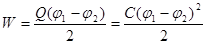 , ,
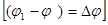
Користуючись виразом для енергії, можна знайти механічну (пондеромоторну) силу, з якою пластини конденсатора притягаються одна до другої. Для цього припустимо, що відстань x між пластинами змінюється, наприклад, на величину dx. Тоді діюча сила виконує роботу dA = Fdx.
За рахунок зменшення потенціальної енергії системи
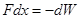
або
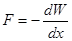
Підставивши в формулу для енергії вираз
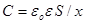 . .
Одержимо
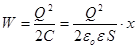
Виконуючи диференціювання при конкретному значенні енергії знайдемо кондемоторну силу:
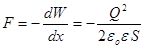 , ,
де знак мінус показує, що сила F намагається зменшити x, тобто являється силою притягання.
ГУСТИНА ЕНЕРГІЇ ЕЛЕКТРИЧНОГО ПОЛЯ
Перетворюємо формулу
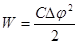 , ,
яка виражає енергію плоского конденсатора з допомогою зарядів та потенціалів, скористувавшись виразами для ємності конденсатора
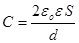
і різниці потенціалів між його обкладинками (Dj = Ed). Тоді одержимо:
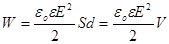 , ,
де V = Sd - об’єм конденсатора.
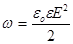
об’ємна густина енергії електричного поля конденсатора.
Для ізотропного діелектрика
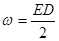 , ,
де D - електричне зміщення; або
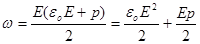 , ,
де p- вектор поляризації, перший додаток у цьому виразі співпадає з густиною енергії поля в вакуумі. А другий додаток являє собою енергію, яка витрачається на поляризацію діелектрика.
Енергія конденсатора виражається через величину, що характеризує електростатичне поле – через напруженість Е. Це показує, що електростатичне поле має енергію.
Відповідь на запитання, яке з двох уявлень про локалізацію електростатичної енергії переважає і являється її носієм – заряди чи поле – може дати лише дослід. Електростатика вивчає постійні в часі поля нерухомих зарядів, тобто в ній поля і виражаючи їх заряди невіддільні одне від другого. Тому електростатика відповісти на поставлені запитання не зможе. Дальніший розвиток теорії і експерименту показує, що змінні поля можуть існувати відокремлено, незалежно від збудивших їх зарядів, і розповсюджуючись в просторі в вигляді електромагнітних хвиль, здатні переносити енергію. Це переконливо підтверджує основні положення теорії близькодії про локалізацію енергії в полі і то, що носієм енергії являється поле.
ВИСНОВКИ
Куля радіусом r має електроємність
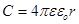 . .
Для того, щоб провідник мав велику ємність, він повинен мати дуже великі розміри.
На практиці використовуються конденсатори. Електроємність плоского конденсатора:
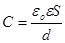
для циліндричного – електроємність має вираз:
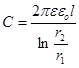 . .
Являючись основним елементом коливального контуру, конденсатори мають широке застосування в техніці зв’язку.
Заряджений конденсатор має енергію:
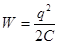 або або 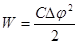 . .
Об’ємна густина енергії електричного поля конденсатора:
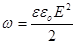 , ,
для ізотропного діелектрика:
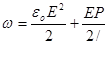 . .
Поле являється носієм енергії.
НАВЧАЛЬНА ЛІТЕРАТУРА
1. Гусева Г.Б. Курс физики. §30 - 32
2. Савельев И.В. Курс физики, т.1, Курс общей физики.-М.: 1989. § 9-12
3. Трофимова Т.И. Курс физики,-М.: Высшая школа, 1985, 432 с. § 83, 86
План лекції
з навчальної дисципліни
ФІЗИКА
Тема ЗАКОНИ ПОСТІЙНОГО СТРУМУ
ОРГАНІЗАЦІЙНО-МЕТОДИЧНІ ВКАЗІВКИ ДО ПРОВЕДЕННЯ ЛЕКЦІЇ
При вивченні постійного електричного струму, необхідно враховувати, що основні поняття постійного струму курсантам відомі із курсу фізики середньої школи. Тому необхідно особливу увагу звернути на основні характеристики постійного струму , одиниці їх вимірювання, а також на нові поняття : закон Ома в диференціальній формі та на узагальнений закон Ома. Необхідно пам’ятати , що матеріал лекції має дуже важливе значення для вивчення спеціальних /ТЕРЦ/ та воєнно-спеціальних дисциплін.
ВСТУП
Протягом віків наука і техніка та їх розвиток були тісно пов’язані з вченням про електрику. Це вивчення є основою науково-технічного прогресу. Заряд електрона є найменшою частинкою електрики в природі, а заряд ядра завжди кратний заряду електрона.
Заряджені частинки, як і самі атоми та молекули, знаходяться в безперервному русі і взаємодіють між собою. Причому, цей рух не впорядкований. Якщо ж виникає впорядкований рух зарядів – виникає електричний струм. На лекції будуть розглянуті основні характеристики та закони електричного струму, які мають важливе практичне значення і, звичайно, вони широко використовуються в військовій техніці зв’язку.
ОСНОВНІ ХАРАКТЕРИСТИКИ ПОСТІЙНОГО ЕЛЕКТРИЧНОГО СТРУМУ
В електростатиці вивчалась взаємодія нерухомих зарядів і поле цих зарядів – електростатичне поле. При рухові зарядів виникають інші явища, виникає електричний струм. Електричним струмом називають упорядкований рух електричних зарядів. В металах електричний струм являє собою упорядкований рух електронів проти електричного поля, в електролітах – іонів різних знаків у протилежних напрямках, у газах - електронів та іонів і ін. Такий струм називають струмом провідності. Якщо ж рух зарядів відбувається разом з тілом. На якому вони знаходяться, то такий струм називають конвекційним . Наприклад, конвекційний струм виникає при падінні заряджених краплин води в атмосфері під дією сили тяжіння. Рух заряджених мікроскопічних частинок під впливом електричного поля в вакуумі називають струмом в вакуумі.
За напрям електричного струму умовились вважати напрям руху позитивних зарядів. Якщо струм створюється негативно зарядженими частинками, то напрям струму вважають протилежним до напряму руху цих частинок. Кількісними характеристиками електричного струму є скалярна величина – сила струму I та векторна величина – густина струму 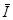 . .
Силою струму називають фізичну величину, яка чисельно дорівнює заряду, що проходить через поперечний переріз провідника за одиницю часу.
Якщо за нескінченно малий проміжок часу dt через поперечний переріз провідника проходить заряд dq, то сила струму
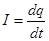 / /1/ / /1/
Формула /1/ виражає миттєве значення струму. Якщо сила струму і його напрям з часом не змінюється, то такий струм називають постійним. Сила постійного струму :
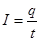 /2/, /2/,
Де q– заряд, який проходить через поперечний переріз провідника за час t.
Сила струму в СІ вимірюється в амперах, причому ампер є основною одиницею в СІ. На практиці використовуються одиниці: 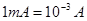 ; ; 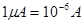 ; ; 
Якщо струм створюється позитивними і негативними зарядами, то сила струму дорівнює арифметичній сумі струмів, створених цими зарядами.
Оскільки електричний струм може бути розподілений по перерізу провідника нерівномірно, то для характеристики розподілу електричного струму по перерізу провідника вводять поняття густини струму.
Вектором густини струму I називають вектор чисельно рівний силі струму . що проходить через одиничну, перпендикулярну до струму . площину і направлений в напрямку струму:
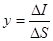 /3/ /3/
Якщо струм розподілений рівномірно по перерізу провідника, тоді :
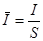 /4/ /4/
В СІ густина струму вимірюється в 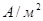 , на практиці – А/мм. , на практиці – А/мм.
Виділяємо в провіднику площину перерізу DS, перпендикулярну до швидкості напрямленого руху зарядів u /рис.1/.
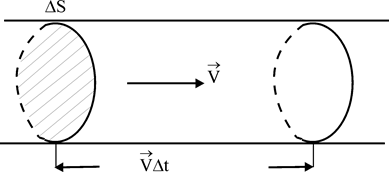
Рис.1
Через цю площину за час t пройдуть ті електрони провідника , які знаходяться в циліндрі , об’ємом V = DS×u×t. Якщо концентрація (число зарядів в одиниці об’єму) зарядів n, то число зарядів
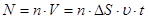 , ,
а заряд , перенесений через поперечний переріз :
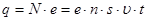 , ,
де е – заряд електрону.
Отже
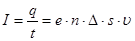 , ,
а густина струму:
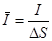 ; ; 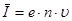 /5/. /5/.
Із формули /5/ можна знайти швидкість упорядкованого руху електронів у провіднику.
Знаючи густину струму, повний струм вираховується за формулою :
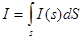 . .
РІЗНИЦЯ ПОТЕНЦІАЛІВ, ЕРС ТА НАПРУГА В КОЛІ ПОСТІЙНОГО СТРУМУ
Струм в провіднику може існувати тільки тоді, коли на його кінцях існує різниця потенціалів. Нехай на кінцях А провідника потенціал 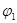 , а на кінці В - , а на кінці В - 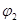 , причому , причому 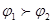 (рис. 2) (рис. 2)
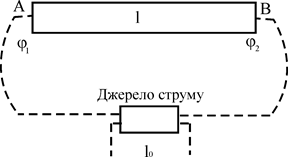
Рис. 2
Тоді між кінцями провідника існує різниця потенціалів
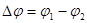
і напруженість електричного поля
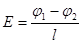 . .
Під впливом цього поля позитивні заряди будуть рухатись від А до В і по провіднику потече струм. Але, внаслідок руху позитивних зарядів потенціал 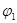 буде зменшуватись , а потенціал буде зменшуватись , а потенціал 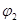 - збільшуватись і - збільшуватись і 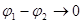 
Струм практично миттєво припиниться.
Отже, якщо створити електричне поле за допомогою зарядів, то постійний струм в ньому неможливий – необхідно на кінцях провідника підтримувати постійну різницю потенціалів;
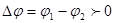 . .
Для цього необхідно безперервно розділяти заряди протилежного знака і переносити позитивні заряди від кінця В до кінця А. Такий розділ зарядів можливий тільки силами сторонніми /хімічними, механічними, магнітними та ін./
Отже, необхідною умовою існування постійного струму є те, що у замкнутому колі повинен бути пристрій, здатний створювати і підтримувати різницю потенціалів за рахунок роботи сил неелектричної природи – сторонніх сил. Такі пристрої називають джерелами електричного струму (рис.2).
Джерело струму виконує роботу по переміщенню зарядів :
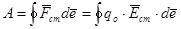 . .
Величину, яка чисельно рівна роботі сторонніх сил по переміщенню одиничного позитивного заряду вздовж контуру, називають електрорушійною силою e. Отже,
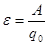 ; ; 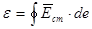 (В) /6/, (В) /6/,
де 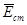 - напруженість електричного поля сторонніх сил, яка практично існує тільки на ділянці l0 джерела струму (рис.2).Тому: - напруженість електричного поля сторонніх сил, яка практично існує тільки на ділянці l0 джерела струму (рис.2).Тому:
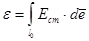 . .
Джерело постійного струму позначається так :
Ділянка електричного кола, в якій включено джерело струму, називається неоднорідною. Розглянемо таку ділянку (рис.3):
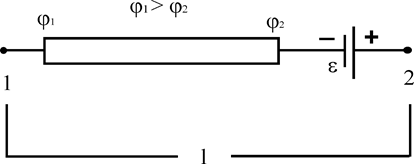
Рис.3
Робота по переміщенню заряду q0 буде дорівнювати :
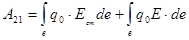 , ,
де Е – напруженість електростатичного (нуклонівського ) поля, а 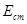 - поля сторонніх сил. - поля сторонніх сил.
Величина, чисельно рівна роботі нуклонівських і сторонніх сил по переміщенню одиничного позитивного заряду на ділянці кола , називається напругою на ділянці кола U.
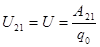 ; ; 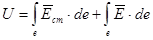 , ,
але
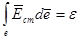 , , 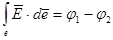 . .
Отже :
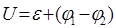 /7/. /7/.
Якщо ділянка кола однорідна, то 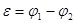 , тобто напруга на однорідній ділянці кола дорівнює різниці потенціалів. , тобто напруга на однорідній ділянці кола дорівнює різниці потенціалів.
ЗАКОН ОМА В ІНТЕГРАЛЬНІЙ ТА ДИФЕРЕНЦІАЛЬНІЙ ФОРМІ
Вивчаючи залежність між струмом і напругою для однорідної ділянки кола , німецький учений Ом в 1826 р. Встановив закон:
Сила струму на ділянці кола прямо пропорційна прикладеній напрузі і обернено пропорційна опору ділянки кола:
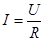 , /8/ , /8/
де R- опір провідника. Якщо провідник однорідний і має циліндричну форму, то
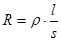 , /9/ , /9/
де l- довжина провідника, S- площа поперечного перерізу, r - питомий опір матеріала провідника . В СІ опір вимірюється в омах ( кілоомах-кОм, мегаомах – МгОм).
В електротехніці замість опору використовують провідність
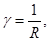
та питому провідність
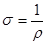 . .
Провідність в СІ вимірюється в сименсах (См). В радіотехніці деталі, які мають опір R ,називають резистором і схематично позначають так :
Формула (8) виражає запис закону Ома в інтегральній формі. Для одержання закону Ома в диференціальній формі підставимо в (8) значення R (9):
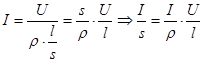
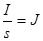 ; ; 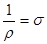 ; ; 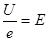
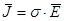 /10/ /10/
Це і є закон Ома в диференціальній формі: густина струму дорівнює добутку питомої провідності на напруженість електричного поля.
РОБОТА І ПОТУЖНІСТЬ ПОСТІЙНОГО СТРУМУ. ЗАКОН ДЖОУЛЯ-ЛЕНЦА
Якщо на ділянці провідника опором R, на кінцях якої напруга U, проходить струм I, то через його поперечний переріз за час dt буде перенесено електричний заряд dq = I×dt. Але при переміщенні заряду сили поля виконують роботу
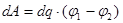 , ,
Або
dA = dq×U.
Отже:
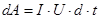 . /11/ . /11/
У випадку постійного струму :
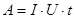 /12/ /12/
На основі закону Ома можна записати :
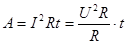 /13/ /13/
Якщо струм змінюється з часом :
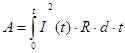
Важливою енергетичною характеристикою електричного струму є потужність Р (N). Потужність постійного струму чисельно дорівнює роботі струму за одиницю часу.
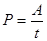 ; ; 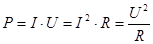 /14/ /14/
Оскільки ЕРС джерела струму дорівнює роботі, що виконується джерелом при перенесенні одиниці заряду по всьому колу, то при постійному струмі I за час t виконується робота
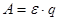 ; ; 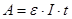 /15/, /15/,
А потужність джерела струму :
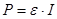 /16/ /16/
Потужність споживачів називають корисною :
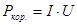 . .
Відношення корисної потужності до загальної потужності джерела струму визначає ККД джерела струму:
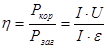 ; ; 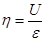 /17/ /17/
При проходженні струму по нерухомому провіднику впорядкований рух зарядів буде непрямолінійний - заряди взаємодіють з частинками провідника і віддають їм частину своєї енергії. Тому внутрішня енергія провідника буде збільшуватись, провідник нагріватиметься.
Вивчаючи теплову дію струму, англійський вчений Д.Джоуль і російський Е.Ленц відкрили закон, який формулюється так
Кількість теплоти Q, що виділяється в провіднику при проходженні в ньому постійного струму, прямо пропорційна квадрату сили струму , опору провідника R і часу проходження струму, тобто:
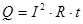 /18/ /18/
Закон Джоуля-Ленца випливає із закону збереження енергії :

В СІ робота постійного струму, теплота вимірюється в джоулях, а потужність в ватах. На практиці використовують позасистемну одиницю роботи та енергії струму: 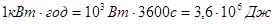
УЗАГАЛЬНЕНИЙ ЗАКОН ОМА. НАПРУГА НА КЛЕМАХ ДЖЕРЕЛА СТРУМУ
Розглянемо закон Ома для неоднорідної ділянки кола, тобто такої ділянки, в якій діє ЕРС джерела струму (рис.4)

Рис.4
ЕРС на ділянці 1-2 позначимо через 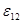 , а прикладену на кінцях ділянки кола різницю потенціалів через , а прикладену на кінцях ділянки кола різницю потенціалів через 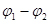 . .
Якщо струм проходить по нерухомим провідникам ділянки кола 1-2, то на основі закону збереження і перетворення енергії робота всіх сил (сторонніх і електростатичних) 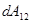 дорівнює теплоті dQ, що виділяється на цій ділянці кола. Згідно (12) і (13) : дорівнює теплоті dQ, що виділяється на цій ділянці кола. Згідно (12) і (13) :
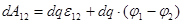
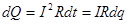 . .
Оскільки
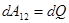 , ,
то
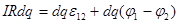 . .
Звідки :
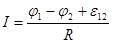 /19/ /19/
Це і є закон Ома для неоднорідної ділянки кола, або узагальнений закон Ома.
ЕРС 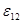 , як і сила струму I – величина скалярна , її необхідно брати з додатнім, або з від’ємним знаком – в залежності від знаку роботи, здійснюваної сторонніми силами. Якщо ЕРС сприяє руху позитивних зарядів в вибраному напрямку (1-2), то , як і сила струму I – величина скалярна , її необхідно брати з додатнім, або з від’ємним знаком – в залежності від знаку роботи, здійснюваної сторонніми силами. Якщо ЕРС сприяє руху позитивних зарядів в вибраному напрямку (1-2), то 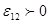 . Якщо ж ЕРС перешкоджає руху позитивних зарядів, то . Якщо ж ЕРС перешкоджає руху позитивних зарядів, то 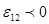 . .
При відсутності на ділянці кола джерела струму 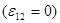 із (19) одержимо закон Ома для однорідної ділянки кола : із (19) одержимо закон Ома для однорідної ділянки кола :
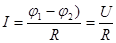 . .
Якщо ж електричне коло замкнуте, то 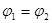 . Тоді із (19) одержимо закон Ома для замкнутого кола : . Тоді із (19) одержимо закон Ома для замкнутого кола :
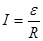 , ,
а
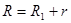
загальний опір кола, де r – внутрішній опір джерела струму, а R1-опір навантаження (зовнішній опір).
Таким чином: сила струму в замкнутому колі прямо пропорційна ЕРС джерела струму і обернено пропорційна повному опору кола:
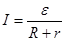 /20/ /20/
Якщо коло розімкнене, то I=0 і з закону Ома (18) одержимо, що
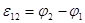
тобто ЕРС дорівнює різниці потенціалів на клемах джерела струму. Таким чином, щоб найти ЕРС джерела струму, треба виміряти різницю потенціалів на його клемах, при розімкненому зовнішньому колі.
Коли ж коло замкнене, то із закону Ома для замкненого кола (20):
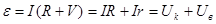 . .
Звідки:
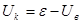 . .
Отже: напруга на клемах джерела струму завжди менша ЕРС на величину напруги на внутрішньому опорові джерела струму Uв.
ВИСНОВКИ
1.Електричний струм виникає тільки при упорядкованому русі електричних зарядів і характеризується силою та густиною струму. Постійний електричний струм може існувати лише при наявності в провідниках вільних зарядів, при наявності джерела струму з ЕРС і коли електричне коло замкнуте. Причому, напруга на кінцях неоднорідного провідника дорівнює сумі ЕРС джерела струму та різниці потенціалів.
2. Залежність між струмом та напругою на кінцях провідника визначається законом Ома для ділянки кола та узагальненим законом Ома для неоднорідної ділянки кола. Велике практичне значення для розрахунків має закон Ома для замкнутого кола. З цього закону випливає, що завжди напруга на клемах джерела струму при замкнутому колі менша ніж ЕРС.
3. Робота, потужність струму та теплота, що виділяється при його проходженні по провіднику , прямо пропорційні квадрату струму або напрузі і часові проходження струму. Вони також залежать від опору ділянки кола. Як робота, так і теплова дія струму широко використовується на практиці, в т.ч. в техніці зв’язку.
НАВЧАЛЬНА ЛІТЕРАТУРА
1. Гусева Г.Б. Курс физики. §42-44
2. Савельев И.В. Курс физики, т.2, Курс общей физики.-М.: 1989. § 31-353.
3. Трофимова Т.И. Курс физики,-М.: Высшая школа, 1985, 432 с. § 96-99.
|