| Задача 1.
Решить задачу линейного программирования симплексным методом.
Вариант 2.
Найти наибольшее значение функции f(X) = x1
– 4x4
при ограничениях
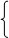 x1
– x2
+ x3
+ x4
= 3 x1
– x2
+ x3
+ x4
= 3
x1
+ x2
+ 2x3
= 5,
xj
³ 0, j = 1, 2, 3, 4.
Решение.
Задача записана в каноническом виде, но не имеет необходимого числа единичных столбцов, т. е. не обладает очевидным начальным опорным решением.
Для нахождения опорного плана переходим к М-задаче:
f(X) = x1
– 4x4
– Мy1
® max
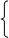 x1
– x2
+ x3
+ x4
= 3 x1
– x2
+ x3
+ x4
= 3
x1
+ x2
+ 2x3
+ y1
= 5,
xj
³ 0, j = 1, 2, 3, 4; y1
³ 0.
Очевидное начальное опорное решение (0; 0; 0; 3; 5).
Решение осуществляется симплекс-методом с искусственным базисом.
Расчеты оформим в симплекс-таблицах
| Номер симплекс-таблицы
|
Базис
|
Cj
Ci
|
B
|
1
|
0
|
0
|
-4
|
-M
|
Q
|
| A1
|
A2
|
A3
|
A4
|
P1
|
| 0
|
A4
|
-4
|
3
|
1
|
-1
|
1
|
1
|
0
|
3:1 = 3
|
| P1
|
-M
|
5
|
1
|
1
|
2
|
0
|
1
|
5:2 = 2,5
|
| j
|
-
|
-5M-12
|
-M-5
|
-M+4
|
-2M-4
|
0
|
0
|
| 1
|
A4
|
-4
|
1/2
|
1/2
|
-3/2
|
0
|
1
|
1/2:1/2=1
|
| A3
|
0
|
5/2
|
1/2
|
1/2
|
1
|
0
|
5/2:1/2=1
|
| j
|
-
|
-2
|
-3
|
6
|
0
|
0
|
| 2
|
A1
|
1
|
1
|
1
|
-3
|
0
|
2
|
| A3
|
0
|
2
|
0
|
2
|
1
|
-1
|
2:2=1
|
| j
|
-
|
1
|
0
|
-3
|
0
|
6
|
| 3
|
A1
|
1
|
4
|
1
|
0
|
3/2
|
1/2
|
| A2
|
0
|
1
|
0
|
1
|
1/2
|
-1/2
|
| j
|
-
|
4
|
0
|
0
|
3/2
|
9/2
|
Начальное опорное решение (0; 0; 0; 3; 5), соответствующее симплекс-таблице 0, неоптимальное, так как в D - строке есть отрицательные значения, наименьшее в столбце А3
. Этот столбец будет направляющим. Минимальное положительное оценочное отношение Q в строке P1
, эта строка направляющая. Направляющий элемент на пересечении направляющих строки и столбца. Столбец P1
выводим из базиса, а А3
- вводим в базис.
При пересчете таблицы столбец Р1
далее можно не рассчитывать.
После пересчета получаем симплекс-таблицу 1. Соответствующее опорное решение (0; 0; 5/2; 1/2; 0) не оптимально, так как в D - строке есть отрицательные значения, в столбце А1
.Этот столбец будет направляющим. Минимальное положительное оценочное отношение Q в строке А4
. В качестве направляющей строки возьмем А4
. Направляющий элемент на пересечении направляющих строки и столбца. Столбец А4
выводим из базиса, а А1
- вводим в базис.
После пересчета получаем симплекс-таблицу 2. Опорное решение, соответствующее симплекс-таблице 2 (1; 0; 2; 0; 0) – не оптимально, так как в D - строке есть отрицательные значения, в столбце А2
. Этот столбец будет направляющим. Минимальное положительное оценочное отношение Q в строке А3
. В качестве направляющей строки возьмем А3
. Направляющий элемент на пересечении направляющих строки и столбца. Столбец А3
выводим из базиса, а А2
- вводим в базис.
Реклама

После пересчета получаем симплекс-таблицу 3. Опорное решение, соответствующее симплекс-таблице 3 (4; 1; 0; 0; 0) – оптимально, так как в D - строке нет отрицательных значений.
Отбрасывая значения переменной y1
, получаем оптимальное решение исходной задачи:
х1
= 4, х2
= 1; х3
= 0; х4
= 0; fmax
= 1×4 + 0×1 + 0×0 – 4×0 = 4.
Задача 2.
Задание 1. Сформулировать экономико-математическую модель исходной экономической задачи.
Задание 2. Решить полученную задачу линейного программирования графическим методом.
Задание 3. Сформулировать двойственную задачу и найти ее оптимальное решение, используя теоремы двойственности.
Вариант 2.
Предприятие производит полки для ванных комнат двух размеров А и Б. Служба маркетинга определили, что на рынке может быть реализовано до 550 полок в неделю, а объем поставляемого на предприятие материала, из которого делаются полки, равен 1200 м2
в неделю. Для каждой полки типов А и Б требуется 2 м2
и 3 м2
материала соответственно, а затраты станочного времени на обработку одной полки типа А и Б составляют соответственно 12 и 30 минут. Общий недельный объем станочного времени равен 160 часов, а прибыль от продажи каждой полки типа А и Б составляет 3 и 4 ден. единиц соответственно. Определить, сколько полок каждого типа следует выпускать в неделю для получения наибольшей прибыли.
Решение.
Задание 1.
Обозначим x1
и x2
количество полок типа А и Б, соответственно (план выпуска). Очевидно, x1
, x2
³ 0 и целые.
Так как объем реализации в неделю составляет до 550 полок, то x1
+ x2
£ 550.
Расход материала составит 2x1
+ 3x2
м2
, эта величина не должна превышать запаса материала 1200 м2
. Следовательно, должно выполняться неравенство 2x1
+ 3x2
£ 1200.
Затраты станочного времени составят 0,2x1
+ 0,5x2
час. и не могут быть больше недельного объема 160 час. Следовательно, должно выполняться неравенство 0,2x1
+ 0,5x2
£ 160. Чтобы не было дробей, умножим его на 10 и получим 2x1
+ 5x2
£ 1600.
Прибыль от реализации полок составит f(X) = 3x1
+ 4x2
ден. единиц, и она должна быть наибольшей
Получаем экономико-математическую модель задачи:
Реклама

Найти максимум функции f(X) при заданных ограничениях
f(X) = 3x1
+ 4x2
® max
x1
+ x2
£ 550
2x1
+ 3x2
£ 1200
2x1
+ 5x2
£ 1600
x1
, x2
³ 0, целые.
Задание 2.
Решаем задачу без условия целочисленности решения. Построим множество допустимых решений задачи.
Прямые ограничения x1,2
³ 0 выделяют первую четверть плоскости.
Проведем прямую x1
+ x2
= 550 через точки (0; 550) и (550; 0). Подставим в первое неравенство координаты точки (0; 0): 1×0 +1×0 = 0 < 550, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.
Проведем прямую 2x1
+ 3x2
= 1200 через точки (0; 400) и (600; 0). Подставим в первое неравенство координаты точки (0; 0): 2×0 + 3×0 = 0 < 1200, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.
Проведем прямую 2x1
+ 5x2
= 1600 через точки (0; 320) и (800; 0). Подставим в первое неравенство координаты точки (0; 0): 2×0 + 5×0 = 0 < 1600, так как неравенство выполняется, то выбираем полуплоскость, содержащую эту точку.
Множество допустимых решений – это многоугольник ABCDO.
Построим линию уровня целевой функции f(X) = 3x1
+ 4x2
3x1
+ 4x2
= 0 через точки (200; -150 ) и (-200; 150).
Вектор-градиент {3; 4} задает направление, перемещаясь вдоль которого, можно увеличить значение целевой функции; перемещаясь в противоположном направлении, можно уменьшить ее значение. На чертеже построен вектор, пропорциональный градиенту (60; 80), так как сам градиент имеет малый масштаб на чертеже.
Из чертежа видно, что наибольшее значение целевой функции будет на линии уровня, проходящей через точку С, являющейся пересечением прямых (1) и (2).
Координаты этой точки найдем из системы
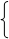 x1
+ x2
= 550, x1
+ x2
= 550,
2x1
+ 3x2
= 1200.
Первое уравнение умножим на 2 и вычтем из второго, получаем x2
= 100 и x1
= 450
fmах
= 3 ×450 + 4 ×100 = 1750 ден. единиц.
Полученное оптимальное решение оказалось целым, следовательно, это решение поставленной задачи. Получили: в оптимальном плане выпуска следует произвести полок типа А 450 шт., а полок типа Б – 100 шт.При этом прибыль от реализации составит 1750 ден. единиц и будет наибольшей.
Задание 3.
Двойственная задача.
Найти минимум функции g(Y) при ограничениях:
g(Y) = 550y1
+ 1200y2
+ 1600y3
® min
y1
+ 2y2
+ 2y3
³ 3
y1
+ 3y2
+ 5y3
³ 4
y1,2,3
³ 0.
Оптимальное решение прямой задачи Х = (450; 100). Подставим его в ограничения этой задачи
1×450 + 1×100 = 550
2×450 + 3×100 = 1200
2×450 + 5×100 = 1400 < 1600
Условия дополняющей нежесткости (вторая теорема двойственности): для оптимальных планов двойственных задач имеют место соотношения:
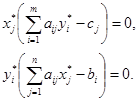
Так как для оптимального решения прямой задачи треть ограничение выполняется как неравенство, то в оптимальном решении двойственной задачи y3
= 0.
Так как для оптимального решения прямой задачи х1
> 0и х2
> 0, то оба ограничения двойственной задачи выполняются как равенство. Для нахождения решения двойственной задачи получаем систему
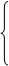 y3
= 0 y3
= 0
y1
+ 2y2
+ 2y3
= 3
y1
+ 3y2
+ 5y3
= 4
Получаем решение: y1
=, y2
= 1, y3
= 0.
Найдем значение целевой функции двойственной задачи:
g(Y) = 550×1 + 1200×1 + 1600×0 = 1750.
Получили gmin
= fmax
= 1750 ден. единиц.
Так как значения прямой и двойственной функций равны, то Y = (1; 1; 0) является оптимальным решением двойственной задачи (по первой теореме двойственности).
Задача 3.
Задание 1. Записать исходные данные задачи в виде транспортной таблицы, определить, открытой или закрытой является транспортная задача.
Задание 2. Сформулировать экономико-математическую модель исходной транспортной задачи.
Задание 3. Найти оптимальный план перевозок, отметив при этом единственность или неединственность оптимального плана.
Вариант 3.
На складах A, B, C, Д находится соответственно 50 т, 40 т, 40 т и 70 т муки, которую нужно доставить четырем хлебозаводам. Первому хлебозаводу требуется 50 т муки, второму – 40 т, третьему – 50 т и четвертому – 60 т муки. Стоимость доставки одной тонны муки со склада А каждому хлебозаводу соответственно равны 8, 3, 5 и 2 ден. единиц, со склада В – 7, 4, 9 и 8 ден. единиц, со склада С – 6, 3, 3 и 1 ден. единиц, со склада Д – 2, 4, 1 и 5 ден. единиц. Составить план перевозки муки, обеспечивающий минимальные транспортные расходы.
Решение.
Задание 1.
| Мощности
поставщиков
|
Мощности потребителей
|
| 50
|
40
|
50
|
60
|
| 50
|
8
|
3
|
5
|
2
|
| 40
|
7
|
4
|
9
|
8
|
| 40
|
6
|
3
|
3
|
1
|
| 70
|
2
|
4
|
1
|
5
|
Сумма мощностей поставщиков (запасы муки на всех складах) 50+40+40+70 = 200, сумма мощностей потребителей (потребности всех хлебозаводов) 50+40+50+60 = 200. Суммы равны, данная задача является транспортной задачей закрытого типа.
Задание 2.
Обозначим xij
объем поставок муки от i – го поставщика (склада) j – му потребителю (хлебозаводу), i = 1, 2, 3, 4; j = 1, 2, 3, 4. Очевидно, xij
³ 0. В закрытой транспортной задаче все ограничения являются равенствами.
Так как потребности должны быть удовлетворены, то выполняются условия:
х11
+ х21
+ х31
+ х41
= 50
х12
+ х22
+ х32
+ х42
= 40 (1)
х13
+ х23
+ х33
+ х43
= 50
х14
+ х24
+ х34
+ х44
= 60
Так как поставки от поставщика всем потребителям не могут быть больше его возможностей, то выполняются условия:
х11
+ х12
+ х13
+ х14
= 50
х21
+ х22
+ х23
+ х24
= 40 (2)
х31
+ х32
+ х33
+ х34
= 40
х41
+ х42
+ х43
+ х44
= 70
Затраты на транспортировку составят
F(X) = 8х11
+ 3х12
+ 5х13
+ 2х14
+
+ 7х21
+ 4х22
+ 9x23
+ 8х24
+
+ 6х31
+ 3х32
+ 3х33
+ 1х34
+
+ 2х41
+ 4х42
+ 1х43
+ 5х44
+.
Требуется найти неотрицательное решение системы уравнений (1) – (2), на котором целевая функция затрат F(X) принимает минимальное значение.
Задание 3.
Начальный план перевозок находим методом минимальной стоимости:
Заполняем клетку (3; 4) х34
= min {60, 40} = 40, от поставщика 3 вывезено все, в строке 3 больше поставок нет. Заполняем клетку (4; 3) х43
= min {50, 70} = 50, потребителю 3 все завезено, в столбец 3 больше поставок нет. Клетка (1; 4) х14
= min {60 - 40, 50} = 20, потребителю 4 все завезено, в столбец 4 больше поставок нет. Клетка (4; 1) х41
= min {50, 70 - 50} = 20, от поставщика 4 вывезено все, в строке 4 больше поставок нет. Клетка (1; 2) х12
= min {40, 50 - 20} = 30, от поставщика 1 вывезено все, в строке 1 больше поставок нет. Клетка (2; 2) х22
= min {40 - 30, 40} = 10, потребителю 2 все завезено, в столбец 2 больше поставок нет. Клетка (2; 1) х21
= 30. Все клетки, в которые даны поставки, считаем занятыми, остальные – свободными. Первоначальный план перевозок задается таблицей 1.
Таблица 1.
| Мощности
поставщиков
|
Мощности потребителей
|
ui
|
| 50
|
40
|
50
|
60
|
| 50
|
8
|
3
30
|
5
|
2
20
|
0
|
| 40
|
7
30
|
4
10
|
9
|
8
|
-1
|
| 40
|
6
|
3
|
3
|
1
40
|
1
|
| 70
|
2
20
|
4
|
1
50
|
5
|
4
|
| vj
|
6
|
3
|
5
|
2
|
Исследуем этот план перевозок на оптимальность методом потенциалов. Потенциалы для занятых клеток удовлетворяют уравнениям: vj
= cij
+
ui
.
Пусть u1
= 0; по клетке (1; 2) находим v2
= 3; по клетке (1; 4) находим v4
= 2; по клетке (2; 2) находим u2
= -1; по клетке (2; 1) находим v1
= 6; по клетке (3; 4) находим u3
= 1; по клетке (4; 1) находим u4
= 4; по клетке (4; 3) находим v3
= 5.
Для всех клеток матрицы перевозок найдем оценки клеток dij
= (ui
+ cij
) - vj
:
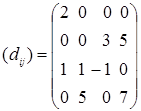
Среди оценок есть отрицательная, следовательно план перевозок Х0
(таблица 1) не оптимальный. Наименьшая оценка в клетке (3; 3).
Составим цикл пересчета и пометим клетки поочередно знаками «+» и «-»:
+ - + - + - + -
(3; 3), (3; 4), (1; 4), (1; 2), (2; 2), (2; 1), (4; 1), (4; 3).
В клетки с «+» переместим из клеток с «-» величину min{40; 30; 30; 50} = 30. В этом случае план перевозок станет таким ( таблица 2).
Таблица 2.
| Мощности
поставщиков
|
Мощности потребителей
|
ui
|
| 50
|
40
|
50
|
60
|
| 50
|
8
|
3
0
|
5
|
2
50
|
0
|
| 40
|
7
|
4
40
|
9
|
8
|
-1
|
| 40
|
6
|
3
|
3
30
|
1
10
|
1
|
| 70
|
2
50
|
4
|
1
20
|
5
|
3
|
| vj
|
5
|
3
|
4
|
2
|
Освободилось две клетки (1; 2) и (2; 1). Клетку (1; 2) считаем занятой с нулевой поставкой.
Среди оценок нет отрицательных, следовательно план перевозок Х0
(таблица 1) оптимальный.
Исследуем этот план перевозок на оптимальность методом потенциалов. Потенциалы для занятых клеток удовлетворяют уравнениям: vj
= cij
+
ui
.
Пусть u1
= 0; по клетке (1; 2) находим v2
= 3; по клетке (1; 4) находим v4
= 2; по клетке (2; 2) находим u2
= -1; по клетке (3; 4) находим u3
= 1; по клетке (3; 3) находим v3
= 4; по клетке (4; 3) находим u4
= 3; по клетке (4; 1) находим v1
= 5.
Для всех клеток матрицы перевозок найдем оценки клеток dij
= (ui
+ cij
) - vj
:
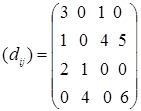
Так как среди оценок свободных клеток нет нулевых, то оптимальный план перевозок единственный.
Общие затраты на перевозки
F(X1
) = 2*50 + 4*40 + 3*30 + 1*10 + 2*50 + 1*20 = 480 ден. единиц
будут минимальными при:
x14
= 50, x22
= 40, x33
= 30, х34
= 10, x41
= 50, x43
= 20, остальные xij
= 0.
По оптимальному плану перевозок следует перевезти муки:
со склада А на четвертый хлебозавод - 50 т;
со склада В на второй хлебозавод - 40 т;
со склада С на третий хлебозавод - 30 т;
на четвертый хлебозавод - 10 т;
со склада Д на первый хлебозавод - 50 т;
на третий хлебозавод - 20 т.
Задача 4
В таблице приведены годовые данные о трудоемкости производства I т цемента (нормо-смен) (N —последняя цифра зачетной книжки студента):
| Текущий номер года (t)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Трудоемкость 1 т цемента (yi
)
|
7,9+0,N
|
8,3+0,N
|
7,5+0,N
|
6,9+0,N
|
7,2+0,N
|
6,5+0,N
|
5,8+0,N
|
4,9+0,N
|
5,1+0,N
|
4,4+0,N
|
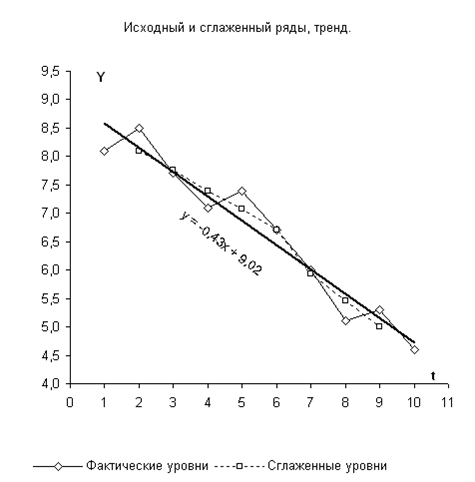
Задание 1. Сгладить временной ряд методом простой скользящей средней, выбрав длину интервала сглаживания m = 3; результаты отразить на графике.
Задание 2. Определить наличие тренда во временном ряду методом Фостера - Стьюарта. Табличные значения статистики Стьюдента ta
принять равными при уровне значимости a = 0.05 ta
= 2,23 , а при a = 0,30 - ta
= 1,09; другие необходимые табличные данные приведены в таблице 4.5 учебника на с.153 (описание метода Фостера - Стьюарта см. учебник с. 151- 153).
Задание 3. Для исходного временного ряда построить линейную трендовую модель 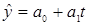 , определив ее параметры на основе метода наименьших квадратов (соответствующую систему нормальных уравнений см. в учебнике на с. 196 формула (5.5)). , определив ее параметры на основе метода наименьших квадратов (соответствующую систему нормальных уравнений см. в учебнике на с. 196 формула (5.5)).
Задание 4. Оценить адекватность построенной модели на основе исследования
а) близости математического ожидания остаточной компоненты (ряда остатков) нулю; критические значения r-критерия принять равным тому числу, как указанно в задании 2;
б) случайности отклонений остаточной компоненты по критерию пиков (поворотных точек); Расчеты выполнить на основе соотношения 5.9. учебника на с. 200;
в) независимости уровней ряда остатков (отсутствие автокорреляции) на основе критерия Дарбина — Уотсона (см. учебник с. 203— 204), используя в качестве критических значений dl
= 1.08 и d2
= 1,36; если критерий Дарбина — Уотсона ответа не дает, исследование независимости провести по первому коэффициенту автокорреляции:
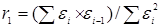 , ,
где ei
-- уровни остаточной компоненты;
Модуль первого коэффициента автокорреляции сравнить с критическим уровнем этого коэффициента, значение которого принять равным 0,36;
г) нормальности закона распределения уровней остаточной компоненты на основе RS-критерия;
В качестве критических значений принять интервал от 2,7 до 3,7 (см. учебник, стр. 201—-202).
Задание 5. Оценить точность построенной трендовой линейной модели, используя показатели среднего квадратического отклонения от линии тренда (формула (5,17) учебника на с. 210, k = 1) и средней относительной ошибки аппроксимации (формула (5.14) учебника на с. 204).
Задание 6. Построить точечный и интервальный прогноз трудоемкости производства 1 т цемента на два шага вперед (формула (5.18) учебника на с. 210). Результаты моделирования и прогнозирования отразить на графике.
Все промежуточные результаты вычислений представить в таблицах, вычисления провести с двумя десятичными знаками в дробной части.
Вариант 2. Условия при N = 2
| Текущий номер года (t)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Трудоемкость 1 т цемента (yi
)
|
8,1
|
8,5
|
7,7
|
7,1
|
7,4
|
6,7
|
6,0
|
5,1
|
5,3
|
4,6
|
Решение.
Задание 1. Сглаживание ряда Y(t) произведем по простой скользящей средней

Результаты в таблице 1.
| Таблица 1.
|
| Сглаживание ряда динамики
|
| t
|
Факт Y(t)
|
Скользящая сумма
|
Скользящее среднее
|
| 1
|
8,1
|
-
|
-
|
| 2
|
8,5
|
24,3
|
8,10
|
| 3
|
7,7
|
23,3
|
7,77
|
| 4
|
7,1
|
22,2
|
7,40
|
| 5
|
7,4
|
21,2
|
7,07
|
| 6
|
6,7
|
20,1
|
6,70
|
| 7
|
6,0
|
17,8
|
5,93
|
| 8
|
5,1
|
16,4
|
5,47
|
| 9
|
5,3
|
15,0
|
5,00
|
| 10
|
4,6
|
-
|
-
|
Задание 2.
Этап 1. Строим две числовые последовательности kt
и lt
| t
|
kt
|
lt
|
| 2
|
1
|
0
|
| 3
|
0
|
1
|
| 4
|
0
|
1
|
| 5
|
0
|
0
|
| 6
|
0
|
1
|
| 7
|
0
|
1
|
| 8
|
0
|
1
|
| 9
|
0
|
0
|
| 10
|
0
|
1
|
Этап 2. Находим величины
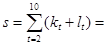 7; 7; 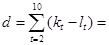 1 – 6 = -5. 1 – 6 = -5.
Этап 3. Для n = 10 выпишем табличные значения m = 3,858; s1
= 1,288; s2
= 1,964.
Вычисляем
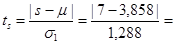 2,44; 2,44; 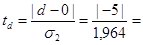 2,55. 2,55.
Этап 4.
Так как расчетные значения ts
= 2,44 и td
= 2,55 больше табличного значения ta
= 2,23, то в данном временном ряду присутствуют тренд и тенденция в дисперсии ряда.
Из таблицы 1 видно, что ряд Y(t) имеет тенденцию к снижению.
Задание 3. Линейную трендовую модель ищем в виде 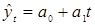 . Параметры модели а0
, а1
найдем, решив систему уравнений . Параметры модели а0
, а1
найдем, решив систему уравнений
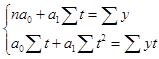 . .
n = 9.
Составим расчетную таблицу 2.
| Таблица 2
|
| t
|
y
|
t2
|
yt
|
| 1
|
8,1
|
1
|
8,1
|
| 2
|
8,5
|
4
|
17,0
|
| 3
|
7,7
|
9
|
23,1
|
| 4
|
7,1
|
16
|
28,4
|
| 5
|
7,4
|
25
|
37,0
|
| 6
|
6,7
|
36
|
40,2
|
| 7
|
6
|
49
|
42,0
|
| 8
|
5,1
|
64
|
40,8
|
| 9
|
5,3
|
81
|
47,7
|
| 10
|
4,6
|
100
|
46,0
|
| 55
|
66,5
|
385
|
330,3
|
Получаем систему
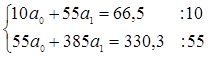 ; ; 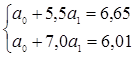 . .
Получили 1,5а1
= -0,64, а1
= -0,64:1,5 = -0,43; а0
= 6,65 - 5,5а1
= 6,65 - 5,5×(-0,43) = 9,02.
Получили трендовую модель: 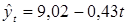 . .
Задание 4.
Оценим качество модели. Для этого найдем расчетные значения Yp
(t), подставляя t =1, …, 10 в трендовую модель, найдем отклонения расчетных значений от исходных E(t) = Y(t) - Yp
(t). Для исследования модели на адекватность составим таблицу 3.
| Таблица 3.
|
| Расчетные величины для оценки адекватности модели
|
| t
|
Y(t)
|
Yр
(t)
|
E(t)
|
k
|
E(t)2
|
E(t)-E(t-1)
|
(E(t)-E(t-1))2
|
E(t)*E(t-1)
|
IE(t)I:Y(t)*100
|
| 1
|
8,1
|
8,59
|
-0,49
|
0,24
|
5,988
|
| 2
|
8,5
|
8,16
|
0,34
|
1
|
0,12
|
0,83
|
0,69
|
-0,17
|
4,059
|
| 3
|
7,7
|
7,73
|
-0,03
|
0
|
0,00
|
-0,37
|
0,14
|
-0,01
|
0,325
|
| 4
|
7,1
|
7,30
|
-0,20
|
1
|
0,04
|
-0,17
|
0,03
|
0,00
|
2,746
|
| 5
|
7,4
|
6,87
|
0,54
|
1
|
0,29
|
0,73
|
0,53
|
-0,10
|
7,23
|
| 6
|
6,7
|
6,44
|
0,27
|
0
|
0,07
|
-0,27
|
0,07
|
0,14
|
3,955
|
| 7
|
6
|
6,01
|
-0,01
|
0
|
0,00
|
-0,27
|
0,07
|
0,00
|
0,083
|
| 8
|
5,1
|
5,58
|
-0,48
|
1
|
0,23
|
-0,47
|
0,22
|
0,00
|
9,314
|
| 9
|
5,3
|
5,15
|
0,15
|
1
|
0,02
|
0,63
|
0,40
|
-0,07
|
2,925
|
| 10
|
4,6
|
4,72
|
-0,12
|
0,01
|
-0,27
|
0,07
|
-0,02
|
2,500
|
| S
|
66,5
|
66,5
|
0,00
|
5
|
1,01
|
2,22
|
-0,22
|
39,125
|
а) Близость математического ожидания остаточной компоненты нулю.
Сумма остатков равна 0. Расчетное значение критерия Стьюдента 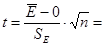 0. 0.
Критическое значение ta
= 2,23 больше расчетного, следовательно, математическое ожидание остаточной компоненты равно нулю.
б) Проверка остатков E(t) на случайность.
Критическое количество поворотных точек для n =10 равно 2.
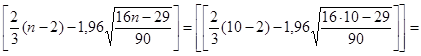 2. 2.
Для данного ряда количество таких точек k = 5. Это больше 2, поэтому остатки E(t) случайные.
в) Проверка остатков E(t) на независимость.
Независимость (отсутствие автокорреляции) проверим, используя критерий Дарбина-Уотсона:
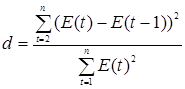 , , 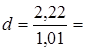 2,20. 2,20.
d > 2, преобразуем d' = 4 - d = 4 - 2,20 = 1,80, получили 1,36 < d' = 1,80 < 2. Это означает, что остатки не зависимы.
г) Проверка остатков на соответствие нормальному закону распределения.
Используется RS - критерий:
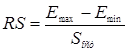 , где , где 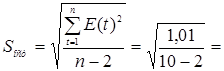 0,36. 0,36.
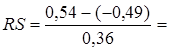 2,87, 2,87,
RSт
= 2,7 - 3,7; так как расчетное значение RS - критерия RSрасч
= 2,87 попадает внутрь интервала от 2,7 до 3,7, то остатки E(t) подчиняются по нормальному закону распределения.
Вывод: так как выполняются все условия адекватности, то модель является полностью адекватной реальному ряду экономической динамики. Ее можно использовать для построения прогнозных оценок.
Задание 5.
Определим точность модели.
Среднее квадратическое отклонение от линии тренда
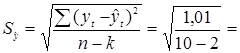 0,36. 0,36.
Средняя относительная ошибка
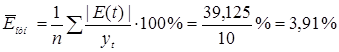 . .
Так как 3,91% < 5%, то точность модели высокая.
Задание 6.
Точечный прогноз для Y получим, подставляя в трендовую модель t =11 и t = 12.
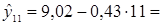 4,285; 4,285; 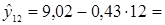 3,855. 3,855.
Для интервального прогноза найдем ширину интервала
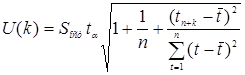 . .
Для числа степеней свободы k = n -2 = 10 - 2 = 8 и уровня значимости a = 0,05 ta
= 2,31.
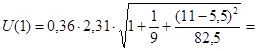 1,00; 1,00; 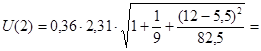 1,04. 1,04.
Границы интервалов прогноза: НГ = Yn+k
- U(k), ВГ = Yn+k
+ U(k).
Результаты прогноза представлены таблицей 4.
Таблица 4.
Точечный и интервальный прогноз
| t
|
U(k)
|
Yn+k p
|
НГ
|
ВГ
|
| 10
|
1,00
|
4,29
|
3,29
|
5,28
|
| 11
|
1,04
|
3,86
|
2,81
|
4,90
|
Построим график.
Задача 5.
В таблице представлены первый (хij
) и второй (Yi
) квадранты схемы межотраслевого баланса производства и распределения продукции для трехотраслевой экономической системы (N — последняя цифра зачетной книжки студента):
| Потребляющие отрасли
|
Производящие отрасли
|
Конечная продукция
|
| 1
|
2
|
3
|
| 1
|
200+10N
|
50+10N
|
300+10N
|
200+10N
|
| 2
|
150+10N
|
250+10N
|
0+10N
|
100+10N
|
| 3
|
230+10N
|
50+10N
|
150+10N
|
300+10N
|
Задание 1. Рассчитать объемы валовой продукции отраслей (формула (6.2) учебника на с. 237).
Задание 2. Рассчитать матрицу коэффициентов прямых затрат А = (aij
) (формула (6.4) учебника на с. 238).
Задание 3. Найти матрицу коэффициентов полных затрат B = (bij
), используя формулу (6.16) учебника на с. 244.
Задание 4. Рассчитать объемы условно чистой продукции отраслей Zj, используя формулу (6.1) учебника на с. 236.
Задание 5. Представить в таблице полную схему межотраслевого баланса (в соответствии с принципиальной схемой МОБ; табл. 6.1 учебника на с.234).
Вариант 3. Условия при N = 2.
| Таблица 1.
|
| Потребляющие отрасли
|
Производящие отрасли
|
Конечная продукция
|
| 1
|
2
|
3
|
| 1
|
220
|
70
|
320
|
220
|
| 2
|
170
|
270
|
20
|
120
|
| 3
|
250
|
70
|
170
|
320
|
Решение.
Задание 1.
Объем валовой продукции находим по формуле
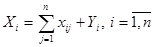 . .
Результаты в таблице 2.
| Таблица 2.
|
| Потребляющие отрасли
|
Производящие отрасли
|
Конечная продукция
|
Валовой продукт
|
| 1
|
2
|
3
|
| 1
|
220
|
70
|
320
|
220
|
830
|
| 2
|
170
|
270
|
20
|
120
|
580
|
| 3
|
250
|
70
|
170
|
320
|
810
|
Задание 2.
Коэффициенты матрицы прямых затрат находим по формуле
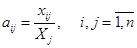
Получаем матрицу А.
| 
|
0,27
|
0,12
|
0,40
|
| А =
|
0,20
|
0,47
|
0,02
|
| 0,30
|
0,12
|
0,21
|
Задание 3. Чтобы найти матрицу коэффициентов полных затрат В, запишем матрицу Е - А, где Е - единичная матрица.
| 
|
0,73
|
-0,12
|
-0,40
|
| Е - А =
|
-0,20
|
0,53
|
-0,02
|
| -0,30
|
-0,12
|
0,79
|
Матрица В находится по формуле
1,96
|
0,67
|
1,00
|
| В = (Е - А)-1
=
|
0,79
|
2,15
|
0,46
|
| 0,87
|
0,58
|
1,72
|
Задание 4. Условно чистую продукцию найдем по формуле

Результаты в таблице 3.
| Таблица 3.
|
| Потребляющие отрасли
|
Производящие отрасли
|
Конечная продукция
|
Валовой продукт
|
| 1
|
2
|
3
|
| 1
|
220
|
70
|
320
|
220
|
830
|
| 2
|
170
|
270
|
20
|
120
|
580
|
| 3
|
250
|
70
|
170
|
320
|
810
|
| Условно чистая продукция
|
190
|
170
|
300
|
Задание 5. Межотраслевой баланс производства и распределения продукции отраслей представлен таблицей 4.
| Таблица 4.
|
| Потребляющие отрасли
|
Производящие отрасли
|
Конечная продукция
|
Валовой продукт
|
| 1
|
2
|
3
|
| 1
|
220
|
70
|
320
|
220
|
830
|
| 2
|
170
|
270
|
20
|
120
|
580
|
| 3
|
250
|
70
|
170
|
320
|
810
|
| Условно чистая продукция
|
190
|
170
|
300
|
660
|
| Валовой продукт
|
830
|
580
|
810
|
2220
|
Литература
1. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В.Федосеев, А.Н.Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. М.: ЮНИТИ, 1999.
2. Экономико-математические методы и прикладные модели. Методические указания по изучению дисциплины и задания к контрольной работе для студентов III курса специальностей 061000 «Государственное и муниципальное управление», 061100 «Менеджмент организации», 061500 «Маркетинг». – М.: ВЗФЭИ, 2002
|