| Содержание
Задача 1
Задача 2
Задача 3
Список литературы
Создание математической модели трехконтурной электрической схемы в среде табличного процессора Excel.
В задаче выполнить следующее:
1. Составить систему уравнений для расчета контурных токов в соответствии с заданной схемой (таблица 1).
2. Составить алгоритм расчета контурных токов на рабочем листе электронной таблицы.
3. Выполнить расчет.
Таблица 1 – Исходные данные для решения задачи 1.
| Исходные данные
|
Последняя цифра шифра – 7
|
| R1 (Oм)
|
2
|
| R2 (Oм)
|
4
|
| R3 (Oм)
|
5
|
| R4 (Oм)
|
2
|
| R5 (Oм)
|
3
|
| R6 (Oм)
|
7
|
| Е1 (В)
|
19
|
| Е2 (В)
|
6
|
| № схемы
|
8
|
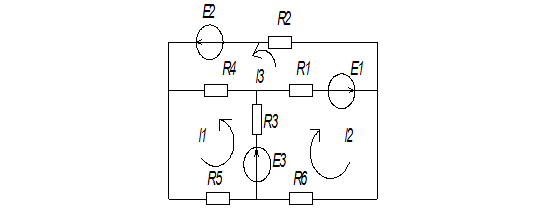
Рисунок 1 – Схема электрической цепи
Решение:
Система уравнений для расчета контурных токов:
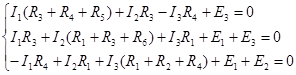
Матрица коэффициентов для расчета токов будет иметь вид:
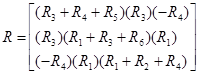
Вектор правой части уравнений:
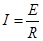
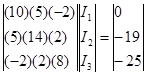
Таблица 2 – Расчет в Excel обратной матрицы
| 10
|
5
|
-2
|
|
0
|
| 5
|
14
|
2
|
|
-19
|
| -2
|
2
|
8
|
|
-25
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| 0,14
|
-0,06
|
0,05
|
|
-0,15
|
| -0,06
|
0,10
|
-0,04
|
|
-0,89
|
| 0,05
|
-0,04
|
0,15
|
|
-2,94
|
Ответ: I1
= - 0,15 A; I2
= - 0,89 A; I3
= - 2,94 A.
Оценка влияния изменения параметров схемы тяговой сети на токи тяговых подстанций.
В задаче требуется выполнить следующее:
1. Составить алгоритм расчета токов подстанции при изменении заданного параметра на рабочем листе электронной таблицы.
2. Составить контрольный пример расчета токов подстанции и решить его вручную.
3. При решении задачи на ЭВМ построить зависимости токов подстанций от заданного параметра. Исходные данные для решения задачи приведены в таблице 3. В таблице указаны токи нагрузок I01
I02
, напряжения холостого хода подстанций U01
и U02
, эквивалентные внутренние сопротивления подстанций RP, сопротивление тяговой сети подстанциями R и меняющийся параметр.
4. При решении задачи принять, что заданный параметр изменяется на ±10%.
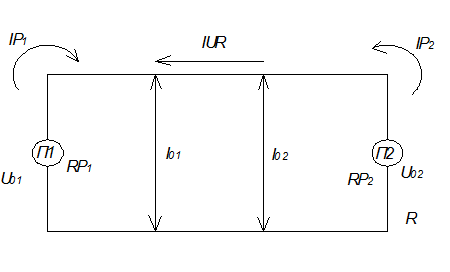
Рисунок 2 – Схема тяговой сети
Таблица 3 – Исходные данные для решения задачи 2.
| Исходные данные
|
Последняя цифра шифра – 7
|
| Ток нагрузки, I01
, А
|
2800
|
| Ток нагрузки, I02
, А
|
2300
|
| Напряжение холостого хода подстанции 1, U01
, В
|
900
|
| Напряжение холостого хода 2 U02
, В
|
890
|
| Эквивалентное внутреннее сопротивление подстанции RP1=RP2 (Ом)
|
0,02
|
| Сопротивление тяговой сети между подстанциями R, Ом
|
0,04
|
| Меняющийся параметр
|
I01
|
Решение:
Таблица 4 – Расчетные показатели
| Ток нагрузки, I01
, А
Реклама

|
2800
|
| Ток нагрузки, I02
, А
|
2300
|
| Напряжение холостого хода подстанции 1, U01
, В
|
900
|
| Напряжение холостого хода 2 U02
, В
|
890
|
| Эквивалентное внутреннее сопротивление подстанции RP1=RP2 (Ом)
|
0,02
|
| Сопротивление тяговой сети между подстанциями R, Ом
|
0,04
|
| Меняющийся параметр
|
I01
|
| к1
|
0,5
|
| к2
|
0,5
|
| iур
|
250
|
| IP1
|
2800
|
| IP2
|
2300
|
Таблица 5 – Зависимость токов подстанции от меняющегося параметра
| Ток нагрузки, I01
, А
|
IP1
|
IP2
|
| 2520
|
2590
|
2230
|
| 2560
|
2620
|
2240
|
| 2600
|
2650
|
2250
|
| 2640
|
2680
|
2260
|
| 2680
|
2710
|
2270
|
| 2720
|
2740
|
2280
|
| 2760
|
2770
|
2290
|
| 2800
|
2800
|
2300
|
| 2840
|
2830
|
2310
|
| 2880
|
2860
|
2320
|
| 2920
|
2890
|
2330
|
| 2960
|
2920
|
2340
|
| 3000
|
2950
|
2350
|
| 3040
|
2980
|
2360
|
| 3080
|
3010
|
2370
|
Рисунок 3 – Зависимость токов подстанции от тока нагрузки
Выбор варианта устройства по минимальному значению критерия оптимизации.
Критерием оптимизации при сравнении вариантов расчета системы электроснабжения являются ежегодные приведенные затраты, которые состоят из 2-х составляющих:
Капитальные вложения ZK и эксплуатационных затрат ZE.
Z=ZK+ZE
Каждая их составляющих является функцией от варианта расчета – х.
т.е. Z(x)=ZK(x)+ZE(x)
В таблице 6 приводятся значения капитальных вложений ZK(x) для каждого варианта расчета. Вторая составляющая – эксплуатационные затраты может быть рассчитана по следующей формуле
ZЕ(х)=а+bx+cx2
Значения параметров a, b, c приводятся в таблице 7.
В задаче требуется выполнить:
1. Составить алгоритм решения задачи на рабочем листе Excel.
2. Выполнить контрольный просчет.
3. Построить график зависимости ежегодных приведенных затрат от варианта расчета Z=f(x).
Таблица 6 – Исходные данные для решения задачи 3.
| Значения составляющей ZK(x) критерия оптимизации
|
| Шифр
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| 7
|
889
|
740
|
618
|
519
|
438
|
371
|
317
|
272
|
235
|
205
|
Таблица 7 – Исходные данные параметров a, b, c
| Последняя цифра шифра
|
7
|
| a
|
30
|
| b
|
80
|
| c
|
0
|
Решение:
Таблица 8 – Расчетные параметры
| Значения составляющей ZK(x) критерия оптимизации
|
| х
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| ZK(x)
|
889
|
740
|
618
|
519
|
438
|
371
|
317
|
272
|
235
|
205
|
| ZE(x)
|
110
|
190
|
270
|
350
|
430
|
510
|
590
|
670
|
750
|
830
|
| Z(x)
|
999
|
930
|
888
|
869
|
868
|
881
|
907
|
942
|
985
|
1035
|
Рисунок 4 – Зависимость Z(x)
1. Волков В.Н. Понятный самоучитель работы в Excel, М.: Питер, 2003 г. 222 с.
2. Заболотный И.П., Гришанов С.А. Математическая модель для расчета динамических режимов электрической системы, М. Электросвязь, 2001 г. 345 с.
3. Пантелеев В.А. Математические модели в расчетах на ЭВМ. Методические указания, 1997 г. 12с.
4. Припачкин Ю.И., Тамм Ю.А. Математическая модель для расчета иерархических телекоммуникационных сетей, М.: Электросвязь, 2001, 268 с.
5. Хазанова Л.З. Математическое моделирование в экономике. Учебное пособие. М.: Бек, 1998. 141 с.
|