Частица вращается по окружности 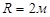 , и уравнение движения , и уравнение движения  . Найти тангенциальное, нормальное и полное ускорение в момент . Найти тангенциальное, нормальное и полное ускорение в момент 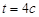 . .
Найдем угловую скорость
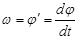 : :
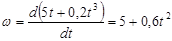 ; ;
Линейная скорость находиться по формуле
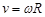
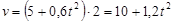
Тангенциальное ускорение
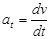 : :
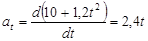 , , 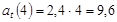 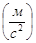
Нормальное ускорение
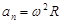 : :
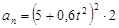 , , 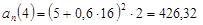 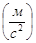
Полное ускорение
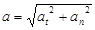 : :
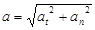 , , 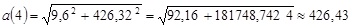 
Ответ: тангенциальное ускорение  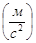 , нормальное ускорение , нормальное ускорение 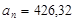 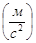 , полное ускорение , полное ускорение 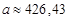 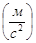 . .
Тело движется вдоль прямой, замедляясь при 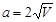 . В начальной точке скорость была . В начальной точке скорость была 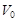 . Какой путь пройдет тело до остановки. . Какой путь пройдет тело до остановки.
Мгновенная скорость 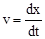 , следовательно , следовательно 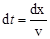
Мгновенное ускорение 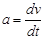 , следовательно
, следовательно 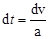
Получаем равенство 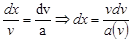
Проинтегрируем равенство 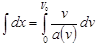
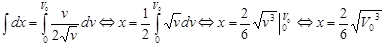
Ответ: тело пройдет путь равный 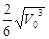
На брусок массой 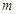 , лежащий на гладкой горизонтальной поверхности, действует сила , лежащий на гладкой горизонтальной поверхности, действует сила 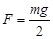 . При прямолинейном движении угол между силой и горизонтом изменяется по закону . При прямолинейном движении угол между силой и горизонтом изменяется по закону 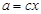 , где , где 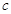 - постоянная. Найти скорость бруска как функцию от - постоянная. Найти скорость бруска как функцию от 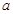 . .
Уравнение движения в проекции 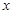 имеет вид имеет вид
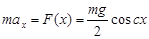
Заменим в уравнении 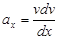 , тогда , тогда
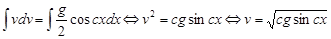
Ответ: скорость бруска равна 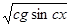
Конькобежец массой 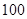 кг, стоя на коньках на льду, толкает камень кг, стоя на коньках на льду, толкает камень 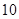 кг под углом 30° к горизонту со скоростью кг под углом 30° к горизонту со скоростью 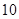 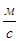 . Найти начальную скорость движения конькобежца. . Найти начальную скорость движения конькобежца.
Импульс и закон сохранения импульса
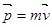 ; ; 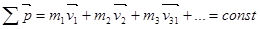 ; ;
Перед броском все тела находились в покое: импульс каждого из них был равен 0, равнялась 0 и их векторная сумма
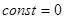
В конце броска импульс груза равен 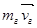 , конькобежца - , конькобежца - 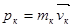
В проекции на ось Ox импульс груза равен 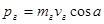 , конькобежца - , конькобежца - 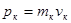 . .
т.к. 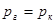 , то , то 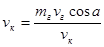
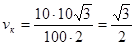  . .
Ответ: 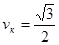 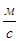 ; ;
Тело массой 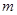 начинает двигаться вдоль оси начинает двигаться вдоль оси 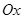 со скоростью со скоростью 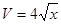 , где , где 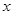 - перемещение. Найти выражение для работы и вычислить работу при - перемещение. Найти выражение для работы и вычислить работу при 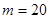 кг за 3с движения. кг за 3с движения.
Найдем ускорение как производную от скорости
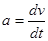 ; ; 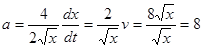 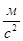 ; ;
Ускорение постоянно, значит движение равноускоренное. Зависимость скорости от времени.
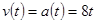
Через 3с скорость будет:
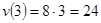 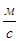
Работа равна изменению кинетической энергии. Т.к. в начале тело находилось в состоянии покоя:
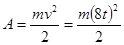 ; ; 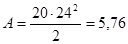 кДж кДж
Ответ: 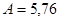 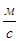 , , 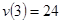 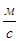 ; ;
Диск массой 10 кг и радиусом 20 см вращается относительно оси симметрии под действием момента сил М = 1,8t2
. Найти угловую скорость колеса через 3 с после начала движения.
Момент инерции диска вычисляется по формуле
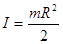 ; ; 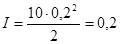 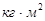
Основной закон динамики вращательного движения
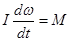
Проинтегрируем выражение по  : :
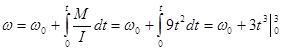
Т.к. 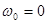 , то , то 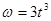
Через 3с угловая скорость будет
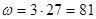 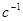
Ответ: 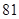 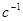
Найти момент инерции стержни сечением S и плотностью р = p0
(1-r/l) , где l - длина, r - расстояние до оси вращения, проходящей черев конец стержня. Вычислить при р = 7800 кг/м3
, S = 2 см2
и I= 80 см.
Выделим бесконечно тонкий участок стержня толщиной 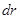 . Его момент инерции: . Его момент инерции:
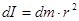 , ,
где 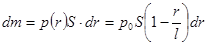 - масса участка. - масса участка.
Т.к. момент инерции аддитивен, момент инерции всего стержня равен сумме моментов инерции всех его участков.
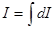
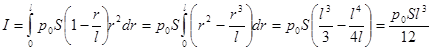
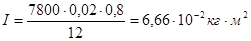
Ответ: 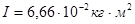
На скамье Жуковского I = 50 кг-м2
стоит человек и держит в руках колесо, момент инерции которого 0,25 кг-м2
и скорость вращения 25 рад/с. Ось колеса совпадает с осью скамьи. Найти угловую скорость вращения скамьи и работу внешних сил, если колесо расположить горизонтально.
Когда колесо повернули горизонтально, момент импульса вокруг вертикальной оси сохранился. То есть
Реклама

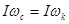 , ,
где 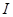 - момент инерции колеса, - момент инерции колеса, 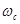 - угловая скорость скамьи, - угловая скорость скамьи, 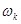 - угловая скорость колеса. - угловая скорость колеса.
Скамья начала вращаться с угловой скоростью
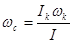 , , 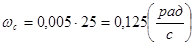
Скорость и энергия внешних сил колеса почти не изменилась. Работа внешних сил пошла на изменение энергии вращения скамьи и равна:
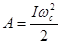 , , 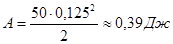
Ответ: 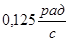 , , 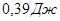 . .
Колебания точки происходят по закону х = Acos(w t+j ). В некоторый момент времени смещение точки равно 5 см, ее скорость V = 20 см/с и ускорение а = - 80 см/с2
. Найти амплитуду А. циклическую частоту w , период колебаний Т и фазу (w t+j ) в рассматриваемый момент времени.
Запишем закон движения и его производные:
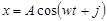 (1), (1),
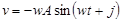 (2), (2),
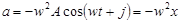 (3). (3).
Подставив 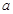 и и 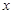 в (3), найдем в (3), найдем 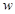 : :
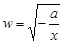 , , 
Преобразуем формулу (2) следующим образом:
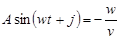 (2’). (2’).
Возведем в квадрат (1) и (2’) и сложим:
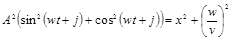
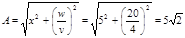 см см
Период колебаний 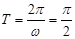 с. с.
Найдем фазу: 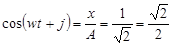 , , 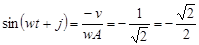
Что соответствует точке на окружности с углом - 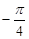
Ответ: 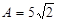 см, см, 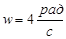 , , 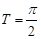 с, с, 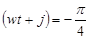 . .
Уравнение колебаний частицы массой 1.6-10 -2
кг имеет вид х = 0,lsin(p t/8 + л/4) (м). Построить график зависимости от времени силы F, действующей на частицу. Найти значение максимальной силы.
Найдем ускорение как вторую производную 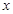 по по 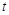 : :
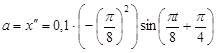
Произведение ускорения на массу даст силу:
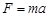 , ,
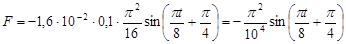
Значение максимальной силы при 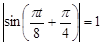
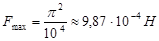
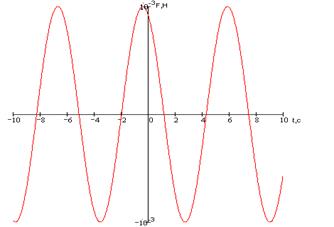
График – синусоида с периодом 16 и смещенная на 2 влево.
Диск радиусом 20 см колеблется около горизонтальной оси, походящей через середину радиуса перпендикулярно плоскости диска. Определить приведенную длину и период колебаний.
Пусть диск повернулся на малый угол 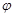 , тогда возвращающий момент сил: , тогда возвращающий момент сил:
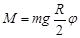 , где , где 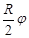 - плечо силы. - плечо силы.
Момент инерции диска относительно центра:
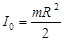
относительно оси вращения:
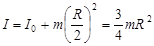
Тогда уравнение движения имеет вид:
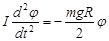 или или 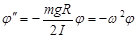
Это уравнение колебаний с частотой:
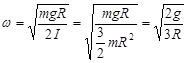
У математического маятника 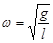
Значит приведенная длина:
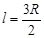 , , 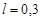 м. м.
Период колебаний:
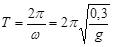
Ответ: 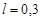 , , 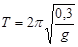 . .
Определить скорость, если разность фаз D j колебаний двух точек среды, отстоящих друг от друга на D x = 10 см, равна p /З. Частота колебаний равна 25 Гц.
Отношение разности фаз к расстоянию между точками есть волновое число 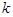
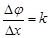 , , 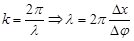 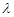 - длина волны. - длина волны.
Выразим частоту:
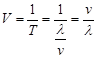 , ,
где 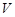 - скорость распространения. - скорость распространения.
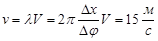
Ответ: 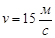 . .
При изменении давления газа на 200 Па объем газа изменится на 3 л. Если давление изменить на 500 Па, объем изменится на 5 л. Найти начальный объем и давление гaзa. Температура газа сохраняется постоянной.
Используем, что при 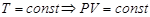 . Тогда . Тогда
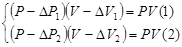
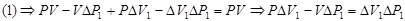 . .
Аналогично для (2)

Выразим из (1) 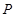 и подставим в (2). и подставим в (2).
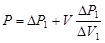
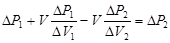 , отсюда , отсюда 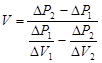 . .
При 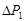 и и 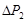 положительных мы не знаем, когда газ сжимается, а когда расширяется. Поэтому выберем все величины отрицательными. положительных мы не знаем, когда газ сжимается, а когда расширяется. Поэтому выберем все величины отрицательными.
Тогда 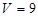 л. Подставив в формулу для л. Подставив в формулу для 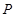 , получим , получим 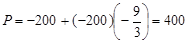 Па. Па.
В обоих случаях газ сжимали.
Ответ: 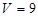 , , 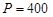 Па. Па.
Найти с помощью распределения Максвелла <V2
x
> среднее значение квадрата проекции скорости молекулы газа при температуре Т.
Распределение Максвелла по проекциям:
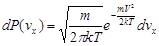
Среднее значение квадрата проекции ищем по формуле:
Реклама

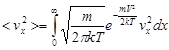
Введем новую переменную 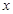
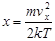 , , 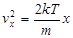 , , 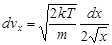
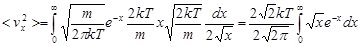
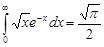 - табличный интеграл. - табличный интеграл.
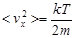
Ответ: 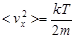 . .
Найти работу, совершающуюся при изотермическом расширении водорода массой 5 г, при температуре 290°К. при увеличении объема газа в три раза.
Количество водорода 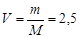 моль. моль.
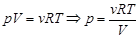
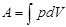
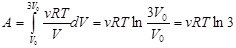 - при расширении от - при расширении от  до до 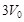 . .
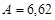 кДж. кДж.
Ответ: 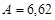 кДж. кДж.
Во сколько раз увеличится КПД цикла Карно при увеличении температуры нагревателя от t1
= 300°К до T 2
= 380 К при температуре холодильника T2
= 200°К?
КПД находим по формуле
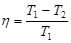 , ,
где 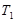 - температура нагревателя, а - температура нагревателя, а 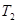 - температура холодильника. - температура холодильника.
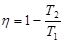
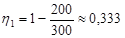
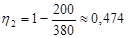
 - во столько раз увеличивается КПД. - во столько раз увеличивается КПД.
Ответ: 1,42.
|