КУРСОВАЯ РАБОТА
Тема: Корреляционный анализ
Задание: Рассчитать полным факторным экспериментом влияние давления, жирности и кислотности на качество продукции
СОДЕРЖАНИЕ
Введение
1. Корреляционный анализ
1.1 Понятие корреляционной связи
1.2 Общая классификация корреляционных связей
1.3 Корреляционные поля и цель их построения
1.4 Этапы корреляционного анализа
1.5 Коэффициенты корреляции
1.6 Нормированный коэффициент корреляции Браве-Пирсона
1.7 Коэффициент ранговой корреляции Спирмена
1.8 Основные свойства коэффициентов корреляции
1.9 Проверка значимости коэффициентов корреляции
1.10 Критические значения коэффициента парной корреляции
2. Планирование многофакторного эксперимента
2.1 Условие задачи
2.2 Определение центр плана (основной уровень) и уровня варьирования факторов
2.3 Построение матрицы планирования
2.4 Проверка однородности дисперсии и равноточности измерения в разных сериях
2.5 Коэффициенты уравнения регрессии
2.6 Дисперсия воспроизводимости
2.7 Проверка значимости коэффициентов уравнения регрессии
2.8 Проверка адекватности уравнения регрессии
Заключение
Список литературы
ВВЕДЕНИЕ
Планирование эксперимента -математико-статистическая дисциплина, изучающая методы рациональной организации экспериментальных исследований — от оптимального выбора исследуемых факторов и определения собственно плана эксперимента в соответствии с его целью до методов анализа результатов. Начало планирования эксперимента положили труды английского статистика Р.Фишера (1935), подчеркнувшего, что рациональное планирование экспериментадаёт не менее существенный выигрыш в точности оценок, чем оптимальная обработка результатов измерений. В 60-х годах 20 века сложилась современная теория планирования эксперимента. Её методы тесно связаны с теорией приближения функций и математическим программированием. Построены оптимальные планы и исследованы их свойства для широкого класса моделей.
Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления.
Реклама

В процессе измерений, последующей обработки данных, а также формализации результатов в виде математической модели, возникают погрешности и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить о ее адекватности. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами.
Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности.
Среди основных методов планирования, применяемых на разных этапах исследования, используют:
- планирование отсеивающего эксперимента, основное значение которого выделение из всей совокупности факторов группы существенных факторов, подлежащих дальнейшему детальному изучению;
- планирование эксперимента для дисперсионного анализа, т.е. составление планов для объектов с качественными факторами;
- планирование регрессионного эксперимента, позволяющего получать регрессионные модели (полиномиальные и иные);
- планирование экстремального эксперимента, в котором главная задача – экспериментальная оптимизация объекта исследования;
- планирование при изучении динамических процессов и т.д.
Целью изучения дисциплины является подготовка студентов к производственно-технической деятельности по специальности с применением методов теории планирования и современных информационных технологий.
Задачи дисциплины: изучение современных методов планирования, организации и оптимизации научного и промышленного эксперимента, проведения экспериментов и обработки полученных результатов.
1. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
1.1
Понятие корреляционной связи
Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, может ли рост влиять на вес человека или может ли давление влиять на качество продукции?
Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь - это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого.
Реклама

Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем больше рост, тем больше вес человека. Однако из этого правила имеются исключения, когда относительно низкие люди имеют избыточный вес, и, наоборот, астеники, при высоком росте имеют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д.
Корреляционные связи - это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. Оба термина - корреляционная связь и корреляционная зависимость - часто используются как синонимы. Зависимость подразумевает влияние, связь - любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого.
Корреляционная зависимость -
это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака.
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Корреляционные связи различаютсяпо форме, направлению и степени (силе).
По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи (рисунок 1). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности.

Рисунок 1 - Связь между эффективностью решения задачи и силой мотивационной тенденции
По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака - низкие значения другого (рисунок 2). При отрицательной корреляции соотношения обратные (рисунок 3). При положительной корреляции коэффициент корреляции имеет положительный знак, при отрицательной корреляции - отрицательный знак[1].

Рисунок 2 – Прямая корреляция
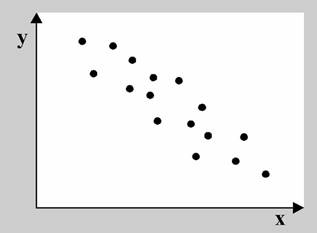
Рисунок 3 – Обратная корреляция

Рисунок 4 – Отсутствие корреляции
Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
1.2
Общая классификация корреляционных связей
В зависимости от коэффициента корреляции различают следующие корреляционные связи:
- сильная, или тесная при коэффициенте корреляции r>0,70;
- средняя (при 0,50<r<0,69);
- умеренная (при 0,30<r<0,49);
- слабая (при 0,20<r<0,29);
- очень слабая (при r<0,19).
1.3 Корреляционные поля и цель их построения
Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения (xi
, yi
) двух признаков. Если экспериментальных данных немного, то двумерное эмпирическое распределение представляется в виде двойного ряда значений xi
и yi
. При этом корреляционную зависимость между признаками можно описывать разными способами. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.
Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения xi
и yi
. Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т.д.), то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами xi
и yi
графически в виде геометрического места точек в системе прямоугольных координат. Эту графическую зависимость называются также диаграммой рассеивания или корреляционным полем.
Данная модель двумерного нормального распределения (корреляционное поле) позволяет дать наглядную графическую интерпретацию коэффициента корреляции, т.к. распределение в совокупности зависит от пяти параметров: μx
, μy
– средние значения (математические ожидания); σx
,σy
– стандартные отклонения случайных величин Х и Y и р – коэффициент корреляции, который является мерой связи между случайными величинами Х и Y.
Если р = 0, то значения, xi
, yi
, полученные из двумерной нормальной совокупности, располагаются на графике в координатах х, у в пределах области, ограниченной окружностью (рисунок 5, а). В этом случае между случайными величинами Х и Y отсутствует корреляция и они называются некоррелированными. Для двумерного нормального распределения некоррелированность означает одновременно и независимость случайных величин Х и Y.

Рисунок 5 - Графическая интерпретация взаимосвязи между показателями
Если р = 1 или р = -1, то между случайными величинами Х и Y существует линейная функциональная зависимость (Y = c + dX). В этом случае говорят о полной корреляции. При р = 1 значения xi
, yi
определяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличением xi
значения yi
также увеличиваются), при р = -1 прямая имеет отрицательный наклон (рисунок 5, б). В промежуточных случаях (-1 < p < 1) точки, соответствующие значениям xi,
yi
, попадают в область, ограниченную некоторым эллипсом (рисунок 5, в, г), причем при p > 0 имеет место положительная корреляция (с увеличением xi
значения yi
имеют тенденцию к возрастанию), при p < 0 корреляция отрицательная. Чем ближе р к 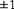 , тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии. Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую другую форму: парабола, гипербола и т. д. В этих случаях мы рассматривали бы так называемую, нелинейную (или криволинейную) корреляцию (риунок 5, д). , тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии. Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую другую форму: парабола, гипербола и т. д. В этих случаях мы рассматривали бы так называемую, нелинейную (или криволинейную) корреляцию (риунок 5, д).
Таким образом, визуальный анализ корреляционного поля помогает выявить не только наличия статистической зависимости (линейную или нелинейную) между исследуемыми признаками, но и ее тесноту и форму. Это имеет существенное значение для следующего шага в анализе ѕ выбора и вычисления соответствующего коэффициента корреляции.
Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида Y = f(X), где признак Y – зависимая переменная, или функция от независимой переменной X, называемой аргументом. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.[2]
1.4
Этапы корреляционного анализа
Практическая реализация корреляционного анализа включает следующие этапы:
а) постановка задачи и выбор признаков;
б) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений, проверка нормальности одномерного распределения);
в) предварительная характеристика взаимосвязей (аналитические группировки, графики);
г) устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции;
д) исследование факторной зависимости и проверка ее значимости;
е) оценка результатов анализа и подготовка рекомендаций по их практическому использованию[3].
1.5
Коэффициенты корреляции
Коэффициенты корреляции является общепринятой в математической статистике характеристикой связи между двумя случайными величинами. Коэффициент корреляции - показатель степени взаимозависимости, статистической связи двух переменных; изменяется в пределах от -1 до +1. Значение коэффициента корреляции 0 указывает на возможное отсутствие зависимости, значение +1 свидетельствует о согласованности переменных.
Различают следующие коэффициенты корреляции:
- дихотомический - показатель связи признаков (переменных) измеряемых по дихотомическим шкалам наименований;
- Пирсона (Pearson product-moment correlation) - коэффициент корреляции, используемый для континуальных переменных;
- ранговой корреляции Спирмена (Spearmen's rank-order correlation) - коэффициент корреляции для переменных, измеренных в порядковых (ранговых) шкалах;
- точечно-бисериальной корреляции (point-biserial correlation) - коэффициент корреляции, применяемый в случае анализа отношения переменных, одна из которых измерена в континуальной шкале, а другая - в строго дихотомической шкале наименований;
- j - коэффициент корреляции, используемый в случае, если обе переменные измерены в дихотомической шкале наименований.
- тетрахорический (четырехпольный) (tetrachoric) - коэффициент корреляции, используемый в случае, если обе переменные измерены в континуальных шкалах[4].
Линейная связь между переменными Xi
и Xj
оценивается коэффициентом корреляции:
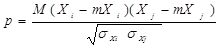 , ,
где Xi
и Xj
– исследуемые переменные; mXi
и mXj
– математические ожидания переменных; σX
и σX
– дисперсии переменных.
Выборочный коэффициент корреляции определяют по формуле:
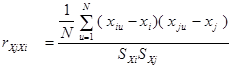 , ,
или по преобразованной формуле:
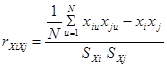 , ,
где i =1, 2, ..., n, j = 1, 2, ..., m, u = 1, 2, ..., N; N – число опытов(объем выборки); xi
, xj
– оценки математических ожиданий; SXi
, SXj
– оценки среднеквадратических отклонений.
Только при совместной нормальной распределенности исследуемых случайных величин Xi
и Xj
коэффициент корреляции имеет определенный смысл связи между переменными. В противном случае коэффициент корреляции может только косвенно характеризовать эту связь[5].
1.6
Нормированный коэффициент корреляции Браве-Пирсона
В качестве оценки генерального коэффициента корреляции р используется коэффициент корреляции r Браве-Пирсона. Для его определения принимается предположение о двумерном нормальном распределении генеральной совокупности, из которой получены экспериментальные данные. Это предположение может быть проверено с помощью соответствующих критериев значимости. Следует отметить, что если по отдельности одномерные эмпирические распределения значений xi
и yi
согласуются с нормальным распределением, то из этого еще не следует, что двумерное распределение будет нормальным. Для такого заключения необходимо еще проверить предположение о линейности связи между случайными величинами Х и Y. Строго говоря, для вычисления коэффициента корреляции достаточно только принять предположение о линейности связи между случайными величинами, и вычисленный коэффициент корреляции будет мерой этой линейной связи.
Коэффициент корреляции Браве–Пирсона (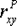 ) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле: ) относится к параметрическим коэффициентам и для практических расчетов вычисляется по формуле:
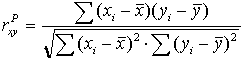
Из формулы видно, что для вычисления 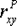 необходимо найти средние значения признаков Х и Y, а также отклонения каждого статистического данного от его среднего необходимо найти средние значения признаков Х и Y, а также отклонения каждого статистического данного от его среднего 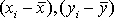 . Зная эти значения, находятся суммы . Зная эти значения, находятся суммы 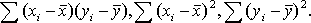 . Затем, вычислив значение . Затем, вычислив значение 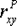 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для f = n –2. Если , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным для f = n –2. Если 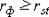 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 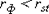 , то между признаками наблюдается недостоверная корреляционная взаимосвязь[2]. , то между признаками наблюдается недостоверная корреляционная взаимосвязь[2].
Пример 1.10 студентам были даны тесты на наглядно-образное и вербальное мышление. Измерялось среднее время решения заданий теста в секундах. Исследователя интересует вопрос: существует ли взаимосвязь между временем решения этих задач? Переменная X — обозначает среднее время решения наглядно-образных, а переменная Y— среднее время решения вербальных заданий тестов.
Решение. Представим исходные данные в виде таблицы 4, в которой введены дополнительные столбцы, необходимые для расчета по формуле.
Таблица 1 – Условия задачи
| № испытуемых |
x |
y |
хi
-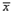 |
(хi
-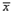 )2 )2
|
yi
-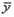 |
(yi
- 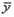 )2 )2
|
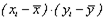 |
| 1 |
19 |
17 |
-16,7 |
278,89 |
-7,2 |
51,84 |
120,24 |
| 2 |
32 |
7 |
-3,7 |
13,69 |
-17,2 |
295,84 |
63,64 |
| 3 |
33 |
17 |
-2,7 |
7,29 |
-7,2 |
51,84 |
19,44 |
| 4 |
44 |
28 |
8,3 |
68,89 |
3,8 |
14,44 |
31,54 |
| 5 |
28 |
27 |
-7,7 |
59,29 |
2,8 |
7,84 |
-21,56 |
| 6 |
35 |
31 |
-0,7 |
0,49 |
6,8 |
46,24 |
-4,76 |
| 7 |
39 |
20 |
3,3 |
10,89 |
-4,2 |
17,64 |
-13,86 |
| 8 |
39 |
17 |
3,3 |
10,89 |
-7,2 |
51,84 |
-23,76 |
| 9 |
44 |
35 |
8,3 |
68,89 |
10,8 |
116,64 |
89,64 |
| 10 |
44 |
43 |
8,3 |
68,89 |
18,8 |
353,44 |
156,04 |
| Сумма |
357 |
242 |
588,1 |
1007,6 |
416,6 |
| Среднее |
35,7 |
24,2 |
Рассчитываем эмпирическую величину коэффициента корреляции по формуле расчета коэффициента корреляции Браве–Пирсона:
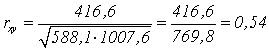
Определяем критические значения для полученного коэффициента корреляции по таблице. При нахождении критических значений для вычисленного коэффициента линейной корреляции Пирсона число степеней свободы рассчитывается как f = n – 2 = 8. rкрит
=0,72 > 0,54 , следовательно, гипотеза Н1
отвергается и принимается гипотеза H0
, иными словами, связь между временем решения наглядно-образных и вербальных заданий теста не доказана[1].
1.7
Коэффициент ранговой корреляции Спирмена
Если потребуется установить связь между двумя признаками, значения которых в генеральной совокупности распределены не по нормальному закону, т. е. предположение о том, что двумерная выборка (xi и yi) получена из двумерной нормальной генеральной совокупности, не принимается, то можно воспользоваться коэффициентом ранговой корреляции Спирмена (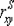 ): ):
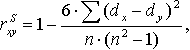
где dx и dy – ранги показателей xi и yi; n – число коррелируемых пар.
Коэффициент ранговой корреляции также имеет пределы 1 и –1. Если ранги одинаковы для всех значений xi и yi, то все разности рангов (dx - dy) = 0 и = 1. Если ранги xi и yi расположены в обратном порядке, то 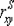 = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi
и yi
. = -1. Таким образом, коэффициент ранговой корреляции является мерой совпадения рангов значений xi
и yi
.
Когда ранги всех значений xi
и yi
строго совпадают или расположены в обратном порядке, между случайными величинами Х и Y существует функциональная зависимость, причем эта зависимость не обязательно линейная, как в случае с коэффициентом линейной корреляции Браве-Пирсона, а может быть любой монотонной зависимостью (т. е. постоянно возрастающей или постоянно убывающей зависимостью). Если зависимость монотонно возрастающая, то ранги значений xi
и yi
совпадают и 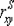 = 1; если зависимость монотонно убывающая, то ранги обратны и = 1; если зависимость монотонно убывающая, то ранги обратны и 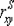 = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y. = –1. Следовательно, коэффициент ранговой корреляции является мерой любой монотонной зависимости между случайными величинами Х и Y.
Из формулы видно, что для вычисления 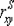 необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)2
. Зная эти значения, находятся суммы необходимо сначала проставить ранги (dx и dy) показателей xi и yi, найти разности рангов (dx - dy) для каждой пары показателей и квадраты этих разностей (dx - dy)2
. Зная эти значения, находятся суммы 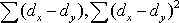 , учитывая, что , учитывая, что 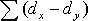 всегда равна нулю. Затем, вычислив значение всегда равна нулю. Затем, вычислив значение 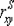 , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с табличным. Если 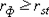 , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если , то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если 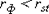 , то между признаками наблюдается недостоверная корреляционная взаимосвязь. , то между признаками наблюдается недостоверная корреляционная взаимосвязь.
Коэффициент ранговой корреляции Спирмена вычисляется значительно проще, чем коэффициент корреляции Браве-Пирсона при одних и тех же исходных данных, поскольку при вычислении используются ранги, представляющие собой обычно целые числа.
Коэффициент ранговой корреляции целесообразно использовать в следующих случаях:
- если экспериментальные данные представляют собой точно измеренные значения признаков Х и Y и требуется быстро найти приближенную оценку коэффициента корреляции. Тогда даже в случае двумерного нормального распределения генеральной совокупности можно воспользоваться коэффициентом ранговой корреляции вместо точного коэффициента корреляции Браве-Пирсона. Вычисления будут существенно проще, а точность оценки генерального параметра р с помощью коэффициента 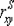 при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций; при больших объемах выборки составляет 91,2% по отношению к точности оценки по коэффициенту корреляций;
- когда значения xi
и (или) yi
заданы в порядковой шкале (например, оценки судей в баллах, места на соревнованиях, количественные градации качественных признаков), т. е. когда признаки не могут быть точно измерены, но их наблюдаемые значения могут быть расставлены в определенном порядке.
Пример 2. Определить достоверность взаимосвязи между показателями веса и максимального количества сгибания и разгибания рук в упоре лежа у 10 исследуемых с помощью расчета рангового коэффициента корреляции, если данные выборок таковы:
xi
,кг~55; 45; 43; 47; 47; 51; 48; 60; 53;50
yi
, кол-во раз ~ 26; 20; 25; 22; 27; 28; 16; 15; 18; 24
Решение
1. Расчет рангового коэффициента корреляции Спирмена произведем по формуле:
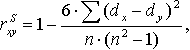
где: dx
и dy
— ранги показателей х
и у
;
n
— число коррелируемых пар или исследуемых.
2 Данные тестирования занести в рабочую таблицу и сделать необходимые расчеты.
Таблица 2 – Данные тестирования
| xi
|
dx
|
yi
|
dy
|
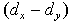 |
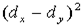 |
| 55 |
9 |
26 |
9 |
0 |
0 |
| 45 |
2 |
20 |
4 |
-2 |
4 |
| 43 |
1 |
25 |
7 |
-6 |
36 |
| 47 |
3.5 |
22 |
5 |
-1.5 |
2.25 |
| 47 |
3.5 |
7 |
8 |
-4.5 |
20.25 |
| 51 |
7 |
28 |
10 |
-3 |
9 |
| 48 |
5 |
16 |
2 |
3 |
9 |
| 60 |
10 |
15 |
1 |
9 |
81 |
| 53 |
8 |
18 |
3 |
5 |
25 |
| 50 |
6 |
24 |
6 |
0 |
0 |
 |
 |
 |
 |
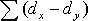 = 0 = 0
|
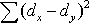 = 186,5 = 186,5 |
Тогда 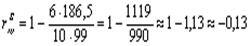
3. Сравнить расчетное значение рангового коэффициента корреляции(rф
=-0,13) с табличным значением для n = 10 при α = 5% и сделать вывод.
Вывод:
1) т.к. rф
= -0,13 < 0, то между данными выборок наблюдается прямая отрицательная взаимосвязь, т.е. увеличением показателей веса вызывает снижение максимального количество сгибаний и разгибаний рук в упоре лежа в группе исследуемых;
2) т.к. rф
= -0,13 < rst
= 0,64 для n = 10 при α = 5%, то с уверенностью Р = 95% можно говорить о том, что выявленная зависимость недостоверна.
1.8
Основные свойства коэффициентов корреляции
К основным свойствам коэффициента корреляции необходимо отнести следующие:
- коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи;
- значения коэффициентов корреляции – это отвлеченные числа, лежащее в пределах от —1 до +1, т.е. -1 < r < 1;
- при независимом варьировании признаков, когда связь между ними отсутствует, r= 0;
- при положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный знак и находится в пределах от 0 до +1, т.е. 0 < r < 1;
- при отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до –1, т.е. -1 < r <0;
- чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к 1. Если r = ±1, то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х будет соответствовать одно или несколько строго определенных значений признака Y;
- только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы f= n –2, где n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции. [2]
1.9
Проверка значимости коэффициентов корреляции
Для проверки значимости коэффициентов корреляции чаще всего используют распределение Стьюдента и условие:
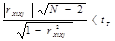 , f = N – 2, α = 0,05. , f = N – 2, α = 0,05.
Если условие выполняется, то гипотеза об отсутствии корреляционной связи принимается[5].
1.10
Критические значения коэффициента парной корреляции
Таблица 3 - Критические значения коэффициента парной корреляции при α=0,05
| Число степеней свободы f |
Критиче-ское значение r |
Число степеней свободы f |
Критиче-ское значение r |
Число степеней свободы f |
Критиче-
ское значение
r
|
1
2
3
4
5
6
7
8
|
0,997
0,950
0,878
0,811
0,754
0,707
0,666
0,632
|
9
10
11
12
13
14
15
16
|
0,602
0,576
0,553
0,532
0,514
0,497
0,482
0,468
|
17
18
19
20
30
50
80
100
|
0,456
0,444
0,433
0,423
0,349
0,273
0,217
0,195
|
 Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным (критическим) значением r, которое приведено в таблице 3. Для пользования этой таблицей нужно знать число степеней свободы f = N – 2 и выбрать определенный уровень значимости, например равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа при проверке нашей гипотезы Р = 1 – α = 0,95, или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.
Для проверки значимости коэффициента парной корреляции нужно сравнить его значение с табличным (критическим) значением r, которое приведено в таблице 3. Для пользования этой таблицей нужно знать число степеней свободы f = N – 2 и выбрать определенный уровень значимости, например равный 0,05. Такое значение уровня значимости называют еще 5%-ным уровнем риска, что соответствует вероятности верного ответа при проверке нашей гипотезы Р = 1 – α = 0,95, или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.
В практических исследованиях 5%-ный уровень риска применяется наиболее часто. Но экспериментатор всегда свободен в выборе уровня значимости, и возможны ситуации, в которых, например, требуется 1%-ный уровень риска. При этом возрастает надежность ответа. Проверка гипотезы сводится к сравнению абсолютной величины коэффициента парной корреляции с критическим значением. Если экспериментально найденное значение r меньше критического, то нет оснований считать, что имеется тесная линейная связь между параметрами, а если больше или равно, то гипотеза о корреляционной линейной связи не отвергается[6].
2. РЕШЕНИЕ ЗАДАЧИ
2.1 Условие задачи
Рассчитать полным факторным экспериментом влияние давления 5-20 МПа, жирности 4-2,5м.д. и кислотности 14-20°Т на качество продукции.
Таблица 1 – Условие задачи
| Фактор |
Номер фактора |
Верхнее значение |
Нижнее значение |
| Давление |
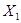 |
20 |
5 |
| Жирность |
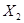 |
4 |
2,5 |
| Кислотность |
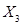 |
20 |
14 |
Таблица 2 – Функция отклика
| У1 |
65 |
60 |
63 |
46 |
47 |
47 |
56 |
54 |
| У2 |
55 |
47 |
46 |
47 |
58 |
56 |
49 |
61 |
| УЗ |
55 |
51 |
61 |
57 |
58 |
53 |
55 |
52 |
2.2 Определение центра плана (основной уровень) и уровня варьирования факторов
Находим центр плана:
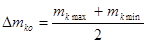 . .
Находим полуразмах:
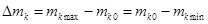 . .
Рассчитываем и оформляем в виде таблицы.
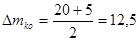 , , 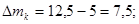
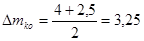 , , 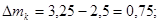
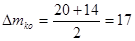 , , 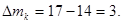
Таблица 3 – Центр плана и полуразмах
| Фактор |
Центр плана 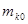 |
Полуразмах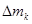 |
| Давление |
12,5 |
7,5 |
| Жирность |
3,25 |
0,75 |
| Кислотность |
17 |
3 |
Рассчитываем нижний уровень варьирования факторов:
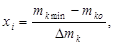
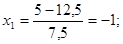
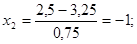
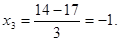
Рассчитываем верхний уровень варьирования факторов:
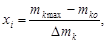
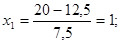
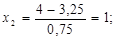
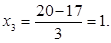
2.3 Построение матрицы планирования
Так как мы имеем 2 уровня варьирования факторов и 3 фактора, то получаем матрицу  . Число опытов равно 8. . Число опытов равно 8.
Таблица 3 – Матрица планирования типа 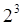
| № опыта |
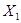 |
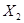 |
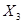 |
| 1 |
+ |
+ |
- |
| 2 |
+ |
+ |
+ |
| 3 |
+ |
- |
+ |
| 4 |
+ |
- |
- |
| 5 |
- |
+ |
- |
| 6 |
- |
+ |
+ |
| 7 |
- |
- |
+ |
| 8 |
- |
- |
- |
Составляем расширенную матрицу планирования для того, чтобы учесть взаимодействие факторов.
Таблица 4 – Расширенная матрица планирования
| № опыта |
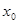 |
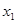 |
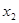 |
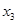 |
 |
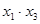 |
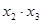 |
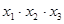 |
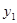 |
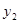 |
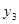 |
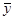 |
| 1 |
+ |
+ |
+ |
- |
+ |
- |
- |
- |
65 |
55 |
55 |
58,3 |
| 2 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
60 |
47 |
51 |
52,7 |
| 3 |
+ |
+ |
- |
+ |
- |
+ |
- |
- |
63 |
46 |
61 |
56,7 |
| 4 |
+ |
+ |
- |
- |
- |
- |
+ |
+ |
46 |
47 |
57 |
50 |
| 5 |
+ |
- |
+ |
- |
- |
+ |
- |
+ |
47 |
58 |
58 |
54,3 |
| 6 |
+ |
- |
+ |
+ |
- |
- |
+ |
- |
47 |
56 |
53 |
52 |
| 7 |
+ |
- |
- |
+ |
+ |
- |
- |
+ |
56 |
49 |
55 |
53,3 |
| 8 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
54 |
61 |
52 |
55,7 |
2.4 Проверка однородности дисперсии и равноточности измерения в разных сериях
Для проверки однородности дисперсии был выбран критерий Кохрена. Для этого рассчитываем дисперсию в каждом опыте по формуле:
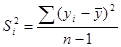 . .
Находим:
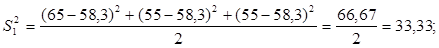
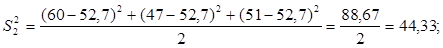
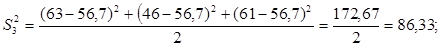
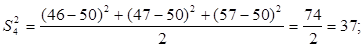
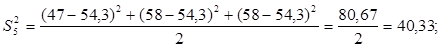
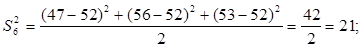
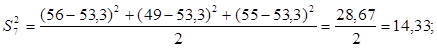
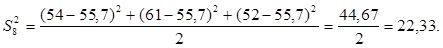
Условия проверки однородности дисперсий по критерию Кохрена:
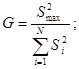
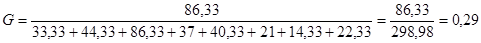
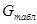 для уровня значимости 0,05 равна 0,32. для уровня значимости 0,05 равна 0,32.
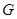 < <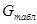 , следовательно, дисперсия однородна и измерения в разных сериях равноточны. , следовательно, дисперсия однородна и измерения в разных сериях равноточны.
2.5 Коэффициенты уравнения регрессии
Находим коэффициенты уравнения регрессии.
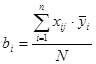 . .
Находим:
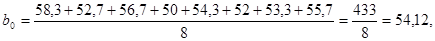
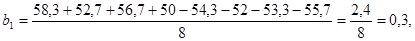
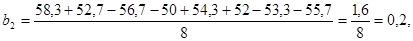
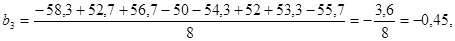
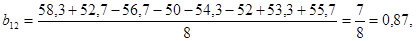
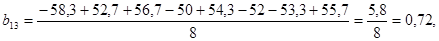
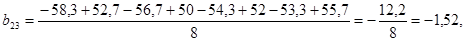
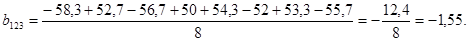
Следовательно, уравнение регрессии примет вид:
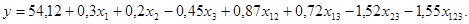
2.6 Дисперсия воспроизводимости
Вычисляем значение дисперсии воспроизводимости по формуле:
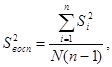
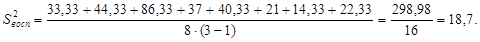
2.7 Проверка значимости коэффициентов уравнения регрессии
Проверяем значимость коэффициентов уравнения регрессии по критерию Стьюдента:
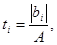 где где 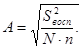
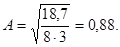
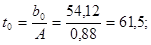
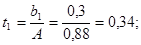
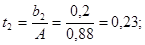
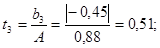
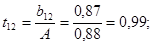
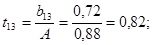
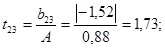
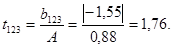
Условие значимости 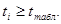 Для уровня значимости α = 0,05 и числа степеней свободы f = N - 1 =8 - 1 = 7 находим табличное значение критерия Стьюдента Для уровня значимости α = 0,05 и числа степеней свободы f = N - 1 =8 - 1 = 7 находим табличное значение критерия Стьюдента 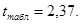
Сравниваем расчетное значение с табличным и видим, что значение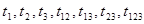 незначительные и их коэффициенты следует исключить из уравнения регрессии. Так как коэффициенты получились незначимы и мы не имеем возможности заново поставить новый эксперимент и продолжаем вычисления, выбрав наиболее близкие к значимым коэффициенты. незначительные и их коэффициенты следует исключить из уравнения регрессии. Так как коэффициенты получились незначимы и мы не имеем возможности заново поставить новый эксперимент и продолжаем вычисления, выбрав наиболее близкие к значимым коэффициенты.
Уравнение регрессии примет вид:
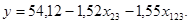
2.8 Проверка адекватности уравнения регрессии
Для проверки используется критерий Фишера:
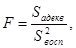
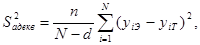
где d – количество коэффициентов уравнения регрессии.
Находим значения 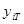 : :
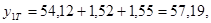
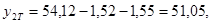
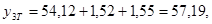
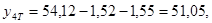
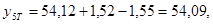
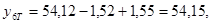
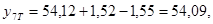
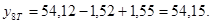
Найдем значение
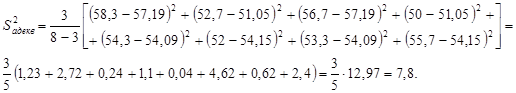
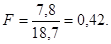
Находим табличное значение критерия Фишера для степеней свободы 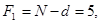 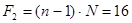 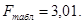
Сравниваем условие 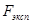 < <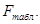 , значит, модель адекватна. , значит, модель адекватна.
Выводы:
- Уравнение регрессии имеет вид: 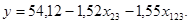
- Анализ значимости коэффициентов уравнении регрессии показал, что влияние всех факторов незначимо.
- Модель адекватна, так как критерий адекватности меньше табличного.
- Измерения в различных серий равноточны.
ЗАКЛЮЧЕНИЕ
Термин «корреляция» был введен в науку выдающимся английским естествоиспытателем Френсисом Гальтоном в 1886 году. Однако точную формулу для подсчета коэффициента корреляции разработал его ученик Карл Пирсон.
Задачи с одним выходным параметром имеют очевидные преимущества. Но на практике чаще всего приходится учитывать несколько выходных параметров. Иногда их число довольно велико. Так, например, при производстве резиновых и пластмассовых изделий приходится учитывать физико-механические, технологические, экономические, художественно-эстетические и другие параметры (прочность, эластичность, относительное удлинение и т.д.). Математические модели можно построить для каждого из параметров, но одновременно оптимизировать несколько функций невозможно.
Обычно оптимизируется одна функция, наиболее важная с точки зрения цели исследования, при ограничениях, налагаемых другими функциями. Поэтому из многих выходных параметров выбирается один в качестве параметра оптимизации, а остальные служат ограничениями. Всегда полезно исследовать возможность уменьшения числа выходных параметров. Для этого и используется корреляционный анализ.
С использованием результатов корреляционного анализа исследователь может делать определённые выводы о наличии и характере взаимозависимости, что уже само по себе может представлять существенную информацию об исследуемом объекте. Результаты могут подсказать и направление дальнейших исследований, и совокупность требуемых методов, в том числе статистических, необходимых для более полного изучения объекта[7].
Особенно реальную пользу применение аппарата корреляционного анализа может принести на стадии ранних исследований в областях, где характеры причин определённых явлений ещё недостаточно понятны. Это может касаться изучения очень сложных систем различного характера: как технических, так и социальных.
СПИСОК ЛИТЕРАТУРЫ
1 Сидоренко Е.В. Методы математической обработки в психологии. Спб.: ООО «Речь», 2000. – 350 с.
2 Лекция на тему: "Корреляционный анализ''// www.kgafk.ru, 2006, 8 с.
3 Ковалев В.В, Волкова О.Н., Анализ хозяйственной деятельности предприятия//polbu.ru, 2005, 2 с.
4 Поляков Л.Е., Коэффициент ранговой корреляции Спирмена//www.eduhmao.ru, 1971, 2 с.
5 Бондарь А.Г., Статюха Г.А. Планирование эксперимента в химической технологии. Киев: Высшая школа, 1976 – 335 с.
6 Адлер Ю.П., Грановский Ю.В., Маркова Е.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.–278 с.
7 Андерсон Т., Введение в многомерный статистический анализ//www.ami.nstu.ru, 1963, 24 с.
|