Южно – Российский государственный университет
экономики и сервиса
Ставропольский технологический институт сервиса
Лабораторный практикум
по физике
Механика.
Молекулярная физика.
Термодинамика
Ставрополь – 2003
Издается по решению Научно-
методического совета СТИС
от 5 декабря 2002 г.
Лабораторный практикум по физике
Механика. Молекулярная физика. Термодинамика
Ставрополь: СТИС, 2003. 24 с.
Пособие к лабораторному практикуму по физике для студентов инженерных специальностей. Содержит пять лабораторных работ, в которых студенты в форме укрупненных дидактических единиц осваивают кинематику и динамику поступательного движения, кинематику и динамику вращательного движения твердого тела, колебательное движение трех типов маятников, вязкость жидкостей и газов, изменение энтропии тела при нагревании и плавлении.
Каждая работа содержит краткое теоретическое введение, описание идеи метода измерений и экспериментальных установок, методику измерений, обработки и представления результатов. В конце работы приводится подробная схема отчета и набор контрольных вопросов и заданий. Работы насыщены заданиями, рассчитаны на 4 академических часа при условии основательной домашней подготовки.
ÓСоставители:
ст. преподаватель Киселев В.В.
канд. ф.-м. н., доцент Козлов С.А.
Рецензент:
доцент, канд. ф.-м. н., Пиунов И.Д.
 
Цель работы
Углубление теоретических представлений о кинематике и динамике поступательного движения материальной точки, экспериментальная проверка основных законов поступательного движения на специальной лабораторной установке – машине Атвуда, дальнейшее закрепление навыков оформления экспериментальных результатов.
1. Экспериментальная установка
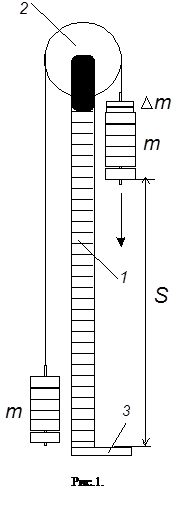 Машина Атвуда (рис.1) состоит из легкого блока 2
, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m
). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1.
Если на правый груз положить небольшой перегрузок D
m
, грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3. Машина Атвуда (рис.1) состоит из легкого блока 2
, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m
). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1.
Если на правый груз положить небольшой перегрузок D
m
, грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.
Время движения грузов измеряется с помощью ручного или стационарного секундомера.
Силы трения в машине Атвуда сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса одного из грузов (в нашей установке – правого) делается немного больше массы другого. Эта операция производится при помощи кусочков пластилина и выполняется с таким расчетом, чтобы а) грузы могли находиться в статическом положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся система приходила в равномерное движение. Масса используемого пластилина столь мала, что в последующих расчетах в массу грузов не включается. Перегрузки D
m
, с помощью которых системе задается движение, укладывают также на правый груз системы.
Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.
Реклама

2. Теоретическая часть
Второй закон Ньютона для каждого из тел системы (рис.2) в предположении невесомости блока и отсутствия трения дает
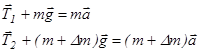 , (1) , (1)
где Т1
,2
– силы натяжения нити, m – масса каждого груза, Dm – масса перегрузка, а – ускорение системы.
В проекциях на вертикальную ось ОY получаем соот3ношения
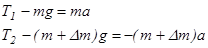 . (2) . (2)
Отсюда, так как Т1
= Т2
, ускорение движения системы равно
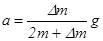 . (3) . (3)
Из выражения (3) видно, во-первых, что ускорение не зависит от времени, что доказывает равноускоренный характер движения грузов. Во-вторых, видно, что изменять ускорение системы можно, меняя перегрузки Dm. В случае равноускоренного движения скорость грузов v и их перемещение DS за время t определяются следующим образом:
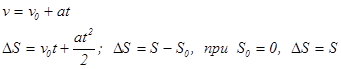 (4) (4)
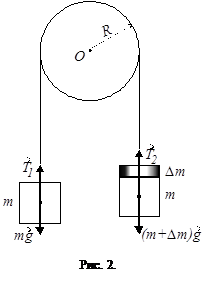 Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то
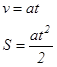 . (5) . (5)
Второе соотношение часто называют законом перемещений: «Перемещение при равноускоренном
движении прямо пропорционально квадрату времени движения».
Соотношение (5) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела
». Действительно, из соотношения (3) следует, что величина ускорения а
движения грузов прямо пропорционально действующей силе D
mg
и обратно пропорционально массе (2
m
+
D
m
)
системы.
3. Экспериментальная часть
Задание 1.
Проверка закона перемещений.
1. Проверьте вертикальность установки машины Атвуда и сбалансированность грузов.
2. На правый груз наложите перегрузок в 2-5 г.
3. Измерьте время прохождения грузом расстояний в 20, 40, 60
и т. д. см
– всего 4-5
опытов. Полученные данные заносите в таблицу 1 отчета.
4. Зависимость S
=
f
(
t
)
– квадратичная функция, а ее график – парабола и ее наглядная идентификация («узнавание») невозможна. Поэтому постройте график зависимости S = f(t2
)
. Точку (t=0, S=0)
на графике не откладывать не надо.
5. Как правило, экспериментальные точки из-за погрешностей измерений не лежат на одной прямой, что затрудняет построение графика зависимости S
=
f
(
t
2
).
Для линеаризации зависимости примените метод наименьших квадратов (МНК) (табл. 2 отчета). Проведите необходимые вычисления, запишите уравнение 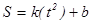 , гдеk
и b
– вычисленные с помощью МНК коэффициенты. Подставляя в полученное уравнение два произвольных значения t2
, найдите координаты двух точек, которые отложите на графике и проведите через них прямую. , гдеk
и b
– вычисленные с помощью МНК коэффициенты. Подставляя в полученное уравнение два произвольных значения t2
, найдите координаты двух точек, которые отложите на графике и проведите через них прямую.
Реклама

6. Значение коэффициента линейной корреляции, его близость к единице указывает на величину разброса экспериментальных точек и достоверность того, что полученный график действительно прямолинейный. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод, выполняется ли закон перемещений,
и если выполняется, то с каким коэффициентом корреляции.
Задание 2.
Определение ускорения движения грузов
В полученном уравнении прямой 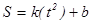 коэффициент k
равен половине ускорения системы: k=a/2
. Это позволяет вычислить ускорение грузов (a
=2
k
) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет. коэффициент k
равен половине ускорения системы: k=a/2
. Это позволяет вычислить ускорение грузов (a
=2
k
) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
Задание 3.
Определение ускорения свободного падения
(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Учитывая погрешности измерения масс грузов, перегрузка и ускорения грузов, определите относительную и абсолютную погрешность измерения ускорения свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.
Задание 4.
Проверка второго закона Ньютона
Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем двух раздельных исследований
4.1.Исследование зависимости ускорения от силы при постоянной массе
1. Тщательно сбалансируйте грузы, выбрав их массы в пределах 150 - 200 г
каждый.
2. Затем на правый груз наложите первый перегрузок D
m
. В результате в системе появляется движущая сила, равная D
mg
. При этом, конечно, общая масса системы незначительно увеличивается, но этим изменением массы по сравнению с массой грузов можно пренебречь и считать массу движущихся грузов постоянной.
3. Измерьте время равноускоренного движения системы на пути, например, 80 см.
Все данные заносят в таблицу 3 отчета.
4. Пользуясь законом путей
(5), вычисляют ускорение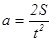 системы.
системы.
5. Поведите еще 4-5
опыта, увеличивая массу перегрузков. Заполните табл. 3.
6. В координатных осях [а,
F
]
постройте график зависимости ускорения движения от действующей силы. Точку (
F
=0,
a
=0)
на графике откладывать не надо. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение грузов действительно прямо пропорционально действующей на них силе.
7. Проанализируйте результаты своих исследований и сделайте вывод.
4.2. Исследование зависимости ускорения от массы при постоянной силе
1. Все опыты проводят с одним и тем же перегрузком. На систему в этом случае действует сила F
=
D
m
(
g
-
a
)
, но с учетом малости ускорения а
в сравнении с g
, можно считать, что на грузы действует не зависящая от ускорения, постоянная по величине сила. Ускорение системы измеряется также как и в предыдущем задании - через путь и время.
2. Для изменения массы системы одновременно на правый и левый груз накладывают дополнительные одинаковые грузы. Масса система обозначена М
. Все данные записывают в таблицу 4 отчета.
3. График зависимости ускорения от массы представляет собой кривую (гиперболу), которую идентифицировать визуально невозможно. Для определения вида зависимости между ускорением и массой 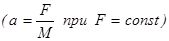 необходимо построить график в координатных осях [1/
M
,
a
].
Если экспериментальные точки ложатся на прямую с незначительным разбросом, то это - прямое подтверждение обратной зависимости между ускорением и массой. необходимо построить график в координатных осях [1/
M
,
a
].
Если экспериментальные точки ложатся на прямую с незначительным разбросом, то это - прямое подтверждение обратной зависимости между ускорением и массой.
4. Проанализируйте результаты своих наблюдений и сформулируйте вывод.
Контрольные вопросы и упражнения
1.Какое движение называется поступательным?
2.Запишите уравнения координат и скоростей для одномерного и двумерного, равномерного и равноускоренного движений.
3.Дайте определение инерциальной системы отсчета. Приведите примеры ИСО и НИСО.
4. Сформулируйте первый закон Ньютона. Приведите примеры его проявления.
5.Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?
6. Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.
7.Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.
8.Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?
9.Графики, полученные при выполнении вами работы, скорее всего не проходят через нуль. Чем это можно объяснить?
10. Выполните дополнительную проверку достоверности выводов задания 4.1.
По угловому коэффициенту D
F
/
D
a
графика 2 определите массу М
грузов и сравните ее с реальной массой.
11. Выполните дополнительную проверку достоверности выводов задания 4.2. По угловому коэффициенту D
a
/
D
(1/
M
)
графика 3 определите значение приложенной силы F
и сравните ее с реально действовавшей в системе силой.
Отчет по лабораторной работе № 1
«Изучение поступательного движения»
выполненной студент . ……….. . . . . курса, ...... Ф. И. ...........
группа …. «…»…………. 200...г.
Цель работы: .............................................................................................................................
 Задание 1
. Проверка закона перемещений Задание 1
. Проверка закона перемещений
Таблица 1
m
1
= … г,
m
2
=… г,
D
m
=… г
| № п/п
|
S,
м
|
t , c
|
t
2
,
c
2
|
| 1
|
| 2
|
| 3
|
МНК Таблица 2
Обозначения:
t
2
=
x
,
S
=
y
| № п/п |
xi
|
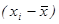 |
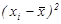
|
yi
|
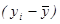 |
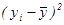 |
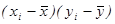 |
| 1 |
| 2 |
| 3 |
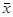 =
= |
S = |
S = |
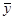 =
= |
S = |
S = |
S = |
Коэффициенты: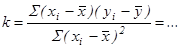 ,
,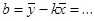 .
.
Уравнение прямой
S= kt2
+ bS = ... (t2
) + …Вычисление коэффициента линейной корреляции и погрешностей измерений
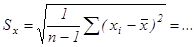 ;
;
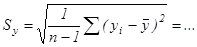 ;
;
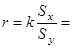 … . … .
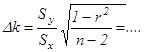 ; ; 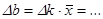 . .
k
= …
±
… м/с2
;b
=...
±
...м
Выводы: .................................................................................................................................……..
Задание 2.
Определение ускорения движения грузов.
а =…
±
… м/с2
;
d
а
=… %
Задание 3.
Вычисление ускорения свободного падения (формула и расчет)
g
=…
±
… м/с2
,
d
g
=… %
Выводы: ........................................................................................................................................
Задание 4
. Проверка второго закона Ньютона
4.1. Исследование зависимости ускорения от силы при постоянной массе
 Таблица 3 Таблица 3
Суммарная масса системы М = … г
| № п/п
|
D
m
´
10-3
,кг
|
F
=
D
mg
, Н
|
S
, м
|
t
, с
|
a
, м/с2
|
| 1
|
| 2
|
| 3
|
Выводы: ………………………………………………………………………………………………
4.2. Исследование зависимости ускорения от массы при постоянной силе
 Таблица 4 Таблица 4
Действующая силаF
=
D
mg
= …Н
| № п/п
|
M
, кг
|
M-1
,
кг
-1
|
S,
м
|
t
,
c
|
a
, м/с2
|
| 1
|
| 2
|
| 3
|
Выводы: ………………………………………………………………………………………….
Дополнительная проверка результатов измерений
1. Вычисление массы системы по углу наклона прямой: M=
D
F/
D
a=
Комментарии:
2. Вычисление силы по углу наклона прямой: F
=
D
a
/
D
(1/
M
) =
Комментарии:

Цель работы
Углубить и закрепить теоретические представления о кинематике и динамике вращательного движения, экспериментально проверить основные законы вращательного движения, продолжить отработку навыков протоколирования, оформления и анализа результатов экспериментальных наблюдений.
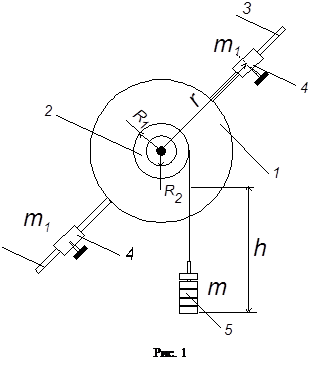
1. Экспериментальная установка
В эксперименте вращательное движение исследуется на специальной установке – маятнике Обербека, представляющем собой систему тел с закрепленной осью вращения, у которой можно изменять момент инерции, задавать разные по величине моменты вращающих сил и измерять скорости и ускорения вращательного движения.
Основная часть маятника Обербека (рис.1) - диск 1
, укрепленный в подшипнике на горизонтальной оси. Соосно с диском закреплены шкивы 2
. Момент вращающих сил можно регулировать, меняя шкив или набор грузов 5.
Момент инерции системы можно изменять, для чего по стержням 3
, укрепленным по диаметру диска, могут передвигаться цилиндры 4
одинаковой массы.
Для определения ускорения падения грузов по шкале измеряют высоту h
и секундомером - время падения t
грузов. Высота падения грузов обычно берется неизменной и максимальной для всех опытов.
Перед каждым опытом маятник следует тщательно сбалансировать. Для этого, сняв платформу со шкива, устанавливают подвижные цилиндры на стержнях симметрично и так, чтобы маятник оказался в безразличном равновесии.
2. Теоретическая часть
 Основное уравнение динамики вращательного движения твердого тела с моментом инерции J
имеет вид Основное уравнение динамики вращательного движения твердого тела с моментом инерции J
имеет вид
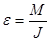 , (1) , (1)
где 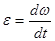 - угловое ускорение, М
– полный момент внешних сил. - угловое ускорение, М
– полный момент внешних сил. Полный момент внешних сил равен
M
=
M
н
– Мтр
, (2)
где Мн
– вращающий момент (в данном случае - момент силы натяжения нити), Мтр
– момент силы трения. С учетом этого основное уравнение динамики вращательного движения принимает вид 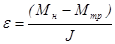 , которому можно придать форму линейной зависимости момента силы натяжения Мн
от e
:
, которому можно придать форму линейной зависимости момента силы натяжения Мн
от e
:
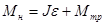 . (3) . (3)
Измерив продолжительность t
падения и перемещение h
груза, можно определить ускорение его поступательного движения
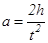 . (4) . (4)
Это ускорение равно линейному ускорению точек шкива и связано с угловым ускорением маятника соотношением:
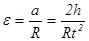 (5) (5)
Момент Мн
силы натяжения Т
нити равен
M
н
=Т
R
.(6)
Силу Т
можноопределить из второго закона Ньютона для поступательного движения, который в проекциях на ось 0
Y
дает
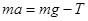 , (7)
, (7)
где m
–
масса груза.
Таким образом, момент сил натяжения нити равен
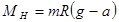 . (8) . (8)
Момент инерции маятника J
может быть определен из экспериментальных наблюдений. С другой стороны, его можно рассчитать суммированием моментов инерции диска, стержней, шкивов и подвижных цилиндров.Суммарные моменты инерции диска, шкива и стержней J
0
указаны в «паспортах» приборов. Момент инерции одного подвижного цилиндра относительно оси маятника определяются с помощью теоремы Штейнера:
J=m1
r2
+m1
l2
/12
, (9)
где m
1
- масса одного цилиндра,r
расстояние от его середины до оси маятника, l
- длина цилиндра. Вторым слагаемым в этой формуле можно пренебречь ввиду его малости. Таким образом, момент инерции всего маятника вычислять по формуле:
J=J0
+N
×
m1
×
r2
, (10)
где N
–
число подвижных цилиндров.
3. Экспериментальная часть
Задание 1.
Оценка момента силы трения, действующей в системе
1. Установите подвижные цилиндры m
1
на минимальном расстоянии от оси вращения. Сбалансируйте маятник.
2. Накладывая на легкую платформу, подвешенную к нити, небольшие грузы определите минимальную массу m0
(сумма масс платформы и грузов), при которой маятник начнет вращаться. Оцените момент сил трения из соотношения:
Мтр
= m0
gR ,
(11)
где R
– радиус шкива, на который намотана нить.
С целью минимизировать влияние силы трения на экспериментальные результаты все последующие наблюдения следует проводить с грузами массой m
³
10
m
0
.
Задание 2
.
Проверка основного уравнения динамики вращательного движения
Поскольку угловое ускорение вращающегося тела является функцией двух переменных – момента силы и момента инерции, то изучение динамики вращательного движения выполняется путем раздельного исследования двух зависимостей.
2.1. Зависимость углового ускорения
e
от действующего момента
силы М при постоянном моменте инерции системы
J
=
cons
t
1. Заранее измерьте высоту h
падения груза, которая может быть оставлена во всех последующих опытах одинаковой.
2. Укрепите цилиндры m1
на стержнях на минимальном расстоянии от оси вращения. Сбалансируйте маятник.
3. Первый опыт проводится при минимальном значении массы груза m
.
Намотайте нить на шкив. Расположите нижний край груза на уровне верхней метки. Отпустите груз, предоставив ему возможность падать. Засеките время падения груза. Измерения повторите трижды. Значения m
,
r
,
h
и среднее значение времени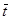 заносите в таблицу 1 отчета.
заносите в таблицу 1 отчета.
4. Измените значение момента сил Мн
, увеличив массу груза. Снова трижды измерьте времени падения. (Момент силы можно также изменить, перенеся нить на шкив другого радиуса).
5. Проведите еще не менее трех опытов, постепенно увеличивая момент силы Мн
.
6. Пользуясь формулами (4), (5), (8), определите для каждого опыта значения линейного ускорения а
, углового ускорения e
и момента силы натяжения нити Мн
. Завершите заполнение таблицы 1.
Обсуждение результатов, полученных в опытах 2.1
Постройте график зависимости углового ускорения e
от момента силы Мн
при постоянном моменте инерции J
=const.
(график 1).
Поскольку e
=
f
(Мн
)
– линейная функция (см. (3)), то ее графики в координатных осях [М,
e
,]
- прямые линии. Если экспериментальные точки не ложатся на прямую, график надо провести так, чтобы «разброс» точек был приблизительно одинаков по обе стороны прямой. Если «разброс» мал, то это свидетельство того, что угловое ускорение действительно прямо пропорционально моменту сил, приложенных к вращающемуся телу
, что подтверждает закон динамики вращательного движения.
Если разброс велик и это затрудняет построение графика, обработайте результаты методом наименьших квадратов или проделайте новую серию измерений.
2.2. Зависимости углового ускорения
e
от момента
инерции
J
системы при постоянном моменте силы М=
const
.
1. Все измерения в данном опыте должны проводятся при неизменном значении момента силы M
н
, который зависит не только от массы груза m
, радиуса шкива R
, но и от ускорения падения груза (формула (10)). Но поскольку ускорение а
оказывается гораздо меньше ускорения свободного падения g
(что видно по результатам первого опыта), момент силы Мн
можно считать приблизительно постоянным, если не менять значения m
и R
. При этом его можно вычислять по формуле:
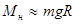 (12) (12)
Таким образом, масса груза и радиус шкива во всех последующих опытах берутся одинаковыми.
2. Укрепите цилиндры m1
на стержнях на минимальном расстоянии от оси вращения. Сбалансируйте маятник. Измерьте расстояние r
от середины подвижных цилиндров до оси вращения. Вычислите по формуле (10) момент инерции маятника в данном случае.
2. Трижды проведите измерение времени падения груза. Используя среднее значение времени падения, рассчитайте по формулам (4) и (5) линейное и угловое ускорение.
3. Переместите цилиндры m
1
на стержнях на несколько сантиметров. Проверьте балансировку маятника. Измерьте расстояние r
и вычисляют момент инерции маятника. Измерьте время падения груза.
4. Вновь переместите цилиндры на стержне, сбалансируйте маятник, вычислите момент инерции и измерьте время падения груза. Шаг перемещения цилиндров должен быть выбран таким образом, чтобы получить еще 3-4
значения момента инерции маятника. Заполните таблицу 2 отчета.
Обсуждение результатов, полученных в опытах 2.2.
В соответствии с законом динамики угловое ускорение обратно пропорционально моменту инерции, т. е. график зависимости e
=
f
(
J
)
представляет собой гиперболу и визуально не идентифицируется. Поэтому проверку зависимости e
=
f
(
J
)
лучше провести в координатных осях [
e
,
J
-1
].
В этом случае график должен представлять собой прямую линию, проходящую через начало координат. Поэтому следует вычислить величины J
-1
= 1/
J
и построить соответствующий график 2.
Если построенный по вашим измерениям график e
=
f
(
J
-1
)
представляет собой прямую линию, то этот факт подтверждает справедливость второй части закона динамики вращательного движения – угловое ускорение обратно пропорционально моменту инерции вращающегося тела.
Если разброс велик и это затрудняет построение графика, обработайте результаты методом наименьших квадратов или проделайте новую серию измерений.
Дополнительная проверка достоверности результатов
Определение момента силы трения, действующей в системе
1. В идеальном случае все графики e
=
f
(
M
н
)
должны проходить через начало координат. Однако реальные прямые отсекают некоторое значение момента сил – существует некоторое минимальное значение момента сил, которое соответствует началу движения маятника. Координата этой точки дает величину момента силы трения скольжения в подшипнике маятника.
Определите по графику 1 значение момента силы трения и сравните полученный результат с Мтр
, измеренномранее в задании 1.
2. Угловой коэффициент наклона графика 1 равен моменту инерции маятника в данной его конфигурации: J
=
D
M
/
D
e
.
Определите момент инерции системы по графику и сравните с его значением, рассчитанным по формуле (10) для этой конфигурации. Если между ними есть различие, то объясните причину и укажите границу погрешности измерений.
3. Угловой коэффициент наклона графика 2 равен моменту приложенных к маятнику сил: 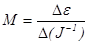 . .
Определите по графику момент сил, приложенных к маятнику, и сравните его со значением, рассчитанным по формуле (12.)
Контрольные вопросы и упражнения
1. Назовите основные характеристики вращательного движения, укажите их обозначения, дайте им определения и назовите единицы измерения. Выделите из них векторные.
2. Запишите уравнения, свзывающие угловую и линейную скорости, угловое и линейное ускорение, период и частоту.
3. Дайте определение момента инерции материальной точки. Назовите единицы измерения момента инерции.
4. Дайте определение момента силы, укажите его направление и назовите единицы измерения.
5. Что исследовалось в данной работе? Из каких заданий состоит вся работа? Как выполняется задание 1? Задание 2? Задание 3?
6. Каковы погрешности использованной в работе экспериментальной установки?
7. Какие выводы сделаны вами на основании анализа экспериментальных результатов?
8. Выполните дополнительно следующие задания контрольного характера.
8.1. Момент силы трения:По результатам задания 1
По графику 1
8.2. Момент инерции системы:По результатам вычислений
По графику 1
8.3. Момент силы: По результатам вычислений
По графику 2
Отчет по лабораторной работе № 2
«Изучение вращательного движения»
выполненной студент . . . . . курса, …...... Ф. И. ...........
группа …. «…»…………. 200...г.
Цель работы: .............................................................................................................................
Задание 1
. Определение момента силы трения
m
0
= …. кг,
R
= … м, Мтр
= Н
×
м
Задание 2
. Проверка основного уравнения динамики вращательного движения
2.1. Зависимость углового ускорения от момента действующих сил при
J
=
const
Таблица 1
r
= …м
J = …кг
×
м 2
h= …
м
|
t1
,
c
|
t2
,
c
|
t3
,
c
|
 ,
,
c
|
a,
м/с2
|
Mп
,
Н
×
м
|
e
,
с-1
|
| R =… м
m
=… кг
|
| R =… м
m
=… кг
|
| R =… м
m
=… кг
|
| R =… м
m
=… кг
|
| R =… м
m
=… кг
|
| R =… м
m
=… кг
|

Вывод:…………………………………………………………………………………………
2.2. Зависимость углового ускорения от момента инерции при
M
=
const
Таблица 2
h = … м
m = …кг
R = … м
М = …Н
×
м
|
t1
,
c
|
t2
,
c
|
t3
,
c
|
c
|
a,
м/с2
|
e
,
с-1
|
J,
,
кгм2
|
J-1
,
,
(кгм2
)-1
|
| r =… м
|
| r =… м
|
| r =… м
|
| r =… м
|
| r =… м
|
     r =… м r =… м
|
Вывод: ………………………………………………………………………………………………
Дополнительная проверка достоверности результатов
Момент силы трения:По результатам задания 1 Мтр
=
По графику 1 Мтр
=
Комментарии:
Момент инерции системы:По результатам вычислений J
=
По графику 1 J
=
Комментарии:
Момент силы: По результатам вычислений М =
По графику 2 М =
Комментарии:

Лабораторная работа №3
ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ

Цель работы:
Углубить знания по теории гармонических колебаний; освоить методику экспериментальных наблюдений и проверить законы незатухающих гармонических колебаний на примере математического, крутильного или физического маятников; закрепить навыки обработки, оформления и представления экспериментальных результатов.
Часть I. Математический маятник
1.1. Теоретическая часть
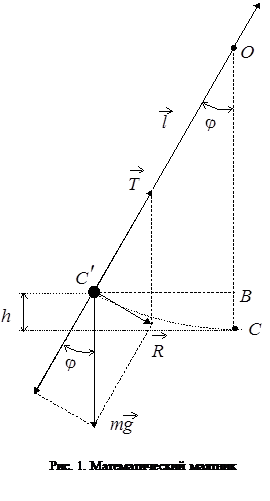 Маятник – тело, совершающее колебательное движение под действием упругой или подобной ей, «квазиупругой» силы. Простейший маятник – массивный груз на подвесе, находящийся в поле силы тяжести. Если подвес нерастяжим, размеры груза пренебрежимо малы по сравнению с длиной подвеса и масса нити пренебрежимо мала по сравнению с массой груза, то груз можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l
от точки подвеса О
. Такой маятник называется математическим
. Маятник – тело, совершающее колебательное движение под действием упругой или подобной ей, «квазиупругой» силы. Простейший маятник – массивный груз на подвесе, находящийся в поле силы тяжести. Если подвес нерастяжим, размеры груза пренебрежимо малы по сравнению с длиной подвеса и масса нити пренебрежимо мала по сравнению с массой груза, то груз можно рассматривать как материальную точку, находящуюся на неизменном расстоянии l
от точки подвеса О
. Такой маятник называется математическим
.
На груз действуют силы: натяжения нити 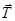 и тяжести и тяжести 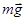 , которые в положении равновесия (точка С, рис.1) компенсируют друг друга
, которые в положении равновесия (точка С, рис.1) компенсируют друг друга 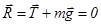 . Для возбуждения колебаний маятник выводят из положения равновесия, например, в точку С`. Теперь на него действует сила . Для возбуждения колебаний маятник выводят из положения равновесия, например, в точку С`. Теперь на него действует сила 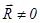 , направленная к положению равновесия и пропорциональная смещению, маятник обладает избыточной потенциальной энергией mgh
по отношению к положению равновесия. Эта энергия обуславливает колебание, происходящее по дуге окружности и описываемое основным уравнением динамики вращательного движения , направленная к положению равновесия и пропорциональная смещению, маятник обладает избыточной потенциальной энергией mgh
по отношению к положению равновесия. Эта энергия обуславливает колебание, происходящее по дуге окружности и описываемое основным уравнением динамики вращательного движения
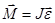 , (1) , (1)
где 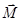 - результирующий вращающий момент, модуль этого вектора равен - результирующий вращающий момент, модуль этого вектора равен 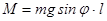 ; ; 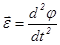 -
угловое ускорение, J = ml2
–
момент инерции груза относительно оси ОО
¢
, проходящей через точку подвеса О
, перпендикулярно плоскости колебаний (плоскости чертежа). -
угловое ускорение, J = ml2
–
момент инерции груза относительно оси ОО
¢
, проходящей через точку подвеса О
, перпендикулярно плоскости колебаний (плоскости чертежа).
Дифференциальное уравнение колебаний математического маятника в отсутствии сил сопротивления имеет вид
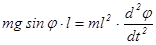 , (2) , (2)
откуда получаем
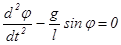 (3) (3)
Для достаточно малых углов (
j
<
5-6
°
)
sin
j
»
j
(в радианах), тогда
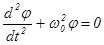 , (4) , (4)
где 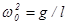 . .
Уравнение (4) представляет собой однородное дифференциальное уравнение второго порядка. Его решением является функция
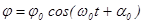 , (5) , (5)
где j
0
– амплитуда,
a
0
– начальная фаза
. В этом можно убедиться, подставив (5) в (4).
Из (5) следует, что угол отклонения маятника из положения равновесия изменяется по гармоническому закону. Величина 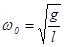 является циклической частотой
собственных колебаний маятника, тогда величина является циклической частотой
собственных колебаний маятника, тогда величина
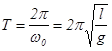 (6)
(6)
-
период колебаний математического маятника.1
Из выражения (6) следуют три закона колебаний математического маятника:
При малых углах отклонения (sin
j
»
j
или j
<
60
) и в отсутствие сторонних сил
1.период колебаний не зависит от массы маятника;
2.период колебаний не зависит от амплитуды;
3.период колебаний определяется формулой 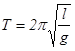 . .
Две из этих закономерностей подлежат проверке в данной работе.
1.2. Экспериментальная часть
Используемый в работе маятник представляет собой модель математического маятника - груз, подвешенный на тонкой нити. В работе используются не менее трех грузов, размеры которых значительно меньше длины нити (примерно как 1:50) и которые существенно отличаются по массе (примерно как 1:2:4), но близки по форме и размерам, чтобы силы сопротивления, возникающие при их движении, были примерно одинаковыми. Следует помнить, что длина маятника – это расстояние от точки подвеса до центра массы груза. Начальный угол отклонения маятника из положения равновесия не следует брать больше, чем 10-15°.
Задание 1. Проверка влияния массы математического
маятника на период его колебаний
1. Закрепив тело на подвесе, измеряют время 10 – 20 полных колебаний при возможно большей длине маятника. Повторяют измерения для других грузов. Данные заносят в таблицу 1.1 отчета.
2. Вычисляют период колебаний с точностью до 0,001 секунды.
3. Вычисляют оценочно относительную инструментальную погрешность измерений d.
4. Сравнивают периоды колебаний. Если различие в периоде колебаний не превышает 1% (приблизительно 0,01 с), то можно сделать вывод о практической независимости периода колебаний математического маятника от его массы.
Задание 2. Изучение зависимости периода колебаний
математического маятника от его длины
1. Подвешивают на нити стальной шарик. Длину подвеса изменяют с таким шагом, чтобы получить с данной нитью 5-6 экспериментальных точек. Число колебаний в каждом опыте 10-15. Угол отклонения маятника из положения равновесия не должен превышать 5-6°. Полученные данные заносят в таблицу 1.2 отчета.
2. Зависимость Т=
f
(
l
)
нелинейная. Поэтому для удобства экспериментальной проверки эту зависимость следует линеаризировать. Можно, например, построить график зависимости квадрата периода колебаний от длины маятника Т2
=
f
(
l
)
. Если экспериментальные точки ложатся на прямую с небольшим разбросом, то можно сделать вывод о выполнении формулы (6) и следовательно, одного из законов математического маятника. Если разброс велик, то следует повторить всю серию измерений.
Контрольное задание
. Определение ускорения свободного падения.
С помощью полученного графика можно определить ускорение свободного падения. Предварительно следует получить точное уравнение экспериментальной прямой. Для этого применяют метод наименьших квадратов (МНК) и определяют угловой коэффициент прямой, т.е.
k
=
D
T
2
/
D
l
= 4
p
2
/
g
, откуда g
=4
p
2
/
k
.
Определите из графика k
=
D
T
2
/
D
l
и вычислите ускорение свободного падения.
По формулам МНК определите погрешность измерения g
.
Часть II. Физический маятник
 2.1. Теоретическая часть 2.1. Теоретическая часть
Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О, не проходящей через центр масс С тела (рис.2).
Если маятник выведен из положения равновесия на некоторый угол j, то составляющая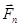 силы тяжести силы тяжести 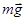 уравновешивается силой реакции оси О, а составляющая уравновешивается силой реакции оси О, а составляющая 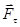 стремится возвратить маятник в положение равновесия. Все силы приложены к центру масс тела. При этом стремится возвратить маятник в положение равновесия. Все силы приложены к центру масс тела. При этом
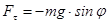 . (7) . (7)
Знак минус означает, что угловое смещение j и возвращающая сила 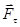 имеют противоположные направления. При достаточно малых углах отклонения маятника из положения равновесия sinj»j, поэтому сила Ft
» -mgj и она ведет себя подобно упругим силам. имеют противоположные направления. При достаточно малых углах отклонения маятника из положения равновесия sinj»j, поэтому сила Ft
» -mgj и она ведет себя подобно упругим силам.
Поскольку маятник в процессе колебаний совершает вращательное движение относительно оси О, то оно может быть описано основным законом динамики вращательного движения
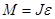 , (8)
, (8)
где М – момент силы Ft
относительно оси О, J – момент инерции маятника относительно оси О, 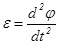 - угловое ускорение маятника. - угловое ускорение маятника.
Момент силы в данном случае равен
M = Ft
×l = -mgj×l , (9)
где l – расстояние между точкой подвеса и центром масс маятника.
С учетом (9) уравнение (8) можно записать в виде
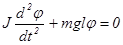 (10) (10)
или
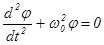 , (11) , (11)
где 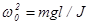
Решением дифференциального уравнения (11) является функция
j
=
j
0
×
cos(
w
0
t+
a
)
, (12)
позволяющая определить положение маятника в любой момент времени t. Из выражения (12) следует, что при малых колебаниях физический маятник совершает гармонические колебания с амплитудой колебаний j0
, циклической частотой  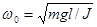 , начальной фазой a и периодом , начальной фазой a и периодом
T
=2
p
/
w
0
= 2
p
{
J
0
+
ml
2
)/
mgl
}1/2
,
(13)
Анализ формулы (13) позволяет сформулировать следующие закономерности колебаний физического маятника:
При малой амплитуде и в отсутствие сторонних сил
1.
период колебаний физического маятника зависит от момента инерции маятника относительно оси вращения (качания);
2.
период колебаний физического маятника при малых смещениях не зависит от амплитуды
колебаний;
3.
период колебаний физического маятника сложным образом зависит от положения центра масс маятника относительно точки подвеса[1]
.
2.2. Экспериментальная часть
Применяемые в данной работе физические маятники представляют собой:
1) однородный стержень, достаточно длинный, чтобы момент инерции относительно центра его массы можно было рассчитывать по формуле J
0
=
ml
2
/12;
2) плоские тела правильной геометрической формы, момент инерции которых может быть рассчитан исходя из их геометрии и массы.
Стержни закрепляются в специальной оправе с призматическим основанием, и после установки на платформу превращаются в маятники.
Плоские тела имеют отверстия для подвешивания на ось вращения.
Период колебаний маятника измеряют с помощью секундомера.
Задание 1.
Изучение зависимости периода колебаний физического маятника от его
момента инерции и расстояния между осью качаний и центром тяжести
маятника
1. Закрепите оправу на конце стержня и установите его на вилку. Измерьте расстояние l1
от оси качаний до центра тяжести стержня.
2. Отклоните стержень на 5 -6
°
и измерьте время 5-10
полных колебаний. Определите период колебаний.
3. Переместите оправу ближе к центру тяжести стержня. Измерьте расстояние l2
. Снова измерьте период колебаний стержня.
4. Тем же образом необходимо провести 5-6 опытов, постепенно перемещая опорную призму к середине стержня. Все результаты измерений занесите в таблицу 2.1. отчета.
4. По результатам опыта вычислите величины l2
и (T2
l)
.
5. Следует построить два графика. Первый график зависимости T=f(l)
отображает сложную зависимость периода колебаний физического маятника от его момента инерции и расстояния до оси качания. Второй график – линеаризация той же зависимости. Если точки на втором графике ложатся на прямую с небольшим разбросом, что объясняется погрешностями измерений, то можно сделать вывод о правильности формулы (13) для периода колебаний физического маятника.
Задание 2. Определение моментов инерции тел различной формы методом
колебаний.
1. Из набора тел к работе возьмите (по указанию преподавателя) одно и измерьте период его колебаний относительно произвольной оси.
2. С помощью формулы (16) вычислите момент инерции тела относительно оси качаний.
3. Произведите необходимые геометрические измерения и, зная массу тела, вычислите момент инерции тела относительно центра масс. С помощью теоремы Гюйгенса – Штейнера рассчитайте момент инерции тела относительно оси, проходящей через ось качаний.
4. Величину моментов инерции, полученных при измерении, сравните с рассчитанными теоретически. Для корректного заключения следует оценить погрешности измеренного и вычисленного моментов инерции. Относительная погрешность измеренного
момента инерции находится по формуле:
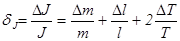 (14) (14)
Относительная погрешность вычисленного
момента инерции определяется из расчетной формулы для заданного вам тела и погрешностей, входящих в нее величин.
Контрольное задание
.
Определение ускорения свободного падения и длины стержня
С помощью полученного графика зависимости (T2
l) = f(l2
)
, можно определить ускорение свободного падения и длину стержня, используемого в опыте. Для этого следует определить угловой коэффициент наклона прямой и величину отрезка, отсекаемого прямой от оси OY
:
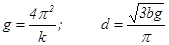 (15) (15)
При вычислении длины стержня используйте экспериментально полученное значение ускорения свободного падения.
В выводе сравните полученные величины g
и d
с их действительными значениями.
Часть
III
. Крутильный маятник
3.1. Теоретическая часть
Крутильный маятник представляет собой стержень, шнур или проволоку, один, (как правило – верхний) конец которой закреплен. К нижнему концу подвешивается тело произвольной формы. Если повернуть на некоторый угол груз с проволокой вокруг ее длинной (вертикальной) оси, и отпустить, то в системе возникнут крутильные колебания. Дифференциальное уравнение малых крутильных колебаний в отсутствие трения имеет привычный вид
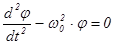 (16) (16)
По аналогии с пружинным маятником, для которого 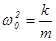 (k – коэффициент упругости, m – масса, как мера инертности), для крутильного маятника может быть записано (k – коэффициент упругости, m – масса, как мера инертности), для крутильного маятника может быть записано 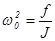 , где f – коэффициент упругости кручения подвеса, J – момент инерции груза. , где f – коэффициент упругости кручения подвеса, J – момент инерции груза.
Таким образом, если масса проволоки ничтожна в сравнении с грузом, то период гармонических колебаний крутильного маятника зависит от момента инерции подвешенного тела и от упругих свойств материала подвеса:
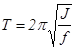 (17) (17)
Между коэффициентом f упругости кручения образца и модулем сдвига G
материала этого образца существует следующее соотношение
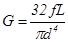 , (18) , (18)
где d
– диаметр цилиндрической проволоки, L
– ее длина.
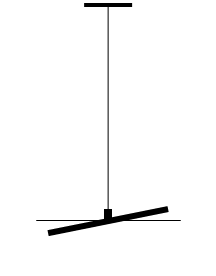
3.1. Экспериментальная часть
В данной работе крутильный маятник (рис 3) представляет собой шнур или проволоку длиной до 1 м, верхний конец которой закреплен в зажиме, например, прибит к верхней части проема двери. На нижнем конце имеется легкая горизонтальная платформа, в которой закрепляется груз. Грузы имеют правильную геометрическую форму (стержни) и известную массу, что облегчает расчет их моментов инерции.
Задание 1. Определение зависимости периода колебаний
крутильного маятника от момента инерции груза.
1. Штангенциркулем измерьте диаметр проволоки, а линейкой ее длину.
2. Измерьте длину стержня и, по известной массе, рассчитайте его момент инерции.
3. Укрепите стержень в платформе так, чтобы он располагался горизонтально, а центр его тяжести совпадал с линией подвеса.
4. Сообщите маятнику вращательный импульс так, чтобы он совершал крутильные колебания с небольшой амплитудой. Измерьте суммарное время 5-10 колебаний маятника. Вычислите период колебаний.
5. Проделайте подобные измерения и расчеты с другими телами из набора. Результаты занесите в таблицу 3.1 отчета.
6. Постройте график зависимости T(J) в координатных осях [J,T2
].
7. По виду графика сделайте вывод о характере зависимости T(J) для крутильного маятника.
Задание 2. Определение модуля сдвига материала методом крутильных колебаний
1. Используя вычисленный ранее момент инерции стержня и период колебаний по формуле (17) рассчитайте коэффициент упругости кручения f подвеса.
2. По формуле (18) рассчитайте модуль сдвига G материала проволоки.
3. Замените проволоку (материал – по указанию преподавателя) и, проделав необходимые измерения, определите коэффициент упругости кручения f и модуль сдвига G ее материала.
4. Рассчитайте абсолютную и относительную погрешности измерений величин f и G.
5. Сравните полученные значения модуля сдвига с табличными значениями и сделайте вывод о точности проделанных измерений. В выводе следует также проанализировать, какая из измеряемых величин вносит наибольшую погрешность в результат измерения.
Задание 3. Определение моментов инерции тел методом крутильных колебаний
1. Подвесив исследуемое тело (кольцо с указанной на нем массой) к проволоке и известным коэффициентом упругости кручения, измерьте период колебаний.
2. По формуле 15 рассчитайте момент инерции исследуемого тела относительно оси, совпадающей с осью проволоки.
3. Рассчитайте момент инерции кольца по его массе и радиусу относительно этой же оси вращения.
4. Сравните экспериментальный и теоретический результаты.
Контрольные вопросы
1.Дайте определение гармонических колебаний и приведите примеры.
2.Какие величины характеризуют гармонические колебания?
3.Запишите дифференциальное уравнение свободных гармонических колебаний.
4.Дайте строгое определение математического маятника и опишите закономерности его колебаний.
5.Какие упражнения были выполнены вами с этим маятником?
6.Дайте строгое определение физического маятника и опишите закономерности его колебаний.
7.Какие упражнения были выполнены вами с физическим маятником?
8.Дайте строгое определение крутильного маятника и опишите закономерности его колебаний.
9.Какие упражнения были выполнены вами с крутильным маятником?
10. Исходя из графика T
=
f
(
l
)
для физического маятника, определите при каком отношении (
l
/
d
)
период колебаний стержня минимальный.
Отчет о выполнении лабораторной работы № 1
«Изучение колебательного движения»,
выполненной студент …...... курса, …...... Ф. И. …........
группа …. «…»…………. 200…г.
Цель работы: ……………………………………………………………………………………
Часть
I
.
Математический маятник
Задание 1.Проверка влияния массы математического маятника на его период
колебаний
Длина маятника l
=…м
.
Первоначальное отклонение j
=…
Таблица 1.1.
| № п/п
|
m
, кг
|
N
|
t
,с
|
T
,с
|
| 1
|
| 2
|
| 3
|
Вывод: …………………………………………………………………………………………….
Задание 2.Изучение зависимости периода колебаний математического маятника
от его длины
Первоначальное отклонение
j =…
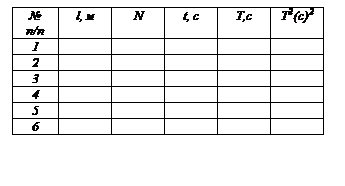 Таблица 1.2. Таблица 1.2.
График зависимости T2
=f(l)
Таблица 1.3. МНК
Обозначения:
l
=
x
,
T
2
=
y
| № п/п |
xi
|
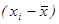 |

|
yi
|
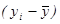 |
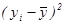 |
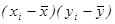 |
| 1 |
| 2 |
| 3 |
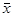 =
= |
S = |
S = |
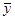 =
= |
S = |
S = |
S = |
Коэффициенты: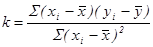 = … ,
= … ,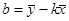 =
=
Уравнение прямой: (
T2
) = …
×
l + …
Вычисление погрешностей измерений
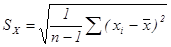 = …
,
= …
,
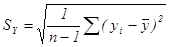 = … ,
= … ,
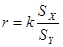 = … . = … .
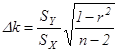 =
…,
=
…, 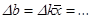
Контрольное задание
. Определение ускорения свободного падения
k =…. g = 4
p
2
/k=….
g =…
±
… м/с2
,
d
g
=… %
Выводы:
…………………………………………………………………………………………..
Часть
II
.
Физический маятник
Задание 1
. Изучение зависимости периода колебаний физического маятника от его
момента инерции и расстояния между осью качаний и центром тяжести
маятника
Первоначальное отклонение j =…
Таблица 2.1
| № п/п
|
l , м
|
N
|
t , c
|
T , c
|
l2
, c2
|
T2
l ,
c2
×м
|
| 1
|
| 2
|
| 3
|
| И т. д.
|
График зависимости T
=
f
(
l
).
График зависимости T
2
l
=
f
(
l
2
)
Выводы:
……………………………………………………………………………………………
Контрольное задание.
Определение ускорения свободного падения и длины стержня
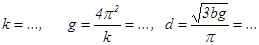
Выводы: …………………………………………………………………………………………..
Задание 2.
Определение моментов инерции тел различной формы методом
колебаний
Форма тела: ………….
Масса тела: m = …
± …. кг
Расстояние от центра тяжести до оси качания: l = …
± … м
Период колебаний тела: Т = …
±… с
Измеренный момент инерции тела относительно оси качания: J = … кг
×м2
Формула для расчета погрешности измеренного момента инерции и расчет погрешности: ………………………………………………………………………………………………………
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = …
± …. кг
× м2
;
d
J
= … %
Геометрические размеры тела (с погрешностями измерений): …………………………….
Вычисленный момент инерции тела относительно центра тяжести:
J = … кг
×м2
Вычисленный момент инерции тела относительно оси качания: J = … кг
×м2
Формулы для расчета погрешностей вычисленных моментов инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = …
± …. кг
× м2
;
d
J
= … %
Выводы:
……………………………………………………………………………………………
Часть
III
. Крутильный маятник
Задание 1.Определение зависимости периода колебаний крутильного маятника от
момента инерции груза
Таблица 3.1.
№
стерж.
|
m, кг
|
l,
м
|
J, кгм2
|
N
|
t,
c
|
T,
с
|
T2
, с2
|
| 1
|
| 2
|
| 3
|
| 4
|
| 5
|
График зависимости T
2
=
f
(
J
)
Вывод
: ……………………………………………………………………………………………..
Задание 2
.
Определение модуля сдвига материала методом крутильных колебаний
Материал подвеса: ............
Диаметр проволоки: d
= ...
±
.... мм = (…
±
…)
´
10-3
м
Длина подвеса: L
= ...
±
... см = (…
±
…)
´
10-2
м
Угловой коэффициент наклона графика:k
=(
D
T
)2
/
D
J
= …
Коэффициент упругости кручения проволоки: f
= 4
p
2
/
k
= ….
Модуль сдвига материала проволоки:
G
= ...
±
... Н/м2
,
d
G
= ... %
Выводы
: .....................................................................................................................................…..
Задание 3
. Определение моментов инерции тел методом крутильных колебаний
Форма тела: ……….
Масса тела: m = …
± …. к
г
Коэффициент упругости кручения проволоки: f
= ….
Период колебаний тела: Т = …
±… с
Измеренный момент инерции тела относительно центра тяжести:
J = … кг
×м2
Формула для расчета погрешности измеренного момента инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = …
± …. кг
× м2
;
d
J
= … %
Геометрические размеры тела (с погрешностями измерений): …………………………….
Вычисленный момент инерции тела относительно центра тяжести:
J = … кг
×м2
Формула для расчета погрешности вычисленного момента инерции и расчет погрешностей: ……………………………………………………………………………………………….
Окончательный результат с абсолютной и относительной погрешностью измерения:
J = …
± …. кг
× м2
;
d
J
= … %
Выводы
……………………………………………………………………………………………..
 |
Лабораторная работа №4
ВЯЗКОСТЬ ЖИДКОСТЕЙ И ГАЗОВ
|
|
 |
Цель работы
Углубить теоретические представления о механизмах возникновения внутреннего трения. Освоить методы измерения вязкости жидкостей и газов.
1. Теоретическая часть
 Макроскопическое движение, возникшее в жидкости или газе под действием внешних сил, постепенно прекращается. Очевидно, что это происходит под действием сил сопротивления, существующих внутри жидкостей и газов. Силы такого внутреннего
трения присущи всем реальным жидкостям и газам и составляют основу понятия вязкости. Макроскопическое движение, возникшее в жидкости или газе под действием внешних сил, постепенно прекращается. Очевидно, что это происходит под действием сил сопротивления, существующих внутри жидкостей и газов. Силы такого внутреннего
трения присущи всем реальным жидкостям и газам и составляют основу понятия вязкости.
1.1. Вязкость жидкостей
Причину возникновения сил вязкого трения в жидкостях можно пояснить с помощью рисунка 1. Пусть два слоя жидкости, середины которых отстоят друг от друга на расстоянии dz
,
имеют скорости v
1
и v
2
.
Co стороны слоя, который движется быстрее, на слой, который движется медленнее, действует ускоряющая сила F
1
.
Наоборот, на быстрый слой действует тормозящая сила F
2
со стороны медленного слоя. Эти силы, направленные по касательной к слоям, называются силами внутреннего трения.
И. Ньютон предложил для их расчета следующую формулу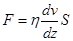 , (1) , (1)
где dv
/
dz
-
градиент скорости движения слоев в направлении, перпендикулярном трущимся слоям, S
-
площади соприкасающихся слоев, h
- динамическая вязкость (вязкость) жидкости или газа
или коэффициент внутреннего трения.
Динамическая вязкость - характеристика данного вещества, численно она равна силе трения, возникающей между двумя слоями этой жидкости площадью по 1 м2
каждый при градиенте скорости, равном 1 м/с на метр. Размерность коэффициента вязкости 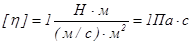 . В некоторых случаях принято пользоваться так называемой кинематической вязкостью,
равной динамической вязкости жидкости, деленной на плотность жидкости . В некоторых случаях принято пользоваться так называемой кинематической вязкостью,
равной динамической вязкости жидкости, деленной на плотность жидкости 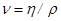 . .
В жидкостях внутреннее трение обусловлено действием межмолекулярных сил. Расстояния между молекулами жидкости сравнительно невелики, а силы взаимодействия значительны. Молекулы жидкости, подобно молекулам твердого тела, колеблются около
положения равновесия, но эти положения не являются постоянными. По истечении некоторого времени молекула скачком переходит в новое положение. Это время называется временем «оседлой жизни» молекулы.
Среднее время «оседлой жизни» молекул называется временем релаксации
t
.
Вязкость жидкости обусловлена силами межмолекулярного взаимодействия, характерными для каждого вещества. Вещества с малой вязкостью - текучи, и наоборот, сильно вязкие вещества могут иметь механическую твердость, как, например, стекло. Вязкость существенно зависит от количества и состава примесей, а также от температуры. С повышением температуры время релаксации уменьшается, что обуславливает рост подвижности жидкости и уменьшение ее вязкости.
1.2. Вязкость газов
Вязкость газов, в отличие от жидкостей, увеличивается при повышении температуры. Различный характер зависимости вязкости газов и жидкостей от температуры указывает на различный механизм их возникновения, хотя формула Ньютона одинаково справедлива и для обоих этих состояний.
              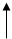  Рассмотрим, как возникает внутреннее трение в газах. В отличие от жидкостей здесь силы внутреннего трения возникают в результате микрофизического процесса
передачи импульса
от одного слоя газа к другому. Переносчиками импульса выступают молекулы газа. Рассмотрим, как возникает внутреннее трение в газах. В отличие от жидкостей здесь силы внутреннего трения возникают в результате микрофизического процесса
передачи импульса
от одного слоя газа к другому. Переносчиками импульса выступают молекулы газа.
Выделим в движущемся потоке газа вдоль вектора скорости два параллельных соприкасающихся слоя. Пусть скорости их движения по величине и направлению таковы, как показано на рисунке 2. Имеющиеся в тепловой скорости, а, следовательно, и в импульсе молекул составляющие р
x
в рассматриваемых слоях неодинаковы. Молекулы, находящиеся в более медленном, «нижнем», слое имеют меньшую составляющую импульса р
x
и, попав в «верхний» слой, затормаживают его. «Верхние»же молекулы, наоборот, переносят импульс больший, чем имеют молекулы «нижнего» слоя, и поэтому ускоряют этот слой.
 Вязкость различных газов неодинакова и тем больше, чем больше молекулярная масса газа. Она увеличивается также с повышением давления, т.е. концентрации молекул, и температуры. Чем выше температура газа, тем интенсивней происходит обмен молекулами между его слоями, тем лучше работает механизм внутреннего трения. Вязкость различных газов неодинакова и тем больше, чем больше молекулярная масса газа. Она увеличивается также с повышением давления, т.е. концентрации молекул, и температуры. Чем выше температура газа, тем интенсивней происходит обмен молекулами между его слоями, тем лучше работает механизм внутреннего трения.
1.3. Движение твердого тела в жидкости
При движении тел в вязкой жидкости возникают силы сопротивления. Происхождение этих сил можно объяснить двумя разными механизмами. При небольших скоростях, когда за телом нет вихрей (ламинарное течение или обтекание
), сила сопротивления обуславливается только вязкостью жидкости. Слои жидкости, прилегающие к телу, неподвижны относительно тела. Граничащие с ними слои увлекаются ими по описанному выше механизму вязкого трения в жидкостях. Так создаются силы, тормозящие относительное движение твердого тела и жидкости. Величину этих силы трения можно рассчитать с использованием формулы Ньютона (1).
Второй механизм сил сопротивления связан с образованием вихрей (рис.3). Давление в жидкости меняется в зависимости от скорости потока так, что в области вихрей оно существенно уменьшается (уравнение Бернулли: p
1
+
r
v
1
2
/2=
p
2
+
r
v
2
2
/2
). Разность давлений D
p
=
r
(
v
1
2
–
v
2
2
)/2 в
областях перед телом и за ним создает силу «лобового» сопротивления и тормозит движение тела. Часть работы, совершаемой силами трения при движении тела в жидкости, идет на образование вихрей, энергия которых переходит затем в теплоту.
Если движение тела в жидкости происходит медленно, без образования вихрей, то сила сопротивления создается только по первому из описанных механизмов. Для тел сферической формы ее величину определяют по формуле Стокса
:
Fc
=6
p
h
rv
(2)
где г -
радиус шарика; v
-
скорость его равномерного
движения; h
- вязкость жидкости.
2. Экспериментальная часть
Часть I.
Определение вязкости жидкости по методу Стокса
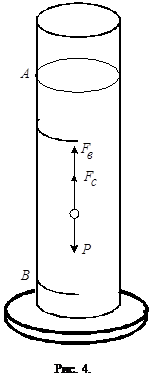 Теория метода Теория метода
Надвижущийся шарик в жидкости действуют трисилы: силатяжести - Р
, выталкивающая сила FA
и сила сопротивления Fc
.
Силу тяжести и выталкивающую силу можно определить через объем шарика, плотность r
шарика и плотность r
0
жидкости:
P=4
p
r3
r
g/3
(3)
FA
=4
p
r3
r
o
g/3
(4)
Сила тяжести и выталкивающая сила постоянны. При малой скорости падения шарика сила сопротивления прямо пропорциональна этой скорости и поэтому на начальном этапе он движется равноускоренно. Затем наступает момент, когда все три силы уравновешиваются, и шарик начинает двигаться равномерно:
P
=
FA
+
Fc
или 4
p
r
3
r
g
/3=
4
p
r
3
r
o
g
/3+6
p
h
rv
, (5)
откуда
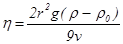 (6) (6)
Экспериментальная установка
Для определения вязкости жидкости по методу Стокса берется высокий цилиндрический сосуд с исследуемой жидкостью (рис.4). На сосуде имеются две кольцевые метки А
и В
. Метка А
соответствует той высоте, где силы, действующие на шарик, уравновешивают друг друга и движение становится равномерным. Нижняя метка В
нанесена для удобства отсчета времени в момент падения шарика.
Бросая шарик в сосуд, отмечают по секундомеру время t
прохождения шариком расстояния l
= АВ
между двумя метками.
Если в формулу (6) подставить выражение для скорости движения v=l/t
и вместо радиуса r
ввести диаметр шарика d
, то окончательная расчетная формула приобретает вид:
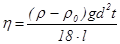 ( 7) ( 7)
Ход выполнения работы
1. Измерьте расстояние между метками А
и В.
2. При необходимости измерьте с помощью ареометра плотность жидкости r
0
.
3. Измерьте микрометром или штангенциркулем диаметр d
шарика.
4. Бросив шарик в сосуд с жидкостью, измерьте время t
прохождения шариком расстояния между метками А
и В.
5. По формуле (7) вычислите вязкость жидкости h
.
6. Аналогичные измерения проделайте с пятью шариками. Результаты измерений и вычислений заносите в таблицу 1 отчета.
7. По результатам всех опытов найдите среднее значение вязкости h
.
8. Для оценки систематической погрешности измерения вязкости используйте расчетную формулу (7). Выведите формулу для вычисления относительной погрешности измерения. При этом условно считается, что табличные величины, входящие в формулу, не имеют погрешностей, а погрешности измеренных величин /, d
,
r
определяются точностью приборов, использованных для их измерения.
9. Полученное значение вязкости сравните с табличной величиной для данной жидкости. При объяснении причин расхождения укажите какой из используемых измерительных приборов вносит в окончательный результат наибольшую погрешность.
Часть II. Определение вязкости воздуха по методу Пуазейля
Теория метода
При ламинарном движении жидкостей и газов по гладким цилиндрическим трубам расход (объем жидкости или газа, протекающих через поперечное сечение трубы за одну секунду), зависит от ее вязкости, диаметра трубы, ее длины и разности давления на ее концах. Соответствующее соотношение было выведено Пуазейлем и носит его имя.
V=
D
p
p
r2
D
t/
h
l
,
куда входят перепад давления, радиус трубы, длительность течения, коэффициент вязкости, длина трубы.
На основании этого соотношения разработан и широко применяется метод измерения вязкости жидкостей и газов - метод Пуазейля.
Для газов он состоит в измерении скорости ламинарного протекания газов в тонком капилляре с известными размерами и при контролируемой разности давлений. В данной работе по методу Пуазейля определяется вязкость воздуха. На величину вязкости газов большое влияние оказывают посторонние примеси. Для атмосферного воздуха, например, следует учитывать содержание водяных паров. В установках для точных измерений воздух перед поступлением в капилляр осушают различными, чаще всего химическими осушителями. Важно также помнить, что вязкость газов в большой степени зависит от их температуры, что также предусмотрено в лабораторных приборах.
Экспериментальная установка
Экспериментальная установка для определения воздуха (рис. 4) состоит из сосуда 1
со сливным шлангом 2, капилляра 3,
мерительного стакана 4
и жидкостного манометра 5.
Перед опытом сосуд заполняется водой. При опущенном шланге 2 уровень воды в сосуде уменьшается и возникает перепад давлений воздуха на концах А
и В
капилляра 3,
который измеряется манометром 5.
Освободившийся объем занимает воздух, проникающий в сосуд через капилляр. При этом объем вытекшей воды равен объему воздуха, прошедшему через капилляр.
Расчетная формула для определения коэффициента вязкости по методу Пуазейля имеет вид:
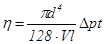 (8) (8)
где d
-
диаметр капилляра, / - его длина, V-
объем прошедшего через капилляр воздуха (объем вытекшей из сосуда жидкости), D
р -
перепад давлений на концах капилляра (показание манометра), t
- время протекания воздуха через капилляр.
Ход выполнения работы
1. Закрепите сливной шланг в вертикальном положении. Заполните сосуд 7 водой до начала его конической части. Плотно закрепите пробку с капилляром в горловине сосуда.
2. Опустите сливной шланг вниз, подставив под него мерный сосуд. Измерьте секундомером время t
,
в течение которого из сосуда вытечет объем V
=200 см3
воды.
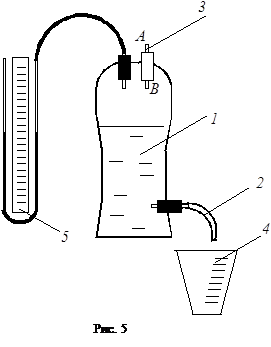 3. Измерьте в это же времени перепад давлений D
р
по манометру. 3. Измерьте в это же времени перепад давлений D
р
по манометру.
Примечание:
При постепенном понижении уровня воды в сосуде скорость истечения уменьшается. Это приводит к изменению перепада давлений воздуха на концах капилляра. Поэтому необходимо брать среднее за время опыта значение D
р.
4. По формуле (8) вычислите вязкость воздуха.
5. Опыт повторите не менее трех раз. Результаты занесите в таблицу 2 отчета.
6. Оцените относительную погрешность измерения вязкости воздуха. Погрешности измерений диаметра и длины капилляра возьмите из «паспорта» прибора.
9. В выводе сравните полученное значение вязкости воздуха с табличным значением (h
=
1,8
×
1
0-5
Па
×
с при 18о
С)
Дополнительное задание
1. Вычислите плотность воздуха по формуле 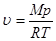 ,
где М
= 0,029
кг/моль –
молярная масса воздуха, R
-
универсальная газовая постоянная, давление и температура - нормальные. ,
где М
= 0,029
кг/моль –
молярная масса воздуха, R
-
универсальная газовая постоянная, давление и температура - нормальные.
2. Вычислите среднюю арифметическую скорость молекул воздуха при данных условиях 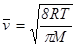 . .
3. Вычислить среднюю длину свободного пробега 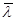 молекул воздуха при нормальных условиях, исходя из формулы Максвелла молекул воздуха при нормальных условиях, исходя из формулы Максвелла 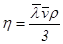 . .
4. Исходя из формулы р
= nkT
,
вычислить концентрацию п
молекул воздуха при нормальных условиях (
k
-
постоянная Больцмана).
5. Вычислить среднее число столкновений молекул, испытываемых одной молекулойза одну секунду 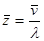 . .
6. Вычислить эффективный диаметр молекул воздуха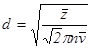
Отчет по лабораторной работе №4
«Вязкость жидкостей и газов»
выполненной студент…. …. курса, ….. Ф.И. ……….
группа ….. «….» …………….. 200 … г.
Цель работы: ………………………………………………………………………………………
Часть I. Определение вязкости жидкости по методу Стокса
Таблица 1
Жидкость....................
Расстояние между метками l
=... ±..... см
Плотность жидкости r
0
= …
±
… г/см3
Плотность материала шарика r
= …
±
… г/см3
| № п/п
|
Диаметр шарика
d
, мм
|
Время движения шарика
t
, с
|
Вязкость жидкости
h
, Па
×
с
|
| 1
|
| 2
|
| 3
|
| 4
|
| 5
|
Среднее значение вязкости жидкости 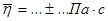
|
Формулы для расчета и расчет погрешности измерения вязкости жидкости1
:
Вывод: ……………………………………………………………………………………………..
Часть П. Определение вязкости воздуха по методу Пуазейля
Таблица 2
Диаметр капилляра d
=... ± ... мм
; Длина капилляра I =... ±.... мм
№ п/п
|
Объем
прошедшего
через капилляр
воздуха
V
,
см3
(или мл)
|
Перепад
давлений,
D
h
,
см вод. ст.
|
Перепад
давлений
D
р,
Па
|
Время
протекания воздуха через капилляр
t
,
с
|
Вязкость воздуха
h
´
10-5
, Па
×
с
|
| 1
|
| 2
|
| 3
|
Среднее значение вязкости воздуха
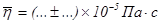 |
Формулы для расчета и расчет погрешности измерения вязкости воздуха[2]
:
Вывод: ……………………………………………………………………………………………..
Дополнительное задание
Нормальные условия:p
= … мм рт. ст.= … Па;
T
= … К
1. Плотность воздуха: r
= … кг/м3
2. Средняя арифметическая скорость молекул воздуха: 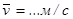
3. Средняя длина свободного пробега молекул воздуха: 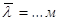
4. Концентрация молекул воздуха: n
=… 1/м3
5. Среднее число столкновений молекул воздуха 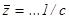
6. Эффективный диаметр молекул воздуха: d
= … м
 

Цель работы:
Углубление теоретических представлений об энтропии, экспериментальное наблюдение процесса плавления и кристаллизации и получение навыков измерения изменения энтропии.
1. Теоретическая часть
Термодинамический процесс обратим, если, протекая в обратном направлении, он возвращает систему в исходное состояние без затрат энергии (упругий удар, колебания маятника в отсутствии сопротивления, идеализированный цикл Карно). Большинство процессов в технике – необратимы или, по крайней мере, содержат этапы, являющиеся необратимыми (неупругий удар, процессы с трением, диффузия, теплообмен). Энтропия является количественной мерой степени необратимости процесса.
Из равенства КПД тепловых двигателей и термического КПД обратимого цикла Карно
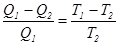 (1) (1)
можно получить выражение
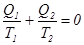 (2) (2)
Это выражение означает, что количество теплоты, полученное или отданное телом при обратимом процессе, пропорционально температуре. Отношение Q
/
T
называется приведенным количеством теплоты.
Сумма приведенных количеств теплоты при любом обратимом процессе равна нулю, что в дифференциальной форме имеет вид 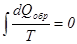 , ,  (3) (3)
причем интеграл берется по замкнутому контуру (круговой процесс). В каждом цикле кругового процесса все термодинамические параметры принимают исходные значения, т.е. их изменение равно нулю. В этом случае равна нулю и сумма приведенных количеств теплоты, что позволяет ввести термодинамический параметр состояния энтропию
S
, как некоторую функцию состояния, дифференциал которой
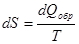 (4)
(4)
Если некоторая термодинамическая система обратимо переходит из состояния 1
, характеризующегося параметрами р1
,
V
1
,
Т1
, в состояние 2
с параметрами р2
,
V
2
, Т2
,
то изменение энтропии системы при таком переходе может быть вычислено по формуле
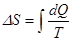 , (5) , (5)
где dQ
—
элементарный приток теплоты в систему, Т
- термодинамическая температура всей системы. Интеграл берется вдоль «траектории» процесса, например абс
при нагревании и плавлении, как показано на рисунке 1.
Возможны следующие три случая:
а)
D
S
=0
– процесс обратим, может протекать как в прямом, так и в обратном направлениях;
б)
D
S
>0
- процесс необратим, самопроизвольно протекает только в одном направлении
в)
D
S
<0
- процесс самопроизвольно протекать не может, необходим подвод энергии извне.
2-й закон термодинамики с использованием понятия энтропии формулируется так:
Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться.
В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом способов, которыми может быть реализовано данное состояние макроскопической системы. Согласно Больцману энтропия системы и термодинамическая вероятность связаны между собой следующим соотношением
S
=
klnW
,
(6)
где k
– постоянная Больцмана. Энтропия является мерой неупорядоченности системы.2. Экспериментальная часть
Установка собрана по схеме, показанной на рисунке 2. Она состоит из электронагревателя малой мощности 2
(трубчатая муфельная печь)
, питание которого осуществляется через понижающий трансформатор 3.
В стеклянной пробирке находится небольшой кусочек олова известной массы 1
. Пробирка закреплена в штативе и может опускаться в нагреватель или подниматься из него. Температуру олова измеряют дифференциальной термопарой. Она состоит из двух термопар,включенных «навстречу» так, что милливольтметр показывает разность термоЭДС. При этом температура t
1
«холодного спая» термопары должна быть постоянной и вполне определенной, для чего этот спай термопары рекомендуется погружать в тающий лед. Искомая температура t2
определяется по градуировочному графику этой термопары или с помощью градуировочного коэффициента. Используемая в данной работе термопара в требуемом интервале температур имеет градуировочный коэффициент a
=19,5 град/мВ.
Если «холодный» спай термопары находится не в тающем льду, а в воздухе, то к полученным из градуировки результатам необходимо приплюсовать комнатную температуру.
В качестве электроизмерительного прибора используется мультиметр, который включается на измерение постоянного напряжения на пределе 200 м
V
.
В данной лабораторной работе определяется изменение энтропии, происходящее при нагревании и плавлении (или при охлаждении и затвердевании) определенной массы олова.
Возрастание энтропии при нагревании можно объяснить возрастанием энергии колебательного движения атомов олова в кристаллической решетке, что приводит к увеличению возможных микросостояний и, следовательно, к росту энтропии, как меры неупорядоченности системы. При плавлении энтропия системы возрастает дополнительно за счет неупорядоченности пространственного распределения атомов в жидкой фазе.
Если первоначально температура олова равна комнатной, то при подведении теплоты олово сначала нагревается до температуры плавления, потом плавится при постоянной температуре. Изменение энтропии на первом этапе – в процессе нагревания, равно:
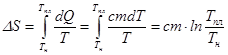 (7) (7)
где Тпл
- температура плавления, Тн
—
начальная температура кристаллической фазы, с
- удельная теплоемкость олова: с =
2,3 • 102
Дж/(кг
×К)
, m
- масса олова.
На втором этапе - при плавлении, изменение энтропии определяется по формуле:
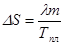 (8)
(8)
где l
— удельная теплота плавления (для олова l
=5,85
×
104
Дж/кг
).
Полное изменение энтропии равно:
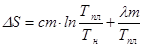 (9) (9)
Эта величина положительна D
S
>0,
если рассматриваемый процесс сопровождается притоком теплоты в систему, т.е. при нагревании и плавлении. При кристаллизации и охлаждении D
S
<
0
. Для вычисления D
S
надо знать параметры, входящие в (9), в частности, необходимо измерить температуру плавления и температуру кристаллизации олова.
Измерения и обработка результатов
1. Изучите описание экспериментальной установки. При работе особое внимание уделить
технике безопасности
:
· Включайте нагреватель только с разрешения преподавателя.
· Не касайтесь металлических деталей установки во время его работы. Опасайтесь ожогов.
· Прежде, чем производить любые манипуляции с прибором выньте вилку трансформатора из розетки.
2. Подготовьте прибор к работе. Для этого опустите пробирку с оловом в горловину печи. Подключить мультиметр к гнездам термопары, выставив его на 200mV
постоянногонапряжения.
3. Включите прибор (с разрешения преподавателя). Через каждые 20 –30
секундзаписывайте показания мультиметра. Данные заносите в таблицу 1 отчета. Когда милливольтметр покажет 12 – 13 мВ
, процесснагревания остановите, отключив электропечь.
4. Для охлаждения образца поднимите его и отведите в сторону от электропечи. Для этого отверните винт крепления муфты штатива, поверните держатель пробирки и закрепить его в новом положении.
5. Произведите измерения температуры в процессе охлаждения образца. Для этого вновь необходимо отмечать показания милливольтметра через каждые 20-30
секунд. Этот процесс завершите при показаниях милливольтметра 4 – 5 мВ
. (таблица 2)
6. Пользуясь градуировочным коэффициентом, переведите показания милливольтметра в градусы Цельсия с учетом комнатной температуры. Заполнить соответствующую строку в таблицах 1 и 2.
7. По полученным результатам постройте графики изменения температуры олова со временем tо
=
f(
t).
Желательно, чтобы в верхней части графики нагревания и охлаждения кончались и начинались из одной точки.
8. Вновь включите электропечь и повторно снимите данные для построения кривых нагревания-плавления и кристаллизации-охлаждения олова. Заполнить таблицы 3 и 4. Постройте на прежней координатной сетке новые графики tо
=f(
t).
По горизонтальным участкам всех четырех кривых определите среднее значение температуры фазовых переходов: плавления Тпл
и кристаллизации Ткр
(по шкале Кельвина).
9. По данным эксперимента, используя выражения (7-9), вычислите:
· Изменение энтропии D
S
1
данного образца олова при изменении температуры от комнатной до температуры плавления олова.
· Изменение энтропии этого образца D
S
2
при плавлении олова.
· Полное изменение энтропии в процессе нагревания и плавления образца.
· Изменение энтропии D
S
3
данного образца олова при кристаллизации образца.
· Изменение энтропии D
S
4
данного образца олова при охлаждении образца от температуры кристаллизации до конечной температуры.
· Полное изменение энтропии образца при его кристаллизации и охлаждении.
Контрольные вопросы
1. Какими энергетическими превращениями сопровождается процесс плавления? Процесс кристаллизации?
2. Приведите примеры обратимых и необратимых термодинамических процессов.
3. Каков физический смысл «приведенной теплоты»? Почему в необратимых процессах сумма приведенных количеств теплоты не равна нулю?
4. Почему имеет смысл изменение энтропии, а не ее значение?
5. Каков вероятностный смысл понятия энтропия? Приведите примеры.
6. Как рассчитать изменение энтропии при нагревании? При фазовом переходе в веществе?
7. Каков принцип действия термопары? Дифференциальной термопары?
Отчет по лабораторной работе № 5
«Изучение изменения энтропии в неизолированной системе»
выполненной студент . . . . . курса, ...... Ф. И. ...........
группа …. «…»…………. 200...г.
Цель работы: .............................................................................................................................
Масса образца m
= .... кг
Удельная теплоемкость олова с = .... Дж/кг
×
К
Удельная теплота плавления олова l
= ... Дж/кг
Комнатная температура t
к
= ...
°
С
Таблица 1
Таблица 2
Таблица 3
Таблица 4
Расчет изменения энтропии
При нагревании образца: Тн
= ... К, Тпл
= ... К,
D
S
1
= ... Дж/К
При плавлении образца: Тпл
= ... К
D
S
2
= ... Дж/К
Полное изменение при нагревании и плавлении: D
S
= ... Дж/К
При кристаллизации образца: Ткр
= ... К, Тк
= ... К,
D
S
3
= ... Дж/К
При охлаждении образца: Ткр
= ... К,
Тк
= ... К,
D
S
4
= ... Дж/К
Полное изменение при кристаллизации и охлаждении: D
S
= ... Дж/К
Выводы: ………………………………………………………………………………………..
[1]
Анализ формулы (13) показывает наличие минимума у периода колебаний при ml2
=
J0
.
[2]
Оценка погрешности измерения производится по данным первого опыта с указанием погрешностей всех величин, входящих в расчетную формулу. В окончательный результат вносится среднее по всем опытам значение вязкости.
|