Термины и единицы измерения при описании электрического тока
Единицы измерения электрического тока
Единица измерения, используемая для выражения скорости потока жидкости, в определенной степени дело вкуса; можно измерять поток воды через трубу, например, в кубических футах в минуту, хотя в некоторых случаях миллиметры в час подходят больше. Сила электрического тока обычно измеряется в кулонах в секунду или в амперах (сокращенно А). Одни кулон соответствует заряду, содержащемуся в 6,24· 1018
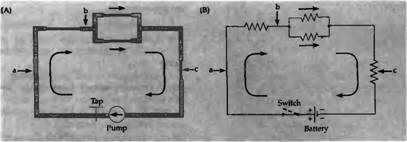
электронах. В электрических цепях и уравнениях ток обычно обозначается I или i. Как поток воды, ток векторная величина, иначе говоря, он имеет определенное направление. Направление тока часто обозначают стрелками, как на графике 1, всегда предполагая, что ток движется от положительного к отрицательному полюсу батареи.
Что означают термины положительный или отрицательный применительно к электрическому току? Здесь аналогия с гидравликой не помогает. В данном случае стоит представить эффект тока, проходящего через химический раствор. Например, представим, что две медные проволоки погружены в раствор сульфата меди н соединены с положительными и отрицательными полюсами батареи. Ионы меди в растворе, отталкиваясь от положительно заряженной проволоки, проходят к отрицательно заряженному стержню. Положительные ионы меди движутся в направлении условно принятом для тока: от положительного полюса к отрицательному. Одновременно ионы сульфата передвигаются в противоположном направлении и накапливаются на положительно заряженной проволоке. В таком случае направление, заданное току, соответствует направлению, в котором движутся положительные заряды в цепи; отрицательные заряды передвигаются в противоположном направлении.
Аналогия с гидравликой также полезна при объяснении источника энергии для тока и понятия электрического потенциала. Поток жидкости, изображенный на рис. 1, зависит от разности давления. Движение тока происходит от области высокого давления по направлению к области с низким давлением. При равном давлении в этих областях движение практически отсутствует. Общее давление в цепи обеспечивается использованием энергии насоса. В электрической цепи, изображенной здесь, «электрическое давление», или потенциал, обеспечивается батареей, в которой запасена химическая энергия. Гидравлическое давление измеряется в г/см2
, а электрический потенциал в вольтах.
Реклама

Символы, использованные в диаграммах параллельных и последовательных электрических цепей, проиллюстрированы на рис. 2. В соответствии с названиями, вольтметр измеряет электрический потенциал и является эквивалентом измерения давления в гидравлике; амперметр измеряет силу тока в цепи и соответствует флоуметру.
| Рис. 1. Гидравлические и электрические цепи. (А, В) соответствующие цепи для для тока воды и электрического тока. Батарея аналогична насосу, который работает при постоянном давлении, переключатель соответствует крану в гидравлической линии, а сопротивления — сужениям трубы. |
|
Рис. 2. Обозначения, применяемые в схемах электрических цепей.
|
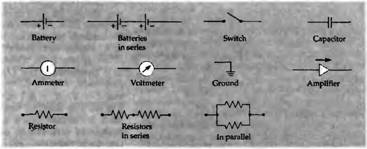 |
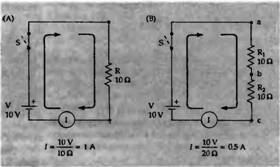
Рис. 3. Закон Ома в простой цепи. (А) Ток I = (10V)/(10) = 1A. (В) Ток I = (10V)/(20) = 0,5 А, и напряжение на каждом сопротивлении 5 V.
|
 |
Закон Ома и электрическое сопротивление
В гидравлических системах, по крайней мере в идеальных условиях, количество тока, проходящего через систему, увеличивается с давлением. Отношение между давлением и скоростью течения тока определяется сопротивлением, собственной характеристикой трубы. Длинные трубы маленького диаметра обладают большим сопротивлением, чем короткие трубы большого диаметра. Аналогичным образом, прохождение тока в электрических цепях зависит от сопротивления цепи. Опять же, тонкие длинные провода обладают большим сопротивлением, чем широкие короткие. Если ток проходит через ионный раствор, его сопротивление увеличится при меньшей концентрации раствора. Это происходит потому, что менее концентрированный раствор имеет меньше ионов, способных переносить электрический ток. В проводниках, таких как металлическая проволока, отношение между током и разностью потенциалов описывается законом Ома, сформулированным в 1820 году. Согласно этому закону, величина тока I, проходящего через проводник, прямо пропорциональна приложенной к нему разности потенциалов, согласно уравнению I = V/R, где R — сопротивление провода.
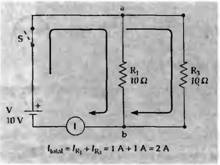
Рис. 4. Параллельные сопротивления. Кода R1
и R3
параллельно включены в цепь, падение напряжения на каждом сопротивлении равно 10 V, а общий ток цепи 2 А.
.
|
 |
Если I измеряется в амперах, V в вольтах, то единицей измерения R является ом (Ом). Величина, обратная сопротивлению, называется проводимостью, и является отражением того, с какой легкостью проходит ток через проводник. Проводимость обозначается g и равна 1/R; единицей измерения проводимости является сименс (См). Таким образом, закон Ома можно также записать в форме I = gV.
Реклама

Применение закона Ома при расчетах (цепей)
Закон Ома действителен, когда кривая зависимости тока от потенциала представлена прямой линией. В любом контуре или той его части, для которой выполнено это условие, можно вычислить каждую переменную, если известны две другие. Например:
1. Можно пропустить известный ток через нервную мембрану, измерить изменение потенциала и затем вычислить сопротивление мембраны по формуле
R = V/I.
2. Измеряя разницу потенциала, производимую неизвестным током, и зная сопротивление мембраны, можно вычислить ток, используя формулу I = V/R.
3. Пропустив известный ток через мембрану и зная ее сопротивление, можно вычислить изменение потенциала:
V = IR.
Необходимо упомянуть два простых, но важных правила (законы Кирхгофа).
1. Алгебраическая сумма всех токов, направленных к одному узлу, равна нулю. Например, в точке а на рис. 4
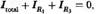
что означает, что
I[ota]
(входящий) = -IR
1
- IR
3
(выходящий),
(это просто означает, что заряд не производится и не разрушается в каком-либо месте цепи).
2. Алгебраическая сумма напряжений батарей равна алгебраической сумме всех IR падений напряжения в цепи. Пример этого показан на рис. 3В:
V = IR1
, + IR2
(это соответствует закону сохранения энергии). Теперь мы можем изучить более детально цепи на рис. 3 и 4, которые необходимы для создания модели мембраны. На рис. 3А изображена батарея (V) на 10 вольт, связанная с сопротивлением (резистором) R в 10 Ом. Переключатель S можно размыкать и замыкать, прерывая или устанавливая таким образом прохождение тока. Напряжение на Я равно 10 вольт, поэтому ток I, измеренный амперметром, согласно закону Ома, равен 1,0 ампер. На рис. 3В один резистор заменен двумя резисторами R1
и R2
, соединенными последовательно. По первому закону Кирхгофа, ток, входящий в точке b, должен быть равен току, выходящему из нее. Поэтому через оба сопротивления должен проходить одинаковый ток I. Согласно второму закону Кирхгофа, IR1
+IR2
= V (10В). Следовательно, ток I = V/(R1
+ R2
) = 0,5 А. Тогда напряжение в bна 5 В больше, чем напряжение в с, а в а на 5В больше, чем в b. Следует заметить, что, поскольку есть только один путь для тока, полное сопротивление, воспринимаемое со стороны батареи, равно просто сумме сопротивлений двух резисторов, то есть
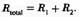
Что произойдет, если, как показано на рис. 4, мы добавим второе сопротивление, также 10 ом, включенное параллельно, а не последовательно? В пепи два резистора R1
и R2
обеспечивают отдельные пути для тока. Оба находятся под напряжением 10 В, так что соответствующие значения тока будут:
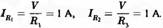
Следовательно, для удовлетворения первого закона Кирхгофа в точку а должно поступать 2 А и 2 А должны выходить из точки Ь. Амперметр в таком случае будет показывать 2 А. Комбинированное сопротивление R1
и R3
равно
R[ota]
= V/I = (10 В)/(2 А) = 5 Ом,
или половине отдельных сопротивлений. Это имеет смысл, если подумать об аналогии в гидравлике: две трубы в параллели предоставят меньшее сопротивление потоку, чем одна из этих труб в одиночку. В электрической цепи в параллели проводимости суммируются:
g[ota]
= g1
+ g3
, или I /R[ota]
= 1 /R1
+ 1 /R3
.
Если теперь мы обобщим для любого количества (n) резисторов, сопротивления в случае последовательного соединения просто суммируются:
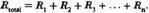
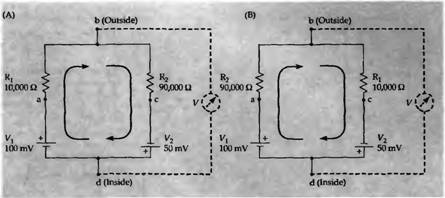 |
Рис. 5. Аналоговая схема мембраны нервной клетки. На А и В сопротивления R1
и R2
поменяны местами, в остальном цепи одинаковы. Источники V1
и V2
включены последовательно. На (А) точка b (потенциал «внешней» стороны мембраны) положительно заряжен относительно точки d («внутренняя» сторона) на 85 mV; на (В) — на 35 mV. Эти цепи иллюстрируют как изменения сопротивления изменяют потенциал при неизменном источнике тока (который представляет равновесные потенциалы ионов).
|
А при параллельном соединении сопротивлений складываются обратные величины:
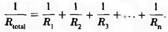
Применение анализа цепи к модели мембраны
На рис. 5А показана цепь, сходная с цепями, которые используются для представления нервных мембран. Следует заметить, что две батареи поставляют ток в цепь в одинаковом направлении, и что сопротивления R1
и R2
соединены последовательно. Какова разность потенциалов между точками b и d (которые представляют внутреннюю и внешнюю среду мембраны)? Полная разность потенциалов на двух резисторах между а и с равна 150 мВ, при этом точка а положительна по отношению к с. Следовательно, ток протекающий из а в с через резистор равен 150 мВ/100000 Ом = 1,5 мкА. Когда 1,5 мкА проходит через 10000 Ом. как между а и Ь, происходит падение потенциала в 15 мВ, если точка а положительна по отношению к Ь. Разница потенциалов между внутренней и внешней средой равна, следовательно, 100 мВ - 15 мВ = 85 мВ. Можно получить тот же результат, вычислив падение потенциала после прохождения R2
(1,5 мкА x 90000 Ом = 135 мВ) и прибавив его к V2
( 135 мВ - 50 мВ = 85 мВ). Это должно быть так, потому что потенциал между b и d должен иметь единое значение.
На рис. 5В R1
, и R2
поменялись местами. Так как общее сопротивление в цепи остается прежним, ток тоже должен быть таким же, как на рис. 5А, то есть 1,5мкА. Теперь падение потенциала после прохождения Л2
, между а и Ь, равно 90 000 Ом x 1,5 мкА = 135 мВ, точка а положительна по отношению к Ь. Теперь потенциал мембраны 100 мВ - 135 мВ = -35 мВ — отрицательный; тот же результат можно, конечно, получить используя ток, проходящий через R1
. Эта простая цепь иллюстрирует важный пункт физиологии мембран: потенциал мембраны может меняться в результате изменения сопротивлений, при том что батареи остаются неизмененными. Общее описание мембранного потенциала в цепи, изображенной на рис. 5А, можно получить таким способом:
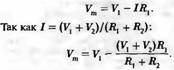
Преобразовав получим:
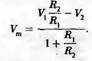
Электрическая емкость и постоянная времени
В цепях, изображенных на рис. 3 и 4, замыкание или размыкание ключа производит мгновенные и одновременные перемены тока и потенциала. Конденсаторы вводят в рассмотрение движения тока элемент времени. Они аккумулируют и хранят электрический заряд, и когда они присутствуют в цепи, перемены тока и напряжения не будут одновременными.
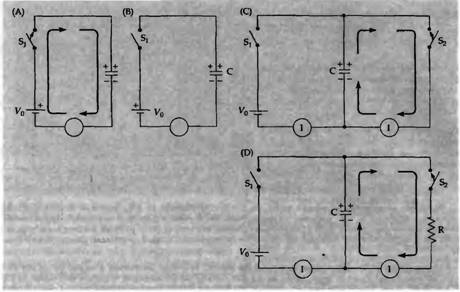 |
Рис. 6. Емкости в электрической цепи. А, В и С представляют собой идеальные цели без сопротивления. Когда ключ S1
замкнут (А), емкость заряжается мгновенно до напряжения V0
. Если затем S1
разомкнуть (В), потенциал останется на емкости. Замыкание ключа S2
(С) мгновенно разряжает емкость. На (О) емкость разряжается через сопротивление R. Максимальный ток разряда I = V0
/R.
.
|
Конденсатор состоит из двух проводящих электричество пластин (обычно металлических), разделенных изолятором (воздухом, слюдой, маслом или пластиком). Когда на пластины прикладывается напряжение (рис. 6А), заряд моментально перемещается с одной пластины на другую по наружной цепи. Однако, когда конденсатор полностью заряжен, ток прекращается, так как он не может проходить через изолятор. Емкость (С) конденсатора определяется количеством заряда (q) который он может сохранять на каждый вольт, приложенный к нему:
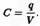
Единица измерения емкости — кулон/вольт, или фарад (Ф). Чем больше размер пластинок и чем они ближе друг к другу, тем больше емкость. Конденсатор емкостью 1 фарад очень большой; часто используемые емкости — порядка микрофарад (мкФ) и меньше.
Когда ключ на рис. 6А замыкается, происходит моментальное разделение зарядов на пластинах. Количество заряда, хранящегося в конденсаторе, пропорционально его емкости и величине приложенного к нему напряжения (V0
,). Когда ключ размыкается, как на рис. 6В, заряд конденсатора остается, так же как и напряжение (V) между пластинками. (Можно иногда получить неожиданную электротравму от электронной аппаратуры, когда она уже была выключена, потому что некоторые конденсаторы в цепи могут остаться заряженными). Конденсатор можно разрядить замыканием второго переключателя, как показано на рис. 6С. Движение тока опять же будет мгновенным, возвращая заряд и напряжение конденсатора к нулю. Если же разряжать конденсатор через сопротивление (R, рис.6D), разрядка будет постепенной. Это происходит потому, что сопротивление ограничивает величину тока. Если напряжение в конденсаторе — V, тогда по закону Ома максимальный ток равен I = V/R. В цепи без сопротивления величина тока увеличивается, становится бесконечно большой и конденсатор разряжается за бесконечно малый промежуток времени; если сопротивление очень большое, конденсатор разряжается очень долго. Скорость разрядки в данный момент времени, dq/dt, соответствует току, протекающему в этот момент. Иначе говоря, dq/dt = -V/R (с отрицательным знаком, потому что заряд уменьшается со временем), где V, первоначально равное напряжению батареи, уменьшается по мере разряжения конденсатора. Так как g = CV, dq/dt = CdV/dt,можно написать CdV/dt = —V/R, или
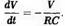
Рис. 7. Зарядка емкости. На (А) емкость заряжается со скоростью, определяемой сопротивлением. На (В) скорость зарядки зависит от двух сопротивлений цепи. На (Е) емкостной ток и напряжение на обкладках емкости показаны как функция времени. Напряжение достигает максимума при полном заряде емкости, то есть когда ток больше не течет через емкость. На (С) и (D) показаны гидравлические аналоги цепей (А) и (В).
|
 |
Это уравнение показывает, что темп потери напряжения в конденсаторе пропорционален остающемуся напряжению. Таким образом, при уменьшении напряжения уменьшается скорость разрядки. Постоянная пропорциональности \/RC является константой скорости (темпа) для процесса, RC — это его постоянная времени. Подобный процесс постоянно возникает в природе. Например, скорость, с которой вода вытекает из ванной уменьшается при уменьшении глубины и, следовательно, давления на водосток. В этом случае процесс разрядки описывается экспоненциальной функцией
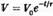
где V0
, — начальный заряд конденсатора, a = RC — постоянная времени. Подобным образом, когда конденсатор заряжается через сопротивление, как показано на рис. 7, процесс зарядки занимает ограниченное время. Напряжение между пластинами увеличивается со временем, пока не достигает напряжения батареи, и ток прекращает проходить. Процесс зарядки станет возрастающим экспоненциально, с постоянной времени = RC:
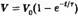
Данные примеры иллюстрируют другое свойство конденсатора. Ток протекает в конденсатор и из конденсатора только при изменении потенциала:
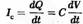
Когда напряжение на конденсаторе постоянно (dV/dt = 0), емкостной ток Iс
равен нулю. Другими словами, емкость имеет «бесконечное сопротивление» для постоянной разности потенциалов и «низкое сопротивление» для быстро меняющегося потенциала. На рис. 7В показана цепь, в которой ток протекает через сопротивление и конденсатор, соединенные параллельно; на рис. 7Е показан временной ход емкостного тока и напряжения.
Свойства конденсатора в электрической цепи могут быть проиллюстрированы аналогией с немного более усовершенствованной гидравлической системой, изображенной на рис. 7С. Конденсатору соответствует эластичная мембрана, образующая перегородку в заполненной жидкостью камере. Когда открывается кран (пробка), жидкость накачивается с одной стороны камеры в другую. Под действием давления, производимого насосом, мембрана деформируется. Жидкость продолжает течь до тех пор, пока из-за своей эластичности мембрана не станет производить равное и противоположное по направлению давление; тогда жидкость прекращает течь и камера полностью заполнена.
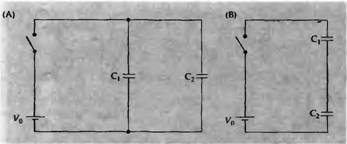 |
Рис.8. Сопротивления, включенные параллельно (А) и последовательно (В).
|
Если параллельно поместить трубу так, как показано на рис. 7D, часть жидкости протекает по этой трубе, а часть идет на расширение мембраны. Степень расширения зависит от сопротивления трубы, а также от емкости камеры. Если сопротивление трубы высокое, тогда для определенного потока разность давлений на ее концах будет относительно большой. В таком случае мембрана будет растягиваться сильнее и растяжение займет больше времени. Аналогично, если емкость камеры больше, больше жидкости потребуется для ее заполнения (или «зарядки») и понадобится больше времени для того, чтобы достичь устойчивого состояния. Поэтому типичная константа времени системы определяется произведением сопротивления и емкости.
Если конденсаторы соединены параллельно, как показано на рис. 8А, общая емкость увеличивается. Общий заряд конденсатора является суммой единичных зарядов, находящихся в каждом конденсаторе:
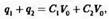
или
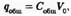
где Собщ
= С1
+ С2
. Напротив, при последовательном соединении конденсаторов емкость уменьшается (рис. 8В). Уравнение оказывается таким же, как и в сопротивлениях, соединенных параллельно. Итак, для n (количества) конденсаторов, соединенных параллельно,
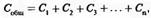
а для соединенных последовательно:
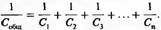
Литература
1. Haque, N.S., Borghesam, P., and Isacson, О. 1997. Mol. Med. Today 3: 175-183.
2. Burgess, D. L., and Noebe/s, J. L. 1999. Ann. N. Y.Acad. Sci. 868: 199-212.
3. Adrian, E. D. 1946. The Physical Background of Perception. Clarendon, Oxford, England.
|