Нижегородский государственный архитектурно-строительный университет
Институт экономики, управления и права
Кафедра железобетонных и каменных конструкций
Пояснительная записка к курсовому проекту по дисциплине
«Железобетонные конструкции» по теме:
«РАСЧЕТ СБОРНЫХ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ МНОГОЭТАЖНОГО ПРОИЗВОДСТВЕННОГО ЗДАНИЯ»
Нижний Новгород – 2010г.
1. Исходные данные
Район строительства – г.Ярославль (IV снеговой район).
Сетка колонн: поперёк здания – 5.7 м х 4 шт, вдоль здания - 6.7 м х 6 шт.
Высота этажа – 3.3 м.
Количество этажей – 4.
Временная нормативная нагрузка – р= 8.5 кН/м2
.
Коэффициенты – к1
= 0.75, К2
= 0.8.
Бетон тяжелый класса для: плиты – В25, ригеля – В20, колонны – В25.
Рабочая арматура класса для: полка сборной плиты – А400, продольные рёбра плиты – А500, ригель – А500, колонны – А400.
Проектирование элементов железобетонных конструкций выполняется в соответствии с действующими Нормами.
В соответствии с заданием проектируются сборные железобетонные конструкции 4-этажного, 3–пролетного производственного здания без подвала, с обычными условиями эксплуатации помещений (относительная влажность воздуха не выше 75%) и временными нагрузками на перекрытиях p= 8.5 кН/м2
.
Здание имеет полный железобетонный каркас с рамами, расположенными в поперечном направлении. Поперечные рамы образуются из колонн, располагаемых на пересечениях осей, и ригелей, идущих поперек здания. Ригели опираются на короткие консоли колонн. Места соединения ригелей и колонн, после сварки выпусков арматуры и замоноличивания стыков, образуют жесткие рамные узлы. Ригели и колонны делаются прямоугольного сечения.
На рамы по верху ригелей опираются плиты перекрытий (покрытия), располагаемой длинной стороной вдоль здания. Номинальная длина плит равна расстоянию между осями рам lк
=6.7 м. У продольных стен укладываются плиты половинной ширины, называемыми доборными. По рядам колонн размещаются связевые плиты, приваренные к колоннам и образующие продольные распорки.
Продольные стены выполняются навесными или самонесущими из легкобетонных панелей. Привязка колонн крайних рядов и наружных стен к продольным разбивочным осям – «нулевая».
План и поперечный разрез проектируемого здания, решенного в сборном железобетоне, представлены на рисунке 1.
Реклама

Сборное железобетонное перекрытие компонуется из двух элементов: сборных ребристых плит (именуемых ниже «плиты») и сборных ригелей. Ригели поперечных рам во всех зданиях направлены поперек, а плиты – вдоль здания.
Ригели проектируются с ненапрягаемой рабочей арматурой. Поперечное сечение ригеля принимается прямоугольным.
4.Расчет сборной ребристой плиты.

Рис. 2. Схема армирования ребристой плиты в поперечном сечении
Для сборного железобетонного перекрытия, представленного на плане и в разрезе на рис. 1, требуется рассчитать сборную ребристую плиту с ненапрягаемой арматурой в продольных ребрах. Сетка колонн l´lк
= 5.7 х 6.7 м. Направление ригелей междуэтажных перекрытий – поперек здания. Нормативное значение временной нагрузки на междуэтажные перекрытия 8.5 кН/м2
. Вся временная нагрузка условно считается длительной. Коэффициент надежности по назначению здания принимается γn
=0,95, коэффициенты надежности по нагрузке: временной - γƒ
= 1,2; постоянной - γƒ
= 1,1. Бетон тяжелый класса В25. По таблицам СНиП 2.03.01-84 расчетные сопротивления бетона Rb
= 14.5 МПа и Rbt
= 1.05 МПа; коэффициент условий работы бетона γb
1
=1,0 С учетом этого значения коэффициента γb
1
, принимаемые далее в расчетах по несущей способности (первая группа предельных состояний) величины расчетных сопротивлений равны:
Rb
= 1,0 ∙ 14.5 = 14.5 МПа;
Rbt
= 1,0 ∙ 1.05 = 1.05 МПа.
Для расчета по второй группе предельных состояний (расчет прогиба и ширины раскрытия трещин) расчетные сопротивления бетона будут Rb
,
ser
= 18.5 МПа, Rbt
,
ser
= 1,55 МПа; модуль упругости бетона Eb
= 30000 МПа (п. 5.2.10).
Основные размеры плиты:
– длина плиты: ln
= lk
– 50 мм = 6700 – 50 = 6650 мм;
– номинальная ширина: В = l:5 = 5700:5 = 1140 мм;
– конструктивная ширина : В1
= В – 15 мм = 1140 – 15= = 1125 мм.
Высоту плиты ориентировочно, принимая всю нагрузку длительной, определяем по формуле:
h=c∙l0
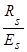 Θ (4.1)
Θ (4.1)
h = 30 ∙ 6400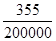 1,5 = 511 мм 1,5 = 511 мм
но не менее h = ln
/15 = 6650/15= 443 мм.
с = 30 – при армировании сталью класса А400
l0
= lк
– b = 6700 – 300 = 6400 мм – пролёт ребра плиты в свету, где
b=300 мм – предварительно принимаемая ширина сечения ригеля;
Rs
=355 МПа – расчётное сопротивление арматуры класса А‑ІІІ (А400) для предельного состояния первой группы;
Es
=2×105
МПа – модуль упругости арматуры;
Реклама

q =1,5.
Принимаем h = 500 мм.
1. Расчет полки плиты.
Толщину полки принимаем h′ƒ
= 50 мм.
Пролет полки в свету l0п
= В1
– 240 мм = 1125 – 240 = 885 мм = 0,885 м.
Расчетная нагрузка на 1 м2
полки:
Постоянная (с коэффициентом надежности по нагрузке γƒ
= 1,1):
a) вес полки: γƒ
∙ h′ƒ
∙ ρ = 1,1 ∙ 0,05 ∙ 25 = 1,375 кН/м2
,
25 кН/м3
– вес 1 куб. м тяжелого железобетона;
b) вес пола и перегородок 1,1 ∙ 2,5 = 2,75 кН/м2
. При отсутствии сведений о конструкции пола и перегородок, их нормативный вес принимаем 2,5 кН/м2
.
Итого постоянная нагрузка: g0
= 1,375+2,75 = 4,125 кН/м2
.
Временная нагрузка (с γƒ
= 1,2): p0
= 1,2 ∙ 8.5 = 10.2 кН/м2
.
Полная расчетная нагрузка (с γn
= 0,95):
q = γn
(g0
+ p0
)=0,95(4,125+10.2) = 13.61 кН/м2
.
Изгибающий момент в полке (в пролете и на опорах) по абсолютной величине равен:
М = , кН∙м. (4.2) , кН∙м. (4.2)
М =13.61·(0.885)2
/11= 0.97 кН∙м.
По заданию полка армируется сварными сетками из обыкновенной арматурной проволоки класса А400.
Расчетное сопротивление Rs
= 355 МПа
h0
= hƒ
′ - a= 50 – 17,5 = 32,5 мм; b = 1000 мм,
где а = 17.5 – 19 мм, примем а = 17.5 мм
По формулам имеем:
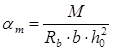 (4.3.) (4.3.)
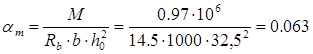
Проверяем условие αm
< αR
:
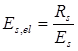 . (4.4.) . (4.4.)
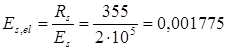
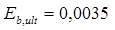
Граничная относительная высота сжатой зоны:
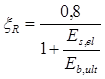 (4.5.) (4.5.)
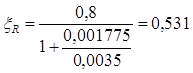
αR
= ξR
(1-0,5 ξR
) (4.6.)
αR
= 0,531(1-0,5∙0,531) = 0,39
Таким образом, условие αm
= 0,063 < αR
= 0,39 выполняется.
Находим площадь арматуры:
Аs
=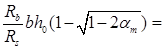 (4.7.) (4.7.)
Аs
=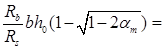 14.5/355·1000·32.5·(1-√1-2·0.063) = 86 мм2 14.5/355·1000·32.5·(1-√1-2·0.063) = 86 мм2
Нижние (пролётные) и верхние (надопорные) сетки принимаем:
С1(С2) 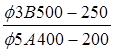 ; Аs
=141 мм2
(+8,5%). ; Аs
=141 мм2
(+8,5%).
Процент армирования полки:
μ%=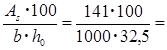 0.43%. 0.43%.
2. Каждое поперечное торцовое ребро армируется C-образным сварным каркасом с рабочей продольной арматурой 3 Ø 6 А400 и поперечными стержнями Ø 4 В500 с шагом 100 мм.
3. Расчет продольных ребер. Продольные ребра рассчитываются в составе всей плиты, рассматриваемой как балка П-образного сечения с высотой h=500 мм и конструктивной шириной В1
=1125 мм (номинальная ширина В=1,14 м). Толщина сжатой полки h′ƒ
= 50 мм.
Расчетный пролет при определении изгибающего момента принимаем равным расстоянию между центрами опор на ригелях:
l=lk
– 0,5b= 6,7 – 0,5 ∙ 0,3 = 6.55 м;
расчетный пролет при определении поперечной силы:
l0
= lk
– b = 6,7 – 0,3=6.4 м,
где b=0,3 м – предварительно принимаемая ширина сечения ригеля.
Нагрузка на 1 пог. м плиты (или на 1 пог. м двух продольных ребер) составит:
а) расчетная нагрузка для расчета на прочность (первая группа предельных состояний, γƒ
>1): постоянная
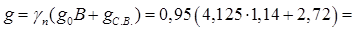 7.29 кН/м 7.29 кН/м
где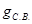 – расчётная нагрузка от собственного веса двух рёбер с заливкой швов – расчётная нагрузка от собственного веса двух рёбер с заливкой швов
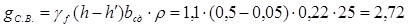 кН/м, где кН/м, где
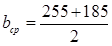 =220 мм – средняя ширина двух рёбер. =220 мм – средняя ширина двух рёбер.
r = 25 кн/м3
.
временная p = γn
p0
B= 0,95 · 10.2 · 1,14 = 11.05 кН/м;
полная q = g + p= 7,29 + 11.05 = 18.34 кН/м;
б) расчетная нагрузка для расчета прогиба и раскрытия трещин (вторая группа предельных состояний, γƒ
=1):
qII
= qn
= 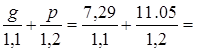 15.84 кН/м. 15.84 кН/м.
Усилия от расчетной нагрузки для расчета на прочность
М =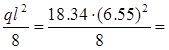 98.4 кН·м; 98.4 кН·м;
Q =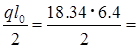 58.7 кН. 58.7 кН.
Изгибающий момент для расчета прогиба и раскрытия трещин
МII
=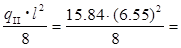 84.95 кН·м. 84.95 кН·м.
4.2 Расчет прочности нормальных сечений
Продольная рабочая арматура в ребрах принята в соответствии с заданием класса А500, расчетное сопротивление Rs
=435 МПа. Сечение тавровое с полкой в сжатой зоне; расчетная ширина полки:
b´f
= B1
– 40 мм = 1125 – 40 = 1085 мм;
h0
= h – a= 500 – 50 = 450 мм (а=50 мм при двухрядной арматуре).
Полагая, что нейтральная ось лежит в полке, имеем:
am
=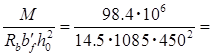 0,031; 0,031;
x=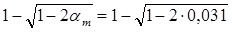 = 0,031; = 0,031;
x = xh0
= 0,031 × 450 = 14 мм < hf
¢=50мм;
Проверяем условие αm
< αR
:
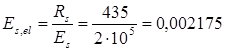
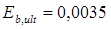
Граничная относительная высота сжатой зоны:
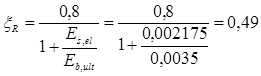
αR
= ξR
(1-0,5 ξR
) = 0,49(1-0,5∙0,49) = 0,370.
Таким образом, условие αm
= 0,031 < αR
= 0,370 выполняется.
Площадь сечения продольной арматуры:
As
=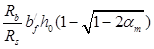
As
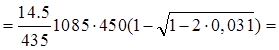 517 мм2 517 мм2
Принимаем продольную арматуру 4Æ14 А400 с Аs
= 616 мм2
по два стержня в каждом ребре.
μ%= 1.37% < 5%. 1.37% < 5%.
4.3 Расчет прочности наклонных сечений на поперечную силу
Поперечная сила на грани опоры Qmax
= 58.7 кН. В каждом продольном ребре устанавливается по одному каркасу с односторонним расположением двух рабочих стержней диаметром d= 14 мм (рис. 2). Диаметр поперечных стержней должен быть не менее 4 мм. Принимаем поперечные стержни диаметром dsw
= 4 мм из проволоки класса В500, Asw
1
=12,6 мм2
; расчетное сопротивление Rsw
= 300 МПа. При Asw
1
=12,6 мм2
и n= 2 (на оба ребра) имеем:
Asw
= nAsw
1
=2×12,6 = 25,2 мм2
.
Бетон тяжелый класса В25 (Rb
= 14.5 МПа; Rbt
= 1.05 МПа; коэффициент условий работы бетона γb
1
=1,0 т.к. кратковременная нагрузка составляет более 10% от всей временной нагрузки).
Шаг хомутов предварительно принимаем:
Sw
1
= 150 мм (S1
≤ 0,5h0
= 0,5 ∙450 = 225 мм; S1
≤300мм)
Sw2
=300мм (S2
≤ 0,75 h0
= 0,75 ∙ 450 = 337мм; S2
≤500мм).
Прочность бетонной полосы проверим из условия (7):
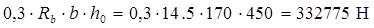 >Qмах
= 58700 Н >Qмах
= 58700 Н
т.е. прочность полосы обеспечена
Интенсивность хомутов определим по формуле:
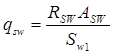 , Н/мм (4.8.) , Н/мм (4.8.)
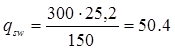 Н/мм Н/мм
Поскольку qsw
=50.4 Н/мм > 0,25Rв
t
b = 0,25×1.05×170 =44.6 Н/мм – хомуты полностью учитываются в расчете и значение Мb
определяется по формуле:
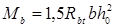 , Н∙мм (4.9.) , Н∙мм (4.9.)
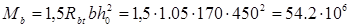 Н∙мм Н∙мм
Определим длину проекции самого невыгодного наклонного сечения с:
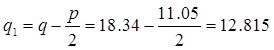 кН/м. кН/м.
Поскольку
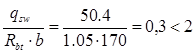 значение с определяем по формуле: значение с определяем по формуле:
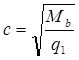 , но не более 3h0
(4.10.) , но не более 3h0
(4.10.)
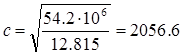 мм > 3h0
=3×450=1350 мм, мм > 3h0
=3×450=1350 мм,
следовательно, принимаем с=1350 мм.
Длина проекции наклонной трещины с0
– принимается равной с, но не более 2h0
. Принимаем
с0
= 2h0
= 2 × 450 =900 мм. Тогда
QSW
= 0,75qSW
×c0
= 0,75 ×50.4 × 900 = 34020 Н = 34.02 кН
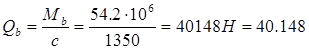 кН, кН,
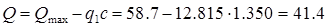 кН. кН.
Проверяем условие
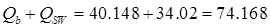 кН > кН >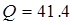 кН. кН.
т.е. прочность наклонных сечений обеспечена.
Проверим требование:
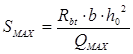 > Sw
1
. (4.11.) > Sw
1
. (4.11.)
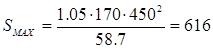 мм > Sw
1
=150 мм. мм > Sw
1
=150 мм.
т.е. требование выполнено.
4.4 Определение приопорного участка
При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от:
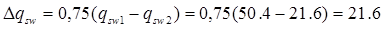 Н/мм, Н/мм,
где 
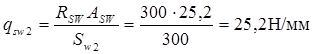 . .
Поскольку
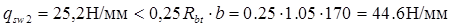 , тогда: , тогда:
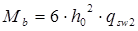 , Н/мм , Н/мм
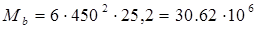 Н/мм Н/мм
Так как 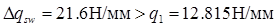 , то длина приопорного участка: , то длина приопорного участка:
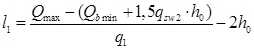 , (4.12.) , (4.12.)
где 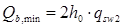 (4.13.) (4.13.)
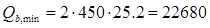 Н Н
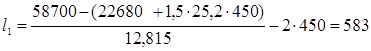 мм мм
1. Расчет прогиба плиты
Исходные данные для расчета:
Изгибающий момент в середине пролета МII
=84.95 кН×м.
Модуль упругости: бетона Eb
=30000 МПа, арматуры Es
=200000 МПа.
Сечение тавровое. С учетом замоноличивания бетоном продольного шва между ребрами расчетная ширина полки будет b¢f
=1140 мм и средняя ширина ребра
b=(255+185)/2=220 мм
Проверяем наличие нормальных к продольной оси трещин в растянутой зоне ребер. Трещины образуются при условии
MII
> Rbt
,
ser
Wpl
. ( 4.14.)
Упругопластический момент сопротивления Wpl
по растянутой зоне находим по формуле при А¢s
=0 и g1
=0:
Wpl
=(0,292+0,75×2m1
a+0,15g1
¢)bh2
, (4.15.)
где g1
¢=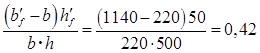
m1
=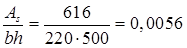
a=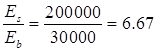
Wpl
=(0,292+1,5×0,0056×6,67+0,15×0,42)·220×5002
= 22,605×106
мм3
.
Rbt
,
ser
Wpl
.=1,55×22,605×106
=35,04×106
Н×мм=35,0 4 кН×м < MII
=84,95 кН×м,
т.е. растянутой зоне образуются трещины.
Кривизну 1/r определяем для элемента с трещинами в растянутой зоне, согласно пп. 4.27-4.29 СНиП 2.03.01-84* [2]. Для железобетонного изгибаемого элемента с ненапрягаемой арматурой формула (160) указанного СНиПа примет вид:
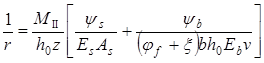 , (4.16.) , (4.16.)
Где yb
= 0,9 – для тяжелого бетона (п. 4.27);
v= 0,15 – для тяжелого бетона при продолжительном действии нагрузки (п. 4.27, табл. 35).
Коэффициент ys
вычисляется по формуле (167) СНиП [2] при исключении третьего члена:
ys
=1,25 - jls
jm
, (4.17.)
где jls
=0,8 (п. 4.29, табл. 36, продолжительное действие нагрузки);
jm
=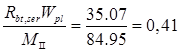 < 1 < 1
(формула (168) для изгибаемого элемента при отсутствии предварительного напряжения).
ys
=1,25 – 0,8×0,41 =0.922 < 1. Согласно п. 4.29 СНиПа [2], принимаем ys
=1,0.
Плечо внутренней пары сил и площадь сжатой зоны бетона определяется по приближенным формулам, полагая:
x=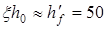 мм, мм,
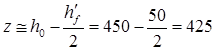 мм, мм,
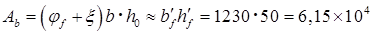 мм2
. мм2
.
Кривизна составит:
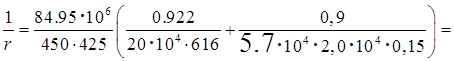 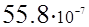 мм мм
Прогиб плиты в середине пролета будет
f=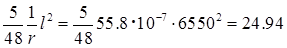 мм < fult
= мм < fult
=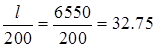 мм, мм,
т. е. прогиб плиты лежит в допустимых пределах (см. [1], табл. 19).
2. Проверка ширины раскрытия трещин, нормальных к оси продольных ребер, производится согласно пп. 4.14 и 4.15 СНиП 2.03.01 – 84* [2]. Ширина раскрытия трещин определяется по формуле (144) СНиПа:
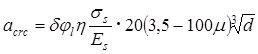
Для рассчитываемой плиты, загруженной только длительной нагрузкой, входящие в расчетную формулу для аcrc
величины согласно п. 4.14 СНиПа равны:
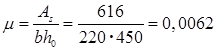 < 0,02; < 0,02;
φl
=1,6-15μ=1,6-15•0,0062=1,507 (тяжелый бетон естественной влажности); δ=1,0; η=1,0; d- диаметр принятой арматуры.
Напряжение в арматуре σs
в сечении с трещиной при расположении арматуры в два ряда по высоте находится на основании формул (147) и (149) СНиПа [2] при значении Р=0 (предварительное напряжение отсутствует):
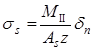 , ,
Где 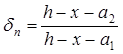
Значения z и x принимаются такой же величины, как при расчете прогиба:
а1
=50 мм; 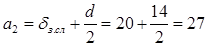 мм; мм;
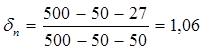 ; ;
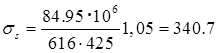 Н/мм2
=340.7 МПа < Rs
,
ser
=500 МПа Н/мм2
=340.7 МПа < Rs
,
ser
=500 МПа
(требование п. 4.15 СНиПа [2]).
Ширина раскрытия трещин составит:
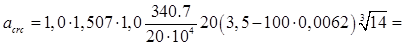 0,36 мм = acrc
2
= 0,36 мм, 0,36 мм = acrc
2
= 0,36 мм,
т.е. ширина раскрытия трещин лежит в допустимых пределах.
Для сборного железобетонного перекрытия, план и разрез которого представлены на рис. 1, требуется рассчитать сборный ригель. Сетка колонн l´lк
= 6.7´5.7 м. Для ригеля крайнего пролета построить эпюры моментов и арматуры.
1. Дополнительные данные
Бетон тяжелый, класс бетона B20, коэффициент работы бетона γb
1
= 1,0. Расчетные сопротивления бетона с учетом γb
1
= 1,0 равны:
Rb
= 1,0∙11,5 = 11,5 МПа;
Rbt
= 1,0∙0,9 = 0,9 МПа.
Продольная и поперечная арматура – класса A500. Коэффициент снижения временной нагрузки к1
=0,75.
2. Расчетные пролеты ригеля
Предварительно назначаем сечение колонн 400´400 мм (hc
= 400 мм), вылет консолей lc
= 300 мм. Расчетные пролеты ригеля равны:
- крайний пролет l1
= l-1,5hc
-2lc
= 5,7 – 1,5 ∙ 0,4 – 2 ∙ 0,3 = 4,5 м;
- средний пролет l2
= l - hc
- 2lc
= 6,7 – 0,4 – 2 ∙ 0,3 = 4,7 м.
3. Расчетные нагрузки
Нагрузка на ригель собирается с грузовой полосы шириной lк
= 6,7 м, равной расстоянию между осями ригелей (по lк
/2 с каждой стороны от оси ригеля).
а) постоянная нагрузка (с γn
= 0,95 и γƒ
= 1,1):
вес железобетонных плит с заливкой швов:
0,95∙1,1∙3∙6,7 = 21 кН/м;
вес пола и перегородок:
0,95∙1,1∙2,5∙6,7 = 17.5 кН/м;
собственный вес ригеля сечением b´h @0,3´0,6 м (размеры задаются ориентировочно)
0,95∙1,1∙0,3∙0,6∙25 = 4,7 кН/м;
итого: постоянная нагрузка g = 43.2 кН/м.
б) Временная нагрузка с коэффициентом снижения к1
= 0,75 (с γn
= 0,95 и γƒ
= 1,2):
ρ = 0,95∙0,75∙1,2∙8.5∙6,0 = 41.42 кН/м.
Полная расчетная нагрузка: q = g + ρ = 43.2 + 41.42 = 84.62 кН/м.
4. Расчетные изгибающие моменты.
В крайнем пролете:
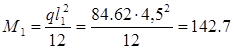 кН×м кН×м
На крайней опоре:
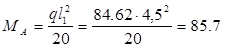 кН×м кН×м
В средних пролетах и на средних опорах:
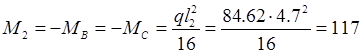 кН×м кН×м
Отрицательные моменты в пролетах при p/ ρ = 41.42 / 43.2 = 0,96 »1,0:
в крайнем пролете для точки «4» при β = - 0,010
M4
=β (g+ρ) l1
2
= -0,010 ∙84.62∙4,5 2
= -17 кН∙м;
в среднем пролете для точки «6» при β= -0,013
M6
=β (g+ρ) l2
2
= -0,013∙84.62∙4.7 2
= - 24.3 кН∙м.
5. Расчетные поперечные силы
На крайней опоре:
QA
= 0,45ql1
= 0,45∙84.62∙4,5 = 171.4 кН.
На опоре B слева:
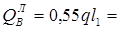 0,55 ×84.62 × 4, 5 = 209.4 кН. 0,55 ×84.62 × 4, 5 = 209.4 кН.
На опоре B справа и на средних опорах:
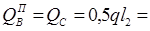 0,5 × 84.62 × 4.7 = 198.9 кН. 0,5 × 84.62 × 4.7 = 198.9 кН.
6. Расчет ригеля на прочность по нормальным сечениям
Для арматуры класса A500 ξR
= 0,49 (см. расчет продольного ребра плиты). Принимаем ширину сечения b=300мм. Высоту ригеля определяем по опорному моменту MB
= 117 кН∙м, задаваясь значением ξ = 0,35 < ξR
= 0,49. Находим αm
= ξ (1 – 0,5ξ) = 0,35(1 – 0,5∙0,35) = 0,289. Сечение рассчитывается как прямоугольное по формуле (1):
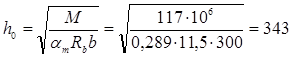  мм; мм;
h = h0
+a = 343+65 = 408 мм;
принимаем h = 450 мм (h/b = 450/300 = 1,5).
Расчет арматуры
Расчетное сопротивление арматуры класса A500 будет Rs
= 435 МПа. Расчет производится по формулам:
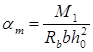
Аs
=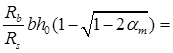
а) Крайний пролет. M1
= 142.7 кН∙м; b = 300 мм; h= 450 мм; h0
= h - a = 450 – 65 = 385 мм (арматура расположена в два ряда по высоте)
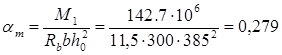
Аs
= 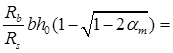 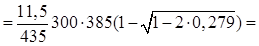 1023 мм2
. 1023 мм2
.
Принимаем арматуру 2Ø16 A500 + 2Ø20 A500 с АS
= 402 + 628 = 1030 мм2
.
Проверяем условие αm
< αR
:
αR
= ξR
(1-0,5 ξR
) = 0,49(1-0,5∙0,49) = 0,37
Таким образом, условие αm
= 0,279 < αR
= 0,37 выполняется, т.е. для сечения ригеля с наибольшим моментом M1
условие выполняется.
б) Средний пролет. M2
= 117 кН∙м; b = 300 мм; h = 450 мм; h0
= h-a = 450-60=390 мм (арматура расположена в два ряда по высоте)
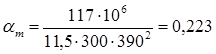
Аs
= 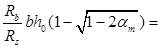
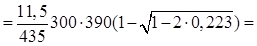 791мм2 791мм2
принято 2Æ14 A500 и 2Æ18 A500 с As
= 308 + 509 = 817 мм2
.
в) Средняя опора. MB
= MC
= M= 117 кН∙м; b = 300 мм; h= 450 мм; h0
= h - a = 450-65 = 385 мм (арматура расположена в один ряд с защитным слоем 50 мм)
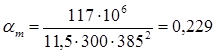
Аs
= 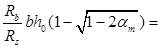
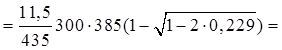 805мм2 805мм2
принято 2Æ25 A500 с As
= 982 мм2
.
г) Крайняя опора. MA
= 85.7 кН∙м; h0
= h - a = 450 – 65 = 385 мм (арматура расположена в один ряд с защитным слоем 50 мм);
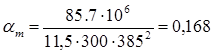
Аs
= 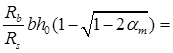
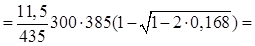 565 мм2 565 мм2
принято 2Æ20 A500 с As
= 628 мм2
.
д) Верхняя пролетная арматура среднего пролета по моменту в сечении «6»
M6
= 24.3 кН∙м; b = 300 мм; h = 450 мм; h0
=
=h - a = 450-35=415мм (однорядная арматура);
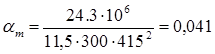
Аs
= 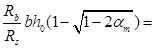
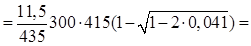 138 мм2 138 мм2
принято 2Æ10 A500 с As
= 157 мм2
.
е) Верхняя пролетная арматура крайнего пролета по моменту в сечении «4»
M4
= 17 кН∙м; h0
= h - a = 415 мм (однорядная арматура);
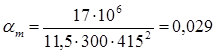
Аs
= 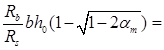
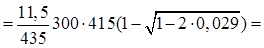 96.9 мм2 96.9 мм2
принято 2Æ8 А500 с As
= 101 мм2
.
7. Расчет ригеля на прочность по наклонным сечениям на действие поперечных сил
В крайнем и средних пролетах ригеля устанавливаем по два плоских сварных каркаса с односторонним расположением рабочих продольных стержней. Наибольший диаметр продольных стержней в каждом каркасе d = 25 мм.
Qmax
= 209.4 кН. Бетон В20 (Rb
= 11,5МПа; Rb
t
= 0,9МПа γb
1
= 1,0
Так как нагрузка на ригель включает ее временную составляющую).
Принимаем во всех пролетах поперечные стержни из стали класса А-II (А300) диаметром dsw
= 6 мм (Asw
= 28.3 мм2
). Принятый диаметр поперечных стержней удовлетворяет требованиям обеспечения качественной сварки, расчетное сопротивление поперечных стержней принимаем, согласно Приложения, равным Rsw
= 300 МПа. Количество поперечных стержней в нормальном сечении равно числу плоских сварных каркасов в элементе, т.е. n=2.
Вычисляем
Asw
=n∙Asw1
=2∙28,3=56.6 мм2
;
Rsw
Asw
= 300∙56.6 = 16980 H.
Сечение прямоугольное с шириной b=300 мм и высотой h = 450 мм. Рабочая высота сечения на приопорных участках h0
= 385 мм (см. расчет продольной арматуры). В крайнем и среднем пролетах ригеля шаг поперечных стержней:предварительно принимаем
Sw1
=100мм (S1
≤0,5h0
; S1
≤300 мм);
Sw2
=250 мм (S2
≤0,75h0
; S2
≤500мм).
1. Проверки на прочность наклонной сжатой полосы:
0,3 ×Rb
×b×h0
= 0,3 × 11,5 × 300 × 385 = 398.48 кH > QMAX
= 209.4 кН
т.е. прочность полосы обеспечена
2. Проверка прочности наклонного сечения
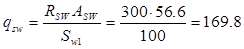 Н/ мм. Н/ мм.
Поскольку qsw
=169.8 Н/мм > 0,25Rb
t
b = 0,25∙0,9∙300 = 67,5 Н/мм - хомуты полностью учитываются в расчете и Мb
определяется по формуле:
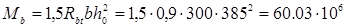 Н мм = 60.03 кН м. Н мм = 60.03 кН м.
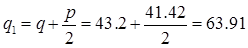 кН/м кН/м
Поскольку
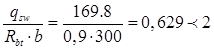
c мм < 3h0
= 3 ∙ 385 = 1155 мм мм < 3h0
= 3 ∙ 385 = 1155 мм
Принимаем c = 969 мм, c0
= 2∙385=770 мм;
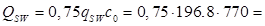 98060 H = 98.06 кН 98060 H = 98.06 кН
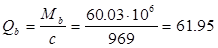 кН кН
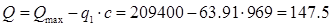 кН (147.5) кН (147.5)
Проверка условия
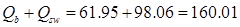 кН > Q=147.5 кН, кН > Q=147.5 кН,
условие прочности обеспечивается.
Проверка требования
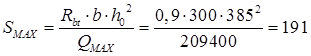 мм > Sw1
=100 мм мм > Sw1
=100 мм
т.е. принятый шаг Sw1
=100 мм удовлетворяет требованиям СП [4].
Определение приопорного участка
При равномерно распределённой нагрузке длина приопорного участка определяется в зависимости от:
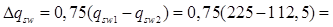 76.41 Н/мм, где: 76.41 Н/мм, где:
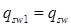
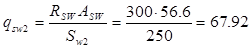 Н/ мм. Н/ мм.
qsw
2
= 67.92 Н/мм > 0,25 Rbt
×b = 0,25 × 0,9 × 300 = 67,5 Н/ мм – условие выполняется, т.е. Mb
и Qb
,
max
не пересчитываем.
Так как 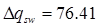 Н/ мм > q1
=63.91 Н/ мм, то: Н/ мм > q1
=63.91 Н/ мм, то:
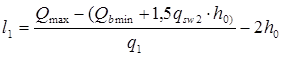 , ,
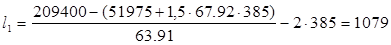 мм мм
где 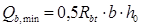 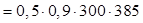 = 51975 Н = 51975 Н
Обрыв продольной арматуры в пролете. Построение эпюры арматуры.
По изложенному выше расчету определяется площадь продольной рабочей арматуры в опасных участках сечения: в пролетах и на опорах, где действует наибольшие по абсолютной величине моменты.
Для определения места обрыва продольной арматуры строятся огибающая эпюра изгибающих моментов от внешних нагрузок и эпюра арматуры, представляет собой изображение несущей способности сечений ригеля Мult
.
Моменты в пяти точках определяются по формуле:
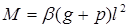
Расчетные моменты эпюры арматуры, которое может воспринять балка в каждом сечении при имеющихся в этих сечениях растянутой арматуры, определяется по формуле:
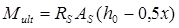 , где , где
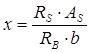 ,мм – высота сжатой зоны. ,мм – высота сжатой зоны.
AS
– площадь арматуры в рассматриваемом сечении.
Место действия обрыва стержней отстаёт от теоретического на расстоянии W, принимаемом не менее величины, определяемой по формуле:
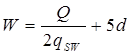
Q – расчетная поперечная сила в месте теоретического обрыва стержня;
qsw
– усилие в поперечных стержнях на единицу длины элемента на рассматриваемом участке;
d – диаметр обрываемого стержня.
При правильном подборе и распределении продольной арматуры по длине ригеля эпюра арматуры Mult
повсюду охватывает огибающую эпюру моментов M, нигде не врезаясь в нее, но и не удаляясь от нее слишком далеко в расчетных сечениях. В таком случае во всех сечениях ригеля, будет выполнятся условие прочности по моменту M<Mult
и обеспечения экономичности расходование арматуры.
Построение эпюры арматуры ниже иллюстрируется на примере рассчитываемого ригеля рамы. Согласно заданию, построение эпюр производиться для крайнего пролета.
Подсчет моментов сведен в табл. 2, при этом отрицательные моменты в пролете вычисляются для отношения
p/g = 41.42/43.2 »1.
Таблица 2
| Крайний пролет «0 - 5» |
| M = bql1
2
= b× 84.62 × 4,52
= 1713.6· b (кН×м) |
| Сечения |
0 |
1 |
2 |
2’ |
3 |
4 |
5 |
| Положительные моменты |
b |
- |
0,037 |
0,079 |
0,0833 |
0,077 |
0,030 |
- |
| +М |
- |
63.4 |
135.4 |
142.7 |
132 |
51.4 |
- |
| Отрицательные моменты |
b |
-0,050 |
-0,003 |
+0,021 |
- |
+0,018 |
-0,010 |
-0,0625 |
| -М |
-85.68 |
-5.14 |
+36 |
- |
+30.8 |
-17 |
-117 |
Нулевые точки эпюры положительных моментов располагаются на расстоянии 0,1 l1
= 0,45 м от грани левой опоры и 0,125 l1
= 0,56 м от грани правой опоры. Огибающая эпюра моментов приведена на рис. 11. Под ней построена эпюра поперечных сил для крайнего пролета.
Ординаты эпюры Мult
вычисляются через площади фактически принятой ранее арматуры и откладываются на том же чертеже.
На положительные моменты
На наибольший положительный момент M1
принята арматура 2Æ20 и 2Æ16 А500 с Аs
= 1030мм2
.
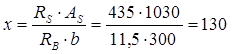 мм мм
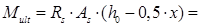 435 × 1030 × (385 – 0,5 × 130) = 143.4 кН×м 435 × 1030 × (385 – 0,5 × 130) = 143.4 кН×м
Ввиду убывания положительного момента к опорам, часть арматуры можно не доводить до опор, оборвав в пролете. Рекомендуется до опор доводить не менее 50% расчетной площади арматуры. Примем, что до опор доводится 2Ø20 A500 с АS
= 628 мм2
. Момент Мult
, отвечающий этой арматуре, получим пропорционально ее площади:
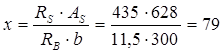 мм мм
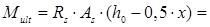 435 × 628 × (385 – 0,5 × 79) = 94.4 кН×м 435 × 628 × (385 – 0,5 × 79) = 94.4 кН×м
На отрицательные опорные моменты:
На момент МA
принята арматура 2Ø20 А500 с АS
=628 мм2
.
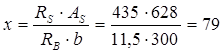 мм, мм,
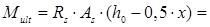 435 × 628 × (385 – 0,5 × 79) = 94.4 кН×м 435 × 628 × (385 – 0,5 × 79) = 94.4 кН×м
На момент МB
= МC
принята арматура 2Ø25 А500 с АS
=982 мм2
.
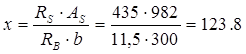 мм мм
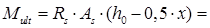 435 × 982 × (385 – 0,5 × 123.8) = 138 кН×м 435 × 982 × (385 – 0,5 × 123.8) = 138 кН×м
На отрицательные пролетные моменты
На момент М4
принята арматура 2Ø8 А500 с АS
=101 мм2
.
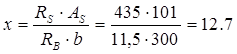 мм мм
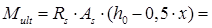 435 × 101 × (415 – 0,5 × 12.7) = 17.95 кН×м 435 × 101 × (415 – 0,5 × 12.7) = 17.95 кН×м
Обрываемые пролетные и опорные стержни заводятся за место теоретического обрыва на величину W. Расстояние от опорных стержней до мест теоретического обрыва стержней а определяется из эпюры графически.
В сечении 2 каркаса ( dsw
= 6 мм; Аsw1
=28.3 мм2
; Аsw
=56.6 мм2
; Rsw
= 300 МПа)
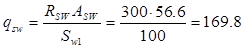 H/мм. H/мм.
Значения W будут (см. рис.11): для пролетных стержней 2Æ25 A- II (А300)
слева: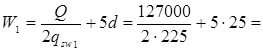 407 мм < 20d= 500 мм 407 мм < 20d= 500 мм
справа: 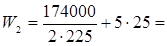 512 мм > 20d= 500 мм; 512 мм > 20d= 500 мм;
для надопорных стержней слева 2Ø28 А300:
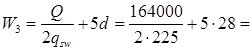 504 мм < 20d= 560 мм 504 мм < 20d= 560 мм
справа 2Æ36 A-II (А300)
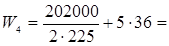 629 мм < 20d= 720 мм 629 мм < 20d= 720 мм
Принято W1
= 500 мм; W2
= 550 мм; W3
= 600 мм; W4
= 750 мм.
Сетка колонн 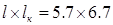 м м
Высота этажей между отметками чистого пола – 3.3 м. Нормативное значение временной нагрузки на междуэтажные перекрытия 8.5 кH/м2
, расчетное значение снеговой нагрузки на покрытие – 2.4 кH/м2
(для г.Ярославля). Кратковременная нагрузка превышает 10% от всей временной. Коэффициент снижения ее на междуэтажных перекрытиях к2
=0,8. Коэффициент надежности по назначению здания gn
=0,95.
Основные размеры ребристых плит и ригелей перекрытий и покрытия принимаются по предыдущему расчету. Толщина пола – 100 мм. Бетон тяжелый класса B25, продольная арматура – класса A400, поперечная арматура – класса A240.
Расчет колонны на сжатие
Полная грузовая площадь для одной внутренней колонны составит
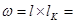 5.7×6,7=38.19 м2
. 5.7×6,7=38.19 м2
.
Подсчет нагрузок на грузовую площадь сведен в таблицу.
Нагрузку от собственного веса конструкций покрытия и междуэтажных конструкций принимаем по данным предыдущего расчёта.
Колонну принимаем сечением 400×400 (мм). Собственный вес колонны длиной 3.3 м с учетом веса двухсторонней консоли будет:
Нормативный – 0,95[0,4×0,4×3.3 +(0,3×0,45+0,3×0,3) ×0,4] ×25 = 14.68кН.
Расчетный – 1,1×14.68 = 16.15 кН.
Расчет колонны по прочности на сжатие производим для двух схем загружения:
За расчетное принимаем верхнее сечение колонны 1-го этажа, расположенное на уровне оси ригеля перекрытия этого этажа. Расчет выполняется на комбинацию усилий Mmax
-N, отвечающую загружению временной нагрузкой одного из примыкающих к колонне пролетов ригеля перекрытия 1-го этажа и сплошному загружению остальных перекрытий и покрытия.
а) Определение усилий в колонне. Расчетная продольная сила N.
Постоянная и временная нагрузки на одну внутреннюю колонну от покрытия и всех межэтажных перекрытий, кроме того перекрытия 1-го этажа; собирается с полной грузовой площади 38.19 м2
. Постоянная нагрузка от перекрытия 1-го этажа собирается с полной грузовой площади.
| Вид нагрузки |
Нагрузка (кН/м2
)×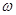 × ×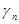 |
Нормативн. нагрузка (кН) |
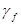 |
Расчетная нагрузка |
| А. Нагрузка на перекрытие |
1. Собственный вес конструкций кровли
(ковер, утеплитель, стяжка и пр.)
2. Вес железобетонной конструкции покрытия.
3. Временная нагрузка (снег)
|
2,95×38.19×0,95
3,8×38.19×0,95
2.4×38.19×0,95
|
107.03
137.9
87.1
|
1,3
1,1
1/0,7
|
139.15
151.7
124.4
|
| Полная нагрузка |
332.03 |
415.25 |
| Б. Нагрузка на межэтажное перекрытие |
1. Вес железобетонных конструкций перекрытия
2. Вес пола и перегородок
3. Временная нагрузка с коэф. снижения к2
=0,8
0,8×8.5=6.8 кН/м2
|
3,8×38.19×0,95
2,5×38.19×0,95
6.8×38.19×0,95
|
137.9
90.7
246.7
|
1,1
1,1
1,2
|
151.7
99.8
296
|
| Полная нагрузка |
475.3 |
547.5 |
Временная нагрузка на перекрытие 1-го этажа собирается с половины грузовой площади, учитывается полосовое ее расположение через пролет. Расчетная продольная сила N в расчетном сечении колонны с учетом собственного веса двух ее верхних этажей, расположенных выше рассматриваемого сечения:
N=415.25+3×547.5-296/2+3×16.15=1958.2 кН.
Расчетный изгибающий момент М.
Для определения момента М в расчетном сечении 1 колонны временную нагрузку на ригеле перекрытия 1-го этажа располагаем в одном из примыкающих к колонне пролетов. Величина расчетной временной нагрузки на 1 м длины ригеля с учетом коэффициента снижения к2
=0,8:
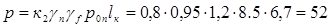 кН. кН.
Расчетные высоты колонн будут: для первого этажа
Н1
=Н1эт
+0.15-hпол
-hпл
-hриг
/2=3.3+0,15-0,1-0,5-0,45 /2=2.625 м.
для второго этажа
Н2
=Н2эт
=3.3 м.
Линейные моменты инерции:
- колонны сечением 400×400 мм:
Для первого этажа 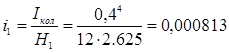 м3 м3
Для второго этажа 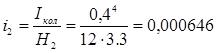 м3
. м3
.
- ригеля сечением 300×450 мм, пролетом l=5.7 м:
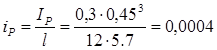 м3
. м3
.
Расчетный изгибающий момент М в расчетном сечении колонны по формуле:
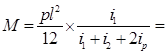 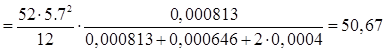 кНм. кНм.
б) Расчет колонны по прочности.
Принимая условно всю нагрузку длительно действующей, имеем
NL
=1958.2 кН и ML
=50,67 кНм; l0
=H1
=2.625 м.
Для тяжелого бетона класса В25 имеем расчетное сопротивление бетона Rb
=14,5×0,9=13.05МПа, модуль упругости бетона Еb
=30000 МПа.
Для продольной арматуры класса А400 расчетное сопротивление Rs
=Rsc
=355 МПа; модуль упругости Еs
=200000 МПа.
h0
=h-a=400-50=350 мм (предварительно а=50 мм).
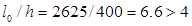 необходим учет прогиба колонны необходим учет прогиба колонны
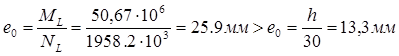
т.е. значение М не корректируем.
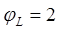 т.к. вся нагрузка принята длительно действующей. т.к. вся нагрузка принята длительно действующей.
Так как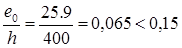 принимаем принимаем 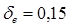
Задаемся μ = 0,0185; 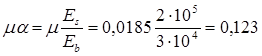
Жесткость колонны:
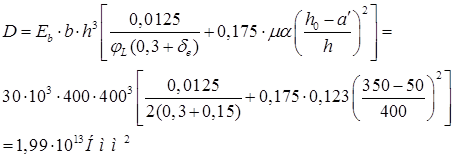
Критическая сила:
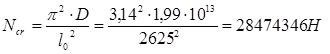 ; ;
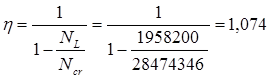 ; ;
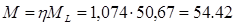 кНм; кНм;
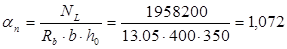
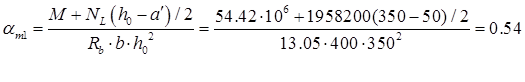
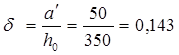 ; ; 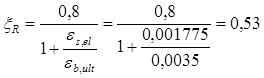 ; ;
Если 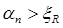 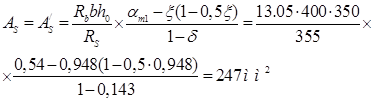
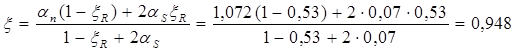
Допускается принимать
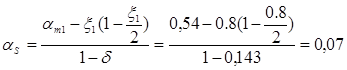
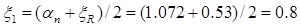
Проверка
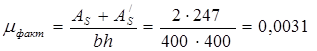 (0.3%) (0.3%)
Расчет колонны по усилиям второй схемы загружения
За расчетное принимается нижнее сечение колонны 1-го этажа, расположенное на уровне верха фундамента. Расчет выполняется на комбинацию усилий Nmax
-M, отвечающих сплошному загружению временной нагрузкой всех междуэтажных перекрытий и покрытия.
а) Определение усилий в колонне. Расчетная продольная сила N.
Постоянная и временная нагрузка на одну внутреннюю колонну от покрытия и всех перекрытий собираются с полной грузовой площади. Учитывается также собственный вес колонны высотой в три этажа. На основании данных таблицы получим:
N=415.25+3×547.5+4×16.15=2122.35 кН.
Расчетный изгибающий момент М.
Поскольку здание имеет жесткую конструктивную схему и пролеты ригеля, примыкающие к рассматриваемой колонне слева и справа, равны, то при сплошном загружении временной нагрузкой покрытия и всех междуэтажных перекрытий изгибающий момент в сечении колонны будет равен нулю.
б) Расчет колонны на прочность.
В нижнем сечении колонны 1-го этажа действует продольная сила N=2122.35 кН. Изгибающий момент в сечении М=0. Поскольку расчетный эксцентриситет с0
=М/N=0, сечение рассчитывается на сжатие продольной силой N=2122.35 кН, приложенной со случайным эксцентриситетом е0
.
Так как вся временная нагрузка принята длительной, то Nl
=N=2122.35 кН. При Nl
/N=1 и l0
/h=6.6 для тяжелого бетона находим
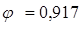
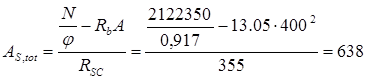 мм2
. мм2
.
Коэффициент армирования:
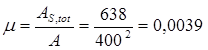
Процент армирования 0.39% т.е. лежит в пределах оптимального армирования.
Таким образом, в результате проведённых расчётов видим, что
Аs,tot
=638 мм2
> Аs
+А¢s
=2×247=494 мм2
.
Поэтому продольную рабочую арматуру подбираем по наибольшей требуемой площади
Аs,tot
=638 мм2
.
Принимаем 6Ø12 A500 с АS
=679 мм2
(+6.4%)
Принятую продольную арматуру пропускаем по всей длине рассчитываемой монтажной единицы без обрывов. Колонна армируется сварным каркасом из арматуры диаметром 8 мм класса А240 с шагом S = 400мм.
7. Расчет консоли колонны
Консоль колонны предназначена для опирания ригеля рамы. Консоли колонны бетонируются одновременно с ее стволом, поэтому выполняется также из тяжелого бетона класса В25 имеем расчетное сопротивление бетона Rb
=13.05 МПа, Rbt
=0,945 МПа,модуль упругости бетона Еb
=30000 МПа. Продольная арматура выполняется из стали класса A400 с расчетным сопротивлением Rs
=355 МПа. Поперечное армирование коротких консолей выполняется в виде горизонтальных двухветвевых хомутов из стержней диаметром 8мм класса А240. Модуль упругости поперечных стержней Еs
=200000МПа. Консоль воспринимает нагрузку от одного междуэтажного перекрытия с грузовой площади ω/2 = 19.095 м2
.
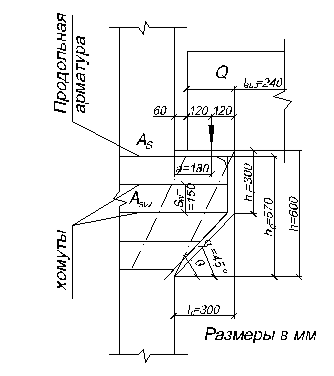
Расчетная поперечная сила передаваемая на консоль, составляет:
Q=547.5/2=273.75 кН.
Принимаем вылет консоли lc
=300 мм, высоту сечения консоли в месте примыкания ее к колонне, h=600мм. Угол наклона сжатой грани консоли к горизонту 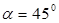 . Высота сечения у свободного края h1
=600-300=300 мм > h/3=200 мм. Рабочая высота опорного сечения консоли h0
=h-a=600-50=550 мм. Поскольку lc
=300<0.9h=495мм, консоль короткая. . Высота сечения у свободного края h1
=600-300=300 мм > h/3=200 мм. Рабочая высота опорного сечения консоли h0
=h-a=600-50=550 мм. Поскольку lc
=300<0.9h=495мм, консоль короткая.
Расстояние от приложения силы Q до опорного сечения консоли будет:
a= lc
-lsup
/2=300-240/2=180мм.
Проверяем прочность бетона на смятие под опорной площадкой:
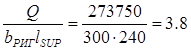 МПа < Rb
=13.05 МПа. МПа < Rb
=13.05 МПа.
Проверяем условие прочности по наклонной сжатой полосе:
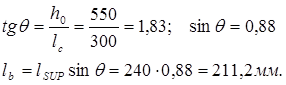
Принимаем шаг горизонтальных хомутов Sw
=150 мм.
Asw
=nAsw1
=2×50.3=100.6 мм2
.
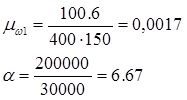
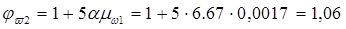
Проверяем условие прочности:
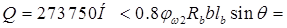
= 0,8 × 1,06 × 13.05 × 400 × 211,2 × 0,88 = 822703 H
Площадь сечения продольной горизонтальной арматуры консоли As
определяют по изгибающему моменту у грани колонны (в опорном сечении консоли), увеличенному на 25% за счет возможности отклонения фактического приложения нагрузки Q на консоль от ее теоретического положения в неблагоприятную сторону: M=1,25Q×a.
М=1,25Q×а=1,25×273.75×0,18=61.59 кН·м.
Площадь сечения арматуры будет равна:
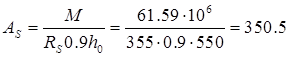 мм2
. мм2
.
Принимаем 2Ø16 A400 с АS
=402 мм2
.
Список литературы
1. СНиП 2.01.07-85*. Нагрузки и воздействия [Текст]: утв. Госстроем России 29.05.2003: взамен СНиП II-6-74: дата введения 01.01.87. – М.: ГУП ЦПП, 2003. – 44 с.
2. СНиП 2.03.01-84. Бетонные и железобетонные конструкции [Текст]: Госстрой СССР – М.: ЦИТП, 1989. – 85 с.
3. СНиП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения [Текст]: утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004. – М.: ГУП НИИЖБ, 2004. – 26 с.
4. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры [Текст]: утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004. – М.: ГУП НИИЖБ, 2004. – 55 с.
5. Руководство по расчету статически неопределимых железобетонных конструкций [Текст]: Научно-исследовательский институт бетона и железобетона Госстроя СССР. – М.: Стройиздат, 1975. – 192 с.
6. Руководство по конструированию бетонных и железобетонных конструкций из тяжелого бетона (без предварительного напряжения) [Текст]: ГПИ Ленингр. Промстройпроект Госстроя СССР, ЦНИИпромзданий Госстроя СССР. – М.: Стройиздат, 1978. – 175 с.
7. Байков, В. Н. Железобетонные конструкции. Общий курс [Текст]: учеб. для вузов / В. Н. Байков, Э. Е. Сигалов. Изд. 5-е, перераб. и доп. – М.: Стройиздат, 1991. – 767 с.: ил.
8. Руководство по расчету статически неопределимых железобетонных конструкций [Текст]. – М.: Стройиздат, 1975.
9. Руководство по конструированию бетонных и железобетонных конструкций из тяжелого бетона (без предварительного напряжения) [Текст]. М.: Стройиздат, 1978.
10. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры. [Текст]. – М.: ЦИТП Госстроя СССР, 1988 г.
|