Государственное образовательное учреждение высшего профессионального образования
Контрольная работа по курсу
Теория машин и механизмов
Кинематическое исследование кривошипно-балансирного механизма
2009 год
Содержание
Кинематическое исследование кривошипно-балансирного механизма
Построение кинематических диаграмм
Построение планов скоростей и ускорений кривошипно-балансирного механизма
Кинетостатический анализ механизма
Задание
1. Построить в выбранном масштабе согласно своему варианту схему механизма для восьми положений кривошипа. Начальное положение ведущего звена (кривошипа ОА
) определяется углом J
0
. Все последующие положения звена ОА
определяются через 45º от первоначального.
2. Построить траектории точек S
и С
2
.
3. Построить диаграмму перемещения точки В
.
4. Методом графического дифференцирования построить диаграммы изменения скорости и ускорения точки В
.
5. Построить планы скоростей и ускорений для восьми заданных положений механизма и определить значения скорости и ускорений характерных точек.
6. Для одного из положений механизма определить силы давления в кинематических парах, учитывая силы инерции звеньев, веса, момента инерции звеньев относительно осей, проходящих через их центры тяжести, полезные сопротивления, приложенные к ведомому звену. Силы полезного сопротивления Р
сопр
и моменты полезного сопротивления М
сопр
следует направить против движения ведомого звена.
7. Пользуясь найденным давлением в шарнире А
, подсчитать уравновешивающий момент на ведущем кривошипе ОА
и затем для проверки определить этот же момент методом рычага Жуковского.
Данные для построения:
| Вариант |
Схема механизма |
Размеры звеньев в мм |
Q
|
φ |
n
,об. /мин ведущего звена |
| ОА
|
АВ
|
ВО
1
|
AS
2
|
BS
3
|
OO
1
|
| 7 в |
Рис.7 |
100 |
400 |
150 |
250 |
60 |
400 |
100 |
10 |
920 |
| Вариант |
Вес звеньев, Н |
Моменты инерции относительно осей, проходящих через центры массы звеньев 2 и 3, кг∙м2
|
Сила сопротив-ления, Н |
Момент сопротив-ления,
Н *м
|
| Звено 2 |
Звено 3 |
Звено 2 |
Звено 3 |
Р
сопр
|
М
сопр
|
| G
2
|
G
3
|
JS
2
|
JS
3
|
| 7 (а, б, в, г, д, е) |
50 |
30 |
0,06 |
0,02 |
- |
400 |
Начертим в выбранном масштабе 1: 4 кинематическую схему механизма (рис. 1).
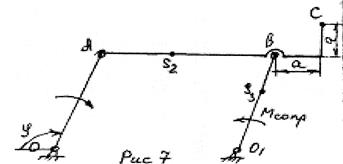
Рис. 1
Для построения плана положений звеньев необходимо:
1. Построить траекторию центра шарнира А
, ведущего звена, для этого проводим окружность радиуса ОА
.
2. Отметить на траектории движения точки А
6÷8÷12 и т.д. положений шарнира А
.
3. Построить траекторию движения точки В
ползуна, совершающего возвратно-поступательное движение.
4. Найти на траектории движения точки В
6÷8÷12 и т.д. положений ползуна, соответствующих отмеченным положениям шарнира А
. Для этого необходимо взять раствор циркуля, равный длине шатуна АВ
, и сделать из каждого положения точки А
засечки на траектории движения точки В
. Полученные точки А
и В
в соответствии соединить прямыми.
Реклама

При вращении кривошипа ОА
ползун В
совершает возвратно-поступательное движение из одного крайнего положения в другое. Под крайним положением звена, совершающего возвратно-поступательное или колебательное движение, понимают положение, соответствующее изменению направления движения звена.
В крайнем правом положении ползун В
будет находиться на наибольшем расстоянии от шарнира О
. Это положение будет тогда, когда кривошип ОА
и шатун АВ
расположатся по одной прямой один за другим. Для нахождения этого положения необходимо из центра шарнира О
радиусом равным (ОА
+ АВ
) = 100+400=500 сделать засечку на траектории движения точки В
.
В крайнем левом положении точка В
должна находиться на наименьшем расстоянии от шарнира О
. Это положение будет тогда, когда кривошип ОА
и шатун АВ
расположатся по одной прямой. Для нахождения этого положения необходимо из центра шарнира О
радиусом, равным (АВ
- ОА
) =400-100=300 сделать засечку на траектории движения точки В
.
Крайние положения точки В
определяют ход ползуна кривошипно-шатунного механизма.
Имея 6÷8÷12 положений звеньев механизма, можно построить траектории положения любой точки любого звена, например центра тяжести S
шатуна АВ
. Положение точки S
определяем делая засечки на прямых А
1
В
1
, А
2
В
2
, …, А
8
, В
8
дугами радиуса А
S
из точек А
1
, А
2
, А
3
, …, А
8
. Соединив последовательно полученные точки S
0
, S
1
, S
2
,..., S
8
плавной кривой, получим траекторию точки S
за один оборот кривошипа.
Построение положения звеньев кривошипно-балансирного механизма и определение положений характерных точек выполняется аналогично КШМ, рассмотренному выше. По заданным координатам определить на чертеже положение неподвижных точек ОО
1
. Затем провести окружность радиуса ОА
и отметить на них восемь положений (А
1
, А
2
,…, А
8
) точки А
ведущего звена, для которых требуется определить положение всех звеньев механизма. Положения остальных звеньев механизма, соответствующие заданным положениям ведущего звена ОА
, определяем методом засечек.
Точка В
движется по дуге окружности радиуса ВО
1
и всегда находится на этой дуге. Положение точек В
1
, В
2
, …, В
8
, соответствующие заданным положениям звена ОА
1
, ОА
2
, …, ОА
8
получим на пересечении дуги с дугой окружности радиуса АВ
, описанной из точек А
1
, А
2
, …, А
8
. Соединив точки В
1
, В
2
, …, В
8
с точками А
1
, А
2
, …, А
8
и О
1
получим положение звеньев АВ
и ВО
1
(рис. 2).
Реклама

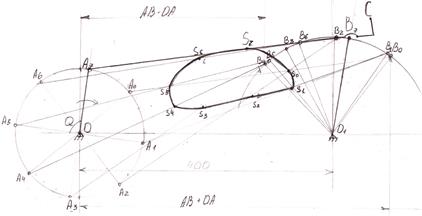
Рис. 2
Кинематической диаграммой называется кривая в прямоугольной системе координат, представляющая зависимость какого-либо параметра движения звена от времени или угла поворота ведущего звена.
Выражение зависимости параметров движения звеньев в виде графиков дает возможность наглядно представить их изменение за определенный промежуток времени.
Построим кинематическую диаграмму перемещения, изменения скорости и ускорения точки В
кривошипно-балансирного механизма.
Для построения необходимо:
1. Выбрать произвольную прямоугольную систему координат s
/t
.
2. На оси абсцисс отложить время t
одного оборота кривошипа ОА
и разделить полученный отрезок на 6÷8÷12 равных частей.
3. Из каждой точки деления оси абсцисс в направлении оси ординат отложить перемещение точки В
, которые определяем из рис.1 за соответствующий промежуток времени (угла поворота кривошипа ОА
). За начало отсчета перемещения точки В
принимаем одно из крайних положений В
0
, В
4
.
4. Соединить плавной кривой полученные точки.
Это и будет диаграмма перемещения ползуна (приложение2).
Для построения диаграммы скорости точки В
необходимо продифференцировать закон S
= f
(t
). Строится диаграмма методом графического дифференцирования диаграммы перемещения точки В
.
Для этого необходимо:
1. Выбрать прямоугольную систему координат v
/t
.
2. По оси абсцисс отложить в том же масштабе время t
одного оборота кривошипа ОА.
3. На отрицательной части оси абсцисс выбрать точку Р
в качестве полюса диаграммы скорости. Расстояние РО
выбирается произвольно, учитывая, что величина отрезка РО
влияет на высоту диаграммы скорости - чем больше РО
, тем выше диаграмма.
4. Провести касательные к соответствующим точкам диаграммы перемещения (1', 2', 3', …, 8').
5. Через полюс Р
провести прямые, параллельные касательным диаграммы перемещения до пересечения с осью ординат. Точки пересечения с осью параллельно перенести на ординаты соответствующих точек деления оси абсцисс.
6. Соединить плавной кривой полученные точки.
Имея диаграмму скоростей v
/t
, аналогично строим диаграмму тангенциальных ускорений, представленную в приложение 2.
На рис.3 представлена кинематическая схема механизма. Требуется построить планы скоростей и ускорений в заданном его положении, если известны размеры звеньев и значение угловой скорости ведущего звена.
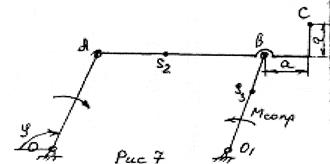
Рис. 3
Для определения скоростей точек звеньев проанализируем движение шарнира А
ведущего звена. Кривошип ОА
совершает вращательное движение, следовательно, скорость точки А
определяется по формуле:
vA
= ω1
· lOA
= (πn
/30) · lOA
(м/c) =9,62;
где ω1
- угловая скорость ведущего звена (рад/с),
n
= 920 число оборотов вращения кривошипа (об. /мин),
lOA
= 0,1 длина кривошипа ОА
(м).
Для определения скорости точки В
шатуна АВ
, совершающего плоскопараллельное движение, разложим это движение на переносно-поступательное вместе с точкой А
и относительно-вращательное движение точки В
вокруг точки А
. Тогда, как известно из теоретической механики, имеем:
 В
= В
= 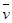 пер. пост
+
пер. пост
+ 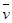 отн. вращ
,
отн. вращ
,
но:
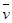 пер. пост
=
пер. пост
= 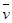 А
,
А
, 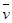 отн. вращ
=
отн. вращ
= 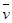 ВА
, ВА
,
и рассмотрим векторное уравнение по величине и направлению:
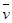 В
= В
= 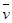 А
+ А
+ 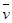 ВА ВА
| Значение |
- |
(πn
/30) · lОА
|
- |
| Направление |
┴ВО
1
|
┴ОА
|
┴АВ
|
Решением этого векторного уравнения является план скоростей.
Построение плана скоростей производится в следующей последовательности:
1) в плоскости чертежа произвольно выбираем точку Р
в качестве полюса плана;
2) из полюса Р
проводим прямую, перпендикулярную кривошипу ОА
, откладываем на ней отрезок Ра
, который изображает в выбранном масштабе 1: 100 см скорость точки А,
;
3) из точки а
проводим прямую, перпендикулярную шатуну АВ
; это направление вектора 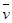 ВА
; ВА
;
4) через полюс Р
проводим прямую, перпендикулярную звену ВО
1
до пересечения с прямой, перпендикулярной шатуну АВ
, точку пересечения обозначим b
.
Фигура Ра
b
является планом скоростей механизма (приложение 3а).
Отрезок Р
b
изображает в выбранном масштабе абсолютную скорость точки В
, которая определена из плана скоростей:
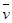 В
= Р
b
· Kv
=9,2
Kv
, В
= Р
b
· Kv
=9,2
Kv
,
где Kv
=0,01
- масштаб скоростей (1: 100).
Отрезок ab
изображает в том же масштабе скорость относительно-вращательного движения 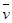 ВА
; величина этой скорости: ВА
; величина этой скорости:
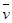 ВА
= ab
· Kv
=3
Kv
. ВА
= ab
· Kv
=3
Kv
.
Угловая скорость относительно-вращательного движения:
ωВА
= 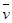 ВА
/ lАВ
. =3/0,4=7,5 ВА
/ lАВ
. =3/0,4=7,5
Для определения абсолютной скорости шатуна воспользуемся методом подобия; следуя этому методу, точка определяется на отрезке ab
из соотношения
АВ
/ab
= AS
/as
= BS
/bs
; 400
/3
= 250
/as
= 60
/bs
откуда: as=1,875; bs=0,45
PS
= 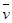 S
= 8,1
S
= 8,1
- абсолютная скорость точки S
.
Определяем ускорения точек механизма методом планов ускорения. Находим ускорение точки А
кривошипа, так как кривошип вращается равномерно, точка А
будет иметь только нормальное (центростремительное) ускорение:
āА
= ā
пер. пост
= ω² · lОА
= 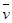 А
2/
lОА
=9,622
/0,1=925,4 А
2/
lОА
=9,622
/0,1=925,4
Точка В
принадлежит шатуну АВ
, который совершает плоскопараллельное движение, разложив его на переносно-поступательное вместе с точкой А
и относительно-вращательное движение точки В
вокруг точки А
, получаем:
āВ
= āА
+ āВА
+ āВА
| Величина |
- |
v
2
А
/lОА
|
v
2
ВА
/lАВ
|
- |
| Направление |
- |
// ОА
от А
к О
|
// АВ
от В
к А
|
┴ АВ
|
Решить данное векторное уравнение нельзя, так как два вектора неизвестны по величине, а один из них неизвестен и по направлению.
Поэтому составляем второе векторное уравнение.
Рассмотрим точку В
как принадлежащую балансиру ВО
1
; тогда ускорение точки В
определяется:
āВ
= āВ
+ āВ
| Значение |
- |
v
²В
/ lВО
1
|
- |
| Направление |
- |
// ВО
1
от В
к О
1
|
┴ ВО
1
|
Решением двух векторных уравнений является план ускорений.
Для того чтобы построить план ускорений, необходимо:
1) в плоскости чертежа выбрать точку π в качестве полюса плана;
2) из точки π провести прямую, параллельную ОА
, и отложить на ней отрезок πа
, равный в выбранном масштабе ускорению точки А
;
3) из точки а
провести прямую, параллельную шатуну АВ
, и отложить на ней отрезок а
n
, равный и параллельный ускорению аВА
;
4) через точку n
провести прямую, перпендикулярную шатуну АВ
;
5) из полюса π провести прямую, параллельную ВО
1
и отложить на ней отрезок πm
, равный в выбранном масштабе 1: 100
āв
= ω² · lВО
1
= 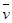 в
2/
lВО
1
=9,22
/0,15=564,3
; в
2/
lВО
1
=9,22
/0,15=564,3
;
6) через точку m
провести прямую, перпендикулярную ВО
1
, до пересечения с прямой, перпендикулярной АВ
, точку пересечения обозначить b
;
7) полюс π соединяем прямой с точкой b
. Отрезок πb
равен в выбранном масштабе āВ
;
8) точки а
и b
соединяем прямой, отрезок а
b
равен в выбранном масштабе ускорению āВА
(приложение 3б).
Для определения ускорения точки S
2
найдем ее расположение на отрезке а
b
из соотношения:
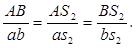
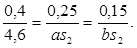 откуда ā
S
2
=2,875; откуда ā
S
2
=2,875;
πS
2
= ā
S
2
- абсолютное ускорение точки S
2
.
Чтобы определить ускорение точки S
3
, найдем ее расположение на отрезке πb
из соотношения:
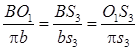 . .
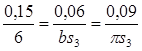 откуда bS
3
=2,4 откуда bS
3
=2,4
πS
3
= bS
3
- абсолютное ускорение точки S
3
.
Угловое ускорение относительно вращательного движения равно:
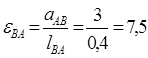 . .
Определим давление во всех кинематических парах и уравновешивающую силу, приложенную к шарниру А
кривошипа кривошипно-балансирного механизма.
Решение:
1. Строим планы скоростей и ускорений механизма
2. Определяем силы инерции и моменты сил инерции для звеньев механизма. Знак минус показывает, что направление силы или момента сил противоположно ускорению.
Звено АВ
совершает плоскопараллельное движение, и действие сил инерции для него сводится к силе и моменту сил инерции:
Р
и2
= -J
2/
q
· as=-50/100*2,875=-1,44
;
М
и2
= -Js
· εВА
= -Js
· (аВА
/ lАВ
) =-0,45.
Сила Р
и2
направлена в сторону, противоположную направлению ускорения а
s
2
. Момент инерции М
и2
- в сторону, противоположную направлению углового ускорения εВА
, а εВА
направлено в ту же сторону, что и касательное ускорение аВА
.
Заменим силу инерции Р
и2
и момент сил инерции М
и2
, действующие на шатун АВ
, одной результирующей силой.
Для этого момент инерции М
и2
заменяем парой сил, где в качестве силы пары берем силу, равную Р
и2
. Одну из сил пары прикладываем к центру тяжести и направляем ее по линии действия Р
и2
в противоположную сторону.
Определяем плечо силы из соотношения:
М
и2
= Р
и2
· h
h
= М
и2
/Р
и2
= М
и2
/Р
и2
=0,3, так как Р
и2
= Р
и2
.
Звено В
(ползун) совершает поступательное движение, поэтому действует только сила инерции
Р
и3
= -mAB
= - (J
3
/g
) · aB
. =-0,66
3. Определяем силы давления в кинематических парах (рис. 16):
а) для определения сил давления в кинематической паре 3-4 выделим группу Ассура и рассмотрим ее равновесие.
Поскольку группа отсоединена от механизма, действие отброшенных частей последнего звена группы нужно заменить силами. Как действуют эти силы, пока не известно, поэтому изображаем их произвольно. Вектор Q
1-2
- сила действия звена 1 на звено 2, вектор Q
4-3
-сила действия звена 4 на звено 3.
Согласно принципу Д’Аламбера, анализируемая группа находится в состоянии равновесия. Можно к ней применить уравнение и определить неизвестные силы.
ΣР
i
= Р
и2
+ J
2
+ Р
и3
+ Р
сопр
+ J
3
+ Q
1-2
+ Q
4-3
= 0
Так как группа Ассура находится в равновесии, то алгебраическая сумма моментов всех сил относительно А
равна нулю.
ΣМА
= Р
и2
· h
1
- J
2
· h
2
+ Q
4-3
· h
3
- J
3
· h
3
+ (Р
и3
+ Р
сопр
) · h
4
= 0
Из этого уравнения выразим Q
4-3
:
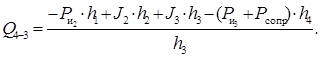
Если в результате арифметических действий Q
4-3
окажется со знаком минус, то это значит, что направление силы выбрано ошибочно и его надо изменить на обратное.
Определив силу Q
4-3
, определяем силу давления в кинематической паре 1-2, построив для этого план сил. Для этого из произвольно выбранного полюса Н
последовательно откладываем векторы сил в выбранном масштабе
Величину силы Q
1-2
определяем из плана сил. Для этого замеряем вектор Q
1-2
и умножаем на масштаб.
Из принципа возможных перемещений вытекает, что сумма моментов сил, приложенных к повернутому плану скоростей относительно полюса Р
, равна нулю.
Составим уравнение моментов сил
Р
и2
· h
1
+ Р
ур
· Ра
- J
2
· h
2
- (Р
и3
+ Рс
) Р
b
= 0.
Из этого уравнения следует:
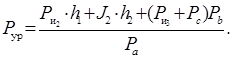
|