1.КИНЕМАТИЧЕСКИЙ И СИЛОВОЙ РАСЧЕТ
1 2.1 Выбор электродвигателя
2.2 Расчет частоты вращения вала электродвигателя
2.3 Кинематические расчеты
3 ВЫБОР МАТЕРИАЛА И РЕЖИМА ТЕРМИЧЕСКОЙ ОБРАБОТКИ
3.1 Выбор материала и режима термической обработки для червяка
3.2 Выбор материала для червячных колес
4 РАСЧЕТ ДОПУСКАЕМЫХ НАПРЯЖЕНИЙ
4.1 Расчет допустимых контактных напряжений
4.2 Расчет допустимых напряжений изгиба
5 ПРОЕКТИРОВАНИЕ ЧЕРВЯЧНОЙ ПЕРЕДАЧИ
5.1 Определение межосевого расстояния
5.2 Подбор основных параметров передачи
5.3 Фактическое передаточное число
5.4 Геометрические размеры червяка и колеса
.5 К.П.Д. передачи
5.6 Силы в зацеплении
5.7 Проверочный расчет червячной передачи на контактную прочность
5.8 Проверочный расчет червячной передачи на изгибную прочность
5.9 Тепловой расчет
6 СМАЗКА
7 КОНСТРУИРОВАНИЕ ВАЛОВ РЕДУКТОРА
7.1 Исходные данные для расчет
7.2 Приближенный расчет быстроходного вала
7.3 Приближенный расчет тихоходного вала
8 ПОДБОР И РАСЧЕТ ПОДШИПНИКО
8.1 Быстроходный вал
8.2 Тихоходный вал
ЛИТЕРАТУРА
ВВЕДЕНИЕ
Червячная передача относится к передачам зацеплением с перекрещивающимися осями валов.
Основные достоинства червячных передач: возможность получения больших передаточных чисел в одной паре, плавность зацепления, возможность самоторможения. Недостатки: сравнительно низкий к.п.д., повышенный износ и склонность к заеданию, необходимость применения для колес дорогих антифрикционных материалов.
Червячные передачи дороже и сложнее зубчатых, поэтому их применяют, как правило, при необходимости передачи движения между перекрещивающимися валами, а также там, где необходимо большое передаточное отношение.
Критерием работоспособности червячных передач является поверхностная прочность зубьев, обеспечивающая их износостойкость и отсутствие выкрашивания и заедания, а также изгибная прочность. При действии в червячном зацеплении кратковременных перегрузок проводится проверка зубьев червячного колеса на изгиб по максимальной нагрузке.
Для тела червяка осуществляется проверочный расчет на жесткость, а также проводится тепловой расчет.
Проектирование осуществляется в два этапа: проектировочный – из условий контактной выносливости определяются основные размеры передачи и проверочный – при известных параметрах передачи в условиях ее работы определяются контактные и изгибные напряжения и сравниваются с допускаемыми по выносливости материала.
Определяются силы, нагружающие подшипники и производится подбор подшипников по грузоподъемности.
1.1.1 Для выбора электродвигателя определяются требуемая его мощность и частота вращения.
Согласно исходным данным на проектирование, требуемую мощность для выполнения технологического процесса можно найти из формулы:
Рвых
=Ft
∙V, (2.1)
где Рвых
– мощность на выходном валу привода, Вт;
Ft
– тяговое усилие, Н;
V – скорость движения рабочего органа, м/с;
Рвых
= 1,5 кВт.
Тогда в соответствии с кинематической цепочкой передачи мощности общий К.П.Д. всего привода рассчитывается по формуле:
ηобщ
= η1
×η2
×η3
×η4
(2.2)
Отсюда
ηобщ
= 0,8×0,95×0,98×0,99 = 0,74.
Таким образом, из расчета общего К.П.Д. стало видно, что в процессе работы привода только 74% мощности от двигателя будет поступать к барабану лебедки.
Определим требуемую мощность двигателя для нормальной работы лебедки:
Реклама

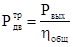 , (2.3) , (2.3)
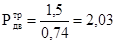 кВт. кВт.
Принимаем двигатель мощностью 2,2 кВт.
Поскольку на данном этапе еще неизвестны передаточные числа передач привода и не известна частота вращения вала двигателя, возникает возможность рассчитать желаемую частоту вращения вала электродвигателя.
Для этого проведены следующие расчеты.
Согласно исходным данным угловая скорость выходного вала рассчитывается по формуле:
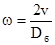 ,(2.4) ,(2.4)
где ω – угловая скорость, с-1
;
Dб
– диаметр барабана, м;
v – скорость движения рабочего органа, м/с.
Тогда,
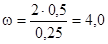 , с-1
. , с-1
.
Найдем частоту вращения, зная угловую скорость по формуле:
 об/мин. (2.5) об/мин. (2.5)
Из анализа кинематической схемы привода электролебедки видно, что общее передаточное число его (uобщ
) образуется за счет передаточного числа редуктора червячной передачи.
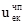 = 16…50 = 16…50
Принимаем uчп
= 50. Взаимосвязь между частотами вращения вала электродвигателя nдв
и выходного вала nз
определяется зависимостью:
nдв
= nз
uобщ
, (2.6)
тогда желаемая частота вращения вала электродвигателя составит:
nдв
= 38,2×50 = 1910 об/мин.
Согласно имеющейся номенклатуре двигателей наиболее близким к желаемой частоте вращения является двигатель с синхронной частотой вращения, равной 1500 об/мин. С учетом вышеизложенного, окончательно принимаем двигатель марки: 90L4/1395. серии АИР, который обладает следующими характеристиками:
Рдв
= 2,2 кВт;
nдв
= 1500 об/мин.
Общее передаточное число:
uобщ
= nдв
/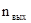 = 1500/38,2=39,3. = 1500/38,2=39,3.
Определим все кинематические характеристики проектируемого привода, которые понадобятся в дальнейшем для детальной проработки передачи. Определение частоты и скоростей вращения. Частоты вращения всех валов легко рассчитать, начиная, от выбранной частоты вращения вала электродвигателя с учетом того, что частота вращения каждого последующего вала определяется через частоту вращения предыдущего по формуле (2.7) с учетом передаточного числа:
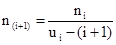 ,(2.7) ,(2.7)
где n(
i
+1)
– частота вращения i+1 вала, об/мин;
ui
–(i+1) – передаточное отношении между i и i+1 валами.
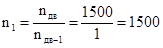 об/мин, об/мин,
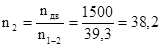 об/мин. об/мин.
Моменты на валах редуктора:
Т1
=9,55×103
(Р/nэ
)= 9,55×103
×(2,2/1500)=14,0 Н×м
Т2
=Т1
×u=14,0×39,3=550 Н×м.
Необходимо помнить, что при работе червячной передачи в контакте витков червяка и зубьев червячных колес присутствует трение скольжения. Поэтому для снижения сил трения и повышения К.П.Д. передачи червяк изготавливают из стали, а червячное колесо из бронзы, латуни, серого чугуна.
Реклама

При выборе конкретного материала и режима термической обработки для червяка необходимо учитывать стоимость и дефицитность материала. Материалом для червяка являются конструкционные качественные среднеуглеродистые или низколегированные стали: сталь 35, сталь 40, сталь 45, 40Х, 40ХМ.
Выбираем сталь 40ХН, твердостью HRC50-56 σт
=750 МПа, улучшение и закалка токами высокой частоты.
Основным критерием для выбора материала червячных колес является скорость скольжения витков червяка по зубьям червячного колеса. Скорость скольжения ориентировочно может быть рассчитана по формуле (3.14).
Vs
= 0,45×10-3
×n2
×u×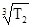 ;(3.1) ;(3.1)
где Vs
- скорость скольжения, м/с;
n2
– частота вращения вала червячного колеса;
u - передаточное число червячной передачи;
Т2
- крутящий момент на валу червячного колеса. 992,6
Vs
= 0,45×10-3
×38,2×50×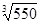 = 7,0 м/с. = 7,0 м/с.
Принимаем: бронзу БрО10Ф1, способ отливки центробежное литье, σв
= 215 МПа, σт
= 135 МПа.
В данном разделе осуществляется расчет допускаемых напряжений материала червяка и червячного колеса. В понятие допускаемых напряжений вкладывается следующие смысл: если в работающей передаче в червячном зацеплении возникают напряжения меньше допустимых, то она будет работать весь установленный период службы, в противном случае превышение напряжений в рабочей передаче выше допустимых вызовет либо существенное сокращение срока службы, либо ее аварийную поломку. Анализ работы закрытых червячных передач показывает, что наиболее нагруженными являются поверхности зубьев в месте их соприкосновения основаниями ножек зубьев. Поэтому все закрытые передачи проверяются по условию не превышения допустимых контактных напряжений [σ]н
и допустимых изгибных напряжений [σ]F
Условный предел контактно-износной выносливости [σ]но
, относящийся к условной базе Νно
= 10×106
цикл.
Расчет допустимых контактных напряжений производят по формуле (4.1).
[σ]н
= Cv
[σ]но
Kн1
,(4.1)
где [σ]н
- допустимые контактные напряжения МПа;
Cv
- коэффициент интенсивности износа зубьев, зависящий от скорости скольжения;
[σ]но
=(0,75…0,9)σв
- условный предел контактно-изноской выносливости;
Кн1
- коэффициент долговечности, учитывающий срок службы передачи.
Так как скорость скольжения Vs=7 м/c, то Cv
= 0,83
Коэффициент долговечности рассчитаем по формуле (3.16)
Кн1
= 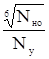 ,(4.2) ,(4.2)
где Nно
10×106
цикл, условная база контактно-усталостного испытания материалов червячного колеса.
Νн
- число циклов контактного напряжения зубьев червячного колеса определяется по формуле (4.3).
Nн
= Lh
×60-n2
×Kpe
в
,(4.3)
где Lh
- моторесурс (чистое время работы);
n2
- частота вращения вала червячного колеса, об/мин;
Крев
- коэффициент реверсивности;
Крев
= 0,5 - при реверсивном режиме (зубья червячного колеса работают обеими сторонами).
Моторесурс рассчитывают по формуле (3.18):
Lh
=Lгод
× 365 × Кгод
× 24 × Ксут
× ПВ, (4.4)
где Lгод
- количество лет работы привода;
Lгод
= 5 лет;
Kгод
= 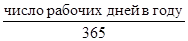 - коэффициент годового использования; - коэффициент годового использования;
Kсут
= 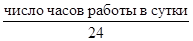 - коэффициент суточного использования; - коэффициент суточного использования;
ПВ = 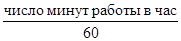 - коэффициент продолжительности включения в течение часа. Из исходных данных имеем: - коэффициент продолжительности включения в течение часа. Из исходных данных имеем:
Kгод
= 0,6
Kсут
= 0,29.
Отсюда по формуле (4.4) находим моторесурс:
Lh
= 5×365×0,6×24×0,29×0,5=3811 час.
Рассчитаем по формуле (4.3) Nн
- число циклов контактного напряжения зубьев червячного колеса.
Nн
= 3811×60×40,2×0,5 = 4595583,6 цикл ≈ 4,6×106
Найдем по формуле (4.2) коэффициент долговечности:
Кн1
= 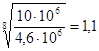 ; ;
[σ]н0
= 0,9×215= 194 МПа;
[σ]н
= 0,83×194×1,1=177 МПа.
Допускаемые напряжения изгиба вычисляют для материала зубьев червячного колеса:
[σ]F
= [σ]F
0
KFL
,(4.5)
Коэффициент долговечности:
KFL
=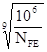 (4.6) (4.6)
Здесь NFL
=25×107
, тогда KFL
=0,815, а [σ]F
=0,815×0,22×215=38,5 МПа.
Межосевое расстояние рассчитывается по формуле (5.1)
аω
≥ 610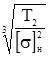 , (5.1) , (5.1)
где аω
- межосевое расстояние, мм;
Т2
- крутящий момент на валу червячного колеса, Н∙м;
Т2
– 550 Н∙м;
[σ]но
- допустимое контактное напряжение червячной передачи;
[σ]но
= 177 МПа.
аω
≥ 610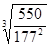 ≥158,5 мм ≥158,5 мм
Округляем до стандартного. Принимаем аω
=160мм.
4.2 Подбор основных параметров передачи
Число витков червяка выбирается с учетом передаточного числа передачи.
Число зубьев червячного колеса находится из соотношения:
z2
= z1
×u, (5.2)
где z1
- число витков червяка, z1
= 1;
u - передаточное отношение;
z2
= 1×39,3=39,3.
Принимаем z2
= 40.
Предварительные значения:
модуля передачи..................................... m=(1,4…1,7)aω
/z2
;
коэффициента диаметра червяка........... q=2aω
/m - z2
.
Принято: m=6,8; q=7,1.
Коэффициент смещения инструмента находится из формулы (5.3).
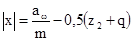 (5.3) (5.3)
тогда
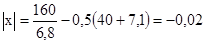 . .
По расчету коэффициент смещения инструмента получается |x| ≤ 1, поэтому значения aω
, m, q и z2
не меняем.
Фактическое передаточное число с учетом найденных значений чисел зубьев определяется по формуле (5.4).
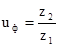 , (5.4) , (5.4)
Тогда
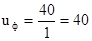 . .
4.4.1 Основные размеры червяка
Делительный диаметр, размеры в мм:
d1
=mq,(5.5)
d1
=6,8×7,1 = 50 мм.
Диаметр вершины витков:
da
1
= d1
+ 2m,(5.6)
da
1
= 50+2×6,8 = 64 мм.
Диаметр впадины:
df
1
=di-2,4m,(5.7)
df
1
= 50 - 2,4 × 6,8 = 34 мм
Делительный угол подъема витков червяка:
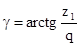 ,(5.8) ,(5.8)
тогда
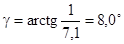 . .
Длина нарезаемой части червяка принимаем:
b1
= (10+5,5|х|+z1
)m,(5.9)
b1
= (10+5,5×0,02+1) 6,8 = 75 мм.
Делительный и начальный диаметры:
d2
= m×z2
,(5.10)
d2
= 6,8×40 = 270 мм.
Диаметр вершины зубьев:
da
2
= d2
+ 2m(l+x),(5.11)
da
2
= 270 + 2×6,8(1+0,02) = 284 мм.
Диаметр впадин:
ds
2
= d2
-2m(1,2 - х);(5.12)
ds
2
= 270 - 2×6,8(1,2-0,02) = 254 мм.
Ширина венца:
b2
≤0,5×dal
,(5.13)
тогда,
b2
=0,5×64 = 32 мм.
Коэффициент полезного действия находится по формуле (5.22).
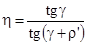 ,(5.14) ,(5.14)
где ρ' - приведенный угол трения с учетом потерь мощности в зацеплении, опорах и на перемешивание масла р'=1,2°.
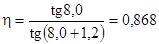 . .
Вследствие того, что оси червяка и червячного колеса перекрещиваются, и что передача в целом находится в силовом равновесии, легко установить зависимости для определения сил в зацеплении.
Окружная сила на колесе равна осевой силе на червяке:
Ft
2
= Fa
1
=  ,(5.15) ,(5.15)
где Т2
- крутящий момент, Н×м.;
d2
- делительный диаметр червячного колеса, м.
Ft
2
= Fa
1
= 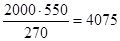 Н. Н.
Окружная сила на червяке, в зацеплении равна осевой силе на колесе:
Ft
1
= Fa
2
= 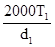 ,(5.16) ,(5.16)
Ft
1
= Fa
2
= 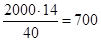 Н. Н.
Радиальные силы:
Fr1
= Fr2
= Ft2
×tgα/cosγ,(5.17)
где α = 20° - стандартный угол зацепления.
Frl
= Fr2
= 4075×tg20°/cos8,0° = 1500 Η.
Окончательно проверить правильность размеров в практикуемой передаче по контактным напряжениям, которые не должны превышать допустимого значения, определенного в п.4.1.
Скорость скольжения витков червяка по зубьям червячного колеса:
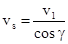 ,(5.18) ,(5.18)
где v1
- окружная скорость на червяке, м/с;
v1
= πd1
×n1
/60000;(5.19)
где n1
– частота вращения червяка;
d1
- делительный диаметр червяка, м;
v1
= 3,93 м/с,
тогда,
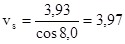 м/с. м/с.
Расчетное контактное напряжение находят из:
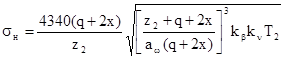 ≤[σ]н
,(5.20) ≤[σ]н
,(5.20)
где d2
- делительный диаметр колеса, м;
Т2
- крутящий момент, Н×м.
kβ
- коэффициент концентрации нагрузки по длине рассчитывается по формуле:
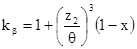 ,(5.21) ,(5.21)
где θ - коэффициент деформации червяка принимают по табл. 6.2 [9, с. 74],
θ = 154;
x- вспомогательный коэффициент, зависящий от характера изменения нагрузки, х=0,3.
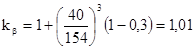 . .
kv
- коэффициент динамики, kv
=1.
Тогда по формуле 5.20
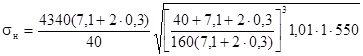 = 150 МПа. = 150 МПа.
Из расчета следует: σн
≤ [σ]н
,
150 < 177
Данный расчет позволяет проверить правильность размеров рассчитанной передачи с точки зрения ее нормальной работы по изгибным напряжениям, которые не должны превышать допустимых значения.
Расчетное напряжение изгиба рассчитывается по формуле
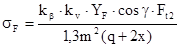 ≤[σ]F
,(5.22) ≤[σ]F
,(5.22)
где m — модуль, м;
YF
– коэффициент формы зуба, определяемый с учетом эквивалентного числа зубьев.
YF
= 1,71,
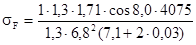 =20,8 МПа. =20,8 МПа.
Из расчета следует, что 20,8≤38,5.
Червячный редуктор в связи с низким значением К.П.Д. и вследствие этого высоким выделением тепла обязательно проверяют на нагрев.
Тепловой расчет передачи представлен в таблице 5.9.
Таблица 5.9
| Наименование параметров |
Обозначение |
Расчетные формулы |
| Приведенный угол трения, ° |
φ′ |
φ′=1,2° |
| К.п.д. червячной передачи |
η |
η =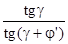 =0,868 =0,868 |
| Мощность на червяке, кВт |
Р |
Р=2,2 кВт |
| Количество тепла, выделяемое в передаче, ккал/ч |
Q |
Q=860(1- η)Р=250 |
| Коэффициент теплоотдачи, ккал/м2
ч° |
КТ
|
КТ
=11 |
| Температура масла в редукторе, °С |
t1
|
t1
=70° |
| Температура окружающей среды, °С |
t0
|
t0
=20° |
| Поверхность охлаждения, м2
|
S |
S=0,196 |
| Количество отдаваемого тепла, ккал/ч |
Q1
|
Q1
= КТ
(t1
- t0
) S=107,8 |
| Условие достаточности естественного охлаждения |
- |
Q≤Q1
; 250≥107,8 |
Как видно из расчета таблицы 5.9, требуется искусственное охлаждение редуктора.
Условия эффективной смазки червячных передач: достаточное покрытие рабочих поверхностей зубьев и подшипников масляным слоем, отвод такого количества тепла, которое требуется для предотвращения чрезмерного нагрева, малое сопротивление смазочной среды.
Смазка передачи осуществляется окунанием. Способ – картерный непроточный. Сорт масла – Автотракторное АК-15 ГОСТ 1862-63.
Вращающий момент на быстроходном валу редуктора Т1
= 14,0 Н×м, на тихоходном валу Т2
= 550 Н×м. силы в червячном зацеплении редуктора:
Ft
1
= Fa
2
= 700 Н;
Ft
2
= Fa
1
= 4075 Н;
Fr
1
= Fr
2
= 1500 Н;
Размеры червяка d1
= 50 мм, df
1
= 34 мм. Размеры червячного колеса d2
= 270 мм.
При расчете валов редуктора необходимо учитывать консольную нагрузку и считать ее приложенной в середине посадочной консольной части вала.
На быстроходном валу радиальную консольную нагрузку определяем по формуле.
Fк1
=80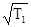 ,(7.1) ,(7.1)
Fк1
=80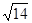 = 300 Н. = 300 Н.
На тихоходном валу радиальную нагрузку определяем по формуле (7.2):
Fк2
=125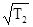 ,(7.2) ,(7.2)
Fк2
= 125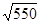 = 2930 Н. = 2930 Н.
В соответствии с конструкцией редуктора заданного типа из эскизной компоновки и ориентировочного расчета валов получим необходимые расстояния до опор валов и приложенных нагрузок.
Материал вала – сталь 40ХН, для которой предел выносливости после улучшения:
σ-1
= 0,35σb
+ (70…120),(7.3)
где σb
= 920 МПа,
σ-1
= 0,35×920 + 100 = 422 МПа.
Допускается напряжение изгиба при симметричном цикле напряжений:
[σn
]-1
= 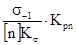 ,(7.4) ,(7.4)
где [n] = 1,7 - – допускаемый коэффициент запаса прочности для опасного сечения;
Kσ
= 2,0 – допускаемый коэффициент концентрации напряжений;
Kpn
= 1 – коэффициент режима нагрузки при расчете на изгиб.
[σn
]-1
= 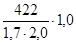 = 124 МПа. = 124 МПа.
Строим эпюры изгибающих моментов.
В вертикальной плоскости YOZ рисунок 7.1.
а) определим опорные реакции от действия сил Ft
1
:
Ray
= Rcy
=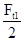 = 350 Н.
= 350 Н.
б) проверим правильность определения реакций:
ΣY = - Ray
+ Ft
1
- Rcy
= -350 + 700 – 350 = 0
Реакции определены верно.
в) строим эпюру изгибающих моментов, для этого определим их значения в характерных сечениях вала:
- в сечении А М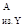 = 0; = 0;
- в сечении B М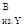 = Ray
×125×10-3
= 350×95×10-3
= 43,8 Н×м; = Ray
×125×10-3
= 350×95×10-3
= 43,8 Н×м;
- в сечении С М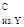 = 0. = 0.
Следовательно, максимальный изгибающий момент будет в сечении В. Откладываем его на сжатом волокне вала (рис. 7.1.г.).
В горизонтальной плоскости XOZ (рис. 7.1.д)
а) определим опорные реакции от действия сил Fr
1
, Fa
1
, Fк1
из условия статики как сумма моментов относительно левой А и правой С опор.
ΣМА
= 0 - Fr
1
×125 – Fa
1
×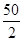 + Rcx
×250 + Fk
1
×335 = 0 + Rcx
×250 + Fk
1
×335 = 0
Rcx
= 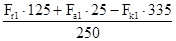 = 755,5 Н. = 755,5 Н.
ΣМС
= 0 RАХ
×250 – Fr
1
×125 + Fa
1
×25 - Fk
1
×85 = 0
RАХ
= 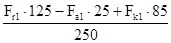 = 444,5 Н. = 444,5 Н.
б) проверим правильность определения реакций
ΣХ = RАХ
- Fr
1
+ Rcx
- Fk
1
=444,5 – 1500 + 755,5 + 300 = 0,
то есть реакции определены верно.
в) строим эпюру изгибающих моментов определяя их значение в характерных сечениях вала:
- в сечении А М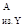 = 0; = 0;
- в сечении В действуют изгибающие моменты от реакций RAX
и Fa
1
, М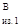 = RAX
×125×10-3
= 444,5×125×10-3
= 55,6 Н×м; М = RAX
×125×10-3
= 444,5×125×10-3
= 55,6 Н×м; М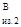 = Fa
1
×25×10-3
= 4075×25×10-3
= 101,9 Н×м. = Fa
1
×25×10-3
= 4075×25×10-3
= 101,9 Н×м.
- в сечении С М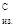 = Fk
1
×85×10-3
= 300×85×10-3
= 25,5 Н×м; = Fk
1
×85×10-3
= 300×85×10-3
= 25,5 Н×м;
- в сечении D М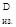 = 0. = 0.
В сечении В направления изгибающих моментов совпадают по направлению. Откладываем значение М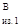 вверх от оси, а затем из этой же точки откладываем М вверх от оси, а затем из этой же точки откладываем М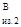 вверх, т.е. вверх, т.е.
М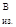 = М = М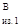 + М + М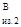 = 55,6 +101,9 = 157,5 Н×м; = 55,6 +101,9 = 157,5 Н×м;
г) проверим правильность определения момента в сечении В от сил
Fk
1
и Rcx
:
М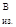 = Rcx
×125×10-3
+ Fk
1
×210×10-3
= 755,5×125×10-3
+ 300×210×10-3
= 157,5 Н×м. = Rcx
×125×10-3
+ Fk
1
×210×10-3
= 755,5×125×10-3
+ 300×210×10-3
= 157,5 Н×м.
д) строим эпюру крутящих моментов (рис. 8.1.ж).
Передача его происходит вдоль вала до середины червяка от середины ступицы муфты Т1
= 14,0 Н×м.
Сечение В.
Суммарный изгибающий момент в сечении равен:
МизΣ
= 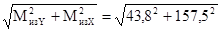 = 163,5 Н×м. = 163,5 Н×м.
Напряжения изгиба:
σиз
= 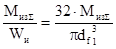 ,(7.5) ,(7.5)
где df
1
– диаметр впадин витка червяка, м.
σиз
= 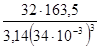 = 42,4 МПа. = 42,4 МПа.
Напряжения кручения:
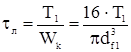 (7.6) (7.6)
где Т1
– крутящий момент на валу, Н×м.
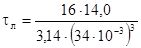 = 1,80 МПа. = 1,80 МПа.
Определим эквивалентное напряжение по энергетической теории прочности и сравним его значение с допустимым:
σэкв
= 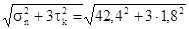 = 42,5 МПа, = 42,5 МПа,
что меньше [σn
]-1
= 124 МПа.
Сечение С.
Изгибающий момент в сечении:
Мизг
= МизХ
= 25,5 Н×м.
Напряжение изгиба определяется по формуле 8.5
σиз
= 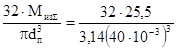 = 4,1 МПа. = 4,1 МПа.
Напряжение кручения находится по формуле 8.6.
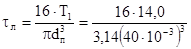 = 1,1 МПа. = 1,1 МПа.
Эквивалентное напряжение:
σэкв
= 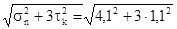 = 4,52 МПа, = 4,52 МПа,
что гораздо меньше [σn
]-1
= 124 МПа.
Примем материал для изготовления вала - сталь 40ХН, для которой σв
= 920 МПа. Тогда допускаемое напряжение изгиба будет равняться по формуле 7.4.
[σn
]-1
= 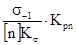 , ,
[σn
]-1
= 0,43×σb
+100;
σ-1
= 0,43×920+100 = 495,6 МПа;
[σn
]-1
= 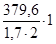 = 146 МПа. = 146 МПа.
Строим эпюры изгибающих моментов.
В вертикальной плоскости YOZ (рисунок 7.2 в)
а) определим опорные реакции сил Ft
2
и Fk
2
:
ΣМk
= 0 - Ft2
×70 + Fk2
×230 – RMY
×140 = 0;
RMY
=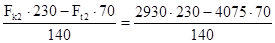 = 2776 Н; = 2776 Н;
ΣМM
= 0 - RKY
×140 + Ft2
×70 + Fk2
×90 = 0;
RKY
=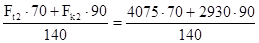 = 3921 Н = 3921 Н
б) проверим правильность определения реакций.
ΣY = RKY
– Ft2
– RMY
+ Fk2
=3921 – 4075 - 2776 + 2930 = 0,
т.е. реакции определены верно по величине и по направлению.
в) строим эпюру изгибающих моментов (рисунок 7.2 г), определяя их значения в характерных сечениях вала:
- в сечении K M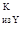 = 0; = 0;
- в сечении LM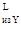 = RKY
×70×10-3
= 4089×70×10-3
= 286,2 Н×м; = RKY
×70×10-3
= 4089×70×10-3
= 286,2 Н×м;
- в сечении MM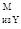 = Fk
2
×70×10-3
= 2930×90×10-3
= 263,7 Н×м; = Fk
2
×70×10-3
= 2930×90×10-3
= 263,7 Н×м;
- в сечении N M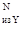 = 0. = 0.
Откладываем найденные значения моментов на сжатом волокне вала. В горизонтальной плоскости XOZ (рисунок 7.2 д).
а) определим опорные реакции от действия сил Fr
2
и Fa
2
ΣМk
= 0 Fr
2
×70 – Fa
2
×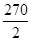 - RMX
×140 = 0; - RMX
×140 = 0;
RMX
=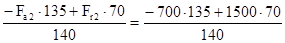 = 75 Н; = 75 Н;
ΣМM
= 0 - Fr
2
×50 – Fa
2
×120 + RKX
×100 = 0;
RKx
=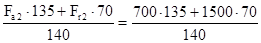 = 1425 Н = 1425 Н
б) проверим правильность определения реакций.
ΣX = - RKX
+ Fr
2
- RMX
= - 1425 + 1500 - 75 = 0,
т.е. реакции определены верно.
в) строим эпюры изгибающих моментов (рисунок 7.2 е), определяя их значения в характерных сечениях вала:
- в сечении K M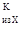 = 0; = 0;
- в сечении LM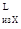 = RKX
×70×10-3
= 1425×70×10-3
= 99,75 Н×м; = RKX
×70×10-3
= 1425×70×10-3
= 99,75 Н×м;
- в сечении MM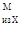 = 0. = 0.
Значение моментов от силы Fа2
и RKX
не совпадают по направлению, поэтому откладываем значения момента M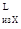 вниз от оси, а значение момента M вниз от оси, а значение момента M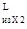 вверх из этой точки, т.е. от значения M вверх из этой точки, т.е. от значения M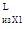 =99,75 Н×м. =99,75 Н×м.
г) проверим правильность определения момента M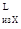 от действия сил RМ
X
. от действия сил RМ
X
.
M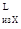 = RМ
X
×70×10-3
= 5,25 Н×м. = RМ
X
×70×10-3
= 5,25 Н×м.
д) строим эпюру крутящих моментов (рисунок 7.2 ж). Передача его происходит вдоль вала до середины червячного колеса:
Т2
= 550 Н×м.
Сечение L.
Суммарный изгибающий момент
МизΣ
=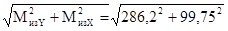 = 303 Н×м. = 303 Н×м.
Диаметр вала в опасном сечении ослаблен шпоночным пазом. При известных значениях его размеров осевой момент сопротивления Wn
и
полярный момент сопротивления Wk
определяем согласно формулам:
Wn
= 0,1×d3
- 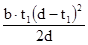 ,(7.7) ,(7.7)
Wk
= 0,2×d3
- 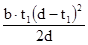 ,(7.8) ,(7.8)
Для вала d = 48 мм, b = 14 мм, t = 5,5 мм.
Подставив в формулы (8.7) и (8.8) исходные данные, получаем:
Wn
= 0,96×10-5
м3
;
Wk
= 2,07×10-5
м3
.
Определим напряжение изгиба:
σn
= 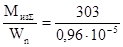 =31,6 МПа. =31,6 МПа.
Напряжение кручения:
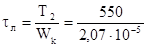 = 26,6 МПа. = 26,6 МПа.
Эквивалентное напряжение:
σэкв
= 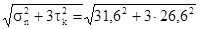 = 55,9 МПа. = 55,9 МПа.
что меньше [σn
]-1
= 146 МПа.
Сечение М.
Изгибающий момент в сечении:
Мизг
= Миз
Y
= 286,2 Н×м.
Напряжение изгиба:
σиз
= 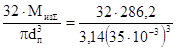 = 68,0 МПа. = 68,0 МПа.
Напряжение кручения:
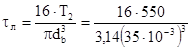 = 65,4 МПа. = 65,4 МПа.
Эквивалентное напряжение:
σэкв
= 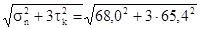 = 132,1 МПа, = 132,1 МПа,
что меньше [σn
]-1
= 146 МПа.
Частота вращения вала n1
=1500 об/мин dn
=40мм. Требуемая долговечность подшипников Ln
= 3811 час. Схема установки подшипников - в распор. На опоры вала действуют силы
RAy
=350 H;
Rax
= 424 Н;
Fa
1
= 4075 Н;
RCy
= 350 Н;
RCx
=755,5 H.
Предварительно примем подшипники роликовые конические средней серии 7308
С=56,0 кН; ℓ = 0,35, у=1,7. Для определения осевых нагрузок на опоры вычислим суммарные реакции опор и приведем схему нагружения вала рис. 8.1
Ra
= 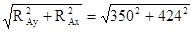 = 550 Н; = 550 Н;
Rс
= 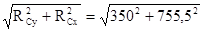 = 833 Н; = 833 Н;
Применительно к схеме получим:
Rz
1
= RA
= 550 Η
RZ
2
=RC
=833 H
Fa
= Fа
l
= 4075 Η
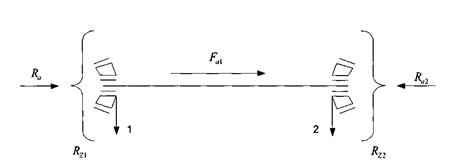
Рисунок 8.1 – Схема нагружения быстроходного вала
Определим осевые составляющие по формуле:
Rs
=0,83×ℓ×Rя
RS
1
= 0,83×ℓ×RZ
1
= 0,83×0,35×550 = 160 Η
RS
2
=0,83×ℓ×RZ
2
=0,83×0,35×833 = 242 Η
так как RS
1
< RS
2
и Fa
> RS
2
- RS
1
= 242 - 160 = 82 H,
то осевые силы, нагружающие подшипники:
Ra1
=RS1
= 160 Η,
Ra2
=Ra1
+ Fa
= 160+ 4075 = 4235 Η.
Сравним отношение 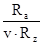 с коэффициентом ℓ и окончательно примем значения коэффициентов xи у. с коэффициентом ℓ и окончательно примем значения коэффициентов xи у.
При 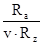 = =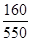 = 0,29 <ℓ = 0,35, = 0,29 <ℓ = 0,35,
x = 1; y = 0.
При 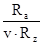 = =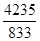 = 5,1 > ℓ = 0,35, = 5,1 > ℓ = 0,35,
x = 0,35; y = 1,7.
Вычислим эквивалентную динамическую нагрузку:
RΕ
=(v·ΧRя
+ yRa
)·ΚΒ
·ΚT
,(8.2.)
где σ = 1 - коэффициент вращения, при вращении внутреннего кольца подшипника;
КБ
= 1,1 - коэффициент безопасности
отсюда,
RE
1
= vXRz
1
×КБ
×Кт
= 1×1×550×1,1×1 = 605 Н,
RЕ2
= (vΧRя
2
+ YRa
2
)×КБ
×Кт
= (1×0,35×833+1,7×4235)×1,1×1 = 8240 Н = 8,24 кН.
Определим расчетную долговечность подшипника при:
Lioh
= 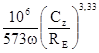 ,(8,3) ,(8,3)
где ω – угловая скорость, с-1
.
Lioh
= 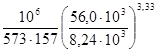 = 6540 час, = 6540 час,
что больше требуемой долговечности
Lh
= 3811 час.
Определим динамическую грузоподъемность:
Сгр
= RЕ
×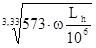 ,(8.4) ,(8.4)
тогда Сгр
= 8,24×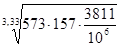 = 47,6 кН, = 47,6 кН,
что меньше Сz
= 56 кН.
подшипник 7211 пригоден.
Частота вращения вала, n2
= 95,5 об/мин, угловая скорость ω2
= 10 с-1
, dn
= 35 мм. Схема установки подшипников - в распор. На опоры вала действуют силы:
Rky
= 3921 Η;
Rmy
=2776 H;
Rkx
= 1425 Η;
Rmx
= 75 Η;
Fa
2
= 700 Η.
Определим суммарную реакцию опор:
Rx
= 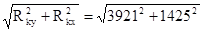 = 4170 Н; = 4170 Н;
Rm
= 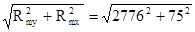 = 2777Н; = 2777Н;
Предварительно примем подшипники роликовые конической серии 7207.
Для него выпишем: CZ
=32,5 кH, ℓ = 0,37, у = 1,62.
Для определения осевых нагрузок на опоры приведем схему нагружения вала рис.8.2 к виду представленному на рис.6.4а [8,с.102]
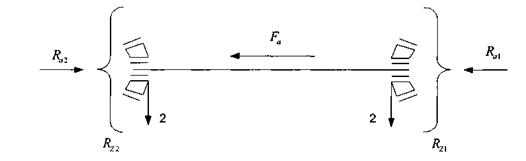
Рисунок 8.2 – Схема нагружения тихоходного вала
Применительно к схеме получим:
RZ
1
=Rm
=2777 Н;
RZ
2
= Rx
=4170 Η;
Fa
= Fa
2
= 700 Η.
Определим осевые составляющие по формуле 8.1
RS
1
= 0,83×ℓ×RZ
1
= 0,83×0,37×2777 = 853 Η
RS
2
=0,83×ℓ×RZ
2
=0,83×0,37×4170 = 1280 Η
так как RS
1
< RS
2
и Fa
> RS
2
- RS
1
= 1280 – 853 = 427 H,
то осевые силы, нагружающие подшипники:
Ra1
=RS1
= 853 Η,
Ra2
=Ra1
+ Fa
= 853+700 = 1553 Η.
Сравним отношение 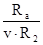 с коэффициентом ℓ и окончательно примем значения коэффициентов x и у. с коэффициентом ℓ и окончательно примем значения коэффициентов x и у.
При  = =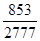 = 0,307 <ℓ = 0,37, = 0,307 <ℓ = 0,37,
x = 1; y = 0.
При  = =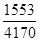 = 0,37 < ℓ = 0,37, = 0,37 < ℓ = 0,37,
x = 1; y = 0.
Вычислим эквивалентную динамическую нагрузку по формуле (9.2.):
RΕ
1
=v·x×RZ
1
×ΚΒ
·ΚT
= 1×1×2777×1,1×1 = 3055 Н,
RΕ
2
=v·x×RZ
2
×ΚΒ
·ΚT
= 1×1×4170×1,1×1 = 4587 Н = 4,59 кН,
Определим расчетную долговечность подшипников в опоре 2 по формуле (8.3):
Lioh
= 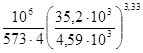 = 385420час, = 385420час,
Что больше требуемой долговечности
Lh
= 3810,6 час.
Определим динамическую грузоподъемность по формуле (8.4):
Сгр
= 4,59×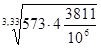 = 8,8 кН, = 8,8 кН,
что меньше Сz
= 35,2,
подшипник 7207 пригоден.
ЛИТЕРАТУРА
1 Каталог электродвигателей постоянного тока серии 2П. - М., 1991.- 250 с.
2 Дунаев П.Ф. Детали машин. Курсовое проектирование. - М., 1990. - 462 с.
3 Иванов М.И. Детали машин. - М., 1991. - 532 с.
|