МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ МАШИНОСТРОИТЕЛЬНАЯ АКАДЕМИЯ
Кафедра "Автоматизация производственных процессов"
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине
"Теория автоматического управления"
Выполнил:
ст. гр. АПП 97-2
И. А. Шкуднов
Проверил:
Доцент Е. В. Пищулина
Краматорск 2000
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ МАШИНОСТРОИТЕЛЬНАЯ АКАДЕМИЯ
Кафедра "Автоматизация производственных процессов"
ЗАДАНИЕ
к курсовой работе по ТАУ
студента группы АПП 97-2 Шкуднова Игоря.
Тема: Расчет линейной непрерывной двухконтурной САУ по заданным требованиям к качеству ее работы
Исходные данные: 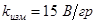 ; ; 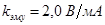 ; ; 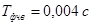 ; ; 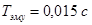 ; ; 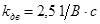 ; ; 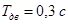 ; ; 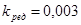 . .
Тип ЛАЧХ: 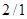 ; ; 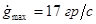 ; ; 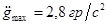 ; ; 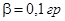 ; ;  ; ; 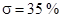 ; ; 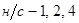 . .
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. АНАЛИЗ ИСХОДНОЙ САУ
1.1 Описание структурной схемы САУ электропривода постоянного тока
1.2 Расчет коэффициента усиления САУ и определение коэффициента передачи предварительного усилителя
1.3 Анализ устойчивости
2. ДИНАМИЧЕСКИЙ СИНТЕЗ САУ ПО ЗАДАННЫМ ТРЕБОВАНИЯМ К КАЧЕСТВУ ЕЕ РАБОТЫ
2.1 Определение желаемой передаточной функции
2.2 Расчет последовательного корректирующего устройства
2.2.1 Определение передаточной функции последовательного корректирующего устройства
2.2.2 Реализация последовательного корректирующего устройства
2.2.3 Оценка качества скорректированной САУ
2.3 Расчет параллельного корректирующего устройства
2.3.1 Определение передаточной функции параллельного корректирующего устройства
2.3.2 Реализация параллельного корректирующего устройства
2.3.3 Оценка качества скорректированной САУ
3. СИНТЕЗ САУ ВО ВРЕМЕННОЙ ОБЛАСТИ
3.1 Описание структурной схемы САУ в пространстве состояний
3.2 Проектирование САУ с использованием обратных связей
3.2.1 Определение коэффициентов обратных связей и коэффициента регулятора
3.2.2 Оценка качества скорректированной САУ
3.3 Определение индекса наблюдаемости САУ
3.4 Проектирование САУ с заданными свойствами с использованием наблюдателя Люенбергера
3.4.1 Построение структурной схемы САУ с наблюдателем Люенбергера
3.4.2 Оценка качества скорректированной САУ
ВЫВОДЫ
ПЕРЕЧЕНЬ ССЫЛОК
В САУ, состоящих только из функционально-необходимых элементов, хотя и уменьшаются ошибки по сравнению с системами, в которых отсутствуют автоматические управляющие устройства (регуляторы), обычно не удается получить требуемых показателей качества. В замкнутых системах это объясняется тем, что условия для достижения высокой точности в установившемся и переходном режимах имеют противоречивый характер. Действительно для уменьшения ошибки в установившемся режиме необходимо повышать коэффициент усиления системы в разомкнутом состоянии 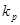 . С увеличением . С увеличением 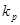 уменьшается запас устойчивости системы и, следовательно, ухудшается переходной процесс. Возможно и то, что система станет раньше неустойчивой, чем удается получить требуемой коэффициент усиления уменьшается запас устойчивости системы и, следовательно, ухудшается переходной процесс. Возможно и то, что система станет раньше неустойчивой, чем удается получить требуемой коэффициент усиления 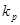 . Для того чтобы при увеличении . Для того чтобы при увеличении 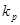 сохранить устойчивость и улучшить показатели качества переходного процесса, необходимо соответствующим образом изменить частотные характеристики системы - осуществить коррекцию системы. сохранить устойчивость и улучшить показатели качества переходного процесса, необходимо соответствующим образом изменить частотные характеристики системы - осуществить коррекцию системы.
Реклама

Под коррекцией САУ понимается изменение их динамических свойств с целью обеспечения требуемого запаса устойчивости, повышения динамической точности и показателей качества переходного процесса. Для коррекции в систему включают корректирующие устройства. Ухудшение переходного процесса и потеря устойчивости при увеличении 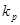 связаны с запаздыванием в системе колебаний по фазе. Следовательно, необходимо частично скомпенсировать запаздывание в некоторой полосе частот. Опережение по фазе может быть допустимо в результате сложения напряжения сигнала рассогласования с производной от него. Такое сложение осуществляется с помощью дифференцирующего фазопередающего устройства. Необходимое функциональное преобразование сигнала рассогласования системы может быть допустимо с помощью корректирующих устройств, включаемых в главный контур управления последовательно элементам системы или в цепи местных обратных связей. связаны с запаздыванием в системе колебаний по фазе. Следовательно, необходимо частично скомпенсировать запаздывание в некоторой полосе частот. Опережение по фазе может быть допустимо в результате сложения напряжения сигнала рассогласования с производной от него. Такое сложение осуществляется с помощью дифференцирующего фазопередающего устройства. Необходимое функциональное преобразование сигнала рассогласования системы может быть допустимо с помощью корректирующих устройств, включаемых в главный контур управления последовательно элементам системы или в цепи местных обратных связей.
Задача курсовой работы заключается в том, чтобы проанализировать данную САУ на устойчивость и качественность работы. Если система не удовлетворяет требованиям устойчивости и качества, то необходимо обеспечить удовлетворение этих требований путем введения в САУ корректирующего звена.
Структурная схема системы автоматического регулирования приведена на рис. 1.1.
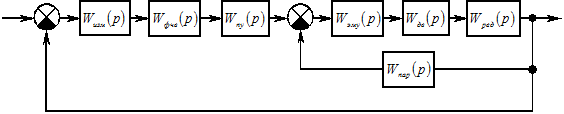
Рисунок 1.1
— Структурная схема САУ электропривода постоянного тока
Здесь:
— 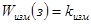 — передаточная функция измерительного устройства (ИУ); — передаточная функция измерительного устройства (ИУ);
— 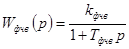 — передаточная функция фазочувствительного выпрямителя (ФЧВ); — передаточная функция фазочувствительного выпрямителя (ФЧВ);
— 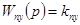 — передаточная функция предварительного усилителя (ПУ); — передаточная функция предварительного усилителя (ПУ);
Реклама

— 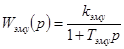 — передаточная функция электромашинного усилителя (ЭМУ); — передаточная функция электромашинного усилителя (ЭМУ);
— 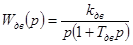 — передаточная функция двигателя постоянного тока; — передаточная функция двигателя постоянного тока;
— 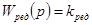 — передаточная функция редуктора. — передаточная функция редуктора.
Измерительное устройство предназначено для измерения (сравнения) входных сигналов 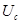 и и 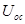 и выдачи сигнала рассогласования и выдачи сигнала рассогласования 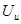 , обработанного соответствующим образом. , обработанного соответствующим образом.
Фазочувствительный выпрямитель предназначается для выпрямления переменного напряжения.
Предварительный усилитель обеспечивает заданную точность САУ. Он представляет собой каскадный усилитель с фиксированным коэффициентом усиления.
Электромашинный усилитель регулирует напряжение питания двигателя и представляет собой генератор постоянного тока с несколькими обмотками возбуждения с фиксированной частотой вращения ротора от приводного двигателя.
Определим общий коэффициент усиления системы:
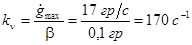 , (1.1) , (1.1)
где 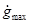 — максимальное значение скорости задающего воздействия; — максимальное значение скорости задающего воздействия;
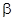 — составляющая ошибки по скорости. — составляющая ошибки по скорости.
С другой стороны:
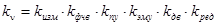 . (1.2) . (1.2)
Принимая 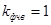 , можно вычислить , можно вычислить 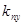 : :
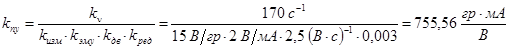 . (1.3) . (1.3)
Согласно полученным данным, структурная схема электропривода будет иметь вид (см. рис. 1.2).
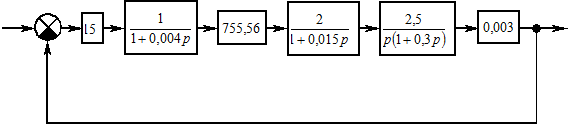
Рисунок
1
.2— Структурная схема исходной САУ
Проанализируем устойчивость САУ, используя критерий Рауса-Гурвица, суть и основные положения которого описаны в источнике [2]. Для анализа по этому критерию необходимо получить характеристический полином. Для получения характеристического полинома найдем передаточную функцию системы:
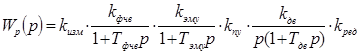 , (1.4) , (1.4)
где 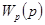 — передаточная функция разомкнутой САУ. — передаточная функция разомкнутой САУ.
Подставляя данные, получим:
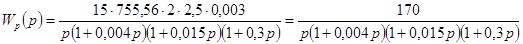 . .
Так как один из корней знаменателя нулевой, то система находится на границе устойчивости.
Теперь получим выражение для замкнутой САУ с единичной отрицательной обратной связью:
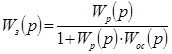 , (1.5) , (1.5)
где 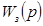 — передаточная функция замкнутой САУ; — передаточная функция замкнутой САУ;
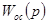 — передаточная функция обратной связи. В данном случае — передаточная функция обратной связи. В данном случае 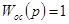 . .
Подставив в формулу (1.5) рассчитанные ранее числовые значения, получим:
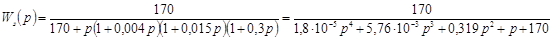 . .
Получили характеристический полином 4-го порядка.
Для определения устойчивости системы запишем определитель Гурвица:
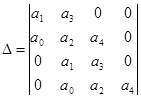 , (1.6) , (1.6)
где 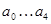 — коэффициенты знаменателя соответственно. — коэффициенты знаменателя соответственно.
Подставляя числа, получим:
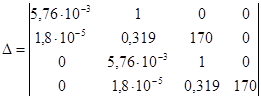 . .
Для устойчивости системы необходимо, чтобы, 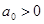 , , 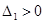 , , 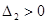 , , 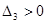 , , 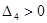 . Проверяем: . Проверяем:
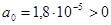 . .
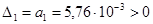 . .
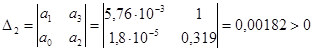 . .
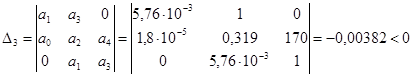 . .
Так как 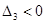 , то система неустойчива, а это значит, что необходимо проектировать корректирующие устройства. , то система неустойчива, а это значит, что необходимо проектировать корректирующие устройства.
В соответствии с вариантом задания принимаем желаемую ЛАЧХ типа 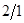 . Ее передаточная функция будет иметь вид: . Ее передаточная функция будет иметь вид:
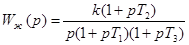 , (2.1) , (2.1)
где 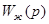 — передаточная функция желаемой системы; — передаточная функция желаемой системы;
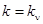 — коэффициент усиления системы; — коэффициент усиления системы;
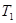 , , 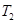 , , 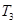 — постоянные времени САУ. — постоянные времени САУ.
Определим частоту среза, исходя из ее связи со временем регулирования:
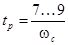 , (2.2) , (2.2)
где 7 — соответствует запасу устойчивости по фазе 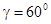 , 9 — , 9 — 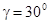 ; ;
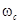 — частота среза желаемой ЛАЧХ. — частота среза желаемой ЛАЧХ.
Запас устойчивости по фазе определим, исходя из перерегулирования:
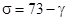 . (2.3) . (2.3)
Подставляя сюда 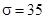 (по условию), получаем, что (по условию), получаем, что 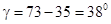 . .
Необходимый коэффициент в формуле (2.2) определим методом интерполяции:
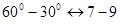 ; ; 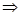 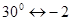 ; ; 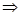 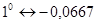 ; ; 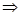 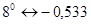 ; ; 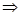
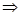 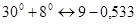 ; ; 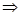 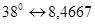 . .
В соответствии с заданием  . Подставляя полученные значения в формулу (2.2), получаем . Подставляя полученные значения в формулу (2.2), получаем 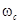 : :
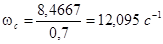 . .
Для вычисления постоянных времени 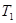 , , 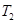 , , 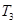 , вычислим сопрягающие частоты , вычислим сопрягающие частоты 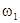 , , 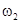 , , 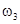 , исходя из соотношения: , исходя из соотношения:
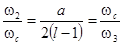 , (2.4) , (2.4)
где 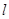 — наклон второй асимптоты ЛАЧХ. В соответствии с заданием принимаем — наклон второй асимптоты ЛАЧХ. В соответствии с заданием принимаем 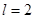 ; ;
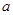 — коэффициент, определяемый из соотношения: — коэффициент, определяемый из соотношения:
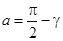 , (2.5) , (2.5)
где 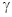 — запас устойчивости по фазе, выраженный в радианах. — запас устойчивости по фазе, выраженный в радианах.
Вычисляем:
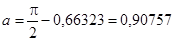 , , 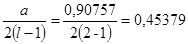 . .
Откуда:
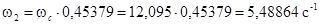 , ,
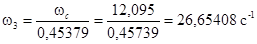 . .
Для ЛАЧХ типа 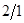 справедливо следующее соотношение: справедливо следующее соотношение:
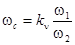 , (2.6) , (2.6)
где 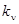 — общий коэффициент усиления системы. — общий коэффициент усиления системы.
Подставляем:
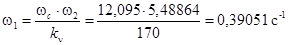 . .
Постоянные времени можно определить из соотношения:
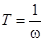 . (2.7) . (2.7)
Численно:
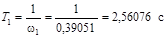 , , 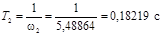 , , 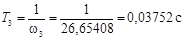 . .
В соответствии с формулой (2.1) записываем передаточную функцию желаемой разомкнутой системы:
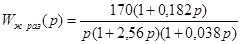 . .
Для построения ЛАЧХ необходимо вычислить логарифмы сопрягающих частот:
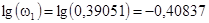 , , 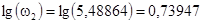 , ,
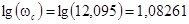 , , 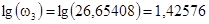 . .
ЛАЧХ желаемой системы представлена на рис. 2.1.

Рисунок 2.1
— Логарифмическая амплитудно-частотная характеристика желаемой передаточной функции
Используя формулу (1.5), запишем передаточную функцию желаемой замкнутой системы с единичной отрицательной обратной связью:
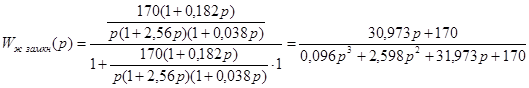 . .
Для расчета переходного процесса воспользуемся программой Perehod.exe, куда введем коэффициенты знаменателя и числителя. Получим график переходного процесса, представленный на рис 2.2.
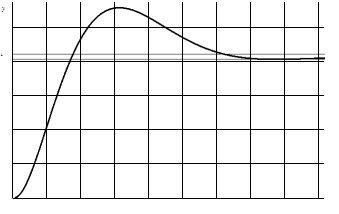
Рисунок 2.2
— Переходный процесс в желаемой передаточной функции
Время переходного процесса и перерегулирование равны:
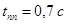 , , 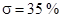 . .
2.2.1Определение передаточной функции последовательного корректирующего устройства
Передаточную функцию последовательного корректирующего устройства найдем графическим методом, исходя из формулы:
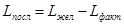 . (2.8) . (2.8)
Для этого построим ЛАЧХ исходной системы, а затем графически вычтем из желаемой ЛАЧХ исходную, получим ЛАЧХ последовательного корректирующего устройства.
Передаточная функция исходной системы имеет вид:
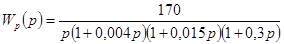 . .
Необходимые для построения ЛАЧХ сопрягающие частоты можно вычислить, преобразовав выражение (2.7):
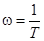 . (2.9) . (2.9)
Откуда:
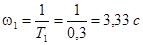 , , 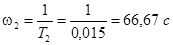 , , 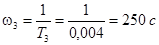 . .
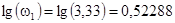 , ,  , , 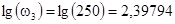 . .

Рисунок 2.3
— Определение ЛАЧХ последовательного корректирующего устройства
В соответствии с рис. 2.3 передаточная функция последовательного корректирующего устройства будет иметь вид:
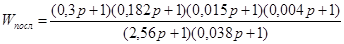 . .
Тогда передаточная функция скорректированной последовательным корректирующим устройством разомкнутой системы будет равна:
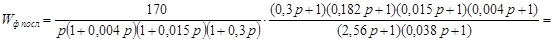
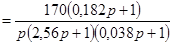 . .
Передаточная функция замкнутой системы в соответствии с формулой (1.5) примет вид:
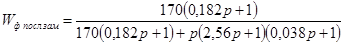 . .
2.2.2Реализация последовательного корректирующего устройства
Используя перечень звеньев, приведенный в источнике [1], произведем реализацию последовательного корректирующего контура с помощью последовательного соединения двух звеньев, электрические схемы которых приведены на рис. 2.4.
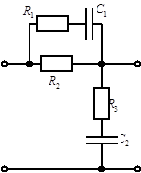 
Рисунок 2.4
— Электрические схемы звеньев последовательного корректирующего устройства
Первая схема реализует следующую передаточную функцию:
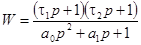 , (2.10) , (2.10)
где 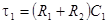 ; ;
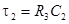 ; ;
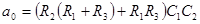 ; ;
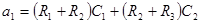 ; ;
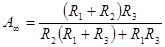 . .
Вторая схема реализует следующую передаточную функцию:
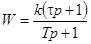 , (2.11) , (2.11)
где 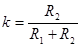 ; ;
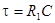 ; ;
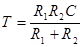 . .
Реализованная последовательным соединением этих двух звеньев передаточная функция будет иметь вид:
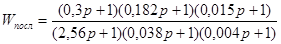 . .
Сопоставляя данную передаточную функцию с выражениями (2.10) и (2.11), получим следующие параметры элементов, используемых в схемах.
Для первой схемы:
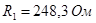 , , 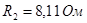 , , 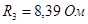 , , 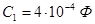 , , 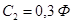 . .
Для второй схемы:
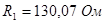 , , 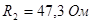 , , 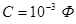 . .
Схема электрическая принципиальная последовательного корректирующего устройства приведена на рис. 2.5.
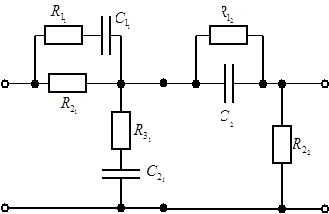
Рисунок 2.5
— Схема электрическая принципиальная последовательного корректирующего устройства
2.2.3Оценка качества скорректированной САУ
Передаточная функция скорректированной последовательным корректирующим устройством разомкнутой системы будет равна:
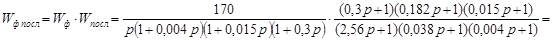
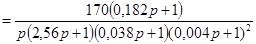 . .
Передаточная функция замкнутой системы в соответствии с формулой (1.5) примет вид:
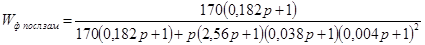 . .
С помощью программы Perehod.exe определяем время переходного процесса и перерегулирование:
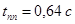 , , 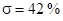 . .
Погрешность по времени переходного процесса будет равна:
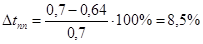 . .
Погрешность по перерегулированию:
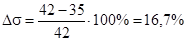 . .
График переходного процесса представлен на рисунке 2.6.
2.3.1Определение передаточной функции параллельного корректирующего устройства
Разделим данную структурную схему на две части: одну из частей будет описывать 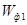 , а вторую — , а вторую — 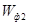 . Второй части данной структурной схемы соответствует последовательное соединение звеньев, охваченное звеном параллельной коррекции. Следовательно: . Второй части данной структурной схемы соответствует последовательное соединение звеньев, охваченное звеном параллельной коррекции. Следовательно:
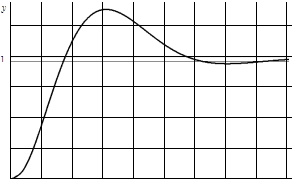
Рисунок 2.6
— Переходной процесс в системе, скорректированной последовательным корректирующим звеном
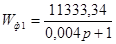 , , 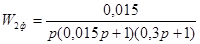 . .
Передаточную функцию параллельного корректирующего устройства найдем графическим методом, исходя из формулы:
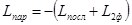 , (2.12) , (2.12)
где 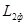 — ЛАЧХ передаточной функции второй части фактической структурной схемы, то есть — ЛАЧХ передаточной функции второй части фактической структурной схемы, то есть 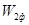 . .
В соответствии с рис. 2.7
передаточная функция параллельного корректирующего устройства будет иметь вид:
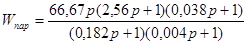 . .
Тогда передаточная функция разомкнутой системы с параллельной коррекцией будет иметь вид:
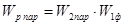 , (2.13) , (2.13)
где 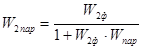 . .
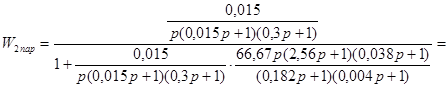
=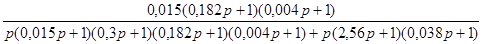 . .
Подставляя 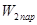 в выражение (2.13), получим передаточную функцию скорректированной параллельным корректирующим устройством разомкнутой системы: в выражение (2.13), получим передаточную функцию скорректированной параллельным корректирующим устройством разомкнутой системы:
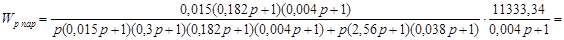
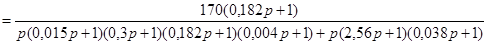 . .
Передаточная функция замкнутой единичной обратной связью системы с параллельной коррекцией в соответствии с формулой (1.5) примет вид:
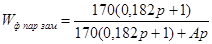 , ,
где 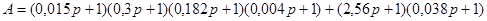 . .

Рисунок 2.7
— Определение ЛАЧХ параллельного корректирующего устройства
2.3.2Реализация параллельного корректирующего устройства
Подбирая необходимые звенья из перечня, приведенного в источнике [1], произведем реализацию параллельного корректирующего контура с помощью последовательного соединения двух типов звеньев, электрические схемы которых приведены на рис. 2.8.
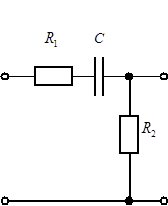 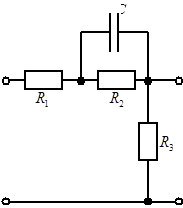
Рисунок 2.8
— Электрические схемы звеньев параллельного корректирующего устройства
Первая схема реализует следующую передаточную функцию:
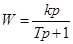 , (2.14) , (2.14)
где ;
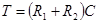 ; ;
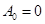 ; ;
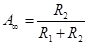 . .
Вторая схема реализует следующую передаточную функцию:
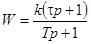 , (2.15) , (2.15)
где 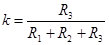 ; ;
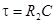 ; ;
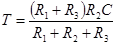 ; ;
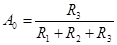 ; ;
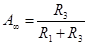 . .
Реализованная последовательным соединением первого и двух вторых звеньев передаточная функция будет иметь вид:
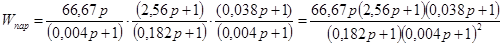 . .
Сопоставляя данную передаточную функцию с выражениями (2.14) и (2.15), получим следующие параметры элементов, используемых в схемах.
Для первого звена (первая схема рис. 2.8):
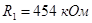 , , 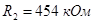 , , 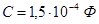 . .
Для второго звена (вторая схема рис. 2.8):
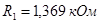 , , 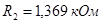 , , 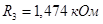 , , 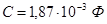 . .
Для третьего звена (вторая схема рис. 2.8):
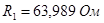 , , 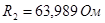 , , 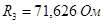 , , 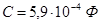 . .
Схема электрическая принципиальная последовательного корректирующего устройства приведена на рис. 2.9.
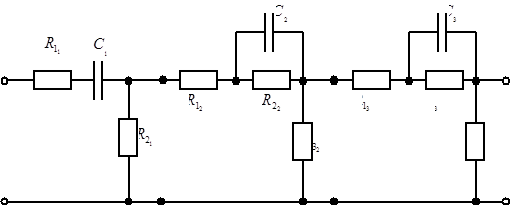
Рисунок 2.9
— Схема электрическая принципиальная параллельного корректирующего устройства
2.3.3Оценка качества скорректированной САУ
Передаточная функция скорректированной параллельным корректирующим устройством разомкнутой системы будет равна:
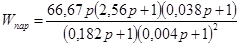 . .
Тогда передаточная функция той части схемы, которая охвачена параллельной коррекцией будет равна:
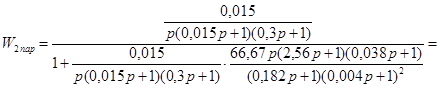
=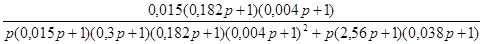 . .
Подставляя 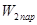 в выражение (2.13), получим передаточную функцию скорректированной параллельным корректирующим устройством разомкнутой системы: в выражение (2.13), получим передаточную функцию скорректированной параллельным корректирующим устройством разомкнутой системы:
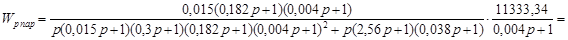
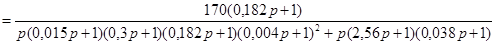 . .
Передаточная функция замкнутой единичной обратной связью системы с параллельной коррекцией в соответствии с формулой (1.5) примет вид:
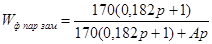 , ,
где 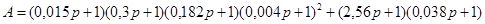 . .
С помощью программы Perehod.exe определяем время переходного процесса и перерегулирование:
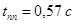 , , 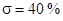 . .
Погрешность по времени переходного процесса будет равна:
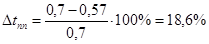 . .
Погрешность по перерегулированию:
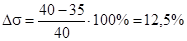 . .
График переходного процесса представлен на рисунке 2.10.
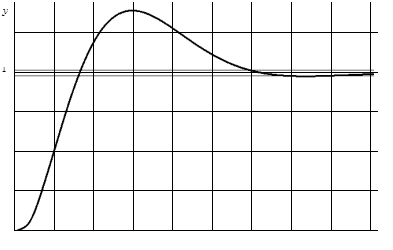
Рисунок 2.10
— Переходной процесс в скорректированной системе
Методы анализа и синтеза САУ в пространстве состояний основаны на том, что любая линейная непрерывная система может быть описана дифференциальными уравнениями первого порядка.
Схематически САУ представляется в виде комбинаций интеграторов, сумматоров и усилителей.
На основании этого строим структурную схему САУ в пространстве состояний (рис. 3.1).

Рисунок 3.1
— Структурная схема САУ в пространстве состояний
На основании структурной схемы САУ в пространстве состояний (рис. 3.1) запишем матрицы коэффициентов, входных сигналов на интеграторы и выходных сигналов с интеграторов, которые будем использовать в дальнейшем для анализа системы:
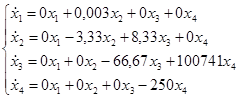 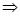 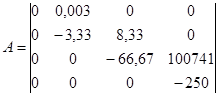 , , 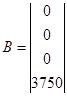 , ,
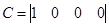 . .
3.2.1Определение коэффициентов обратных связей и коэффициента регулятора
Используя программу Stvarfdbk.exe для разомкнутой системы, полученной в п. 3.1, получим следующие данные для проектирования САУ с использованием обратных связей:
— коэффициенты знаменателя: 0; 55502,78; 17722,01; 320; 1;
— корни: -250; -3,33; -66,67; 0;
— коэффициенты числителя: 9440691.
Для дальнейших расчетов с использованием программы Stvarfdbk.exe, нам необходима передаточная функция желаемой системы:
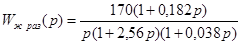 . .
Для того чтобы использовать данную программу, нам необходимо, чтобы знаменатель передаточной функции был четвертого порядка. Используем апериодическое звено первого порядка с 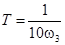 : :
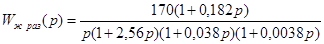 . .
В соответствии с формулой (1.5) передаточная функция замкнутой системы будет иметь вид:
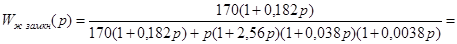
 . .
Используя программу Stvarfdbk.exe в режиме проектирования, задав полученные выше значения, получим следующие данные:
— коэффициенты числителя:
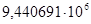 ; ; 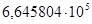 ; ; 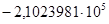 ; ; 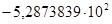 ; ;
— корни: 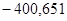 ; ; 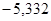 ; ; 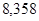 ; ;
— коэффициенты обратной связи: 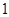 ; ; 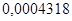 ; ; 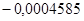 ; ; 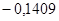 ; ;
— коэффициент усиления: 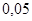 ; ;
— характеристический полином замкнутой системы:
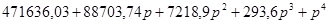 ; ;
— корни: 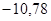 ; ; 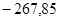 ; ; 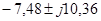 ; ;
— максимальная нормализованная ошибка: 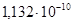 . .
Используя полученные данные, получим структурную схему САУ с коррекцией обратными связями (рис. 3.2).

Рисунок 3.2
— Структурная схема скорректированной обратными связями САУ
На основании структурной схемы САУ в пространстве состояний (рис. 3.2) запишем матрицы коэффициентов, входных сигналов на интеграторы и выходных сигналов с интеграторов:
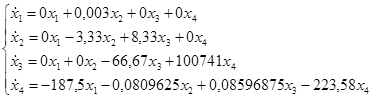 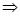
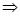 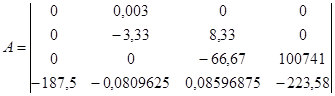 , , 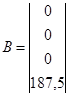 , , 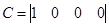 . .
Используя программу Stvarfdbk.exe, получим следующие данные:
— коэффициенты знаменателя: 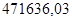 ; ; 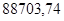 ; ; 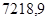 ; ; 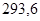 ; ; 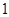 ; ;
— корни: 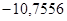 ; ; 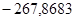 ; ; 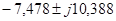 ; ;
— коэффициенты числителя:  . .
Передаточная функция скорректированной системы имеет вид:
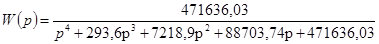 . .
3.2.2Оценка качества скорректированной САУ
С помощью программы Perehod.exe, куда вводим полученную выше передаточную функцию, определяем время переходного процесса и перерегулирование:
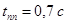 , , 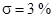 . .
Погрешность по времени переходного процесса будет равна:
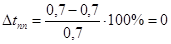 . .
Погрешность по перерегулированию:
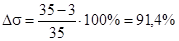 . .
График переходного процесса представлен на рисунке 3.3.
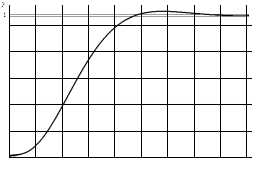
Рисунок 3.3
— Переходной процесс в скорректированной системе
Для определения индекса наблюдаемости системы используется программа Observ.exe. Индекс наблюдаемости используется в программе Luen.exe для определения порядка необходимого корректирующего фильтра.
Индексом наблюдаемости системы называется такое минимальное целое число 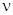 , при котором матрица , при котором матрица 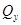 , определяемая выражением , определяемая выражением 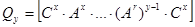 , имеет ранг равный , имеет ранг равный 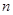 . В общем случае . В общем случае 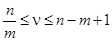 . Если ранг . Если ранг 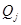 равен равен 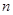 , в то время как ранг , в то время как ранг 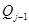 меньше меньше 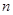 , то индекс наблюдаемости , то индекс наблюдаемости 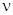 равен равен 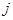 . Если ранг . Если ранг 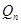 меньше меньше 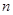 , то система считается ненаблюдаемой. , то система считается ненаблюдаемой.
Для расчета индекса наблюдаемости 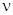 необходимо ввести порядок матрицы необходимо ввести порядок матрицы 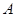 и матрицы и матрицы 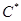 . Так как по условию наблюдаемыми состояниями являются . Так как по условию наблюдаемыми состояниями являются 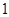 , , 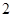 и и 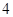 , то матрица , то матрица 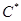 будет иметь вид: будет иметь вид:
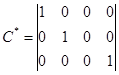 . (3.1) . (3.1)
Использовав программу Observ.exe, получим значение индекса наблюдаемости 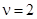 . Порядок наблюдателя Люенбергера определяется из соотношения: . Порядок наблюдателя Люенбергера определяется из соотношения:
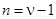 . (3.2) . (3.2)
Таким образом, в системе будет использоваться наблюдатель Люенбергера первого порядка, то есть наблюдатель будет состоять из одного интегратора.
3.4.1Построение структурной схемы САУ с наблюдателем Люенбергера
Используя программу Luen.exe, получим следующие значения параметров, необходимых для построения структурной схемы САУ с наблюдателем Люенбергера:
— собственные значения наблюдателя: 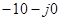 ; ;
— коэффициенты характеристического полинома: 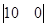 ; ;
— матрица F: 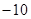 ; ;
— матрица G1: 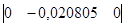 ; ;
— матрица G2: 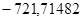 ; ;
— коэффициенты ОС по выходу 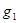 : : 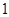 ; ; 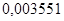 ; ; 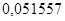 ; ;
— коэффициенты ОС наблюдателя 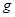 : : 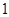 . .
Для наблюдателя Люенбергера справедлива следующая система уравнений:
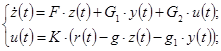 (3.3) (3.3)
Используя систему (3.3), построим структурную схему САУ с наблюдателем Люенбергера (рис. 3.4).
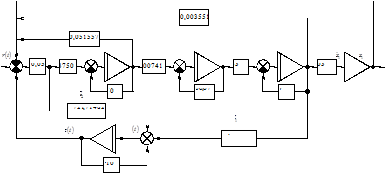
Рисунок 3.4
— Структурная схема САУ с наблюдателем Люенбергера
3.4.2Оценка качества скорректированной САУ
На основании структурной схемы САУ в пространстве состояний (рис. 3.4) запишем матрицы коэффициентов, входных сигналов на интеграторы и выходных сигналов с интеграторов:
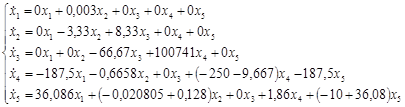 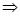
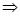 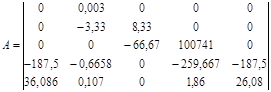 , , 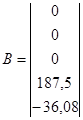 , , 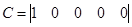 . .
Используя программу Stvarfdbk.exe, получим следующую передаточную функцию системы с наблюдателем Люенбергера:
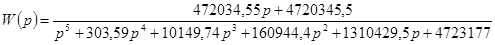 . .
С помощью программы Perehod.exe определяем время переходного процесса и перерегулирование:
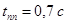 , , 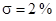 . .
Погрешность по времени переходного процесса будет равна:
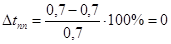 . .
Погрешность по перерегулированию:
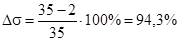 . .
График переходного процесса представлен на рисунке 3.5.
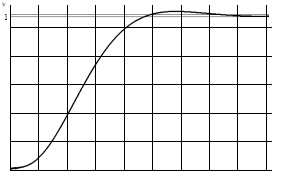
Рисунок 3.5
— Переходной процесс в скорректированной системе
В процессе выполнения работы была проанализирована автоматическая система — электропривод постоянного тока. Для нее были выполнены последовательная и параллельная коррекция.
Последовательное корректирующее устройство вводит производную по рассогласованию, что увеличивает запас устойчивости системы и улучшает качество переходных процессов. При реализации этого вида коррекции были достигнуты следующие параметры точности:
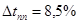 , , 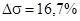 . .
Недостатки этого вида коррекции:
— в процессе эксплуатации при изменении параметров последовательных элементов системы, уменьшается эффект коррекции;
— 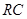 -контуры чувствительны к высокочастотным помехам. -контуры чувствительны к высокочастотным помехам.
Параллельные корректирующие устройства работают при меньшем уровне помех, чем последовательные, так как сигнал поступает на него пройдя в начале через всю систему, являющуюся фильтром низких частот. Благодаря этому эффективность действия параллельного корректирующего устройства при наложении помех на сигнал ошибки снижается в меньшей мере, чем последовательного. Здесь были достигнуты следующие параметры точности:
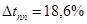 , , 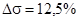 . .
Коррекция с помощью обратных связей обладает следующими достоинствами:
— нелинейные свойства элементов, охваченных обратной связью, линеаризуются, так как передаточные свойства охваченного участка определяются параметрами контура в цепи обратной связи.
Вместе с достоинствами есть и недостатки, такие как:
— сложность и большая стоимость их реализации;
— трудности при суммировании сигнала обратной связи и сигнала обратной связи и сигнала ошибки;
— контур обратной связи сам по себе может оказаться неустойчивым.
Последовательная коррекция применяется в маломощных системах, а коррекция с ОС в мощных системах.
Наблюдатель Люенбергера является наилучшим корректирующим устройством, которое приближает переходной процесс к желаемому, но его реализация сложна, так как необходимо выполнить еще одно интегрирующее устройство, а также устройство сложения и сравнения сигналов от различных интеграторов. Этот вид коррекции применяется в тех случаях, когда ОС нельзя поставить во все измеряемые точки.
Наблюдатель Люенбергера по нескольким измеряемым состояниям, после обработки и сравнения данных судит о протекающем технологическом процессе и выдает соответствующие сигналы на регулятор, который корректирует САУ.
ПЕРЕЧЕНЬ ССЫЛОК
1. Зайцев Г. Ф. Теория автоматического управления и регулирования. — К.: "Высшая школа", 1989, — 431с.
2. Юревич Е. И. Теория автоматического управления. Учебник для студентов высших технических учебных заведений. Издание 2-е, переработанное и дополненное —Л.: "Энергия", 1975.
3. Сборник задач по теории автоматического регулирования и управления, под редакцией В. А. Бесекерского, 5-е издание, переработанное. — М.: "Наука", 1978, — 512с.
4. Клюев А. С. Автоматическое регулирование. Издательство 2-е, переработанное и дополненое. — М.: "Энергия", 1973.
5. Солодовников В. В. Основы теории и элементы системы автоматического регулирования. — М.: "Машиностроение", 1985, - 476с.
6. Воронов А. В. Теория автоматического управления. — М.: "Машиностроение", 1977, - 455с.
|