Московский Государственный Технический Университет
им. Н.Э. Баумана
Калужский филиал
Кафедра М2-КФ
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
на тему «Расчет и проектирование сварных конструкций»
Вариант № 21
Калуга
Содержание
1. Краткое описание металлоконструкции крана
2. Выбор материалов и расчетных сопротивлений
3. Построение линий влияния
3.1 Определение усилий в главной балке
3.2 Определение усилий в стержнях вертикальной вспомогательной фермы
3.3 Определение усилий в стержнях горизонтальной вспомогательной фермы
4. Определение расчетных усилий от заданных нагрузок в элементах моста
4.1 Вертикальная вспомогательная ферма
4.2 Горизонтальная вспомогательная ферма
5. Подбор сечений элементов моста.
5.1 Подбор сечения главной балки
5.2 Подбор сечения вертикальной вспомогательной фермы
5.3 Подбор сечения горизонтальной вспомогательной фермы
6. Расчет концевой балки
7. Расчет сварных швов
7.1 Расчет сварных швов главной балки
7.2 Расчет сварных швов вертикальной вспомогательной фермы
7.3 Расчет сварных швов горизонтальной вспомогательной фермы
7.4 Узлы вертикальной вспомогательной фермы
7.5 Узлы горизонтальной вспомогательной фермы
8. Допускаемый прогиб балки
Список литературы
Конструкция моста является симметричной фигурой относительно двух взаимно перпендикулярных вертикальных плоскостей – продольной и поперечной. При помощи горизонтальных ферм и диагональных связей между поясами вертикальных ферм достигается пространственная жесткость конструкции.
Главная балка воспринимает нагрузки от собственного веса и давления ходовых колес грузовой тележки. Вертикальная вспомогательная ферма воспринимает нагрузки от собственного веса. Горизонтальные фермы воспринимают горизонтальные инерционные нагрузки при разгоне и торможении крана (равномерно распределенные – от веса кран, сосредоточенные – от веса тележки с грузом). Концевые банки нагружены сосредоточенными силами в вертикальной плоскости от действия главных и вспомогательных ферм к горизонтальным инерционным силам при разгоне и торможении тележки.
2. Выбор материалов и расчетных сопротивлений
Для всех основных элементов крана выбираем низкоуглеродистую конструкционную сталь ВСт3 сп5, изготовленную по ГОСТ380-71. Сталь данной марки широко применяется в машиностроении, особенно в изготовлении различных металлоконструкций. Эта сталь характеризуется высоким пределом текучести, она пластична, хорошо работает при различных силовых воздействиях и позволяет получать высококачественные сварные соединения. К тому же сталь ВСт3 сп5 является одной из наиболее дешевых сталей. Поэтому ее выгодно использовать в изготовлении сварных конструкций.
Реклама

Механические свойства:
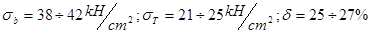
Химический состав:
C-0.14%; Si-0.12%; Mn-0.4%; S-<0.05%; P-<0.04%
Расчетные сопротивления:
Растяжение, сжатие
Изгиб
Срез
|
R=19 kH/cm2
RH
=20 kH/cm2
Rср
=12 kH/cm2
|
Для компенсации упрощенного расчета вводят коэффициент неполноты расчета m: для главной балки m=1; для вертикальной вспомогательной фермы m=0.55; для концевой балки m=0.5.
3. Построение линий влияния
3.1 Определение усилий в главной балке
Необходимо построить линии влияния моментов, чтобы знать их максимально возможные значения в разных сечениях балки.
0,1lM1
= 0,09l = 1,62 м
0,2lM2
= 0,16l = 2,88 м
0,3lM3
= 0,21l = 3,78 м
0,4lM4
= 0,24l = 4,32 м
0,5lM5
= 0,25l = 4,5 м
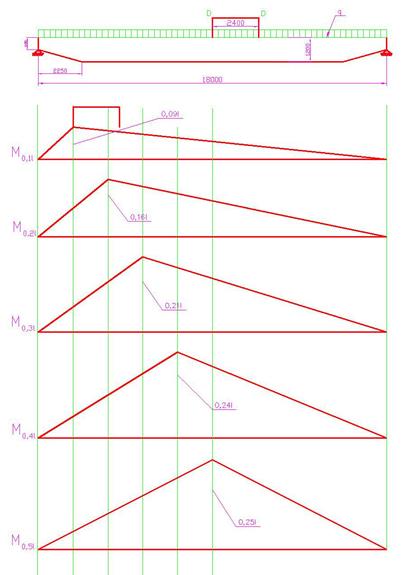
Определим моменты от веса тележки в каждом из сечений 0,1l, 0,2l и т.д. с учетом того, что один из сосредоточенных грузов располагается над вершиной линии влияния, а второй занимает положение, показанное на рис. 1.
Величина изгибающего момента от сосредоточенных сил вычисляется по формуле:
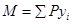 , ,
где уi
– ордината линии влияния;
Р – величина сосредоточенного груза.
В сечениях при l = 18 м и d = 2,4 м:
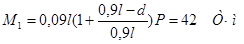
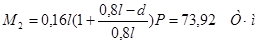
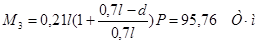
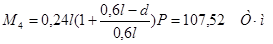
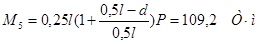
Наибольшие значения М для сечений балки от Р показаны на рис. 2.
Определим изгибающие моменты от равномерно распределенной нагрузки. Момент в сечении x от равномерно распределенной нагрузки определяется по формуле:
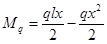 . .
В сечениях:
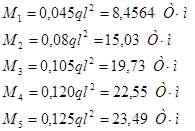
Значения М для сечений балки от q показаны на рис. 3.
Вычислим суммарные величины моментов в сечениях от сосредоточенных сил и равномерной нагрузки:
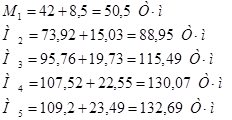
Таким образом, расчетной величиной момента для балки является М = 132,69 Т м = 13269000 кГ см.
Требуемый момент сопротивления балки для этого усиления равен:
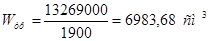 . .
Построим линии влияния поперечной силы:
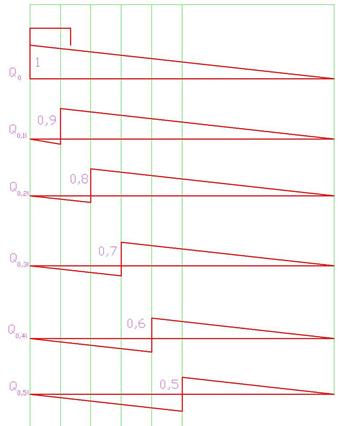
в сечении x= 0, ордината влияния Q0
= 1;
в сечении x= 0,1l, ордината Q1
= 0,9;
в сечении x= 0,2l, ордината Q2
= 0,8 и т.д.
Определим расчетные усилия от сосредоточенных сил в каждом из указанном сечений с учетом того, что одна из них располагается над вершиной линии влияния.
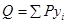 . .
В сечении x = 0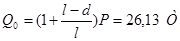 . .
Аналогично в сечениях при l = 18 м и d = 2 м:
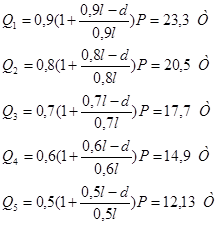
Поперечные силы Q от собственного веса q равны:
Реклама

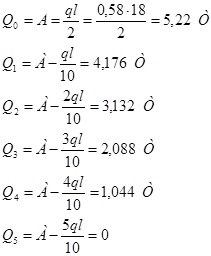
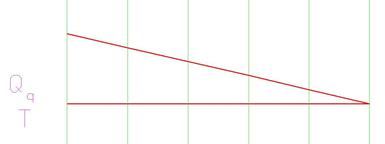
Расчетные значения поперечных сил от сосредоточенных и равномерно распределенных нагрузок будут следующими:
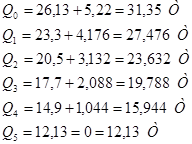
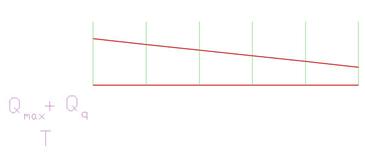
Усилия определяют методом линий влияния. Построим линии влияния для панели 5-6. Моментной точкой изгиба является узел 18. Пусть груз находится справа от разрезанной панели: 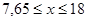 м. Рассмотрим равновесие левой части: м. Рассмотрим равновесие левой части:
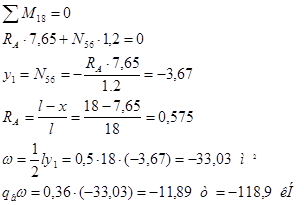
Линия влияния имеет вид треугольника с ординатой y1
= -3,67
Построим линии влияния для панели 18-19. Моментная точка – 7. Пусть груз находится справа 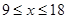 м. Рассмотрим равновесие левой части: м. Рассмотрим равновесие левой части:
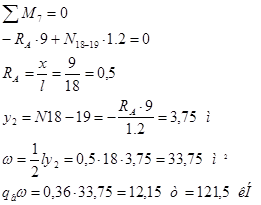
Линия влияния имеет вид треугольника с ординатой y1
=3,75 м.
Построим линию влияния для раскоса 18-7. Пусть груз находится справа от разрезаемой панели: 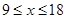
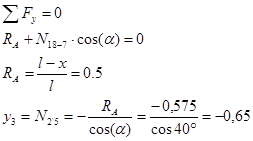
Пусть груз находится слева от панели, т.е. 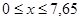 : :
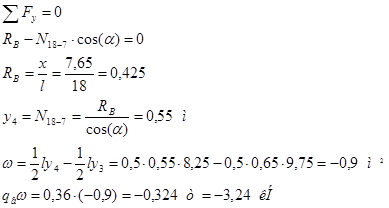
Построим линию влияния для стойки 0-15. Она работает лишь при нахождении единичного груза в панели 0-1. При нахождении груза равного 1 в узле 0 усилие в стойке 0-15 равно 0.
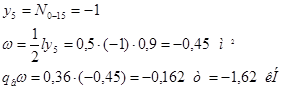
Построим линию влияния для стойки 2-16. Стойка 2-16 работает лишь при нахождении единичного груза в панелях 1-2 и 2-3. При прохождении груза равного 1 в узле 1 усилие в стойке 2-16 равно 1. При нахождении указанного груза в узле 1 и левее его, а также в узле 3 и правее его усилие в стойке 2-16 равно 0.
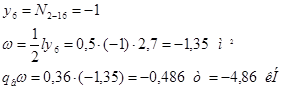
Аналогично усилия распределяются в стойке 4-17.
Линия влияния для стоек 0-15, 2-16, 4-17 имеют вид треугольника с высотой равной 1(в узлах 0; 2; 4 соответственно).
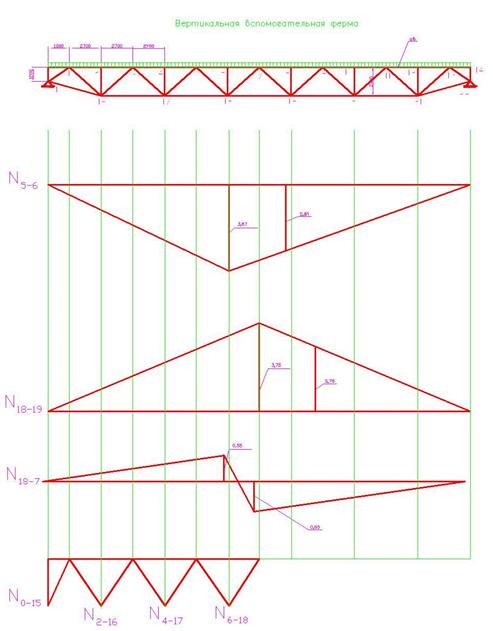
Построим линии влияния для панели 5’-6. Моментная точка – узел 18. Пусть груз находится справа от разрезаемой панели 5’-6. Рассмотрим равновесие левой части:  м. м.
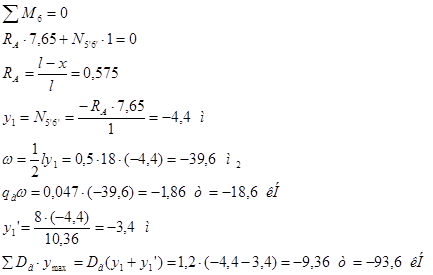
Линия влияния имеет вид треугольника с ординатой y1
= -3,4 м.
Построим линию влияния для панели 6’-8’. Моментная точка – узел 7`. Пусть груз находится справа от разрезаемой панели 6’-8’: 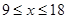 . Рассмотрим равновесие левой части: . Рассмотрим равновесие левой части:
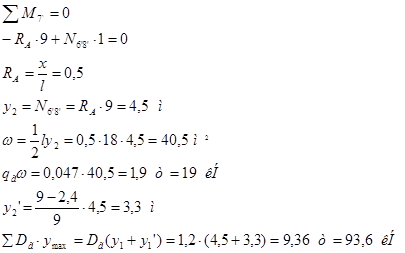
Линия влияния имеет вид треугольника с ординатой y1
=3,3 м.
Построим линию влияния для раскоса 6-7`. Пусть груз находится справа от разрезаемой панели 6-7`: 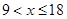 . Сумма проекций на ось y: . Сумма проекций на ось y:
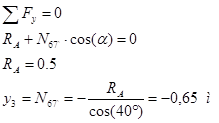
Пусть груз слева от разрезаемой панели 6-7’: 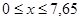 . Сумма проекций на ось y: . Сумма проекций на ось y:
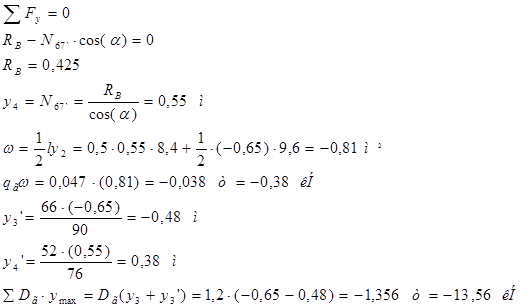
Построим линию влияния для стойки 0-0`. Она работает лишь при нахождении единичного груза в панели 0`-1`. При нахождении груза равного 1 в узле 0 усилие в стойке 0-0` равно 0.
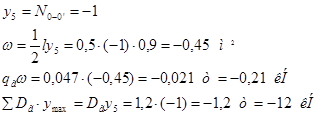
Построим линию влияния для стойки 2-2`. Стойка 2-2` работает лишь при нахождении единичного груза в панелях 1`-2` и 2`-3`. При прохождении груза равного 1 в узле 1` усилие в стойке 2-2` равно 1. При нахождении указанного груза в узле 1` и левее его, а также в узле 3` и правее его усилие в стойке 2-2` равно 0.
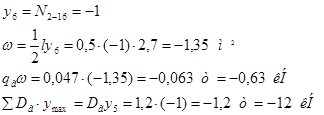
Аналогично усилия распределяются в стойке 4-4` и 6-6`.
Линии влияния стоек 0-0`, 2-2`, 4-4`, 6-6` будут иметь вид аналогичный линиям влияния стоек вертикальной вспомогательной фермы.
4. Определение расчетных усилий от заданных нагрузок
в элементах моста
4.1 Вертикальная вспомогательная ферма
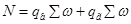
Верхний пояс:
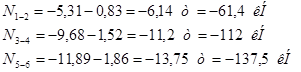
Нижний пояс:

Раскосы:
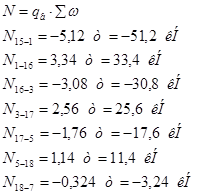
Стойки:
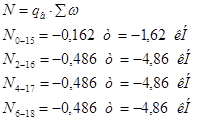
Раскосы:

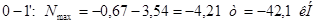
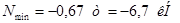
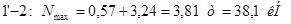
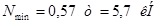
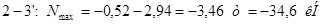
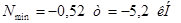
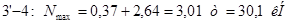
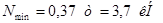
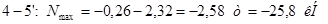
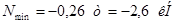
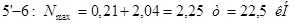
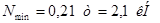
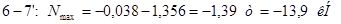
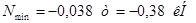
Стойки:
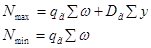
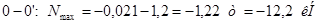
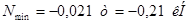
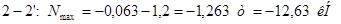
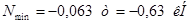
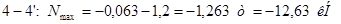
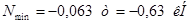
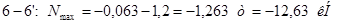
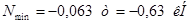
5. Подбор сечений элементов моста
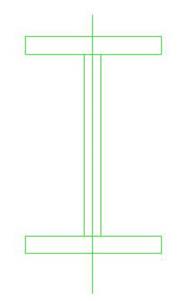
По требованиям СНИП минимальная толщина стенки принимается 6 мм, а полки 8 мм.
Принимаем 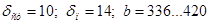 мм. мм.
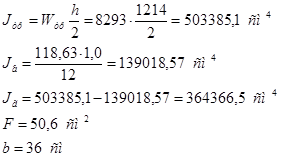
Принимаем сечение горизонтального листа 360x14мм.
Определим уточненное значение момента инерции подобранного поперечного сечения балки:
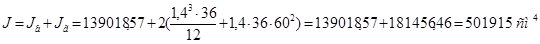
Наибольшее нормальное напряжение в крайнем волокне балки:
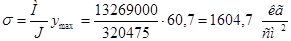
Определим касательное напряжение на уровне центра тяжести балки в опорном ее сечении:
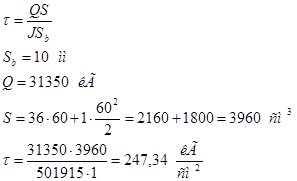
Определим эквивалентные напряжения в сечении, в котором имеется наибольший изгибающий момент М = 13269000 кГ см и Q = 12130 кГ.
Эквивалентные напряжения вычисляются на уровне верхней кромки вертикального листа в зоне резкого изменения ширины сечения.
Вычислим в этом волокне балки напряжения от М:
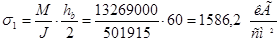 . .
В этом же волокне напряжение от Q:
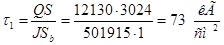 , ,
где 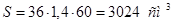 э э
Эквивалентное напряжение:
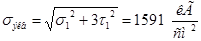 , ,
что меньше наибольшего нормального напряжения в крайнем волокне.
Общая устойчивость балки
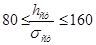 ; ;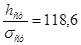
Требуются вертикальные ребра жесткости.
Расстояние между ними:
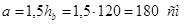 . .
В этом случае следует знать следующие величины:
1) нормальное напряжение в верхнем волокне вертикального листа:
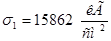 ; ;
2) среднее касательное напряжение τ от поперечной силы. В середине пролета Q = 12130 кГ, среднее напряжение равно:
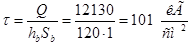 ; ;
3) местное напряжение под сосредоточенной силой:
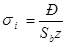 ;m=1. ;m=1.
Для среднего значения режима:
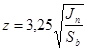 . .
Примем сечение рельса 50x50 мм.
Ордината центра тяжести сечения пояса и рельса относительно верхней кромки пояса равна:
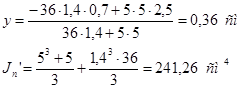
Найдем момент инерции относительно оси x0
, проходящей через центр тяжести сечения пояса с рельсом ( F = 75,4 см2
).
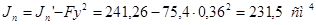 . .
Вычислим условную длину:
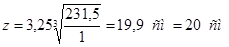 . .
Находим напряжение 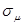 от Р = 14000 кГ: от Р = 14000 кГ:
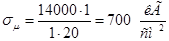 . .
Для проверки правильности постановки ребер жесткости надлежит выяснить три вспомогательные величины:
1) 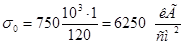 ; ;
2) 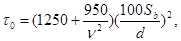
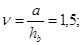 d = 120 см. d = 120 см.
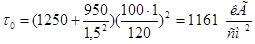 . .
3) 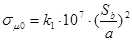 , ,
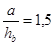 k1 = 8,6. k1 = 8,6.
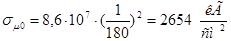 . .
Проверим, обеспечена ли требуемая устойчивость:
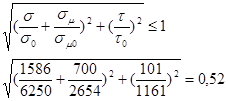
Устойчивость вертикального листа в середине пролета вполне обеспечена.
Посмотрим, обеспечена ли устойчивость в опорных сечениях.
На опоре 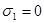 . .
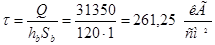 . .
Проверяем снова устойчивость для опорного сечения, полагая 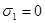 . .
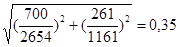
Устойчивость в опорном сечении обеспечена.
Переходим к расчету поясных швов
.
Катеты верхних и нижних поясных швов примем равными k = 6 мм.
В нижних поясных швах действуют касательные напряжения:
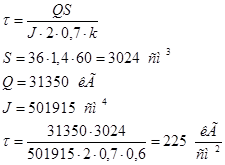
В верхних поясных швах при определении напряжений следует вычислять Sс учетом наличия рельса:
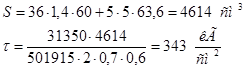
Местное напряжение в шве:
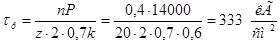 . .
Условное результирующее напряжение:
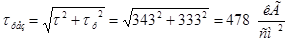 . .
Допускаемое напряжение в поясных швах:
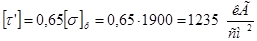 . .
Катеты швов, приваривающих ребра жесткости к поясам и вертикальному листу принимаем k = 6 мм.
m=0,55
Верхний пояс
:
Верхний пояс сжатый. С точки зрения уменьшения сборочно-сварочных работ принимаем сечение из одного равнобокого уголка.
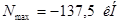
1) Требуемая площадь сечения:
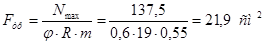
Примем уголок 100х100х12, F=22,8 см2
, 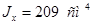 , , 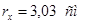 . .
2) Проверка на устойчивость:
Находим гибкость:
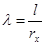 , ,
где l– свободная длина элемента (l= 135 см);
rx
– радиус инерции поперечного сечения гибкого элемента.
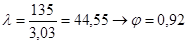
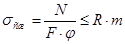
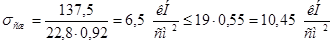
3) Проверка на выносливость:
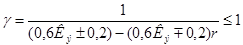 , ,
где Кэ
– коэффициент концентрации напряжений (Кэ = 1,2);
r– характеристика нагружения панели верхнего пояса.
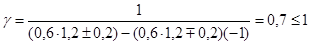
Принимаем 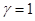 . .
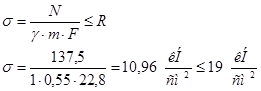
Нижний пояс
:
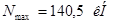
1) Требуемая площадь сечения
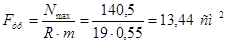
Примем уголок 90х90х8; F=13,90 см2
, 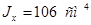 , , 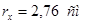 . .
2) Гибкость:
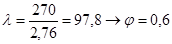
3) Проверка на прочность:
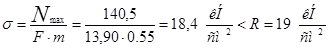
4) Проверка на выносливость:
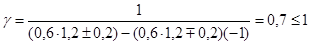
Принимаем 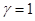 . .
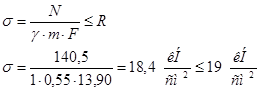
Раскосы
:
Растяжение: Nmax
=33,4 (kH); lp
=144,48 cм.
Сжатие: Nmax
= -52,2 (kH); lp
=86,54 cм.
Сжатые раскосы:
1) Требуемая площадь
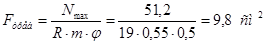
Примем уголок 75х75х7; F=10,10 см2
; 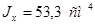 , , 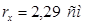 . .
2) Гибкость:
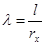 , где , где 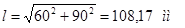
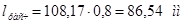
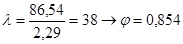
3) Проверка на устойчивость
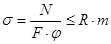
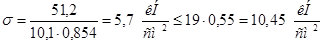
4) Проверяем на прочность:
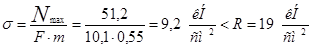
Растянутые раскосы:
1) Требуемая площадь
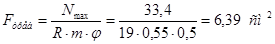
Примем уголок 70х70х5; F=6,86 см2
; 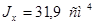 , , 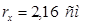 . .
2) Гибкость
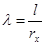 , где , где 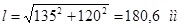
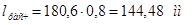
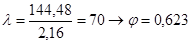
3) Проверка на устойчивость:
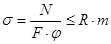
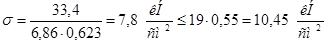
4) Проверяем на прочность:
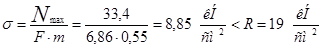 . .
Стойки
:
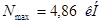
1) Требуемая площадь сечения:
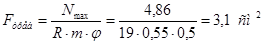
Выбираем уголок 50х50х5; F=4,8 см2
; 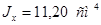 , , 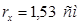 . .
lp
=120 cм.
2) Гибкость:
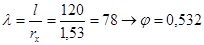
3) Проверка на устойчивость
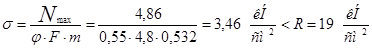
4) Проверка на выносливость:
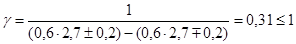
(Кэ = 2,7)
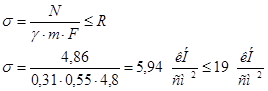
m=0,55
Раскосы
:
Растяжение: Nmax
= 38,1 (kH); Nmin
= 5,7 (kH); lp
= 107,63 cм.
Сжатие: Nmax
= -42,1 (kH); Nmin
= -6,7 (kH) ; lp
= 134,4 cм.
Сжатые раскосы:
1) Требуемая площадь
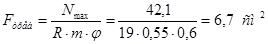
Примем уголок 70х70х5; F=6,86 см2
; 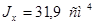 , , 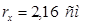 . .
2) Гибкость:
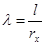 , где , где 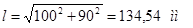
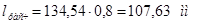
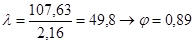
3) Проверяем на прочность:
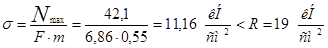
4) Проверка на выносливость:
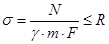
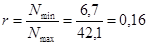
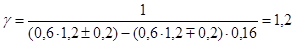
Принимаем 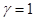 . .

Растянутые раскосы:
1) Требуемая площадь
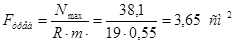
Примем уголок 50х50х5; F=4,8 см2
; 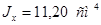 , , 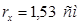 . .
2) Гибкость
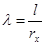 , где , где 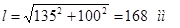
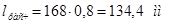
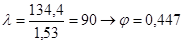
3) Проверяем на прочность:
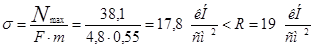
4) Проверка на выносливость:
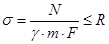
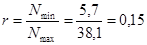
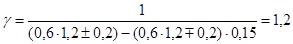
Принимаем 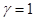 . .
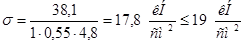
Стойки:
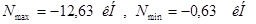
1) Требуемая площадь сечения:
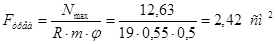
Выбираем уголок 50х50х5; F=4,8 см2
; 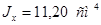 , , 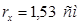 . .
lp
=120 cм.
2) Гибкость:
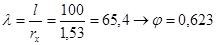
3) Проверка на устойчивость:

4) Проверка на прочность:
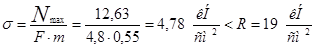
5) Проверка на выносливость:
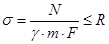
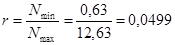
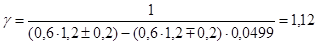
Принимаем 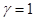 . .
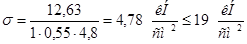
Сечение концевой балки состоит из двух вертикальных и двух горизонтальных листов. Концевая балка нагружена сосредоточенными силами в местах крепления главной балки и вспомогательных ферм, от которых возникают моменты в горизонтальных и вертикальных плоскостях.
m=0,55
1) Давление со стороны механизма передвижения
:
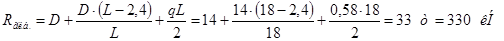
2) Давление вспомогательной фермы со стороны механизма передвижения:
3)
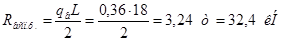
4) Горизонтальная сила при торможении
тележки:
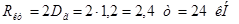
5) Определение реакций 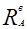 и и
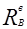
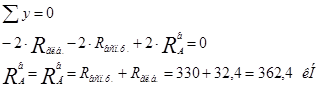
6) Определение реакций 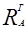 и и
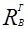 : :
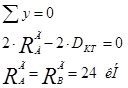
7) Изгибающий момент в вертикальной плоскости
:
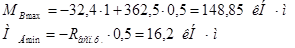
8) Изгибающий момент в горизонтальной плоскости
:
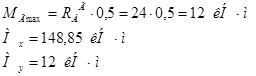
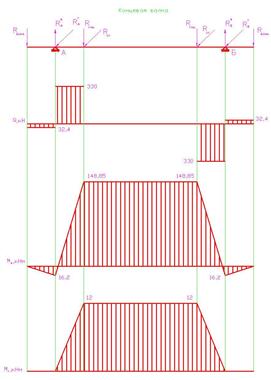
9) Подбор сечения концевой балки
:
Примем данные сечения:
Площадь 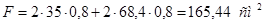
Момент инерции относительно осиx:
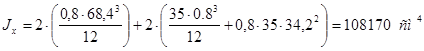
Момент инерции относительно оси y:
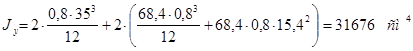
Балка составленная из двух сечений соединена накладками и болтами.

За счет ослабления отверстиями под болты:
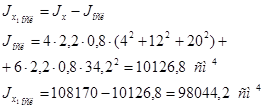
Момент сопротивления сечения относительно оси х:
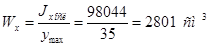
Напряжения в вертикальной плоскости:
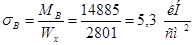
С учетом ослабления:
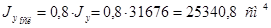
Момент сопротивления относительно оси y:
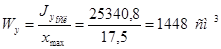
Напряжения в горизонтальной плоскости:
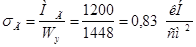
Суммарное напряжение:
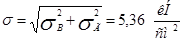
10) Определение необходимого количества болтов в стыке концевой балки.
Допускаемое напряжение в болте принимаем: 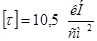 . .
Площадь среза:
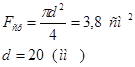
Принимаем М20 по ГОСТ 3805-70 повышенной прочности.
Допустимое усилие на болт по его сопротивлению срезу:
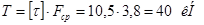 . .
Определим момент воспринимаемый всеми болтами, находящимися в одном поперечном сечении балки:
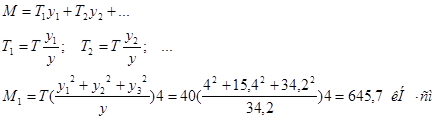
Требуемое число рядов болтов:
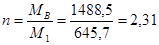
Принимаем по 2 ряда с каждой стороны стыка.
Расстояние между болтами 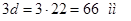 . .
Расстояние от центра болта до накладки:
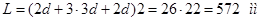 . .
Принимаем 580 мм.
Толщину горизонтальных накладок принимаем 18 мм, на вертикальных листах – 12 мм.
10) Напряжение в сечении стыка главной фермы и концевой балки:
1) 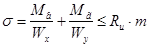
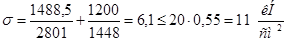
2) 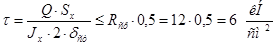
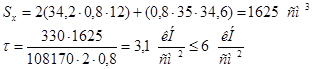
3) 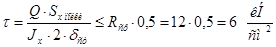

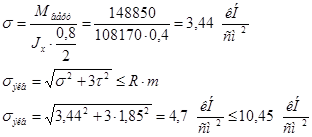
Расчет поясных швов балки:
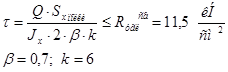
Sx
– статический момент горизонтального листа относительно центра тяжести
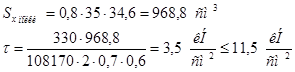
Расчет швов соединения главной балки с концевой:
При расчете сварных швов узла сопряжения главной балки с концевой принимаем силу: 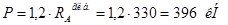 . Это усилие воспринимается двумя швами. Толщину швов принимаем k = 6 мм. . Это усилие воспринимается двумя швами. Толщину швов принимаем k = 6 мм.
Напряжение среза в шве будет равно:
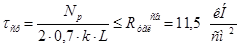
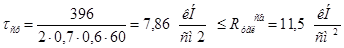
Величина реакций 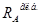 применяется от своего наибольшего значения при крайнем левом положении ненагруженной тележки: применяется от своего наибольшего значения при крайнем левом положении ненагруженной тележки:
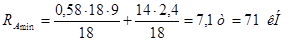
Коэффициент снижения допускаемых напряжений в случае работы шва при переменных нагрузках:
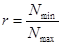 , ,
заменяем на отношение 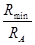 . .
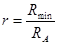 , где , где 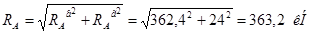 . .
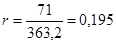 . .

Вычислим допускаемое напряжение к рассматриваемым швам:
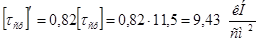 , т.к. , т.к. 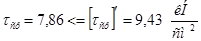 . .
Подобранные швы для концевой балки выбраны верно, т.е. прочность подобранного шва обеспечена.
Длина швов рассчитывается по формуле:
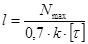
Раскосы:
Сжатый раскос:
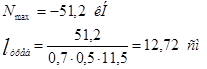
Длина шва на обушке:
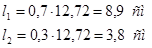
Растянутый раскос:
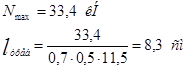
Длина шва на обушке:
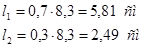
Верхний пояс:
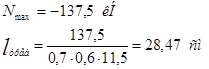
Длина шва на обушке:
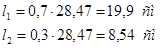
Нижний пояс:
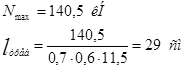
Длина шва на обушке:
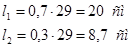
Стойки:
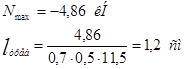
Раскосы:
Сжатый раскос:
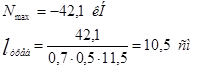
Длина шва на обушке:
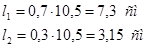
Растянутый раскос:
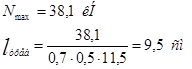
Длина шва на обушке:
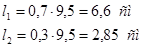
Стойки:
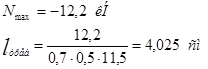
Длина шва на обушке:
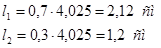
Раскосы и стойки прикрепляют к косынкам, привариваемым к вертикальной полке уголков пояса. Длину швов назначают с учетом технологических и конструктивных особенностей.
Узел 3.
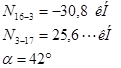
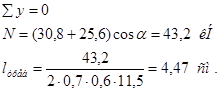
Из конструктивных соображений принимаем l = 60 мм. Шов прерывистый.
Узел 5.
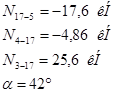
Для нахождения N сложим векторно все силы, действующие на узел:
Требуемая длина швов равна:
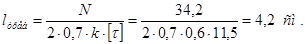
Из конструктивных соображений принимаем l = 60 мм. Шов прерывистый.
Узел 6.
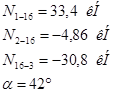
Для нахождения N сложим векторно все силы, действующие на узел:
Требуемая длина швов равна:
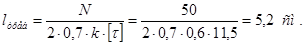
Из конструктивных соображений принимаем l = 60 мм. Шов прерывистый.
Узел 4.
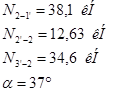
Для нахождения N сложим векторно все силы, действующие на узел:
Требуемая длина швов равна:
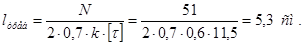
Из конструктивных соображений принимаем l = 60 мм. Шов прерывистый.
Узел 7.
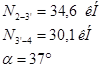
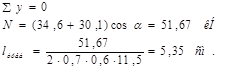
Из конструктивных соображений принимаем l = 60 мм. Шов прерывистый.
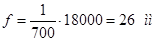 . .
Список литературы
1. Ф.А. Николаев, С.А. Куркин, В.А. Винокуров «Расчет, проектирование и конструирование сварных конструкций», М: Высшая школа, 1971;
2. Справочник по сварке, т.3 (под редакцией В.А. Винокурова), М: Машиностроение, 1979.
3. В.И. Андреев: «Справочник конструктора-машиностроителя». М.: «Машиностроение», 1978 г.
4. Н.В. Дружинин, В.М. Хохов: «Проектирование и расчет сварных конструкций». Москва, 1982 г.
5. ГОСТ2312-72. Обозначение сварных швов на чертежах.
|