МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РТ
АЛЬМЕТЬЕВСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ИНСТИТУТ
Факультет инженерной механики
Кафедра транспорта и хранения нефти
КУРСОВАЯ РАБОТА
по дисциплине "Гидравлика"
на тему: "Расчет гидравлической циркуляционной установки"
Альметьевск, 2009
Содержание
1. Введение
2. Описание циркуляционной установки
3. Схема установки
4. Расчет циркуляционной установки
4.1 Определение геометрической высоты всасывания насоса Н2
4.1.1 Определение расхода жидкости
4.1.2 Определение потерь напора
4.2 Определение показания дифманометра (или дифпьезометра) скоростной трубки
4.3 Построение эпюр скоростей для сечения в месте установки скоростной трубки и т.д.
4.4 Определение установившегося уровня жидкости в промежуточной ёмкости Н1
4.5 Определение разности показания манометров Рм2
и Рм3
4.6 Определение суммарных потерь напора в местных сопротивлениях и их суммарную эквивалентную длину
4.7 Определение необходимого диаметра самотечного трубопровода dс, обеспечивающего установление заданного постоянного уровня в верхнем резервуаре Н3
4.8 Определение минимальной толщины стальных стенок трубы d2,при которой не происходит ее разрыва в момент возникновения прямого гидравлического удара
4.9 Определение полезной мощности насоса
Заключение
Список литературы
Гидравлика занимается изучением законов равновесия и движения жидкостей, а также взаимодействие между жидкостями и твердыми телами, полностью или частично погруженными в жидкость.
Чтобы познать рассматриваемые явления, установить причины их возникновения, а также условия протекания, в гидравлике широко используются упрощенные приемы решения некоторых задач для получения приближенных, но иногда крайне необходимых ответов на вопросы инженерной практики.
Изучением законов равновесия и движения жидкостей занимается и другая наука-гидромеханика, в которой применяются лишь строго математические методы, позволяющие получать общие теоретические решения различных задач, связанных с равновесием и движением жидкостей. Долгое время гидромеханика рассматривала преимущественно невязкую (идеальную) жидкость, т.е. некоторую условную жидкость с абсолютной подвижностью частиц, считающуюся абсолютно несжимаемой, не обладающей вязкостью - не сопротивляющейся касательным напряжениям. В последнее время гидромеханика стала разрешать также проблемы движения вязких (реальных) жидкостей, а потому роль эксперимента в гидромеханике значительно возросла. Таким образом, изучением законов равновесия и движения жидкостей занимаются две науки: гидравлика (техническая механика жидкостей) и гидромеханика.
Реклама

Гидравлика делится на две части: гидростатику и гидродинамику. Гидростатика изучает законы равновесия жидкостей и действие их на соприкасающиеся с ними твердые тела. Гидродинамика изучает законы движения жидкостей и взаимодействия их с соприкасающимися с ними покоящимися или движущимися твердыми телами.
Гидравлика может быть определена как прикладная механика жидкости. Она является основой таких дисциплин, как гидроэнергетика, водоснабжение и канализация, гидравлические машины (турбины, насосы, компрессоры), трубопроводный транспорт. Значительна роль этой науки в химической технологии, легкой промышленности, автоматики.
В современной промышленности нет области, где не проводятся гидравлические расчеты процессов, устройств и механизмов.
Особое значение гидравлика имеет для нефтяной и газовой промышленности, так как все ее процессы, начиная от бурения разведочных скважин и кончая транспортировкой готовой продукции потребителю, связаны с перемещением и хранением жидкости.
Для каждой из этих отраслей характерен свой круг гидродинамических задач и соответствующих методов их решения. Однако все они основываются на общих законах движения и покоя жидкостей и газов, а также на некоторых общих методах описания гидродинамических явлений.
Вопросами гидравлики человек интересовался еще с древности. За несколько тысяч лет до нашей эры в Египте, странах Ближнего и Среднего Востока, в Индии и Китае люди уже умели строить платины и каналы. Примерно в тоже время появились первые гидравлические двигатели - водяные колеса.
Первым научным трудом о законах равновесия жидкостей считают трактат Архимеда "О плавающих телах", написанный за 250 лет до нашей эры. После этого появились работы Леонардо да Винчи "О движении и измерении воды" (1452-1519).
В 1565 г. была опубликована работа голландского ученого Симона Стевина (1548-1620 гг.) "Начала гидростатики". В работах Галилея (1564-1642 гг.) рассмотрены закономерности пребывания тел в воде. Торричелли (1608-1647 гг.), исследуя течение жидкости из отверстия, нашел известную формулу для скорости течения. Паскаль (1623-1662 гг.) вывел закон о передаче давления в жидкостях.
Реклама

Исаак Ньютон (1642-1724 гг.) впервые предложил основные законы течения в жидкости. В 1738 г. в книге "Гидродинамика" Даниил Бернулли опубликовал уравнение, в котором устанавливалась связь между давлением, скоростью движения и положением рассматриваемой массы жидкости при установившемся движении.
В 1755 и 1756 гг. появляются работы Леонарда Эйлера, где он впервые дает полную систему уравнений движения идеальной жидкости.
Основоположниками гидравлики как самостоятельной науки являются члены Петербургской академии наук Д. Бернулли и Л. Эйлер. В 1738 г. была опубликована работа Д. Бернулли "Гидродинамика или записки о силах движения жидкости", в которой установлена связь между давлением и скоростью в элементарной струйке тяжелой "идеальной" жидкости.
М.В. Ломоносов (1711-1765 гг.) изучал условия работы гидротехнических сооружений и занимался исследованием движения воздуха в родниках.
В 1791 г. вышло первое русское печатное руководство по гидравлике А. Колмакова "Карманная книжка для вычисления количества воды, вытекающей через трубы, отверстия или по желобам, а также и силы, какою они ударяют, стремясь с данной скоростью".
В конце ХVХ и начале Х1Х веков во Франции появляются работы Шези по движению воды в каналах и трубах и Дарси - по напорному движению воды в трубах.
В 1883 г. Н.П. Петров разработал гидродинамическую теорию смазки, уточнил гипотезу о внутреннем трении в движущейся жидкости.
В 1889 вышла работа Н. Жуковского "О гидравлическом ударе в водопроводных трубах", в которой дана теория гидравлического удара. Жуковским впервые были введены основные дифференциальные уравнения движения грунтовых вод.
Л.С. Лейбензоном (1879-1951 гг.) и его учениками создана российская армия фильтрации.
В развитии нефтяной гидравлики роль русских и советских ученых проявилась особенно ярко. В. Шухов (1853-1939 гг.) разработал основы гидравлического расчета трубопроводов, которые затем развили Л. Лейбензон (1879-1951 гг.) и его ученики И. Чарный (1909-1967 гг.), В. Черникин (1912-1965 гг.) и др. На базе работ Павловского Н.Н. (1884-1937 гг.) Лейбензон заложил основы новой науки "Подземная гидравлика", которую успешно развивали его ученики И.А. Чарный, В.Н. Щелкачев, Б.В. Лапук и созданные ими школы.
Жидкость по самотечному трубопроводу поступает из верхнего резервуара А в нижний резервуар В, откуда насосом перекачивается в промежуточную емкость С и из нее выливается в резервуар А.
На всасывающей линии насосной установки имеется всасывающая коробка с обратным клапаном 1, поворотное колено 2, задвижка 3, вакуумметр Рв. На нагнетательной линии установлены манометры Рм1, Рм2, Рм3, скоростная трубка 5 и расходомер Вентури 6. Промежуточная емкость С в донной части имеет насадок 7.
ИСХОДНЫЕ ДАННЫЕ
| Вариант 13 |
| Величина |
Значение |
| r1
, кг/м3
|
760 |
| n1
, см2
/с |
0,007 |
| l1
, м |
10 |
| l2
, м |
8 |
| l3
, м |
3 |
| l4
, м |
1 |
| l5
, м |
3 |
| l6
, м |
100 |
| l7
, м |
50 |
| l8
, м |
5 |
| l9
, м |
190 |
| l10
, м |
3 |
| lc
, м |
20 |
| lэкв.,
м |
2 |
| d1
, мм |
81 |
| d2
, мм |
68 |
| , мм |
0,1 |
| с
, мм |
0,2 |
| Н3
, м |
0,5 |
| кор
|
10 |
| кол
|
1 |
| зад
|
2 |
| dвен
, мм |
30 |
| μвен
|
0,94 |
hвен,
мм рт. ст
|
166 |
| 2
, кг/м3
|
0 |
| РВ,
кПа |
40 |
| Рм1
, кПа |
145 |
| dнас
, мм |
30 |
| μнас
|
0,82 |
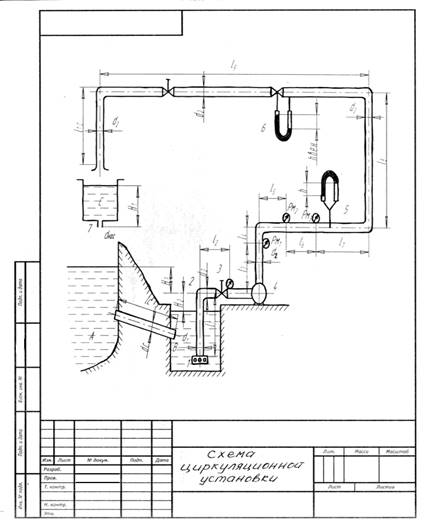
Для определения геометрической высоты воспользуемся известным уравнением Бернулли. Для его применения необходимо выбрать плоскость сравнения. Плоскостью сравнения может служить любая горизонтальная плоскость. Также необходимо выбрать два сечения. Сечения проводятся перпендикулярно вектору скорости. Нумерация сечений производится по направлению движения жидкости. Уравнение Бернулли для установившегося движения реальной несжимаемой жидкости записывается:
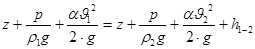 (1) (1)
где: z-расстояние от выбранных сечений соответственно до некоторой произвольно выбранной плоскости сравнения (м). Если сечение лежит ниже плоскости сравнения, то z отрицательна.
р - абсолютное или манометрическое давление в сечениях (Па);
ρ - плотность несжимаемой жидкости (кг/м³);
α - коэффициент кинетической энергии (коэффициент Кориолиса). Обычно принимается равным единице.
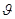 - средняя скорость в сечениях (м/с); - средняя скорость в сечениях (м/с);
g - ускорение свободного падения (м/с²);
h1-2 - потери напора между сечениями. Они представляют собой сумму потерь напора по длине и сумму потерь напора на местных сопротивлениях:
h1-2 = hм + hд
На схеме циркуляционной установки удобно выбрать два сечения, где:
А-А это поверхность жидкости в нижнем резервуаре В;
В-В в месте установки вакуумметра Рв во всасывающей линии насосной установки.
Тогда уравнение Бернулли для этих сечений запишется в виде:
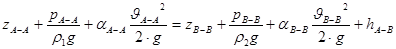 (2) (2)
где zА-А и zВ-В - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости;
РА-А, РВ-В - давления в сечениях А-А и В-В соответственно;
ρ - плотность циркуляционной жидкости;
g - ускорение свободного падения;
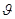 А-А и А-А и 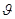 В-В - скорость течения жидкости в сечении А-А и В-В соответственно; В-В - скорость течения жидкости в сечении А-А и В-В соответственно;
hА-В - потери напора на участках между выбранными сечениями.
Если выбрать поверхность жидкости в нижнем резервуаре за начало отсчета, т.е. сечение А-А, тогда zА-А=О, а zВ-В=Н2.
Поскольку в нижнем резервуаре (В) уровень установившийся, значение скорости 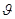 будет равным нулю. А так как резервуар открыт, то давление в сечении А-А можно принять равным атмосферному РА-А=Ратм. Давление же в сечении В-В представляет собой разность атмосферного и вакуумного давления РВ-В =Ратм - Рвак. При решении практических задач коэффициент Кориолиса (α), как уже говорилось, можно принять равным единице и в расчетах не учитывать. Тогда в уравнении Бернулли остается лишь одна неизвестная величина - скорость будет равным нулю. А так как резервуар открыт, то давление в сечении А-А можно принять равным атмосферному РА-А=Ратм. Давление же в сечении В-В представляет собой разность атмосферного и вакуумного давления РВ-В =Ратм - Рвак. При решении практических задач коэффициент Кориолиса (α), как уже говорилось, можно принять равным единице и в расчетах не учитывать. Тогда в уравнении Бернулли остается лишь одна неизвестная величина - скорость 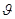 в. Скорость определяется по формуле в. Скорость определяется по формуле
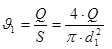 (3) (3)
где Q- расход жидкости (м³/с);
S- площадь поперечного сечения (м²);
В результате, формула (2) примет вид:
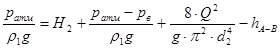 (4) (4)
В полученной формуле известны все величины, кроме Н2 и hА-В. Поэтому для определения геометрической высоты всасывания насоса (Н2) предварительно необходимо определить hА-В.
Расходом потока называется количество жидкости, протекающее через некоторое поперечное сечение потока в единицу времени. Это сечение должно быть сделано так, чтобы обязательно пересекало каждую элементарную струйку и только один раз. Обычно за поверхность сечение принимают живое сечение потока. Для аналитического вычисления расхода необходимо знать закон распределения скоростей по сечению потока.
Наиболее простыми и вместе с тем точными способами измерения расхода жидкости являются объемный и весовой способы.
При весовом способе взвешиванием на весах находят вес всей жидкости, поступившей в мерник за определенное время, определяют весовой расход по формуле, и, зная удельный вес жидкости, вычисляют объемный расход.
В практике, как правило, для измерения расхода жидкости пользуются специальными приборами, которые предварительно тарируются объемным или весовым способом.
Одним из таких основных приборов является трубчатый водомер, или водомер Вентури. Большим достоинством этого водомера является простота конструкции и отсутствие в нем каких-либо движущихся частей. Трубчатые водомеры могут быть горизонтальными и вертикальными.
Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури.
Запишем уравнение неразрывности для сечений 1-1 и 2-2:
Q1 = Q2, следовательно 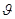 1 · S1 = 1 · S1 = 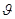 2 ·S2 (5) 2 ·S2 (5)
Из полученного равенства выразим скорость V2:
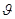 2 = 2 = 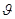 1· S1/S2 (6) 1· S1/S2 (6)
Запишем уравнение Бернулли для двух сечений 1-1 и 2-2:
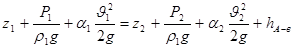 (7) (7)
где z1 и z2 - расстояния от сечений А-А - и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости; р-давления в сечениях А-А и В-В соответственно; ρ-плотность циркулирующей жидкости; g-ускорение свободного падения; 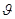 - скорость течения жидкости в сечениях А-А и В-В соответственно; α-силы Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно; hА-В - потери напора на участках между выбранными сечениями. Выберем ось трубопровода за начало отсчета, тогда z1=z2=0, т.к трубопровод горизонтален. Предположим, что по трубопроводу течет идеальная жидкость. Тогда потери напора hА-В = 0. - скорость течения жидкости в сечениях А-А и В-В соответственно; α-силы Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно; hА-В - потери напора на участках между выбранными сечениями. Выберем ось трубопровода за начало отсчета, тогда z1=z2=0, т.к трубопровод горизонтален. Предположим, что по трубопроводу течет идеальная жидкость. Тогда потери напора hА-В = 0.
α1 = α2 = 1.
Теоретический расход будет меньше, т.к существуют потери напора. Учтем это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.
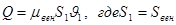 (8) (8)
С учетом всех преобразований: 
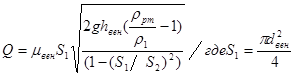 (9) (9)
В итоге имеем:
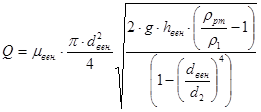 (10) (10)
Q= 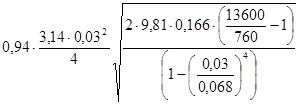 =0,005м³/с =0,005м³/с
| Вариант |
Значение Q, м3
/с |
| 13 |
0,005 |
Определение величины потерь напора при движении реальных жидкостей является одной из основных задач практической гидравлики. При движении реальной жидкости энергия движения (напор) жидкости будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости. В гидравлике различают два основных вида сопротивлений:
1
. Потери напора по длине
, т.е. сопротивления, проявляющиеся по всей длине потока
, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток. Это линейные потери. Они определяются по формуле Дарси-Вейсбаха:
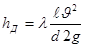 (11) (11)
где 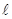 - длина трубы (или участка трубы) на котором определяются потери напора"; - длина трубы (или участка трубы) на котором определяются потери напора"; 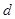 - диаметр трубы; - диаметр трубы; 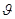 - средняя скорость в трубе; λ
= λ
(Re, ∆/
d
) - коэффициент гидравлического сопротивления трения. Коэффициент гидравлического сопротивления трения (λ) зависит от двух безразмерных параметров Rе
- числа Рейнольдса и ∆/
d
- относительной шероховатости трубы. Число Рейнольдса определяется по формуле: - средняя скорость в трубе; λ
= λ
(Re, ∆/
d
) - коэффициент гидравлического сопротивления трения. Коэффициент гидравлического сопротивления трения (λ) зависит от двух безразмерных параметров Rе
- числа Рейнольдса и ∆/
d
- относительной шероховатости трубы. Число Рейнольдса определяется по формуле:
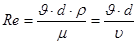 (12) (12)
где μ
- динамическая вязкость жидкости (Па·с); 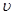 - кинематическая вязкость жидкости (м²/с). Для определения коэффициента гидравлического сопротивления трения существуют много различных формул. Удобно пользоваться следующими формулами. Для ламинарного режима движения: - кинематическая вязкость жидкости (м²/с). Для определения коэффициента гидравлического сопротивления трения существуют много различных формул. Удобно пользоваться следующими формулами. Для ламинарного режима движения:
λ =64/
Rе
, Rе
< 2000÷2320.
Для турбулентного режима движения (формула Альтшуля):
λ=0,11 (68/
Rе+ ∆/
d) 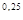 , Rе
>2000÷2320
, Rе
>2000÷2320
2. Местные потери напора
, так называемые местные сопротивления
, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям в величине или направлении скорости течения жидкости. Потери напора на местных сопротивлениях определяются по формуле
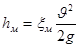 (м) (13) (м) (13)
где 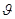 - средняя скорость движения жидкости; - средняя скорость движения жидкости;
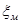 - коэффициент местного сопротивления. - коэффициент местного сопротивления.
Потеря напора на местном сопротивлении может определяться как по скорости до местного сопротивления, так и по скорости после местного сопротивления. Так как скорости по величине могут быть разными, то в этих случаях для одного и того же местного сопротивления будут разные значения 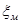 . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления. . Принято определять потери напора по скорости после местного сопротивления. Исключение составляет расширение трубопровода (выход потока из трубы в бак), где потери определяются по скорости до местного сопротивления.
Для определения потерь напора по данной курсовой работе будем учитывать как потери напора по длине трубопровода, так и местные сопротивления.
hА-В =
hд +
hм
(м) (14)
где hд
- потери напора по длине трубопровода (м);
hм
- потери напора от местных сопротивлений.
а) Вначале определим hм
- потери напора от местных сопротивлений. Для этого сложим все местные сопротивления на рассматриваемом участке:
hм =
hкор+
hкол +
hзад
где hкор
- потери напора на коробке всасывающей линии;
hкол
- потери напора на колене всасывающей линии;
hзад
- потери напора на задвижке всасывающей линии.
Используя формулу (13) получим:
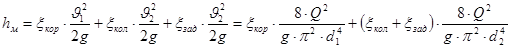 (15) (15)
hм
= 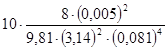 + +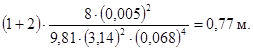
б) Теперь рассчитаем hд
- потери напора по длине трубопровода. Они определяются как сумма потерь напора на участке трубопровода 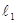 и потерь напора на участке трубопровода и потерь напора на участке трубопровода 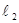 : :
hд =
hд1 +
hд2
(м) (16)
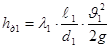 (м) (м) 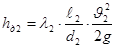 (м) (м)
где λ1
и λ2
- коэффициенты гидравлического сопротивления 1 и 2 участков.
Для определения λ1
и λ2
необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Рейнольдса для этих участков по формуле (12):
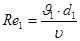 = =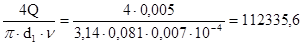
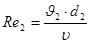 = =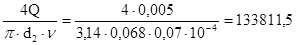
где ν - кинематическая вязкость циркуляционной жидкости.
По полученным результатам вычисления чисел Rе
определяем режим течения - турбулентный или ламинарный.
Затем определим тип трубопровода (шероховатый или гладкий) на участках трубопровода 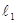 и и 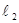 . Для этого находим значения величин обратной относительной шероховатости для обоих рассматриваемых участков по данным значениям d
и ∆
: . Для этого находим значения величин обратной относительной шероховатости для обоих рассматриваемых участков по данным значениям d
и ∆
:
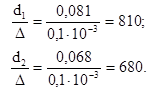
Оба участка принадлежат зоне шероховатых труб, если их числа Rе
принадлежат промежуткам:
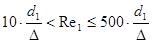
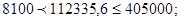
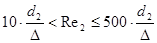
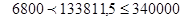
Оба участка принадлежат зоне шероховатых труб, т. к выполняются оба условия.
Для определения λ
1
и λ
2
воспользуемся формулой Альтшуля:
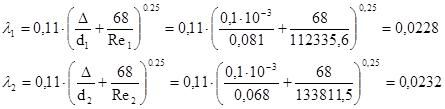
Теперь, когда известны все величины, можно найти суммарные потери напора на участках 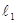 и и 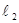 (по формуле (16)): (по формуле (16)):
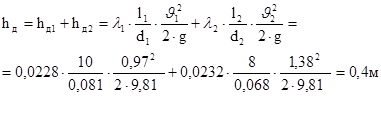
Подставим полученные значения в формулу (14) определим необходимую величину hА-В:
hА-В =
hд +
hм =
0,4+0.77 =1,17м. Результаты занесем в таблицу.
| Вариант |
Значение hА-В
, м |
| 13 |
1,17 |
Заканчивая расчетную часть по первому пункту задания, т.е. нахождение геометрической высоты всасывания насоса H
2
, воспользуемся формулой (4):
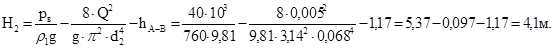
| Вариант |
Значение H
2
, м |
| 13 |
4,1 |
Для выполнения задания достаточно уравнения Бернулли для осевой трубки:
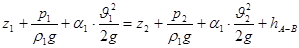 (17) (17)
где 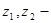 расстояние от сечений А-А
и В-В
соответственно до некоторой произвольно выбранной горизонтальной плоскости; расстояние от сечений А-А
и В-В
соответственно до некоторой произвольно выбранной горизонтальной плоскости;
р
- давления в сечениях А-А
и В-В
соответственно;
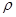 - плотность циркулирующей жидкости; - плотность циркулирующей жидкости;
g-
ускорение свободного падения;
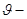 скорость течения жидкости в сечении А-А
и В-В
; скорость течения жидкости в сечении А-А
и В-В
;
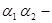 коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А
и В-В
соответственно; коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А
и В-В
соответственно;
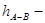 потери напора на участках между выбранными сечениями. потери напора на участках между выбранными сечениями.
Пренебрегаем очень небольшими на малой длине между сечениями А-А
и В-В
потерями напора (hА-В
= 0).
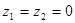 , если выбираем ось трубопровода за начало. , если выбираем ось трубопровода за начало.
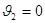 , так как жидкость внутри дифманометра почти неподвижна. , так как жидкость внутри дифманометра почти неподвижна.
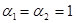 (для практических расчетов). (для практических расчетов).
В итоге имеем:
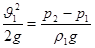 (18) (18)
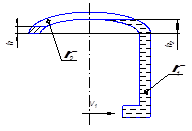
Из рисунка видно разность давлений:
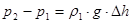 (19) (19)
В результате уравнение (1) примет вид:
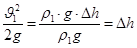 (20) (20)
Имеем расчетную формулу для определения показания дифманометра:
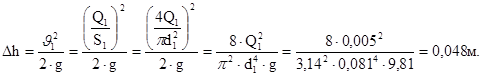
Полученные результаты занесем в таблицу:
| Вариант |
Значение ∆
h
, м |
| 13 |
0,048 |
Анализируя схему циркуляционной установки можно сделать вывод, что расход жидкости постоянный в любом сечении трубопровода. Следовательно, режим течения жидкости зависит от диаметра трубопровода на рассматриваемом участке. Это, в свою очередь, говорит об идентичности режима течения на участках трубопровода с одинаковыми диаметрами. В месте установки скоростной трубки режим течения идентичен режиму течения на участке трубопровода всасывающей линии. Следовательно, мы имеем турбулентный режим течения, который происходит в зоне сопротивления шероховатых труб.
Формула для распределения скоростей в круглой трубе при турбулентном режиме в зоне шероховатых труб имеет следующий вид:
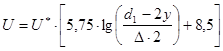 (21) (21)
где U - местная скорость в данной точке сечения;
U٭ - динамическая скорость; 
d1 -диаметр трубопровода;
y - расстояние от оси трубопровода;
∆ - эквивалентная шероховатость стенок труб;
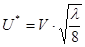 (22) (22)
где 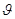 - средняя скорость течения жидкости; - средняя скорость течения жидкости;
λ - коэффициент гидравлического сопротивления;
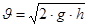 (23) (23)
где h - показание дифманометра (или дифпьезометра) скоростной трубки. Подставив (22) и (23) в (21) получим:
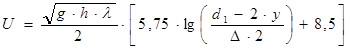 (24) (24)
где 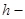 показание дифманометра скоростной трубки. показание дифманометра скоростной трубки.
Для построения эпюры скоростей зададим значения 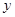 в интервале от 0 до в интервале от 0 до 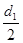 =40.1мм с шагом 2 мм (чем меньше шаг, тем точнее эпюра). Вычислим для каждого значения =40.1мм с шагом 2 мм (чем меньше шаг, тем точнее эпюра). Вычислим для каждого значения 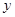 местную скорость. Если количества полученных точек не достаточно для определения траектории кривой, то необходимо взять больше значений. По результатам составим таблицу и построим график. местную скорость. Если количества полученных точек не достаточно для определения траектории кривой, то необходимо взять больше значений. По результатам составим таблицу и построим график.
| y |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
| u |
1,729 |
1,720 |
1,710 |
1,700 |
1,689 |
1,677 |
1,664 |
1,651 |
1,637 |
1,621 |
1,604 |
| 22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
| 1,585 |
1,564 |
1,540 |
1,513 |
1,481 |
1,442 |
1,393 |
1,325 |
1,217 |
0,921 |
Эпюра скоростей
Для определения установившегося уровня жидкости в промежуточной ёмкости Н1
составим уравнение Бернулли для сечений 1-1 и 2-2:
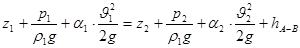 (25) (25)
где 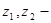 расстояние от сечений А-А
и В-В
соответственно до некоторой произвольно выбранной горизонтальной плоскости (м
); расстояние от сечений А-А
и В-В
соответственно до некоторой произвольно выбранной горизонтальной плоскости (м
);
р
- давления в сечениях А-А
и В-В
соответственно (Па
);
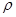 - плотность циркулирующей жидкости (кг/м3
); 1 1 - плотность циркулирующей жидкости (кг/м3
); 1 1
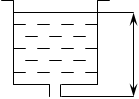 g-
ускорение свободного падения (м/с2
); g-
ускорение свободного падения (м/с2
);
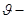 скорость течения жидкости в Н1 скорость течения жидкости в Н1
сечении А-А
и В-В
соответственно (м/с
);
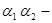 коэффициенты Кориолиса, которые учитывают 2 2 коэффициенты Кориолиса, которые учитывают 2 2
неравномерность распределения скоростей в сечениях А-А
и В-В
соответственно. 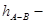 потери напора на участках между выбранными сечениями. Плоскость сравнения совместим с сечением 2-2, тогда потери напора на участках между выбранными сечениями. Плоскость сравнения совместим с сечением 2-2, тогда 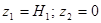 . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора . Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора 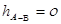 . . 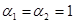 (для практических расчетов).Т. к. диаметр промежуточной ёмкости во многом больше диаметра насадки (для практических расчетов).Т. к. диаметр промежуточной ёмкости во многом больше диаметра насадки 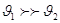 , значит , значит 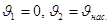
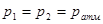 , т.к емкости открытые. Запишем уравнение Бернулли (1) с учётом всех утверждений: , т.к емкости открытые. Запишем уравнение Бернулли (1) с учётом всех утверждений:
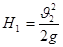 (26) (26)
Зная расход можно определить 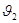 : :
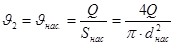 (27) (27)
Подставляя (3) в (2) получим:
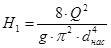 (28) (28)
В действительности при прохождении жидкости в ёмкости через насадок возникают потери напора, учтём их с помощью коэффициента расхода 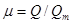 , подставив его в формулу (28): , подставив его в формулу (28):
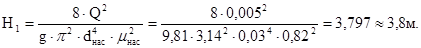
| Вариант |
Значение Н1, м |
| 13 |
3,8 |
Для сечений Рм2
и Рм3
уравнение Бернулли имеет вид:
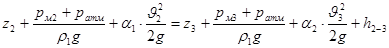 (29) (29)
где 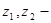 расстояние от сечений Рм2
и Рм3
соответственно до некоторой произвольно выбранной горизонтальной плоскости (м
); расстояние от сечений Рм2
и Рм3
соответственно до некоторой произвольно выбранной горизонтальной плоскости (м
);
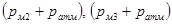 - давления в сечениях Рм2
и Рм3
соответственно (Па
); - давления в сечениях Рм2
и Рм3
соответственно (Па
);
 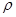 - плотность циркулирующей жидкости (кг/м3
); - плотность циркулирующей жидкости (кг/м3
);
g-
ускорение свободного падения (м/с2
);
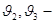 скорость течения жидкости в сечении Рм2
и Рм3
соответственно (м/с
); скорость течения жидкости в сечении Рм2
и Рм3
соответственно (м/с
);
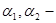 коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях Рм2
и Рм3
соответственно. коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях Рм2
и Рм3
соответственно.
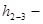 потери напора на участках между выбранными сечениями. потери напора на участках между выбранными сечениями.
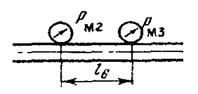
Выберем ось трубопровода за начало отсчета, тогда 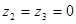 , т.к трубопровод горизонтален. , т.к трубопровод горизонтален. 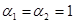 , (для практических расчетов). , (для практических расчетов).
Потери напора между выбранными сечениями 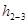 определяются только потерями напора по длине трубопровода, т.к местных сопротивлений на данном участке нет. определяются только потерями напора по длине трубопровода, т.к местных сопротивлений на данном участке нет. 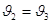 , т.к расход и площадь поперечного сечения одинаковы для сечений Рм2
и Рм3
. В итоге формула (29) примет вид: , т.к расход и площадь поперечного сечения одинаковы для сечений Рм2
и Рм3
. В итоге формула (29) примет вид:
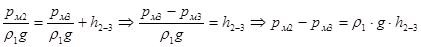 (30) (30)
Потери напора по длине трубопровода определяется по формуле Дарси-Вейсбаха:
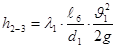 (31) (31)
Подставим (31) в (30):
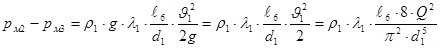 (32) (32)
Подставим в (32) значения параметров и получим конечный результат.
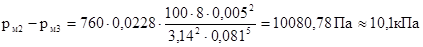
Результат заносим в таблицу.
| Вариант |
Значения рм2 -рм3, кПа |
| 13 |
10,1 |
Потери напора в местных сопротивлениях складываются из потерь на фланце, в угольниках, расходомера Вентури, на задвижках и выходе из трубы. Из справочника найдём значения коэффициента местных сопротивлений: 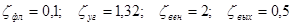 . .
Запишем формулу Вейсбаха для нагнетательной линии:
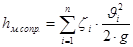 , ,
где 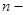 количество местных сопротивлений на рассматриваемом участке. В нашем случае имеем (с учетом количество местных сопротивлений на рассматриваемом участке. В нашем случае имеем (с учетом 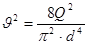 ) )
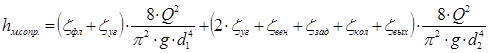 (33) (33)
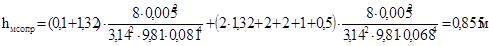
Потери напора в местных сопротивлениях можно выразить через эквивалентную длину, т.е. такую длину трубопровода, для которой
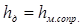 и и 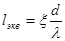
Суммарная эквивалентная длина определяется по формуле:
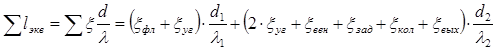 (34) (34)
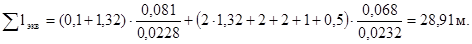
Подставим значения параметров и найдем необходимые величины.
| Вариант |
Значение hм сопр, м |
Σ lэкв, м |
| 13 |
0,855 |
28,91 |
Для определения dс используется графоаналитический способ решения с использованием ПК (программа MicrosoftExcel). Задаемся интервалом dciот 1 мм до 200 мм с шагом 1 мм. И для каждого варианта рассчитываются потери напора, возникающие при прохождении жидкости по самотечному трубопроводу.
Потери напора определяются по формуле:
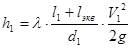 , ,
где lэкв - суммарная эквивалентная длина местных сопротивлений самотечного трубопровода.
Вычислим поэтапно потери напора для dc
от 0 до 200 мм:
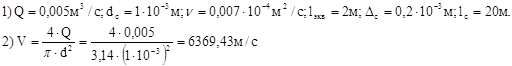
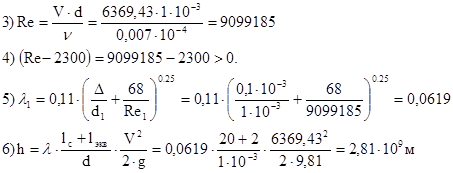
По результатам вычисления dс составим таблицу и построим график зависимости h=f (dc).
| dc
, мм |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
| h, мм |
879,69 |
27,50 |
3,62 |
0,86 |
0,28 |
0,11 |
0,05 |
0,03 |
0,01 |
0,01 |
График зависимости h=f (dc
)
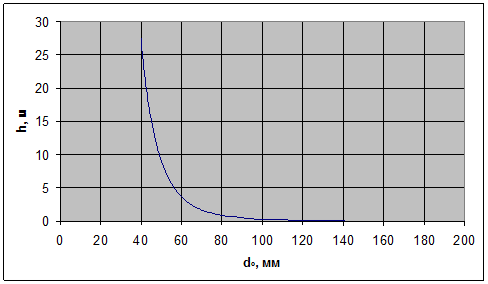
Для определения необходимого значения диаметра трубопровода по полученному графику определяем dc для значения h=H2+H3=const, т.к уровень установившийся - это и есть потери напора при прохождении жидкости по самотечному трубопроводу: h=4,1+0,5= 4,6 м.
Имеем, что при h=4,6м значение диаметра примерно равно dc
=57 мм.
Под гидравлическим ударом понимают резкое увеличение давления в трубопроводах при внезапной остановке движущейся в них жидкости. Гидравлический удар может иметь место, например, при быстром закрытии различных запорных приспособлений, устанавливаемых на трубопроводах (задвижка, кран), внезапной остановке насосов, перекачивающих жидкость и т.д. Особенно опасен гидравлический удар при длинных трубопроводах, в которых движутся значительные массы жидкости с большими скоростями. В этих случаях, если не принять соответствующих предупредительных мер, гидравлический удар может привести к повреждению мест соединений отдельных труб (стыки, фланцы, раструбы), разрыву стенок трубопровода, поломке насосов и т.д.
Повышение давления при гидравлическом ударе определяется формулой Н.Е. Жуковского:
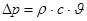
где ρ - плотность жидкости;
с - скорость распространения ударной волны;
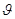 - средняя скорость движения жидкости. - средняя скорость движения жидкости.
Скорость ударной волны определяется по формуле:
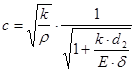 , ,
где 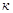 - модуль упругости стенок трубопровода (Па), - модуль упругости стенок трубопровода (Па),
δ-толщина стенок трубопровода (м).
Мы имеем дело с трубами бесшовными и марки стали - Ст20, для которой модуль упругости Е =2·10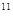 Па, а модуль упругости жидкости k=1,35·10 Па, а модуль упругости жидкости k=1,35·10 Па. Па.
При выполнении расчетов в курсовой работе для стальных труб принимают с = 1200 м/с.
Для борьбы с гидравлическим ударом применяются различного рода устройства, увеличивающие время закрытия задвижек и кранов; на трубопроводах устанавливаются также автоматически действующие предохранительные клапаны и воздушные колпаки, которые располагаются перед задвижками и играют роль своеобразных воздушных буферов, воспринимающих повышенное давление.
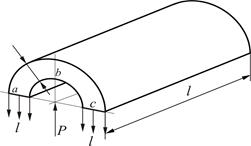
Опасным сечением для трубы будет любое ее диаметральное сечение.
На цилиндрическую поверхность трубы действует сила давления жидкости. Если пренебречь весом жидкости, можно эту силу определить как силу давления проекции цилиндрической поверхности на диаметральную плоскость "ас" по известной формуле:
Р = р·d·l (35)
где р - давление;
d·l- площадь рассматриваемой плоскости.
Но эта сила давления воспринимается двумя сечениями стенки трубы, поэтому
р·d·l = 2·σдоп·δмин·l
где σдоп -допустимое напряжение для материала трубы. Из этой формулы определяем минимальную толщину стенки трубы:
δмин = 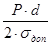 (36) (36)
где Р=Рман + ∆Р, а d=d2. Из полученого видно, что отсутствует величина ∆Р. Она определяется по формуле Жуковского:
∆Р=с·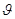 ·ρ (где ·ρ (где 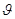 = =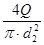 ) (37) ) (37)
Для стальных труб принимаем с=1200 м/с, из справочника находим для стали марки Ст20 σдоп:
σдоп=0,16·10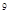 (Па) (Па)
Находим сначала 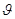 , затем ∆Р (по формуле (3)). После чего Р и , затем ∆Р (по формуле (3)). После чего Р и 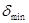 (по формуле (36)). (по формуле (36)).
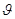 = =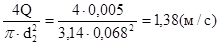
∆Р=с·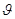 ·ρ=1200·1,38·760=1258560 (Па) ·ρ=1200·1,38·760=1258560 (Па)
Р=Рман + ∆Р=145000+1258560=1403560 (Па)
δмин = 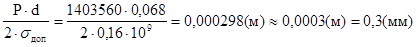
Результат расчетов заносим в таблицу:
| Вариант |
Значение δ, мм |
| 13 |
0,3 |
Устройство и работа гидравлических машин основана на использовании принципов гидравлики. Гидравлические машины это такие, в которых основным рабочим телом является жидкость.
По своему назначению в зависимости от характера происходящих в них энергетических процессов гидравлические машины можно разделить на две большие группы: гидравлические двигатели и насосы.
Гидравлические двигатели служат для преобразования гидравлической энергии потока жидкости в механическую энергию, получаемую на валу двигателя и используемую в дальнейшем для различных целей, в основном для привода различных машин.
Насосами называются гидравлические машины для перемещения жидкостей путем повышения энергии рабочей среды. Механическая энергия, подводимая к насосам от двигателей, приводящих эти машины в действие, преобразуется в них в гидравлическую энергию жидкости.
По принципу действия различают гидравлические машинылопастного типа (центробежные насосы, турбины) и машины, действующие по принципу вытеснения жидкости твердым телом (поршневые насосы).
Полезная мощность-работа, потребляемая насосом в единицу времени.
Полезная работа, потребляемая насосом в единицу времени (мощность) будет равна:
N= γ·Q·H (кВт) (1 кВт=1, 36 л. с)
где γ - удельный вес жидкости, γ = ρ·g;
Q- производительность насоса, т.е. расход жидкости, подаваемой насосом в трубопровод;
Н - полный (манометрический) напор.
Действительная мощность, потребляемая насосом и подводимая к нему от двигателя, будет больше полезной мощности ввиду неизбежных потерь энергии в насосе. В формуле для определения полезной мощности насоса Н=Ннас, тогда Nнас=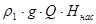 , где , где 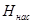 определяется по формуле: определяется по формуле:
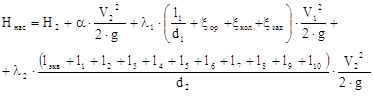
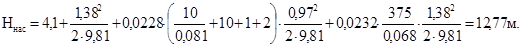
Nнас=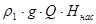 = 7609,810,00512,77=476,04 Вт=0,476 кВт = 7609,810,00512,77=476,04 Вт=0,476 кВт
где Н-высота подъема, т.е. Н=Н2·αi. Для практических расчетов принимаем
αi=1. Индекс "в" на всасывающей линии, "н" - на нагнетательной линии.
| Вариант |
Значение Nнас, кВт |
| 13 |
0,476 |
В ряде участков гидравлической установки режим течения жидкости - турбулентный, в результате мы имеем большие потери напора. Как следствие это влечет за собой экономические затраты. Рекомендую добавить в циркуляционную жидкость небольшие количества таких веществ, как, например, высокомолекулярные полимеры (полиокс, полиакриламид - ПАА), гуаровая смола, поливиниловый спирт - ПВС. Будучи растворенными в жидкости, они обладают способностью значительно снижать гидравлические сопротивления при турбулентном режиме.
Механизм происходящих при этом явлений полностью пока не выяснен, но есть основания полагать. Что частицы этих веществ (их длинные и гибкие молекулы), внесенные в поток жидкости, тесно взаимодействуя с ее пульсирующими частицами, существенно изменят характер турбулентного течения.
Указанные изменения проявляются, прежде всего, в близкой к стенкам, ограничивающим поток, весьма малой по толщине области пограничного слоя. Здесь снижаются пристеночные поперечные пульсации скоростей и давлений, и это оказывает решающее влияние на общий уровень турбулентности и поведение потока в целом. Причем достаточно нескольких миллионных долей полимера по отношению к растворителю, чтобы достигалось значительное уменьшение гидравлического сопротивления.
1. Нефтегазовая гидромеханика / Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. - Москва-Ижевск: Институт компьютерных исследований, 2003. - 480 с.
2. Техническая гидромеханика/ Емцев Б.Т. - 2-е изд., перераб. И доп. - М.: Машиностроение, 1987. - 440 с.: ил.
3. Основы теоретической механики: Учебник.2-е изд., перераб. и дополн. - М.: Изд-во МГУ, 2000. - 719 с.
4. Сопротивление материалов: Учебник для вузов/ Под общ. Ред. Акад. АН УССР Г.С. Писаренко. - 4-е изд. перераб. и доп. - Киев: Высшая школа, 1979. - 696 с.30106.2105000000.
5. Бурдин Г.Д., Базакуза В.А., Единицы физических величин: Справочник-Харьков: Высшая школа, 1984.
6. Стоцкий Л.Р. Физические величины и их единицы. - М.: Просвещение, 1984.
7. Теория механизмов и машин: Терминология. Буквенное обозначение величин. - М.: Наука, 1984.
8. Курсовое проектирование и его унификация в Московском институте нефти и газа имени И.М. Губкина.4.1 и 4.2 - М. - : МИНГ, 1987.
9. Методическое пособие для выполнения курсовой работы по гидравлике / Зозуля Н.Е., Альметьевск, 2001.
|