Оглавление
Заданиедля контрольной работы
1 Определение мощности на приводном валу
2 Выбор электродвигателя
3 Кинематический расчет привода
4 Расчет параметров зубчатых колес
4.1 Определение механических свойств материалов
4.2 Расчет параметров передачи
5 Конструирование валов редуктора
5.1 Расчет диаметров валов
5.2 Расчет шпоночных соединений
5.3 Расчет зубчатой муфты
5.4 Разработка чертежа вала редуктора
6 Проверочный расчет быстроходного вала
6.1 Определение реакций опор
6.2 Расчет статической прочности вала
6.3 Уточненный расчет прочности вала
7 Подбор подшипников качения
Список использованной литературы
Задание для контрольной работы
Провести проектировочный и проверочный расчет деталей механизма привода на основании его сборочного чертежа. Произвести выбор электродвигателя, расчет соединений, муфт и основных деталей редуктор, а также ориентировочного значения коэффициента полезного действия. Выполнить рабочий чертеж вала.
Кинематическая схема.
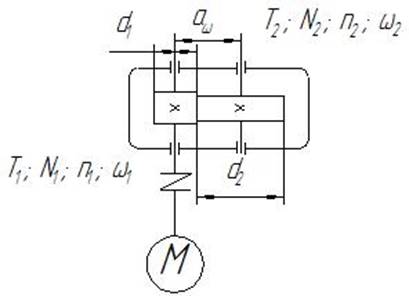
Исходные данные:
Долговечность привода tΣ
, ч: 11600
Мощность тихоходного вала N2
, кВт: 3,3
Частота вращения тихоходного вала n2
, мин-1
: 435
Материал вала: сталь 45 с термообработкой улучшением
1 Определение мощности на приводном валу
КПД редуктора:
η = ηзп
· ηм
· ηп
2
ηзп
= 0,95…0,98; принимаем ηзп
= 0,98 – КПД закрытой цилиндрической передачи;
ηм
= 0,995 – КПД муфты;
ηп
= 0,99 – КПД пары подшипников качения.
η = 0,98 · 0,995 · 0,992
= 0,955
Требуемая мощность двигателя:
N1
= N2
/ η = 3,3 / 0,955 = 3,46 кВт.
2 Выбор электродвигателя
Выбираем электродвигатель с запасом мощности: 4А112МВ6Y3 со следующими характеристиками:
Nдв
= 4 кВт; nдв
c
= 1000 мин-1
; dдв
= 38 мм; ψmax
= 2,2.
Частота вращения двигателя при номинальной нагрузке:
n1
= nдв
= nдв
c
· (1-s) = 1000 · (1-0,04) = 960 мин-1
, где:
s – коэффициент скольжения, принимаем s = 0,04.
3 Кинематический расчет привода
Передаточное число редуктора:
u = n1
/ n2
= 960 / 435 = 2,2
Принимаем ближайшее стандартное значение (второй ряд): u = 2,24.
Уточним частоту вращения тихоходного вала редуктора:
n2
= n1
/ u = 960 / 2,24 = 429 мин-1
Реклама

Угловые скорости вращения валов:
ω1
= πn1
/ 30 = 3,14 · 960 / 30 = 100,5 с-1
;
ω2
= πn2
/ 30 = 3,14 · 429 / 30 = 44,9 с-1
.
Вращающие моменты на валах:
Т1
= N1
/ ω 1
= 3,46 · 103
/ 100,5 = 34,43 Н·м;
T2
= (N2
/ ω 2
) · η = T1
· u · η = 34,43 · 2,24 · 0,955 = 73,65 Н·м.
4
Расчет параметров зубчатых колес
4.1
Определение механических свойств материалов
Выбираем для шестерни сталь 45 с термообработкой улучшением НВ 240, а для колеса тоже сталь 45 с термообработкой нормализацией НВ 215.
Примем предварительно: для шестерни диаметр заготовки до 100 мм, а для колеса до 400 мм. Тогда:
- для материала шестерни: предел текучести σт
= 440 МПа, предел прочности σв
= 780 МПа;
- для материала колеса: предел текучести σт
= 280 МПа, предел прочности σв
= 550 МПа.
По заданной долговечности определяем число рабочих циклов:
- шестерни Nц1
= 60 · 960 · 11600 = 6,7 · 108
;
- колеса Nц2
= 60 · 429 · 11600 = 3 · 108
.
Так как Nц
> 107
принимаем коэффициент долговечности КHL
= 1.
Коэффициент безопасности примем: [n] = 1,15.
При НВ ≤ 350 НВ: σН
limb
= 2 · HB + 70, тогда:
- для шестерни σН
limb
1
= 2 · 240 + 70 = 550 МПа
[σH
]1
= (σН
limb
1
· КHL
) / [n] = (550 · 1) / 1,15 = 478,3 МПа
- для колеса σН
limb
2
= 2 · 215 + 70 = 500 МПа
[σH
]2
= (σН
limb
2
· КHL
) / [n] = (500 · 1) / 1,15 = 434,8 МПа
4.2 Расчет параметров передачи
Введем коэффициент, учитывающий динамичность нагрузки и неравномерность зацепления kH
= 1,2.
Коэффициент ширины колеса: ψba
= 0,4.
Межосевое расстояние из условия контактной прочности зубьев:
αW
= (u + 1) 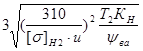 = (2,24 + 1) = (2,24 + 1) 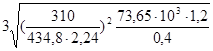 = 91,3 мм. = 91,3 мм.
Принимаем αW
= 100 мм.
m = (0,01-0,02) αW
= 1-2 мм, принимаем m = 1 мм.
Определяем суммарное число зубьев шестерни и колеса:
zΣ
= 2 αW
/ m = 2 · 100 / 1 = 200,
а также отдельно для быстроходной ступени передач:
z1
= 2 αW
/ m(u + 1) = 2 · 100 / 1 · (2,24 + 1) = 61,7; z1
= 62
Для тихоходной ступени:
z2
= z1
u = 61,7 · 2,24= 138,2; z2
= 138
Уточняем передаточное число:
u = z2
/ z1
= 138 / 62 = 2,23
Делительные диаметры:
d1
= mz1
= 1 · 62 = 62 мм
d2
= mz2
= 1 · 138= 138 мм
Диаметры вершин зубьев:
da
1
= d1
+ 2m = 62 + 2 · 1 = 64 мм
da
2
= d2
+ 2m = 138 + 2 · 1 = 140 мм
Ширина колеса прямозубой передачи при ψba
= 0,4:
Реклама

b2
= ψва
· αW
= 0,4 · 100 = 40 мм
Ширина шестерни:
b1
= b2
+ 4 = 40 + 4 = 44 мм
Диаметры окружности впадин:
df
1
= d1
– 2,5m = 62 – 2,5 · 1 = 59,5 мм
df
2
= d2
– 2,5m = 138– 2,5 · 1 = 135,5 мм
Коэффициент ширины шестерни по диаметру:
Ψbd
= b1
/d1
= 44 /62 = 0,71
5 Конструирование валов редуктора
5.1 Расчет диаметров валов
Диаметр выходного конца вала, исходя из расчета на кручение:
d = 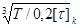 , ,
где [τ]k
– допускаемые напряжения кручения, определяемые механическими свойствами материала вала.
[τ]k
= 0,1σт
Ведущий вал выполним за одно целое с шестерней. В качестве материалов валов возьмем: сталь 45 с термообработкой улучшением.
Тогда для ведущего вала:
[τ]k
= 0,1σт
= 0,1 · 440 = 44 МПа
dВ1
= 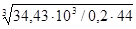 = 15,8 мм = 15,8 мм
Так как диаметр вала двигателя dдв
= 38 мм, то окончательно берем dВ1
= 38 мм. Диаметр вала под подшипники принимаем 50 мм.
Для ведомого вала:
[τ]k
= 0,1σт
= 0,1 · 440 = 44 МПа
dВ2
= 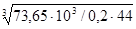 = 20,3 мм = 20,3 мм
Принимаем: выходной диаметр Ø25 мм, под подшипники – Ø35 мм, под колесо - Ø45 мм.
5.2 Расчет шпоночных соединений
Размеры призматических шпонок выбираем по диаметру вала:
Ведущий вал:
dВ1
= 38 мм, берем шпонку: 10х8, t1
= 5 мм.
Ведомый вал:
dВ2
= 25 мм, берем шпонку: 8х7, t1
= 4 мм.
dВ2.1
= 45 мм, берем шпонку: 14х9, t1
= 5,5 мм.
Длину призматической шпонки выбираем из стандартного ряда в соответствии с расчетом на смятие по боковым сторонам шпонки:
lр
≥ (2 · Т · 103
)/( d(h – t1
) · [σсм
])
Допускаемые напряжения смятия:
[σсм
] = σт
/ [s],
где [s] – допускаемый коэффициент запаса.
Для шпонок из чистотянутой стали 45Х принимаем σт
= 400 МПа. Принимаем: [s] = 2,3
[σсм
] = 400 / 2,3 = 173,9 МПа
Ведущий вал:
lр1
= (2 · 34,43 · 103
)/(38 · (8 – 5) · 173,9) = 3,47 мм
l1
= lр1
+ b = 3,47 + 10 = 13,47 мм
Окончательно берем: l1
= 20 мм
Ведомый вал:
lр2
= (2 · 73,65 · 103
)/(25 · (7 – 4) · 173,9) = 11,3 мм
l2
= lр2
+ b = 11,3 + 8 = 19,3 мм
Окончательно берем: l2
= 20 мм
lр3
= (2 · 73,65 · 103
)/(45 · (9 – 5,5) · 173,9) = 5,4 мм
l3
= lр3
+ b = 5,4 + 14 = 19,4 мм
Окончательно берем: l3
= 20 мм
Ширина колеса 40 мм – шпонка подходит.
5.3 Расчет зубчатой муфты
В приводе будем использовать зубчатую муфту. Выбор муфты производится в зависимости от диаметра вала и передаваемого крутящего момента по критерию:
Трасч
= k · Тдл.
≤ Ттабл.
Принимаем k = 1, тогда:
Трасч
= Т1
= 34,43 Н·м
Диаметр муфты:
dМ
≥ 10 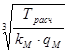 = 10 = 10 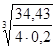 = 35 мм = 35 мм
qM
= 0,2 – 0,25
kМ
= 4 – 6 – при твердости 40-50 HRC
Выбираем зубчатую муфту dМ
= 60 мм, Т = 4000 Н · м.
5.4 Разработка чертежа вала редуктора
Основные размеры вала редуктора были получены в результате его проектирования. Недостающие размеры определим на основании выбранного варианта исполнения.
Вал редуктора спроектирован ступенчатым, это дает ряд преимуществ: удобство сборки; изготовление сопрягаемых деталей в системе отверстия.
Размеры под посадочные места под сопрягаемые детали выберем по их соответствующим размерам и условиям соединений.
Для обеспечения возможности выхода шлифовального камня при обработке
посадочных поверхностей вала введем канавку.
Для обеспечения требований взаимозаменяемости и обеспечения необходимого качества соединений проставим на чертеже допуски на размеры.
Укажем шероховатость обрабатываемых поверхностей. В технических требованиях укажем термообработку.
6 Проверочный расчет быстроходного вала
6.1 Определение реакций опор
Для проверочного расчета статической и усталостной прочности ступенчатого вала составим его расчетную схему.
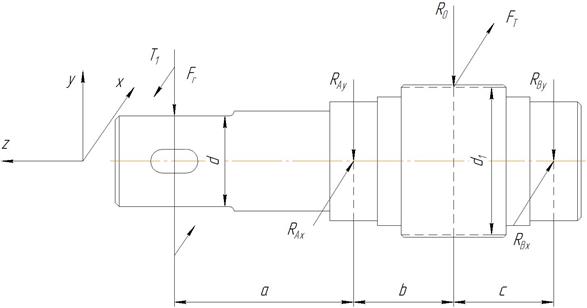
Расчетная схема вала.
Геометрические параметры вала определим на основании чертежа:
а = 75 мм; b = 42 мм; с = 42 мм.
Рассмотрим внешние силы, нагружающие быстроходный вал редуктора.
Со стороны муфты от электродвигателя на вал действует крутящий момент Т1
и поперечная сила Fr
; со стороны зацепления окружная сила FT
и поперечная R0
:
FT
= 2T1
/ d1
= 2 · 34,43 · 103
/ 62 = 1111 Н
R0
= FT
· tgα = 1111 · tg 20° = 404 Н
Fr
= (0,1 – 0,3)Ft
,
где Ft
– окружное усилие, действующее на зубья муфты.
Ft
= 2T1
/ dМ
= 2 · 34,43 · 103
/ 60 = 1148 Н
Принимаем Fr
= 344,4 Н
Рассмотрим плоскость YOZ:
ΣМАу
= 0; -RBy
· (c+b) – R0
· b + Fr
· a = 0
RBy
= (Fr
· a – R0
· b) / (c+b) = (344,4 · 75 – 404 · 42) / 84 = 105,6 H
ΣМB
у
= 0; RAy
· (c+b) + R0
· c + Fr
· (a + b + c) = 0
RAy
= (-Fr
· (a + b + c) – R0
· c) / (c+b) = (-344,4 · 159 – 404 · 42) / 84 = - 854 H
Проверка:
ΣFу
= 0; -Fr
- RAy
– R0
- RBy
= -344,4 + 854 – 404 – 105,6 = 0
Построение эпюры Му
:
Участок 0 ≤ z ≤ a, a = 0,075 м.
Му
= - Fr
· z
Му
(0) = 0
Му
(0,075) = -344,4 · 0,075 = -25,8 Н · м
Участок a ≤ z ≤ a + b, a = 0,075 м, b = 0,042 м.
Му
= - Fr
· z - RAy
· (z – a)
Му
(0,075) = - Fr
· z = -344,4 · 0,075 = -25,8 Н · м
Му
(0,117) = -344,4 · 0,117 – (- 854) · (0,117 – 0,075) = -4,4 Н · м
Плоскость XOZ.
ΣМАх
= 0; -FT
· b – RBx
(c + b) =0
RBx
= - FT
· b / (c + b) = -1148 · 42 / 84 = -574 Н
ΣМВх
= 0; FT
· с + RА
x
(c + b) =0
RА
x
= - FT
· с / (c + b) = -1148 · 42 / 84 = -574 Н
Проверка:
ΣFx
= 0; RА
x
+ RBx
+ FT
= 0
-574 – 574 + 1148 = 0
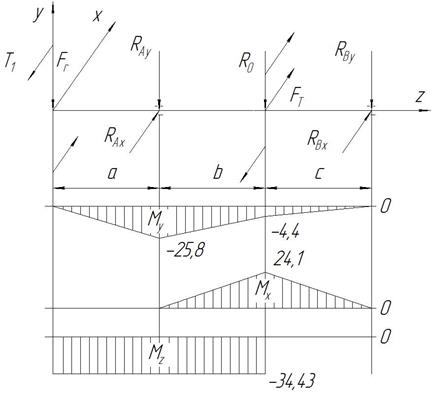
Построение эпюры Мх
.
Участок 0 ≤ z ≤ a, a = 0,075 м.
Мх
(0) = 0
Мх
(0,075) = 0 – на этом участке нет изгибающих сил.
Участок a ≤ z ≤ a + b, a = 0,075 м, b = 0,042 м.
Мх
(0,075) = 0
Мх
(0,117) = RА
x
· b = 574 · 0,042 = 24,1 Н · м
Результирующие реакции опор.
RA
= 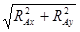 = = 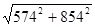 = 1029 H = 1029 H
RB
= 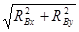 = = 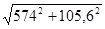 = 583,6 H = 583,6 H
Построение эпюры Мz
.
T1
= 34,43 Н · м
Участок 0 ≤ z ≤ a + b
Mz
= - T1
= -34,43 Н · м
6.2 Расчет статической прочности вала
На основании эпюр можно сделать следующие выводы.
Опасными сечениями для рассматриваемого вала, которые необходимо проверить на прочность, являются сечения: (z = 0), как наименее жесткое при кручении dВ1
= 38 мм, а также сечения (z = a) и (z = a + b), где действуют наибольшие изгибающие моменты.
В сечении (z = 0) находится еще и шпоночный паз, ослабляющий его жесткость. Сечение (z = a), где действует изгибающий момент:
Ма
=  = =  = 25,8 Н·м = 25,8 Н·м
И крутящий момент Мz
= 34,43 Н·м, находится в сложном напряженном состоянии и при этом имеет диаметр, незначительно превышающий наименьший. В сечении (z = a + b) изгибающий момент достигает величины:
Ма +
b
= 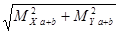 = = 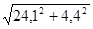 = 24,5 Н·м = 24,5 Н·м
Рассчитаем наибольшие напряжения в опасных сечениях.
В сечении (z = 0) нормальные напряжения от осевых сил и изгибающих моментов равны нулю, касательные напряжения τmax
определяются крутящим моментом
Мz
= 34,43 Н·м и полярным моментом сопротивления сечения Wp
цилиндрического конца вала со шпоночным пазом, глубиной t1
= 5 мм.
Wp
= 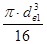 - - 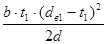 = = 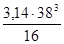 - - 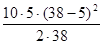 = 10052 мм3 = 10052 мм3
Тогда наибольшие касательные напряжения:
τmax
= Мz
/ Wp
= 34,43 / 10052 · 10-9
= 3,4 МПа,
а условие прочности вала в сечении (z = 0):
τmax
= 3,4 МПа ≤ [τ]k
= 44 МПа
выполняется.
В сечении (z = a) наибольшие нормальные напряжения определяются величиной изгибающего момента Ма
= 25,8 Н·м и моментом сопротивления сечения вала.
Wa
= 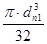 = = 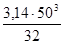 = 12266 мм3 = 12266 мм3
σmax
= Ма
/ Wa
= 25,8 / 12266 · 10-9
= 2,1 МПа,
а наибольшие касательные напряжения этого сечения с полярным моментом:
Wp
= 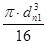 = = 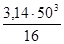 = 24532 мм3
, равны: = 24532 мм3
, равны:
τmax
= Мz
/ Wp
= 34,43 / 24532 · 10-9
= 1,4 МПа
В качестве допустимых напряжений на изгиб примем:
[σ] = 0,8 · σT
= 0,8 · 440 = 352 МПа
При этом условие статической прочности по приведенным напряжениям выполняется.
σпр
= 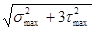 = = 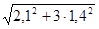 = 3,2 МПа ≤ [σ] = 352 МПа, = 3,2 МПа ≤ [σ] = 352 МПа,
В сечении (z = a + b) рассчитаем аналогично, с учетом того, что наибольшие нормальные напряжения определяются величиной изгибающего момента
Ма +
b
= 24,5 Н·м и моментом сопротивления сечения вала (с диаметром шестерни по впадинам):
Wa
= 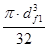 = = 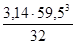 = 20670 мм3 = 20670 мм3
σmax
= Ма +
b
/ Wa
= 24,5 / 20670 · 10-9
= 1,2 МПа
Wp
= 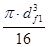 = = 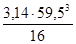 = 41340 мм3 = 41340 мм3
τmax
= Мz
/ Wp
= 34,43 / 41340 · 10-9
= 0,8 МПа
Условие статической прочности по приведенным напряжениям выполняется.
σпр
= 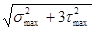 = = 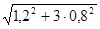 = 1,8 МПа ≤ [σ] = 352 МПа, = 1,8 МПа ≤ [σ] = 352 МПа,
6.3 Уточненный расчет прочности вала
Определим усталостные характеристики материала вала – шестерни, изготовленной из стали 45 с улучшением (σт
= 440 МПа, σв
= 780 МПа). При симметричном цикле (R = -1) имеем:
σ-1
= 0,43 · σв
= 0,43 · 780 = 335,4 МПа
τ-1
= 0,6 · σ-1
= 0,6 · 335,4 = 201,2 МПа
При пульсационном цикле (R = 0) имеем:
σ0
= 1,6 · σ-1
= 1,6 · 335,4 = 536,6 МПа
τ0
= 1,6 · τ-1
= 1,6 · 201,2 = 321,9 МПа
Рассчитаем коэффициенты, отражающие соотношение пределов выносливости при симметричном и пульсирующем циклах соответственно изгиба и кручения:
ψσ
= (2 · σ-1
- σ0
) / σ0
= (2 · 335,4 – 536,6) / 536,6 = 0,25
ψτ
= (2 · τ-1
- τ0
) / τ0
= (2 · 201,2 – 321,9) / 321,9 = 0,25
Из графика [3] определим коэффициенты влияния абсолютных размеров:
- в сечении (z = 0) при dв1
= 38 мм получим εσ
= ετ
= 0,82
- в сечении (z = а) при dп1
= 50 мм получим εσ
= ετ
= 0,77.
Зададим коэффициенты шероховатости [3] в зависимости от шероховатости поверхности Ra:
- в сечении (z = 0) при Ra = 1,25 получим kσ
n
= kτ
n
= 1,1
- в сечении (z = а) при Ra = 2,5 получим kσ
n
= kτ
n
= 1,2.
Эффективные коэффициенты концентрации напряжений определим из графика [1]:
- в сечении (z = 0) для концентратора в виде шпоночного паза имеем эффективные коэффициенты концентрации при изгибе и кручении соответственно
kσ
= 2,3 и kτ
= 2,1.
- в сечении (z = а) для концентратора в виде посадки с гарантированным натягом подшипника на вал имеем:
kσ
/ εσ
= 3,9; kτ
/ ετ
= 1 + 0,6(kσ
/ εσ
– 1) = 1 + 0,6 · 2,9 = 2,74
Примем коэффициент упрочнения в расчетных сечениях равным kу
= 1, поскольку поверхность вала не упрочняется. Рассчитаем коэффициенты перехода:
- для сечения (z = 0):
kσ
D
= (kσ
/ εσ
+ kσ
n
– 1) / kу
= (2,3 / 0,82 + 1,1 – 1) / 1 = 2,9
kτ
D
= (kτ
/ ετ
+ kτ
n
– 1) / kу
= (2,1 / 0,82 + 1,1 – 1) / 1 = 2,66
- для сечения (z = a):
kσ
D
= (kσ
/ εσ
+ kσ
n
– 1) / kу
= (3,9 + 1,2 – 1) / 1 = 4,1
kτ
D
= (kτ
/ ετ
+ kτ
n
– 1) / kу
= (2,74 + 1,2 – 1) / 1 = 2,94
Определим коэффициенты долговечности kСσ
и kСτ
[3]. Для этого рассчитаем эквивалентное число циклов при наибольшем значении показателя степени m = 9:
NΣ
= 60 · n1
· tΣ
· 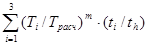 = 60 · 960 · 11600 · (19
· 0,1 + 0,89
· 0,25 + + 0,69
· 0,65) = 5,3 · 106 = 60 · 960 · 11600 · (19
· 0,1 + 0,89
· 0,25 + + 0,69
· 0,65) = 5,3 · 106
Коэффициент долговечности: kСσ
= 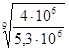 = 0,96 < 1, следовательно, = 0,96 < 1, следовательно,
kСσ
= kСτ
= 1.
Поскольку вал не испытывает осевой нагрузки, то будем считать, что нормальные напряжения, возникающие в поперечном сечении вала, изменяются по симметричному циклу, т.е. σm
= 0, амплитуда цикла нормальных напряжений равна наибольшему номинальному напряжению изгиба, соответственно: для сечения (z = 0), σa
= 0 МПа; для сечения (z = a), σa
= σmax
= 2,1 МПа
Исходя из неблагоприятных условий примем, что напряжения кручения изменяются по нулевому (пульсирующему) циклу, тогда:
- для сечения (z = 0) τа
= τm
= τmax
/ 2 = 3,4 / 2 = 1,7 МПа;
- для сечения (z = a) τа
= τm
= τmax
/ 2 = 1,4 / 2 = 0,7 МПа.
Тогда коэффициент запаса прочности по касательным напряжениям для сечения
(z = 0):
nτ
= τ-1
/ ((kτ
D
/ kСτ
) · τа
+ ψτ
· τm
) = 201,2 / (2,66 · 1,7 + 0,25 · 1,7) = 40,7
Для сечения (z = a) коэффициент запаса прочности определим по нормальным и касательным напряжениям соответственно:
nσ
= σ-1
/ ((kσ
D
/ kСσ
) · σa
+ ψσ
· σm
) = 335,4 / (4,1 · 2,1) = 39
nτ
= τ-1
/ ((kτ
D
/ kСτ
) · τа
+ ψτ
· τm
) = 201,2 / (2,94 · 0,7 + 0,25 · 0,7) = 90,1
Окончательно получим для сечения (z = a):
n = (nσ
· nτ
) / 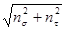 = (39 · 90,1) / = (39 · 90,1) / 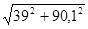 = 35,8 = 35,8
Поскольку допускаемые значения коэффициента запаса принимают [n] = 1,5 – 2, то условие достаточной прочности n ≥ [n] выполняется.
7 Подбор подшипников качения
Определим ресурс:
Тихоходный вал:
L = (tΣ
· 60 · n) / 106
= (11600 · 60 · 435) / 106
= 302,8 млн. об.
Быстроходный вал:
L = (tΣ
· 60 · n) / 106
= (11600 · 60 · 960) / 106
= 668,2 млн. об.
Подсчитаем эквивалентные нагрузки:
Р = V · Rp
· Кб
· Кт
V = 1 – вращается внутреннее кольцо;
Кб
= 1,3 - 1,5 – коэффициент безопасности;
Кт
= 1 – температурный коэффициент;
Rp
– силы возникающие в подшипнике.
Для быстроходного вала:
Р = 1 · 1029 · 1,5 · 1 = 1544 Н
Для тихоходного вала:
Р = 1 · 574 · 1,5 · 1 = 861 Н
Динамическая грузоподъемность:
С = Р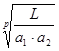 , где: , где:
а1
= 1 – коэффициент надежности,
а2
= 0,7 - 0,8 – обобщенный коэффициент.
Для быстроходного вала:
С = 1544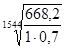 = 1551 Н = 1551 Н
Для тихоходного вала:
С = 861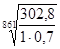 = 867 Н = 867 Н
Для быстроходного вала: dп1
= 50 мм, С = 1551 Н, берем подшипник средней серии №310 (С = 61800 Н). [2]
Для тихоходного вала: dп1
= 35 мм, С = 867 Н, берем подшипник легкой серии №207 (С = 25500 Н). [2]
Список использованной литературы
1. Курсовое проектирование деталей машин. /Под общ. ред. В. Н. Кудрявцева. – Л.: Машиностроение, 1984. – 400с.
2. Анурьев В. И. Справочник конструктора – машиностроителя. М.: Машиностроение. 1979. Т. 1-3.
3. Кудрявцев В. Н. Детали машин. Л.: Машиностроение, 1980. 464 с.
4. Гжиров Р. И. Краткий справочник конструктора. – Л.: Машиностроение. 1983. – 464 с.
|