| Министерство общего и профессионального образования
Российской Федерации
Сибирский государственный аэрокосмический университет
имени академика М. Ф. Решетнева
С. Н. Козловский
Основы теории и технологии контактной точечной сварки
Монография
Красноярск 2005
УДК 621.791.763
ББК
К 59
Рецензенты:
Печатается по решению Редакционно – издательского совета университета
Козловский С.Н.
К 59 Основы теории и технологии контактной точечной сварки: Монография / С. Н. Козловский; СибГАУ. — Красноярск:, 2003. — ??? с. ISBN
В монографии изложены основы теории и технологии контактной точечной сварки. Рассмотрены основные процессы, протекающие при контактной точечной сварке: деформирования свариваемых деталей при их сближении до соприкосновения; формирования механических и электрических контактов, электрической проводимости зоны сварки; нагрева металла в зоне сварки и методы количественной его оценки; объемные пластические деформация металла в зоне точечной сварки. Приведены математические модели основных термодеформационных процессов, протекающих в зоне сварки на стадии нагрева: равновесия силовой системы электрод–детали–электрод; теплового состояния зоны сварки; силового взаимодействия деталей в площади свариваемого контакта; пластической деформации металла в зоне точечной сварки. Описаны методики расчетного определения: размеров ядра и средних значений температуры в зоне сварки; среднего значения нормальных напряжений в площади контакта деталь–деталь; давления расплавленного металла в ядре; сопротивления пластической деформации металла в условиях формирования точечного соединения; определения степени и скорости пластической деформации металла в зоне сварки, его температуры;
высоты уплотняющего пояска в свариваемом контакте. Описаны методики математического моделирования процессов формирования точечных сварных соединений. Показано изменение параметров основных термодеформационных процессов, протекающих в зоне сварки на стадии нагрева и влияние на них режимов сварки. Рассмотрены технологические аспекты повышения устойчивости процесса формирования точечных сварных соединений и их качества.
Монография предназначена для научных и инженерно-технических работников, занимающихся совершенствованием существующих и разработкой новых сварочных технологий контактной точечной сварки. Она может быть полезна аспирантам, студентам вузов и техникумов сварочных специальностей.
Реклама

УДК 621.791.763
ББК
ISBN
© Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева, 2005
© С.Н. Козловский
| ВВЕДЕНИЕ
|
| 1.
Сущность и технологии традиционных способов контактной
точечной сварки
|
| 1.1.
|
Двусторонняя точечная сварка, ее разновидности и основные параметры точечных сварных соединений
|
| 1.2.
|
Основные технологические приемы контактной точечной сварки
|
| 1.2.1.
|
Термодеформационные процессы, протекающие в зоне сварки и общая схема формирования точечного сварного соединения ....
|
| 1.2.2.
|
Технологические приемы традиционных способов контактной точечной сварки
|
| 1.2.3.
|
Контактная точеная сварка с обжатием периферийной зоны соединений
|
| 1.3.
|
Параметры режимов — факторы регулирования процесса точечной сварки
|
| 1.3.1
|
Время сварки
|
| 1.3.2
|
Сила сварочного тока
|
| 1.3.3
|
Усилие сжатия электродов
|
| 1.3.4
|
Форма и размеры рабочих поверхностей электродов
|
| 1.3.5
|
Критерии подобия для определения режимов сварки
|
| 2.
Основные процессы, протекающие при контактной точечной
сварке
|
| 2.1
|
Сближение свариваемых деталей
|
| 2.1.1
|
Деформирование свариваемых деталей при их сближении ..
|
| 2.1.2.
|
Влияние деформирования деталей на усилие сжатия в свариваемом контакте
|
| 2.1.3.
|
Экспериментально-расчетный метод определения усилия
деформирования деталей при их сближении
|
| 2.2
|
Формирование контактов при сжатии деталей электродами
|
| 2.2.1
|
Формирование механических контактов
|
| 2.2.2
|
Формирование электрических контактов
|
| 2.3
|
Электрическая проводимость зоны сварки
|
| 2.3.1
|
Электрические сопротивления контактов при точечной сварке
|
| 2.3.2.
|
Электрические сопротивления собственно свариваемых
деталей
|
| 2.3.3
|
Общее электрические сопротивления зоны сварки
|
| 2.4.
|
Нагрев металла в зоне сварки и методы количественной его
оценки
|
| 2.4.1
|
Источники теплоты в зоне формирования сварного соединения..
|
| 2.4..
|
Температурное поле в зоне формирования соединения
|
| 2.4.3
|
Тепловой баланс в зоне сварки и расчет сварочного тока
|
| 2.5.
|
Объемная пластическая деформация металла в зоне формировании точечного сварного соединения
|
| 2.5.1.
|
Методики экспериментальных исследований макродеформаций металла в зоне сварки
|
| 2.5.2.
|
Характер пластических деформаций металла в зоне сварки на стадии нагрева
|
| 3.
Математические модели основных термодеформационных
процессов, протекающих в зоне точечной сварки
|
| 3.1.
|
Термодеформационное равновесие силовой системы электрод–детали–электрод при традиционных способах сварки
Реклама

|
| 3.2.
|
Термодеформационное равновесие силовой системы электрод–
–детали–электрод при контактной точечной сварке с обжатием периферийной зоны соединения
|
| 3.2.1
|
Способ контактной точечной сварки с обжатием периферийной зоны соединений вне контура уплотняющего пояска
|
| 3.2.2.
|
Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения
|
| 3.3
|
Оценка теплового состояния зоны сварки на стадии нагрева
|
| 3.3.1.
|
Экспериментально-расчетный метод оценки теплового
состояния зоны сварки на стадии нагрева
|
| 3.3.2.
|
Методики расчетного определения размеров ядра и средних значений температуры в зоне сварки
|
| 3.4.
|
Математические модели силового взаимодействия деталей в площади свариваемого контакта при формировании соединения
|
| 3.4.1.
|
Методика расчета среднего значения нормальных напряжений в площади контакта деталь–деталь
|
| 3.4.2.
|
Методика расчета давления расплавленного металла в ядре
|
| 3.5.
|
Методики определения параметров термодеформационных
процессов, протекающих в зоне точечной сварки
|
| 3.5.1.
|
Сопротивление пластической деформации металла в условиях деформирования при повышенных температурах
|
| 3.5.2.
|
Определение степени и скорости пластической деформации
металла в зоне точечной сварки
|
| 3.5.3.
|
Определение температуры металла в зоне пластических
деформаций
|
| 3.5.4.
|
Определение высоты уплотняющего пояска в свариваемом
контакте
|
4. Математическое моделирование процессов формирования
точечных сварных соединений
|
| 4.1.
|
Методики расчета изменения диаметра уплотняющего пояска в процессе контактной точечной сварки
|
| 4.1.1.
|
Методика расчета изменения диаметра уплотняющего пояска при традиционных способах контактной точечной сварки
|
| 4.1.2.
|
Методика расчета изменения диаметра уплотняющего пояска при точечной сварке с обжатием периферии соединения
|
| 4.2
|
Изменение термодеформационных процессов на стадии нагрева при традиционных способах точечной сварки
|
| 4.2.1
|
Изменение параметров термодеформационных процессов при традиционных способах точечной сварки
|
| 4.2.2.
|
Особенности термодеформационных процессов при точечной сварке с обжатием периферийной зоны соединения
|
| 4.2.3.
|
Влияние режимов сварки на параметры термодеформационных процессов, протекающих в зоне формирования соединения
|
| 4.3.
|
Критерий оценки режимов контактной точечной сварки
|
| 5. Технологические аспекты получения качественных сварных
соединений
|
| 5.1.
|
Дефекты сварных соединений, причины и механизмы их
образования
|
| 5.1.1.
|
Непровары
|
| 5.1.2.
|
Выплески
|
| Устойчивость процесса контактной точечной сварки
|
| 5.3.1.
|
Методика определения устойчивости процесса точечной сварки
|
| 5.3.2.
|
Регулирование устойчивости процесса точечной сварки
|
| Глава 6. Программированные режимы традиционных способов точечной сварки
|
| 7. Программированные режимы способов точечной сварки с обжатием периферийной зоны соединения
|
ВВЕДЕНИЕ
Контактная точечная сварка (КТС) — это один из способов контактной сварки, который наиболее широко применяется в машиностроении, в особенности в массовом производстве. Так, например, в автомобилестроении около 70 % объема сварочных работ выполняется именно этим способом. Значительное применение КТС получила и в других отраслях: в тракторном и сельскохозяйственном машиностроении, при производстве пассажирских и товарных вагонов и других отраслях промышленности и строительства. Этому способствовали положительные особенности процесса КТС: незначительные остаточные деформации, высокая производительность, высокий уровень механизации и автоматизации, гибкость и универсальность технологического процесса, отсутствие вспомогательных сварочных материалов, высокая экологичность и культура производства.
Вместе с тем, описанных выше достоинств КТС становилось недостаточно по мере расширения использования КТС для получения неразъемных соединений в изделиях ответственного назначения из современных конструкционных материалов: низко- и среднелегированных, коррозионностойких, теплостойких и жаропрочных сталей и сплавов, алюминиевых, магниевых, титановых и других сплавов, например, в авиационной и космической промышленности, которые работают при повышенных температурах, в агрессивных средах, при динамических нагрузках. В этих случаях к качеству точечных сварных соединений предъявляются повышенные требования по надёжности и стабильности прочностных характеристик, уровню остаточных деформаций, а также, в ряде случаев, по гарантированному уровню надёжности полного отсутствия таких дефектов, как непровары и выплески.
Технологии традиционных способов КТС (к ним относят способы точечной сварки, при осуществлении которых детали сжимают токопроводящими электродами и в периоды сжатия, действия импульса тока и проковки соединений параметры режима сварки, как правило, не изменяют) к началу 70-х годов ХХ века достигли своего совершенства и практически исчерпали возможности своего развития. Они вполне удовлетворяли требованиям массового производства, но во многих случаях не могли обеспечить требуемый уровень качества при сварке изделий ответственного назначения. Поэтому в этот период и стали развиваться способы КТС с программированным изменением параметров режима (сварочного тока, усилия сжатия электродов) в период формирования соединений, которые позволяют управлять термодеформационными процессами, протекающими в зоне сварки. Они открывали новые возможности повышения качества получаемых точечных соединений.
В данной работе сделана попытка обобщить теоретические и технологические разработки способов КТС с программированным воздействием на зону формирования точечных сварных соединений.
1. Сущность И технологии традиционных способов контактной точечной сварки
Технологии электрической контактной точечной сварки за более чем вековой период своего развития (привилегия (патент) из Департамента торговли и мануфактур России на изобретение точечной сварки выдана русскому инженеру Н. Н. Бенардосу в 1887 г.) достигли весьма высокого уровня совершенства и отличаются большим разнообразием способов их практического осуществления. Для создания наиболее оптимальных условий формирования точечных соединений при сварке конкретных деталей из различных материалов, отличающихся теплофизическими свойствами, применяют разные виды тока (переменный, постоянный, низкочастотный и др.) и разные циклы параметров режимов сварки, отличающиеся параметрами усилия сжатия электродов и сварочного тока в разные периоды процесса сварки. Ниже рассмотрены сущность и наиболее распространенные технологии двусторонней точечной сварки, общая схема формирования точечных сварных соединений и основные термодеформационные процессы, которые протекают в зоне сварки и наиболее значимо влияют на конечное качество получаемых сварных соединений.
1.1
. Двусторонняя
точечная сварка, ее разновидности и основные параметры точечных сварных соединений
Электрическая контактная точечная сварка (КТС) — это способ контактной сварки (рис. 1.1), при котором свариваемые детали 1, расположенные перед сваркой внахлестку, сжимают токопроводящими электродами 2 и 3 сварочным усилием F
СВ
, а затем от источника питания ИП (например, трансформатора) пропускают импульс сварочного тока I
СВ
длительностью t
СВ
и таким образом сваривают их по отдельным участкам касания, называемым сварными точками 4 [1, 2]. При КТС для образования физического контакта между свариваемыми поверхностями и их активации в месте формирования соединения затрачивается тепловая и механическая энергия, которая подводится извне сжатием деталей электродами и пропусканием через зону сварки импульса сварочного тока [3, 4]. Наиболее надежным способом, который обеспечивает образование физического контакта и способствует возникновению межатомарных связей в зоне формирования соединений, является расплавление металла в приповерхностных слоях деталей с образованием общего его объема. Поэтому в технологии КТС, за редким исключением [5, 6], принято, что необходимым условием образования точечного сварного соединения является образование общей зоны расплавленного металла соединяемых деталей
. В специальной литературе по сварке общую зону расплавленного металла свариваемых деталей обычно называют «литое ядро», «ядро расплавленного металла» или просто «ядро» [2...4, 7…17].
Параметрами, которые наиболее значимо влияют на процесс формирования точечного сварного соединения и различают между собой все многообразие известных способов двусторонней точечной сварки, являются род сварочного тока и форма его импульса. Это их различие (рис. 1.2) обусловлено в основном особенностями устройства силовых электрических контуров машин контактной точечной сварки [18, 19]. Поэтому способы КТС по роду сварочного тока и форме его импульса разделяют на следующие группы [2, 3, 15, 16]:
- контактная точечная сварка переменным током (рис. 1.2, а
);
- низкочастотная контактная точечная сварка (током пониженной частоты монополярными или униполярными импульсами) (рис. 1.2, б
);
- конденсаторная контактная точечная сварка (рис. 1.2, в
);
- контактная точечная сварка постоянным током (рис. 1.2, г
);
Каждая из этих групп способов КТС имеет свои особенности, преимущества и недостатки в технологическом и техническом аспектах. Кроме того, они различаются и экономической эффективностью [20, 21].
Точечное сварное соединение (рис. 1.3), поскольку сварку в подавляющем числе случаев осуществляют электродами с цилиндрической рабочей частью, обычно считают осесимметричным. Такое соединение (сварную точку (рис. 1.3, а
)) приято характеризовать геометрическими параметрами в плоскости оси электродов, которые называют «конструктивными элементами соединения
». Кроме того, геометрическими параметрами характеризуют также и рабочие части электродов (рис. 1.3, б
). Основными из них, наиболее часто используемыми и в большинстве случаев регламентируемыми, являются параметры, которые описывают ядро расплавленного металла (диаметр и высота ядра, проплавление деталей), остаточные деформации деталей (глубина вмятин от электродов), а также рабочие поверхности электродов (диаметр плоской и радиус сферической).
Ядро расплавленного металла (рис. 1.3, а
, б
) в большинстве случаев характеризуют его размерами: диаметром d
Я
в плоскости контакта
деталь-деталь (свариваемого контакта), а также его высотой h
Я
или проплавлением деталей А1
и А3
..
Последние определяют отдельно для каждой детали как отношение к толщине деталей s
1
и s
2
расстояний h
1
и h
2
от плоскости свариваемого контакта до границы зоны расплавленного металла
(см. рис. 1.1) и выражают обычно в процентах [2, 3, 14…16]:
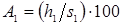 %, %, 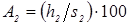 %. (1.1) %. (1.1)
При точечной сварке деталей одноточечные соединения применяют относительно редко. В подавляющем числе случаев точечной сварки осуществляют многоточечные соединения деталей (рис. 1.4). Последние выполняют в виде одного (рис. 1.4, а
) или нескольких (рис. 1.4, б
) рядов сварных точек, расположенных вдоль нахлестки деталей.

К основным конструктивным элементам, характеризующим многоточечные соединения, относят: ширину нахлёстки В
, расстояние (шаг) между точками t
Ш
в ряду (в шве), расстояниями между осями швов b
, а также расстоянием u
между крайними осями швов и кромками листов.
Перечисленные выше конструктивные элементы сварных соединений существенно влияют как на процесс их формирования при КТС, так и на показатели качества готовых сварных соединений. Поэтому их допускаемые значения в подавляющем большинстве случаев регламентируются как в зарубежной [22], так и отечественной практике КТС, например, в ГОСТах [23], ОСТах, отраслевых технологических рекомендациях, стандартах предприятий [14].
Размеры ядра (его диаметр dЯ
и высота h
Я
, а также проплавление деталей А1
и А2
) наиболее значимо влияют на свойства точечного соединения, в первую очередь, на прочностные. Поэтому получение оптимальных значений этих параметров, которые должны находиться в пределах между минимальными и максимальными допускаемыми их значениями, и является основной задачей технологии точечной сварки.
Минимально допускаемые значения диаметра ядра
определяются влиянием целого ряда факторов точечной сварки, например, таких как прочность сварных соединений и стабильность ее значений, устойчивость процесса КТС против образования выплесков, непроваров и др. Их значения зависят от толщины s
свариваемых деталей [3, 10, 23]:
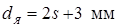 , (1.2) , (1.2)
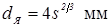 . (1.3) . (1.3)
Они регламентированы ГОСТ 15878 – 79 (табл. 1.1). Эти табличные значения диаметров ядра выработаны многолетней практикой КТС.
Таблица 1.1
Минимально допускаемые значения диаметра ядра для соединений
группы А по ГОСТ 15878 – 79.
| Толщина деталей,
s = s1
|
Минимальный диаметр ядра,
dЯ
|
Минимальная ширина нахлестки, В
|
Минимальный шаг между точками, tШ
|
| алюминиевые, магниевые, медные сплавы
|
стали, титановые сплавы
|
алюминиевые, магниевые, медные сплавы
|
стали,
|
| 0,5
1,0
1,2
1,5
2,0
2,5
3,0
4,0
5,0
6,0
|
3
4
5
6
7
8
9
12
14
16
|
10
14
16
18
20
22
16
32
40
50
|
8
11
13
14
17
19
21
28
34
42
|
10
15
17
20
25
30
35
45
55
65
|
Величина проплавления деталей А1
и
А2
в большинстве случаев должна находиться в пределах 20…80 % от толщины деталей. На титановых сплавах верхний предел увеличивают до 95 %, а на магниевых — уменьшают до 70 %.
Минимально допускаемое расстояние между осями швов
b
устанавливают из условия отсутствия влияния шунтирования тока на процесс КТС. Его выбирают таким, чтобы расстояние до соседних точек в любом направлении, например t
1
, было не меньше минимально допускаемого шага между точками t
Ш
.
Минимальную ширину нахлестки В
, а также минимальное расстояние от центра точки или оси шва до края нахлестки
u
устанавливают по условию отсутствия объемных пластических деформаций металла на краю нахлестки. Причем минимальные значения и
должны быть не менее 0,5В
.
Глубина вмятин
от электродов с1
и с2
не должна превышать 20 % от толщины деталей, поскольку они ухудшают внешний вид соединений и обычно уменьшают их прочность. Только при сварке деталей неравных толщин или в труднодоступных местах её допускают увеличивать до 30 % [2, 3, 15, 16].
Широкое применение в современном машиностроении точечных сварных соединений вместо клепаных, в том числе при изготовлении узлов летательных аппаратов, обусловлено не только преимуществами их технико-экономических показателей [22, 23], но и конкурентной способностью эксплуатационных свойств [2, 3, 9, 11, 15, 17]. Прежде всего, это относится к их прочности, которую в основном определяют размеры ядра расплавленного металла в совокупности с другими конструктивными элементами сварных соединений, причем в первую очередь — к прочности динамической [24...29]. Именно поэтому соответствие полученных при КТС размеров ядра заданным оптимальным значениям, в первую очередь его диаметра и проплавления деталей, является одним из основных критериев качества и надёжности соединений деталей, выполненных контактной точечной сваркой
[10, 11, 14, 15].
1.2
. Основные технологические приемы контактной точечной сварки
При КТС энергетическое воздействие на металл зоны формирования соединения осуществляют импульсом тока, а силовое – сжатием деталей электродными устройствами в месте сварки. Количественно это воздействие характеризуют параметрами режима сварки и представляют обычно в виде циклограмм их изменения во времени. Значения параметров тока и усилия сжатия электродов, характер их изменения в отдельные периоды цикла сварки определяют параметры термодеформационных процессов, протекающих в зоне сварки, и таким образом влияют на устойчивость процесса формирования соединения, в частности против образования непроваров и выплесков, на размеры ядра, местные и общие остаточные деформации и, в конечном итоге, на эксплуатационные свойства сварного соединения. Этим в основном и различаются отдельные способы точечной сварки, наиболее распространенные из которых рассмотрены ниже.
1.2.1.
Термодеформационные процессы, протекающие в зоне сварки и общая схема формирования точечного сварного соединения
В общем случае для формирования сварных соединении деталей, в том числе и при контактной точечной сварке, необходимо образование физического контакта между соединяемыми их поверхностями, химических связей в нем и развитие релаксационных процессов в объемах металла зоны сварки. В каждой элементарной точке эти процессы идут последовательно, а по отношению ко всей соединяемой поверхности могут протекать одновременно. При КТС их зарождение и развитие обеспечивается комплексным тепловым и силовым воздействием на металл зоны формирования соединения [2, 3, 16, 30, 31].
Термодеформационные процессы, протекающие в зоне формирования точечного сварного соединения, в соответствии со значимостью их влияния на конечный результат сварки принято условно разделять на основные процессы и процессы сопутствующие [2, 3, 16].
К основным термодеформационным процессам относят процессы, без протекания которых формирование точечного сварного соединения в принципе невозможно. К ним относят, в частности, следующие:
- нагрев и расплавление металла проходящим током;
- образование общей зоны расплавленного металла (ядра) и его кристаллизацию на последней стадии формирования соединений;
- микроскопические деформации металла в контактах и макроскопические в зоне формирования соединения.
К сопутствующим термодеформационным процессам сварки относят процессы, которые не только не обязательны для формирования сварного соединения, но некоторые из них и нежелательны, так как ухудшают условия формирования соединения и конечные результаты сварки. При КТС они являются неизбежным следствием протекания в зоне сварки процессов основных. В частности, к сопутствующим процессам относят следующие:
- дилатацию металла в зоне формирования соединений;
- перемешивание жидкого металла в ядре и удаление окисных
пленок;
- воздействие термодеформационного цикла сварки на свойства металла в зоне сварки и прилегающей к ней области;
- образование остаточных напряжений и деформаций в деталях;
- массоперенос в контактах электрод – деталь.
Несмотря на изменение значимости влияния каждого из перечисленных выше основных термодеформационных процессов, в процессе сварки общая схема формирования соединения происходит по единой схеме. Поэтому цикл сварки во временной последовательности условно разделяют на отдельные этапы, в соответствии со значимостью влияния какого-либо из основных факторов в их период [3, 16]. По-видимому, цикл сварки во временной последовательности целесообразно разделить на следующие четыре этапа (рис. 1.5), которые отличаются не только значимостью влияния какого-либо из основных факторов на процесс формирования соединения, но и основными технологическими задачами, выполняемыми сочетанием параметров режима в этот период:
1-й этап
— от начала сжатия деталей электродами усилием F
Э
до начала импульса тока IСВ
;
2-й этап
— от начала импульса тока IСВ
до начала расплавления металла в контакте деталь – деталь (до начала формирования ядра);
3-й этап
— от начала формирования ядра диаметром dЯ
в контакте деталь – деталь до окончания импульса сварочного тока IСВ
;
4-й этап
— от окончания импульса сварочного тока IСВ
до снятия усилия F
Э
сжатия деталей электродами. На первом этапе
сжатие деталей электродами вызывает микропластические деформации в контактах деталь-деталь и электрод-деталь, следствием которых является формирование механических и электрических контактов. Главная задача на этом этапе — это обеспечение стабильности параметров контактов, что является исходным условием устойчивого течения процесса сварки и получения стабильных размеров ядра.
На втором этапе
включение тока приводит к нагреву металла в зоне сварки, который интенсифицирует процессы микропластических деформаций, разрушения окисных пленок, формирования механических и электрических контактов. Нагретый металл зоны сварки расширяется, деформируется преимущественно в зазор между деталями, вследствие чего в контакте деталь – деталь образуется рельеф (уплотняющий поясок). Это приводит к расхождению электродов Δ
. Динамика увеличения уплотняющего пояска на этом этапе определяет изменение плотности тока в зоне сварки и скорость тепловыделения в ней. Главная задача на этом этапе — это обеспечение оптимальной скорости нагрева металла в зоне сварки.
На третьем этапе
происходит расплавление металла в области контакта деталь-деталь, образование ядра и уплотняющего пояска вокруг него, который предотвращает выброс расплавленного металла. По мере прохождения тока продолжается нагрев металла в зоне сварки, ядро растет по диаметру и высоте, происходит перемешивание металла, удаление поверхностных пленок и образование металлических связей в жидкой фазе. Продолжаются процессы теплового расширения металла в зоне сварки и его пластической деформации. Главная задача на этом этапе — это обеспечение оптимальной степени макродеформаций металла в зоне сварки, которая бы обеспечивала оптимальную скорость нагрева металла в зоне сварки и предотвращала выброс расплавленного металла.
На четвёртом этапе
происходит охлаждение металла в зоне сварки и его кристаллизация в ядре, параметры которого определяют эксплуатационные свойства точечного сварного соединения. При охлаждении металла уменьшается его объем, вследствие чего возникают остаточные напряжения и деформации. Главная задача на этом этапе — это обеспечение степени макродеформаций металла в зоне сварки, достаточной для компенсации усадки металла.
1.2.2.
Технологические приемы традиционных способов контактной точечной сварки
Среди циклов традиционных способов КТС (рис. 1.6), по-видимому, наиболее распространенным является цикл изменения параметров режима (рис. 1.6, а
), предложенный еще Н. Н. Бенардосом. При сварке по этому циклу детали сжимают токопроводящими электродами (см. рис. 1.1) неизменным усилием F
СВ
и через определенное время сжатия t
СЖ
пропускают импульс сварочного тока заданной силы I
СВ
и длительности t
СВ
, а затем через определенное время проковки t
ПР
, достаточное для кристаллизации и охлаждения зоны сварки, усилие сжатия электродов снимают. Его технологические возможности до настоящего времени удовлетворяют требованиям практики КТС не только сварки деталей из малоуглеродистых сталей в автомобиле- и сельхозмашиностроении [10, 17], но и сварки некоторых специальных сталей и сплавов [9, 15].
С целью предотвращения образования в ядре дефектов усадочного характера (трещин, пор) при сварке деталей из материалов, склонных к их образованию, например, относительно толстых деталей или деталей, склонных к закалке, а также деталей из высокопрочных материалов, применяют цикл (рис. 1.6, б
), в котором при кристаллизации расплавленного металла в ядре и охлаждения зоны сварки (в период t
ПР
проковки) усилие сжатия электродов увеличивают (прикладывают ковочное усилие F
К
). Этим увеличивают в ней степень пластической деформации металла, компенсирующей его усадку при кристаллизации и охлаждении.
Величину ковочного усилия F
К
[3]:
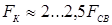 , (1.4) , (1.4)
и момент его приложения t
К
(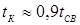 ) задают с учетом термодеформационных процессов, протекающих в зоне сварки, и увеличивают обычно монотонно с заданной скоростью, но иногда и ступенчато. И все же достичь поставленной цели только приложением F
К
не всегда удается, поскольку его величина ограничивается прочностью электродов и техническими возможностями машин точечной сварки [14...19, 32...37]. ) задают с учетом термодеформационных процессов, протекающих в зоне сварки, и увеличивают обычно монотонно с заданной скоростью, но иногда и ступенчато. И все же достичь поставленной цели только приложением F
К
не всегда удается, поскольку его величина ограничивается прочностью электродов и техническими возможностями машин точечной сварки [14...19, 32...37].
В технологии КТС известны и циклы (рис. 1.6, в
), при осуществлении которых в период проковки соединения t
ПР
усилие сжатия электродов не только не увеличивают, но даже и уменьшают [38]. Например, при сварке свинцовых деталей со стальными.
При сварке деталей из углеродистых и низколегированных сталей с целью предотвращения образования в соединении закалочных структур и трещин путем уменьшения скорости его охлаждения применяют цикл
(рис. 1.6, г
), в котором сжатие деталей электродами вообще прекращают одновременно с окончанием импульса сварочного тока [39]. Для решения этой же задачи, а также с целью улучшения условий проковки соединений и уменьшения требуемой величины ковочного усилия, а иногда для термообработки соединения в сварочных электродах применяют цикл, в котором после окончания импульса сварочного тока I
СВ
в период проковки соединения t
ПР
пропускают дополнительный подогревающий импульс тока I
Д
(рис. 1.6, д
). Дополнительный подогревающий импульс тока I
Д
, уменьшающий сопротивление деформации металла в зоне сварки, может применяться в сочетании с любой циклограммой изменения усилия сжатия электродов. Подогревающий ток пропускают обычно в виде отдельного дополнительного импульса I
Д
, но иногда и как модулированное продолжение импульса сварочного [3, 11, 15, 16, 40…46].
Для получения оптимальных значений начальных электрических сопротивлений в контактах, в особенности при сварке деталей из высокопрочных материалов или деталей с относительно невысоким качеством подготовки поверхностей, в практике точечной сварки применяют цикл (рис 1.6, е
), в котором перед импульсом сварочного тока в период сжатия деталей t
СЖ
производят их обжатие повышенным усилием сжатия электродов F
0
(усилием обжатия). Этот технологический прием используют и для предупреждения наружных и внутренних начальных выплесков, а также для вытеснения пластичных прослоек грунта, клея [3, 9, 11, 15, 16]. Величину усилия предварительного обжатия деталей обычно принимают равной величине ковочного усилия [3]:
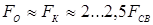 . (1.5) . (1.5)
Причем, применение при КТС равных усилий обжатия и проковки соединения упрощает конструкцию приводов сварочных машин.
Однако в ряде случаев только предварительным обжатием деталей не удаётся получить оптимальные значения начальных электрических сопротивлений в контактах. В этом случае применяют цикл (рис 1.6, ж
), в котором металл в зоне сварки предварительно, перед сварочным импульсом I
СВ
, подогревают отдельным либо совмещенным со сварочным дополнительным подогревающим I
П
импульсом тока [3, 14, 15, 47…49].
Последние исследования процессов КТС показывают, что во многих случаях точечной сварки стабилизировать процесс формирования соединения можно интенсификацией микро- и макропластических деформаций металла в зоне сварки путем уменьшения его сопротивления пластической деформации на стадиях сжатия и проковки соединения. В таких случаях одном цикле рационально использовать и предварительный, и дополнительный подогревающие импульсы тока, в частности, даже при сварке деталей из легких сплавов [3, 50]. Подогревающие импульсы тока I
П
и I
Д
можно использовать в сочетании с любой циклограммой изменения усилия сжатия электродов (рис 1.6, з
). Для достижения указанных выше целей иногда используют цикл (рис. 1.6, и
), в котором до импульса сварочного тока и после его окончания, осуществляют колебания электродов с инфразвуковой, звуковой [51], или ультразвуковой [52, 53] частотой.
В ряде случаев, например, при сварке деталей из жаропрочных материалом, рационально применять даже цикл (рис 1.6, к
), в котором усилие сжатия электродов F
Э
во время t
СВ
действия импульса сварочного тока уменьшают по определенной программе [54].
Кроме того, программированное изменение усилия сжатия электродов во время импульса сварочного тока позволяет повысить и энергетическую эффективность процесса КТС, а также его устойчивость против образования непроваров. Для достижения этих целей применяют циклы, в которых усилие сжатия электродов в процессе сварки изменяют. Причем, в процессе КТС усилие сжатия электродов чаще всего увеличивают от начального до конечного его значения. И осуществляют это ступенчато (рис. 1.6, л
) или монотонно (рис 1.5, м
) [10, 15, 18, 54...58].
Нагрев металла в зоне сварки осуществляют обычно одним импульсом сварочного тока и регулируют изменением его силы и длительности. Форму импульса тока при сварке на серийных машинах, как правило, не регулируют. Характер его нарастания и спада определяется естественным модулированием, зависящим от индуктивности вторичных контуров сварочных машин (рис 1.2). Это обусловлено ограниченными возможностями изменения силы сварочного тока путем фазового его регулирования при небольшой длительности импульсов и промышленной частоте тока 50 Гц. Только при сварке сталей на машинах переменного тока, иногда представляется возможным регулировать нарастание и спад импульса тока, а также регулировать спад тока при сварке деталей из легких сплавов, на низкочастотных машинах и машинах постоянного тока [2…4, 7...19].
1.2.3.
Контактная точеная сварка с обжатием периферийной зоны
соединений
Выше было показано, что традиционные способы КТС отличаются весьма большим многообразием используемых технологических приемов. Несмотря на это уровень дефектности сварных точек в серийном производстве даже при изготовлении узлов летательных аппаратов, достигает
5 % [32]. В условиях точечной сварки в обычных отраслях машиностроения он еще выше. Это говорит о том, что традиционные способы практически исчерпали свои технологические возможности. В этой связи весьма перспективным направлением развития технологии КТС является совершенствование и разработка новых способов точечной сварки с целенаправленным программированным воздействием на процесс формирования соединения. Одним из таких перспективных способов КТС является так называемая «контактная точечная сварка с обжатием периферийной зоны соединений» [3, 16].
При контактной точечной сварке с обжатием периферийной зоны соединений (рис. 1.7) свариваемые детали сжимают токопроводящими электродами усилием F
Э
и прикладывают вокруг них обжимными втулками автономное дополнительное сжимающее усилие F
0
(усилие обжатия).
В основе способов КТС с обжатием периферийной зоны соединений лежит изобретенный в 1930 г. П. Н. Львовым специальный электрод (рис. 1.8) [59]. Этот электрод (рис. 1.8, а
) содержит собственно токопроводящий электрод 2 и концентрично расположенный вокруг него силовой пуансон (обжимную втулку) 3, соединенный с приводом обжатия, которым служит упругий элемент 7.
Данное электродное устройство позволяет общее усилие сжатия деталей F
СВ
, которое задают приводом сварочной машины, разделить на две его составляющих. Одна его часть F
Э
(см. рис. 1.7, а
), как и при традиционных способах КТС, сжимает свариваемые детали посредством токопроводящих электродов в центральной части зоны формирования соединения (над ядром). Другая же его часть F
0
— посредством силовых пунсонов обжимает свариваемые детали в периферийной ее области (в области уплотняющего пояска). Таким образом, в силу конструктивных особенностей данное электродное устройство предопределяет основные признаки способа КТС с обжатием периферийной зоны соединений в области уплотняющего пояска [16, 60], при котором в любой момент соотношение усилий определяется следующей зависимостью (см. рис. 1.7, б
):
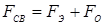 . (1.6) . (1.6)
Проведенные за истекший период исследования показали высокую эффективность данного способа КТС по предотвращению выплесков и непроваров. Устойчивость процесса формирования соединения против образования выплесков повышается вследствие увеличения усилия сжатия деталей в области уплотняющего пояска [3, 16, 61]. Устойчивость же процесса сварки против образования непроваров можно повысить вследствие уменьшения вероятности образования выплесков при обжатии периферии соединения, проводя сварку на более жестких режимах [3, 16]. Кроме того, обжатие периферийной зоны соединений позволяет предотвращать дефекты усадочного характера (трещины, поры) [62], уменьшить глубину вмятин от электродов, зазоры между деталями в нахлестке и ее ширину [3, 16]. Применение этого способа КТС позволяет также увеличить прочность соединений, в том числе и динамическую, путем прогиба деталей в направлении оси электродов до начала импульса тока [63], обжатием во время его действия [16] или же проковкой периферии соединения на стадии охлаждения зоны сварки [64].
Наряду с выявлением технологических возможностей способа КТС с обжатием периферийной зоны соединений совершенствовались и конструкции электродных устройств для их осуществления. В результате был разработан ряд электродных устройств (рис 1.8), отличающихся в основном конструкциями приводов усилий на электроде или обжимной втулке.
Весьма привлекательной, позволяющей получить практически любую программу изменения усилия обжатия F0
, кажется конструкция устройства (рис. 1.8, б
) с электромагнитным приводом 6 усилия на обжимной втулке 3 [65]. Однако в нем усилие F0
зависит от осевого смещения втулки 3 относительно токопроводящего электрода 2,
что уменьшает стабильность усилия обжатия вследствие отклонений глубины вдавливания электрода в поверхности детали 1. Кроме того, при современных токопроводящих материалах электромагнитный привод должен иметь катушку значительных геометрических размеров, чтобы получить требуемые усилия обжатия (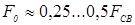 ). Это затрудняет использование данного электродного устройства в практике КТС. ). Это затрудняет использование данного электродного устройства в практике КТС.
Следует отметить, что конструкции электродных устройств с упругими элементами в приводах усилия на обжимной втулке F0
(рис. 1.8, а
) или усилия на токопроводящем электроде FЭ
(рис. 1.8, в
) проработаны более глубоко. В них требуемые усилия обеспечиваются путем деформации упругих элементов 7 или 8 на заранее установленную величину h
при сжатии деталей. В первой конструкции таких электродных устройств [59, 66…68] усилие FЭ
на электроде 2 задается приводом машины посредством силового элемента 5,
а на обжимной втулке 3 — упругим элементом 7 (рис. 1.8, а
). Во второй же конструкции (рис. 1.8, в
) наоборот — привод машины 5 задает усилие обжатия F0
на обжимной втулке, а на токопроводящем электроде 2 усилие FЭ
задается упругим элементом 8 [69].
Несмотря на некоторые конструктивные различия, эти электродные устройства имеют одинаковые преимущества (относительно простую конструкцию и малые габаритные размеры) и общий недостаток — усилия F0
(рис. 1.8, а
) или FЭ
(см. рис. 1.8, в
) также зависит от перемещения обжимной втулки 3 относительно токопроводящего электрода 2. Это приводит к их отклонениям при сварке вследствие вдавливания токопроводящих электродов 2 в поверхности деталей 1. Кроме того, конструкции этих электродов не вполне удовлетворяют требованиям по технологичности, так как очень трудоемка настройка электрода на требуемое при сварке усилие обжатия вследствие высокой жесткости упругого элемента.
По-видимому, их использование возможно при сварке деталей малых толщин, когда величины усилий FЭ
и F0
, а следовательно и жесткость упругих элементов, а также взаимные осевые смещения электрода и втулки в процессе формирования соединений относительно малы. В этом случае отклонения силового воздействия на детали от заданных значений в меньшей степени влияет на качественные показатели соединений ввиду кратковременности цикла сварки и инерционности механических процессов в силовых приводах сварочных машин.
Наиболее приемлемым для сварки деталей малых, средних и больших толщин является электродное устройство с гидравлическим приводом [70]. В нем (рис. 1.8, г
) усилие F0
на обжимной втулке 3 задается приводом машины посредством силового элемента 5, а усилие FЭ
на токопроводящем электроде 2 — гидроприводом 9. Достоинством данной конструкции является то, что гидропривод можно расположить в верхней части электрододержателя 4 и уменьшить габариты рабочей части устройства. Но это усложняет подвод тока к подвижному электрододержателю 4. Такой привод позволяет получать стабильные усилия, независящие от осевого смещения обжимной втулки относительно электрода. Здесь следует отметить, что для него не разработаны специализированные устройства, которые задавали бы требуемое для КТС давление рабочей жидкости.
Широкому использованию в условиях реального производства способов КТС с обжатием периферийной зоны соединения, несмотря на их высокую технологическую эффективность, препятствуют рабочие характеристики электродных устройств, в первую очередь относительно низкая стойкость токопроводящего электрода 2. Это обусловлено тем, что обжатие деталей в области уплотняющего пояска диаметром dП
вызывает необходимость уменьшения внутреннего диаметра dВВ
обжимной втулки 3 и, следовательно, наружного диаметра DЭ
рабочей части электрода 2 до значений, близких к диаметру ядра dЯ
, которые значительно меньше стандартных. Поэтому увеличивается уровень сжимающих напряжений в рабочей части электрода 2,
ухудшается температурный режим его работы из-за повышения плотности сварочного тока и затрудненного охлаждения. В результате интенсифицируются пластические деформации в приконтактных объемах металла электродов и процессы взаимодействия металлов в контактах электрод-деталь.
Таким образом, формирование точечных сварных соединений как при традиционных способах сварки, так и при сварке с обжатием периферийной зоны соединений происходит по единой схеме и способы КТС различаются между собой в основном количественными параметрами термодеформационных процессов, протекающих в зоне сварки на разных этапах формирования соединения, которые определяются внешним энергетическим и силовым воздействием на металл зоны сварки (параметрами режима). Процесс КТС с обжатием периферийной зоны соединений предоставляет больше возможностей силового воздействия на зону сварки и потому весьма перспективен в технологическом плане.
1.3
. Параметры режимов — факторы регулирования процесса точечной сварки
Режимы точечной сварки конкретного соединения (марка металла и сочетание толщин деталей) определяются совокупностью параметров, из которых основными являются: сила I
СВ
импульса сварочного тока; длительность t
СВ
импульса сварочного тока (время сварки); усилие сжатия электродов F
СВ
; форма и размеры рабочих поверхностей электродов (d
Э
— при плоской и R
Э
— при сферической).
Режимы КТС принято подразделять на два типа: «жесткие» режимы, характеризующиеся малым t
СВ
и большим I
СВ
, и «мягкие» режимы с относительно большим t
СВ
и малым I
СВ
[2…4, 7...11, 13…17].
Известны предложения, по которым можно количественно оценивать жесткость режимов, например, по отношению отдельных параметров режима КТС: 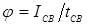 , по показателям, представляющим собой различные интерпретации критерия Фурье [71, 72], среди которых наиболее распространен критерий А.С. Гельмана [10]: , по показателям, представляющим собой различные интерпретации критерия Фурье [71, 72], среди которых наиболее распространен критерий А.С. Гельмана [10]:
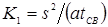 , (1.7) , (1.7)
где s
— толщина свариваемых деталей; a
— коэффициент температуропроводности их материала;
а также по критерию технологического подобия [13]:
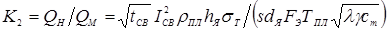 , (1.8) , (1.8)
где Q
Н
— энергия, выделившаяся в объеме ядра; Q
М
— тепловые потери в массу свариваемых деталей; ρПЛ
— удельное электрическое сопротивление металла при температуре плавления ТПЛ
; d
Я
и h
Я
— диаметр и высота ядра расплавленного металла; σТ
—
предел текучести свариваемого металла в холодном состоянии; F
Э
—
усилие сжатия электродов. a
— коэффициент теплопроводности; γ
— плотность; cm
— удельная массовая теплоемкость.
При увеличении жесткости режимов увеличивается мощность источников теплоты и уменьшается роль теплоотвода в формировании температурного поля, вследствие чего увеличивается проплавление деталей. Вместе с этим возрастает и склонность процесса КТС к образованию выплесков. Поэтому при сварке на жестких режимах применяют большие усилия сжатия электродов, чем при сварке на мягких режимах. [3, 15]
Энергетическое и силовое воздействие на металл зоны формирования соединения при КТС обеспечивается конкретным сочетанием параметров режима. При этом изменение каждого из них приводит к интенсификации или, наоборот, подавлению отдельных термодеформационных процессов, протекающих на отдельных или всех этапах процесса сварки. В конечном итоге, это сказывается на устойчивости процесса формирования соединения и размерах ядра (рис. 1.9).
1.3.1.
Время сварки
В теории и практике КТС под термином «время сварки» понимается длительность t
СВ
импульса сварочного тока I
СВ
. При неизменной силе сварочного тока I
СВ
время сварки t
СВ
определяет количество теплоты Q
ЭЭ
, которое в этом случае выделяется в зоне формирования соединения пропорционально длительности импульса тока. Поэтому с увеличением времени сварки растет проплавление деталей А
и, в большей мере, диаметр d
Я
ядра расплавленного металла (рис. 1.9, а
).
Вместе с этим при увеличении t
СВ
возрастает и влияние теплоотвода на характер распределения температуры в зоне сварки, которое сопровождается большим разогревом деталей и увеличением деформаций. Кроме того, при увеличении t
СВ
все большая часть Q
ЭЭ
отводится в окружающий зону сварки металл Q
2
и в электроды Q
3
, что приводит к уменьшению энергетического КПД процесса КТС (см. п. 2.4). При некотором t
СВ
может наступить состояние теплового равновесия, при котором вся выделившаяся теплота отводится из зоны сварки, то есть 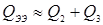 , а количество теплоты в зоне сварки Q
1
не изменяется. Это приводит к тому, что ядро (А
и d
Я
) расплавленного металла перестаёт расти. Следовательно, увеличение t
СВ
дальше момента теплового равновесия и энергетически, и технологически нецелесообразно потому, что ни к чему кроме увеличения разогрева деталей не приводит. , а количество теплоты в зоне сварки Q
1
не изменяется. Это приводит к тому, что ядро (А
и d
Я
) расплавленного металла перестаёт расти. Следовательно, увеличение t
СВ
дальше момента теплового равновесия и энергетически, и технологически нецелесообразно потому, что ни к чему кроме увеличения разогрева деталей не приводит.
1.3.2.
Сила сварочного тока
Сила сварочного тока I
СВ
является одним из основных параметров режима КТС, поскольку при неизменной длительности его импульса t
СВ
определяет не только количество энергии, выделяющейся в зоне сварки, но и, что наиболее важно для процесса формирования соединения, градиент её увеличения по времени. Вследствие этого именно сила сварочного тока определяет скорость нагрева металла в зоне формирования соединения.
В ряде случаев сварки, в особенности при малом расстоянии (шаге) между сварными точками, сила сварочного тока I
СВ
, т. е. тока который протекает через зону формирования соединения и определяет тепловыделение в ней, и сила тока, который протекает во вторичном контуре сварочной машины I
2
, могут различаться между собой. Причиной этого может являться ток шунтирования I
Ш
, который протекает вне зоны сварки, в частности, через ранее сваренные точки (рис. 1.10) или контакты деталь-деталь, расположенные вне зоны формирования соединения, например, при точечной сварке с обжатием периферийной зоны соединения. Таким образом, значение вторичного тока сварочной машины I
2
зависит от сварочного тока I
СВ
и тока шунтирования I
Ш
:
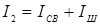 (1.9) (1.9)
Ток шунтирования
. Зона проводимости тока шунтирования представляет собой электрическую цепь с сопротивлением r
Ш
, параллельную электрической цепи зоны сварки с сопротивлением r
ЭЭ
. Вследствие этого силу тока шунтирования можно вычислить по формуле [3]:
 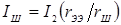 , (1.10) , (1.10)
где 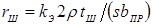 — электрическое сопротивление шунтирующей ветви; ρ
— удельное электрическое сопротивление металла свариваемых деталей; — электрическое сопротивление шунтирующей ветви; ρ
— удельное электрическое сопротивление металла свариваемых деталей;
k
Э
— коэффициент (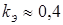 ); );
s
— толщина детали; b
ПР
— ширина шунта, приведенная с учётом растекания тока и равная 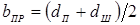 ; d
П
и d
Ш
— диаметры уплотняющего пояска и шунтирующего контакта соответственно. ; d
П
и d
Ш
— диаметры уплотняющего пояска и шунтирующего контакта соответственно.
Сварочный ток.
От силы сварочного тока размеры ядра расплавленного металла зависят в наибольшей степени (рис. 1.9, б
). С увеличением I
СВ
проплавление деталей А
и диаметр ядра d
Я
растут почти прямо пропорционально изменению I
СВ
.
Силу сварочного тока I
СВ
, по той же причине, что и t
СВ
, пока определяют только ориентировочно по технологическим рекомендациям или по эмпирическим зависимостям [2…4, 7…11, 13, 15…17]. В отличие от t
СВ
, для определения которого расчетные методики вообще отсутствуют, для определения I
СВ
в теории КТС предложено много самых разнообразных зависимостей, к сожалению, не отличающихся высокой точностью и универсальностью, например, зависимостей следующего вида [73...76]:
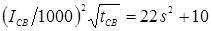 ; ; 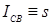 ; ;
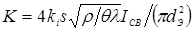 ; ; 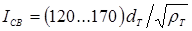 , ,
где s
— толщина деталей; d
Э
— диаметр рабочей поверхности электрода;
ki
– опытный коэффициент; θ
— температура плавления (с учетом скрытой теплоты плавления); ρ
и λ
— удельное электрическое сопротивление и коэффициент теплопроводности; d
Т
— диаметр ядра (см); ρТ
— удельное электрическое сопротивление металла в момент его плавления (мкОм/см).
В практике традиционных способов КТС для сварочного импульса, длительностью t
СВ
, усредненную силу сварочного тока I
СВ
чаще всего приближенно рассчитывают по следующей зависимости, которая получена из общеизвестного закона Джоуля – Ленца [8…11, 16]:
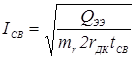 , [3] (1.11) , [3] (1.11)
где Q
ЭЭ
— количество теплоты, выделяющееся в зоне сварки, которое требуется для образования сварного соединения заданных размеров (величина Q
ЭЭ
определяется по уравнению теплового баланса (см. ниже п. 2.4.3));
mr
— коэффициент, который учитывает изменение сопротивления зоны сварки r
ЭЭ
в процессе формирования соединения (для низкоуглеродистых сталей он равен  , для алюминиевых и магниевых сплавов — , для алюминиевых и магниевых сплавов — 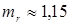 , для коррозионно-стойких сталей — , для коррозионно-стойких сталей — 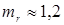 , для сплавов титана — , для сплавов титана — 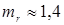 ; r
ДК
— электрическое сопротивление деталей в конце сварки (определение r
ДК
см. ниже п. 2.3.3). ; r
ДК
— электрическое сопротивление деталей в конце сварки (определение r
ДК
см. ниже п. 2.3.3).
1.3.3
. Усилие сжатия электродов
Усилие сжатия электродов (сварочное усилие) F
СВ
— один из важнейших параметров режима КТС, который оказывает влияние на все основные процессы, ответственные за формирование соединения, в частности, на микро- и макропластические деформации, на выделение и перераспределение теплоты, на охлаждение металла в зоне сварки и кристаллизацию его в ядре.
С увеличением F
СВ
увеличиваются пластические деформации металла в зоне сварки и площади контактов, уменьшается плотность тока в них, уменьшается электрическое сопротивление участка электрод–электрод и стабилизируется его величина. Поэтому при постоянстве остальных параметров режима увеличение F
СВ
вызывает уменьшение размеров ядра
(рис. 1.9, в
), прочности сварных точек при одновременном понижении и их стабильности. Если же увеличение F
СВ
сопровождается таким увеличением I
СВ
или t
СВ
, что размеры ядра остаются неизменными, то с ростом величины сварочного усилия прочность точек возрастает и становится более стабильной. [10, 77…79]
Как и сварочный ток, сварочное усилие определяют в основном по эмпирическим зависимостям, предложенным для приближенного расчета или пересчета сварочного усилия и основанным на подобии процессов КТС. Методики пересчета F
СВ
исходят из подобия процессов формирования соединений при сварке деталей из одних и тех же металлов разных толщин. Все они, к сожалению, также не отличаются ни высокой точностью, ни универсальностью. В частности, для пересчетов и расчетов F
СВ
предложены следующие зависимости [10, 15, 73, 80...82]:
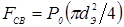 ; ; 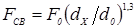 ; ;
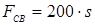 ; ; 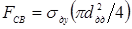 ; ; ; ;
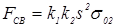 ; ; 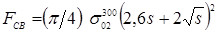 , ,
где F
0
— удельное сварочное усилие; d
Я
— диаметр ядра расплавленного металла с известным F
СВ
; d
Я
— диаметр ядра, для которого рассчитывают F
СВ
; P
0
— удельное давление, определяемое экспериментально; d
Э
— диаметр рабочей поверхности электрода; s
— толщина деталей; k
1
и k
2
—коэффициенты, учитывающие сопротивление деформации металла и конструктивную жесткость изделия; σ
02
— условный предел текучести свариваемого металла при нормальной температуре; 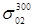 — предел текучести свариваемого металла при температуре 300о
С; — предел текучести свариваемого металла при температуре 300о
С;
1.3.4.
Форма и размеры рабочих поверхностей электродов
Форма и размеры рабочих поверхностей электродов (рис. 1.3: d
Э
— при плоской и R
Э
— при сферической), контактирующие со свариваемыми деталями, существенно влияют на качество получаемых сварных соединений. Увеличение площади контакта электрод–деталь, например, из-за износа рабочей поверхности электродов приводят к уменьшению плотности тока и давления в зоне сварки, а, следовательно, к уменьшению размеров ядра и снижению качества готовых точечных соединений (рис. 1.9, г
).
Применяемая форма электродов зависит от свойств материала свариваемых деталей. Так, например, для сварки титановых, алюминиевых и магниевых сплавов, как правило, применяют электроды со сферическими рабочими поверхностями. Стали же, в основном сваривают электродами с плоской рабочей поверхностью.
Размеры рабочих поверхностей электродов в большинстве случаев выбирают исходя из толщины свариваемых деталей.
Радиус сферы электрода R
Э
определяют, ориентируясь на конечный диаметр отпечатка и допустимую глубину вмятины, которая не должна превышать 10 % от толщины детали [83]. Исходя из этого условия предложены следующие зависимости для определения минимального R
Э
MIN
и максимального R
Э
MAX
радиусов рабочих поверхностей электродов в зависимости от толщины s
свариваемых деталей [84]:
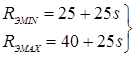 . .
Диаметры плоских рабочих поверхностей электродов выбирают с учетом диаметров ядра, которые в свою очередь задают по толщине деталей. Значения d
Э
определяют по следующим зависимостям [85, 86]:
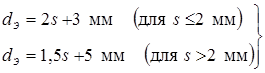 , , 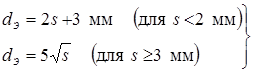 . .
Однако в практике КТС размеры рабочих поверхностей электродов обычно не рассчитывают. Значения d
Э
и R
Э
, как правило, выбирают по технологическим рекомендациям (табл. 1.2), в которых они близки к значениям, рассчитанным по приведенным выше зависимостям. Окончательные значения t
СВ
, I
СВ
, F
СВ
и R
Э
или d
Э
определяют и корректируют на образцах технологической пробы [3, 15].
 Поскольку приемлемые по точности для практики КТС методики оптимизации режимов сварки (сочетаний I
СВ
, t
СВ
и F
СВ
) пока не разработаны параметры одного из них, как правило, время сварки t
СВ
, определяют ориентировочно по технологическим рекомендациям, основанным на экспериментальных исследованиях процессов КТС и опыте их практического использования в промышленности. После этого для принятого значения t
СВ
по приближенным методикам, определяют силу I
СВ
и усилие сжатия электродов F
СВ
[2…4, 7…11, 13, 15…17]. Поскольку приемлемые по точности для практики КТС методики оптимизации режимов сварки (сочетаний I
СВ
, t
СВ
и F
СВ
) пока не разработаны параметры одного из них, как правило, время сварки t
СВ
, определяют ориентировочно по технологическим рекомендациям, основанным на экспериментальных исследованиях процессов КТС и опыте их практического использования в промышленности. После этого для принятого значения t
СВ
по приближенным методикам, определяют силу I
СВ
и усилие сжатия электродов F
СВ
[2…4, 7…11, 13, 15…17].
Таким образом, существующие расчетные методики определения основных параметров режима весьма не совершенны. У них можно отметить общий недостаток — они не отражают физической сущности процессов, протекающих при КТС, не являются универсальными и применимы только для тех ограниченных областей толщин и металлов, на основании результатов исследований которых они и получены. Они не могут использоваться для решения задач, связанных с программированным изменением термодеформационных процессов, протекающих при формировании точечных сварных соединений.
1.3.5
. Критерии подобия для определения режимов сварки
Выше, в п. 1.2.1 отмечалось, что, несмотря на изменение значимости влияния на отдельных этапах формирования соединения каждого из основных термодеформационных процессов, протекающих в зоне сварки, на процесс сварки общая схема формирования соединения происходит по единой схеме. При этом исследователями процесса КТС давно было подмечено, что при сварке деталей разных толщин параметры основных термодеформационных процессов изменяются по одинаковым закономерностям, то есть подобно. На основании результатов экспериментальных исследований рядом исследователей были разработаны основы теории подобия процессов КТС и предложен ряд критериев — безразмерных величин, математически описывающих это подобие [3, 4, 13, 16, 74…76, 87, 88].
Физические процессы подобны, если они описываются одним и тем же дифференциальным уравнением и имеют подобные начальные и граничные условия. Подобие выражается в том, что при определенных условиях в сходственных точках тел, т. е. в точках с одной и той же относительной координатой, например, в точках, расположенных в середине или на краю листа, достигаются одни и те же значения переменных параметров, в частности температуры или деформации.
По этим критериям, определяемым по моделям, рассчитывают масштабные коэффициенты для определения параметров процесса. Процессы точечной свирки деталей разной толщины могут быть подобны при равенстве критериев подобия, например, следующих [16]:
- критерий геометрического подобия
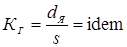 ; (1.12) ; (1.12)
- критерий гомохронности (подобия по времени — критерий Фурье)
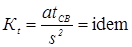 ; (1.13) ; (1.13)
- критерий подобия тепловыделения
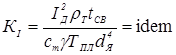 ; (1.14) ; (1.14)
- критерий подобия пластических деформаций
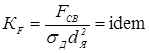 , (1.15) , (1.15)
где s
— толщина деталей; d
Я
— диаметр ядра; I
Д
и t
СВ
— действующее значение сварочного тока и время его протекания; F
СВ
— сварочное усилие; с
m
, γ, ТПЛ
, и σД
— соответственно, массовая теплоёмкость, плотность, температура плавления и сопротивление деформации свариваемого металла.
Применение теории подобия позволяет по одному экспериментально определенному режиму с использованием критериев подобия рассчитать параметры режима сварки деталей других толщин. Значения критериев определяют по единичным опытам [3, 4, 15].
Однако часто расчеты по зависимостям (1.12…1.15) приводят к значительным погрешностям. Обусловлено это прежде всего тем, что в практике сварки не соблюдается критерий геометрического подобия
(см. табл. 1.1). Поэтому для приближенной оценки параметров режима в относительно малом диапазоне толщин (1…4 мм) пользуются рядом других, в основном эмпирических, соотношений, аналогичных по структуре указанным выше, например, [15].
Таким образом, различие способов точечной сварки определяется внешним силовым энергетическим и силовым воздействием на зону формирования соединения. Это воздействие влияет на параметры термодеформационных процессов, протекающих в зоне сварки, которые рассмотрены ниже, и определяющих качество получаемых соединений.
2. основные Процессы, протекающие при
контактной точечной сварке
Сварная точка является результатом сложных термодеформационных процессов, протекающих в зоне формирования соединения в течение цикла сварки. Некоторые из этих процессов протекают последовательно, а некоторые и параллельно. Параметры последних зависят не только от внешнего энергетического и силового воздействия на металла в зоне сварки, но и от сложного их взаимного влияния. Ниже рассмотрены закономерности протекания термодеформационных процессов, оказывающих наиболее значимое влияние на конечный результат сварки.
2.1.
Сближение свариваемых деталей
Технологической операцией, которая первой выполняется в любом цикле КТС, является сближение свариваемых поверхностей до соприкосновения, поскольку собранные для сварки детали практически никогда плотно не прилегают между собой. Обусловлено это тем, что между свариваемыми деталями всегда имеются зазоры. Они являются следствием либо искривления деталей при выполнении технологических операций, которые предшествуют сварке, либо дефектов сборки деталей перед сваркой, или деформаций деталей непосредственно в процессе сварки предшествующих точек [3, 10, 11, 14…16].
В сближении свариваемых деталей до соприкосновения следует выделить два фактора, которые оказывают значимое влияние как на формирование начальных контактов, так и на процесс сварки в целом: геометрический фактор, который проявляется в искривлении деталей при их деформировании в процессе сближения, и силовой фактор, следствием влияния которого является отклонение усилия сжатия в контакте деталь–деталь от усилия сжатия электродов [14…16, 89… 91].
2.1.1.
Деформирование свариваемых деталей при их сближении
Реальная деформация свариваемых деталей в процессе их сближения (рис. 2.1) представляет сложное сочетание признаков, близких как к чистому изгибу пластины (рис. 2.1, а
), так и к чистому ее прогибу по типу мембраны (рис. 2.1, д
). При этом переход от первого ее состояния ко второму происходит плавно (рис. 2.1, б...г
) по мере увеличения расстояния u
от кромки нахлестки до центра электродов. Причем этот переход происходит тем быстрее (при меньшей величине u
), чем меньше расстояние t
Ш
до точек опоры вдоль нахлестки.
Наличие зазоров между деталями и операции их сближения до соприкосновения, которое приводит к сложному искривлению деталей, существенно изменяет как распределение напряжений в контактах, так и характер, протекающих в них микро- и макродеформаций. При отсутствии зазора (рис. 1.5, этап
1) можно допустить, что в контакте деталь-деталь деформируются две плоские поверхности, а при большом расстоянии от кромки листов до электродов (рис. 2.1, д
) — две сферические поверхности. В практике же сварки в основном встречаются промежуточные более сложные, несимметричные виды деформирования свариваемых деталей при их сближении (рис. 2.1, б...в
) [91].

Сложное искривление деталей при их сближении приводит как к уменьшению размеров ядра, так и к искажению его формы (рис. 2.2). Основной причиной этого является изменение формы контакта (рис. 2.3).
Исследования влияния величины зазора δ
, шага между точками t
=2
t
Ш
, расстояния от кромки нахлестки u
и F
СВ
на величину и форму начального контакта выявили сложную их зависимость от перечисленных выше факторов. При этом измерение контурной площади контакта производили по известной методике угольных плёнок [92…94].
 Форма контакта оценивалась коэффициентом формы k
Ф
, который характеризует отклонение формы контакта от окружности, т. е. эллипсоидность контакта. В этом случае реальный контакт принимается в форме эллипса, в котором взаимно перпендикулярные наибольшее и наименьшие значения диаметров контакта принимаются равными наибольшей 2а
и наименьшей 2
b
оси эллипса (рис. 2.3). Эти оси сравниваются с диаметром d
0
условной окружности, площадь которой равна площади эллипса. В этом случае коэффициент формы контакта определяется по зависимости Форма контакта оценивалась коэффициентом формы k
Ф
, который характеризует отклонение формы контакта от окружности, т. е. эллипсоидность контакта. В этом случае реальный контакт принимается в форме эллипса, в котором взаимно перпендикулярные наибольшее и наименьшие значения диаметров контакта принимаются равными наибольшей 2а
и наименьшей 2
b
оси эллипса (рис. 2.3). Эти оси сравниваются с диаметром d
0
условной окружности, площадь которой равна площади эллипса. В этом случае коэффициент формы контакта определяется по зависимости
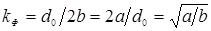 . (2.1) . (2.1)
Очевидно, что коэффициент формы контакта показывает относительное отклонение формы контакта от окружности. Во всех случаях прогиба деталей при наличии зазора между ними контакт вытягивается вдоль оси, перпендикулярной линии края нахлестки (рис. 2.4). Увеличение расстояния от края листа u
при постоянстве остальных параметров приводит к уменьшению контурной площади сварочного контакта S
К
относительно ее величины при отсутствии зазора S
0
(S
К
/S
0
) и уменьшению коэффициента её формы k
Ф
, т. е. его эллипсоидности
(рис. 2.4, а
). Это объясняется плавным переходом вида деформации детали
 |
от изгиба к прогибу по типу мембраны. Увеличение расстояния между точками t
приводит к увеличению контурной площади контакта и увеличению искажения его формы (рис. 2.4, б
). Причем увеличение k
Ф
происходит до некоторого значения t
, зависящего от величины зазора δ
, а затем с увеличением t
эллипсоидность контакта k
Ф
уменьшается. Это также объясняется изменением вида деформации деталей в контакте. Так, увеличение S
К
при уменьшении u
и увеличении t
можно объяснить увеличением усилия сжатия F
в площади контакта, так как усилие, которое затрачивается на деформацию деталей при их сближении при таком изменении t
и u
уменьшается. Уменьшение же k
Ф
при увеличении u
объясняется переходом от изгиба детали в месте сжатия к ее прогибу по типу мембраны. Начальное увеличение k
Ф
при увеличении t
, наоборот, обусловлено переходом от прогиба детали по типу мембраны к ее изгибу, а дальнейшее уменьшение k
Ф
обусловлено уменьшением искривления деталей при увеличении t
.
При увеличении зазора δ
(рис. 2.4, в
) площадь контакта S
К
вначале уменьшается, что можно объяснить уменьшением усилия в площади контакта, а затем резко увеличивается вплоть до первоначальных размеров. Последнее обусловлено тем, что при достижении зазором некоторой величины δ
, которое зависит от конкретного сочетания значений t
и u
, происходит резкий переход от изгиба детали к её прогибу по типу мембраны. Дальнейшее же увеличение забора приводит к монотонному уменьшению площади контакта, причиной чего является уменьшение усилия сжатия в площади контакта. Эллипсоидность контакта при увеличении зазора вначале увеличивается, а затем монотонно уменьшается. Это объясняется описанным выше изменением вида деформации деталей. Причем, положение точек перегиба (δ =
2…2,5 мм
, и t
=
100…125 мм
) на кривых изменения S
К
/S
0
и k
Ф
не является постоянным, а изменяется при изменении сочетаний значений t
, δ
и F
.
Увеличение усилия F
сжатия деталей (рис. 2.4, г
) во всех случаях приводит к монотонному увеличению площади контакта деталь–деталь, обусловленному увеличением давления в его площади. При этом монотонно уменьшается и искажение формы контакта.
Таким образом, контурная площадь контакта деталь–деталь всегда уменьшается при наличии зазора между ними, а искажение её формы зависит от конкретных сочетаний расстояния между точками и расстояния до кромки нахлёстки, а также значений зазора и усилия сжатия деталей. При величинах зазоров, встречающихся в практике КТС, искажение формы контакта однозначно увеличивается с увеличением расстояния между точками и уменьшением расстояния до кромки нахлёстки.
2.1.2.
Влияние деформирования деталей на усилие сжатия
в свариваемом контакте
Из силовой схемы двусторонней точечной сварки (см. рис.1.1) следует, что усилие сжатия в контактах электрод–деталь и деталь–деталь равны усилию сжатия деталей электродами. Однако это всегда справедливо только для контактов электрод–деталь. Что же касается усилия сжатия в контакте деталь–деталь, то во многих случаях сварки оно отличается от усилия сжатия деталей электродами. И причиной этого являются зазоры, которые приводят к тому, что некоторая часть усилия сжатия электродов (в дальнейшем будем обозначать ее — F
Д
) затрачивается на деформирование свариваемых деталей при их сближении до соприкосновения. Вследствие этого усилие в площади свариваемого контакта FC
меньше усилия сжатия электродов F
Э
на величину F
Д
.
Оценка величины отклонения FC
от F
Э
важна не только для формирования начальных контактов, а для всего процесса формирования соединений при КТС. Так, устойчивость процесса формирования соединений против образования выплесков при традиционных способах сварки связывают, в частности, с наличием зазоров между свариваемыми деталями. При этом основной причиной образования выплесков при наличии зазоров считают значительное уменьшение усилия сжатия деталей в свариваемом контакте, несмотря на то, что величину зазоров при КТС жестко регламентируют (табл. 2.1) [10, 11, 91, 95].
Очевидно, что такие допуски, в особенности при сборке крупногабаритных изделий, например, при сборке обечаек диаметром в несколько метров с перегородками или набором, выдержать весьма проблематично. Такие ограничения, несомненно, удорожают технологию сборки и сварки. При этом, конкретные результаты исследований, которые бы установили степень влияния F
Д
на отклонение F
С
от F
Э
в процессе КТС и тем самым обосновали бы такое объяснение причин повышенной склонности процесса сварки к образованию выплесков и такие жесткие допуски на величину зазоров, очень немногочисленны.
Таблица 2.1
Допускаемая величина зазоров при КТС
| Длина
участка
(мм)
|
Толщина более тонкой детали — s
, мм
|
| 0,3 ≤ s < 1
|
1 ≤ s < 1,5
|
1,5 ≤ s < 2,5
|
s ≥ 2,5
|
| Допускаемая величина зазоров δ
, мм
|
| 100
|
0,5
|
0,4
|
0,3
|
0,2
|
| 200
|
1,0
|
0,8
|
0,6
|
0,4
|
| 300
|
1,5
|
1,2
|
0,9
|
0,6
|
По-видимому, наименее трудоемким было бы расчетное определение величины F
Д
, например, решением известного уравнения С. Жермен – Лагранжа, описывающего прогиб пластинки [96],
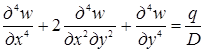 , (2.2) , (2.2)
где w
– величина прогиба пластинки; x
и y
– координаты; q
– внешняя нагрузка; D
– цилиндрическая жесткость листа, равная
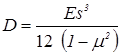 ; ;
здесь E
– модуль упругости; s
– толщина листа; μ
– коэффициент Пуассона.
Однако точное решение уравнения (2.2) даже для идеализированных граничных условий представляет большие трудности и, например, по мнению автора работы [97], не всегда оправдано. Кроме того, аналитическое определение величины F
Д
затрудняется еще и тем, что схема закрепления деталей при точечной сварке, например, посредством уже сваренных точек весьма неопределенна. Она не имеет близких аналогов среди идеализированных схем закрепления пластинок в известных [96…98] аналитических решениях этой задачи.
В экспериментальных исследованиях силового взаимодействия деталей при наличии зазоров [91, 99, 100], величина усилия F
Д
, необходимая для сближения свариваемых деталей, определялась как функция комплексного влияния ряда технологических факторов точечной сварки (рис. 2.5):
F
Д
= F(t, t*
, u, α,
δ
, s, R
Э
),
где t
–
расстояние между сваренными точками; t
*
–
расстояние до соседних сваренных точек; u
–
расстояние от кромки листа до центра свариваемой точки, которое, как правило, равно половине ширины В
нахлестки; α
–
угол раскрытия зазора в нахлестке; δ –
величина зазора в месте сварки; s
–
толщина деталей; R
Э
–
радиус сферы рабочей поверхности электродов. Так как при точечной сварке зона нагрева ограничена и составляет относительно небольшую часть зоны упругопластической и упругой деформации деталей при их сближении, то считается, что усилие прогиба деталей в процессе сварки не изменяется [95]. Такое допущение позволяет проводить эксперименты по определению F
Д
на холодных образцах вне сварочной машины.
Моделирование зазоров производилось по известной методике, показанной на (рис. 2.6). В этом случае образцы 1 в местах имитации уже сваренных точек сжимались специальными струбцинами 2 усилием 2…8 кН, которое вполне обеспечивало жесткое закрепление образцов толщиной 1…4 мм при их деформировании электродами в месте сварки (рис. 2.6, а
). Величина зазора δ
, а также угол α
раскрытия зазора в нахлестке устанавливались прокладками 3. Кроме того, зазоры моделировали и по известной методике [95], в соответствии с которой образцы сваривали через размерные прокладки (рис. 2.6, б
).
 |
Деформация образцов производилась на экспериментальной установке изготовленной на базе разрывной машины УММ-5 (рис. 2.7).  В ней верхний 1 и нижний 2 электрододержатели с установленными в них электродами закреплены в губках разрывной машины 3 и 4. На нижнем электрододержателе 2 жестко закреплена направляющая скоба 5, в направляющей 6 которой верхний электрододержатель 1 установлен с возможностью осевого перемещения. На кронштейне 7, жестко закрепленном на верхнем электрододержателе 1, установлен индикатор перемещения часового типа 8, установка нуля на котором производится регулировочным винтом 9. Деформируемые детали 10 помещаются между электродами перпендикулярно их оси. Поддерживающее приспособление 11 служит для фиксации пространственного положения деформируемых деталей. В ней верхний 1 и нижний 2 электрододержатели с установленными в них электродами закреплены в губках разрывной машины 3 и 4. На нижнем электрододержателе 2 жестко закреплена направляющая скоба 5, в направляющей 6 которой верхний электрододержатель 1 установлен с возможностью осевого перемещения. На кронштейне 7, жестко закрепленном на верхнем электрододержателе 1, установлен индикатор перемещения часового типа 8, установка нуля на котором производится регулировочным винтом 9. Деформируемые детали 10 помещаются между электродами перпендикулярно их оси. Поддерживающее приспособление 11 служит для фиксации пространственного положения деформируемых деталей.
Прогиб ω
деформируемых деталей 10 измерялся с точностью ± 0,005 мм по сближению h
электродов 1 и 2, а величина деформирующего усилия измерялась по шкале разрывной машины с точностью ± 10 Н. Погрешность Δ
h
измерения сближения деталей h
учитывалась как среднестатистическая поправка. Она появляется из-за деформации элементов конструкции установки при нагружении, внецентренного расположения индикатора перемещения и вдавливания электродов в детали. Величина погрешности Δ
h
, которую определяли при сжатии одного листа, зависит от сжимающего усилия F
Д
(рис. 2.8). В итоге прогиб одного листа определялся по выражению
 . .
 В экспериментах использовались образцы из сплавов АМц, Д16Т, АМг6 и МА2-1 размером 300 × 400 мм и толщиной 1...5 мм. Измерения деформирующего усилия F
Д
при сочетании факторов каждой ячейки производились три раза. В экспериментах использовались образцы из сплавов АМц, Д16Т, АМг6 и МА2-1 размером 300 × 400 мм и толщиной 1...5 мм. Измерения деформирующего усилия F
Д
при сочетании факторов каждой ячейки производились три раза.
Для определения значимости влияния на величину F
Д
усилия сопротивления деталей их сближению до соприкосновения семи технологических факторов точечной сварки, которые показаны выше (рис. 2.5), планировались четырёхфакторный эксперимент в пяти уровнях (латинский квадрат) и трехфакторный эксперимент в семи уровнях по известным методикам [101…105].
При проведении четырехфакторного эксперимента в пяти уровнях осуществляли проверку значимости влияния на величину F
Д
факторов t
*
, α,
R
Э
и s
при неизменных значениях параметров t
, δ
и u
. В результате получены отношения дисперсий факторов к дисперсии воспроизводимости, которые соотносятся с критерием Фишера, для условий данного эксперимента равным 3,9, следующим образом:
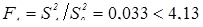 ; ; 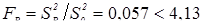 ; ;
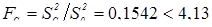 ; ; 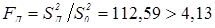 . .
Таким образом, из этого эксперимента следует, что влияние фактора Д, т. е. толщины деталей s
, на величину F
Д
значимо, а влияние факторов А, В и С, т. е. t
*
, α
и R
Э
— не значимо.
Проверку значимости влияния исследуемых факторов t
, δ,
u
на величину F
Д
при неизменных значениях параметров t
*
, α,
R
Э
и s
осуществляли проведением трехфакторного эксперимента в семи уровнях. В результате также получены отношения дисперсий факторов к дисперсии воспроизводимости, которые соотносятся с критерием Фишера, который для условий данного эксперимента равен 3,9, следующим образом:
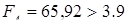 ; ; 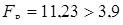 ; ; 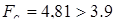 . .
Следовательно, все исследуемые в данном эксперименте факторы А, В и С, т. е. расстояние между сваренными точками t
,
величина зазора в месте сварки δ
и расстояние от кромки листа до центра свариваемой точки u
на величину F
Д
влияют значимо.
Степень влияния каждого из факторов на величину усилия сопротивления деталей деформации при их сближении F
Д
можно оценить по соотношению дисперсий. Тогда значимо влияющие на величину F
Д
факторы в порядке уменьшения их влияния располагаются следующим образом:
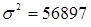 ; ; 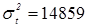 ; ; 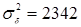 ; ; 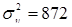 . .
Таким образом, из семи исследуемых технологических факторов значимо влияют на величину F
Д
только четыре вышеуказанных: толщина деталей s
, расстояние между точками t
, величина зазора в месте сварки δ
и расстояние от кромки листа до центра свариваемой точки u
(рис. 2.9). Влияние же расстояния до соседних сваренных точек t
*
, угла раскрытия зазора в нахлестке α
и радиуса сферы рабочей поверхности электродов R
Э
в исследуемом диапазоне их изменения не значимо и находится в пределах статистического разброса измеренных значений F
Д
. Зависимость F
Д
от значимо влияющих на его величину факторов однозначна при любых их сочетаниях. Величина F
Д
возрастает с увеличением s
, δ
и u
, а также с уменьшением t
(рис. 2.9). При этом градиент изменения F
Д
, характеризующий степень влияния каждого из факторов, согласуется с приведенным выше соотношением их дисперсий.
Для определения количественной зависимости между усилием сопротивления свариваемых деталей их прогибу F
Д
и значимо влияющими на его величину технологическими факторами КТС проводились однофакторные эксперименты по общеизвестной методике. Проведенными исследованиями установлено следующее.

С увеличением толщины деталей s
характер увеличения усилия сопротивления свариваемых деталей их прогибу F
Д
практически не изменяется при всех сочетаниях остальных значимых факторов (рис. 2.10). Это же можно сказать и о характере уменьшения F
Д
при увеличении расстояния между сваренными точками t
(рис. 2.11).
Влияние величины зазора δ
и расстояния до кромки листа u
на усилие сопротивления свариваемых деталей их прогибу F
Д
не столь однозначно (рис. 2.12). Так, при сжатии деталей у кромки нахлестки, т. е. при небольших значениях u
(кривая 1 на рис. 2.12, а
) или при небольших отношениях δ
/t
(рис. 2.12, б
), что имеет место при малой величине зазора δ
или большом шаге между точками t
, увеличение F
Д
происходит практически пропорционально увеличению зазора. Это объясняется тем, что при таких условиях искривление деталей в месте сжатия небольшое, характер деформации листов близок к чистому изгибу и детали деформируются в упругой области (см. рис. 2.1).
При увеличении отношения δ
/t
деформирование листов переходит от их изгиба к прогибу по типу мембраны. Кривизна деталей в месте сжатия увеличивается и деформации могут выходить за пределы области упругих. В этом случае детали в области, прилегающей к месту сжатия, могут деформироваться упруго-пластически или даже пластически. В следствие этого прямо пропорциональная зависимость усилия F
Д
от величины зазора δ
нарушается и рост величины F
Д
замедляется (рис. 2.12, а
). С увеличением расстояния до кромки нахлестки u
усилие сопротивления свариваемых деталей их прогибу увеличивается F
Д
(рис. 2.13). Однако в этом случае рост F
Д
происходит только до определенного соотношения между параметрами δ,
u
и t
, а затем прекращается (рис. 2.13, а
, б
).

Это объясняется тем (см. рис. 2.1), что по мере увеличения отношения u
/
t
характер деформации деталей изменяется от состояния, близкого к чистому изгибу (при малых значениях отношений u
/
t
и δ/
t
), к состоянию, близкому к чистому прогибу по типу мембраны (при увеличении отношений u
/
t
и δ/
t
). При достижении отношением u
/
t
определенного значения, которое зависит от соотношения s
и δ
, соответствующего переходу к прогибу по типу мембраны (рис. 2.1, г
), дальнейшее увеличение u
на усилие F
Д
практически не влияет.
2.1.3.
Экспериментально-расчетный метод определения усилия
деформирования деталей при их сближении
В связи с тем, что точно рассчитать величину усилия сопротивления свариваемых деталей их прогибу F
Д
решением уравнения (2.2) для условий точечной сварки представляет большие трудности, то для решения технологических задач рационально использовать приближенный экспериментально-расчетный метод определения при КТС усилий, необходимых для деформирования деталей до их соприкосновения [91, 100]. Его суть заключается в следующем.
Результаты экспериментальных измерений величины усилия сопротивления свариваемых деталей их прогибу F
Д
при различных сочетаниях технологических факторов значимо влияющих на его величину, приближенно можно описать следующими функциями, которые выражают зависимость F
Д
от каждого из них при неизменных значениях остальных:
 , ,
где f
1
, f
2
, f
3
, f
4
– функции удовлетворяющие равенствам, которые представляется возможным определить по экспериментальным результатам деформирования свариваемых деталей при конкретных условиях точечной сварки; w
– прогиб одной свариваемой детали.
Тогда можно предположить, что существует некая функция f
5
, которая удовлетворяет условию
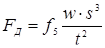 . (2.3) . (2.3)
Толщину деформируемых деталей в зависимости (2.3) можно выразить через цилиндрическую их жесткость D
по зависимости 2.2
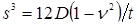 , ,
а величину прогиба свариваемой детали w
— через величину зазора δ
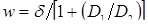 ,
,
где D
1
, D
2
— цилиндрическая жесткость деталей, причем D
1
жесткость более тонкой детали.
С учетом приведенных выше зависимостей выражение (2.3) можно преобразовать к следующему виду:
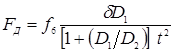 , (2.4) , (2.4)
где f
6
– функция, удовлетворяющая равенству.
Эмпирическая зависимость (2.4) структурно согласуется с зависимостями, полученными при аналитических решениях задач прогиба пластинки для идеализированных граничных условий, например, в работе [97].
Анализом результатов экспериментальных исследований зависимости величины усилия сопротивления свариваемых деталей их прогибу F
Д
от значимо влияющих на неё технологических факторов точечной сварки установлено, что параметры u
/
t
, (w
/t
) и s
влияют на величину F
Д
не однозначно. Так, в области упругих деформаций прогиба деталей значение функции f
6
в основном зависит только от параметра  . В области же деформаций упругопластических — значения функции f
6
уменьшаются с увеличением параметра (w
/t
) и толщины деталей s
. . В области же деформаций упругопластических — значения функции f
6
уменьшаются с увеличением параметра (w
/t
) и толщины деталей s
.
Определено, что с достаточной для приближенных технологических расчетов точностью функции f
6
может быть аппроксимирована зависимостью вида
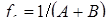 , ,
где А
и В
– экспериментально определяемые коэффициенты, которые зависят, соответственно, от параметров (u
/t
) — 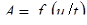 и от параметров (w
/t
) и s
— и от параметров (w
/t
) и s
— 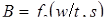 (рис. 2.14). (рис. 2.14). Тогда, с учетом сказанного выше, зависимость (2.4) для расчетного определения величины усилия F
Д
сопротивления свариваемых деталей их прогибу можно преобразовать к следующему окончательному виду
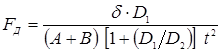 , (2.5) , (2.5)
где δ
— величина зазора в месте сжатия; D
1
и D
2
— цилиндрическая жесткость деталей (см. зависимость 2.2), причем при неодинаковой их толщине: D
1
жесткость более тонкой детали; А
и В
– экспериментально определяемые коэффициенты (рис. 2.14); t
— расстояние между точками.
Сравнение значений F
Д
при различных сочетаниях значимо влияющих на него технологических факторов, в частности, приведенных в
табл. 2.2, показало, что относительное отклонение усилия в плоскости свариваемого контакта ε
F
от усилия сжатия деталей электродами F
Э
при сварке деталей этих толщин, равное
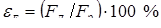 , (2.6) , (2.6)
даже при исследуемых величинах зазоров (до 3-х мм) находятся в пределах 0,5…10 %. При встречающихся в практике КТС сочетаниях t
, δ
и s
значения ε
F
не превышают 2…5 %.
Таким образом, полученная зависимость (2.5), позволяет при решении технологических задач расчетным путем приближенно определять величину усилия F
Д
, необходимого для сближения свариваемых деталей до соприкосновения их поверхностей при конкретных условиях сварки, и с достаточной для практики точностью прогнозировать возможное отклонение усилия сжатия в площади свариваемого контакта от усилия сжатия деталей электродами.
2.2.
Формирование контактов при сжатии деталей электродами
Исходным условием осуществления процесса контактной точечной сварки является наличие электрической проводимости между токопроводящими электродами, что невозможно без наличия её в контактах деталь–деталь и электрод–деталь. То, что величина и стабильность начального электрического сопротивления контактов существенно влияют на тепловые процессы в зоне сварки и, в конечном итоге, на качество готового соединения можно считать однозначно установленным. Это подтверждается многочисленными результатами исследований процесса КТС как отечественных [3, 4, 7...17, 106...115], так и зарубежных [116…120] исследователей. И только в немногочисленных исследованиях [121, 122] получены противоположные результаты.
В свою очередь, образованию электрических контактов деталь–деталь или электрод–деталь должно предшествовать образование между ними хотя бы очагов контактов механических [4, 13].
Таблица 2.2
Значения
F
Д
при различных сочетаниях
s
,
t
,
u
и
δ
| №
пп
|
Сочетания факторов
|
F
Д
(кН)
|
Отклонения FДэксп
от FДрасч.
(%)
|
F
Э
(кН)
|
Отклонения εF
(%)
|
| s
|
t
|
u
|
δ
|
Экспериментальные значения
|
Расчетные значения
|
| 1
|
1,0
|
30
|
8
|
0,5
|
0,110
|
0,133
|
17,6
|
5,0
|
2.6
|
| 2
|
-″-
|
-″-
|
-″-
|
1,0
|
0,280
|
0,256
|
9,3
|
-″-
|
5,1
|
| 3
|
-″-
|
-″-
|
-″-
|
1,5
|
0,350
|
0,373
|
6,5
|
-″-
|
7,4
|
| 4
|
-″-
|
-″-
|
-″-
|
2,0
|
0,460
|
0,487
|
5,8
|
-″-
|
9,6
|
| 5
|
-″-
|
100
|
-″-
|
1,0
|
0,020
|
0,014
|
4,2
|
-″-
|
0,2
|
| 6
|
-″-
|
-″-
|
-″-
|
2,0
|
0,030
|
0,027
|
11,1
|
-″-
|
0,5
|
| 7
|
-″-
|
-″-
|
-″-
|
3,0
|
0,040
|
0,041
|
2,6
|
-″-
|
0,8
|
| 8
|
2,0
|
50
|
10
|
0,5
|
0,270
|
0,303
|
11,4
|
11,0
|
2,7
|
| 9
|
-″-
|
-″-
|
-″-
|
1,0
|
0,640
|
0,607
|
5,5
|
-″-
|
5,4
|
| 10
|
-″-
|
-″-
|
-″-
|
1,5
|
0,930
|
0,896
|
3,8
|
-″-
|
8,1
|
| 11
|
-″-
|
-″-
|
-″-
|
2,0
|
1,130
|
1,182
|
4,4
|
-″-
|
10,7
|
| 12
|
-″-
|
100
|
-″-
|
1,0
|
0,100
|
0,116
|
15,2
|
-″-
|
1,0
|
| 13
|
-″-
|
-″-
|
-″-
|
2,0
|
0,250
|
0,235
|
6,3
|
-″-
|
2,2
|
| 14
|
-″-
|
-″-
|
-″-
|
3,0
|
0,360
|
0,349
|
3,2
|
-″-
|
3,2
|
| 15
|
3,0
|
70
|
13
|
0,5
|
0,470
|
0,511
|
6,0
|
16,0
|
3,1
|
| 16
|
-″-
|
-″-
|
-″-
|
1,0
|
0,940
|
1,011
|
7,0
|
-″-
|
6,3
|
| 17
|
-″-
|
-″-
|
-″-
|
1,5
|
1,610
|
1,509
|
6,6
|
-″-
|
9,9
|
| 18
|
-″-
|
-″-
|
-″-
|
2,0
|
0,207
|
1,979
|
4,7
|
-″-
|
12,3
|
| 19
|
-″-
|
100
|
-″-
|
1,0
|
0,460
|
0,438
|
5,0
|
-″-
|
2,6
|
| 20
|
-″-
|
-″-
|
-″-
|
2,0
|
0,850
|
0,864
|
1,6
|
-″-
|
5,3
|
| 21
|
-″-
|
-″-
|
-″-
|
3,0
|
1,320
|
1,278
|
3,2
|
-″-
|
7,9
|
Таким образом, формирование контактов при КТС включает в себя, по крайней мере, два, различающихся между собой, процесса: формирование механических контактов; формирование электрических контактов, которые во временной последовательности протекают одновременно после сближения свариваемых деталей до соприкосновения их поверхностей.
2.2.1.
Формирование механических контактов
Реальные поверхности деталей всегда имеют микроскопические неровности (рис. 2.15), поскольку они образуются не только при механической обработке поверхностей [12, 13], но даже и при кристаллизационных [12] или рекристаллизационных [123] процессах в металлах. Эти неровности в технологии машиностроения характеризуют шероховатостью и волнистостью. Их параметры, включая и терминологию, регламентированы ГОСТами [124, 125].
 Если бы поверхности деталей были идеально гладкими и плоскими, то контакты между ними существовали бы по всей площади сопрягаемых поверхностей. Эту площадь принято называть «номинальной площадью контакта» и обозначать Аа
(рис. 2.16). Следовательно, при точечной сварке «номинальной площадью контакта» Аа
является вся площадь нахлестки. Наличие на поверхностях реальных деталей шероховатости и волнистости приводит к тому, контакт между ними не будет сплошным. Лишь отдельные участки поверхностей воспринимают усилия сжатия. Сумма таких дискретных площадок контакта образует «фактическую площадь контакта», которую принято обозначать А
r
. Единичные пятна фактического контакта располагаются неравномерно, отдельными областями. Эти области сосредоточения пятен фактических контактов, обведенные контурами, в сумме составляют «контурную площадь контакта», которую обозначают Ас
. Тогда можно считать, что при контактной точечной сварке «контурной площадью контакта» Ас
является вся площадь внутри контура уплотняющего пояска. Такая классификация площадей контактов общепринята в технологии машиностроения [126, 127] и сварки [4, 12, 13, 92, 128, 129]. Если бы поверхности деталей были идеально гладкими и плоскими, то контакты между ними существовали бы по всей площади сопрягаемых поверхностей. Эту площадь принято называть «номинальной площадью контакта» и обозначать Аа
(рис. 2.16). Следовательно, при точечной сварке «номинальной площадью контакта» Аа
является вся площадь нахлестки. Наличие на поверхностях реальных деталей шероховатости и волнистости приводит к тому, контакт между ними не будет сплошным. Лишь отдельные участки поверхностей воспринимают усилия сжатия. Сумма таких дискретных площадок контакта образует «фактическую площадь контакта», которую принято обозначать А
r
. Единичные пятна фактического контакта располагаются неравномерно, отдельными областями. Эти области сосредоточения пятен фактических контактов, обведенные контурами, в сумме составляют «контурную площадь контакта», которую обозначают Ас
. Тогда можно считать, что при контактной точечной сварке «контурной площадью контакта» Ас
является вся площадь внутри контура уплотняющего пояска. Такая классификация площадей контактов общепринята в технологии машиностроения [126, 127] и сварки [4, 12, 13, 92, 128, 129].

При контактировании жестких тел величина контурной площади контакта определяется геометрическими характеристиками их поверхностей, в основном волнистостью, а также, хотя и в значительно меньшей мере, и шероховатостью [126, 127, 130...135]. При точечной сварке кроме волнистости и шероховатости на контурную площадь контактов оказывает влияние распределение нагрузки, которое зависит от площади (при плоской) или радиуса (при сферической) рабочих поверхностей электродов, и толщина свариваемых деталей вследствие относительно небольшой жесткости последних [4, 13,81, 92, 136].
В теории контактной точечной сварки наиболее известны две методики расчетного определения контурной площади контактов АС
[10, 13]:
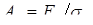 , (2.7) , (2.7)
 , (2.8) , (2.8)
где F
Э
— усилие сжатия электродов; σТ
— предел текучести материала деталей; Аа
— номинальная площадь контакта; Z
— показатель степени, который учитывает нагрузку и сопротивление деформации металла деталей
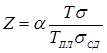 или или 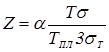 ; ;
здесь α —
опытный коэффициент; Т —
температура в контакте; σ
— удельная нагрузка: 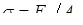 ; ТПЛ
—
абсолютная температура плавления металла; σСД
— сопротивление деформации металла в масштабе волнистости. ; ТПЛ
—
абсолютная температура плавления металла; σСД
— сопротивление деформации металла в масштабе волнистости.
Значения контурной площади АС
, рассчитанные по зависимости (2.7), значительно превышают экспериментальные значения, например, приведенные в работах [92, 128, 129]. Экспериментальные данные, а также теоретические исследования [81, 136] однозначно показывают, что при точечной сварке контурная площадь практически не зависит от площади нахлестки, то есть от номинальной площади контакта Аа
. Поэтому возможность применения зависимости (2.8) для практических расчетов в условиях точечной сварки весьма проблематична. Кроме того, вычисления по зависимости (2.8) весьма трудоемки, так как могут быть произведены только методом итераций, поскольку искомая величина АС
входит и в правую ее часть для определения величины удельной нагрузки σ
.
Сведения же о фактической площади контактов при точечной сварке и механизме ее формирования весьма ограничены. Так, в работе [92] экспериментально установлено, что она составляет 1…25 % от контурной площади контакта. При этом отмечается, что в случае сжатия деталей электродами с плоской рабочей поверхностью пятна единичных микроконтактов распределяются почти равномерно по всей контурной площади. В случае же сжатия деталей электродами со сферической рабочей поверхностью плотность единичных контактов растет к ее периферии.
Для расчета фактической площади контакта А
r
в работе [13] предложена зависимость, которая структурно аналогична зависимости (2.8)
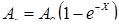 , (2.9) , (2.9)
где: Х
— показатель степени, равный
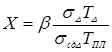 или или 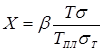 ; ;
здесь β —
опытный коэффициент; σΔ
— давление, действующее в площади единичного микроконтакта; ТΔ
—
температура микровыступов в контакте; σСДΔ
— сопротивление деформации металла в масштабе микровыступов.
Расчеты фактической площади контакта А
r
по зависимости (2.9) затрудняются теми же обстоятельствами, что и расчет контурной площади по зависимости (2.8). Причем определение температуры и свойств металла в масштабе микровыступов весьма неопределенно.
При сварке деталей из алюминиевых и магниевых сплавов относительные деформации микрошероховатостей на их поверхности достигают 60…70 %. Причем их значения в контакте электрод–деталь в 1,3...1,4 раза больше, чем в контакте деталь–деталь [129]. Такой уровень микродеформаций в контактах электрод–деталь может приводить к схватыванию металлов детали и электрода (по механизму сварки давлением в твердой фазе [12, 137]) и такому нежелательному при точечной сварке явлению, как массоперенос металлов между поверхностями деталей и электродов [128].
2.2.2.
Формирование электрических контактов
Образование механических микроконтактов в фактических площадях контактов еще не гарантирует наличие в нем контакта электрического [4, 13]. Это обусловлено тем, что идеально чистая (ювенильная), металлическая поверхность существует только короткие моменты времени (доли секунды) в изломе металла или в первые мгновения после её механической обработки [4, 12, 13]. Очистка и предотвращение последующего возникновения поверхностного загрязнения деталей в технологических процессах сварки давлением в основном удаётся только в вакуумных устройствах [137...140]. В силу конструктивных особенностей таких устройств [141...144] использовать их при точечной сварке экономически и технологически не целесообразно.
 |
Реальные же поверхности свариваемых деталей всегда покрыты окисной пленкой, состав и толщина которой зависит от рода металла или сплава, от состава, давления и температуры газовой фазы, а так же от продолжительности их воздействия (рис. 2.17). На поверхности окисных пленок возможно наличие адсорбированных газов, влаги и органических веществ, и прочих наслоений [3, 4, 12, 13, 145...151]. Последние значительно затрудняют сближение металлических поверхностей, так как вещество граничного слоя при сжатии приобретает упругость твердого тела [12, 148]. Поэтому фактическую площадь даже единичного контакта условно можно разделить на три (см. рис. 2.16). К первой, А
r
м
— относятся участки с металлическим контактом, в которых электрический ток протекает без заметного переходного сопротивления, как это имеет место между кристаллами в компактном металле. Ко второй, А
r
пл
— участки с квазиметаллическим контактом, поверхность которых покрыта тонкой пленкой, легко пропускающей ток благодаря туннельному эффекту [152] или фриттинг эффекту [13]. К третьей же, А
r
мо
— участки, не проводящие ток и покрытые мономолекулярными плёнками (окислы, сульфаты и т. п.), которые практически играют роль изоляторов [13, 152].
С целью создания наиболее благоприятных условий для формирования электрических контактов перед их сваркой, как правило, проводят специальную подготовку поверхностей деталей, например, травление с последующей пассивацией или механическую зачистку. При этом время хранения подготовленных деталей до сварки регламентируют. А непосредственно перед ней контролируют электрическое сопротивление участка электрод–электрод [7...17, 111...115].
Таким образом, формирование контактов электрод–деталь и деталь–деталь со стабильными параметрами представляет сложную задачу технологии точечной сварки, так как этот процесс зависит от большого числа факторов, параметры которых на практике зачастую носят случайный характер и имеют большой статистический разброс: от усилия сжатия электродов и геометрии их рабочих поверхностей; от макро- и микрогеометрии поверхностей деталей; сопротивления деформации металла микро- и макромасштабах; поверхностных пленок и др.
2.3
. Электрическая проводимость зоны сварки.
Электрическая проводимость зоны сварки характеризуется электрическим сопротивлением участка электрод–электрод r
ЭЭ
(рис. 2.18).
В общем случае, электрическое сопротивление участка электрод–электрод r
ЭЭ
представляют в виде суммы последовательно соединенных активных сопротивлений собственно свариваемых деталей r
Д1
и r
Д2
, сопротивлений контакта между ними r
ДД
, а также сопротивлений контактов между деталями и электродами r
ЭД1
и r
ЭД2
[3, 16]:
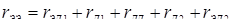 . (2.10) . (2.10)
При сварке деталей равной толщины и из одного и того же материала эту зависимость можно упростить и записать в следующем виде:
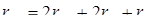 . (2.11) . (2.11)
Для определения общего электрического сопротивления зоны сварки по зависимости (2.11) необходимо в любой момент процесса сварки опре делить величину всех ее составляющих. Очевидно, что математически точно решить эту задачу вряд ли представляется возможным из-за чрезвычайно сложного влияния и взаимовлияния на проводимость зоны сварки параметров термодеформационных процессов, которые протекают в зоне сварки. Например, таких как нестационарный нагрев металла в зоне сварки, обусловленный процессами выделения теплоты и ее отвода в электроды и детали, изменение удельного сопротивления металла при нагреве, микропластические деформации в контактах деталь–деталь и электрод–деталь, макропластические деформации металла в зоне сварки и др. Поэтому в технологических расчетах величину электрического сопротивления зоны сварки определяют приближенно, в большинстве, по эмпирическим зависимостям. делить величину всех ее составляющих. Очевидно, что математически точно решить эту задачу вряд ли представляется возможным из-за чрезвычайно сложного влияния и взаимовлияния на проводимость зоны сварки параметров термодеформационных процессов, которые протекают в зоне сварки. Например, таких как нестационарный нагрев металла в зоне сварки, обусловленный процессами выделения теплоты и ее отвода в электроды и детали, изменение удельного сопротивления металла при нагреве, микропластические деформации в контактах деталь–деталь и электрод–деталь, макропластические деформации металла в зоне сварки и др. Поэтому в технологических расчетах величину электрического сопротивления зоны сварки определяют приближенно, в большинстве, по эмпирическим зависимостям.
2.3.1
. Электрические сопротивления контактов при точечной сварке
Наличие электрических контактных сопротивлений обусловлено относительно небольшой площадью электрического контакта по сравнению с номинальной площадью контактирующих поверхностей. Это происходит из-за наличия неровностей на поверхностях деталей и электродов, а также из-за различных не электропроводных поверхностных образований: оксидных и гидрооксидных пленок, адсорбированных влаги, масел, пыли и т.п. С увеличением сопротивлений контактов, как правило, уменьшается и стабильность их значений. Большие и не стабильные значения электрических сопротивлений контактов являются основными возмущающими факторами процесса КТС, которые могут приводить не только к отклонениям параметров качества сварных соединений, но и к образованию дефектов типа выплеск или непровар. На сопротивление контактов деталь–деталь и электрод–деталь при точечной сварке наиболее значимо влияют исходное состояние поверхностей деталей и усилие их сжатия (рис. 2.19).
Влияние состояния поверхности на контактное сопротивление очень велико. При этом на его величину оказывает влияние и шероховатость поверхностей, и сопротивление деформации металла в поверхностном слое, и параметры поверхностных пленок. Увеличение параметров шероховатости, а также толщины и прочности поверхностных пленок, при одинаковых остальных условиях, приводят к увеличению контактного сопротивления в десятки, сотни, а иногда и тысячи раз (табл. 2.3).

С увеличением усилия сжатия электродов при контактной точечной сварке деталей любых толщин и из любых материалов однозначно уменьшаются как величина сопротивления контактов, так и разброс их значений. Такое изменение контактных сопротивлений при увеличении усилия сжатия происходит вследствие интенсификации процессов микропластических деформаций в контактах, которые приводят к смятию микровыступов, разрушению поверхностных пленок и увеличению площадей фактических контактов [3, 4, 7...17, 107...120, 153, 154].
Механические и электрические процессы, протекающие в сварочных контактах в процессе формирования соединений за цикл сварки и определяющие его электрические параметры, очень сложны. Это затрудняет их математическое описание, т. е. разработку математических моделей контактов при КТС. Задача осложняется еще и неопределенностью, а также случайностью параметров, которые характеризуют шероховатость поверхностей после их технологической обработки и поверхностные пленки. Так, о реальном профиле шероховатых поверхностей авторы работы [127] замечают следующее: «…Надо обладать большим воображением, чтобы в реальных очертаниях выступов увидеть правильную геометрическую фигуру. …Существование неровностей с заостренными вершинами вообще представляется маловероятным».
Для условий точечной сварки наиболее адекватной считается ситовая модель проводимости контактов. На ее основе разработан ряд методик для расчетного определения электрического сопротивления контактов. Из них наибольшую известность получили две методики.
Одна из них — это методика Р. Хольма, разработанная им для шинных контактов и приведенная, например, в более поздней работе [152]. Эта формула затем Ф. И. Кислюком [7, 106] была введенная в теорию контактной точечной сварки и до настоящего времени не претерпела существенных изменений [3]:
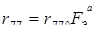 , (2.12) , (2.12)
где r
ДД0
и а
— коэффициенты, определяемые экспериментально; F
Э
— усилие сжатия электродов.
Другая же методика, первоначально разработанная К. А. Кочергиным для стыковой сварки [107], а затем распространенная им же и на сварку точечную, учитывает в определенной мере реальные микропластические деформации в контактах. В ней микрогеометрия шероховатой поверхности моделируется правильными четырехгранными пирамидами одинаковой высоты и рассчитывается сопротивление системы этих пирамид в условиях их деформирования. По крайней мере, эта методика описывает реальные микропластические деформации качественно [4, 13]:
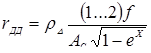 , (2.13) , (2.13)
где: ρΔ
— удельное электрическое сопротивление металла в масштабе микрошероховатости; (1…2) f
— толщина контактного слоя; АС
— контурная площадь контакта; Х
— функция нагрузки и сопротивления деформации металла (определение АС
и Х
см. в зависимостях (2.8) и (2.9)).
Электрические же сопротивления контактов электрод–деталь r
ЭД
. до сих пор, как правило, отдельно не рассчитывают. Их, по предложению
А. С. Гельмана [155], принимают равными половине величины сопротивлений в контактах деталь–деталь r
ДД
, т. е.:
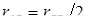 . (2.14) . (2.14)
Следует отметить, что возможность использования зависимостей (2.13) или (2.14) в современных методиках решения технологических задач точечной сварки весьма проблематична. Очевидно, что зависимость (2.12) не отражает физической сущности проводимости контактов и представляет собой функцию, аппроксимирующую экспериментальные измерения r
ДД
. Поэтому она может быть использована только для тех условий сварки, при которых определялись её коэффициенты. Специализированных же банков данных их значений, как отмечается в работе [156], пока нет, а имеющиеся их значения не точны и зачастую представлены в некорректной форме. Это же в полной мере можно отнести и к значениям ρΔ
в зависимости (2.13). Кроме того, вычисление в ней значений АС
(см. зависимость (2.8)) при точечной сварке весьма неопределенно.
Таким образом, несмотря на то, что исследования механизма формирования контактов при контактной точечной сварке и их влияния на процесс формирования соединения весьма многочисленны и глубоки, их, по-видимому, нельзя считать завершенными. Отсутствуют приемлемые для решения современных технологических задач методики расчётного определения электрического сопротивления участка электрод–электрод и, в частности, сопротивления контактов. Так, в работе [156] при разработке современных САПР ТП для точечной сварки рекомендуется использовать все ту же зависимость (2.12). В работе же [4] автор зависимости (2.13)
К. А. Кочергин отмечает, что существующие методики расчетов описывают процессы, протекающие в контактах, в основном только качественно, и точность количественных расчетов по данным методикам весьма низкая.
Поэтому, в большинстве случаев, даже когда решают задачи по определению в зоне сварки полей распределения потенциалов и температуры в относительно точной постановке, например, численным решением дифференциальных уравнений, сопротивления контактов либо вообще не учитывают, либо задают их по зависимостям типа (2.12).
2.3.2. Электрические сопротивления собственно свариваемых деталей
Электрическое сопротивление собственно деталей — это сопротивление, которое определенным образом распределено в объеме деталей, расположенном между сжимающими их электродами.
Величину электрического сопротивления собственно детали r
Д
в большинстве случаев определяют по методике А. С. Гельмана. Еще в 40-х годах 20-го в. им была теоретически определено распределение потенциалов в свариваемых деталях путем решения методом конечных разностей дифференциального уравнения, описывающего электрическое поле
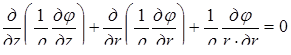 , (2.15) , (2.15)
где φ —
потенциал в рассматриваемой точке; z
и r
— цилиндрические координаты пространства.
Решением этого уравнения с граничными условиями, отражающими особенности протекания электрического тока при точечной сварке на участке электрод–детали–электрод, им определена топография растекания линий тока в деталях до диаметра dj
(см. рис 2.18) при различных условиях сварки и разработана инженерная методика расчета электрического сопротивления r
Д
собственно свариваемых деталей [16, 85, 155]:
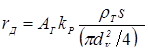 , (2.16) , (2.16)
где: АГ
— коэффициент (рис.2.20), учитывающий уменьшение сопротивления детали r
Д
относительно сопротивления цилиндра r
Ц
, высотой s
и диаметром d
К
, которое происходит из-за растекания линий тока до диаметра dj
; ρТ
— удельное электрическое сопротивление металла деталей; k
Р
— коэффициент, учитывающий неравномерность нагрева деталей.
 Следует отметить поразительную, для того времени и тех вычислительных средств (расчетов на арифмометрах), точность решения Следует отметить поразительную, для того времени и тех вычислительных средств (расчетов на арифмометрах), точность решения
А. С. Гельмана. В 70-х годах многие исследователи подобные задачи начали решать на ЭВМ. Естественно, что некоторые из них пытались уточнить решение А. С. Гельмана. Как это ни удивительно, но значения коэффициента АГ
(сейчас его так и называют — «коэффициент Гельмана»), полученные с помощью арифмометра [155] и ЭВМ, например, в работе [157], практически совпадают.
При решении этой же задачи растекание линий тока в деталях
К. А. Кочергин моделирует их токопроводящее сечение в виде двух усеченных конусов, вершинами обращённых к контактам (показаны штриховыми линиями на рис 2.18). Это же сопротивление деталей r
Д
он рассматривает как сумму сопротивлений конусов и сопротивлений за счет искривления линий тока в близи контакта (уменьшения площади токопроводящего сечения). В результате такого решения [4, 13] величину r
Д
им предложено определять по следующей зависимости:
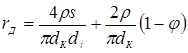 , (2.17) , (2.17)
где φ
— коэффициент, который представляет собой отношение электрического сопротивления конусов к сопротивлению цилиндра диаметром d
К
и высотой, равной толщине деталей s
.
При расчетах r
Д
по зависимости (2.17) значение диметра dj
, до которого происходит растекание линий тока в деталях, т. е. диаметра основания конуса, определяется через тот же коэффициент А.С. Гельмана АГ
:
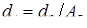 . .
Таким образом, по существу эти методики расчета электрического сопротивления свариваемых деталей представляют собой одно и то же решение данной задачи. Они различаются только тем, что в зависимости (2.16) рассчитывается уменьшение r
Д
, которое происходит из-за растекания линий тока в деталях до диаметра dj
, относительно сопротивления цилиндра, диаметром d
К
, а в зависимости (2.17) — наоборот, рассчитывается увеличение r
Д
относительно сопротивления цилиндра, диаметром dj
, которое происходит из-за сужения линий тока у контактов до диаметра d
К
.
Преимущественное применение в практике расчетов зависимости (2.16) объясняется, во-первых, тем, что диаметр контакта d
К
, в отличие от dj
, в процессе сварки можно легко измерить, а во-вторых, по-видимому, и тем, что методика А.С. Гельмана предложена намного раньше.
2.3.3.
Общее электрическое сопротивления зоны сварки
Многочисленными исследованиями процесса КТС к настоящему времени однозначно установлены зависимости электрического сопротивления участка электрод–электрод r
ЭЭ
от основных факторов, воздействующих на него при точечной сварке. В общем случае величина r
ЭЭ
и ее изменение при КТС зависят от параметров режима сварки, толщины деталей и свойств их металла, формы и размеров рабочих поверхностей электродов. Наибольшее влияние на исходную величину электрического сопротивления участка электрод–электрод r
ЭЭ
оказывают свойства материала деталей, состояние их поверхностей и время t
В
выдержки деталей от момента зачистки до сварки, усилие сжатия электродов F
Э
, форма и размеры их рабочих поверхностей (d
Э
или R
Э
).
С увеличением усилия сжатия электродов F
Э
исходное электрическое сопротивление участка электрод–электрод всегда уменьшается
(рис. 2.21). При этом одновременно с уменьшением величины r
ЭЭ
уменьшается и разброс его значений, т. е. повышается их стабильность. Именно поэтому применение повышенного усилия сжатия электродов является одним из основных и наиболее простых технологических приемов, которым в практике КТС повышают стабильность показателей качества получаемых сварных соединений [2, 3, 8…11, 14…17].
С увеличением времени выдержки деталей от момента зачистки до сварки t
В
увеличивается как величина r
ЭЭ
, так и разброс его значений. То есть в этом случае, наоборот, стабильность электрического сопротивления участка электрод–электрод уменьшается. Причем наиболее интенсивно рост величины r
ЭЭ
и разброса его значений идет в первые двое – трое суток. Это обусловлено увеличением контактных сопротивлений из-за окисления свариваемых деталей, то есть ростом толщины окисных пленок на их поверхностях. Именно поэтому в практике КТС проведение технологических мероприятий (подготовки поверхностей деталей перед сваркой), направленных на уменьшение величины контактных сопротивлений и повышение стабильности их значений, является исходным условием получения качественных сварных соединений. Последнее обстоятельство особенно существенно для технологии сварки деталей из алюминиевых и магниевых сплавов [3, 9, 10, 14, 114].
При увеличении диаметра d
Э
(при плоской) или радиуса R
Э
(при сферической) рабочих поверхностей электродов величина r
ЭЭ
несколько уменьшается. Это обусловлено увеличением площади токопроводящего сечения в свариваемых деталях. Разброс же значений r
ЭЭ
при этом увеличивается, то есть стабильность их уменьшается. Это является следствием уменьшения давления в контактах, которое происходит из-за увеличения их площади при неизменном усилии сжатия электродов. Однако влияние этого фактора на процесс КТС не столь существенно, как двух описанных выше. Геометрические параметры электродов (d
Э
, d
Э
или R
Э
) обычно выбирают по технологическим рекомендациям в зависимости от толщины свариваемых деталей (см. табл. 1.2) [3, 9, 11, 15].
При КТС в процессе формирования точечного сварного соединения величина электрического сопротивления участка электрод–электрод r
ЭЭ
всегда уменьшается (рис. 2.22). В динамике уменьшения r
ЭЭ
выделяют два этапа: I и II, которые существенно различаются градиентом скорости изменения электрического сопротивления участка электрод–электрод.

Этап I характеризуется быстрым уменьшением сопротивления участка электрод – электрод. В основном это обусловлено быстрым уменьшением при нагреве контактных сопротивлений r
ДД
и 2r
ЭД
.
В течение этапа II величина сопротивления r
ЭЭ
в основном определяется величиной сопротивления деталей 2r
Д
, так как сопротивление контактов электрод–деталь 2r
ЭД
невелико, а сопротивление контакта деталь–деталь r
ДД
к этому времени уменьшается практически до нуля. В этот период характер изменения r
ЭЭ
определяется в основном двумя процессами: увеличением сопротивления зоны сварки из-за его нагрева и уменьшением ее сопротивления вследствие увеличения площадей контактов. Небольшой спад r
ЭЭ
на этом участке обусловлен преимущественным влиянием увеличения площади электрических контактов, диаметры которых к концу нагрева достигают значений d
Э
и d
П
[3, 4, 7…17, 107, 155, 156].
В общем случае характер изменения r
ЭЭ
в процессе сварки зависит от свойств металла, толщины деталей, режима сварки, формы импульса тока, размеров ядра, формы рабочей поверхности электродов и т. п.
Естественно, что величина общего сопротивления участка электрод-электрод r
ЭЭ
меньше для сплавов с более низким удельным электросопротивлением (сплавы на основе меди и алюминия (рис. 2.23)). Это обусловлено также и тем, что для всех толщин деталей, независимо от материалов из которых они изготовлены, отношения геометрических параметров рабочих поверхностей электродов и диаметров ядра к толщине деталей примерно одинаковые (см. п. 1.3.4, табл. 1.1 и 1.2).
 С увеличением толщины деталей общее сопротивление участка электрод–электрод и конечное его значение r
ЭЭК
заметно снижаются в основном за счет увеличения площади контакта в процессе сварки (см. табл. 2.4). Увеличение диаметра ядра при С увеличением толщины деталей общее сопротивление участка электрод–электрод и конечное его значение r
ЭЭК
заметно снижаются в основном за счет увеличения площади контакта в процессе сварки (см. табл. 2.4). Увеличение диаметра ядра при 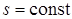 , которое достигается повышением силы тока или времени сварки приводит, как правило, к снижению r
ЭЭ
и r
ЭЭК
. , которое достигается повышением силы тока или времени сварки приводит, как правило, к снижению r
ЭЭ
и r
ЭЭК
.
Изменение параметров режима точечной сварки оказывает заметное влияние на r
ЭЭ
вследствие изменения теплового состояния металла и площади контактов. Так, увеличение FCB
или I
СВ
приводит к росту диаметра контактов и снижению r
ЭЭ
. Переход к режимам с большим временем сварки при сохранении одного и того же диаметра ядра также приводит к некоторому снижению r
ЭЭ
и r
ЭЭ К
из-за уменьшения сопротивления пластической деформации и роста размеров контактов.
При точечной сварке используются электроды со сферической и плоской рабочей поверхностью.
Сварка электродами со сферической рабочей поверхностью отличается меньшими размерами контакта на первом этапе, соответственно большей плотностью тока и большей скоростью тепловыделения. Зона расплавления возникает раньше, чем при сварке электродами с плоской рабочей поверхностью, и поэтому область I на рис. 2.22 менее протяженна и значения r
ЭЭ
в этой области заметно выше. При этом скорость повышения r
ЭЭ
возрастает с уменьшением радиуса сферы. Характер изменения r
ЭЭ
области II для обоих типов электродов примерно одинаков, но в течение всего цикла сварки среднее значение r
ЭЭ
при сварке электродами со сферической рабочей поверхностью на 10…15 % выше, чем при сварке электродами с плоскими рабочими поверхностями.
Таблица
2.4
Значения
r
ЭЭ К
в конце процесса КТС
| Материал
|
Толщина деталей, мм
|
| 0,3
|
0,5
|
1
|
1,5
|
2
|
2,5
|
| Д16АТ
|
18
|
16
|
13
|
11
|
10
|
8
|
| Л62
|
76
|
48
|
30
|
24
|
20
|
18
|
| 08 кп
|
150
|
135
|
115
|
100
|
90
|
75
|
| 30ХГСА
|
115
|
145
|
125
|
110
|
100
|
90
|
| Х15Н5Д2Т
|
145
|
165
|
135
|
120
|
110
|
100
|
| 12Х18Н10Т
|
215
|
185
|
150
|
130
|
120
|
110
|
| ОТ4-1
|
240
|
210
|
165
|
145
|
133
|
120
|
| Примечание. Данные приведены для двух деталей одинаковой толщины с минимальным диаметром ядра
|
Таким образом, основным фактором, дестабилизирующим электрическое сопротивление зоны сварки (участка электрод–электрод) и, в конечном итоге, параметры качества получаемых соединений, является в основном электрическое сопротивление контактов. Поэтому при приближённых технологических расчётах, например, сварочного тока по зависимости (1.11), сопротивление зоны сварки r
ЭЭ
обычно принимают равным его значению в конце процесса КТС r
ЭЭК
. [3]
Для упрощения расчета r
ЭЭ
= 2r
Д
(при сварке двух деталей одинаковой толщины) используют условную схему термодеформационного состояния металла зоны сварки. В частности, учитывая, что в контакте электрод–деталь его диаметр dK
ЭД
примерно равен диаметру рабочей поверхности электрода d
Э
(dK
ЭД
≈ d
Э
) (см. табл. 1.1), а диаметр контакта деталь–деталь dK
ДД
приближённо равен диаметру уплотняющего пояска d
П
(dK
ДД
≈ d
П
) и то, что d
Э
мало отличается от d
П
, условно принимают d
П
≈ d
Э
(где d
П
≤ 1,2 d
Я
). Кроме того, принимают также, что сопротивления контактов r
ЭД
и r
ДД
равны нулю.
При таких допущениях определяемое сопротивление r
ЭЭ
представляют как сумму сопротивлений двух условных пластин одинаковой толщины s
, каждая из которых нагрета до некоторой средней температуры Т1
и Т2
(рис. 2.24). Тогда искомое сопротивление r
ЭЭК
определяется следующей зависимостью [3]:
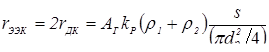 . (2.18) . (2.18)
Удельные электросопротивления деталей ρ1
и ρ2
(см. рис. 2.23) определяют соответственно по температурам Т1
и Т2
для полулистов, прилегающих к электродам и контакту деталь–деталь соответственно (рис. 2.24). В частности, при сварке деталей из низкоуглеродистых сталей Т1
и Т2
принимают соответственно равными 1200 и 1500 °С, а для алюминиевых сплавов — 450 и 630 °С. Коэффициент kP
, учитывающий неравномерность нагрева деталей, для сталей принимают равным ~ 0,85, для алюминиевых и магниевых сплавов — ~ 0,9. При сварке деталей толщиной 0,8…3 мм коэффициент А. С. Гельмана АГ
(см. рис. 2.20) принимают равным ~ 0,8 [3].
 Значения сопротивлений, рассчитанные по зависимости (2.18), как правило, согласуются с экспериментальными данными, в частности, приведенными в табл. 2.4. Значения сопротивлений, рассчитанные по зависимости (2.18), как правило, согласуются с экспериментальными данными, в частности, приведенными в табл. 2.4.
Таким образом, электрическая проводимость зоны сварки, определяемая электрическим сопротивлением свариваемых деталей и контактов электрод–деталь и деталь–деталь, зависит от большого числа технологических факторов точечной сварки и отличается значительной нестабильностью, в первую очередь, из-за нестабильности электрических сопротивлений контактов электрод–деталь и деталь–деталь. Поэтому при приближенных решениях технологических задач КТС проводимость зоны сварки оценивают по электрическому сопротивлению только свариваемых деталей.
2.4.
Нагрев металла в зоне сварки и методы количественной его оценки
Для решения технологических задач точечной сварки в большинстве случаев требуется определить количество теплоты, выделившееся в зоне сварки, и распределение в ней температуры. Характер температурного поля в зоне формирования соединения определяют в основном два процесса, одновременно протекающие и противоположно направленные: тепловыделение сварки и теплопередача из нее в окружающий холодный металл и электроды [2…4, 158].
Наиболее точные значения параметров тепловыделения и распределения температуры получают путем решения дифференциальных уравнений распределения потенциалов и теплопроводности. Вместе с тем, при проектировании технологий КТС в основном применяют приближенные инженерные методики расчетов этих параметров, поскольку они более наглядно отражают тепловые процессы, которые протекают в зоне формирования точечного сварного соединения, и, в ряде случаев, вполне удовлетворяют по точности расчетов.
2.4.1.
Источники теплоты в зоне формирования сварного соединения
При КТС в зоне сварки действует несколько источников теплоты. Нагрев металла в зоне сварки происходит в основном за счет генерирования теплоты в свариваемых деталях, а также на электрических сопротивлениях участка электрод–электрод, при прохождении через них электрического тока (рис. 2.25).
 Основное количество теплоты, выделяющейся при прохождении сварочного тока, в процессе точечной сварки (> 90 % от общего его количества Q
ЭЭ
, выделяющегося за цикл сварки в зоне формирования соединения на участке электрод–электрод [3]) происходит в свариваемых деталях, где действует ее источник, распределенный в объеме металла деталей, проводящем электрический ток. Основное количество теплоты, выделяющейся при прохождении сварочного тока, в процессе точечной сварки (> 90 % от общего его количества Q
ЭЭ
, выделяющегося за цикл сварки в зоне формирования соединения на участке электрод–электрод [3]) происходит в свариваемых деталях, где действует ее источник, распределенный в объеме металла деталей, проводящем электрический ток.
Линии электрического тока j
в свариваемых деталях претерпевают заметные искривления, вследствие чего площадь элементарной силовой трубки тока Δ
S
меняется в зависимости от ее длины dl
. С учетом этого суммарное количество теплоты Q
Д
, которое выделяется в деталях на собственно их сопротивлениях r
Д
, может быть определено по закону Джоуля – Ленца, записанному следующим образом [4, 13]:
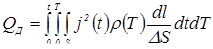 , (2.19)
, (2.19)
где j
— плотность тока; ρ
— удельное электрическое сопротивление металла свариваемых деталей, по которому протекают линии тока j
; S
— площадь сечения, по которому растекаются линии тока; T
и t
— координаты температуры и времени.
Кроме того, некоторое количество теплоты (< 10 % от Q
ЭЭ
[3]) генерируется в контактах деталь–деталь и электрод–деталь и в областях прилегающим к ним, где, хотя и в относительно короткий период (~ 0,1t
СВ
), действуют ее плоские источники. В них генерируется теплота Q
МГ
за счет электрического сопротивления микровыступов r
МГ
(T
), непосредственно образующих контакт, которое в процессе сварки относительно быстро уменьшается вплоть до нулевых значений из-за деформирования (смятия) микровыступов вследствие их разупрочнения при увеличении температуры T
, а также теплота Q
ПЛ
, которая генерируется за счет электрического сопротивления естественных оксидных пленок или (в некоторых случаях практики КТС) в искусственных покрытиях. Для условий КТС, характеризуемых непрерывным изменением силы сварочного тока и температуры металла в зоне формирования соединения, количество теплоты Q
МГ
и Q
ПЛ
можно определить соответственно по следующим зависимостям [4, 13]:
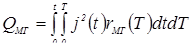 , (2.20)
, (2.20)
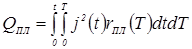 . (2.21)
. (2.21)
При точных расчетах, как дополнительные источники теплоты следует учитывать теплоту Q
ПТ
, выделяющуюся в контактах электрод–деталь вследствие проявления эффекта Пельтье [9, 10, 159] или же вследствие проявления полупроводниковых свойств окисной пленки [160]. Теплота Пельтье генерируется по границам пленок с металлом или по границам жидкого металла с твердым, или же по границам разнородных металлов. Ее количество может быть определено по зависимости [4, 13]:
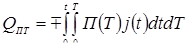 , (2.22)
, (2.22)
где П
(Т
) — коэффициент Пельтье для данной границы.
Таким образом, общее количество теплоты Q
ЭЭ
, которое выделяется в зоне сварки при протекании через нее сварочного тока I
СВ
в течение длительности его импульса t
СВ
(времени сварки) может быть определено как сумма количеств теплоты, выделившейся на указанных выше источниках:
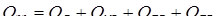 . (2.23) . (2.23)
При приближенных решениях задач технологии КТС, например при определении для конкретных условий сварки ориентировочных значений сварочного тока, теплоту, выделяющуюся в контактах, т. е. Q
МГ
, Q
ПЛ
и Q
ПТ
, по зависимостям (2.20)…(2.22) не рассчитывают. И вообще ее, как правило, в расчетах не учитывают, или же учитывают усредненно через различные поправочные коэффициенты [2, 3, 15].
Таким образом, в технологических расчетах теплоту, выделяющуюся в зоне сварки Q
ЭЭ
, в основном определяют как теплоту Q
Д
, выделяющуюся только в свариваемых деталях. Поскольку в большинстве случаев температуру в зоне сварки усредняют, то зависимость (2.19) преобразуют виду
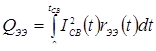 , (2.24) , (2.24)
где I
СВ
— сила сварочного тока, из которого при усреднении по времени силы сварочного тока I
СВ
и электрического сопротивления зоны сварки r
ЭЭ
и получают расчетные зависимости типа (1.11) [2, 3].
2.4.2.
Температурное поле в зоне формирования соединения
Распределение температуры в зоне формирования соединения измерить непосредственно при КТС пока никому не удалось, несмотря на многочисленные общеизвестные попытки это сделать. Поэтому и мнения о значениях температуры, например, в центре зоны сварки, расходятся от температуры плавления металла до температуры его кипения [7, 11, 107, 161]. Анализ известных аналитических методик расчетов температуры в зоне сварки [107, 158, 162, 163], которые учитывают выделение и перераспределении теплоты в ней, например, приведенный в работе [164], показывает, что пытаться удовлетворить требованиям современной технологии КТС по точности определения температуры в зоне сварки этим путем весьма проблематично. Поэтому и работы в этом направлении, по-видимому, бесперспективны.
А. С. Гельман для исследования температурных полей в зоне сварки, по-видимому, первым применил решение дифференциальных уравнений распределения потенциалов и теплопроводности, которые осуществил численным методом, а точнее — методом конечных разностей [155, 164]. Это позволило ему при решении поставленных задач учесть изменение в процессе КТС теплофизических характеристик металла, геометрических параметров соединений, а также влияние энергетического и силового воздействия на зону сварки и скрытую теплоту плавления металла в ядре.
Эту методику, которая заключается в совместном решении дифференциальных уравнений распределения потенциалов и теплопроводности, в дальнейшем с уточнением граничных условий стали широко использовать при решении различных задач технологии точечной сварки методом конечных разностей и методом конечных элементов, как отечественные [157, 165…174], так и зарубежные [175…179] исследователи.
При исследованиях тепловых процессов в зоне формирования точечного сварного соединения в большинстве случаев осуществляют совместное решение дифференциального уравнения (2.15), описывающего электрическое поле, и дифференциального уравнения теплопроводности Фурье, которое при условии, что теплоемкость и плотность металла не зависят от температуры, записывают чаще всего в следующем виде [3, 16]:
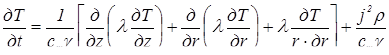 , (2.25) , (2.25)
где с
m
, γ
, λ
и ρ
— соответственно, массовая теплоемкость, плотность, коэффициенты теплопроводности и удельного электрического сопротивления металла; j
— плотность тока.
Сведения о температуре металла в зоне сварки, полученные расчетом по данным методикам, по-видимому, являются наиболее близкими к истинным ее значениям при конкретных условиях сварки. Так, расчетные изотермы температуры плавления (рис. 2.26) по конфигурации и геометрическому положению весьма близки к границам ядра расплавленного металла, экспериментально определяемым на различных стадиях его формирования [165, 172…174].
2.4.3.
Тепловой баланс в зоне сварки и расчет сварочного тока
Теплоту Q
ЭЭ
, которая должна выделиться в зоне формирования соединения для получения ядра заданных размеров, можно рассчитать через теплосодержание металла в ней к концу процесса сварки и количество теплоты, отведенное из зоны сварки в процессе формирования соединения. Для этого используют условные схемы теплопередачи в зоне сварки и распределения в ней температуры (рис. 2.27).

В данной методике расчета допускают, что вся теплота Q
ЭЭ
выделяется в цилиндре, диаметр которого равен диаметру d
Э
контакта электрод-деталь. Выделившуюся теплоту Q
ЭЭ
условно разделяют на теплоту Q
1
, которая расходуется на нагрев и плавление металла в выделенном цилиндре (Q
1
≈ 20...30 % от Q
ЭЭ
[3]), а также на теплоту Q
2
, которая отводится в окружающий его металл деталей (Q
2
≈ 20 % от Q
ЭЭ
[3]), и теплоту Q
3
, которая отводится в электроды (Q
3
> 50 % от Q
ЭЭ
[3]). Относительно очень небольшая часть теплоты Q
ЭЭ
отводится с поверхностей деталей радиационной Q
4
и конвективной Q
5
теплоотдачей. Такое распределение теплоты Q
ЭЭ
описывается так называемым «уравнением теплового баланса», которое было предложено еще в 30-х годах прошлого века [180] и используется до настоящего времени в инженерных методиках расчетного определения силы сварочного тока [3, 10, 16]:
 . (2.26) . (2.26)
За прошедший период методики расчета его составляющих неоднократно изменялись и уточнялись [3, 7…11, 16, 85, 87, 161, 164]. По-видимому, наиболее точные, с учетом результатов исследований тепловых процессов с применением ЭВМ [165], методики расчета составляющих уравнения теплового баланса приведены в работе [3].
При расчетах по уравнению теплового баланса (2.26) общего количества теплоты Q
ЭЭ
, требуемой для формирования соединения заданных размеров, радиационной Q
4
и конвективной Q
5
теплоотдачей с поверхностей деталей обычно пренебрегают из-за их относительно малых величин.
Для расчета теплоты в зоне сварки делают ряд допущений. Так, принимают, что средняя температура в цилиндре, диаметром d
Э
, который приближенно равен диаметру ядра, и высотой, равной суммарной толщине двух деталей 2
s
, принимается равной температуре плавления ТПЛ
. Считается, что заметное повышение температуры металла в деталях из-за отвода в них теплоты Q
2
наблюдается на расстоянии х2
от границы цилиндра, которое определяется временем сварки t
СВ
и коэффициентом температуропроводности металла аМ
:
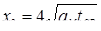 . .
При этом принимается, что средняя температура кольца шириной х2
вокруг цилиндра диаметром d
Э
, равна 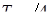 . .
Определение потерь тепла в электроды производится аналогичным образом. При этом принимается, что за счет тепла Q
3
нагревается до средней температуры, равной 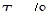 , участок электрода длиной , участок электрода длиной
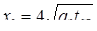 , ,
где аЭ
— коэффициент температуропроводности металла электродов.
С учетом сказанного сокращенное уравнение теплового баланса

в развернутом виде описывают обычно следующим выражением [3]:
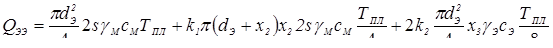 ,(2.27) ,(2.27)
где γМ
и γЭ
— плотность металла свариваемых деталей и электродов; сМ
и сЭ
— теплоемкость металла свариваемых деталей и электродов; k
1
— коэффициент, который учитывает неравномерность распределения температуры в кольце; k
2
— коэффициент, учитывающий влияние на теплоотвод формы рабочей части электродов.
С увеличением времени точечной сварки доля теплоты, отводимой в окружающий металл и электроды, всегда увеличивается, т. е. с увеличением времени сварки всегда уменьшается КПД процесса нагрева [181...184].
Количество теплоты Q
ЭЭ
, которое требуется для образования точечного сварного соединения заданных размеров, используют в основном для приближённого определения силы сварочного тока I
СВ
по зависимости (1.11), обеспечивающего выделение этой теплоты.
2.5.
Объемная пластическая деформация металла в зоне
формирования точечного сварного соединения
Объемная пластическая деформация (ПД) металла при точечной сварке — это один из основных термодеформационных процессов, протекающих в зоне формирования соединения и способствующих его образованию. Она вызывается как внешними факторами, в первую очередь силовым воздействием на детали электродов, так и внутренними факторами, в частности, напряжениями, возникающими при несвободном тепловом расширении (дилатации) металла в зоне сварки между электродами сварочной машины. Пластическое течение металла имеет место на протяжении всего процесса сварки — от формирования начальных контактов, до проковки соединения при его охлаждении. На стадии нагрева во время действия импульса сварочного тока металл в зоне сварки деформируется в основном пластически [3, 16].
Пластическая деформация металла в зоне сварки оказывает решающее влияние на характер электрического и температурного полей, а также на процесс формирования ядра расплавленного металла. В первую очередь, величина объемной пластической деформации влияет на процесс нагрева, так как определяет плотность тока в зоне сварки через площади контактов деталь–деталь и электрод–деталь. При этом нагрев металла в зоне формирования соединения, в свою очередь, оказывает влияние на его пластическую деформацию через изменение сопротивления пластической деформации. В результате такой взаимосвязи и такого взаимовлияния описанных выше процессов осуществляется как бы саморегулирование процесса точечной сварки. Это предполагает, что при устойчивом процессе в зоне сварки должно существовать определенное соответствие между нагревом в ней металла и пластической его деформацией [3, 183, 185…187].
Охлаждение металла в зоне сварки и его кристаллизация в ядре сопровождается температурным и фазовым уменьшением объема, которое приводит на этой стадии формирования соединения к возникновению неравномерного поля остаточных растягивающих напряжений. Это является одной из основных причин образования в соединениях дефектов усадочного характера (трещин, пор, раковин). Только пластическое течение металла в этот период может компенсировать его усадку и предотвратить образование вышеуказанных дефектов сварных соединений [3, 16, 62, 188, 189].
Сведения о пластических деформациях при КТС носят преимущественно качественный характер. Это обусловлено как трудностями их экспериментальных исследований, в первую очередь, из-за закрытого характера зоны сварки и малого ее объема [3, 16, 62, 188, 189], так и трудностями точной математической постановки и решения задачи по определению параметров напряжений и деформаций в условиях динамичного процесса формирования соединений [190...195]. Даже численные методы решения дифференциальных уравнений с применением ЭВМ не позволяют пока достаточно точно определить все сложные взаимовлияния и взаимосвязи термодеформационных процессов, протекающих в зоне формирования соединения [169…172, 174...176, 196...198].
В этой связи весьма перспективным представляется использование для исследований термодеформационных процессов при КТС приближенных теорий напряжений и деформаций, а также расчетно-экспериментальных методов, основы которых изложены, например, в работах [199, 200].
2.5.1.
Методики экспериментальных исследований макродеформаций металла в зоне сварки
Известные экспериментальные исследования процессов макропластических деформаций металла в зоне формирования соединения при КТС проводились в основном по трем методикам.
По первой из них параметры пластической деформации металла в зоне формирования точечного сварного соединения определяли на образцах с направленной текстурой, как, например, в работе [185]. Суть этой методики заключается в следующем.
Свариваемые образцы изготовляются из заготовок, имеющих ярко выраженную, направленную текстуру (проката, поковок). При этом плоскость поверхностей деталей должна быть либо перпендикулярной, либо параллельной к направлению линий текстуры. О деформации металла в зоне сварки судят по искривлениям текстурных линий (рис. 2.28). Однако эта методика не позволяет количественно определять параметры деформаций металла в зоне сварки и отражает лишь качественную картину пластического течения металла в процессе формирования соединения.
По второй методике [62, 189] исследования деформаций при КТС проводились на моделях деталей, рассеченных по плоскости оси электродов и изготовленных из упругих материалов, в частности, из резины. Основное ее достоинство заключается в том, что она относительно легко осуществима технически. Однако корректность полученных результатов вызывает сомнения, поскольку в этой методике не соблюдается один из
основных принципов пластического деформирования металла: неизменность объема металла при пластическом его течении. 
Третья методика — это так называемая «методика координатных сеток», которая широко используется для исследований процессов ПД, например, при обработке металлов давлением. Экспериментальные исследования процессов пластической деформации металла в зоне формирования соединения при контактной точечной сварке по этой методике проводятся на натурных образцах с предварительно нанесенной координатной сеткой, технология изготовления которых предложена и описана в работе [128].
При исследованиях пластических деформаций в плоскостях контактов деталь–деталь и электрод–деталь координатная сетка наносилась на поверхности образцов (рис. 2.29). После этого такие образцы сваривались по обычной технологии точеной сварки, соответствующей материалу деталей и их толщине, а после сварки соединения разрушались. Для выявления динамики изменения параметров макропластических деформаций при КТС по изменению координатной сетки процесс сварки прерывали через заданные промежутки времени, кратные 0,02 с.
При исследовании деформаций в плоскости оси электродов образцы изготовлялись разъемными и координатная сетка наносилась на торцевые поверхности образцов. Перед сваркой образцы совмещались торцевыми поверхностями и зажимались в специальном приспособлении. В этом случае сварку осуществляли так, чтобы плоскость совмещенного разъема образцов совпадала с осью электродов. После сварки такие образцы разрушались по торцевому разъему и производились измерения искажений координатной сетки (рис. 2.30).

Обработка результатов экспериментов в части количественного измерения параметров пластической деформации осуществлялась по методике, описанной в работах [201, 202]. При этом деформация оценивалась только по деформации сторон координатной сетки. Оценить же сдвиговые деформации металла в различных точках зоны сварки затруднительно из-за высокой погрешности измерений угла сдвига, которая в данном случае получается соизмеримой с его величиной.
Относительные смещения металла в зоне сварки  и относительные его деформации и относительные его деформации  по координатам z
и r
в соответствии с принятой методикой оценивались по следующим зависимостям: по координатам z
и r
в соответствии с принятой методикой оценивались по следующим зависимостям:
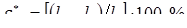 , (2.28) , (2.28)
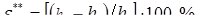 , (2.29) , (2.29)
где l
0
и l
1
— расстояния от базы измерений до и после сварки (при измерении радиальных смещений по координате r
в плоскости сварочного контакта и в плоскости оси электродов за базу принималась ось электродов, а при измерении осевых смещений по координате z
за базу принималась плоскость свариваемого контакта); h
0
и h
1
– длина сторон координатной сетки до и после сварки.
2.5.2.
Характер пластических деформаций металла в зоне сварки
на стадии нагрева
Проведенными экспериментальными исследованиями [203, 204] установлено, что радиальные (координата r
) относительные деформации и смещения металла в плоскости поверхностей свариваемых деталей, в частности в плоскостях контактов электрод–деталь и деталь–деталь (рис.2.31), а также в плоскости оси электродов (координата z
) распределяются неравномерно как по площади контактов, так и по толщине деталей.
При точечной сварке легких сплавов относительные радиальные (по координате r
) смещения  металла в плоскости контакта деталь–деталь (рис. 2.31, а
, в
, д
) не превышают 2...4 %. Причем, зона пластических деформаций распространяется за контур уплотняющего пояска не больше, чем на 5...15 % от его диаметра d
П
. В плоскости контакта электрод–деталь величину относительных осевых (по координате z
) смещений металла в плоскости контакта деталь–деталь (рис. 2.31, а
, в
, д
) не превышают 2...4 %. Причем, зона пластических деформаций распространяется за контур уплотняющего пояска не больше, чем на 5...15 % от его диаметра d
П
. В плоскости контакта электрод–деталь величину относительных осевых (по координате z
) смещений  можно считать вообще незначительной, так как они в течение процесса сварки не превышает 0,5...1 % (рис. 2.31, б
, г
, ж
). можно считать вообще незначительной, так как они в течение процесса сварки не превышает 0,5...1 % (рис. 2.31, б
, г
, ж
).
Относительные радиальные (по координате r
) деформации металла в плоскости контактов электрод–деталь и деталь–деталь 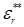 распределяются неравномерно. При этом они даже меняют знак. распределяются неравномерно. При этом они даже меняют знак.
В контуре контакта деталь–деталь координатная сетка растягивается. Наибольшая степень деформаций растяжения  , которая достигает 1,5...3 %, наблюдается на оси электродов. На периферии контакта и за его пределами металл сжимается. Причем сжатие металла локализовано на самой периферии уплотняющего пояска и в относительно узком кольце вокруг контактов деталь–деталь, ширина которого не превышает 5...15 % от их диаметров. Здесь степень деформаций сжатия металла , которая достигает 1,5...3 %, наблюдается на оси электродов. На периферии контакта и за его пределами металл сжимается. Причем сжатие металла локализовано на самой периферии уплотняющего пояска и в относительно узком кольце вокруг контактов деталь–деталь, ширина которого не превышает 5...15 % от их диаметров. Здесь степень деформаций сжатия металла  весьма значительна и достигает 7...15 %. весьма значительна и достигает 7...15 %.
В плоскости контакта электрод–деталь в направлении оси электродов (по координате z
) металл сжимается (рис. 2.31, б
, г
, ж
). Однако степень деформации  металла по оси z
относительно не велика. Она даже на периферии контакта, не превышает 2...3 %. металла по оси z
относительно не велика. Она даже на периферии контакта, не превышает 2...3 %.
Вместе с тем, относительные осевые смещения  металла в плоскости оси электродов по координате z
весьма значительны. Наибольшие относительные осевые смещения металла в плоскости оси электродов по координате z
весьма значительны. Наибольшие относительные осевые смещения  металла в плоскости оси электродов наблюдаются в центре контакта. Их величина к концу процесса достигает значений 8...13 % (рис. 2.31, ж
). По толщине детали их величина относительно стабильна. Это объясняется тем, что осевые относительные деформации металла в плоскости оси электродов наблюдаются в центре контакта. Их величина к концу процесса достигает значений 8...13 % (рис. 2.31, ж
). По толщине детали их величина относительно стабильна. Это объясняется тем, что осевые относительные деформации  металла не велики и, как показали исследования, не превышают 0.5...3 %. Причем, наименьшие значения они имеют в срединной полосе свариваемых деталей. металла не велики и, как показали исследования, не превышают 0.5...3 %. Причем, наименьшие значения они имеют в срединной полосе свариваемых деталей.

Результаты подобных измерений весьма приближённы. Но всё же они позволяют установить качественную картину пластических деформаций металла в зоне сварки, которую можно описать следующей физической моделью.
 При КТС металл в зоне сварки нагревается, в результате чего в ее объеме V
Д
(рис. 2.32), деформируемом пластически (выделен темным цветом), он переходит в пластическое состояние, а в объеме ядра V
Я
, нагретом выше температуры плавления, он расплавляется. Вследствие этого объём металла в зоне сварки увеличивается (проявляется так называемый эффект дилатации) за счет температурного расширения, а в объеме ядра — дополнительно и за счет изменения фазового состояния. Своеобразная форма зоны формирования соединения, неравномерный нагрев металла в ней, его дилатация и разупрочнение, а также схема силового воздействия на детали определяют неравномерное распределение нормальных и касательных напряжений в контактах и в объеме зоны сварки. В результате наблюдается направленное течение металла (показано стрелками), в основном, к границам контакта деталь–деталь. Причем интенсивные пластические деформации в основном локализованы в объёме V
Д1
(заштрихован косой линией), расположенном в области уплотняющего пояска, диаметр d
Д
которого на 5...15 % превышает диаметр d
П
уплотняющего пояска. Объём же металла V
Д2
(заштрихован сеткой), расположенный над ядром, «проседает» в объём ядра практически не деформируясь. При КТС металл в зоне сварки нагревается, в результате чего в ее объеме V
Д
(рис. 2.32), деформируемом пластически (выделен темным цветом), он переходит в пластическое состояние, а в объеме ядра V
Я
, нагретом выше температуры плавления, он расплавляется. Вследствие этого объём металла в зоне сварки увеличивается (проявляется так называемый эффект дилатации) за счет температурного расширения, а в объеме ядра — дополнительно и за счет изменения фазового состояния. Своеобразная форма зоны формирования соединения, неравномерный нагрев металла в ней, его дилатация и разупрочнение, а также схема силового воздействия на детали определяют неравномерное распределение нормальных и касательных напряжений в контактах и в объеме зоны сварки. В результате наблюдается направленное течение металла (показано стрелками), в основном, к границам контакта деталь–деталь. Причем интенсивные пластические деформации в основном локализованы в объёме V
Д1
(заштрихован косой линией), расположенном в области уплотняющего пояска, диаметр d
Д
которого на 5...15 % превышает диаметр d
П
уплотняющего пояска. Объём же металла V
Д2
(заштрихован сеткой), расположенный над ядром, «проседает» в объём ядра практически не деформируясь.
Такой характер пластических деформаций приводит к образованию рельефа в контакте деталь–деталь (уплотняющего пояска) диаметром d
П
, а также зазоров между деталями в нахлестке и вмятин от электродов сВМ
на внешних поверхностях.
Таким образом, за цикл сварки в зоне формирования соединения последовательно во времени и одновременно протекает ряд термодеформационных процессов, например, таких как деформирование свариваемых деталей и их сближение, микроскопические деформации металла в контактах и макроскопические в зоне формирования соединения, формирование механических и электрических контактов, нагрев и расплавление металла, его кристаллизация на последней стадии формирования соединений, которые и определяют конечный результат сварки.
3.
Математические модели основных термодеформационных процессов, протекающих в зоне точечной сварки
Нагрев и пластическая деформация металла в зоне сварки относятся к термодеформационным процессам, наиболее значимо влияющим на устойчивость процесса формирования соединения и во многом предопределяющим его конечные результаты. Это можно считать признанным всеми специалистами. Если нагреву посвящено много экспериментальных и теоретических исследований, предложено большое количество расчетных методик определения его параметров, как аналитических, так и численных, то сведения о процессах пластических деформаций носят в основном самый общий характер. Практически отсутствует их математическое описание (см. раздел 2.5). Вместе с тем, очевидно, что при отсутствии математических моделей этих процессов, методик расчетов количественных значений их параметров, ни о каком научно обоснованном программировании параметров режима точечной сварки не может быть и речи, не говоря уже о создании систем автоматического проектирования технологических процессов (САПР ТП).
Оптимизация параметров силового и энергетического воздействия на детали в современных способах КТС, в том числе и с программированием их параметров режима, затруднительна без определения количественного соотношения между параметрами основных термодеформационных процессов, протекающих в зоне формирования сварного соединения. Определение же количественного соотношения между параметрами основных термодеформационных процессов, протекающих в зоне сварки, невозможно без формального математического их описания, то есть без разработки их математических моделей.
Точное описание формальным языком изменения параметров термодеформационных процессов, протекающих в зоне формирования соединения, а также их взаимозависимости и взаимовлияния, затрудняются их сложностью и динамичностью. Поэтому наиболее рациональным методом решения поставленной задачи является метод идентификации реальных процессов с идеализированными моделями, которые представляется возможным описать математическим языком.
Разработка математической модели термодеформационного равновесия процесса точечной сварки по существу представляет собой математическое описание физической модели процесса формирования соединения, описанной выше в п. 2.5.2. Иными словами, математическая модель термодеформационного равновесия процесса КТС — это математическое описание напряженно-деформированного состояния металла в зоне сварки при формировании точечного сварного соединения. Она основана на результатах экспериментальных исследований процесса сварки, в частности, на вышеуказанном выводе о том, что между тепловыми и деформационными процессами в зоне формирования соединения должно существовать определенное равновесное соотношение, которое зависит от режима сварки, теплофизических свойств металла и геометрических параметров деталей и электродов. При этом подразумевается, что при условиях формирования точечного сварного соединения, близких к условиям оптимальным, система электрод–детали–электрод в силовом отношении замкнута, и силы, действующие на каждый ее элемент, уравновешены в любой момент процесса сварки. Нагрев, разупрочнение, плавление, дилатация и пластическая деформация металла в зоне сварки не нарушают этого равновесия. Выплески же или непровары являются следствием нарушения этого равновесного состояния, вызванного воздействием каких-либо возмущающих факторов. Экспериментальным подтверждением сказанного выше являются как пространственная неподвижность зоны сварки, так и изменение площадей контактов деталь–деталь и электрод–деталь в процессе формирования соединения.
3.1
Термодеформационное равновесие силовой системы
электрод - детали – электрод при традиционных способах сварки
Математическая модель [205, 206], описывающая силовое взаимодействие свариваемых деталей и электродов в контактах деталь–деталь и электрод–деталь, по существу представляет собой математическое описание силового равновесия деталей в процессе формирования соединения при контактной точечной сварке.
Рассмотрим элемент системы электрод–детали–электрод — одну свариваемую деталь, в равновесии в какой-либо фиксированный момент времени t
после момента t
НП
начала плавления металла в контакте деталь–деталь до момента t
СВ
окончания его нагрева, т. е. при  (рис 3.1). Равновесие свариваемой детали в дискретный момент t
будем рассматривать в цилиндрической системе координат.
(рис 3.1). Равновесие свариваемой детали в дискретный момент t
будем рассматривать в цилиндрической системе координат.
Пусть в какой-либо дискретный момент времени t
распределение нормальных, относительно плоскости свариваемого контакта, напряжений по площади S
Э
t
контакта электрод–деталь описывается функцией:
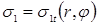 [1]
, (3.1) [1]
, (3.1)
а по площади S
П
t
свариваемого контакта, внутри контура уплотняющего пояска, функцией:
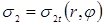 . (3.2) . (3.2)
В свариваемых деталях наблюдается растекание сварочного тока и угол α между линиями тока j
в приконтактных областях деталей меньше 180°. А поскольку ток в них протекает в противоположных направлениях, то между этими линиями тока действуют элементарные электродинамические силы отталкивания Fj
, которые стремятся раздвинуть и свариваемые детали. Пусть их распределение по площади Sjt
растекания тока, приведенное к плоскости свариваемого контакта и направленных нормально к ней, описывается функцией:

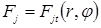 . (3.3) . (3.3)
В работах [3, 16, 207] показано, что давление расплавленного металла в ядре имеет градиент по координате r
, который обусловлен воздействием магнитного поля на жидкий металл. Поэтому распределение давления по площади S
Я
t
ядра в плоскости свариваемого контакта в общем случае следует описывать функцией координат r
и φ
:
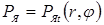 . (3.4) . (3.4)
При сближении свариваемых деталей из-за упругой их деформации в них возникают напряжения. Составляющие этих напряжений, нормальные к плоскости свариваемого контакта, препятствуют сближению свариваемых деталей, т. е., как показано в п. 2.1.2, они уравновешивают часть усилия сжатия электродов. Пусть распределение этих напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является граница контакта деталь–деталь, и ограниченной плоскостями поверхностей свариваемых деталей, описывается функцией:
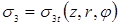 . (3.5) . (3.5)
Для того, чтобы эта система, имеющая одну степень свободы — возможность перемещения в направлении оси электродов, находилась в равновесии, необходимо, чтобы сумма проекций всех сил на координату z
равнялась нулю. В данном случае это условие равновесия можно записать следующим образом:
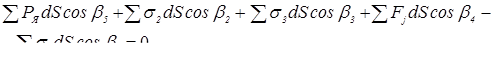 , ,
где β1
, β2
, β3
, β4
, β5
— углы между соответствующими элементарными силами и координатой z
, в данном случае равные нулю, потому что по принятым в зависимостях (3.1)…(3.5) условиям элементарные силы нормальны к плоскости свариваемого контакта; dS
—
площадь действия элементарной силы.
При условии равенства нулю углов β
соответствующие значения  будут равны единице. Тогда написанное выше уравнение равновесия можно преобразовать к следующему виду: будут равны единице. Тогда написанное выше уравнение равновесия можно преобразовать к следующему виду:
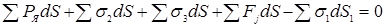 . (3.6) . (3.6)
Условие равновесия (3.6) фактически является интегральным и в цилиндрической системе координат, в интегральной форме может быть записано следующим образом:
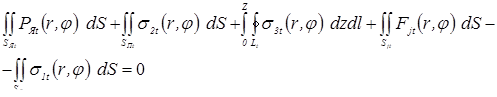 , (3.7) , (3.7)
где Lt
– контур контакта деталь–деталь.
Данное интегральное условие равновесия включает в себя два важных взаимосвязанных технологических параметра: напряжения в контакте электрод–деталь —  , и площадь уплотняющего пояска — S
П
t
, т. е. параметры внешнего силового воздействия на зону сварки и деформирования в ней металла. Это дает возможность при известных остальных его составляющих, выражающих параметры внутренних термодеформационных процессов, определять величину одного из них при заданном значении другого. Кроме того, все составляющие условия (3.7) зависят от термодинамического состояния металла в зоне сварки, характеризуемого температурой и фазовым состоянием, а потому описывают изменение и взаимовлияние всех основных термодеформационных процессов, протекающих в зоне сварки. Поэтому его можно назвать «уравнением термодеформационного равновесия процесса контактной точечной сварки». , и площадь уплотняющего пояска — S
П
t
, т. е. параметры внешнего силового воздействия на зону сварки и деформирования в ней металла. Это дает возможность при известных остальных его составляющих, выражающих параметры внутренних термодеформационных процессов, определять величину одного из них при заданном значении другого. Кроме того, все составляющие условия (3.7) зависят от термодинамического состояния металла в зоне сварки, характеризуемого температурой и фазовым состоянием, а потому описывают изменение и взаимовлияние всех основных термодеформационных процессов, протекающих в зоне сварки. Поэтому его можно назвать «уравнением термодеформационного равновесия процесса контактной точечной сварки».
Точные вычисления непосредственно по уравнению (3.7) весьма затруднительны. Это объясняется отсутствием или сложностью аналитических решений ряда частных задач, входящих в данное уравнение. Например, таких, как распределение напряжений в контактах и их изменение в ходе процесса формирования соединения, определение значений давления в ядре и его градиента в плоскости свариваемого контакта, а также функций, точно описывающих граничные условия и их изменение в процессе сварки. Поэтому для приближенных решений технологических задач уравнение (3.7) целесообразно упростить.
Допущение об осесимметричности зоны формирования соединения при КТС значительно упрощает определение пределов интегрирования. Тогда, для рассматриваемой в равновесии одной детали уравнение (3.7) можно переписать со следующими пределами интегрирования:
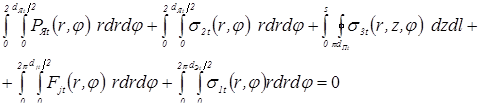 , (3.8) , (3.8)
где s
–
толщина свариваемых деталей, d
Я
t
, d
П
t
, d
Э
t
, djt
, –
диаметры соответственно ядра, контакта деталь–деталь, контакта электрод–деталь и площади растекания линий сварочного тока в момент времени t
.
Приближенные вычисления значений Fjt
показали, что при применяемых режимах сварки электродинамические силы, раздвигающие свариваемые детали из-за растекания в них сварочного тока, очень малы и составляют незначительную часть от сварочного усилия (меньше 0,5 %). Поэтому, при приближенных технологических расчетах этими силами можно пренебречь и 4-й интеграл в (3.8) можно принять равным нулю:
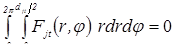 . .
Очевидно, что интегрирование напряжений в контакте электрод-деталь по площади этого контакта, при любом их распределении, даст величину, равную усилию сжатия деталей электродами. Поэтому 5-й интеграл в (3.8), выражающий сумму напряжений в площади контакта электрод–деталь, можно принять равным усилию сжатия электродов F
Э
t
в момент времени t
:
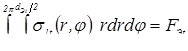 . .
Третий интеграл в (3.8), описывающий сумму напряжений от упругой деформации деталей при их прогибе, после вычислений по цилиндрической поверхности равен усилию F
Д
t
,
которое необходимо для сближения свариваемых деталей до их соприкосновения:
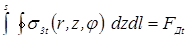 . .
Усилие F
Д
t
в условиях сварки может достигать 10 % [100]. Оно практически не изменяется в процессе формирования соединения [81] и при выборе режимов сварки может учитываться как постоянная составляющая. При приближенных технологических расчетах величину F
Д
t
можно вычислять по зависимости (2.5).
Приближенные расчеты по зависимостям, приведенным в работах [3, 16, 207] показали, что градиент давления в ядре, обусловленный электродинамическим действием сварочного тока, не превышает 5 % от средней его величины, которая определяется термодеформационными процессами в зоне сварки. Поэтому, с целью упрощения расчетов, можно считать, что градиент давления в ядре отсутствует, т. е. допустить, что давление в ядре постоянно по всему объему и не зависит от координат r
и φ
. Тогда после вычисления 1-го интеграла в (3.8), который выражает величину усилия F
Я
t
, развиваемого давлением жидкого металла в площади ядра, получаем:
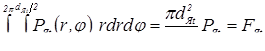 , (3.9) , (3.9)
где РЯ
t
– среднее значение давления расплавленного металла в ядре;
Напряжения во 2-м интеграле уравнения (3.8), который выражает сумму нормальных напряжений в площади уплотняющего пояска, рационально учитывать через их среднее значение, не зависящее от координат r
и φ
. По теореме о среднем [208] — среднее значение напряжений в площади уплотняющего пояска σСР
t
можно выразить следующим образом:
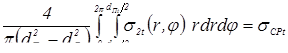 . .
Отсюда интеграл, который выражает сумму нормальных напряжений в площади уплотняющего пояска, можно определить следующим образом:
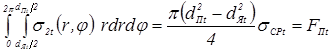 , (3.10) , (3.10)
где F
П
t
–
усилие в площади уплотняющего пояска.
Тогда интегральное уравнение (3.8) термодеформационного равновесия процесса формирования соединений при традиционных способах КТС можно, с учетом сказанного выше, преобразовать к окончательному виду, удобному для практических расчетов:
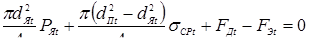 , (3.11) , (3.11)
где, для момента времени t
, d
Я
t
и d
П
t
– диаметры, соответственно, ядра расплавленного металла и уплотняющего пояска; P
Я
t
– давление расплавленного металла в ядре; σ
СР
t
– среднее значение нормальных напряжении в площади уплотняющего пояска; F
Д
t
– усилие, необходимое для сближения свариваемых деталей до соприкосновения их поверхностей; F
Э
t
– усилие сжатия деталей электродами.
Уравнение термодеформационного равновесия процесса контактной точечной сварки (3.11) позволяет для любого момента процесса формирования соединения решать две задачи.
Первая из этих задач — технологическая. Решение данной задачи позволяет рассчитывать усилие сжатия электродов F
Э
t
, как параметр режима сварки, которое необходимо для формирования уплотняющего пояска заданного диаметра d
П
t
, величину которого можно задавать из условия устойчивого формирования соединения при КТС.
Вторая задача — исследовательская. Ее решение может быть использовано при отработках новых технологий КТС. При решении этой задачи, наоборот, для любого момента процесса формирования соединения, по уравнению (3.11) можно рассчитывать диаметр уплотняющего пояска d
П
t
при заданном значении усилия сжатия электродов F
Э
t
.
Очевидно, что оба этих решения имеют большое практическое значение. Первое решение позволяет определить требуемое усилие сжатия электродов при выборе режимов сварки, а второе — моделировать термодеформационные процессы, протекающие в зоне сварки. При этом, для решении любой из этих задач необходимо для любого момента процесса сварки определять все составляющие уравнения (3.11), т. е. количественно определять параметры основных термодеформационных процессов, которые протекают в зоне формирования соединения.
3.2.
Термодеформационное равновесие силовой системы
электрод-детали-электрод при контактной точечной сварке
с обжатием периферийной зоны соединения
Способы КТС с обжатием периферийной зоны соединений, описанные в п. 1.2.3, в которых обжатие осуществляют в области уплотняющего пояска (см. рис. 1.7), не нашли широкого практического применения в основном из-за относительно низкой стойкости токопроводящего электрода. Причиной этого является то, что обжатие деталей в области уплотняющего пояска вызывает необходимость уменьшения внутреннего диаметра обжимной втулки и, следовательно, наружного диаметра рабочей части токопроводящего электрода до значений, близких к диаметру ядра, которые значительно меньше стандартных. В результате токопроводящий электрод перегревается из-за высокой плотности тока и ухудшения условий его охлаждения вследствие уменьшения площади сечения его токопроводящей части. В связи с этим был разработан способ КТС с обжатием периферийной зоны соединений вне контура уплотняющего пояска, в котором силовое взаимодействие деталей значительно сложнее, чем при традиционных способах КТС, и уже не описывается уравнением (3.11).
3.2.1. Способ контактной точечной сварки с обжатием периферийной зоны соединений вне контура уплотняющего пояска
Способ контактной точечной сварки с обжатием периферийной зоны соединений вне контура уплотняющего пояска [209] заключается в том, что в нем, как и в описанных выше, соединяемые детали сжимают токопроводящими электродами, прикладывают вокруг них дополнительное периферийное усилие для обеспечения сжатия в уплотняющем пояске и пропускают импульс сварочного тока. Отличается он тем, что дополнительное периферийное усилие прикладывают вне контура уплотняющего пояска.
 При осуществлении данного способа КТС токопроводящие электроды 1 (рис. 3.2) с диаметром рабочей части D
Э
и обжимные втулки 2 с внутренним диаметром d
ВВ
и наружным диаметром d
ВН
сжимают свариваемые детали 3, соответственно, усилиями токопроводящих электродов F
Э
и обжимных втулок F
О
. В плоскости сварочного контакта эти усилия уравновешиваются силой F
Я
, развиваемой давлением расплавленного металла в ядре (диаметром d
Я
) по его площади, усилием в площади уплотняющего пояска F
П
и усилием в площади кольцевого контакта F
К
, расположенного вне контура уплотняющего пояска L
1
. Вследствие того, что при сварке металл вытесняется в направлении контакта деталь–деталь с образованием в контуре уплотняющего пояска L
1
рельефа высотой h
П
, представляется возможным передавать часть усилия обжатия F
О
в зону сварки (в контур L
1
) за счет силового сопротивления деталей F
У
их прогибу между контурами уплотняющего пояска L
1
и кольцевого контакта L
2
. Таким образом, в зону сварки может быть передана часть усилия обжатия F
О
, прилагаемого между контурами L
2
и L
3
, за вычетом его части, уравновешиваемой в кольцевом контакте F
К
и упругим сопротивлением деталей F
Д
при их сближении до соприкосновения (передаваемое усилие не может быть больше усилия F
У
сопротивления деталей их суммарному прогибу между контурами L
1
и L
2
на величину высоты рельефа h
П
). Это предоставляет возможность увеличить внутренние диаметры обжимных втулок d
ВВ
и диаметры D
Э
электродов и, следовательно, их стойкость. При осуществлении данного способа КТС токопроводящие электроды 1 (рис. 3.2) с диаметром рабочей части D
Э
и обжимные втулки 2 с внутренним диаметром d
ВВ
и наружным диаметром d
ВН
сжимают свариваемые детали 3, соответственно, усилиями токопроводящих электродов F
Э
и обжимных втулок F
О
. В плоскости сварочного контакта эти усилия уравновешиваются силой F
Я
, развиваемой давлением расплавленного металла в ядре (диаметром d
Я
) по его площади, усилием в площади уплотняющего пояска F
П
и усилием в площади кольцевого контакта F
К
, расположенного вне контура уплотняющего пояска L
1
. Вследствие того, что при сварке металл вытесняется в направлении контакта деталь–деталь с образованием в контуре уплотняющего пояска L
1
рельефа высотой h
П
, представляется возможным передавать часть усилия обжатия F
О
в зону сварки (в контур L
1
) за счет силового сопротивления деталей F
У
их прогибу между контурами уплотняющего пояска L
1
и кольцевого контакта L
2
. Таким образом, в зону сварки может быть передана часть усилия обжатия F
О
, прилагаемого между контурами L
2
и L
3
, за вычетом его части, уравновешиваемой в кольцевом контакте F
К
и упругим сопротивлением деталей F
Д
при их сближении до соприкосновения (передаваемое усилие не может быть больше усилия F
У
сопротивления деталей их суммарному прогибу между контурами L
1
и L
2
на величину высоты рельефа h
П
). Это предоставляет возможность увеличить внутренние диаметры обжимных втулок d
ВВ
и диаметры D
Э
электродов и, следовательно, их стойкость.
Так, например, производилась сварка образцов из стали 12Х18Н10Т на машине МТПУ-300 с использованием цилиндрических обжимных втулок и электродов с плоской рабочей поверхностью из сплава Бр.Х. Параметры режимов, максимально допустимые внутренние диаметры обжимных втулок d
ВВМАХ
, при которых обеспечивалась передача упругостью деталей технологически требуемого усилия сжатия в площади уплотняющего пояска (в приведенных примерах 95 % от F
О
) приведены в табл. 3.1.
При этом диаметры рабочих поверхностей d
Э
задавались в соответствии с известными рекомендациями для обычных способов сварки, обеспечивающих наибольшую стойкость электродов. Диаметры же цилиндрических поверхностей электродов D
Э
задавались по внутреннему диаметру обжимной втулки d
ВВ
, которые определяли из условий способов: при сварке по способу с обжатием в области уплотняющего пояска d
ВВ
задавались в пределах контура уплотняющего пояска d
П
, а при сварке по данному способу в пределах d
ВВМАХ
.
Таблица 3.1
Параметры режимов и электродов при сварке с обжатием периферийной зоны соединения
| Толщина
деталей
s
,
мм
|
Параметры режимов
|
Параметры соединения и
электродов, мм
|
| I
СВ
,
кА
|
t
СВ
,
c
|
F
СВ
,
даН
|
F
Э
,
даН
|
F
О
,
даН
|
d
ВВМАХ
мм
|
d
Я
,
мм
|
d
Э
|
d
П
|
D
Э
|
| Прото
тип
|
Новый
|
| 1+1
2+2
3+3
|
6,2
8,9
11,3
|
0,16
0,28
0,36
|
460
900
1350
|
270
548
830
|
190
360
520
|
7,7
15
34
|
5.0
7.0
9.0
|
5.0
8.0
10.0
|
6.5
9.4
11.9
|
6,0
9,0
11.0
|
8,0
16,0
25,0
|
Стойкость электродов оценивалась по количеству сваренных точек, приводящих к увеличению рабочих поверхностей электродов на 10 %. При этом получены следующие результаты: при сварке по способам с обжатием в области уплотняющего пояска и вне его среднеарифметическое количество точек при сварке трех серий образцов каждой толщины соответственно составило: 1 + 1 мм — 17 и 63; 2 + 2 мм — 23 и 187; 3 + 3 мм — 27 и 276. Таким образом, стойкость электродов при сварке по данному способу увеличивается в 4...10 раз, что показывает высокую эффективность данного способа в части повышения стойкости электродов.
Очевидно, что для способов КТС с обжатием периферийной зоны соединений необходима другая математическая модель силового взаимодействия деталей, учитывающая их особенности.
3.2.2.
Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения
Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения [210...212], от модели термодеформационного равновесия при традиционных способах КТС, описанной выше, отличается в основном математическим описанием деформационных процессов, протекающих вне контура уплотняющего пояска. Особенности этих процессов, в частности, возможность разделения в процессе формирования соединения контакта деталь–деталь на два отдельных, установлены экспериментально (рис 3.3).

Причиной разделения контакта деталь–деталь являются прогибы ω1
и ω2
свариваемых деталей 3, вследствие увеличения высоты h
П
уплотняющего пояска между ними в процессе КТС с обжатием периферийной зоны соединения, которое происходит вследствие дилатации и объемных пластических деформаций металла в зоне сварки. В результате из общего контакта деталь–деталь, который формируется при сжатии холодных деталей, образуются два раздельных: свариваемый контакт, который формируется как и при традиционных способах КТС в площади уплотняющего пояска, ограниченного наружным контуром L
1
t
, и замкнутый кольцевой контакт в области сжатия деталей обжимными втулками (с внутренним L
2
t
и наружным L
3
t
контурами). Это возможно в том случае, если внутренний контур обжимных втулок L
4
больше контура уплотняющего пояскаL
1
t
, т. е. в том случае, если обжатие осуществляется вне контура уплотняющего пояска.
В рассматриваемой модели процесса формирования соединения, в любой момент времени t
, внутри изменяющегося контура уплотняющего пояска L
1
t
протекают те же процессы, что и при традиционных способах КТС. Поэтому напряжения и силы, действующие в зоне формирования соединения и нормальные относительно плоскости свариваемого контакта, обозначим теми же функциями, что и в модели традиционных способов контактной точечной сварки без обжатия периферийной зоны соединений (см. зависимости (3.1)…(3.5)):
- 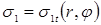 — напряжения в площади S
Э
t
контакта электрод–деталь; — напряжения в площади S
Э
t
контакта электрод–деталь;
- 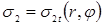 — напряжения в площади S
П
t
свариваемого контакта деталь–деталь; — напряжения в площади S
П
t
свариваемого контакта деталь–деталь;
- 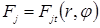 — распределение электродинамических сил по площади Sjt
растекания тока, которые приведены к плоскости контакта и нормальны к ней; — распределение электродинамических сил по площади Sjt
растекания тока, которые приведены к плоскости контакта и нормальны к ней;
- 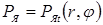 — распределение давления по площади S
Я
t
ядра в плоскости свариваемого контакта; — распределение давления по площади S
Я
t
ядра в плоскости свариваемого контакта;
- 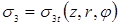 — напряжения,
возникающее из-за упругой деформации деталей при их сближении до соприкосновения, которые распределены так же по цилиндрической поверхности, но отличающейся тем, что ее направляющей является не контур уплотняющего пояска L
1
t
, а внешний контур L
3
t
кольцевого контакта. — напряжения,
возникающее из-за упругой деформации деталей при их сближении до соприкосновения, которые распределены так же по цилиндрической поверхности, но отличающейся тем, что ее направляющей является не контур уплотняющего пояска L
1
t
, а внешний контур L
3
t
кольцевого контакта.
Применительно к данной модели, пусть распределение нормальных напряжений σ4
, относительно плоскости свариваемого контакта, в площади S
В
t
кольцевого контакта обжимная втулка–деталь описывается функцией:
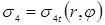 , (3.12) , (3.12)
а в площади S
К
t
кольцевого контакта деталь–деталь функцией:
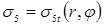 . (3.13) . (3.13)
Тогда равновесие элемента замкнутой силовой системы электрод–детали–электрод (одной детали), имеющей при сварке одну степень свободы — перемещение по координате z
(ось электродов), в цилиндрической системе координат, аналогично уравнению (3.7), с учетом функций (3.12) и (3.13), описывается следующим интегральным уравнением:
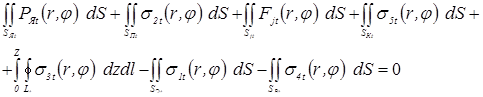 (3.14) (3.14)
В данной модели параметры термодеформационных процессов внутри контура L
1
t
уплотняющего пояска и вне внешнего контура L
3
t
кольцевого контакта деталь–деталь аналогичны параметрам при традиционном способе сварки. Поэтому 1-ый, 2-ой, 5-ый и 6-ой интегралы в уравнении (3.14) с такими же допущениями, как и в уравнении (3.8): зона сварки осесимметрична, давление расплавленного металла в ядре постоянно по всему объему, вычисляют так же, как и для традиционных способов КТС. Поскольку электродинамические силы отталкивания деталей, как и при обычных условиях КТС незначительны по сравнению с усилием сжатия в свариваемом контакте, то 3-ий интеграл в уравнении (3.14), как и в уравнении (3.8), можно принять равным нулю. Очевидно, что значения 7-го и 4-го интегралов равны усилиям сжатия, распределенным по площадям кольцевых контактов втулка–деталь F
О
t
и деталь–деталь F
К
t
:
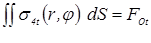 , (3.15) , (3.15)
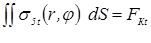 . (3.16) . (3.16)
Тогда с учетом сказанного и зависимостей (3.9), (3.10), (3.15) и (3.16) уравнение (3.14) можно преобразовать к форме, аналогичной уравнению (3.11) и удобной для практических расчетов:
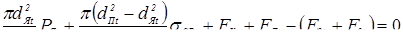 . (3.17) . (3.17)
Здесь, для момента времени t
, d
Я
t
и d
П
t
—
диаметры, соответственно, ядра расплавленного металла и уплотняющего пояска; P
Я
t
—
давление расплавленного металла в ядре; σ
СР
t
—
среднее значение нормальных напряжении в площади уплотняющего пояска; F
Д
t
—
усилие, необходимое для сближения свариваемых деталей до соприкосновения их поверхностей; F
К
t
—
усилие сжатия деталей в кольцевом контакте; F
Э
t
—
усилие сжатия деталей токопроводящими электродами; F
О
t
—
усилие обжатия деталей втулками.
Наибольшую практическую ценность представляют решения уравнения (3.17) относительно F
Э
t
и F
О
t
(расчет режимов) при заданных значениях d
П
t
и d
ВВ
, либо относительно d
П
t
(анализ процесса) при заданных значениях F
Э
t
, F
О
t
и d
ВВ
.
При этом значения РЯ
t
, d
Я
t
, σСР
t
и F
Д
t
могут быть рассчитаны по тем же методикам, что и в уравнении (3.11).
При практических расчетах по уравнению (3.17) усилие F
К
t
, распределенное по площади кольцевого контакта втулка–деталь всегда равно усилию обжатия F
О
t
, которое либо задается, либо рассчитывается как параметр режима сварки. Усилие же, распределенное по площади кольцевого контакта деталь–деталь F
К
t
можно определить из условия равновесия кольцевого элемента детали (рис. 3.4), ограниченного контурами L
1
t
и L
3
t
, которое в интегральной форме можно записать следующим образом:
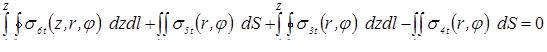 , (3.18) , (3.18)
где 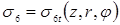 – распределение напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является контур L
1
t
. – распределение напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является контур L
1
t
.

Очевидно, что в уравнении (3.18) 2-ой, 3-ый и 4-ый интегралы при тех же допущениях, аналогичны соответствующим интегралам уравнения (3.14) и равны, как и в (3.17), соответственно, F
К
t
, F
Д
t
и F
О
t
.
Точно вычислить 1-ый интеграл в уравнении (3.18) для определения F
К
t
в уравнении (3.17), то есть решить дифференциальное уравнение
С. Жермен-Лагранжа, в настоящее время затруднительно по причинам, описанным в п. 2.1.2. Но если учесть, что температура по ширине уплотняющего пояска изменяется от температуры плавления ТПЛ
металла (на границе ядра) до температуры, равной примерно 0,2ТПЛ
(на внешнем его контуре), то решение можно упростить. В этом случае можно допустить (поскольку модуль упругости Е
→ 0), что при упругом прогибе деталей между контурами L
1
t
, и L
2
t
, который происходит вследствие увеличения высоты уплотняющего пояска h
П
t
, металл в области уплотняющего пояска работает как пластический шарнир. Тогда, учитывая изложенное выше и схему воздействия сил на детали, их прогиб между контурами L
1
t
, и L
2
t
приближенно можно рассчитать как деформацию круглой пластинки с отверстием, за которое принимается область внутри контура L
1
t
, жестко закрепленной по внутреннему контуру обжимной втулки L
2
t
, силами σ6
t
,
распределенными по цилиндрической поверхности, направляющей которой является контур L
1
t
. Применяя известное решение этой задачи [213] 1-ый интеграл в уравнении (3.18) определяется следующим выражением:
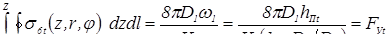 , (3.19) , (3.19)
где D
1
и D
2
— цилиндрическая жесткость свариваемых деталей равная:
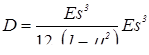 , ,
причем D
1
— меньшая; h
П
t
— высота уплотняющего пояска; Е —
модуль упругости; s
—
толщина детали; μ
— коэффициент Пуассона; F
У
t
— сила упругого сопротивления деталей прогибу 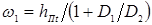 ; Kt
— коэффициент, равный: ; Kt
— коэффициент, равный:
 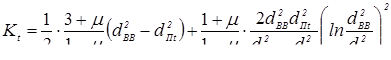 ; ;
d
ВВ
—
внутренний диаметр втулки; d
П
t
— диаметр уплотняющего пояска.
Тогда уравнение (3.18) с учетом (3.19) можно преобразовать к виду, удобному для практических расчетов,
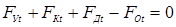 . (3.20) . (3.20)
Относительно диаметра уплотняющего пояска d
П
t
при заданных значениях усилий F
Э
t
и F
О
t
, а также заданном внутреннем диаметре обжимной втулки d
ВВ
, уравнение (3.17), как и уравнение (3.11), решается однозначно. При решении задач по выбору параметров режима (расчет по уравнению (3.17) значений усилий F
Э
t
и F
О
t
и, в случае необходимости, диаметра обжимной втулки d
ВВ
при заданных значениях диаметров уплотняющего пояска d
П
t
) одно и то же усилие в площади свариваемого контакта F
C
t
(в контуре L
1
t
), равное
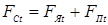 . (3.21) . (3.21)
где F
Я
t
и F
П
t
— усилия сжатия в площадях ядра и уплотняющего пояска (см. зависимости (3.9) и (3.10)); может быть получено при различных сочетаниях F
Э
t
и F
О
t
в пределах, обусловленных упругостью деталей (максимальной величины F
У
t
= F
У
t
МАХ
).
Эта неопределенность устраняется наложением на уравнение (3.17) дополнительных технологических условий, определенных при экспериментальных исследованиях известных способов контактной точечной сварки с обжатием периферийной зоны соединения. Их можно сформулировать следующим образом:
- наиболее оптимальные условия формирования соединения создаются в том случае, если в конце процесса, т. е. при t
=
t
СВ
, упругостью деталей F
У
t
,
передается в контур уплотняющего пояска L
1
t
50...100 %, от требуемого условием отсутствия выплеска усилия сжатия в площади уплотняющего пояска F
П
t
;
- величину усилия сжатия в площади кольцевого контакта F
К
t
целесообразно ограничить пределами возможных отклонений усилия в приводах машин для точечной сварки (они не должны превышать 5...10 % от усилия сжатия в контуре уплотняющего пояска F
С
t
[9…11, 14…16, 17...19]), поскольку при F
К
t
> 0 (при соприкосновении деталей в области обжимной втулки) F
У
t
= F
У
t
МАХ
, и увеличение усилия обжатия F
О
t
приводит только к увеличению усилия в кольцевом контакте F
К
t
(зависимость (3.20)), без увеличения усилия в контуре уплотняющего пояска F
С
t
.
Оговоренные выше технологические условия, приняв обозначения такими же, как и в уравнениях (3.8) и (3.14), можно выразить следующими зависимостями, в которых отсутствие индекса t
указывает на их справедливость только для момента окончания процесса сварки (при t
=
t
СВ
):
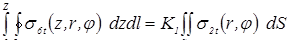 , ,
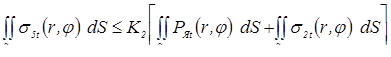 . .
Эти интегральные выражения после вычисления интегралов с допущениями и граничными условиями, аналогичными уравнению (3.17), можно преобразовать к следующему виду:
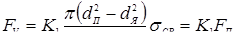 или или 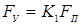 , (3.22) , (3.22)
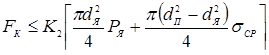 или или 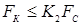 , (3.23) , (3.23)
где для момента t
=
t
СВ
, F
У
– усилие, передаваемое упругостью деталей в контур уплотняющего пояска при t
=
t
СВ
; F
К
– усилие сжатия в площади кольцевого контакта; F
С
— усилие сжатия деталей в площади свариваемого контакта; К1
, К2
—
коэффициенты, равные: К1
= 0,5…1, К2
= 0,05…0,1; d
Я
, d
П
, P
Я
и σСР
— значения d
Я
t
, d
П
t
, P
Я
t
и σСР
t
при t
=
t
СВ
.
Очевидно, что при выполнении условия (3.22) и большой жесткости деталей, либо при уменьшении расстояния между контурами L
1
t
и L
2
(d
ВВ
– d
П
t
→ 0) наличие кольцевого контакта не является обязательным условием процесса сварки (F
К
t
→ 0). В этом случае соприкосновение деталей вне контура уплотняющего пояска может отсутствовать (при F
У
t
МАХ
>
F
О
t
значение F
К
t
=
0). При этом 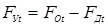 (из зависимости (3.20)). (из зависимости (3.20)).
Из сказанного выше следует, что уравнения (3.8) и (3.11) для традиционных способов сварки являются частным случаем уравнений равновесия (3.14) и (3.17) для КТС с обжатием периферийной зоны соединения, поскольку при d
ВВ
≤ d
П
t
значение F
К
t
=
0 и если (F
Э
t
+
F
О
t
) считать одним усилием, то уравнения (3.14) и (3.17) превращаются, соответственно, в уравнения (3.8) и (3.11). Следовательно, по уравнению (3.17) можно рассчитывать параметры усилия и для обычных условий формирования соединения при традиционных способах КТС. Это позволяет использовать одну и ту же компьютерную программу при расчетах параметров усилия для любых известных способов точечной сварки.
Для практических расчетов по уравнениям термодеформационного равновесия процесса точечной сварки (3.11) или (3.17) необходимо иметь методики определения значений всех их составляющих для любого момента процесса формирования соединения.
3.
3. Оценка теплового состояния зоны сварки на стадии нагрева
Температура металла в зоне сварки является основным фактором, определяющим его сопротивление пластической деформации. Оно же, в свою очередь, через процессы микро- и макропластических деформаций определяет интенсивность процессов выделения и перераспределения теплоты и, в конечном итоге, размеры ядра расплавленного металла. Кроме того, нагрев вследствие дилатации металла, является активным фактором процесса макропластических деформаций при формировании соединения. В силу этого математическое моделирование изменения температурного поля при КТС является исходным условием разработки математических моделей других термодеформационных процессов. При этом анализ термодеформационных процессов на аналитических моделях становится возможным только в том случае, если математическая модель температурного поля удовлетворяет, по крайней мере, двум условиям: описывается непрерывной функцией; в достаточной степени точно отражает динамику его изменения в процессе формирования соединения.
Очевидно, что численные методы расчета температуры при КТС методами конечных разностей или конечных элементов (см. п. 2.4.2), хотя и наиболее точные в настоящее время, не удовлетворяют условию непрерывности функции. В аналитических моделях их иногда рационально использовать на стадии количественных расчетов.
Известные же аналитические методы, также приведенные в п. 2.4.2, как показывают сравнения расчетных и экспериментальных значений температуры, не удовлетворяют требованиям современных способов точечной сварки по точности получаемых результатов.
Вместе с тем, в теории и практике обработки металлов давлением для исследований термодеформационных процессов часто используют расчетно-экспериментальные методы. Анализ результатов исследований тепловых процессов в зоне точечной сварки показывает, что для исследований термодеформационных процессов в ряде случаев и при КТС допустимо использование подобных методов. При решении таких задач использование расчетно-экспериментального метода оценки теплового состояния зоны формирования соединения является компромиссным вариантом удовлетворения вышеуказанных условий. Причем, применительно к условиям точечной сварки их разработка облегчается такими свойствами процессов КТС, установленными рядом исследователей [73...76], как монотонность и подобие изменения параметров термодеформационных процессов при формировании точечных сварных соединений.
Ниже изложен метод оценки теплового состояния зоны формирования точечного сварного соединения на стадии нагрева (по содержанию типичный расчетно-экспериментальный) [214, 215], специально разработанный для аналитического моделирования термодеформационных процессов в условиях точечной сварки [206, 216].
3.3.1
Экспериментально - расчетный метод оценки теплового
состояния зоны сварки на стадии нагрева
Температурное поле при конкретных условиях формирования соединения и его изменение во время импульса сварочного тока можно описать функциями, аппроксимированными по экспериментально определенным характерным пространственно-временным точкам. Например, при точечной сварке относительно просто экспериментально можно определить ряд параметров температурного поля в зоне формирования соединения:
- изменение по времени и максимальную температуру в контакте электрод–деталь ТЭ
;
- время tНП
, за которое температура в контакте деталь-деталь достигает значений температуры плавления ТПЛ
свариваемого металла;
- изменение геометрического положения изотермы температуры плавления ТПЛ
во времени (границы ядра расплавленного металла);
- температуру в контакте деталь-деталь ТД
и температуру на границе уплотняющего пояска ТП
.
В общем случае, задача идентификации является задачей оценки параметров априорно заданной функции. Если тип нелинейной функции неизвестен, то аппроксимация истинной нелинейности может быть выполнена, например, с помощью полиномов. Однако во всех случаях идентификацию можно проводить только в предположении некоторого специфического типа нелинейной аппроксимирующей функции, параметры которой подлежат идентификации.
Для нахождения вида аппроксимирующих функций (рис. 3.5), которые с достаточной точностью отображали бы изменение температуры в плоскости оси электродов по координатам z
(рис. 3.5, а
) и r
(рис. 3.5, б
) для конкретного процесса сварки в любой его момент экспериментально можно определить значение температуры, по крайней мере, в четырёх характерных точках. По координате z
:
- температуру ТЭ
в контакте электрод-деталь (2 точки);
- температуру плавления ТПЛ
по координатам границы (2 точки);
и по координате r
:
- температуру плавления ТПЛ
по координатам границы ядра (2 точки);
- температуру плавления ТПЛ
по координатам границы ядра (2 точки);

Анализом имеющихся экспериментальных результатов и результатов, полученных расчетом температуры в зоне точечной сварки методом конечных разностей, установлено, что изменение температуры по координатам z
и r
(рис. 3.5) удовлетворительно описывается функцией вида
 , (3.24) , (3.24)
где x
— произвольная переменная; a
и b —
коэффициенты, которые можно определять по имеющимся экспериментальным значениям температуры.
Из анализа известных результатов экспериментальных и расчётных исследований можно сделать заключение о том, что изменение температуры по времени на стадии нагрева в любой точке зоны сварки подобно характеру изменения температуры в контакте электрод–деталь (рис. 3.6). При этом общеизвестно, что температура в контакте электрод–деталь в процессе сварки на стадии нагрева возрастает монотонно (рис. 3.6, а
).
При точечной сварке непосредственное измерение температуры в контакте деталь–деталь и свариваемых деталях затруднено малыми размерами и закрытым характером зоны формирования соединения, а также быстротечностью процесса КТС. Вместе с тем, о характере изменения температуры в центре контакта деталь–деталь можно судить по трем характерным точкам, которые представляется возможным определить экспериментально (рис. 3.6, б
):
- в начале процесса температура в центре контакта равна температуре окружающей среды (при t
= 0 — Т
t
= 0);
- в момент начала плавления t
НП
она равна температуре плавления ТПЛ
металла (при t
= t
НП
— Т
t
= ТПЛ
);
- в момент выключения сварочного тока t
СВ
она достигает максимального Т
M
значения (при t
= t
СВ
— Т
t
= Т
M
).

Приемлемую сходимость расчетных и экспериментальных значений температуры в интервале времени до начала плавления металла (0 ≤
t
≤
t
НП
) позволяют получить показательная и логарифмическая функции вида:
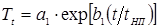 и и 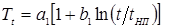 , ,
где a1
и b1
– коэффициенты, которые могут быть определены по имеющимся экспериментальным значениям температуры.
Однако при сварке на относительно жестких режимах, когда отношение t
НП
/
t
СВ
= 0,15...0,3, а — ТМ
/ТПЛ
= 1,1...1,25, что обычно и имеет место при сварке на режимах средней жесткости, показательная функция в интервале t
НП
…t
СВ
имеет локальный максимум температуры, что противоречит имеющимся экспериментальным и расчетным данным о монотонном характере увеличения температуры во время действия импульса сварочного тока. Логарифмическая же функция не имеет этого недостатка. Поэтому она и была принята для описания изменения температуры по времени в первоначальном варианте данного экспериментально-расчетного метода [214], разработанном для условий КТС деталей из легких сплавов электродами со сферической рабочей поверхностью. Однако окончательные зависимости для расчетов параметров термодеформационных процессов при описании изменения температуры по времени логарифмической функцией получались неоправданно громоздкими [216]. Поэтому, в дальнейшем, при его совершенствовании применительно к особенностям сварки деталей из сталей электродами с плоской рабочей поверхностью, а также точечной сварки с обжатием периферийной зоны соединений, логарифмическая функция была заменена на степенную [210, 215, 217] вида:
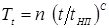 , (3.25) , (3.25)
где n
и c
– коэффициенты, которые подлежат идентификации.
Данная функция при указанных выше соотношениях t
НП
/
t
СВ
и ТМ
/ТПЛ
не имеет локального максимума в интервале t
НП
…t
СВ
, хотя несколько и завышает значения температуры при t
≤
t
НП
по сравнению с результатами, которые получаются при расчетах численными методами. Вместе с тем эксперименты показывают, что действительная скорость нарастания температуры в контакте деталь–деталь очень высока, так как следы оплавления на поверхностях деталей, по крайней мере, при сварке сталей, наблюдаются уже через один полупериод протекания сварочного тока. При относительной простоте степенная функция дает хорошую сходимость расчетных и экспериментальных результатов.
Разработка математической модели температурного поля по расчетно-экспериментальному методу, в сущности, сводится к определению и математическому описанию взаимосвязей аппроксимирующих функций (3.24), описывающих изменение температуры по координатам z и r
, и функции (3.25), описывающей ее изменение по времени t
.
При описании изменения температуры TZt
по оси электродов (по координате z
), в дискретный момент времени t
, значения коэффициентов b
и a
в зависимости (3.24) применительно к конкретному процессу сварки можно найти, если представляется возможным экспериментально определить значения температуры в характерных точках в разные моменты процесса сварки. Для этого, предварительно для момента времени t
преобразовав зависимость (3.24) к виду
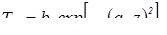 , (3.26) , (3.26)
можно составить систему уравнений, учитывая, что при z
=
h
Я
t
/2 температура TZt
=
T
ПЛ
, а при z
=
s
— TZt
=
T
Э
t
:
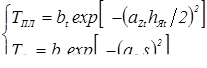 , ,
где для момента времени t
, h
Я
t
— высота ядра расплавленного металла;
T
Э
t
— температура на поверхности деталей под электродами; T
ПЛ
— температура плавления свариваемого металла; s
— толщина деталей.
Решив эту систему уравнений, находим значения коэффициентов bt
и aZt
:
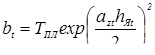 , ,  , ,
подставив которые в (3.26) получим зависимость для расчета температуры TZt
на оси электродов в точке с координатой z
в момент времени t
. После преобразований она будет иметь следующий вид:
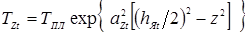 . (3.27) . (3.27)
Эта зависимость имеет хорошую сходимость результатов при расчете изменения температуры по координате z
, с результатами расчетов температуры численными методами, в частности, методом конечных разностей (рис. 3.7). Это, например, подтверждается на изменением температуры по оси электродов в момент выключения сварочного тока при сварке сплава АМг6 (рис. 3.7, а
), рассчитанное по формуле (3.27) и методом конечных разностей в работе [165].
Для расчета в момент времени t
изменения температуры Trt
по координате r
зависимость (3.24) преобразуем к виду
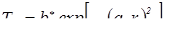 . (3.28) . (3.28)
Определить коэффициенты  и а
rt
можно аналогично тому, как определяли коэффициенты aZt
и bt
, по известным значениям температуры Trt
в характерных точках (рис. 3.5, б
): при r
= d
П
t
/2 значение температуры Trt
на границе уплотняющего пояска равно T
П
, то есть Trt
= T
П
, при r
= d
Я
t
/2 — Trt
= T
ПЛ
и при r
= 0 — Trt
= T
М
. и а
rt
можно аналогично тому, как определяли коэффициенты aZt
и bt
, по известным значениям температуры Trt
в характерных точках (рис. 3.5, б
): при r
= d
П
t
/2 значение температуры Trt
на границе уплотняющего пояска равно T
П
, то есть Trt
= T
П
, при r
= d
Я
t
/2 — Trt
= T
ПЛ
и при r
= 0 — Trt
= T
М
.
Поскольку в точке с координатами  и и  температура имеет максимальное значение T
М
, то из зависимостей (3.27) и (3.28) можно записать следующее соотношение: температура имеет максимальное значение T
М
, то из зависимостей (3.27) и (3.28) можно записать следующее соотношение:
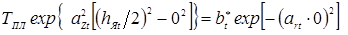 , ,
из которого можно определить коэффициент  для данных условий для данных условий
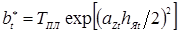 , ,
а зависимость для расчета температуры по координате r
можно записать следующим образом:
 . .
Поскольку на границе ядра расплавленного металла при 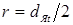 металл нагрет до температуры его плавления T
ПЛ
, то из этой зависимости можно определить значение коэффициента а
rt
, которое будет равно металл нагрет до температуры его плавления T
ПЛ
, то из этой зависимости можно определить значение коэффициента а
rt
, которое будет равно
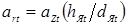 . (3.29) . (3.29)
Тогда зависимость для расчета изменения температуры по координате r
в окончательном варианте имеет следующий вид
 . (3.30) . (3.30)
Изменение температуры по координате r
в момент выключения сварочного тока, рассчитанное по зависимости (3.30), также хорошо согласуется с результатами расчетов методом конечных разностей (рис.3.7, б
). Для расчетов изменения температуры в любой точке плоскости z
–
r
зависимости (3.27) и (3.30) следует объединить. Это можно сделать, если учесть, что температурное поле неразрывно, а температура на оси электродов TZt
при любом значении координаты z
является максимальным значением температуры ТМ
по координате r
, т. е. при r
=
0 значение TZt
= ТМ
.
Из зависимостей (3.27) и (3.30) это соотношение температур по координатам z
и r
можно выразить следующим образом:
 . .
Отсюда после преобразований получаем зависимость для расчета температуры в момент времени t
в любой точке плоскости z
–
r
в пределах зоны сварки, которая имеет следующий вид:
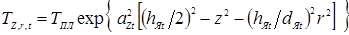 . (3.31) . (3.31)
Характер изменения температурного поля по координатам z
и r
, рассчитанный по зависимости (3.31) в момент выключения сварочного тока, показан на рис. 3.8.
Зависимость (3.31) описывает изменение температурного поля в любой точке плоскости z
–
r
только в отдельные дискретные моменты
времени t
.
Для анализа термодеформационных процессов в зоне сварки необходимо математически описать изменение температуры в каждой ее точке и по времени. Это можно сделать, если с зависимостью (3.31) функционально увязать зависимость (3.25), которая и описывает изменение тем
пературы по времени. Определить значения коэффициентов n
и c
в зависимости (3.25) можно исходя из следующего.
В момент времени t
НП
начала плавления металла в контакте деталь–деталь температура в точке с координатами z
=
0 и r
=
0 равна значениям температуры плавления металла ТПЛ
, т. е. при t
=
t
НП
— Tt
=
ТПЛ
. В момент же окончания импульса тока t
СВ
температура в контакте деталь-деталь достигает максимальных значений ТМ
, т. е. при t
=
t
СВ
— Tt
=
ТМ
. Это позволяет составить следующую систему уравнений
 , ,
после решения которой и находим искомые коэффициенты n
и c
:
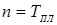 , , 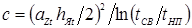 . .
Тогда зависимость для расчета изменения температуры в центре контакта деталь–деталь можно записать в виде
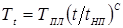 , (3.32) , (3.32)
где с
—
коэффициент, определяемый для момента t
=
t
СВ
, т. е. по конечной высоте ядра h
Я
, и равный
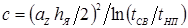 , ,
где aZ
– значение коэффициента aZt
, определяемого по зависимости (3.27) также для момента t
=
t
СВ
, т. е. так же по конечной высоте ядра h
Я
и максимальной температуре T
Э
в контакте электрод–деталь:
 . .
Характер изменения температуры в центре свариваемого контакта, рассчитанный по зависимости (3.32) для различных условий сварки, показан на рис.3.9. Такое изменение температуры вполне согласуется с имеющимися данными, полученными как экспериментально, так и расчетами методом конечных разностей.
Выразим значение температуры плавления металла ТПЛ
в формуле (3.32) через ТМ
из формулы (3.31) при z
=
0 и r
= 0
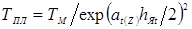
и подставим это выражение в зависимость (3.32). Тогда эту зависимость можно преобразовать к следующему виду:
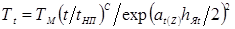 . (3.33) . (3.33)
Если допустить, что характер изменения температуры по времени от нуля до ее максимальных значений в любой точке зоны формирования соединения подобен характеру изменения температуры в центре контакта деталь–деталь, то значение ТМ
в зависимости (3.33) равно значению Т
z
,
r
,
t
рассчитанному по зависимости (3.31). Тогда зависимость (3.33) с учетом (3.31) и (3.29) можно преобразовать к следующему виду:
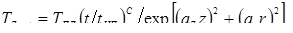 . (3.34) . (3.34)
Зависимость (3.34) описывает изменение температуры в зоне сварки на стадии нагрева по координатам z
и r
, а также по времени t
при допущении, что характер изменения температуры по времени во всех точках зоны формирования точечного сварного соединения подобен характеру изменения температуры в центре контакта деталь–деталь.
 Однако, в действительности, как показали расчеты температурных полей методом конечных разностей, характер изменения температуры по времени на периферии зоны сварки несколько иной, чем характер изменения температуры в центре контакта деталь–деталь. Это означает, что величина коэффициентов az
и ar
,
характеризующих градиент температуры по координатам z
и r
,
должна изменяться по времени и зависеть от условий сварки, в частности, от формы рабочей поверхности электродов. Однако, в действительности, как показали расчеты температурных полей методом конечных разностей, характер изменения температуры по времени на периферии зоны сварки несколько иной, чем характер изменения температуры в центре контакта деталь–деталь. Это означает, что величина коэффициентов az
и ar
,
характеризующих градиент температуры по координатам z
и r
,
должна изменяться по времени и зависеть от условий сварки, в частности, от формы рабочей поверхности электродов.
Проведенные исследования показали, что изменение значений коэффициентов az
и ar
может быть аппроксимировано функцией вида [217]
 , (3.35) , (3.35)
где at
и a
– текущие и конечные значения коэффициента az
или ar
при их изменении по времени; т
и п –
экспериментально определяемые коэффициенты аппроксимации.
Тогда окончательно формулу для расчета изменения температуры в любой точке зоны сварки в любой момент времени в интервале 0 < t
≤
t
СВ
с учетом сказанного выше можно представить в следующем виде:
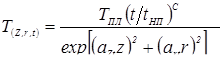 , (3.36) , (3.36)
где t
—
координата времени; c
, azt
и art
– коэффициенты, характеризующие изменение в процессе сварки градиента температуры по цилиндрическим координатам z
и r
и времени t
:
 , , 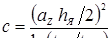 , , 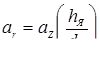 , ,
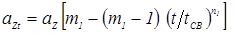 , , 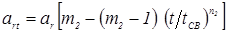 ; ;
ТЭ
—
максимальное значение температуры в контакте электрод–деталь;
t
НП
— время начала плавления металла в контакте деталь–деталь; m
1
, n
1
, m
2
и n
2
— опытные коэффициенты, учитывающие изменение во времени градиента температуры по координатам z
и r
(см. ниже табл. 3.2).
Известные трудности при расчетах температуры по зависимости (3.36) представляет точное определение для конкретных условий сварки момента начала плавления металла в контакте деталь–деталь t
НП
,
максимальной температуры в контакте электрод–деталь ТЭ
, а также коэффициентов m
1
, n
1
, m
2
и n
2
, которые учитывают изменение во времени градиента температуры по координатам z
и r
. Несомненно, что при решении научно-исследовательских задач они в каждом конкретном случае должны определяться индивидуально. При приближенных технологических расчетах они могут быть определены по приведенным ниже обобщенным данным.
Наиболее просто определять момент t
НП
начала плавления металла в контакте деталь–деталь. Это можно осуществить прерыванием процесса сварки (на серийных машинах это можно сделать с шагом 0,02 или 0,01 с). Установлено, что с увеличением жесткости режима сварки момент начала плавления металла t
НП
смещается к началу процесса и существует корреляционная зависимость между значением t
НП
и проплавлением деталей, выраженным отношением высоты ядра расплавленного металла к суммарной толщине деталей h
Я
/2
s
. Усредненная для способов КТС зависимость значений t
НП
от проплавления деталей h
Я
/2
s
, показанная на рис. 3.10, вполне удовлетворительно описывается функцией, интерполированной по полиному Лагранжа [217]:
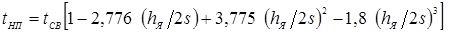 , (3.37) , (3.37)
где t
СВ
–
время сварки; h
Я
– высота ядра; s
–толщина детали.
 Экспериментальное определение максимального значения температуры в контакте электрод-деталь ТЭ
не имеет принципиальных препятствий. Это можно сделать по любой из известных методик, например, описанным в работах [14, 207]. Основная трудность таких измерений — это их относительно большая трудоемкость. Экспериментальное определение максимального значения температуры в контакте электрод-деталь ТЭ
не имеет принципиальных препятствий. Это можно сделать по любой из известных методик, например, описанным в работах [14, 207]. Основная трудность таких измерений — это их относительно большая трудоемкость.
Проведенными исследованиями и обработкой известных результатов экспериментов других исследователей, а также результатов расчетов температуры методом конечных разностей, установлено наличие корреляционной зависимости между максимальным значением температуры в контакте электрод–деталь ТЭ
и относительным проплавлением деталей h
Я
/
2s
(рис. 3.10). Зависимость 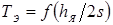 удовлетворительно описывается следующей, относительно простой, аппроксимированной функцией: удовлетворительно описывается следующей, относительно простой, аппроксимированной функцией:
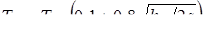 , (3.38) , (3.38)
где ТПЛ
— температура плавления металла; h
Я
— высота ядра; s
—толщина свариваемых деталей.
Наиболее трудоемко определение изменения в процессе формирования соединения коэффициентов azt
и art
, характеризующих изменение градиента температуры по координатам z
и r
. Для этого необходимо измерять значения температуры в характерных точках (см. рис. 3.5), а затем определять значения azt
и art
обратным расчетом по зависимости (3.36). Трудоемкость определения этих коэффициентов можно несколько уменьшить после начала плавления металла. Для этого экспериментально следует измерять изменение высоты h
Я
t
и диаметра d
Я
t
ядра, а коэффициенты azt
и art
так же определять обратным расчетом по зависимостям (3.40) и (3.41). Обработкой значительного числа экспериментальных данных установлено, что характер изменения коэффициентов azt
и art
в процессе формирования точечных сварных соединений зависит в основном от геометрии рабочей поверхности электродов и жесткости режимов сварки.
Наиболее близкий характер изменения градиента температуры по координатам z
и r
в процессе формирования соединения при сварке электродами со сферической рабочей поверхностью (рис. 3.11). При сварке электродами со сферической рабочей поверхностью плавление металла начинается в относительно небольшом объёме и увеличение высоты h
Я
t
(рис. 3.11, а
) и диаметра d
Я
t
(рис. 3.11, б
) ядра происходит плавно. Это обусловлено тем, что градиент изменения температуры по координатам z
и r
в начале процесса нагрева весьма высок, а в процессе сварки плавно уменьшается, вследствие чего уменьшаются и значения коэффициентов azt
(рис. 3.11, а
) и art
(рис. 3.11, б
).
Изменения градиента температуры по координатам z
и r
в процессе формирования соединения при сварке электродами с плоской рабочей поверхностью различаются в большей степени, в особенности в начале процесса сварки (рис. 3.12). 
При сварке электродами с плоской рабочей поверхностью плавление металла начинается по большей площади контакта, чем при сварке электродами со сферической рабочей поверхностью, что обусловлено меньшим градиентом температуры по координате r
. Затем, увеличение высоты h
Я
t
(рис. 3.12, а
) и диаметра d
Я
t
(рис. 3.12, 6
) ядра также происходит плавно. Градиент изменения температуры по координате z
изменяется аналогично предыдущему, соответственно изменяется и azt
(рис. 3.12, а
). Отличия носят лишь количественный характер. Градиент же изменения температуры по координате r
в процессе сварки, в отличие от предыдущего случая, почти не изменяется, хотя в начальной стадии наблюдается повышенный его разброс. Это предопределяет относительно большие начальные значения диаметров ядра (рис. 3.12, б
) и относительно не большие изменения значений art
(рис. 3.12, б
).

При точечной сварке с обжатием периферийной зоны соединения плавление металла начинается по еще большей площади контакта, чем при сварке электродами с плоской рабочей поверхностью (рис. 3.13).

Затем, увеличение высоты h
Я
t
(рис. 3.13, а
) и диаметра d
Я
t
(рис. 3.13, б
) ядра также происходит плавно. Градиент изменения температуры по координате z
изменяется аналогично предыдущим случаям, соответственно изменяется и azt
(рис. 3.13, а
). Отличия носят лишь количественный характер. Градиент же изменения температуры по координате r
, в отличие от предыдущих случаев, в начале процесса сварки меньше чем в конце и монотонно возрастает в процессе формирования соединения. Это предопределяет несколько большие начальные значения диаметров ядра (рис. 3.13, б
) и увеличение значений art
в процессе сварки (рис. 3.12, б
).
Конечно, полученные таким образом значения коэффициентов azt
и art
весьма приближённы, но, как показали сравнения расчётных и экспериментальных значений температуры и размеров ядра, приемлемы для решения приближенных технологических задач. Для практических расчетов полученные значения коэффициентов azt
и art
обобщены аппроксимированными функциями, описывающими их изменение в процессе формирования соединений (зависимости (3.35) и (3.36)). Значения коэффициентов m
1
, n
1
, m
2
и n
2
, необходимые для расчетов температуры в зоне формирования соединения по данному расчетно-экспериментальному методу, для различных условий сварки обобщены в табл. 3.2 [215, 217].
Таблица
3.2
Значения коэффициентов m
1
, n
1
, m
2
и n
2
для расчетов температуры в зоне формирования соединения при различных условиях сварки
| Условия точечной сварки
|
Значения коэффициентов*)
|
| m
1
|
n1
|
m2
|
n2
|
| Электродом со сферической рабочей поверхностью
|
1,9...2,1
|
0,5...0,7
|
1,4...2,1
|
0,5...0,7
|
| Электродом с плоской рабочей поверхностью
|
1,6...1,9
|
0,35...0,45
|
1,9...2,1
|
0,45...0,55
|
| С обжатием периферии сварной точки
|
1,2...1,8
|
0,25...0,35
|
0,05...0,8
|
0,35...0,45
|
| *)
Большие значения относятся к более жестким режимам
|
Изменение температуры в процессе КТС в различных точках зоны сварки, рассчитанное по данному расчетно-экспериментальному методу, в частности, в центре контакта деталь–деталь, в контакте электрод–деталь вполне согласуется с имеющимися данными, полученными экспериментально (осциллографированием) и расчетами методом конечных разностей и конечных элементов (рис 3.14).

Так, температура в центре контакта деталь–деталь (кривая 1) быстро, за время равное 0,1...0,2 t
СВ
, нарастает до температуры, близкой к температуре плавления, а затем рост температуры замедляется. Причем изменение температуры в центре контакта деталь–деталь, рассчитанное по формулам (3.34) и (3.36) совпадает. Это объясняется тем, что она не зависит от координат, т. е. градиента температуры в зоне сварки, и фактически определяется зависимостью (3.33). Изменение же температуры в контакте электрод–деталь, рассчитанное по зависимости (3.36) (кривая 2), ближе к экспериментальным результатам (кривые 3), чем рассчитанное по зависимости (3.34) (кривая 4), поскольку она учитывает различия градиента температуры в разных точках зоны сварки.

Температурное поле в зоне сварки по координатам и времени отличается весьма высоким градиентом температур (рис. 3.15).
Характер изменения температурного поля по координатам и времени вполне соответствует имеющимся данным, полученным как экспериментально, так и решениями дифференциальных уравнений методами конечных разностей и конечных элементов.
3.3.2
Методики расчетного определения размеров ядра и средних
значений температуры в зоне сварки
При решении большинства технологических задач КТС, в частности определения силовых параметров режимов сварки, возникает необходимость в расчетном определении размеров ядра (как правило, его диаметра и высоты) и средних значений температуры в определенных участках зоны формирования соединения.
Размеры ядра
расплавленного металла можно определить по положению изотермы температуры плавления, в частности, высоту h
Я
t
и диаметр d
Я
t
ядра можно определить по координатам пересечения изотермы температуры плавления ТПЛ
с координатными осями z
и r
. Положение изотермы любой температуры в зоне формирования соединения в любой момент времени можно определить из зависимости (3.36), если значение температуры изотермы ТИ
подставить в ее левую часть. После преобразований получаем выражение:
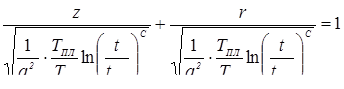 , (3.39) , (3.39)
которое является общеизвестным [208] уравнением эллипса, но только с изменяющимися по времени полуосями.
Например, расположение изотерм (рис. 3.16), показанных сплошными линиями и рассчитанных по зависимости (3.39) для тех же условий сварки, для которых они рассчитывались в работе [165] решением дифференциальных уравнений методом конечных разностей (пунктирные линии), почти совпадают между собой. В частности, в приведенном примере положение изотермы ТИ
= 600 ºС показывает контур ядра расплавленного металла (температура плавления ТПЛ
сплава АМг6 ~ 623 ºС). Причем изотерма ТИ
= 600 ºС, рассчитанная по зависимости (3.39), в большей мере совпадает с контуром ядра, определённым по макрошлифу. Это объясняется тем, что расчетно-экспериментальный метод закладываются конечные размеры (высота h
Я
и диаметр d
Я
) ядра. Таким образом, при ТИ
= ТПЛ
зависимость (3.39) описывает контур ядра расплавленного металла:
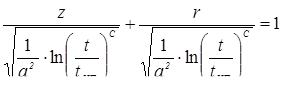 . .
Поскольку полуоси эллипса изотермы температуры плавления равны половине высоты 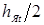 и диаметра и диаметра 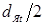 ядра, то по этой зависимости можно определить их значения в любой момент времени t
процесса формирования ядра. После преобразований получены формулы для расчета высоты h
Я
t
и диаметра d
Я
t
ядра в любой момент времени t
после начала плавления металла (времени t
НП
, которое можно определить по зависимости (3.37)) до окончания импульса сварочного тока (при t
НП
<
t
≤
t
СВ
) [217]: ядра, то по этой зависимости можно определить их значения в любой момент времени t
процесса формирования ядра. После преобразований получены формулы для расчета высоты h
Я
t
и диаметра d
Я
t
ядра в любой момент времени t
после начала плавления металла (времени t
НП
, которое можно определить по зависимости (3.37)) до окончания импульса сварочного тока (при t
НП
<
t
≤
t
СВ
) [217]:
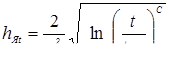 , (3.40) , (3.40)
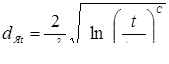 , (3.41) , (3.41)
где azt
и art
— коэффициенты, характеризующие изменение градиентов температуры по координатам z
и r
, которые можно определить по зависимости (3.36) с использованием данных табл. 3.2.
Изменение высоты и диаметра ядра в процессе его формирования, рассчитанные по формулам (3.40) и (3.41), вполне согласуются с данными, полученными из практики КТС (рис. 3.17). Данные формулы дают удовлетворительную сходимость расчетных и экспериментальных результатов (показаны точками), расхождение которых не превышает ± 10 %.

Среднюю температуру
по одной из координат z
или r
, или же по участку плоскости z
—
r
в момент времени t
можно определить из зависимости (3.36), используя общеизвестную [208] теорему о среднем, согласно которой средняя температура по координатам z
или r
на участках z
2
–
z
1
или r
2
–
r
1
, а также по элементу площади S
П
t
в плоскости z
—
r
, может быть выражена следующими зависимостями:
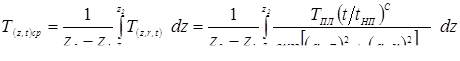 , ,
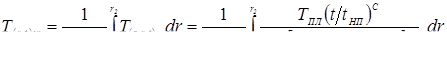 , ,
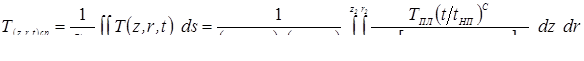 . .
Точные вычисления средних значений температуры в зоне сварки по приведенным выше зависимостям невозможны из-за того, что интегралы вида 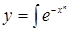 , которые содержатся в вышеуказанных зависимостях, при четных значениях n
аналитически не вычисляются [208]. В таких случаях, как правило, подобные интегралы путем подстановок сводят к интегралам, значения которых вычислены приближенными методами. Для данного случая наиболее подходящим из вышеуказанных является интеграл вида erf (y
), который называют erf-функцией
или функцией ошибок
. Его табличные значения приведены справочниках, например, в [208]. , которые содержатся в вышеуказанных зависимостях, при четных значениях n
аналитически не вычисляются [208]. В таких случаях, как правило, подобные интегралы путем подстановок сводят к интегралам, значения которых вычислены приближенными методами. Для данного случая наиболее подходящим из вышеуказанных является интеграл вида erf (y
), который называют erf-функцией
или функцией ошибок
. Его табличные значения приведены справочниках, например, в [208].
После подстановок, вычисления интегралов и преобразований зависимости для количественных расчетов средних значений температуры в зоне сварки по координатам z
или r
, а также по площади S
П
t
в плоскости
z
—
r
, имеют следующий вид:
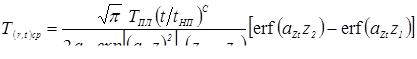 , (3.42) , (3.42)
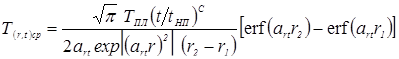 , (3.43) , (3.43)
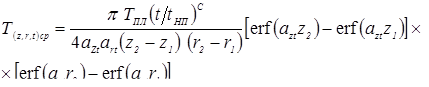 , (3.44) , (3.44)
где для момента времени t
, Т(
z
,
t
)ср
— средняя температура по координате z
на участке z
2
–
z
1
при любом значении r
; Т(
r
,
t
)ср
— средняя температура по координате r
на участке r
2
–
r
1
при любом значении z
; Т(
z
,
r
,
t
)ср
— средняя температура по любому прямоугольному элементу площади 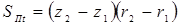 в плоскости оси электродов z
— r
; erf (y
) —
функция ошибок, которая представляет собой интеграл вида в плоскости оси электродов z
— r
; erf (y
) —
функция ошибок, которая представляет собой интеграл вида
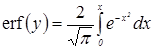 . .
Для распределения температуры в зоне сварки Tz
и Tr
по координатам z
и r
(рис. 3.18), рассчитанного по зависимости (3.36) для момента окончания нагрева, значения средней температуры по координатам z
и r
в пределах ядра расплавленного металла (кривая 1), на оси электродов от границы ядра h
Я
до поверхности листа, толщиной s
(кривая 2), в плоскости свариваемого контакта между границами ядра d
Я
и пояска d
П
(кривая 3), рассчитанные по зависимостям (3.42) и (3.43), а также значение средней температуры в плоскости z
—
r
по площади зоны сварки, которая ограничена уплотняющим пояском d
П
и поверхностью свариваемых деталей, рассчитанное по зависимости (3.44) при z
1
= r
1
=
0, z
2
= s
, r
2
=
d
П
, вполне соответствует существующим представлениям о нагреве металла в процессе формирования точечного сварного соединения.

Таким образом, данный расчетно-экспериментальный метод оценки теплового состояния зоны КТС на стадии нагрева во время действия импульса сварочного тока при относительной простоте расчета, позволяет достаточно точно оценить температуру в любой точке зоны сварки в любой момент процесса формирования точечного сварного соединения. При этом зависимости, выражающие изменение температуры по координатам и времени, являются непрерывными аналитическими функциями и позволяют производить операции математического анализа.
3.4
. Математические модели силового взаимодействия деталей
в площади свариваемого контакта при формировании соединения
Согласно принятым моделям термодеформационного равновесия процесса точечной сварки без обжатия (рис. 3.1) и с обжатием (рис. 3.3) периферийной зоны соединения силовое взаимодействие деталей, сжимаемых электродными устройствами, в площади контура уплотняющего пояска осуществляется металлом, который находится в твёрдой (до начала плавления во всей площади контура уплотняющего пояска) или в твёрдой (после начала плавления в площади уплотняющего пояска, окружающего ядро) и жидкой (в площади ядра расплавленного металла) фазах. Поэтому основными задачами математического моделирования взаимодействия деталей в площади свариваемого контакта при формировании соединения является определение напряжений в площадях контактов, в которых металл находится в твёрдой фазе, и давления в ядре.
3.4.1.
Методика расчета среднего значения нормальных напряжении в контакте деталь - деталь
 Точно рассчитать распределение напряжений в контактах при КТС по-видимому не представляется возможным из-за сложности и динамичности, протекающих в них термодеформационных процессов. Приближённое решение данной задачи [206, 217, 218] основано на допущении, что характер распределения напряжений в контакте деталь–деталь при точечной сварке подобен характеру распределения напряжений в контакте пуансон–деталь при осадке полосы. Это предположение сделано на основании анализа опубликованных работ С. И. Губкина, Е. П. Унксова, В. В. Соколовского и других исследователей, посвященных определению напряжений в контактах. Ими установлено, что в общем случае в площади контакта имеется три участка, которые отличаются распределением касательных напряжений (рис. 3.19). Качественно такой характер распределения нормальных напряжений в контактах электрод–деталь и деталь–деталь при точечной сварке подтверждается экспериментами по затеканию (пластической деформации) металла в узкую щель в электроде (рис. 3.20) и характером деформации периодического рельефа на поверхности детали (рис. 3.21). Точно рассчитать распределение напряжений в контактах при КТС по-видимому не представляется возможным из-за сложности и динамичности, протекающих в них термодеформационных процессов. Приближённое решение данной задачи [206, 217, 218] основано на допущении, что характер распределения напряжений в контакте деталь–деталь при точечной сварке подобен характеру распределения напряжений в контакте пуансон–деталь при осадке полосы. Это предположение сделано на основании анализа опубликованных работ С. И. Губкина, Е. П. Унксова, В. В. Соколовского и других исследователей, посвященных определению напряжений в контактах. Ими установлено, что в общем случае в площади контакта имеется три участка, которые отличаются распределением касательных напряжений (рис. 3.19). Качественно такой характер распределения нормальных напряжений в контактах электрод–деталь и деталь–деталь при точечной сварке подтверждается экспериментами по затеканию (пластической деформации) металла в узкую щель в электроде (рис. 3.20) и характером деформации периодического рельефа на поверхности детали (рис. 3.21).
Можно предположить, что и при сварке в площади контакта в момент времени t
имеется три участка (рис 3.19 и 3.22), отличающихся распределением касательных напряжений τ
, подобно осадке полосы [219]:
1) зона скольжения (участки a
1
b
1
и b
2
a
2
) 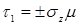 ; ;
2) зона торможения (участки b
1
c
1
и c
2
b
2
) 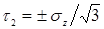 ; ;
3) зона застоя (участки c
1
о
и о
c
2
) 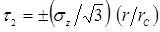 ; ;
где σ
Z
— напряжения, нормальные к плоскости свариваемого контакта;
μ
— коэффициент трения; r
— радиальные координаты точек в плоскости поверхности деталей.
Наличие таких участков в контактах при КТС экспериментально подтверждается, например, в работе [129]. Решением приближенного уравнения равновесия, предложенного
Е. П. Унксовым [219, 220],
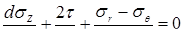 , ,
где s
— толщина детали; σ
z
, σ
r
,
и σθ
— соответственно, нормальные относительно плоскости свариваемого контакта, радиальные и окружные напряжения; совместно с условием пластичности Губера – Мизеса
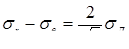 , (3.45) , (3.45)
где σД
— это сопротивление пластической деформации металла в области уплотняющего пояска; получены функции, описывающие изменение нормальных напряжений σ1
Z
, σ2
Z
, σ3
Z
на различных участках контакта, которые, применительно к условиям точечной сварки, имеют следующий вид:
- первый участок при rb
≤
r
≤
ra
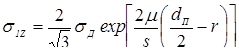 ; (3.46) ; (3.46)
- второй участок при rc
≤
r
≤
rb
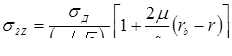 ; (3.47) ; (3.47)
- третий участок при 0 ≤
r
≤
rc
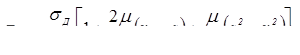 . (3.48) . (3.48)
Здесь μ
– коэффициент трения; d
П
– диаметр контурной площади контакта (уплотняющего пояска).
Координату границы зоны торможения rb
можно определить по зависимости, приведенной в работе [221], которая, применительно к условиям точечной сварки имеет вид
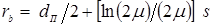 .
(3.49)
.
(3.49)
 Поскольку при КТС в контакте электрод–деталь и, в особенности, деталь–деталь наблюдается схватывание металла [128, 129], то коэффициент трения μ
можно принять равным 0,5. Тогда, согласно (3.49) при μ
= 0,5 — координата Поскольку при КТС в контакте электрод–деталь и, в особенности, деталь–деталь наблюдается схватывание металла [128, 129], то коэффициент трения μ
можно принять равным 0,5. Тогда, согласно (3.49) при μ
= 0,5 — координата 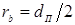 , т. е. зона скольжения (участки a
1
b
1
и a
2
b
2
) отсутствуют, а зона торможения (участки b
1
c
1
и b
2
c
2
) доходит до границы контакта.
, т. е. зона скольжения (участки a
1
b
1
и a
2
b
2
) отсутствуют, а зона торможения (участки b
1
c
1
и b
2
c
2
) доходит до границы контакта.
Расчеты показали, что, пренебрегая уменьшением касательных напряжений в зоне застоя (с1
о
и ос2
(см. рис. 3.19)), получаем абсолютную ошибку при определении средней величины нормальных напряжений σСР
, не превышающую 5...10 %, причем в свариваемом контакте только до начала плавления металла. Поэтому, чтобы упростить расчеты, можно допустить, что распределение касательных напряжений τ
в области 0 ≤
r
≤
d
П
/
2 равномерно и зона торможения распространяется до центра контакта, т. е. r
С
= 0.
Тогда по известной теореме о среднем, после подстановки в нее зависимости (3.47), среднее значение сжимающих нормальных напряжений в свариваемом контакте σСР
t
в любой момент процесса формирования соединения t
можно определить следующим образом
 , (3.50) , (3.50)
где r
1
t
и r
2
t
– соответственно нижний и верхний пределы интегрирования.
При КТС нижний r
1
t
и верхний r
2
t
пределы интегрирования изменяются в течение процесса формирования соединения. До момента начала образования ядра контакт твердого металла осуществляется по всей площади уплотняющего пояска. Поэтому в этот период пределы интегрирования r
1
t
= 0 и r
2
t
= d
П
t
/
2 и интегрирование зависимости (3.47) следует проводить в интервале 0…d
П
t
/
2. При появлении ядра контакт твердого металла осуществляется по уплотняющему пояску шириной b
П
t
= d
П
t
/
2 – d
Я
t
/
2. Следовательно, интегрирование зависимости (3.47) в этот период следует проводить в интервале d
Я
t
/
2…d
П
t
/
2. Поскольку до начала плавления металла d
Я
t
= 0, то интервал интегрирования d
Я
t
/
2…d
П
t
/
2 может быть принят для любого момента КТС при 0 ≤ t
≤ t
СВ
. Тогда, после подстановки в (3.50) зависимостей (3.47) и (3.49) количественное значение σСР
t
можно определить следующим интегральным выражением
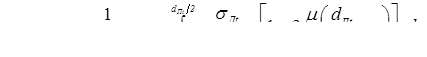 , ,
из которого после вычисления интеграла с вышеуказанными переменными пределами интегрирования получаем формулу для приближенных количественных расчетов среднего значения нормальных напряжений σСР
t
в контакте деталь–деталь в любой момент t
процесса формирования соединения
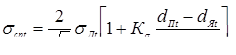 . (3.51) . (3.51)
Здесь, для момента t
процесса формирования соединения, σД
t
— сопротивление деформации металла; d
Я
t
и d
П
t
— текущие значения диаметров, соответственно, ядра и уплотняющего пояска; Кσ
– коэффициент, характеризующий неравномерность распределения в площади контакта нормальных напряжений по координате r
,
который для условий КТС следует принимать в пределах 0,25...0,5.
Согласно выражению (3.47) напряжения σ2
Z
на краю контакта при 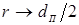 во всех случаях стремятся к значениям сопротивления деформации металла во всех случаях стремятся к значениям сопротивления деформации металла 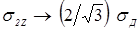 , а в центре контакта при , а в центре контакта при 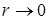 они растут с увеличением отношения диаметра контакта к толщине детали они растут с увеличением отношения диаметра контакта к толщине детали 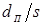 : : 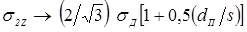 . Это изменение неравномерности распределения напряжений по координате r
, как следует из формулы (3.51), существенно влияет и на средние их значения σСР
t
в площади контакта. Так, минимальные значения . Это изменение неравномерности распределения напряжений по координате r
, как следует из формулы (3.51), существенно влияет и на средние их значения σСР
t
в площади контакта. Так, минимальные значения 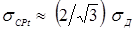 получаются при получаются при 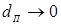 , в случае отсутствия ядра расплавленного металла, или же при уменьшении ширины уплотняющего пояска, т. е. разности , в случае отсутствия ядра расплавленного металла, или же при уменьшении ширины уплотняющего пояска, т. е. разности 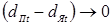 после начала расплавления металла. Причем, это влияние увеличивается с уменьшением толщины свариваемых деталей вследствие увеличения отношения d
П
t
/
s
. после начала расплавления металла. Причем, это влияние увеличивается с уменьшением толщины свариваемых деталей вследствие увеличения отношения d
П
t
/
s
.
 Точность методики расчета σСР
t
до начала плавления металла представляется возможным оценить прямыми измерениями, поскольку при этом условии σСР
t
равно среднему давлению в контакте, которое можно определить делением усилия сжатия электродов F
Э
на его площадь S
К
: Точность методики расчета σСР
t
до начала плавления металла представляется возможным оценить прямыми измерениями, поскольку при этом условии σСР
t
равно среднему давлению в контакте, которое можно определить делением усилия сжатия электродов F
Э
на его площадь S
К
: 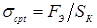 . Например, свариваемые детали сжимали между электродами на экспериментальной установке, описанной в п. 2.1.2 (рис. 2.7), и измеряли при этом контурную площадь контакта по методике угольных пленок (рис. 2.3). Затем определяли экспериментальные значения σСР
и сравнивали их со значениями, рассчитанными по формуле (3.51). Пример такого сравнения для холодных контактов показан на рис. 3.23. Проведенные исследования показали удовлетворительную сходимость экспериментальных (показаны точками) и расчетных (кривая 1) значений напряжений в контактах. . Например, свариваемые детали сжимали между электродами на экспериментальной установке, описанной в п. 2.1.2 (рис. 2.7), и измеряли при этом контурную площадь контакта по методике угольных пленок (рис. 2.3). Затем определяли экспериментальные значения σСР
и сравнивали их со значениями, рассчитанными по формуле (3.51). Пример такого сравнения для холодных контактов показан на рис. 3.23. Проведенные исследования показали удовлетворительную сходимость экспериментальных (показаны точками) и расчетных (кривая 1) значений напряжений в контактах.
Все, сказанное выше, не противоречит существующим представлениям о распределении нормальных напряжений в контактах.
3.4.2.
Методика расчета давления расплавленного металла в ядре
Сведения о давлении расплавленного металла в ядре в литературе по сварке носят в основном предположительно-описательный характер. Это объясняется особенностями точечной сварки, не позволяющими измерить его экспериментально, и сложностью термодеформационных процессов в зоне сварки на стадии нагрева, которая затрудняет расчетное определение его величины.
Ниже изложена методика, разработанная [206, 218, 222] на основании приведенных исследований термодеформационных процессов, протекающих в зоне сварки на стадии нагрева, которая позволяет приближенно рассчитать давление расплавленного металла в ядре в любой момент процесса его формирования. Поставленная цель достигается тем, что реальный процесс пластической деформации металла, окружающего ядро, с определенными допущениями, в частности, об осесимметричности зоны сварки, сводится к решению задачи о деформировании сферической оболочки внутренним давлением Р
(рис. 3.24).
Согласно решению данной задачи Ляме [223] компоненты напряжений в сферических полярных координатах определяются зависимостями:
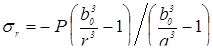 , ,
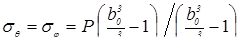 , ,
где σ
r
,
и σθ
, σφ
— радиальное и окружные напряжения; Р —
давление в полости, b
0
— наружный радиус сферы; а —
радиус полости.
Р. Хилл [224], применив условие пластичности Треска – Сен-Венана
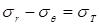 , (3.52) , (3.52)
где σТ
—
предел текучести, распространил это решение на случай упругопластического деформирования внутренним давлением толстостенной сферической оболочки. Согласно этому решению распределение напряжений в толстостенной сферической оболочке при упругопластическом ее деформировании внутренним давлением Р
(слева на рис. 3.24) описывается следующими зависимостями: в упругой области, при c
≤
r
≤
b
0
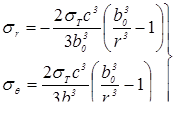 , (3.53) , (3.53)
в пластической области, при а ≤
r
< с
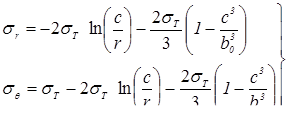 , (3.54) , (3.54)
где a
—
радиус полости; b
0
— наружный радиус сферы; с —
радиус границы пластической области.
В упругой области оба компонента напряжения уменьшаются с увеличением координаты r
. В области пластических деформаций с увеличением r
радиальное напряжение уменьшается по величине, тогда как, по условию пластичности, окружное напряжение увеличивается. Максимальное значение окружного напряжения достигается на границе пластического и упругого состояний металла (радиус с
). Аналогичный характер изменения напряжений по координате r
получен при решении подобной задачи и в работе [225].
Экспериментально установлено (см. п. 2.5.2), что на стадии нагрева максимальные относительные пластические деформации свариваемых деталей по координате r
,
достигающие 15 %, локализованы в области контура сварочного контакта, диаметром d
П
t
, и в узком поясе (шириной
≤ 0,05...0,15 d
П
t
) вокруг него. Упругие же радиальные деформации свариваемых деталей вне этой зоны незначительны, и поэтому ими можно пренебречь. Тогда процесс деформации металла в зоне формирования соединения при контактной точечной сварке можно уподобить процессу деформации металла сферической оболочки с бесконечно толстыми стенками,
т. е. при b
0
→ ∞ (справа на рис 3.24).
 Так как металл, выдавливаемый в зазор деталь–деталь, при несвободном расширении в площади уплотняющего пояска, шириной Так как металл, выдавливаемый в зазор деталь–деталь, при несвободном расширении в площади уплотняющего пояска, шириной 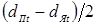 , преодолевает силу реакции противоположной детали, то можно предложить, что он находится в объемно-сжатом напряженном состоянии аналогично металлу зоны а — д
при деформации сферической оболочки. При сварке давление в ядре и напряжения в уплотняющем пояске стремятся раздвинуть свариваемые детали аналогично тому, как и давление в полости сферы и напряжения в зоне объемно-сжатого металла , преодолевает силу реакции противоположной детали, то можно предложить, что он находится в объемно-сжатом напряженном состоянии аналогично металлу зоны а — д
при деформации сферической оболочки. При сварке давление в ядре и напряжения в уплотняющем пояске стремятся раздвинуть свариваемые детали аналогично тому, как и давление в полости сферы и напряжения в зоне объемно-сжатого металла
а — д
при деформировании сферической оболочки. При деформировании сферической оболочки разъединению полусфер препятствует металл с растягивающими окружными σθ
напряжениями при r
>
c
, в процессе же сварки разъединению деталей препятствует усилие сжатия электродов F
Э
. Поскольку ядро в плоскости свариваемых деталей имеет форму круга, в плоскости оси электродов — эллипса, а пластические деформации металла локализованы в области уплотняющего пояска, то можно допустить, что характер напряженного состояния пластически деформируемого металла в приконтактной области уплотняющего пояска подобен характеру напряженного состояния металла в объемно-сжатой зоне а — д
при деформировании сферической оболочки с бесконечно толстой стенкой.
Поэтому процесс деформации металла в зоне сварки на стадии роста ядра можно приближенно уподобить процессу деформации при расширении сферической полости в оболочке с бесконечно толстыми стенками, если оболочку мысленно рассечь по диаметральной плоскости, и сумму растягивающих окружных напряжений σθ
, при r
> д
заменить усилием сжатия электродов, т. е. принять, что:
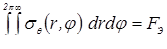 . (3.55)
. (3.55)
Таким образом, определить давление Р
в ядре можно, решая задачу только в пластической области, так как упругие деформации влияния на его величину практически не оказывают. При этом контуром уплотняющего пояска можно считать границу металла при деформировании сферической оболочки, находящегося в объемно-сжатом состоянии.
Тогда изменение напряжений по координате r
в пластической области (а ≤
r
< с
) при b
0
→ ∞,
согласно зависимостям (3.54) можно описать следующим образом:
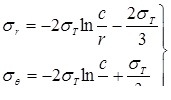 . (3.56) . (3.56)
Более точные результаты, по мнению ряда исследователей [220, 225], получаются при использовании условия пластичности не Треска – Сен-Венана (3.52), а Губера – Мизеса (3.45).
При высоких скоростях деформации и высокой температуре деформируемого металла, что имеет место при точечной сварке, «деформируемость» металла точнее характеризуется не пределом текучести σТ
, а сопротивлением пластической деформации σД
металла с учетом процессов его упрочнения и разупрочнения [226]. Поэтому для условий пластической деформации металла при точечной сварке предел текучести σТ
в условии пластичности (3.45) рационально заменить сопротивлением пластической деформации σД
. Тогда давление в полости сферической оболочки, которое равно радиальному напряжению металла на поверхности полости, но с обратным знаком, необходимое для осуществления пластического течения металла до радиуса с
, по зависимости (3.56) можно рассчитать следующим образом:
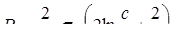 . (3.57) . (3.57)
Координату пластической области с
можно выразить через координату д
границы объемно-сжатого металла из зависимостей (3.56), так как при r
= д
окружные напряжения σθ
=
0. После преобразований получаем следующее соотношение с
и д
:
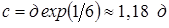 . (3.58) . (3.58)
Согласно принятой модели можно записать следующее соотношение координат элементов сферической оболочки и зоны сварки: д =
d
П
t
/
2, а
а =
d
Я
t
/
2. Причем, значение координаты области пластических деформаций, выраженной зависимостью (3.58), практически совпадает с координатой, полученной при экспериментальных исследованиях пластических деформаций металла в зоне формирования соединения при КТС (см. п. 2.5.2).
С учетом сказанного выше зависимость (3.57) для расчета давления расплавленного металла в ядре РЯ
t
в любой момент времени t
процесса формирования соединений при КТС можно преобразовать к следующему окончательному виду:
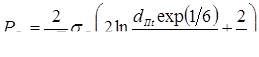 , (3.59) , (3.59)
где для момента времени t
, РЯ
t
– давление расплавленного металла в ядре; σД
t
–сопротивление пластической деформации металла в области уплотняющего пояска; d
Я
t
и d
П
t
– диаметры, соответственно, ядра и уплотняющего пояска.
Из формулы (3.59) следует, что давление расплавленного металла в ядре прямо пропорционально сопротивлению пластической деформации металла и логарифму отношения диаметра уплотняющего пояска к диаметру ядра. Поэтому давление расплавленного металла в ядре в процессе его формирования может только уменьшаться, поскольку всегда уменьшается как сопротивление деформации металла σД
t
, так и отношение d
П
t
/d
Я
t
. Очевидно, что при при уменьшении ширины уплотняющего пояска, то есть разности 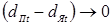 , давление в ядре, как средние значения напряжений σСР
t
, стремятся к минимальному значению: , давление в ядре, как средние значения напряжений σСР
t
, стремятся к минимальному значению: 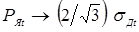 . .
Проверить точность расчетной методики прямым измерением давления расплавленного металла в ядре пока не представляется возможным. Поэтому экспериментальную оценку точности зависимостей для расчета давления в ядре РЯ
t
(3.59) и средних значений нормальных напряжений σСР
t
(3.51) производили косвенно. Такую экспериментальную оценку, пример которой показан на рис. 3.25, осуществляли следующим образом.
 Сваривали образцы деталей, последовательно прерывая процесс сварки на различных его стадиях (через 0,02 с). При этом для моментов прерывания измеряли текущие значения (показаны круглыми точками) диаметров уплотняющего пояска (свариваемого контакта) d
П
и ядра d
Я
(после начала плавления металла). По ним определяли экспериментальные значения среднего давления по площади свариваемого контакта Сваривали образцы деталей, последовательно прерывая процесс сварки на различных его стадиях (через 0,02 с). При этом для моментов прерывания измеряли текущие значения (показаны круглыми точками) диаметров уплотняющего пояска (свариваемого контакта) d
П
и ядра d
Я
(после начала плавления металла). По ним определяли экспериментальные значения среднего давления по площади свариваемого контакта 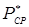 — — 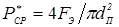 (показаны треугольными точками). Кроме того, для этих же моментов процесса сварки, используя измеренные значения d
Я
и d
П
, рассчитывали РЯ
и σСР
по зависимостям (3.59) и (3.51), а также значения среднего давления по площади свариваемого контакта (показаны треугольными точками). Кроме того, для этих же моментов процесса сварки, используя измеренные значения d
Я
и d
П
, рассчитывали РЯ
и σСР
по зависимостям (3.59) и (3.51), а также значения среднего давления по площади свариваемого контакта 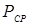 по зависимости: по зависимости: 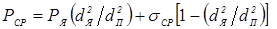 (значения сопротивления деформации металла σД
t
в зависимостях (3.59) и (3.51) определяли по методике, описанной ниже в разделе 3.5). (значения сопротивления деформации металла σД
t
в зависимостях (3.59) и (3.51) определяли по методике, описанной ниже в разделе 3.5).
Очевидно, что до начала плавления металла (~ 0,375 t
СВ
) значения РСР
и σСР
совпадают (показаны сплошной линией). После начала плавления металла значения σСР
меньше, чем значения РСР
(показаны пунктирной линией), так часть усилия сжатия уравновешивается давлением РЯ
расплавленного металла в ядре.
Об адекватности расчетных значений РЯ
и σСР
и их значений в реальном процессе КТС судили по расхождению значений 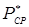 и и 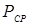 для различных условий сварки (они не превышают 10...20 %). Это, по-видимому, можно считать вполне приемлемым для приближенных методик расчета. для различных условий сварки (они не превышают 10...20 %). Это, по-видимому, можно считать вполне приемлемым для приближенных методик расчета.
Таким образом, разработанные модели силового взаимодействия деталей в площади свариваемого контакта позволяют в любой момент процесса сварки рассчитать давление расплавленного металла в ядре и величину нормальных напряжений в площади свариваемого контакта. Однако для этого необходимо в любой момент процесса иметь возможность определять сопротивление пластической деформации металла в зоне сварки, величина которого входит в зависимости (3.51) и (3.59).
3.5.
Методики определения параметров термодеформационных процессов в условиях формирования точечного сварного соединения
Количественное определение сопротивления пластической деформации (СПД) металла в зоне сварки σД
t
, по-видимому, является наиболее ответственным, так как в основном определяет точность расчётов σСР
t
и РЯ
t
по зависимостям (3.51) и (3.59), и сложным элементом при решении технологических задач по уравнениям (3.11) и (3.17) термодеформационного равновесия процессов КТС. В то же время это понятие применительно к условиям точечной сварки в теории КТС является весьма неопределенным. Так, предложенное в работах [3, 80] понятие «условного сопротивления пластической деформации», определяемое как отношение усилия сжатия электродов F
Э
к площади контакта деталь–деталь 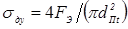 , по сути представляет собой, описанное выше, среднее давление , по сути представляет собой, описанное выше, среднее давление 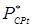 в свариваемом контакте. Причем определяется оно только экспериментально и не может быть использовано в расчетных методиках в свариваемом контакте. Причем определяется оно только экспериментально и не может быть использовано в расчетных методиках
Ниже изложена методика количественного определения сопротивления пластической деформации металла в зоне формирования точечного сварного соединения, которая адаптирована к условиям КТС и позволяет рассчитать его количественные значения в любой момент процесса сварки на стадии нагрева [203, 206, 210, 215… 217].
3.5.1.
Сопротивление пластической деформации металла в условиях деформирования при повышенных температурах
Под сопротивлением пластической деформации металла понимается интенсивность напряжений, достаточная для осуществления в теле или его части пластической деформации (ПД) при заданных термомеханических условиях деформирования [221, 226…230].
На величину СПД металла при пластическом деформировании его при высоких температурах, что, в частности, является характерным и для КТС на стадии нагрева, одновременно влияют несколько технологических факторов: температура деформируемого материала, а также степень и скорость деформации. Это обусловлено тем, что в деформируемом металле при температуре выше температуры рекристаллизации ТРЕКР
, которую ориентировочно принимают равной ТРЕКР
≈ 0,4ТПЛ
[231], одновременно протекают два противоположных процесса: упрочнение — из-за наклепа зерен, и разупрочнение — из-за их рекристаллизации. Конечный результат зависит от соотношения между скоростью деформации и скоростью рекристаллизации металла [221]. С увеличением температуры СПД металла уменьшается, а пластичность, характеризующая возможную степень ПД без нарушения его сплошности, увеличивается [219, 220].
Упрочнение металла в процессе пластической деформации объясняется увеличением числа дефектов кристаллического строения (дислокаций, вакансий, междоузельных атомов). В частности, связь между пределом текучести σТ
и плотностью дислокации ρ
выражается формулой [232]:
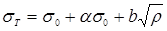 , ,
где σ0
— напряжение сдвига при пластической деформации; b
—
вектор Бюргерса; α
— коэффициент, зависящий от типа решетки и состава сплава.
Так, Тейлор и Илом установили, что упрочнение при деформации монокристалла алюминия происходит по параболическому закону [233]:
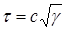 , ,
где τ —
касательное напряжение в плоскости скольжения; γ — сдвиг.
При увеличении скорости пластической деформации напряжение текучести возрастает, а пластичность падает. С увеличением скорости ПД резко падает пластичность некоторых магниевых сплавов, высоколегированной стали и медных сплавов некоторых марок. Значительно менее чувствительны к скорости деформации большинство алюминиевых сплавов, низколегированные и углеродистые стали [221, 234, 235].
Из определения понятия «сопротивление пластической деформации», общепринятого в теориях пластичности и обработки металлов давлением следует, что оно является характеристикой деформируемого металла, которая зависит от термомеханических условий пластической деформации, а именно: степени ε
и скорости u
деформации, а так же от температуры деформируемого объема ТД
[236]. Поэтому оценивать величину СПД в условиях точечной сварки рациональнее не измерением его в ходе процесса КТС, так как осуществить это технически сложно, практически невозможно, а расчетом — с использованием данных и опыта теории и технологии обработки металлов давлением.
Известны ряд эмпирических формул для расчета величины СПД в зависимости от изменения технологических факторов, характеризующих термомеханические условия процесса пластической деформации.
Для определения изменения прочностных характеристик с изменением температуры Т
известен ряд зависимостей, в частности, С. И. Губкина [226] для определения временного сопротивления металла σВ
в области температур, составляющих 0,7...1,0 ТПЛ
:
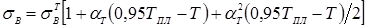 , ,
где 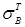 — временное сопротивление при температуре 0,95ТПЛ
и скорости растяжения 40...50 мм/мин; ТПЛ
— температура плавления сплава (о
С); — временное сопротивление при температуре 0,95ТПЛ
и скорости растяжения 40...50 мм/мин; ТПЛ
— температура плавления сплава (о
С);
αТ
— температурный коэффициент, и зависимость Н. С. Курнакова [237]:
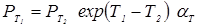 , ,
где 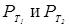 — значения прочностной характеристики при температуре, соответственно, Т1
и Т2
; αТ
— температурный коэффициент, постоянный для данного сплава, если в этом интервале температур в нем отсутствуют физико-химические превращения. — значения прочностной характеристики при температуре, соответственно, Т1
и Т2
; αТ
— температурный коэффициент, постоянный для данного сплава, если в этом интервале температур в нем отсутствуют физико-химические превращения.
Для оценки деформационного упрочнения в процессе пластической деформации известна зависимость [123]:
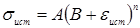 , ,
где σист
и εист
— истинное напряжение и истинная деформация;
А, В
и п
— постоянные, определяемые экспериментально.
Известен ряд формул, отражающих зависимость деформационных характеристик металла от скорости u
его деформирования, в частности, следующие [221, 238]:
П. Людвика — 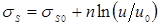 , ,
А. Рейто — 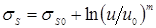 , ,
Е. Зибеля и А. Помпа — 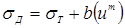 , ,
А. Надаи — 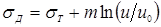 , ,
где σД
— сопротивление деформации металла; σТ
— предел текучести при статической деформации; b
и т
— постоянные коэффициенты, зависящие от материала; σ
S
и σ
S
0
— напряжения текучести, соответственно, при скоростях деформирования u
и u
0
; т
и п —
константы.
Более комплексно реальные процессы упрочнения и релаксации при пластической деформации металла отражены в зависимости, предложенной А. И. Целиковым и В. А. Персианцевым [239], для определения сопротивления деформации σД
:
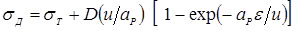 , ,
где D
У
– модуль упрочнения; a
Р
–
коэффициент, представляющий собой скорость релаксации (c-1
); σТ
– предел текучести при статической деформации; ε
– степень деформации; u
– средняя скорость деформации.
Выше приведены лишь наиболее известные решения задачи по определению характеристик металла при их пластическом деформировании. Однако использовать эти формулы применительно к процессу точечной сварки не представляется возможным, поскольку ни одна из них не учитывает одновременного влияния на величину сопротивления пластической деформации основных факторов — температуры, степени и скорости ПД металла, как это имеет место в процессе КТС. Кроме того, для большинства из этих зависимостей не определены значения коэффициентов.
На основании анализа известных методик для определения сопротивления пластической деформации металла и проведенных исследований сделан вывод о том, что для решения поставленной задачи при КТС рационально использовать приближенные, расчетно-экспериментальные методы. В частности, был сделан вывод о том [203, 206, 240], что для определения сопротивления пластической деформации металла в условиях формирования точечного сварного соединения наиболее приемлем метод, предложенный В. И. Зюзиным [241], так называемый «метод термомеханических коэффициентов». По этому методу изменение сопротивления деформации выражается в относительных единицах (коэффициентах) в зависимости от каждого параметра (температуры деформируемого объема ТД
t
, степени ε
t
и скорости ut
пластической деформации) в отдельности. Применительно к условиям КТС расчетное значение сопротивления деформации металла σД
t
определяется по следующей зависимости [203, 206]:
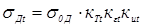 , (3.60) , (3.60)
где σ0Д
— базисное значение сопротивления пластической деформации, при определенных условиях испытаний; кТ
t
, кε
t
и к
Ut
— соответственно, температурный, степенной и скоростной термомеханические коэффициенты в момент времени t
.
При практическом использовании данного метода определения СПД металла используют значения базисного сопротивления пластической деформации σ0Д
, а также термомеханических коэффициентов: температурного кТ
, степенного кε
и скоростного к
U
, которые определяют экспериментально для разных условий деформирования металла. Их значения представлены в справочной литературе по обработке металлов давлением в виде табличных данных, графиков или аппроксимированных по ним функций. Типичное изменение коэффициентов кТ
, кε
и к
U
в зависимости от изменения соответствующих факторов показан на рис. 3.26.

Таким образом, из существующих методов расчетного определения сопротивления пластической деформации металлов, экспериментально-расчетный метод термомеханических коэффициентов является наиболее приемлемым для условий ПД при точечной сварке. Он позволяет учитывать одновременное и комплексное влияние на величину СПД основных факторов процесса пластической деформации металла — температуры, степени и скорости , как это и имеет место в процессе КТС. Кроме того, для наиболее используемых в машиностроении сталей и сплавов определены базисные значения СПД σ0Д
и значения коэффициентов кТ
, кε
и к
U
, которые приведены, например, в работе [242].
Для практических расчетов сопротивления пластической деформации металла по формуле (3.60) в условиях КТС необходимо в любой момент процесса формирования точечного сварного соединения количественно определить степень и скорость деформации, а также температуру деформируемого металла в зоне сварки.
3.5.2
Определение степени и скорости пластической деформации
металла в зоне точечной сварки
По-видимому, в теории точечной сварки понятия степени и скорости пластической деформации металла в зоне формирования соединения определяются не совсем корректно (см. п. 2.5) и математические зависимости для расчёта их параметров не в полной мере отражают сущность этих процессов при КТС и не пригодны для решения практических задач. Ниже описана методика определения степени и скорости деформации в процессе формирования соединения [203, 215, 240], разработанная для условий КТС и вполне приемлемая для решения технологических задач.
В теориях пластичности и обработки металлов давлением, деформацией называют изменение размеров и формы рабочего тела без изменения его массы и объема. При этом, понятие «деформация» относят как к изменению размеров и формы элементарных объемов тела, так и к изменению макроскопических параметров формы и размеров. Количественное определение абсолютной, относительной либо логарифмической (истинной) деформации неизбежно связано с измерением расстояний между точками тела, в том числе и внутри его, поскольку пластическая деформация представляет собой перемещение элементарных объемов тела (точек) относительно друг друга [220, 221, 225, 226]. Однако в условиях точечной сварки сделать это экспериментально с достаточной степенью точности, используя существующие методики (см. п. 2.5.1), не представляется возможным.
Вместе с тем, в теории обработки металлов давлением известен так называемый «метод определения степени пластической деформации по смещенному объёму». Так, при деформации (осадке) цилиндра объёмом VД
силами σ
(рис. 3.27), которые распределены по его торцевым поверхностям, степень деформации ε
, определяемая по смещенному объему VСМ
(заштрихован), равна [221]:
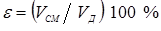 . .
 На основании физической модели процессов макропластических деформаций при формировании точечных сварных соединений, которая была сформулирована выше в п. 2.5.2, процесс пластической деформации металла зоны сварки на стадии нагрева может быть уподоблен описанному выше процессу деформации цилиндра при его осадке (рис. 3.28). Это можно сделать на основании результатов экспериментальных исследований пластических деформаций металла в зоне сварки, в частности приведенных в разделе 2.5.2 и в работе [204], если физическую модель (см. рис. 2.32) несколько идеализировать, сделав следующие допущения (рис. 3.28, а
): На основании физической модели процессов макропластических деформаций при формировании точечных сварных соединений, которая была сформулирована выше в п. 2.5.2, процесс пластической деформации металла зоны сварки на стадии нагрева может быть уподоблен описанному выше процессу деформации цилиндра при его осадке (рис. 3.28). Это можно сделать на основании результатов экспериментальных исследований пластических деформаций металла в зоне сварки, в частности приведенных в разделе 2.5.2 и в работе [204], если физическую модель (см. рис. 2.32) несколько идеализировать, сделав следующие допущения (рис. 3.28, а
):
- пластические деформации металла при КТС локализованы в объеме металла зоны сварки Vt
, ограниченном наружными поверхностями свариваемых деталей и цилиндрической поверхностью, образующей которой является контур L
1
, а направляющей — линия, на 10...18 % выходящая за контур уплотняющего пояска:  (см. зависимость (3.58)) (см. зависимость (3.58))
- зона пластических деформаций Vt
вне контура L
1
окружена жесткой оболочкой, так как радиальные деформации металла в относительно узком (вследствие большого градиента температуры) поясе V
УП
между контурами L
1
и L
2
, находящегося в упругопластическом состоянии, а также окружающего холодного металла V
У
вне контурами L
1
и L
2
, который деформируется только упруго, незначительны и ими можно пренебречь;
- 
осевое пластическое течение (выдавливание) металла, формирующее уплотняющий поясок и являющееся причиной образования вмятин на поверхности электродов, вне контуров контактов деталь–деталь и электрод–деталь отсутствует.
В любой дискретный момент времени t
процесса формирования соединения при КТС на цилиндрический пластически деформируемый объем Vt
металла зоны сварки, со стороны жесткого кольца V
У
холодного металла, который деформируется только упруго, через относительно узкий пояс металла V
УП
, находящегося в упругопластическом состоянии, действуют радиальные напряжения σ
r
. В результате этого при КТС пластическое течение металла возможно в основном лишь в осевом направлении. Перемещение основного объема деформируемого металла, вследствие наличия осевого градиента температуры, происходит в направлении свариваемого контакта (см. п. 2.5.2). При этом элементарные объемы металла при его пластическом течении в зоне сварки перемещаются так же, как при деформации цилиндров 1 и 2, сжатых силами σ1
, радиальными напряжениями σ
r
, которые распределены по боковым их поверхностям (рис. 3.28, б
). Таким образом, пластическое течение элементарных объемов металла в зоне сварки при КТС и при деформации цилиндров, напряжениями σ
r
, распределенными по боковым их поверхностям, происходит так же, как при описанной выше пластической деформации цилиндра при его осадке (см.
рис. 3.27), но только в обратном направлении.
Степень деформации металла в зоне сварки
ε
t
, в любой момент времени t
процесса формирования соединения при при контактной точечной сварке, на основании сказанного выше (см. рис. 3.28, б
) можно определить по зависимости (рис. 3.29):
 , (3.61) , (3.61)
где V
СМ
t
и Vt
— смещенный и деформируемый объемы в момент времени t
.
Физическая модель процессов макропластических деформаций при формировании точечных сварных соединений (см. п. 2.5.2) и сделанные выше допущения, позволяют определить смещенный объем металла при КТС 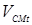 (рис. 3.29). В любой момент t
процесса формирования точечного сварного соединения смещенный объем металла (рис. 3.29). В любой момент t
процесса формирования точечного сварного соединения смещенный объем металла 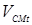 равен сумме приращения равен сумме приращения 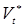 деформируемого объема Vt
вследствие температурного расширения, включая и нагрев выше температуры плавления в объеме ядра V
Я
t
, увеличения деформируемого объема Vt
вследствие температурного расширения, включая и нагрев выше температуры плавления в объеме ядра V
Я
t
, увеличения 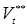 объема металла ядра V
Я
t
при его плавлении, а также объемов металла объема металла ядра V
Я
t
при его плавлении, а также объемов металла 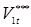 и и 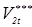 , вытесняемых при вдавливании электродов в детали на глубину c
1
t
и c
2
t
: , вытесняемых при вдавливании электродов в детали на глубину c
1
t
и c
2
t
:
 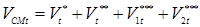 . . (3.62) (3.62)
 Элементарные объемы dV
в разных областях зоны сварки, ограниченной контуром L
1
, испытывают различное тепловое воздействие, а также претерпевают разные агрегатные превращения. С учетом этого в любой момент t
процесса КТС на стадии нагрева приращение Элементарные объемы dV
в разных областях зоны сварки, ограниченной контуром L
1
, испытывают различное тепловое воздействие, а также претерпевают разные агрегатные превращения. С учетом этого в любой момент t
процесса КТС на стадии нагрева приращение  смещенного объема смещенного объема 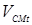 из-за температурного расширения металла деформируемого объема Vt
, и приращение из-за температурного расширения металла деформируемого объема Vt
, и приращение  смещенного объема смещенного объема 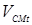 из-за увеличения объема металла ядра V
Я
t
при его плавлении могут быть определены по следующим интегральным зависимостям: из-за увеличения объема металла ядра V
Я
t
при его плавлении могут быть определены по следующим интегральным зависимостям:
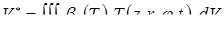 , (3.63) , (3.63)
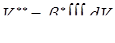 , (3.64) , (3.64)
где для момента времени t
,
β
T
(Т
) — температурный коэффициент объемного расширения; Т(
z
,
r
,φ,
t
)
— функция, описывающая изменение температуры в зоне сварки; β*
– коэффициент объемного расширения при плавлении металла, примеры значений которого показаны в табл. 3.3.
Приращения смещенного объема 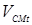 из-за объемов металла из-за объемов металла 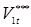 и и 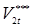 , смещаемых при вдавливании электродов в детали, для момента времени t
могут быть определены как объемы геометрических фигур по следующим интегральным зависимостям: , смещаемых при вдавливании электродов в детали, для момента времени t
могут быть определены как объемы геометрических фигур по следующим интегральным зависимостям:
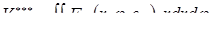 , (3.65) , (3.65)
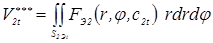 , (3.66) , (3.66)
где для момента времени t
, 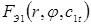 и и 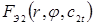 — функции, описывающие геометрию рабочих поверхностей электродов и их положение относительно поверхностей свариваемых деталей; с1
t
и с2
t
– глубины вдавливания электродов в поверхности деталей; S
1Э
t
и S
2Э
t
— площади соответствующих контактов электрод–деталь. — функции, описывающие геометрию рабочих поверхностей электродов и их положение относительно поверхностей свариваемых деталей; с1
t
и с2
t
– глубины вдавливания электродов в поверхности деталей; S
1Э
t
и S
2Э
t
— площади соответствующих контактов электрод–деталь.
Подставив зависимости (3.63…3.66) в (3.62) получаем интегральное выражение, которое позволяет определить смещенный объем металла V
СМ
t
в любой момент процесса точечной сварки:
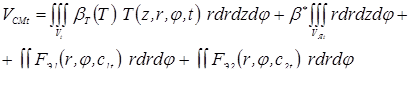 . (3.67) . (3.67)
Выразив деформируемый объём Vt
интегральной зависимостью
и подставив ее совместно с (3.67) в формулу (3.61), получаем интегральное выражение, которое позволяет определить степень пластической деформации металла в зоне формирования точечного сварного соединения, в любой момент времени t
на стадии нагрева [203, 240]:
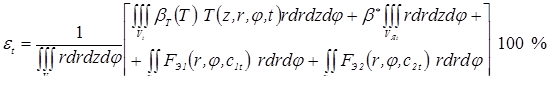 . (3.68) . (3.68)
 Для точных расчетов степени деформации при конкретных условиях точечной сварки необходимо в интегральную зависимость (3.68) подставить подынтегральные функции. А именно, функции, которые описывали бы изменение в процессе КТС: объема деформируемого металла; изменения в нем температуры; объема расплавленного металла; объема металла, вытесняемого электродами; зависимость температурного коэффициента объёмного расширения от изменения температуры. Кроме того, пределы интегрирования необходимо выразить через функции, которые описывали бы поверхности объема деформируемого металла Vt
и объема ядра расплавленного металла V
Я
t
, а также функции Для точных расчетов степени деформации при конкретных условиях точечной сварки необходимо в интегральную зависимость (3.68) подставить подынтегральные функции. А именно, функции, которые описывали бы изменение в процессе КТС: объема деформируемого металла; изменения в нем температуры; объема расплавленного металла; объема металла, вытесняемого электродами; зависимость температурного коэффициента объёмного расширения от изменения температуры. Кроме того, пределы интегрирования необходимо выразить через функции, которые описывали бы поверхности объема деформируемого металла Vt
и объема ядра расплавленного металла V
Я
t
, а также функции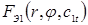 и и 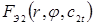 , описывающие геометрию рабочих поверхностей электродов и их положение в момент времени t
относительно поверхностей свариваемых деталей. Учитывая, что вышеназванные функции весьма сложны, а некоторые вообще не определены, то точные аналитические расчеты значений степени пластической деформации по зависимости (3.68) затруднительны, а для решения приближенных технологических задач точечной сварки может быть и не рациональны. , описывающие геометрию рабочих поверхностей электродов и их положение в момент времени t
относительно поверхностей свариваемых деталей. Учитывая, что вышеназванные функции весьма сложны, а некоторые вообще не определены, то точные аналитические расчеты значений степени пластической деформации по зависимости (3.68) затруднительны, а для решения приближенных технологических задач точечной сварки может быть и не рациональны.
Приближенные технологические расчеты по зависимости (3.68) можно упростить, если кроме допущений, описанных выше, принять и следующие:
- зона сварки осесимметрична;
- детали имеют одинаковые теплофизические свойства и одинаковую толщину, т. е. зона сварки симметрична относительно плоскости свариваемого контакта;
- температурный коэффициент объемного расширения металла β
T
не зависит от градиента температуры по координатам и принимается по ее усредненной величине, т. е. 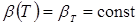 ; ;
- электроды имеют одинаковую геометрию рабочих поверхностей и вдавливаются в поверхности деталей на одинаковую глубину, т. е.:
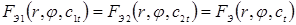 , , 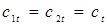 и и 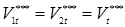 . .
Тогда, приняв допущения, что зона интенсивных пластических деформаций при КТС ограничена поверхностями деталей в контактах электрод–деталь и цилиндрической поверхностью, образующая которой параллельна оси электродов, а направляющей является контур контакта деталь–деталь, интеграл в зависимости (3.68), который определяет объем деформируемого металла Vt
, при толщине деталей s
и диаметре уплотняющего пояска d
П
t
будет равен:
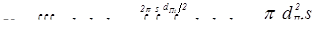 . (3.69) . (3.69)
Сделанные допущения, в частности, о том, что температурный коэффициент объемного расширения металла β
T
не зависит от температуры, т. е. β
T
=
const, позволяют упростить вычисление первого тройного интеграла (в квадратных скобках) в зависимости (3.68), который определяет приращения 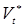 деформируемого объема металла Vt
, вследствие его температурного расширения (зависимость 3.63). Тогда, учитывая, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r
и симметрична относительно плоскости свариваемого контакта по координате z
, этот интеграл можно преобразовать к следующему виду: деформируемого объема металла Vt
, вследствие его температурного расширения (зависимость 3.63). Тогда, учитывая, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r
и симметрична относительно плоскости свариваемого контакта по координате z
, этот интеграл можно преобразовать к следующему виду:
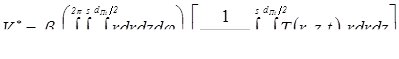 . (3.70) . (3.70)
Очевидно, что тройной интеграл в круглых скобках аналогичен зависимости (3.69), а выражение с двойным интегралом в квадратных скобках аналогично зависимости (3.44), если в нее подставить следующие пределы интегрирования: z
1
= 0, z
2
= s
, r
1
= 0, r
2
= d
П
t
/
2. Тогда, с учетом (3.44) и (3.69), а также того, что температурный коэффициент объемного расширения β
T
и температурный коэффициент линейного расширения α
T
связаны между собой следующим соотношением: β
T
= 3α
T
[123], зависимость (3.70) можно преобразовать к следующему виду:
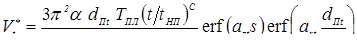 . (3.71) . (3.71)
Допущение об осесимметричности зоны сварки значительно упрощает вычисление и второго тройного интеграла (в квадратных скобках) в зависимости (3.68), который определяет приращение  объема металла ядра при его плавлении. В этом случае объем ядра в любой момент его формирования можно рассчитать как объем тела вращения. Объем ядра V
Я
t
(рис. 3.30) можно представить как объем тела, ограниченного изотермой температуры плавления, выраженной функцией объема металла ядра при его плавлении. В этом случае объем ядра в любой момент его формирования можно рассчитать как объем тела вращения. Объем ядра V
Я
t
(рис. 3.30) можно представить как объем тела, ограниченного изотермой температуры плавления, выраженной функцией 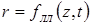 , при вращении ее вокруг координаты z
.
Тогда тройной интеграл в зависимостях (3.64) и (3.68) можно преобразовать следующим образом [208]: , при вращении ее вокруг координаты z
.
Тогда тройной интеграл в зависимостях (3.64) и (3.68) можно преобразовать следующим образом [208]:
 , (3.72) , (3.72)
 где z
1
и z
2
— координаты точек, в которых изотермы температуры плавления пересекают ось электродов. где z
1
и z
2
— координаты точек, в которых изотермы температуры плавления пересекают ось электродов.
Функцию, выражающую зависимость координаты r
от координаты z
в уравнении изотермы температуры плавления: 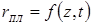 , можно получить из выражения (3.39). После преобразований эта функция может быть записана в следующем виде: , можно получить из выражения (3.39). После преобразований эта функция может быть записана в следующем виде:
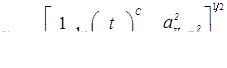 . .
Подставив ее в зависимость (3.72) и вычислив интеграл при переменных пределах интегрирования 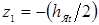 и и 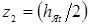 , в которых значение высоты ядра h
Я
t
выражено формулой (3.40), получаем: , в которых значение высоты ядра h
Я
t
выражено формулой (3.40), получаем:
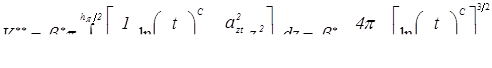 . (3.73) . (3.73)

В практике точечной сварки наиболее распространены электроды (рис. 3.31) со сферической рабочей поверхностью (рис. 3.31, а
), а также конические (рис. 3.31, б
) и цилиндрические (рис. 3.31, в
) электродами с плоскими рабочими поверхностями.
Все они являются телами вращения, а потому объемы 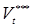 , вытесняемые электродами при их вдавливании в поверхности деталей, могут быть определены не только по зависимостям (3.65) или (3.66), но и гораздо проще по зависимости (3.72). Однако и в этом нет необходимости, так как общеизвестны формулы, согласно которым вытесняемые объемы равны: , вытесняемые электродами при их вдавливании в поверхности деталей, могут быть определены не только по зависимостям (3.65) или (3.66), но и гораздо проще по зависимости (3.72). Однако и в этом нет необходимости, так как общеизвестны формулы, согласно которым вытесняемые объемы равны:
- при сферической рабочей поверхности электрода
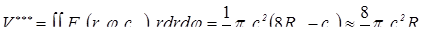 , (3.74) , (3.74)
- при конической форме электрода
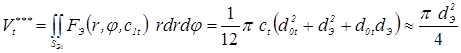 , (3.75) , (3.75)
- при цилиндрической форме электрода
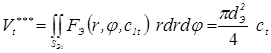 , (3.76) , (3.76)
где ct
— глубина вдавливания электродов в момент времени t
; R
Э
— радиус сферической рабочей поверхности электрода; d
Э
— диаметр плоской рабочей поверхности электрода; dOt
— диаметр отпечатка (контакта) электрод-деталь в момент времени t
.
Вторым слагаемым в зависимости (3.74) можно пренебречь потому, что глубина вдавливания электродов при КТС обычно не превышает 10...20 % от толщины s
свариваемых деталей, т. е. 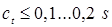 , а радиусы электродов со сферической рабочей поверхностью , а радиусы электродов со сферической рабочей поверхностью 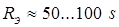 , при которых , при которых 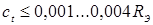 и практически не влияет на результат расчета объема и практически не влияет на результат расчета объема  . По этой же причине можно пренебречь разностью между d
Э
и dOt
в зависимости (3.75), так как при . По этой же причине можно пренебречь разностью между d
Э
и dOt
в зависимости (3.75), так как при 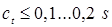 и и 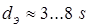 , т. е. при , т. е. при 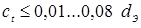 , и определять объем , и определять объем  по зависимости (3.76) как при цилиндрическом, так и коническом электродах. по зависимости (3.76) как при цилиндрическом, так и коническом электродах.
Наиболее сложной задачей при расчетах вытесненного электродами объема  по зависимостям (3.74) и (3.76) является определение глубины вдавливания электродов ct
в процессе формирования соединения. В настоящее время можно прогнозировать лишь качественный характер изменения этого параметра. Определить же значения ct
расчетным путем в процессе КТС с учетом напряженно-деформированного состояния металла области зоны сварки, прилегающей к электроду, пока не удается из-за сложности протекающих там термодеформационных процессов. Поэтому в данной методике значения ct
приближенно определяются через диаметр контакта электрод–деталь. С точностью до 0,01 % значения ct
можно выразить через диаметр отпечатка d
о
(контакта электрод–деталь) при сварке электродами со сферическими рабочими поверхностями [84]: по зависимостям (3.74) и (3.76) является определение глубины вдавливания электродов ct
в процессе формирования соединения. В настоящее время можно прогнозировать лишь качественный характер изменения этого параметра. Определить же значения ct
расчетным путем в процессе КТС с учетом напряженно-деформированного состояния металла области зоны сварки, прилегающей к электроду, пока не удается из-за сложности протекающих там термодеформационных процессов. Поэтому в данной методике значения ct
приближенно определяются через диаметр контакта электрод–деталь. С точностью до 0,01 % значения ct
можно выразить через диаметр отпечатка d
о
(контакта электрод–деталь) при сварке электродами со сферическими рабочими поверхностями [84]: 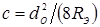 . .
 Экспериментальные исследования показали, что диаметр d
Э
t
контакта электрод–деталь при точечной сварке изменяется подобно изменению диаметра d
П
t
контакта деталь–деталь (рис.3.32). При этом установлено, что в начале процесса КТС d
Э
t
,
на 5...15 % больше d
П
t
,
а в конце процесса — наоборот, d
П
t
примерно на столько же больше, чем d
Э
t
. Поэтому, для приближенных расчетов можно принять, что d
Э
t
и d
П
t
изменяются при сварке одинаково. Тогда изменение значений глубины вмятин от электродов в поверхностях деталей ct
в процессе сварки электродами со сферической рабочей поверхностью при расчетах вытесняемого ими объема металла Экспериментальные исследования показали, что диаметр d
Э
t
контакта электрод–деталь при точечной сварке изменяется подобно изменению диаметра d
П
t
контакта деталь–деталь (рис.3.32). При этом установлено, что в начале процесса КТС d
Э
t
,
на 5...15 % больше d
П
t
,
а в конце процесса — наоборот, d
П
t
примерно на столько же больше, чем d
Э
t
. Поэтому, для приближенных расчетов можно принять, что d
Э
t
и d
П
t
изменяются при сварке одинаково. Тогда изменение значений глубины вмятин от электродов в поверхностях деталей ct
в процессе сварки электродами со сферической рабочей поверхностью при расчетах вытесняемого ими объема металла 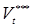 по зависимости (3.74) можно выразить через изменение диаметра уплотняющего пояска следующим образом: по зависимости (3.74) можно выразить через изменение диаметра уплотняющего пояска следующим образом:
 . (3.77) . (3.77)
Практика сварки электродами со сферической и плоской рабочими поверхностями показывает, что при сварке на режимах близких к оптимальным, например, рекомендованных в работах [3, 9, 11, 15...17], глубина их вдавливания в поверхности деталей в процессе формирования соединения изменяется примерно одинаково. Поэтому, при приближенных технологических расчетах значений 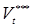 по зависимости (3.76) величину ct
можно определять по зависимости (3.77) и для условий сварки электродами с плоской рабочей поверхностью, если подставить фиктивное значение R
Э
, рекомендованное для этой же толщины деталей, например, в работах [3, 11, 16]. по зависимости (3.76) величину ct
можно определять по зависимости (3.77) и для условий сварки электродами с плоской рабочей поверхностью, если подставить фиктивное значение R
Э
, рекомендованное для этой же толщины деталей, например, в работах [3, 11, 16].
Тогда зависимость (3.68) для расчета степени пластической деформации металла в зоне сварки ε
t
в любой момент t
процесса формирования соединения на стадии нагрева с учетом сказанного выше и зависимостей (3.71), (3.73) и (3.77) можно преобразовать к следующему окончательному виду, удобному для практических расчетов [210, 217]:
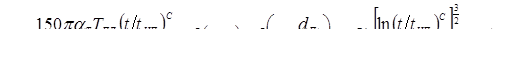 (%), (3.78) (%), (3.78)
где для момента времени t
, αТ
— температурный коэффициент линейного расширения; azt
, art
и с
— коэффициенты (см. зависимость 3.36); t
НП
—
время начала плавления металла (см. зависимость 3.37); 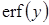 —
функция ошибок (см. зависимость (3.42)... (3.44)); s
—
толщина деталей; d
П
t
— диаметр уплотняющего пояска; β*
— коэффициент увеличения объема металла ядра при его плавлении; —
функция ошибок (см. зависимость (3.42)... (3.44)); s
—
толщина деталей; d
П
t
— диаметр уплотняющего пояска; β*
— коэффициент увеличения объема металла ядра при его плавлении; 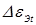 — приращение степени пластической деформации ε
t
металла зоны сварки при вдавливании электродов, равное: — приращение степени пластической деформации ε
t
металла зоны сварки при вдавливании электродов, равное:
при сферической рабочей поверхности электрода
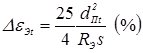 , ,
при конической и цилиндрической форме электрода
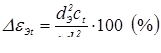 ; ;
R
Э
и d
Э
– радиус (при сферической) и диаметр (при плоской) рабочих поверхностей электродов; с
t
— глубина вдавливания электродов в поверхности деталей (см. зависимость 3.77).
Таким образом, зависимость (3.78) позволяет при технологических расчетах приближенно определить степень пластической деформации ε
t
металла в процессе формирования точечного сварного соединения в любой его момент t
на стадии нагрева.
Скорость деформации
, как это общепринято в теориях пластичности и обработки металлов давлением — это изменение степени деформации ε
t
в единицу времени [220, 221, 227,228], т. е.:
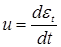 . (3.79) . (3.79)
Размерность скорости деформации зависит от размерности ее степени и может быть  или или  : : 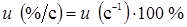 . .
В соответствии с выражением (3.79) скорость деформации можно определить как производную от функции, описывающей изменение по времени степени пластической деформации металла зоны сварки, т. е. производную от зависимости (3.78). Однако в связи с тем, что она содержит не дифференцируемую аналитически erf – функцию, то точное аналитическое определение скорости деформации по (3.79) невозможно. Даже при приближенном дифференцировании функции 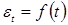 [216] получается очень громоздкая и неудобная для практических расчетов зависимость скорости деформации от времени. Поэтому скорость деформации ut
для любого момента t
процесса сварки рациональнее определять численным дифференцированием зависимости (3.78) , т. е. [210, 217]: [216] получается очень громоздкая и неудобная для практических расчетов зависимость скорости деформации от времени. Поэтому скорость деформации ut
для любого момента t
процесса сварки рациональнее определять численным дифференцированием зависимости (3.78) , т. е. [210, 217]:
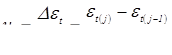 , (3.80) , (3.80)
где Δε
t
— приращение степени деформации 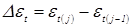 за отрезок времени за отрезок времени 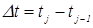 между текущим между текущим 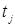 и предыдущим и предыдущим 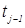 моментами расчета скорости деформации моментами расчета скорости деформации 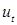 . .
3.5.3.
Определение температуры металла в зоне пластических
деформаций
Методика, по которой рассчитывается изменение сопротивления пластической деформации металла при КТС, предопределяет осреднение температуры в объеме металла зоны интенсивных пластических деформаций. Рассчитать среднюю температуру металла пластически деформируемого в зоне сварки можно по зависимости (3.44).
В разделе 2.5.2 экспериментально определено, что пластические деформации металла зоны сварки на стадии нагрева в основном локализованы в области, ограниченной контуром L
1
, диаметр которого d
Д
t
на 5...15 % больше диаметра d
П
t
уплотняющего пояска, т. е. 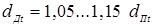
(рис. 3.33). При расчете же давления в ядре радиус внешней границы металла, находящегося в пластическом состоянии, определен и теоретически. Из зависимостей (3.58) и (3.59) получаем: 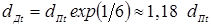 . Поскольку эти результаты приближенно равны, при расчете средней температуры внешней границей зоны интенсивных пластических деформаций рационально принять окружность диаметром . Поскольку эти результаты приближенно равны, при расчете средней температуры внешней границей зоны интенсивных пластических деформаций рационально принять окружность диаметром 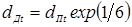 . Внутренней же границей пластических деформаций до начала плавления металла является ось электродов (рис. 3.33, слева), а после появления ядра расплавленного металла (рис. 3.33, справа) — окружность с диаметром d
Я
t
.
Поскольку приняты допущения, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r
и симметрична относительно плоскости свариваемого контакта по координате z
, то среднюю температуру деформируемого металла можно определять только в одной четверти зоны точечной сварки. Следовательно, для определения ТД
t
по зависимости (3.44) в нее следует подставить следующие пределы интегрирования: . Внутренней же границей пластических деформаций до начала плавления металла является ось электродов (рис. 3.33, слева), а после появления ядра расплавленного металла (рис. 3.33, справа) — окружность с диаметром d
Я
t
.
Поскольку приняты допущения, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r
и симметрична относительно плоскости свариваемого контакта по координате z
, то среднюю температуру деформируемого металла можно определять только в одной четверти зоны точечной сварки. Следовательно, для определения ТД
t
по зависимости (3.44) в нее следует подставить следующие пределы интегрирования:  , ,  , , 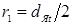 , , 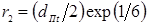 . .
 После подстановки этих пределов интегрирования, вычисления интегралов и преобразований по зависимости (3.44) получаем формулу для расчета средней температуры деформируемого в зоне сварки металла ТД
t
в любой момент t
процесса формирования точечного сварного соединения при После подстановки этих пределов интегрирования, вычисления интегралов и преобразований по зависимости (3.44) получаем формулу для расчета средней температуры деформируемого в зоне сварки металла ТД
t
в любой момент t
процесса формирования точечного сварного соединения при 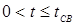 [210, 217]: [210, 217]:
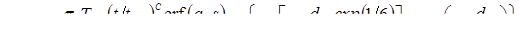 , (3.81) , (3.81)
где для момента времени t
, ТПЛ
— температура плавления свариваемого металла; t
НП
—
время начала плавления металла (см. зависимость 3.37);
azt
, art
и с
— коэффициенты (см. зависимость 3.36); 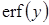 —
функция ошибок (см. зависимость (3.42)... (3.44)); s
—
толщина деталей; d
Я
t
и d
П
t
— диаметры ядра и уплотняющего пояска соответственно. —
функция ошибок (см. зависимость (3.42)... (3.44)); s
—
толщина деталей; d
Я
t
и d
П
t
— диаметры ядра и уплотняющего пояска соответственно.
3.5.4. Определение высоты уплотняющего пояска в свариваемом
контакте
Для решения технологических задач точечной сварки с обжатием периферийной зоны соединений по уравнению (3.17) в любой момент процесса формирования соединения необходимо определять высоту уплотняющего пояска h
П
t
(рис. 3.34), которая входит в зависимость (3.19).
 В процессе формирования точечного сварного соединения происходит пластическое течение металла в зоне сварки к контакту деталь – деталь вследствие его температурного расширения, увеличения объема при расплавлении в ядре, неравномерного нагрева и сложного объемного напряженного состояния (см. п. 2.5.2). Как показано выше в п. 3.5.2, при пластической деформации металла в зоне сварки к контакту между деталями смещается объём V
СМ
t
в результате чего между свариваемыми деталями образуется рельеф (уплотняющий поясок) высотой h
П
t
. Поскольку считается, что металл при пластической деформации не сжимается [200, 219...221, 224...230], высоту уплотняющего пояска h
П
t
в любой момент t
процесса формирования соединения можно определить следующим образом: В процессе формирования точечного сварного соединения происходит пластическое течение металла в зоне сварки к контакту деталь – деталь вследствие его температурного расширения, увеличения объема при расплавлении в ядре, неравномерного нагрева и сложного объемного напряженного состояния (см. п. 2.5.2). Как показано выше в п. 3.5.2, при пластической деформации металла в зоне сварки к контакту между деталями смещается объём V
СМ
t
в результате чего между свариваемыми деталями образуется рельеф (уплотняющий поясок) высотой h
П
t
. Поскольку считается, что металл при пластической деформации не сжимается [200, 219...221, 224...230], высоту уплотняющего пояска h
П
t
в любой момент t
процесса формирования соединения можно определить следующим образом:
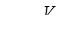 , (3.82) , (3.82)
где в момент времени t
, V
СМ
t
— объем металла зоны сварки, смещенный к свариваемому контакту; S
К
t
— площадь контакта деталь–деталь.
Изменение смещённого объёма V
СМ
t
в процессе точечной сварки описывается интегральным выражением (3.67). Тогда, выразив площадь контакта деталь–деталь S
К
t
интегральной зависимостью
 (3.83) (3.83)
и подставив ее совместно с зависимостью (3.67) в формулу (3.82) получаем интегральное выражение, которое позволяет в любой момент времени t
на стадии нагрева определить высоту уплотняющего пояска h
П
t
, [204, 210]:
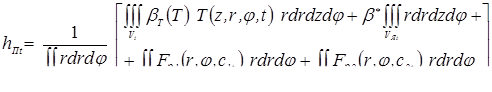 , (3.84) , (3.84)
где обозначения полностью соответствуют зависимости (3.67).
Точные аналитические расчеты по зависимости (3.84) затруднительны, а для решения технологических задач может быть и не рациональны, по тем же причинам, что и зависимости (3.68). При допущениях же, которые были сделаны для зависимости (3.68), в частности, об осесимметричности зоны сварки и о ее симметричности относительно плоскости свариваемого контакта, по зависимости (3.82) можно производить приближённые технологические расчёты. В этом случае, вычислив интеграл в (3.83)
 (3.85) (3.85)
и подставив его, совместно с зависимостями (3.70)…(3.77), в выражение (3.84) после преобразований получаем формулу для расчетов высоты уплотняющего пояска в любой момент t
процесса формирования соединения при сварке деталей одинаковой толщины [204, 243]:
 , (3.84) , (3.84)
где для момента времени t
, αТ
— температурный коэффициент линейного расширения; ТПЛ
— температура плавления свариваемого металла;
t
НП
—
время начала плавления металла (см. зависимость 3.37); azt
, art
и с
— коэффициенты (см. зависимость 3.36); 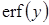 —
функция ошибок (см. зависимость (3.42)...(3.44)); s
—
толщина деталей; d
П
t
— диаметр уплотняющего пояска; β*
— коэффициент увеличения объема металла ядра при его плавлении; —
функция ошибок (см. зависимость (3.42)...(3.44)); s
—
толщина деталей; d
П
t
— диаметр уплотняющего пояска; β*
— коэффициент увеличения объема металла ядра при его плавлении; 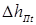 — приращение высоты уплотняющего пояска h
П
t
за счет вдавливания электродов, равное: — приращение высоты уплотняющего пояска h
П
t
за счет вдавливания электродов, равное:
при сферической рабочей поверхности электрода
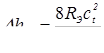 , ,
при конической и цилиндрической форме электрода
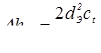 ; ;
R
Э
и d
Э
– радиус (при сферической) и диаметр (при плоской) рабочих поверхностей электродов; с
t
— глубина вдавливания электродов в поверхности деталей (см. зависимость 3.77).
Таким образом, описанные выше методики расчетного определения степени и скорости пластической деформации, температуры металла в зоне сварки, сопротивления его пластической деформации, а также изменения высоты уплотняющего пояска при формировании сварного соединения, позволяют проводить практические расчёты по уравнениям термодеформационного равновесия процессов сварки (3.11) и (3.17), как для традиционных способов сварки, так и для способов сварки с обжатием периферийной зоны соединений.
4.
Математическое моделирование процессов
формирования точечных сварных соединений
Общеизвестно то, что величина (степень) объемной пластической деформации в зоне сварки значимо влияет на процесс нагрева, так как определяет плотность тока через площади ее сечений в плоскостях контактов деталь–деталь и электрод–деталь. Вместе с тем, общеизвестно и то, что нагрев металла в зоне формирования соединения, в свою очередь, тоже оказывает влияние на его пластическую деформацию, поскольку влияет на изменение его сопротивления пластической деформации. Таким образом осуществляется как бы саморегулирование процесса точечной сварки. Это предполагает, что при устойчивом процессе формирования соединения в зоне сварки должно существовать определенное соответствие между нагревом в ней металла и пластической его деформацией [3, 165, 185… 187], которое количественно характеризуется критерием жесткости режимов контактной точечной сварки [3, 15].
Однако указанные выше известные гипотезы и предположения лишь качественно определяют возможные взаимосвязи между основными термодеформационными процессами точечной сварки. Описанные же выше математические модели основных термодеформационных процессов, протекающих при КТС, позволяют количественно определить параметры основных термодеформационных процессов в зоне сварки и закономерности их изменений. Это, в частности, можно сделать при решении интегральных уравнений термодеформационного равновесия процессов контактной точечной сварки относительно диаметра уплотняющего пояска. Кроме того, решение этой задачи предопределяет необходимость расчетного определения параметров всех основных термодеформационных процессов, протекающих в зоне сварки.
Таким образом, решение уравнений (3.11) или (3.17) термодеформационного равновесия процесса контактной точечной сварки относительно диаметра уплотняющего пояска фактически позволяют моделировать процесс КТС. Возможность же варьировать при этом параметры режимов сварки фактически предопределяет возможность проведения численных экспериментов.
4.1.
Методики расчета изменения диаметра уплотняющего пояска в процессе контактной точечной сварки
Математическое моделирование процессов контактной точечной сварки осуществляется решением уравнений термодеформационного равновесия процесса сварки (3.11) или (3.17) относительного диаметра уплотняющего пояска d
П
t
в отдельные дискретные моменты времени t
от начала до окончания импульса тока. При этом параметры внешнего силового воздействия на детали (усилия сжатия электродов F
Э
t
) заданы, как параметры режима сварки. В силу использования для оценки теплового состояния зоны сварки расчетно-экспериментального метода, выраженного зависимостью (3.36), подразумевается, что величина сварочного тока заданна такой, чтобы обеспечивала получение заданных геометрических размеров ядра (высоты h
Я
и диаметра d
Я
). В процессе решения уравнений (3.11) или (3.17) относительно d
П
t
для каждого момента времени t
рассчитывается и все остальные его составляющие, которые отражают изменение термодеформационных процессов, протекающих в зоне сварки на стадии нагрева.
Расчет изменения диаметра уплотняющего пояска в процессе формирования соединения решением уравнений (3.11) или (3.17) относительно d
П
t
осложняется тем, что эти уравнения относительно d
П
t
являются трансцендентными. Поэтому в методиках расчета изменений диаметра уплотняющего пояска в процессе сварки, описанных ниже, решение уравнений (3.11) и (3.17) относительно d
П
t
осуществляется методом итераций.
4.1.1.
Методика расчета изменения диаметра уплотняющего пояска
при традиционных способах контактной точечной сварки
Расчет изменения диаметра уплотняющего пояска в процессе формирования соединения при традиционных способах контактной точечной сварки осуществляется решением уравнения (3.11) относительно d
П
t
для условий сварки деталей одинаковых толщин из одного и того же материала. Алгоритм [206, 210, 253] решения поставленной задачи по моделированию КТС рассчитан на машинный счет и осуществляется следующим образом (рис. 4.1). решением уравнения (3.11) относительно d
П
t
для условий сварки деталей одинаковых толщин из одного и того же материала. Алгоритм [206, 210, 253] решения поставленной задачи по моделированию КТС рассчитан на машинный счет и осуществляется следующим образом (рис. 4.1).
Блок 2 алгоритма осуществляет ввод исходных данных, которые рационально разбить на три группы. В особенности это целесообразно делать при расчетах нескольких вариантов одного и того же задания.
Первая группа исходных данных предназначена для управления работой программы. В ней задается, например, число шагов расчета по времени, условия вывода результатов расчетов и т. п.
Вторая группа исходных данных содержит параметры теплофизических и прочностных характеристик свариваемого материала (табл. 4.1).
Таблица
4.1
Исходные данные для расчетов по уравнениям термодеформационного
равновесия процесса сварки
| №
пп
|
Параметры
|
Обозначение
|
Единицы измерения
|
| Характеристики свариваемого материала
|
| 1
|
Температура плавления
|
ТПЛ
|
°
С
|
| 2
|
Температурный коэффициент линейного расширения
|
α
|
1/о
С
|
| 3
|
Коэффициент расширения при плавлении
|
β*
|
%
|
| 4
|
Предел текучести
|
σТ
|
Па
|
| 5
|
Температура расчёта σТ
|
Тσ
|
°
С
|
| 6
|
Базисное значение сопротивление деформации
|
σД0
|
Па
|
| 7
|
Данные для аппроксимации изменения термомеханических коэффициентов: кТ
, кε
и к
U
и предела текучести σ02
|
АТ
, ВТ,
nT
,
Аε
, Вε,
n
ε,
А
u
, В
u
, В
σ
,
nσ
|
б/р
|
| 8
|
Коэффициент Пуассона
|
μ
|
б/р
|
| 9
|
Модуль Юнга
|
Е
|
Па
|
| Данные по технологии и режиму сварки
|
| 10
|
Толщина свариваемыхдеталей
|
s
|
м
|
| 11
|
Конечные диаметр и высота ядра
|
d
Я
,
h
Я
|
м
|
| 12
|
Шаг между точками*
|
t
|
м
|
| 13
|
Ширина нахлёстки*
|
c
|
м
|
| 14
|
Величина зазора*
|
δ
|
м
|
| 15
|
Радиус или диаметр рабочих поверхностей электродов
|
R
Э
,
d
Э
|
м
|
| 16
|
Время сварки
|
t
СВ
|
c
|
| 17
|
Время начала плавления металла**
|
t
НП
|
c
|
| 18
|
Максимальная температура под электродом**
|
ТЭ
|
°
С
|
| 19
|
Коэффициенты для формул (3.36) и (3.51)
|
m
1
,
n
1
,
m
2
,
n
2
, Кσ
|
б/р
|
| *
— могут не вводиться при δ
= 0;
**
—– могут не вводиться и рассчитываться по зависимостям (3.37) и (3.38)
|
Поскольку зависимость термомеханических коэффициентов от степени и скорости деформации металла, от его температуры, а также зависимость предела текучести от последнего параметра в справочной литературе (например в [242]) в большинстве приводится в виде графиков (см. рис. 3.26) или таблиц, то вводить их рационально в виде аппроксимированных функций, например, вида:
 , (4.1) , (4.1)
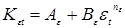 , (4.2) , (4.2)
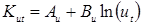 , (4.3) , (4.3)
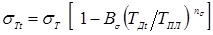 , (4.4) , (4.4)
для которых коэффициенты аппроксимации определяется по графическим или табличным справочным данным.
Третья группа исходных данных (табл. 4.1) характеризует в основном технологию и режим сварки. Поскольку известны способы точечной сварки как неизменными во время импульса тока параметрами усилия сжатия электродов (см. п.1.2.2), так и с изменяющейся их величиной по определенной программе [3, 54, 58, 253, 260, 261], то в последнем случае рационально их также задавать в виде аппроксимированных функций.
Практически любую известную в технологии точечной сварки программу изменения усилия сжатия токопроводящих электродов F
Э
t
в процессе формирования соединения можно описать двумя степенными функциями изменения программированного параметра Р
с одной точкой разрыва Bi
в момент времени t
1
(рис. 4.2). В общем случае, для аппроксимации подобного изменения в процессе точечной сварки любого параметра Р
функции можно записать следующим образом:
 , (4.5) , (4.5)
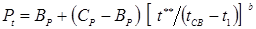 , (4.6) , (4.6)
где АР
, ВР
и C
Р
— значения программируемого параметра в момент времени 0,
t
1
и t
СВ
; a
,
b
— показатели степени.
В случае, если изменение программируемого параметра Р
t
может быть описано одной функцией, то t
1
рационально принимать равным 0,
т. е. изменение параметра Р
t
описывать в интервале времени t
1
… t
СВ
.
Коэффициенты аппроксимации АР
, ВР,
C
Р,
t
1,
a
,
b
, которые в этом случае определяются для программы изменения F
Э
в процессе КТС, водятся в исходных данных (табл. 4.2).
 Поскольку многие ошибки в исходных данных приводят к прерываниям вычислений (например, деление на нуль, логарифм отрицательного числа и т. п.), то рационально осуществлять их контроль после ввода (блок 3). Если обнаружена такая ошибка, то об этом выводится информация (блок 15) выполнение задачи прекращается. Поскольку многие ошибки в исходных данных приводят к прерываниям вычислений (например, деление на нуль, логарифм отрицательного числа и т. п.), то рационально осуществлять их контроль после ввода (блок 3). Если обнаружена такая ошибка, то об этом выводится информация (блок 15) выполнение задачи прекращается.
В блоке 4 рассчитываются параметры, которые не зависят от времени[2]
. Причем, в нем же осуществляется подготовка к выполнению циклов по времени t
, в частности, определяется шаг расчета по времени Δ
t
=
t
СВ
/п
, где п —
число шагов расчета, обнуляются требуемые переменные и задаются их начальное значения. Цикл по времени выполняется блоками 5...13 и заканчивается при выполнении заданного числа i
шагов расчета.
Таблица
4.2
Исходные данные силового воздействия на детали при расчете диаметра уплотняющего пояска по уравнению (3.11)
| №
пп
|
Параметры
|
Обозначение
|
Единица
измерения
|
| 1
|
Неизменное усилие сжатия электродов
|
F
Э
|
Н
|
| 2
|
Данные для аппроксимации программированного усилия сжатия электродов
|
А
Р
,
В
Р,
CР,
t1,
a, b
|
б/р
|
Вычисление диаметра пояска d
П
t
в фиксированный момент t
, осуществляется методом итераций путем последовательного приближения с уменьшением шага Δ
d
П
(рис. 4.3). Поэтому в блоке 6 задается начальное значение d
П
t
, равное диаметру ядра d
Я
t
: d
П
t
=
d
Я
t
. Это означает, что до начала плавления металла при t
≤ t
НП
начальное значение d
П
t
=
0, а при t
> t
НП
значение d
П
t
задается равным d
Я
t
.
 С блока 7 начинается участок алгоритма, осуществляющий цикл по диаметру уплотняющего пояска (блоки 8...11). В нем при каждом цикле по d
П
t
его текущее значение изменяется на Δ
d
П
. В блоке 8 последовательно осуществляются вычисления значений параметров термодеформационных процессов, которые заканчиваются расчетом усилия сжатия С блока 7 начинается участок алгоритма, осуществляющий цикл по диаметру уплотняющего пояска (блоки 8...11). В нем при каждом цикле по d
П
t
его текущее значение изменяется на Δ
d
П
. В блоке 8 последовательно осуществляются вычисления значений параметров термодеформационных процессов, которые заканчиваются расчетом усилия сжатия  в площади уплотняющего пояска по уравнению равновесия (3.11), с учетом зависимостей (3.9) и (3.10), преобразованному к следующему виду: в площади уплотняющего пояска по уравнению равновесия (3.11), с учетом зависимостей (3.9) и (3.10), преобразованному к следующему виду:
 , (4.7) , (4.7)
где F
Я
t
– усилие, развиваемое давлением жидкого металла в площади ядра; F
П
t
–
усилие в площади уплотняющего пояска; F
Д
t
— усилие, необходимое для деформации деталей при их сближении до соприкосновения.
Горячая обработка металлов давлением производится, как правило, при температурах выше температуры рекристаллизации. Для этого интервала температур и определены в основном параметры сопротивления деформации материалов. Для области низких температур эти данные зачастую отсутствуют. Поэтому при расчетах с использованием параметров сопротивления деформации металла, его значения на область низких температур остается только экстраполировать. Однако для этих интервалов температур для большинства материалов известны зависимости от температуры их пределов текучести. Поэтому, при температурах материала, меньше которых не определены значения сопротивления деформации σ
Д
t
(при T
Д
t
< T
σ
), его значения рационально принимать равными пределу текучести σ
Т
t
(блок 8). Это условие, при отсутствии значений сопротивления деформации, позволяет расчеты вообще производить по пределу текучести.
Использование в расчетах σ
Д
t
и σ
Т
t
оправдало двумя обстоятельствами. Во-первых, при сварке значения T
Д
t
достигают значений T
σ
как правило за время t
< 0,05…0,1 t
СВ
.
Во-вторых, разница значений σ
Д
t
и σ
Т
t
быстро уменьшается по мере уменьшения жесткости режимов сварки и увеличения толщины свариваемых деталей.
Рассчитанное в блоке 8 значение усилие сжатия электродов 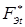 сравнивается с заданным F
Э
t
(блок 9). Пока выполняется условие, что сравнивается с заданным F
Э
t
(блок 9). Пока выполняется условие, что 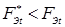 , цикл по d
П
t
продолжается с тем же шагом Δ
d
П
j
переходом в блок 7. Если же это условие не выполняется, то есть , цикл по d
П
t
продолжается с тем же шагом Δ
d
П
j
переходом в блок 7. Если же это условие не выполняется, то есть 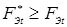 , то абсолютная разность между ними , то абсолютная разность между ними 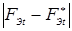 сравнивается с заданной погрешностью е
F
(блок 10). В случае, если сравнивается с заданной погрешностью е
F
(блок 10). В случае, если 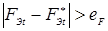 , то значение d
П
t
уменьшается на Δ
d
П
j
, а Δ
d
П
j
уменьшается вдвое (блок 11) и осуществляется переход в блок 7, где d
П
t
увеличивается на измененное значение Δ
d
П
j
и циклы по d
П
t
продолжаются[3]
. Если же , то значение d
П
t
уменьшается на Δ
d
П
j
, а Δ
d
П
j
уменьшается вдвое (блок 11) и осуществляется переход в блок 7, где d
П
t
увеличивается на измененное значение Δ
d
П
j
и циклы по d
П
t
продолжаются[3]
. Если же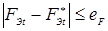 , то абсолютная разность между истинным значением диаметра уплотняющего пояска d
П0
и расчётным d
П
i
меньше или равна допускаемой погрешности е
d
: , то абсолютная разность между истинным значением диаметра уплотняющего пояска d
П0
и расчётным d
П
i
меньше или равна допускаемой погрешности е
d
: 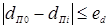 (см. рис. 4.3). На этом циклы по d
П
t
заканчиваются и фиксируются результаты расчётов (блок 12). При условии, что i
<
n
+
1 (блок 13), осуществляется переход в блок 5 и цикл по времени продолжается на следующем шаге расчета по t
. После выполнения заданного числа шагов расчетов по времени t
производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается. (см. рис. 4.3). На этом циклы по d
П
t
заканчиваются и фиксируются результаты расчётов (блок 12). При условии, что i
<
n
+
1 (блок 13), осуществляется переход в блок 5 и цикл по времени продолжается на следующем шаге расчета по t
. После выполнения заданного числа шагов расчетов по времени t
производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается.
Диаметр уплотняющего пояска относится к тем немногочисленным параметрам процесса точечной сварки, которые можно легко измерить экспериментально. Вследствие этого, измеряя изменение диаметра уплотняющего пояска в процессе формирования соединения, представляется возможность оценить точность методики расчетов как диаметра уплотняющего пояска, так и обобщенно всех параметров термодеформационных процессов, используемых при решении уравнения (3.11).
Для проверки описанной выше термодеформационной модели процесса точечной сварки детали сваривали с прерываниями его в моменты ti
(через 0,02 с) и измеряли полученный диаметр уплотняющего пояска. Для этих же условий сварки и моментов ti
процесса формирования соединения производили расчет диаметра уплотняющего пояска d
П
t
по описанной выше методике и сравнивали расчетные его значения с его величиной, измеренной экспериментально. Например, на рис. 4.4 показано изменение диаметра уплотняющего пояска в процессе формирования соединения, полученная экспериментально (кривая 1) и расчетом по описанной выше методике математического моделирования процесса КТС (кривая 2).
 Многочисленные сравнения расчетных и экспериментальных значений диаметра уплотняющего пояска показали, что их расхождения не превышает 5…15 %. Это, в определенной мере, отражает степень адекватности термодеформационной модели процесса формирования соединения и реального процесса точечной сварки, подтверждает приемлемость сделанных допущений и показывает допустимость использования данной модели для приближенных решений технологических задач КТС [206, 217]. Многочисленные сравнения расчетных и экспериментальных значений диаметра уплотняющего пояска показали, что их расхождения не превышает 5…15 %. Это, в определенной мере, отражает степень адекватности термодеформационной модели процесса формирования соединения и реального процесса точечной сварки, подтверждает приемлемость сделанных допущений и показывает допустимость использования данной модели для приближенных решений технологических задач КТС [206, 217].
4.1.2.
Методика расчета изменения диаметра уплотняющего пояска при контактной точечной сварки с обжатием периферии соединения
Расчет изменения диаметра уплотняющего пояска при контактной точечной сварки с обжатием периферии соединения, как и при традиционных способах КТС, представляет собой математическое моделирование процесса формирования соединения. Он также осуществляется в отдельные дискретные моменты времени t
от начала до окончания импульса тока, но только решением относительного диаметра уплотняющего пояска d
П
t
уравнения (3.17) термодеформационного равновесия процесса сварки с обжатием периферийной зоны соединения. При этом параметры внешнего силового воздействия на детали заданы как параметры режима сварки.
Последовательность и логика выполнения алгоритма (рис. 4.5) для расчета изменения диаметра уплотняющего пояска при КТС с обжатием периферии соединения [211, 212, 243], организация и выполнение в нем циклов по времени t
с неизменным шагом Δ
t
(по блокам 5…13) и по диаметру уплотняющего пояска d
П
t
с изменяющимся шагом Δ
d
П
j
(по блокам 7…11) такие же, как и в алгоритме для традиционных способов КТС, показанном на рис. 4.1. Решение задачи также осуществляется методом итераций, так как уравнение (3.17) относительно d
П
t
является трансцендентным. Осуществляется алгоритм следующим образом.
 Вводимые исходные данные, рационально также разбить на три группы. Первая группа исходных данных, предназначенная для управления работой программы, естественно должна учитывать ее особенности. Вторая же и третья группы исходных данных, содержащие характеристики свариваемого материала, а также технологии и режима сварки, такие же, как и при решении этой задачи для традиционных способов точечной сварки (табл. 4.1). Вводимые исходные данные, рационально также разбить на три группы. Первая группа исходных данных, предназначенная для управления работой программы, естественно должна учитывать ее особенности. Вторая же и третья группы исходных данных, содержащие характеристики свариваемого материала, а также технологии и режима сварки, такие же, как и при решении этой задачи для традиционных способов точечной сварки (табл. 4.1).
В большинстве известных способов точечной сварки с обжатием периферийной зоны соединения [59…70, 245] силовое воздействие на детали задают двумя силовыми параметрами режима: усилием F
СВ
t
сжатия деталей приводом сварочной машины и усилием F
0
t
их обжатия кольцевыми силовыми пуансонами в периферийной зоне соединения (см. рис.1.7) как неизменными, так и программированными по величине. В последнем случае их рационально задавать в виде аппроксимированных функций, например, выраженных зависимостями (4.5) и (4.6). Коэффициенты аппроксимации А
F
св
, В
F
св,
CF
св,
t
1,
a
1
,
b
1
и А
F
о
, В
F
о,
CF
о,
t
1,
a
2
,
b
2
в этом случае водятся в исходных данных (табл. 4.3).
Усилие же сжатия на токопроводящем электроде F
Э
t
определяется из соотношения (1.6) усилий сжатия деталей приводом сварочной машины F
СВ
, токопроводящими электродами F
Э
t
и обжимными втулками F
0
t
, которое, с учётом необходимости расчетов в дискретные моменты t
процесса КТС, можно преобразовать к следующему виду:
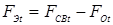 . (4.8) . (4.8)
Вычисление диаметра пояска d
П
t
в фиксированный момент t
, осуществляется также методом итераций путем последовательного приближения (рис. 4.3). Цикл по диаметру уплотняющего пояска d
П
t
с уменьшением шага Δ
d
П
j
осуществляется блоками 8...12. В блоках 8...10 последовательно вычисляются значения параметров термодеформационных процессов, протекающих при КТС с обжатием периферийной зоны соединения.
Таблица
4.3
Исходные данные силового воздействия на детали при расчете диаметра уплотняющего пояска по уравнению (3.17)
| №
пп
|
Параметры
|
Обозначение
|
Единица
измерения
|
| 1
|
Неизменное усилие сжатия приводом сварочной машины
|
F
СВ
|
Н
|
| 3
|
Неизменное усилие обжатия периферийной зоны соединения
|
F
0
|
Н
|
| 2
|
Данные для аппроксимации программированного усилия сжатия приводом сварочной машины
|
А
F
св
t
, В
F
св
t
,
CF
св
t
,
t
1,
a
1
,
b
1
|
б
/
р
|
| 4
|
Данные для аппроксимации программированного усилия обжатия периферийной зоны соединения
|
А
F
о
t
,
В
F
о
t,
CF
о
t,
t1,
a2
, b2
|
б/р
|
При КТС с обжатием периферийной зоны соединения не все усилие (F
Э
t
+
F
О
t
) сжатия деталей электродными устройствами может передаваться в контур уплотняющего пояска. Частично оно может уравновешиваться усилием F
Д
t
, необходимым для сближения деталей до соприкосновения их поверхностей при наличии между ними зазоров. Кроме того, если сумма усилия F
Д
t
и усилия F
У
t
, передаваемого в контур уплотняющего пояска от обжимных втулок меньше, чем усилие сжатия ими деталей F
О
t
, т. е. 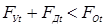 , оно частично, на величину F
К
t
, зависящую от цилиндрической жесткости деталей и расстояния между контурами уплотняющего пояска и обжимной втулки (см. зависимость (3.19)), которую можно определить по зависимости (3.20), преобразованной к следующему виду: , оно частично, на величину F
К
t
, зависящую от цилиндрической жесткости деталей и расстояния между контурами уплотняющего пояска и обжимной втулки (см. зависимость (3.19)), которую можно определить по зависимости (3.20), преобразованной к следующему виду:
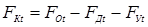 , (4.9) , (4.9)
уравновешивается в кольцевом контакте.
Поэтому для расчётов d
П
t
уравнение (3.17) рационально преобразовать к виду:
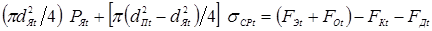 . .
Левая часть этого равенства согласно (3.9), (3.10) и (3.21) равна усилию F
C
t
, уравновешиваемому в площади свариваемого контакта давлением в ядре РЯ
t
и напряжениями в уплотняющем пояске σ
CР
t
. Правая же его часть равна усилию  , которое передаётся в контур уплотняющего пояска от воздействия на детали токопроводящими электродами F
Э
t
и обжимными втулками F
0
t
: , которое передаётся в контур уплотняющего пояска от воздействия на детали токопроводящими электродами F
Э
t
и обжимными втулками F
0
t
:
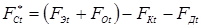 . (4.10) . (4.10)
При итерациях по диаметру уплотняющего пояска d
П
t
сравниваются значения 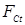 и и 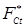 (блок 9). Пока выполняется условие, что (блок 9). Пока выполняется условие, что 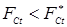 , циклы по d
П
t
продолжаются с тем же шагом Δ
d
П
j
переходом в блок 7. Если же это условие не выполняется, т. е. , циклы по d
П
t
продолжаются с тем же шагом Δ
d
П
j
переходом в блок 7. Если же это условие не выполняется, т. е.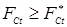 , а , а 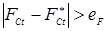 (блок 10), то d
П
t
уменьшается на Δ
d
П
j
, затем уменьшается Δ
d
П
j
(блок 11) и циклы по d
П
t
продолжаются. Если же (блок 10), то d
П
t
уменьшается на Δ
d
П
j
, затем уменьшается Δ
d
П
j
(блок 11) и циклы по d
П
t
продолжаются. Если же 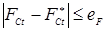 , циклы по d
П
t
заканчиваются, фиксируются результаты расчётов (блок 12) и осуществляется переход в цикл по времени (блок 13). После выполнения заданного числа шагов расчетов по времени производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается. , циклы по d
П
t
заканчиваются, фиксируются результаты расчётов (блок 12) и осуществляется переход в цикл по времени (блок 13). После выполнения заданного числа шагов расчетов по времени производится заданный вывод полученных результатов (блок 14) и решение задачи заканчивается.
Оценку адекватности термодеформационной модели процесса точечной сварки с обжатием периферийной зоны соединения реальному процессу формирования соединения производили так же обобщенно, как и проверку описанной выше термодеформационной модели для традиционных способов точечной сварки. Так же при сварке деталей осуществляли прерывания процесса формирования соединения и измеряли диаметр уплотняющего пояска, а затем сравнивали его значения с расчетными для тех же условий сварки и моментов формирования соединения.
Многочисленные сравнения расчетных и экспериментальных значений диаметра уплотняющего пояска для условий сварки деталей толщиной 1….4 мм из высоколегированных и углеродистых сталей, а также алюминиевых сплавов, показали, что их расхождения не превышают 10…20 %, что в определенной мере, отражает приемлемую для приближенных решений технологических задач степень адекватности термодеформационной модели процесса формирования соединения и реального процесса точечной сварки с обжатием периферийной зоны соединения [210…212, 243].
4.2
. Изменение термодеформационных процессов на стадии
нагрева при традиционных способах точечной сварки
Описанные выше методики расчета основных термодеформационных процессов, протекающих в зоне сварки на стадии нагрева, предоставляют возможность определить их количественные значения в любой момент процесса формирования соединения при заданных параметрах режима сварки. Практически, это означает, что решение уравнений (3.11) или (3.17) относительно диаметра уплотняющего пояска при заданных параметрах режима сварки позволяет проводить численные эксперименты.
Моделированием процессов формирования точечных сварных соединений как при традиционных способах сварки, так и при способах сварки с обжатием периферии соединения по описанным выше методикам расчетов подтверждается существующее мнение [3, 16] о том, что формирование точечных соединений происходит по единой схеме, несмотря на изменение значимости влияния отдельных термодеформационных процессов, протекающих в зоне сварки, на формирование соединения на отдельных этапах цикла сварки, а также различия количественных их параметров. Так, во всех случаях контактной точечной сварки сохраняется временная последовательность протекания отдельных термодеформационных процессов в зоне сварки, значимость их влияния на процесс формирования соединения и характер изменения при сварке: температура металла в зоне сварки во время импульса сварочного тока, хотя и неравномерно, всегда увеличивается; среднее значение давления в свариваемом контакте, напряжения в площади уплотняющего пояска, а после начала плавления металла в свариваемом контакте и давление в ядре всегда уменьшаются по величине; разупрочнение металла в зоне сварки всегда возрастает, что сопровождается его пластическим течением и непрерывным увеличением площади свариваемого контакта [203…206, 210…212, 218, 243].
4.2.1.
Изменение параметров термодеформационных процессов при традиционных способах точечной сварки
Из всех параметров процесса точечной сварки к настоящему времени экспериментально измерено с достаточной степенью надежности только изменение в процессе формирования соединения диаметра уплотняющего пояска, размеров ядра расплавленного металла и температуры в контактах электрод–деталь. Сведения об остальных в большинстве носят предположительный характер.
Решение уравнения (3.11) термодеформационного равновесия процесса формирования соединения для традиционных способов сварки впервые (алгоритм показан на рис. 4.1) позволило рассчитать изменение в процессе КТС параметров основных термодеформационных процессов, определить их взаимовлияние и влияние на устойчивость процесса сварки. При этом установлено следующее (рис. 4.5) [203…206, 214…216, 218].
В процессе формирования точечного сварного соединения на стадии нагрева во время t
СВ
действия импульса сварочного тока происходит уменьшение среднего давления РСР
t
в контуре контакта деталь–деталь, сопровождаемое его пластическим течением и непрерывным увеличением площади (диаметра d
П
t
) свариваемого контакта (рис. 4.5, а
). Это является следствием того, что среднее значение напряжений в контуре уплотняющего пояска σ
СР
t
, а после начала плавления металла в свариваемом контакте и давление РЯ
t
в ядре, уменьшаются по величине. Причем, до начала плавления металла средние значения давления РСР
t
и напряжений σ
СР
t
в контакте деталь–деталь совпадают по величине.
Основными факторами, определяющими такое изменение напряжений в контуре уплотняющего пояска σ
СР
t
и давление РЯ
t
в ядре, являются разупрочнение металла в зоне сварки, которое проявляется в уменьшении его сопротивления пластической деформации σ
Д
t
, а также уменьшение ширины уплотняющего пояска b
П
t
, равной b
П
t
= (d
П
t
– d
Я
t
)/2 (см. зависимости (3.51) и (3.59)), из-за более быстрого увеличения диаметра ядра d
Я
t
по сравнению с увеличением диаметра d
П
t
уплотняющего пояска.

Основным фактором, определяющим уменьшение сопротивления пластической деформации металла в зоне сварки σ
Д
t
является его разупрочнение вследствие увеличения температуры ТД
t
(рис. 4.5, а
), которое по своему влиянию не только полностью компенсирует, но и превосходит упрочняющее действие монотонно увеличивающейся в процессе формирования соединения степени пластической деформации. Кроме того, уменьшению в процессе КТС сопротивления пластической деформации металла в зоне сварки σ
Д
t
способствует и уменьшение при сварке скорости пластической деформации ut
.
Монотонное изменение в процессе КТС напряжений в контуре уплотняющего пояска σ
СР
t
и давления РЯ
t
в расплавленного металла ядре не приводит к нарушению термодеформационного равновесия в площади свариваемого контакта. Оно сопровождается лишь изменением в его площади характера силового взаимодействия деталей (рис. 4.5, в
).
Так, в приведенном на рис. 4.5 примере, детали в месте сварки собраны с зазором δ
= 0,5 мм. Поэтому в соответствии с уравнением (3.11) усилие сжатия в площади свариваемого контакта FCt
(3.21) меньше усилия сжатия деталей электродами F
Э
t
, на величину F
Д
t
(см. зависимость (2.5)), затраченную на деформацию деталей при их сближении до соприкосновения поверхностей. В течение все процесса КТС усилие сжатия в свариваемом контакте FCt
меньше усилия сжатия деталей электродами F
Э
t
на величину F
Д
t
и в данном случае остается неизменным.
До начала плавления металла все усилие FCt
сжатия в свариваемом контакте уравновешивается металлом, находящимся в твёрдой фазе. В этом случае все усилие в площади свариваемого контакта FCt
уравновешивается напряжениями, интегральная сумма которых в площади уплотняющего пояска равна усилию F
П
t
, т. е. в этот период согласно зависимостям (3.10) и (3.21) FCt
= F
П
t
.
В период после момента t
НП
начала плавления металла в свариваемом контакте до окончания импульса тока (при t
НП
< t
≤ t
СВ
) часть усилия сжатия в свариваемом контакте FCt
уравновешивается давлением РЯ
t
расплавленного металла в ядре, которое по его площади развивает усилие F
Я
t
(3.9), а часть — напряжениями в уплотняющем пояске, которые по его площади составляют усилие F
П
t
(3.10). При этом, несмотря на уменьшение давления в ядре РЯ
t
в процессе его формирования, усилие F
Я
t
в его площади увеличивается, что обусловлено более быстрым увеличение площади ядра по сравнению с уменьшением в нем давления. Поэтому по мере роста ядра происходит перераспределение усилий сжатия в свариваемом контакте при неизменной величине FCt
: доля усилия FCt
, уравновешиваемая в его площади усилием F
Я
t
, увеличивается, а доля, уравновешиваемая в площади уплотняющего пояска усилием F
П
t
, уменьшается на величину F
Я
t
.
Такое взаимосвязанное изменение параметров термодеформационных процессов, протекающих в зоне сварки, и параметров силового взаимодействия деталей в площади свариваемого контакта обеспечивает устойчивое формирование соединения в условиях их непрерывного изменения при КТС.
4.2.2.
Особенности термодеформационных процессов при точечной сварке с обжатием периферийной зоны соединения
Формирование сварного соединения при точечной сварке с обжатием его периферийной зоны происходит по той же схеме, что и при традиционных способах КТС. В месте с тем, особенности силового воздействия на детали при КТС с обжатием периферийной зоны соединения, которые заключаются в сжатии деталей токопроводящими электродами усилием F
Э
и автономном обжатии периферийной зоны соединения кольцевыми силовыми пуансонами усилием F
О
(см. п. 1.2.3), при сохранении общего характера протекания основных термодеформационных процессов в зоне сварки приводят к существенному изменению количественных их параметров.
Математическое моделирование процесса КТС с обжатием периферийной зоны соединения, путем решения уравнения (3.17) термодеформационного равновесия этого процесса сварки (алгоритм показан на рис. 4.1), впервые позволило определить не только характер изменения основных термодеформационных процессов в зоне формирования соединения при этом способе сварки, но и рассчитать их количественные параметры. При этом установлено следующее (рис. 4.7) [204, 210…212, 243].

В процессе формирования точечного сварного соединения на стадии нагрева во время t
СВ
действия импульса сварочного тока при КТС с обжатием периферийной зоны соединения, как и при традиционных способах сварки, в зоне сварки происходит пластическое течение металла и монотонное увеличение площади (диаметра d
П
t
) свариваемого контакта
(рис. 4.7, а
). Это является следствием того, что среднее значение напряжений в контуре уплотняющего пояска σ
СР
t
, а после начала плавления металла в свариваемом контакте и давление РЯ
t
в ядре, также уменьшаются по величине в течение действия импульса сварочного тока.
Факторы, следствием воздействия которых является такое изменение напряжений в контуре уплотняющего пояска σ
СР
t
и давления РЯ
t
расплавленного металла в ядре, те же: разупрочнение металла в зоне сварки и снижение его сопротивления пластической деформации σ
Д
t
, а также уменьшение ширины уплотняющего пояска b
П
t
, равной b
П
t
= (d
П
t
– d
Я
t
)/2, из-за более быстрого роста диаметра ядра d
Я
t
по сравнению с увеличением диаметра d
П
t
уплотняющего пояска.
Основным фактором, определяющим уменьшение сопротивления пластической деформации σ
Д
t
металла в зоне сварки во время действия импульса сварочного тока также, как и при традиционных способах КТС, является его разупрочнение вследствие увеличения температуры ТД
t
(рис. 4.5, б
), которое по своему влиянию превосходит упрочняющее действие монотонно увеличивающейся в процессе формирования соединения степени пластической деформации. Так, в период времени после начала формирования ядра, несмотря на существенное увеличение температуры Т0
t
в центре контакта деталь–деталь температуры ТЭ
t
в контакте электрод–деталь, температура деформируемого металла ТД
t
увеличивается незначительно, что хорошо коррелируется с изменением в этот период его сопротивления пластической деформации.
Кроме того, как и при традиционных способах КТС, уменьшению в процессе КТС сопротивления пластической деформации металла в зоне сварки σ
Д
t
также способствует и уменьшение при сварке скорости пластической деформации ut
.
Основное отличие характера протекания термодеформационных процессов при КТС с обжатием периферийной зоны соединения от их протекания при традиционных способах сварки заключается в особенностях характера силового взаимодействия деталей в контакте деталь–деталь, в частности, в возможности их силового взаимодействия вне контура уплотняющего пояска в площади кольцевого контакта деталь–деталь (см. рис. 3.2). Это оказывает существенное влияние на количественные параметры всех основных термодеформационных процессов, протекающих в зоне сварки, в частности, на величину напряжений в контуре уплотняющего пояска σ
СР
t
и давления РЯ
t
в расплавленного металла ядре.
Так, в приведенном на рис. 4.7 примере, детали в месте сварки сжимаются токопроводящими электродами неизменным усилием F
Э
t
=
6 кН и обжимными втулками также неизменным усилием обжатия F
О
t
=
3,4 кН (рис. 4.5, в
). При этом в одном варианте сварки детали обжимаются втулками с внутренним диаметром d
ВВ
, равным 16 мм (изменение параметров термодеформационных процессов в этом варианте сварки показано сплошными линиями), а в другом — 24 мм (в этом варианте сварки —штриховыми линиями).
Поскольку в приведенном примере детали в месте сварки собраны без зазора (δ
= 0 → F
Д
t
= 0), то в соответствии с уравнением (3.17) к моменту начала импульса тока усилие сжатия в площади свариваемого контакта FCt
равно усилию сжатия деталей токопроводящими электродами F
Э
t
, а усилие в кольцевом контакте F
К
t
вне контура уплотняющего пояска равно усилию обжатия деталей F
О
t
кольцевыми силовыми пуансонами.
С момента начала импульса тока вследствие нагрева и расширения металла в зоне сварки в контакте деталь–деталь начинает формироваться рельеф (уплотняющий поясок), увеличивающаяся высота которого h
П
t
определяется по зависимости (3.84). Вследствие этого детали между контурами уплотняющего пояска и внутреннего диаметра обжимной втулки прогибаются и своей упругостью передают в зону сварки часть усилия обжатия деталей F
О
t
, равную усилию F
У
t
, величину которого можно определить по зависимости (3.19), сопротивления деталей их суммарному прогибу на высоту уплотняющего пояска. Таким образом, в процессе сварки на стадии нагрева усилие сжатия в свариваемом контакте FCt
увеличивается пропорционально увеличению высоты h
П
t
уплотняющего пояска на величину F
У
t
, а усилие сжатия деталей в кольцевом контакте F
К
t
на эту же величину уменьшается.
Это сказывается на количественных параметрах всех термодеформационных процессов, протекающих в зоне сварки. Так, увеличение внутреннего диаметра обжимной втулки с 16 до 24 мм приводит к уменьшению усилия упруго прогиба деталей F
У
t
, усилия сжатия в площади свариваемого контакта FCt
, уменьшению диаметра уплотняющего пояска d
П
t
, повышению температуры ТД
t
деформируемого металла и уменьшению его сопротивления пластической деформации σ
Д
t
, а следовательно к уменьшению среднего значения напряжений в площади уплотняющего пояска σ
СР
t
и давления расплавленного металла в ядре РЯ
t
.
При КТС с обжатием периферийной зоны соединения также, как и при традиционных способах сварки, до начала плавления металла все усилие сжатия в свариваемом контакте FCt
уравновешивается металлом, находящимся в твёрдой фазе, и следовательно в этот период согласно зависимостям (3.10) и (3.21) FCt
= F
П
t
.
В период после момента t
НП
начала плавления металла в свариваемом контакте до окончания импульса тока (при t
НП
< t
≤ t
СВ
) часть усилия сжатия в свариваемом контакте FCt
уравновешивается давлением РЯ
t
расплавленного металла в ядре, которое по его площади развивает усилие F
Я
t
(3.9), а часть — напряжениями в уплотняющем пояске, которые по его площади составляют усилие F
П
t
(3.10). При этом, несмотря на уменьшение давления в ядре РЯ
t
в процессе его формирования, усилие F
Я
t
в его площади увеличивается, что обусловлено более быстрым увеличение площади ядра по сравнению с уменьшением в нем давления, что приводит к увеличению доли усилия FCt
, уравновешиваемой усилием F
Я
t
в площади ядра, и уменьшению на эту же величину доли усилия FCt
, уравновешиваемой усилием F
П
t
в площади уплотняющего пояска.
Таким образом, при КТС с обжатием периферийной зоны соединения в процессе сварки происходит не только перераспределение усилий сжатия в свариваемом контакте между уплотняющим пояском и ядром расплавленного металла, но и увеличение усилия сжатия в площади уплотняющего пояска. Это благоприятно сказывается на устойчивости процесса формирования соединения в части увеличения тепловыделения в начале процесса сварки и повышения устойчивости против образования выплесков в его конечной стадии.
4.2.3.
Влияние режимов сварки на параметры термодеформационных процессов, протекающих в зоне формирования соединения
Параметры термодеформационных процессов, протекающих в зоне формирования соединения, зависят от многих факторов точечной сварки, в частности, рассмотренных выше. Кроме того, на них существенное влияние оказывают особенности технологий и параметры режимов точечной сварки, которое и рассмотрим ниже. В частности, исследованием влияния режимов сварки деталей из сплавов АМг6 и АМц, толщиной 1…4 мм, которые приведены в табл. 4.4, установлено следующее.
Таблица
4.4
Параметры режимов точечной сварки и размеры полученных соединений
| №
п/п
|
Материал деталей
|
Толщина деталей, мм
|
Параметры режимов сварки
|
Размеры ядра
|
| Время сварки t
СВ
, с
|
Сварочное усилие
F
СВ
, кН
|
Сварочный ток
I
СВ
, кН
|
Диаметр
d
Я
,
мм
|
Высота
h
Я
, мм
|
| 1
|
АМг6
|
1 + 1
|
0,06
|
6,5
|
38
|
5,0
|
1,2
|
| 2
|
0,08
|
5,5
|
31
|
1,0
|
| 3
|
0,10
|
4,5
|
27
|
0,75
|
| 4
|
2 + 2
|
0,06
|
12,0
|
49
|
8,0
|
2,6
|
| 5
|
0,08
|
42
|
2,1
|
| 6
|
0,10
|
37
|
1,2
|
| 7
|
3 + 3
|
0,16
|
20,0
|
76
|
10,0
|
4,0
|
| 8
|
0,24
|
18,0
|
63
|
3,0
|
| 9
|
0,30
|
17,0
|
57
|
2,1
|
| 10
|
4 + 4
|
0,20
|
28,0
|
85
|
13,0
|
5,1
|
| 11
|
0,26
|
77
|
3,9
|
| 12
|
0,32
|
65
|
2,3
|
| 13
|
АМц
|
1 + 1
|
0,06
|
2,5
|
34
|
5,0
|
1,25
|
| 14
|
0,08
|
26
|
1,0
|
| 15
|
0,10
|
21
|
0,6
|
| 16
|
2 + 2
|
0,10
|
7,0
|
51
|
8,0
|
2,7
|
| 17
|
0,14
|
6,0
|
37
|
2,2
|
| 18
|
0,18
|
5,5
|
32
|
1,3
|
| 19
|
3 + 3
|
0,12
|
10,0
|
78
|
10,0
|
4,1
|
| 20
|
0,16
|
62
|
3,2
|
| 21
|
0,20
|
51
|
2,1
|
| 22
|
4 + 4
|
0,16
|
18,5
|
82
|
13,0
|
4,9
|
| 23
|
0,20
|
16,0
|
73
|
4,1
|
| 24
|
0,24
|
19,0
|
61
|
2,8
|
Температура деформируемого металла
ТД
t
в зоне сварки является основным фактором, определяющим его сопротивление пластической деформации σ
Д
t
. Многочисленные расчеты показали, что нагрев деформируемого объема металла в зоне сварки во время импульса сварочного тока протекает неравномерно (рис. 4.6, б
, рис. 4.7, б
). За первые 10…20 % от времени сварки t
СВ
он нагревается до температуры, которая составляет 65...85 % от конечных ее значений. Затем рост его температуры замедляется. При этом, в случае сварки электродами со сферической рабочей поверхностью рост температуры деформируемого металла наблюдается в течение всего периода действия импульса сварочного тока (рис. 4.6, б
), то при сварке электродами с плоской рабочей поверхностью и, в особенности, с обжатием периферийной зоны соединений увеличение температуры деформируемого металла во второй половине периода их нагрева весьма ограничено (рис. 4.7, б
).
Такое неравномерное увеличение температуры деформируемого металла (рис. 4.8) характерно для любых условий точечной сварки [203, 206, 214…216]. Это в дальнейшем было подтверждено и более точными тепловыми расчетами с решением дифференциальных уравнений, например, в работе [168].

Причинами такого изменения температуры являются, с одной стороны, радиальное перемещение от оси электродов границ деформируемого объема металла из-за увеличения диаметров уплотняющего пояска d
П
t
и ядра расплавленного металла d
Я
t
(см. рис. 4.4, 4.6, а
, 4.7, а
), а с другой — изменения условий процессов выделения и распространения теплоты. Во-первых, увеличение в процессе сварки площадей контактов деталь–деталь и электрод–деталь приводит к уменьшению электрического сопротивления зоны сварки (см. п. 2.3) и, как следствие—к уменьшению тепловыделения. Во-вторых, увеличение площадей контактов электрод–деталь приводит и к увеличению теплоотвода из зоны сварки. Кроме того, замедление увеличения температуры происходит из-за плавления металла в ядре, так как на это затрачивается часть вводимой энергии (см. п. 2.4).
Максимальная температура деформируемого объема металла, которой он достигает в конце процесса формирования соединения, в зависимости от условий сварки изменяется в относительно широких пределах, составляющих 60…95 % от температуры плавления ТПЛ
свариваемого металла.
Изменение толщины свариваемых деталей в пределах 1…4 мм приводит к изменению температуры деформируемого металла, примерно на 5…15 % от ТПЛ
. Причем, с увеличением толщины деталей она возрастает (рис. 4.8), что в основном объясняется уменьшением ее градиента в направлении координаты r
.
Изменение времени сварки влияет на максимальную температуру металла в большей степени (рис. 4.9), чем изменение толщины деталей. Так, изменение времени сварки в пределах, применяемых в практике КТС режимов, приводит к изменению температуры металла на 10…25 % от ТПЛ
. При этом с увеличением времени сварки (уменьшением жесткости режимов) она возрастает. Это обусловлено некоторым уменьшением градиента температуры в металле зоны сварки, прилегающем к ядру.
Такие результаты расчетов температуры металла в зоне сварки вполне согласуются с существующими представлениями, результатами экспериментальных и теоретических исследований процессов выделения и перераспределения теплоты в условиях формирования точечных сварных соединений.
Степень пластической деформации металла в зоне сварки
монотонно увеличивается в течение всего процесса его нагрева, т. е. в течение длительности действия импульса сварочного тока при любых условиях точечной сварки. Причем, во время формирования соединения степень деформации увеличивается неравномерно (рис. 4.10). За первые 5…20 % от времени t
СВ
действия импульса сварочного тока она достигает значений, составляющих 25…40 % от конечных. После этого степень деформации металла в зоне сварки увеличивается практически линейно.
 Динамика изменения степени пластической деформации металла в зоне сварки и ее величина определяются в основном его температурным расширением. Так, характер изменения ε
t
в процессе формирования соединения определяется в основном ее приращением за счет температурного расширения ε
t
1
,
(первое слагаемое в зависимости 3.78), плавления металла в ядре ε
t
2
(второе слагаемое) и вдавливания электродов в поверхности деталей ε
t
3
(третье слагаемое). В момент выключения тока при t
=
t
СВ
приращение степени пластической деформации за счет температурного расширения металла ε
t
1
,
составляет 55…65 % от всей ее конечной величины ε
t
, за счет вдавливания электродов в поверхности деталей ε
t
2
— 20…30 %, за счет приращения объема металла ядра при его расплавлении ε
t
3
— 8…17 %. Динамика изменения степени пластической деформации металла в зоне сварки и ее величина определяются в основном его температурным расширением. Так, характер изменения ε
t
в процессе формирования соединения определяется в основном ее приращением за счет температурного расширения ε
t
1
,
(первое слагаемое в зависимости 3.78), плавления металла в ядре ε
t
2
(второе слагаемое) и вдавливания электродов в поверхности деталей ε
t
3
(третье слагаемое). В момент выключения тока при t
=
t
СВ
приращение степени пластической деформации за счет температурного расширения металла ε
t
1
,
составляет 55…65 % от всей ее конечной величины ε
t
, за счет вдавливания электродов в поверхности деталей ε
t
2
— 20…30 %, за счет приращения объема металла ядра при его расплавлении ε
t
3
— 8…17 %.

К моменту окончания импульса сварочного тока при t
=
t
СВ
степень пластической деформации металла в зоне сварки может достигать значений 12…15 %. При проплавлении деталей на 40…60 %, которое наиболее характерно для большинства соединений в практике точечной сварки, конечная степень деформации составляет 9…12 %.
При сварке на жестких режимах с меньшей длительностью импульса сварочного тока степень деформации на 5…12 % меньше, чем на мягких (рис. 4.11). Это объясняется большим градиентом температуры металла в зоне сварки и большей зоной его нагрева.
С увеличением толщины свариваемых деталей от 1 до 4 мм степень пластической деформации металла в зоне сварки также уменьшается на 8…14 % (рис. 4.12), что объясняется в основном увеличением зоны нагрева при формировании точеного сварного соединения.
  Скорость пластической деформации
ut
металла в зоне сварки изменяется в соответствии с изменение степени его деформации (рис. 4.13), поскольку является ее производной (см зависимость 3.79). Скорость пластической деформации
ut
металла в зоне сварки изменяется в соответствии с изменение степени его деформации (рис. 4.13), поскольку является ее производной (см зависимость 3.79).
Наибольшие ее значения наблюдаются в начале процесса нагрева и составляют через 10 % от времени t
СВ
действия импульса сварочного тока 0,2…3,6 с-1
. В процессе формирования соединения скорость деформации металла зоны сварки уменьшается неравномерно. За последующие 10…15 % от времени нагрева она уменьшается на 20…60 % от значений, которые были при t
≈ 0,1t
СВ
.
После этого она либо монотонно уменьшается до конечных значений, либо остается практически неизменной.

С увеличением жесткости режима сварки скорость деформации возрастает (рис 4.14). Причем, в начале процесса сварки она возрастает примерно в 2,5…3,5 раза, а в конце процесса нагрева — в 1,5…2.5 раза. С увеличением же толщины свариваемых деталей от 1 до 4 мм она уменьшается в 5…6 раз. Это в основном обусловлено увеличением времени сварки t
СВ
, поскольку степень ε
t
деформации металла зоны сварки с увеличением толщины деталей уменьшается всего на 8…14 %.

Сопротивление пластической деформации
σД
t
металла в области уплотняющего пояска в процессе КТС монотонно уменьшается (рис. 4.15).
Причем, уменьшение сопротивления пластической деформации происходят неравномерно, что обусловлено, в основном, неравномерным изменением теплового состояния металла в области уплотняющего пояска (см. рис. 4.6, б
и 4.7, б
). Наибольший градиент его уменьшения, как и уменьшения температуры, наблюдается в первые 10 ¸ 25 % от времени t
СВ
длительности импульса сварочного тока. Это является следствием того, что основным фактором, определяющим сопротивление пластической деформации металла процессе формирования точечного сварного соединения, является его температура. Такое заключение подтверждается характером изменения при сварке термомеханических коэффициентов кТ
, кε
, ки
(рис. 4.16) и их соотношением в дискретные моменты процесса формирования соединения, а также характером изменения их комплексного воздействия на металл зоны сварки, которое можно охарактеризовать коэффициентом разупрочнения 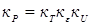 (см. зависимость (3.60)). (см. зависимость (3.60)).

С увеличением жесткости режима сварки сопротивление пластической деформации металла увеличивается в довольно широком диапазоне (на 15…80 %) (рис. 4.17). При этом кратность его увеличения возрастает с повышение прочности металла. С увеличением толщины свариваемых деталей от 1 до 4 мм сопротивление пластической деформации уменьшается: при сварке на жестких режимах — в 1,5…2 раза, а при сварке на мягких режимах — на 10…30 %. Причем кратность уменьшения в начале процесса сварки больше, чем в конце импульса тока и зависит она как от теплофизических свойств металла, так и от параметров режима сварки.
Основным фактором, определяющим сопротивление пластической деформации металла при сварке, является его температура. Вместе с тем и роль степени и скорости пластической деформации металла, как упрочняющих факторов, весьма существенна. Они повышают сопротивление пластической деформации металла зоны сварки на 30…60 % по сравнению со статическим пределом текучести при той же температуре. На рис. 4.18 показано изменение в процессе сварки сопротивления пластической деформации металла (кривая 1) рассчитанное по вышеописанной методике и изменение предела текучести металла (кривая 2) для той же температуры. Поэтому при решении теплодеформационных задач точечной сварки, определяя механические характеристики металла зоны формирования соединения, следует учитывать процессы его упрочнения и разупрочнения, в особенности при сварке деталей малых толщин на жестких режимах.
Среднее значение напряжений
в площади уплотняющего пояска и давление расплавленного металла
в ядре в процессе формирования соединения монотонно уменьшаются (рис. 4.19 и 4.20). Это обусловлено тем, что их величину σСР
t
и РЯ
t
(см. зависимости (3.51) и (3.59)) в основном определяют одни и те же параметры деформационных процессов: сопротивление деформации металла в области уплотняющего пояска σД
t
и ширина уплотняющего пояска, которая в зависимости (3.51) выражена разностью диаметров уплотняющего пояска d
П
t
и ядра d
Я
t
, а в зависимости (3.59) — их отношением. А поскольку при любых условиях точечной сварки, как было показано выше, и сопротивление деформации металла, и ширина уплотняющего пояска в процессе формирования соединения на стадии нагрева всегда уменьшаются, то вследствие этого уменьшается и величина напряжений в площади уплотняющего пояска, и давление расплавленного металла в ядре. Их значения к концу процесса нагрева монотонно приближаются к величине сопротивления деформации металла в области уплотняющего пояска.

С увеличением жесткости режимов сварки как среднее значение напряжений в площади уплотняющего пояска (рис. 4.21), так и давление расплавленного металла в ядре (рис. 4.22) увеличивается. Это в основном является следствием увеличения сопротивления пластической деформации металла в области уплотняющего пояска из-за снижения в нем средней температуры, которое происходит вследствие увеличения в в области уплотняющего пояска ее градиента.

С увеличением толщины свариваемых деталей как среднее значение нормальных напряжений в площади уплотняющего пояска, так и давление расплавленного металла в ядре уменьшаются. Основной причиной этого является то, что с увеличением толщины свариваемых деталей увеличивается и разогрев металла в области уплотняющего пояска. Кроме того, с увеличением толщины свариваемых деталей весьма существенно уменьшается скорость пластической деформации металла и, следовательно, его влияние как упрочняющего фактора. Изменение этих факторов приводит к уменьшению сопротивления пластической деформации металла и, в конечном итоге, к уменьшению напряжений в площади уплотняющего пояска и давления расплавленного металла в ядре.
Таким образом, параметры основных термодеформационных процессов, протекающих в зоне формирования точечных сварных соединений, существенно зависят от параметров режимов сварки. Вследствие этого выбор оптимальных параметров режима КТС является исходным условием устойчивого протекания процесса формирования соединении и получения его высокого качества. Наиболее комплексным показателем оптимальности режимов контактной точечной сварки для конкретных ее условий является показатель их жесткости, который рассмотрен ниже.
4.3
. Критерий оценки режимов контактной точечной сварки
Описанное выше изменение основных термодеформационных процессов, протекающих в зоне сварки, показывает, что при устойчивом процессе формирования соединения в зоне сварки существует определенное соответствие между нагревом в ней металла и пластической его деформацией, и подтверждает, существовавшее ранее [3, 165, 185… 187] об этом предположение. Кроме того, взаимозависимость и взаимовлияние основных термодеформационных процессов, в особенности нагрева и пластической деформации металла, зависимость их от параметров режима точечной сварки, что количественно характеризуется критерием жесткости режимов контактной точечной сварки, подтверждает: саморегулирование процесса КТС существует.
В настоящее время оценку и сравнение режимов контактной точечной сварки по показателю их жесткости в основном производят только качественно, несмотря на то, что этот показатель является наиболее комплексным показателем из всех известных, предназначенных для решения этих задач. Это обусловлено тем, что, несмотря на известные предложения количественно оценивать жесткость режимов, например, по отношению отдельных параметров режима КТС, по показателям, представляющим собой различные интерпретации критерия Фурье и т. п., «абсолютный показатель степени жесткости режима пока не найден [15]» (см п. 1.3).
Общепринятым можно считать, что понятие «жесткость режима» отражает положение процесса КТС между его противоположными и предельными состояниями — непроваром и выплеском. К предельно мягким режимам относят такие режимы, при которых возникают непровары, а к предельно жестким — режимы, при которых возникают выплески. Соответственно и значения показателей жесткости таких режимов являются предельными. Например, в работе [4] указано, что при оценке жесткости режима по показателю K
2
(см зависимость (1.8)) для любых сочетаний толщин и материалов деталей при K
2
< 25 режимы КТС уже недопустимо мягкие, а при K
2
> 50 — граница выплесков, т. е. режимы сварки уже предельно жесткие.
Вместе с тем, классификация режимов, отработанных практикой КТС (например, приведенных в табл. 4.5 и близких к рекомендуемым [2, 3, 7…11, 15] для данных деталей), по известным показателям жесткости (в частности, по критериям К1
(см зависимость (1.7)) и К2
) показывает, что они не всегда располагаются в соответствии с этим понятием. Так, при оценке режимов по К1
не бесспорно соотношение их жесткости не только при различной толщине деталей, что объясняется не соблюдением в практике КТС критерия геометрического подобия сварных соединений (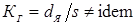 [15] (см. зависимость 1.12)), но и при одинаковой толщине деталей, например, из сплава АМг6 и стали 12Х18Н10Т. Не бесспорно и то, что при оценке по К2
жесткость режимов КТС деталей из сплава АМг6 и стали 08кп примерно одинакова, а режимы КТС деталей из стали 12Х18Н10Т относятся к недопустимо мягким (К2
< 25) и их жесткость меньше, чем при КТС деталей из стали 08кп. [15] (см. зависимость 1.12)), но и при одинаковой толщине деталей, например, из сплава АМг6 и стали 12Х18Н10Т. Не бесспорно и то, что при оценке по К2
жесткость режимов КТС деталей из сплава АМг6 и стали 08кп примерно одинакова, а режимы КТС деталей из стали 12Х18Н10Т относятся к недопустимо мягким (К2
< 25) и их жесткость меньше, чем при КТС деталей из стали 08кп.
Характеристики материалов, при которых проводили расчеты показателей жесткости режимов КТС, в частности, показателей К1
и К2
, приведены в табл. 4.6.
Таблица
4.5
Результаты расчетов при сравнении режимов сварки по критериям
их жесткости КЖ
, К1
и К2
| Мате
риал
|
s
мм
|
I
СВ
кА
|
t
СВ
c
|
F
Э
кН
|
d
Я
|
d
П2
|
d
ПС
|
Δ
Q
ЭЭ
кДж
|
η
|
Kσ
|
КЖ
|
К1
|
К2
|
| мм
|
| Сплав
АМгб
|
0,5
|
33
|
0.04
|
2,0
|
4
|
4.9
|
3.7
|
0.24
|
0.12
|
2.86
|
2.27
|
0.14
|
48.9
|
| 1,0
|
42
|
0,06
|
4.0
|
5
|
6.7
|
5.3
|
0.62
|
0.16
|
2,80
|
2.12
|
0.38
|
44.4
|
| 1,5
|
46
|
0.08
|
5.0
|
6
|
7.8
|
6.2
|
1.08
|
0,19
|
2.77
|
2.09
|
0.64
|
35.9
|
| 2,0
|
55
|
0.10
|
7.0
|
7
|
9,5
|
7.5
|
1.88
|
0.21
|
2.74
|
2,05
|
0,91
|
35.1
|
| 2,5
|
65
|
0.12
|
9.0
|
8
|
10,9
|
8.6
|
2.84
|
0,23
|
2.72
|
2.25
|
1.18
|
36,5
|
| 3,0
|
73
|
0.16
|
12,0
|
9
|
12.5
|
9.9
|
4,41
|
0.24
|
2.70
|
2.26
|
1.28
|
35.5
|
| 4,0
|
85
|
0,20
|
16.0
|
11
|
15.0
|
11,8
|
7,59
|
0,26
|
2.70
|
2,19
|
1.82
|
33,0
|
| Сталь
12Х18Н10Т
|
0,5
|
5
|
0.1
|
2.8
|
4
|
5.0
|
3.7
|
0.63
|
0.16
|
3.01
|
1.40
|
0,36
|
20.8
|
| 1,0
|
6
|
0.16
|
4.5
|
5
|
6.6
|
5.0
|
1.53
|
0,22
|
3.29
|
1.53
|
1.40
|
18,8
|
| 1,5
|
7.5
|
0.22
|
6.5
|
6
|
7.8
|
6.0
|
2.87
|
0.26
|
3.37
|
1.46
|
2.29
|
19.9
|
| 2,0
|
8.5
|
0,2Ь
|
8,5
|
7
|
9.4
|
7.2
|
4.84
|
0,30
|
3.33
|
1.38
|
3,45
|
18,2
|
| 2,5
|
10
|
0.32
|
10.5
|
8
|
10.5
|
8.1
|
7.07
|
0.32
|
3.58
|
1.45
|
4.37
|
19.8
|
| 3,0
|
11.5
|
0.36
|
13,0
|
9
|
12.0
|
9.2
|
10.2
|
0.34
|
3.57
|
1,43
|
5.6
|
19,9
|
| Сталь
08кп
|
0,6
|
7
|
0.1
|
1.0
|
4
|
4.8
|
3,4
|
0.81
|
0,15
|
9.37
|
0,93
|
0.21
|
37,8
|
| 1,0
|
8.5
|
0.2
|
2.0
|
5
|
6.2
|
4.5
|
2.15
|
0.16
|
8,89
|
0.89
|
0.29
|
39.1
|
| 1,5
|
10.5
|
0.34
|
3.5
|
6
|
7,9
|
5.8
|
4,96
|
0,17
|
8.22
|
0.92
|
0,38
|
31.4
|
| 2,0
|
12
|
0.48
|
5.0
|
7
|
9.5
|
6.9
|
9.02
|
0.18
|
7.90
|
0,44
|
0,48
|
29,2
|
| 2,5
|
13
|
0.6
|
6.5
|
8
|
10,8
|
8.0
|
13.7
|
0,19
|
7,73
|
0.87
|
0.61
|
25,8
|
| Примечание
. Расчеты проводили при 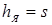 , Т0
= 273 K, σД1
= σТ
, Δ
t
= t
СВ
. , Т0
= 273 K, σД1
= σТ
, Δ
t
= t
СВ
.
|
Основным общим недостатком известных показателей жесткости режимов КТС, в частности К1
и К2
, является то, что они отражают только одну сторону процесса формирования соединения — выделение и перераспределение теплоты в зоне сварки. Вместе с тем, известно [16, 206], что устойчивое формирование соединения (без непроваров и выплесков) происходит в том случае, когда в течение всего процесса КТС обеспечивается определенное равновесное соотношение между нагревом и пластическим деформированием металла в зоне сварки. Его нарушение может привести к чрезмерно быстрому увеличению площадей контактов, уменьшению плотности тока, скорости нагрева и, в конечном итоге — к непровару. Противоположное отклонение перечисленных параметров приводит к выплеску.
На основе математических моделей термодеформационных процессов, протекающих в зоне сварки, и методик математического моделирования процесса точечной сварки на стадии нагрева, описанных выше (см. р. 3, и п. 4.1), разработан критерий оценки жесткости режима контактной точечной сварки [259]. Он комплексно учитывает влияние на формирование точечного сварного соединения тепловых и деформационных процессов, а также параметров режима сварки.
Таблица
4.2
Теплофизические характеристики материалов
| Материал
|
ТПЛ
,
°
С
|
λ,
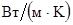
|
сm
,
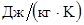
|
γ,
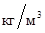
|
ρ0
,
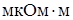
|
αρ
,
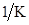
|
σТ
,
МПа
|
| Сплав АМг6
|
620
|
100
|
820
|
2780
|
0.075
|
8·10-4
|
150
|
| Сталь12Х18Н10Т
|
1440
|
16
|
460
|
7800
|
0,75
|
6·10-4
|
230
|
| Сталь 08 кп
|
1530
|
63
|
470
|
7800
|
0.13
|
6·10-3
|
180
|
| Бронза БрХ
|
–
|
360
|
410
|
8230
|
–
|
–
|
–
|
| Обозначение
: αρ
— температурный коэффициент увеличения ρТ
.
|
Физическая сущность этого критерия жесткости режима контактной точечной сварки основана на теоретических и экспериментальных исследованиях процессов КТС, частично описанных выше, которые показали, что существуют взаимосвязи между изменениями параметров термодеформационных процессов, протекающих в зоне формирования соединения, и устойчивостью процесса КТС против образования выплесков и непроваров. В частности, установлено, что изменение отношения скорости нагрева к скорости пластического деформирования металла в зоне сварки коррелируется с изменением устойчивости процесса против образования непроваров и выплесков при различных сочетаниях параметров режима КТС. Поэтому количественное значение отношения этих параметров может служить показателем жесткости режима КТС при любых сочетаниях толщин и материалов свариваемых деталей. Кроме того, значения этого показателя при КТС деталей из материалов, относящихся к одной группе свариваемости [15, 16], относительно стабильны. Поэтому при таких условиях они могут использоваться в качестве критериев оптимизации при выборе параметров режима КТС. Такие выводы можно подтвердить следующим.
Поскольку известные критерии (см. п. 1.3.5), которые описывают соотношение параметров, характеризующих процессы формирования точечных сварных соединений, в подавляющем большинстве безразмерны, то и критерий жесткости режима должен быть таким же. Это позволит сопоставлять результаты оценки разных режимов сварки деталей различных сочетаниях толщин и материалов свариваемых деталей. Поэтому изменение параметров должно выражаться в относительных единицах.
Нагрев металла зоны сварки в процессе формирования точечного сварного соединения можно описать функцией изменения его относительной температуры, имеющей следующий вид
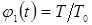 , (4.11) , (4.11)
где Т
— текущее значение средней температуры в зоне сварки; Т0
—
характерное неизменное значение температуры.
Изменение деформированного состояния металла в зоне сварки в процессе формирования соединения можно описать функцией отношения давления в контуре свариваемого контакта (уплотняющего пояска диаметром d
П
), выраженного сжимающими напряжениями в его площади σ
, которое обусловлено внешним силовым воздействием на детали, к сопротивлению деформации металла в области уплотняющего пояска σД
:
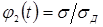 . (4.12) . (4.12)
Это оправдано тем, что в любой момент процесса КТС, как это следует из уравнений термодеформационного равновесия (3.11) и (3.17), в свариваемом контакте среднее значение давления σ
, обусловленного внешним силовым воздействием, уравновешивается противоположно направленными контактными напряжениями σ
Z
, а также (после начала плавления металла) давлением РЯ
расплавленного металла в ядре [218]. Величина σ
Z
и РЯ
, как это следует из зависимостей (3.51) и (3.59), пропорциональны сопротивлению деформации металла σД
. В силу этого и изменение функции 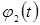 , пропорциональное σД
, пропорционально также изменению площади свариваемого контакта. Поэтому можно считать, что изменение функции , пропорциональное σД
, пропорционально также изменению площади свариваемого контакта. Поэтому можно считать, что изменение функции 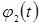 адекватно отражает изменение деформированного состояния металла в зоне сварки. адекватно отражает изменение деформированного состояния металла в зоне сварки.
Исходя из сказанного выше критерий жесткости режима точечной сварки КЖ
, определяемый как отношение скоростей нагрева и пластического деформирования металла в зоне формирования соединения
, можно выразить через отношение производных от функций (4.11) и (4.12) следующим образом:
 . (4.13) . (4.13)
Принимая в качестве независимых переменных температуру Т
и сопротивление деформации металла σД
, в соответствии с теоремой Лагранжа зависимость (4.13) можно преобразовать к виду
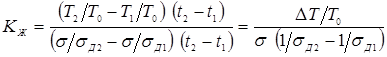 , (4.14) , (4.14)
где Т1
и Т2
, σД1
и σД2
— значения Т
и σД
соответственно в начале t
1
и конце t
2
рассматриваемого отрезка времени Δ
t
=
t
2
- t
1
; Δ
T
— разность значений Т
за время Δ
t
; σ
— среднее значение давления в отрезке времени Δ
t
, равное 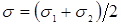 ; σ1
и σ2
— значения σ
соответственно в начале t
1
и конце t
2
рассматриваемого отрезка времени Δ
t
. ; σ1
и σ2
— значения σ
соответственно в начале t
1
и конце t
2
рассматриваемого отрезка времени Δ
t
.
С относительно небольшой погрешностью можно допустить, что на стадии нагрева наиболее интенсивные термодеформационные процессы локализованы в зоне сварки объемом Vt
, ограниченном внешними поверхностями деталей и цилиндрической поверхностью, направляющей которой является контур свариваемого контакта (см. п. 3.5.3, рис. 3.33). Тогда температуру Т
в зависимости (4.13) можно выразить как среднее значение температуры в изменяющемся объеме Vt
, а ее разность Δ
T
в зависимости (4. 14), обозначив Δ
T
С
— через приращения теплосодержания Δ
Q
1
металла в объеме V
t
, и тепловыделения Δ
Q
ЭЭ
на участке электрод – электрод. Для этого, в частности, можно использовать известные решения по определению составляющих уравнения (2.27) теплового баланса при КТС. Тогда, определив теплосодержание Δ
Q
1
через теплоемкость и тепловыделение
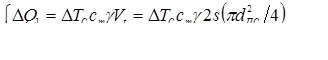 . .
Приравняв правые части этих соотношений значение Δ
T
С
можно выразить следующей зависимостью:
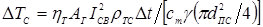 , ,
где d
ПС
— среднее значение диаметра уплотняющего пояска d
П
при его изменении за период Δ
t
от d
П1
до d
П2
, равное 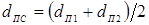 ; ηТ
— тепловой КПД процесса КТС, равный ; ηТ
— тепловой КПД процесса КТС, равный 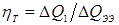 ; АГ
—
коэффициент ; АГ
—
коэффициент
А. С. Гельмана (см. зависимость (2.16)), учитывающий уменьшение электрического сопротивления деталей за счет растекании линий тока; ρTC
— среднее значение удельного электрического сопротивления ρT
при его изменении за период Δ
t
от ρT
1
до ρT
2
, равное 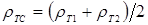 . .
Теперь зависимость (4.14) можно преобразовать к следующему виду:
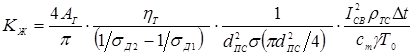 . (4.15) . (4.15)
Известно, что при встречающихся в практике КТС отношениях 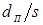 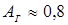 [10, 15]. Тогда можно принять, что в зависимости (4.15) отношение [10, 15]. Тогда можно принять, что в зависимости (4.15) отношение 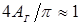 . Поскольку σ
— это среднее значение давления в отрезке времени Δ
t
[см. зависимость (4.14)], а d
ПС
— среднее значение диаметра уплотняющего пояска d
П
за этот же период, то в зависимости (4.15) выражение . Поскольку σ
— это среднее значение давления в отрезке времени Δ
t
[см. зависимость (4.14)], а d
ПС
— среднее значение диаметра уплотняющего пояска d
П
за этот же период, то в зависимости (4.15) выражение 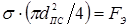 , где F
Э
— усилие сжатия электродов. Тогда, зависимость (4.15) для расчетов показателя жесткости режима точечной сварки КЖ
можно преобразовать к окончательному виду: , где F
Э
— усилие сжатия электродов. Тогда, зависимость (4.15) для расчетов показателя жесткости режима точечной сварки КЖ
можно преобразовать к окончательному виду:
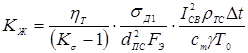 , (4.16) , (4.16)
где 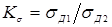 — коэффициент разупрочнения металла в объеме Vt
; — коэффициент разупрочнения металла в объеме Vt
;
Т0
—
температура металла перед сваркой, K.
Основной физический смысл показателя K
Ж
выражен зависимостью (4.13). Вместе с тем качественный анализ зависимости (4.16) позволяет детализировать его содержание. Так, из нее следует, что жесткость режима возрастает с увеличением силы сварочного тока I
СВ
, теплового КПД процесса точечной сварки ηТ
, и удельного электрического сопротивления свариваемого металла ρTC
, а также с уменьшением удельной теплоемкости с
т
и плотности γ
последнего. Общеизвестно, что такое изменение перечисленных параметров приводит к увеличению тепловыделения и скорости нагрева металла в зоне сварки. К этому же приводит и повышение сопротивления деформации металла σД
вследствие увеличения плотности тока в свариваемом контакте из-за уменьшения d
П
. Увеличение же усилия сжатия электродов F
Э
приводит к противоположному изменению d
П
и уменьшению жесткости режима КТС.
Важным фактором, влияющим на жесткость режима, является разупрочнение металла в процессе КТС. Так, при его уменьшении K
σ
→
1, а
K
Ж
→
∞. Это вполне согласуется с тем, что при увеличении сопротивления деформации металла давление в ядре увеличивается (см. зависимость (3.59)) и вероятность образования выплеска возрастает. Таким образом, при отсутствии разупрочнения металла, когда значения K
σ
→
1, а K
Ж
→
∞, при реальных усилиях сжатия деталей образование выплеска становится практически неизбежным из-за увеличения давление расплавленного металла в ядре. Увеличение времени сварки, выраженного t
СВ
в числителе зависимости (4.16), также приводит к уменьшению показателя КЖ
,
т. к. при неизменном диаметре ядра, необходимо уменьшить сварочный ток I
СВ
, который в большей степени влияет на тепловыделение. Все это не противоречит существующим представлениям о процессе КТС.
В табл. 1 приведены результаты расчетов КЖ
по зависимости (4.16), а также некоторых промежуточных параметров (Δ
Q
ЭЭ
, ηТ
, K
σ
, d
ПС
и d
П2
), достаточных для проведения проверочных расчетов. При расчетах K
Ж
изменение средней температуры деформируемого металла ТС
, его сопротивления пластической деформации σД
и диаметра уплотняющего пояска d
П
в процессе КТС определяли по методикам, описанным в п. 4.1.
При этом, как следует из результатов расчетов КЖ
при КТС деталей разных толщин s
из одного и того же материала при h
Я
≈
s
, а Δt
=
t
СВ
значения ТС
относительно стабильны. Так, например, при сварке деталей из сплава АМг6 ТС
≈
560 °С, из сталей 12Х18Н10Т и 08кп — 1300 и 1380 °С соответственно. С учетом скрытой теплоты плавления металла в ядре это в определенной мере оправдывает допущение о том, что ТС
≈
ТПЛ
в методиках расчетов Δ
Q
1
и Δ
Q
ЭЭ
[3], по которым определяли их значения при расчетах значений теплового КПД ηТ
.
Результаты расчетов, в частности, приведенные в табл. 1. показывают, что при оптимальных режимах КТС деталей разных толщин из материалов, относящихся к одной группе свариваемости, значения КЖ
относительно стабильны. То есть, для этих условий КТС показатель КЖ
обладает свойствами критерия. Но это означает
только то, что практикой КТС отработаны режимы, при которых устойчивость процессов сварки против выплесков и непроваров примерно одинакова, т. е. они имеют одинаковую жесткость. Так, например (рис. 4.23), различные сочетания I
СВ
, t
СВ
и F
Э
позволяют получать неизменный диаметр ядра d
Я
(рис. 1, а
), а также значения КЖ
для этих режимов. Из приведенного примера видно, что значения КЖ
при уменьшении t
СВ
и неизменном d
Я
отражают возрастающую жесткость режимов КТС, которая на практике проявляется в повышении проплавления деталей и склонности процесса к образованию выплесков.
Расчеты показателя жесткости режима КТС КЖ
, проведенные по описанной выше методике для большого числа отработанных практикой режимов сварки, которые рекомендованы как наиболее оптимальные [3, 7…12, 15…17], показали следующее. Для режимов КТС, которые принято относить к режимам мягким значения показателя жесткости режима КТС КЖ
<
1, а для режимов, которые принято относить к режимам жестким — КЖ
>
2. Для режимов, которые обычно характеризуют как режимы средней жесткости, значения показателя жесткости КЖ
=
1…2.

В отличие от известных аналогов значения критерия жесткости КЖ
можно рассчитать по зависимости (4.16) для любого отрезка времени Δ
t
процесса формирования соединения. Это позволяет определить жесткость режима КТС не только усредненно для всего времени сварки t
СВ
, по и на отдельных этапах формирования соединения. Так, на рис. 2 показано изменение показателя КЖ
в процессе формирования соединения, рассчитанное с шагом Δ
t
= 0,01 с. В этом случае расчет КЖ
производится так же, как и при Δ
t
= t
СВ
, за исключением того, что переменные параметры в зависимости (4.16) последовательно принимают свои текущие значения.
Результаты расчетов текущих значений КЖ
в процессе формирования точечных соединений показывают, что при КТС с неизменными значениями силы сварочного тока I
СВ
, и усилия сжатия электродов F
Э
показатель КЖ
в период времени Δ
t
≈
0,5…0,6t
СВ
достигает максимальных значений. Относительно невысокие его значения в начале процесса КТС обусловлены не низкой скоростью нагрева (согласно кривой изменения Т
C
в этот период она максимальна), а более высокой скоростью пластического деформирования металла. Высокая скорость пластического деформирования металла, является следствием с одной стороны, высокой скорости разупрочнения металла (см. изменение K
σ
), а с другой стороны — относительно больших значений отношения 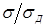 в начале процесса формирования соединения. Бόльшие значения КЖ
на рис. 2 в начале процесса формирования соединения обусловлены, по-видимому, допущением, что сварочный ток I
СВ
не меняется в течение процесса КТС. Если же учитывать реальное нарастание сварочного тока в этот период, определяемое индуктивностью сварочного контура, то изменение КЖ
получается таким, как показано штриховой линией. В конце процесса, несмотря на то, что разупрочнение металла замедленно (K
σ
≈ 1,04), значения КЖ
уменьшаются. Это обусловлено в основном увеличением в процессе КТС диаметра уплотняющего пояска, d
П
, и уменьшением теплового КПД ηТ
, замедляющими рост температуры Т
C
. в начале процесса формирования соединения. Бόльшие значения КЖ
на рис. 2 в начале процесса формирования соединения обусловлены, по-видимому, допущением, что сварочный ток I
СВ
не меняется в течение процесса КТС. Если же учитывать реальное нарастание сварочного тока в этот период, определяемое индуктивностью сварочного контура, то изменение КЖ
получается таким, как показано штриховой линией. В конце процесса, несмотря на то, что разупрочнение металла замедленно (K
σ
≈ 1,04), значения КЖ
уменьшаются. Это обусловлено в основном увеличением в процессе КТС диаметра уплотняющего пояска, d
П
, и уменьшением теплового КПД ηТ
, замедляющими рост температуры Т
C
.
Такое изменение показателя КЖ
при формировании соединения, характерное для циклов КТС с неизменными величинами I
СВ
и F
Э
свидетельствует о целесообразности применения циклов с программированным изменением параметров режима. В этом случае КЖ
может быть использован как параметр оптимизации при определении программ изменения I
СВ
или F
Э
.
По-видимому, неслучайно и то, что при неизменных и близких к оптимальным значениях I
СВ
и F
Э
, выплески обычно образуются в момент времени 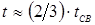 [3, 11, 15], т. е. при относительно высоких значениях КЖ
. [3, 11, 15], т. е. при относительно высоких значениях КЖ
.
То, что показатель жесткости КЖ
в действительности комплексно отражает взаимосвязь тепловых и деформационных процессов при КТС можно подтвердить и следующим.
Выразим в зависимости (4.16) значение температуры свариваемого металла перед сваркой Т0
(K) через температуру его плавления 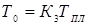 .
Поскольку при оптимальных режимах КТС в момент .
Поскольку при оптимальных режимах КТС в момент 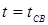 средние значения диаметра уплотняющего пояска приближенно равны диаметру ядра средние значения диаметра уплотняющего пояска приближенно равны диаметру ядра 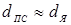 (см. табл. 1), то заменим в ней значения (см. табл. 1), то заменим в ней значения 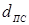 на на 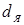 . После этого, умножив числитель и знаменатель зависимости (4.16) на . После этого, умножив числитель и знаменатель зависимости (4.16) на 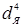 , преобразуем ее к следующему виду при , преобразуем ее к следующему виду при 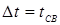 : :
 . (4.17) . (4.17)
Тогда второй множитель в зависимости (4.17), а также ее знаменатель представляют собой выражения известных критериев, разработанных для точечной сварки: числитель — это выражение критерия подобия тепловыделения KI
, знаменатель — это выражение критерия подобия пластических деформаций KF
при КТС (см зависимости (1.14) и (1.15)).
Следовательно, для случая технологических расчетов при 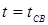 зависимость (4.17) можно записать в следующем виде зависимость (4.17) можно записать в следующем виде
 . (4.18) . (4.18)

Известно, что при изменении толщины свариваемых деталей s
значения критериев подобия тепловыделения KI
и подобия пластических деформаций KF
не остаются неизменными. Они изменяются вследствие того, что не соблюдается критерий геометрического подобия: (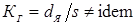 [15] (см. зависимость 1.12)). На рис. 3 показано изменение значений KI
и KF
в зависимости от толщины свариваемых деталей, с увеличением которой значения KI
и KF
уменьшаются. В этих условиях значения показателя жесткости КЖ
, в отличие от известных критериев и при изменении толщины деталей остаются неизменными. В основном это обусловлено увеличением теплового к. п. д. ηТ
процесса КТС, которое наблюдается при увеличении толщины свариваемых деталей, так как влияние изменения разупрочнения металла относительно невелико (см. изменение K
σ
). Такое изменение указанных параметров характерно для традиционных циклов сварки различных материалов всех толщин, встречающихся в практике контактной точечной сварки. [15] (см. зависимость 1.12)). На рис. 3 показано изменение значений KI
и KF
в зависимости от толщины свариваемых деталей, с увеличением которой значения KI
и KF
уменьшаются. В этих условиях значения показателя жесткости КЖ
, в отличие от известных критериев и при изменении толщины деталей остаются неизменными. В основном это обусловлено увеличением теплового к. п. д. ηТ
процесса КТС, которое наблюдается при увеличении толщины свариваемых деталей, так как влияние изменения разупрочнения металла относительно невелико (см. изменение K
σ
). Такое изменение указанных параметров характерно для традиционных циклов сварки различных материалов всех толщин, встречающихся в практике контактной точечной сварки.
Описанное выше математическое выражение показателя жесткости режимов контактной точечной сварки, который комплексно отражает взаимосвязь тепловых и деформационных процессов при формировании точечных сварных соединений. Он позволяет количественно оценить отношение скорости нагрева металла в зоне сварки к скорости его пластического деформирования как за цикл сварки в целом, так и его изменение в процессе КТС. Этот показатель позволяет количественно оценить соотношение жесткостей режимов сварки деталей различных сочетаний толщин и материалов, а также может быть использован как критерий оптимизации при выборе параметров режима КТС.
Таким образом, описанные выше в данном разделе методики расчетов изменения диаметра уплотняющего пояска как для традиционных способов КТС, так и способов КТС с обжатием периферийной зоны соединения, позволяют одновременно математически моделировать изменение параметров силового взаимодействия в контактах электрод-деталь и деталь-деталь, а также изменение параметров основных термодеформационных процессов при формировании точечных сварных соединений, таких как теплового состояния металла в зоне сварки, его разупрочнения и объемных пластических деформаций, изменения напряжений в контактах и давления расплавленного металла в ядре. Это позволяет для различных условий точечной сварки определять как характер их изменения, так и количественные их параметры, определять параметры их взаимозависимостей и взаимовлияний, влияние на их изменение параметров режимов и условий сварки, теплофизических характеристик свариваемых материалов и геометрических параметров соединяемых деталей.
Решение этих задач при разработке новых технологий КТС фактически позволяет математически моделировать процесс формирования точечных сварных соединений, чем значительно снижать трудоемкость выполнения этих работ.
[1]
Здесь и далее символ
t
в индексе означает, что значение параметра относится к дискретному моменту времени
t
процесса формирования точечного сварного соединения.
[2]
Здесь и далее в алгоритмах расчетов в скобках указываются номера зависимостей, по которым осуществляется расчет параметра.
[3]
При машинном счете для предотвращения зацикливания рационально считать число j
циклов и ограничивать их максимальное число
|