Министерство образования и науки Украины
Харьковский государственный технический университет строительства и архитектуры
Заочный факультет
Кафедра экономической кибернетики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине:
"Основы системного анализа"
Харьков
2009
Задание
Найти объем бетонной строительной конструкции по данным периферического, серединного и корневого сечений.
Решение
Найдем площадь периферического поперечного сечения строительной конструкции по данным таблицы:
| x |
Выпуклая часть переф. сечения |
Вогнутая часть переф. сечения |
| 0 |
2,5 |
0 |
| 22 |
17 |
12 |
| 42 |
28,5 |
23 |
| 62 |
37,5 |
31 |
| 82 |
46 |
38 |
| 102 |
51 |
44 |
| 122 |
54 |
48 |
| 142 |
55 |
50 |
Проведем аппроксимацию выпуклой и вогнутой кривых с помощью Excel.
Как базовую функцию используем полином второго порядка:
f(x) = ao
+ a1
x + a2
x2
В результате получим диаграммы с уравнениями аппроксимации для периферического сечения:
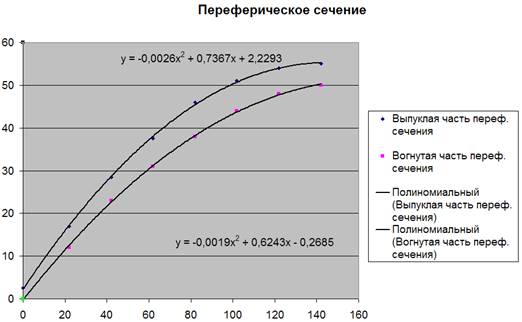
В результате решения получаем ao
= 2,2293 , a1
=0,7367, a2
= -0,0026 для выпуклой части и ao
= -0,2685 , a1
= 0,6243 , a2
= -0,0019 – для вогнутой.
Определим площади Sп,в
и под выпуклой и вогнутой кривыми как определенные интегралы функции f(x) на интервале (0;142) с соответствующими коэффициентами.
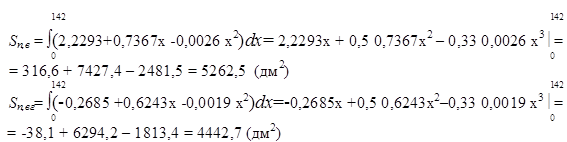
Тогда площадь периферического сечения равна:
Sп
= Sп,вг
– Sп,вг
= 5262,5 – 4442,7 = 819,8 (дм2
) .
Аналогично для серединного сечения по данным таблицы:
| x |
Выпуклая часть серединного сечения |
Вогнутая часть серединного сечения |
| 0 |
2,5 |
0 |
| 22 |
19,5 |
13 |
| 42 |
31,5 |
22 |
| 62 |
40 |
28 |
| 82 |
43 |
31 |
| 102 |
41 |
30 |
| 122 |
35 |
25 |
Получим диаграммы с уравнениями аппроксимации для серединного сечения:
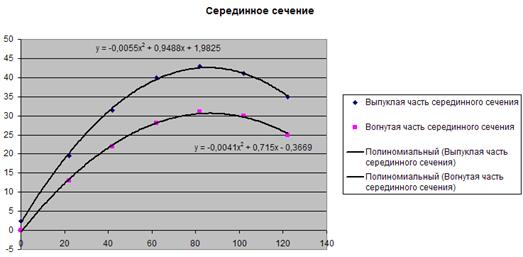
В результате решения получаем ao
= 1,9825 , a1
= 0,9488, a2
= -0,0055 для выпуклой части и ao
= -0,3669 , a1
= 0,715 , a2
= -0,0041 – для вогнутой.
Определим площади Sп,в
и под выпуклой и вогнутой кривыми как определенные интегралы функции f(x) на интервале (0;142) с соответствующими коэффициентами.
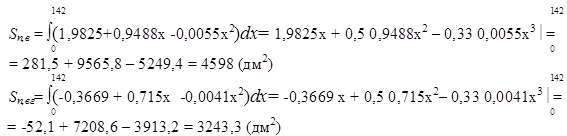
Тогда площадь периферического сечения равна:
Sп
= Sп,вг
– Sп,вг
= 4598 – 3243,3 = 1354,7 (дм2
) .
Аналогично для серединного сечения по данным таблицы:
| x |
Выпуклая часть корневого сечения |
Вогнутая часть корневого сечения |
| 0 |
2,5 |
0 |
| 22 |
26 |
13,3 |
| 42 |
39,8 |
20,6 |
| 62 |
43,2 |
21,8 |
| 82 |
36,2 |
16,7 |
Получим диаграммы с уравнениями аппроксимации для серединного сечения:
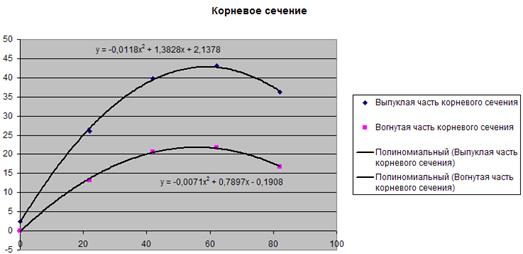
В результате решения получаем ao
= 2,1378 , a1
= 1,3828, a2
= -0,0118 для выпуклой части и ao
= -0,1908 , a1
= 0,7897 , a2
= -0,0071 – для вогнутой.
Определим площади Sп,в
и под выпуклой и вогнутой кривыми как определенные интегралы функции f(x) на интервале (0;142) с соответствующими коэффициентами.
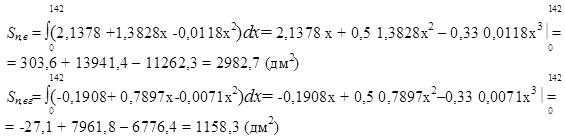
Тогда площадь периферического сечения равна:
Sп
= Sп,вг
– Sп,вг
= 2982,7 – 1158,3 = 1824,4 (дм2
) .
Для расчета целевой функции V(a0
, … a12
) получим аналитическую зависимость F(z). Для этого проведем аппроксимацию полученных ранее данных с помощью Excel:
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
F(z) = b0
+ b1
z+ b2
z2
| F(z) |
| 0 |
1824,4 |
| 102 |
1354,7 |
| 202 |
819,8 |
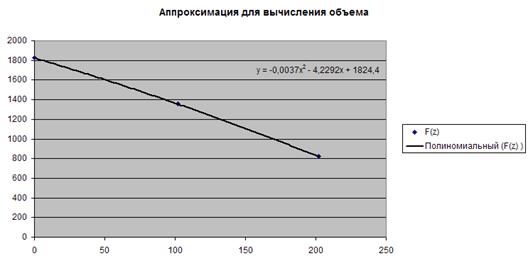
F(0)= 1824,4 F(102)= 1354,7 F(202)= 819,8 b0
=1824,4 b1
= - 4,2292
b2
= -0,0037 F(z) =1824,4 – 4,2292z – 0,0037z2
Далее, интегрируя, получим
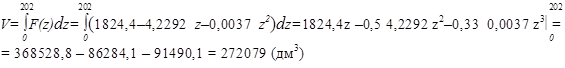
Ответ: V = 272079 дм3
|
