Кафедра “Основы проектирования машин”
Курсовое проектирование
Механизм поперечно-долбежного станка
Содержание
Введение
1 Синтез и анализ рычажного механизма
1.1 Структурный анализ механизма
1.2 Определение недостающих размеров
1.3 Определение скоростей точек механизма
1.4 Определение ускорений точек механизма
1.5 Диаграммы движения выходного звена
1.6 Определение угловых ускорений и скоростей
1.7 Определение ускорений центров масс звеньев механизма
1.8 Аналитический метод расчёта механизма
2 Силовой расчет рычажного механизма
2.1 Определение сил инерции
2.2 Расчет диады 4-5
2.3 Расчет диады 2-3
2.4 Расчет кривошипа
2.5 Определение уравновешивающей силы
2.6 Определение мощностей
2.7 Определение кинетической энергии и приведенного момента инерции механизма
3 Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет зубчатой передачи
3.2 Определение передаточного отношения планетарной ступени и подбор чисел зубьев колес
3.3 Определение частот вращения зубчатых колес
4 Синтез и анализ кулачкового механизма
4.1 Масштабные коэффициенты диаграмм
4.2 Выбор минимального радиуса и построение профиля кулачка
4.3 Определение максимальной линейной скорости и ускорения толкателя
Список использованных источников
Введение
Долбежный станок предназначен для обработки фасонных отверстий (квадратных, шестигранных, шлицевых и др.), прорезание шпоночных пазов и канавок в конических и цилиндрических отверстияx, а также для строгания наружных коротких плоских и фасонных линейчатых поверхностей.
На рис. 3 изображена схема привода долбежного станка. От электродвигателя I движение через планетарный редуктор II и зубчатую передачу z5 –z6 передается на кривошипный вал 01 —01 кулисного механизма III долбежного станка.
На одном валу с зубчатым колесом z5 находится кулачок. Кулачковый механизм IV связан c насосом, предназначенным для смазки станка.
На рис. I изображена кинематическая схема передачи z5 –z6 кулисного механизма и кулачкового механизма.
На рис. 2 изображен график сил сопротивления резанию действующих на долбяк 5 при рабочем ходе.
На рис. 4 дается, схема зубчатого механизма согласно варианту задания.
На рис. 5 задается закон движения толкателя кулачкового механизма.
Реклама

1 Синтез и анализ рычажного механизма
Исходные данные: а/BO2 = 0.5,BC/BO2 =4,Н = 140 мм; β = 360 ; nдв= 950 мин‾¹; к = 1,57.
1.1 Структурный анализ механизма
Степень подвижности механизма
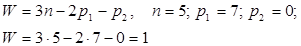
Формула строения механизма: 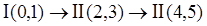
Механизм II класса, 2 порядка.
1.2 Определение недостающих размеров
Угол размаха кулисы:
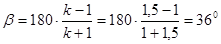 ; ;
Длина кривошипа:
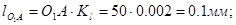
Масштабный коэффициент построения схемы:
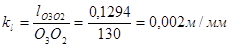
Строим 12 планов механизма, приняв за начало отсчета крайнее правое положение, соответствующее началу рабочего хода механизма (в масштабе кl).
1.3 Определение скоростей звеньев механизма
Угловая скорость кривошипа равна:
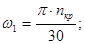
где 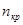 =130 – частота вращения кривошипа. =130 – частота вращения кривошипа.
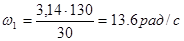
Кинематическая скорость точки А кривошипа в первом положении:
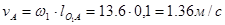
Масштабный коэффициент скоростей:
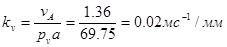
Скорость точки А1 кулисы определяем решая графически совместно систему:
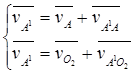
причем: 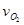 =0; =0;
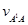 -скорость скольжения камня вдоль кулисы; -скорость скольжения камня вдоль кулисы;
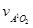 - скорость вращения точки А относительно точки о2 перпендикулярно кулисе. - скорость вращения точки А относительно точки о2 перпендикулярно кулисе.
На плане скоростей pva1 =66.5мм . Абсолютная величина скорости точки А1 кулисы из плана скоростей:
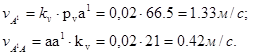
Скорость точки В находим по свойству подобия из соотношения:
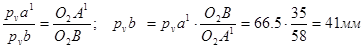
Абсолютная величина скорости т. В:
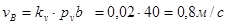
Скорость точки С определяем решая совместно систему:
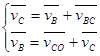
На плане pvс = 14 мм. Абсолютная величина скорости точки С:
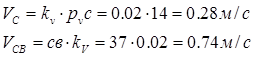
Пример расчета выше для первого положения. Для остальных 11 положений скорости определяются аналогично, их значения приведены в таблице 1.1
Таблица 1.1 - Значения скоростей
| Скорости, м/с |
Положение механизма |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| uА |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
1.36 |
| uА’ |
1.33 |
1.32 |
1.38 |
1.4 |
1.36 |
1.38 |
1.3 |
1.34 |
1.38 |
1.4 |
1.36 |
1.3 |
| uC |
0.28 |
0.38 |
0.58 |
0.78 |
0.74 |
0.68 |
0.28 |
0.56 |
1.38 |
1.24 |
0.42 |
0 |
| uB |
0.78 |
0.7 |
0.68 |
0.74 |
0.76 |
0.8 |
0.92 |
1.14 |
1.36 |
1.46 |
1.2 |
0.96 |
1.4 Определение ускорений точек механизма
Ускорение точки А кривошипа :
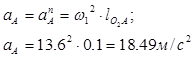 
Ускорение 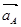 направлено по кривошипу к центру вращения О1. направлено по кривошипу к центру вращения О1.
Масштабный коэффициент ускорения:
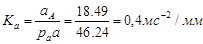
На плане ускорений изображаем ускорение точки А отрезком paa =46.24мм.
Ускорение точки А1 определяем решая совместно систему:
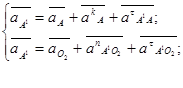
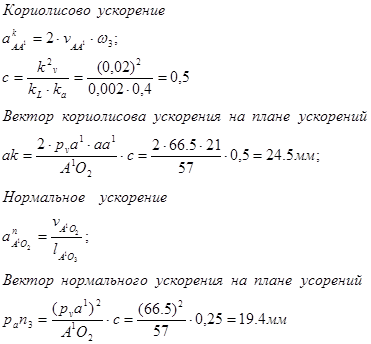
Значения ускорений из плана ускорений.
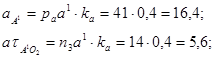
Ускорение точки В определяем по свойству подобия.
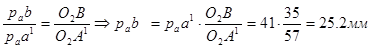
Абсолютная величина ускорения точки В.
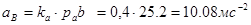
Ускорение точки С находим решая совместно систему векторных уравнений:
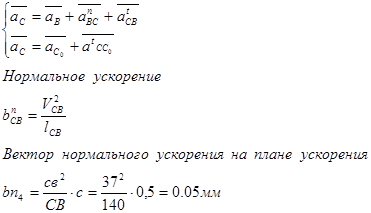
Значения ускорений из плана ускорений.
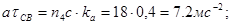
Абсолютная величина ускорения точки С:
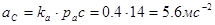
Пример расчета ускорения выполнен для первого положения. Ускорения для остальных положений механизма определяются аналогично. Значения ускорений сводим в таблицу 1.2.
Таблица 1.2- Значения ускорений.
| Ускорения, м/с2 |
Положение механизма |
| 1 |
3 |
5 |
7 |
9 |
11 |
0 |
| aA |
18,49 |
18,49 |
18,49 |
18,49 |
18,49 |
18,49 |
18,49 |
| aAk |
24,5 |
3,2 |
5,2 |
12,8 |
9,6 |
13,26 |
13,2 |
| aA’ |
16,4 |
14,4 |
14,4 |
26,8 |
30,4 |
25,6 |
18,8 |
| aв |
10,08 |
7,6 |
8 |
18,4 |
29,6 |
22,4 |
13,2 |
| aCВ |
7,6 |
7,6 |
7,2 |
11,6 |
29,6 |
6,8 |
6,4 |
| aC |
5,6 |
3,6 |
3,2 |
17,6 |
8.6 |
18,4 |
8,8 |
1.5 Диаграммы движения выходного звена
Диаграмму перемещения S-t строим, используя полученную из плана механизма траекторию движения точки С.
По заданному графику перемещения S-t, Диаграммы скоростей V-t и ускорений а-t определяются из полученных 12-ти планов скоростей и планов ускорений.
Реклама

Масштабные коэффициенты диаграмм:
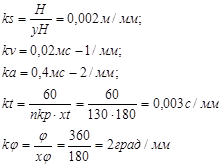
1.6 Определение угловых скоростей и ускорений
Угловые скорости и ускорения звеньев механизма определяются для первого положения:
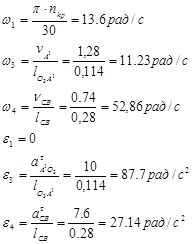
Определение относительных угловых скоростей:
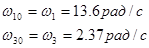
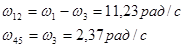
1.7 Определение ускорений центров масс звеньев механизма
Ускорение центров масс звеньев механизмов определяется из плана ускорений:
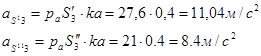
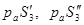 находим по свойству подобия. находим по свойству подобия.
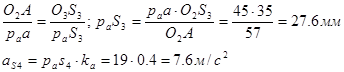
Скорости центров масс звеньев механизмов определяются из планов скоростей:
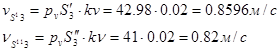
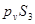 находим по свойству подобия. находим по свойству подобия.
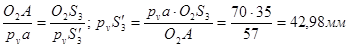
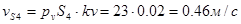
1.8 Аналитический метод расчета
Исходные данные:
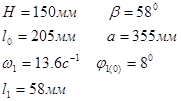
1. Расчет ведется для третьего положения кулисы:
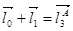
2. В проекциях на координатные оси
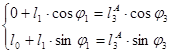
3. Поделим второе уравнение на первое
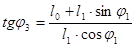
4. Берем производную от левой и правой части
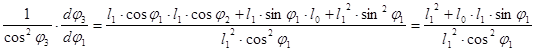
5.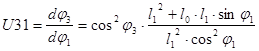
6.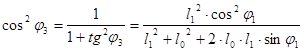
7. Угловая скорость кулисы:
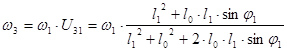
8. 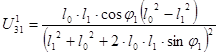
9. Угловое ускорение кулисы:
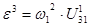
10. 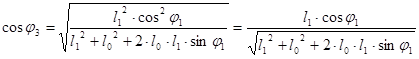
11. 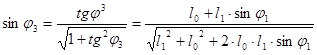
12. Составляем векторное уравнение:
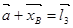
13. Проектируем на оси координат:
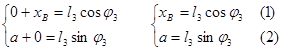
14. Делим уравнение (1) на (2):
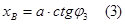
15. Для определения аналога скорости дифференцируем уравнение (3)
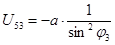 (4) (4)
16. Определение скорости точки С.
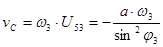
17. Для определение аналога ускорения дифференцируем по координате 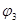 уравнение (4): уравнение (4):
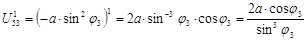
18. Определяем ускорение точки С:
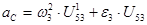
1.9 Расчет скоростей и ускорений для первого положения механизма.
1. Угловая скорость кулисы:
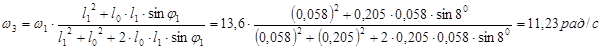
2. 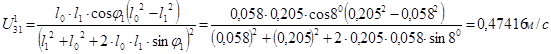
3. Угловое ускорение кулисы:
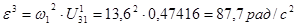
4. 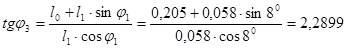
5. 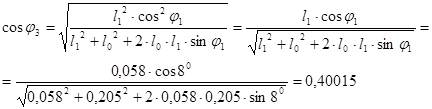
6. 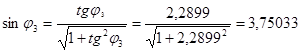
7. Аналог скорости 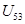 : :
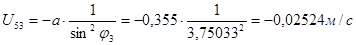
8. Определение скорости точки С.
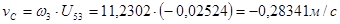
9. Аналогично ускорение 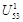
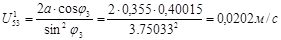
10. Ускорение точки С:
Private Sub TTM()
Dim I1 As Double
Dim 12 As Double
Dim wl As Double
Dim el As Double
Dim fl As Double
Dim f2 As Double
Dim vc(l To 12) As Double
Dim ac(l To 12) As Double
Dim u31 As Double
Dim u311 As Double
Dim u43 As Double
Dim u431 As Double
Dim u531 As Double
Dim u53 As Double
Dim i, n As Integer
= 0,12
=0.058 131 =0.176 1311=0.205
= 0.355
= 0.15 wl=17.5 e1= 0
f 1 = 30
f3=85
n= 12
For i = 1 To n
u31 =(l1^2 + 10*11 *Sin(fl))/(l1 л2 + l0л2 + 2* 10*11 *Sin(fl))
u311 =( 10* 11 *Cos(fl)*(I0^2+ll^2+2*I0*l1*sin(fl))-
2*10*1 l*cos(fl)*(l1^2+I0*l1*sin(fI)/(l1^2+I0^2+2*I0*l1*sin(fl))^2
u431 = (-l3l1 * Sin(f3)*l4*cos(f4) -l3l1 *cos(f3) * l4 * Sin(f4)) / l4^2* cos(f3)^2
u43=I3 l1 *cos(f3)/l4*cos(f4)
w3 = wl *u31
e3=wl ^2*u3ll +el* u31
w4 = u43 * w3
Sin(f4)=(13l1 *Sin(f3)-l5)/l4
Cos(f'4)=sqr(l-Sin(f4)^2)
u531 =-1311 * Cos(f3) + u43 * 14 * Sin(f4) - u43 * l4 *Cos(f4)
u53 =-13 * Sin(f3) +l4*Sin(f4)*u43
vs(i) = w3 *ls3
asn(i) = w3^ 2 *ls3
asr(i)=e3*ls3
as(i)=sqr(asn(i)^2+asr(i)^2)
vc=u53*w3
ac=u53l*w3^2+u53*e3
f1 = fl + 30
Nexti
n= 12
For i = 1 To n
Worksheets( I ).Range("a" & i & "").Value = vs(i)
Worksheets( I ).Range("b" & i & "").Value = as(i)
Next i
End Sub
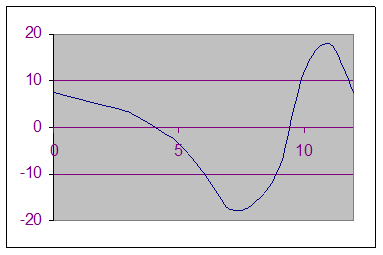
График скоростей
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 0 |
0,28 |
0,45 |
0,58 |
0,68 |
0,66 |
0,52 |
-0,28 |
-0,56 |
-1,38 |
-1,24 |
-1,24 |
0 |
График ускорений| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 7.6 |
6 |
4.6 |
3.2 |
0.4 |
-3.4 |
-10 |
-17.4 |
-16 |
-8.6 |
12 |
18 |
7.6 |
2 Силовой анализ механизма
Определение сил инерции
Исходные данные:
w1= 13.6 рад/с;
Q=7000 Н;
m5= 150 кг;
m3’= 5 кг;
m3’’= 2 кг;
m4= 80 кг;
диаметр цапф, 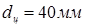
коэффициент трения, 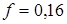
2.1 Определение сил инерции и сил тяжести
Силы тяжести:
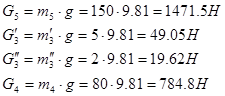
Силы инерции:
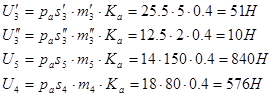
2.2 Расчет диады 4-5
Для расчета этой диады изобразим ее со всеми приложенными к ней силами: силами тяжести, полезного сопротивления и реакциями.
Эти реакции в поступательных парах известны по направлению, но неизвестны по модулю. Определяем с помощью плана сил. Составим уравнение равновесия диады 4-5.
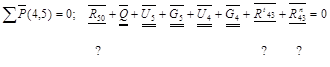
Уравнение содержит три неизвестных, поэтому составляем дополнительное уравнение равновесия в форме моментов сил относительно точки С.
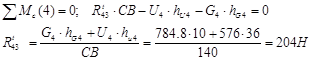
Строим план сил диады в масштабе сил
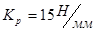
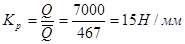
Рассчитаем вектора сил
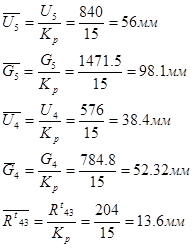
Строим план сил по уравнению сил, в том порядке как силы стояли в уравнении.
Значения сил из плана сил
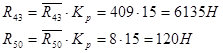
2.3 Расчет диады 2-3
Изобразим диаду со всеми приложенными к ней силами. В точках А и О2 взамен отброшенных связей прикладываем реакции 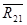 . В точке В прикладываем ранее найденную реакцию . В точке В прикладываем ранее найденную реакцию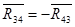 . Составляем уравнение равновесия диады 2-3. . Составляем уравнение равновесия диады 2-3.
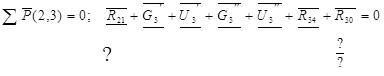
Уравнение содержит три неизвестных, поэтому составляем дополнительное уравнение равновесия в форме моментов сил относительно точки О2.
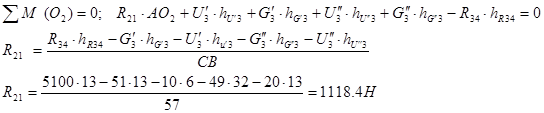
Плечи измеряем на плане. В уравнении сил две неизвестных, поэтому строим план сил и определяем реакцию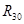 , как замыкающий вектор. , как замыкающий вектор.
Строим план диады в масштабе сил 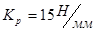 . Значения сил из плана сил. . Значения сил из плана сил.
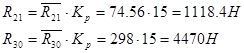
Для рассмотрения внутренних реакций в диаде 2-3 необходимо рассмотреть равновесие одного звена, звена 2.
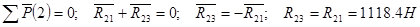
2.4 Расчет кривошипа
Изобразим кривошип с приложенными к нему силами и уравновешивающей силой 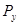 , эквивалентной силе действия на кривошип со стороны двигателя. Действие отброшенных связей учитываем вводя реакции , эквивалентной силе действия на кривошип со стороны двигателя. Действие отброшенных связей учитываем вводя реакции 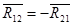 и и 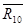 . Определяем уравновешивающую силу, считая, что она приложена в точке А кривошипа, перпендикулярно ему. Составляем уравнение равновесия кривошипа. . Определяем уравновешивающую силу, считая, что она приложена в точке А кривошипа, перпендикулярно ему. Составляем уравнение равновесия кривошипа.
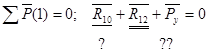
Строим план диады в масштабе сил 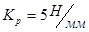 . Значение силы определяем из плана сил. . Значение силы определяем из плана сил.
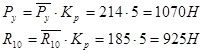
2.5 Определение уравновешивающей силы методом Жуковского
Строим повернутый на 900 план скоростей и в соответствующих точках прикладываем все внешние силы, включая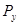 и силы инерции. Составим уравнение моментов относительно точки и силы инерции. Составим уравнение моментов относительно точки 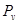 , считая , считая 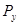 неизвестной: неизвестной:
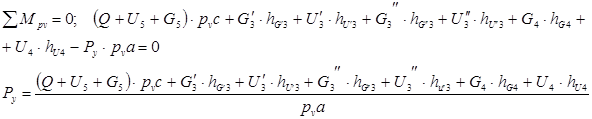
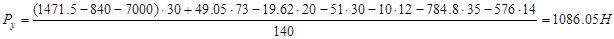
Подлинность графического метода:
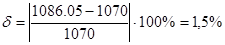
2.6 Определение мощностей
Потери мощности в кинематических парах:
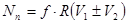
Потери мощности на трение во вращательных парах:
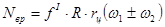
где 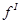 - коэффициент - коэффициент
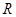 - реакция во вращательной паре, - реакция во вращательной паре,
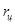 - радиус цапф. - радиус цапф.
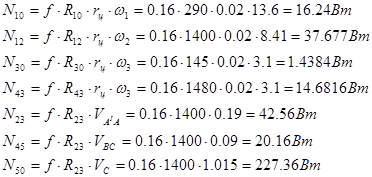
Суммарная мощность трения
 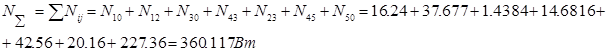
Мгновенно потребляемая мощность
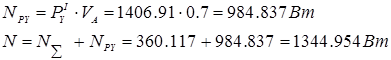
Мощность привода, затрачиваемая на преодоление полезной нагрузки.
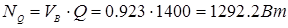
2.7 Определение кинетической энергии механизма
Кинетическая энергия механизма равна сумме кинетических энергий входящих в него массивных звеньев.
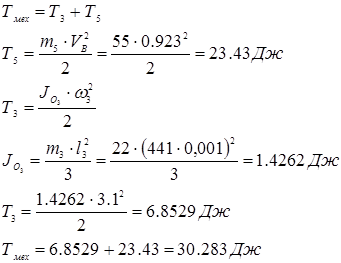
Приведенный момент инерции
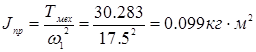
3. Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет равносмещенного зубчатого зацепления.
Исходные данные:
Число зубьев на шестерне 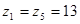
Число зубьев на колесе 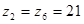
Модуль 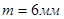
Угол профиля рейки 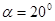
Коэффициент высоты головки зуба 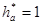
Коэффициент радиального зазора 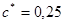
Суммарное число зубьев колес 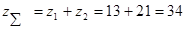
Поскольку 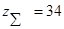 , то проектируем равносмещенное зубчатое зацепление. , то проектируем равносмещенное зубчатое зацепление.
Коэффициент смещение
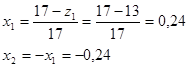
Угол зацепления 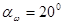
Делительное межосевое расстояние
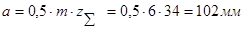
Начальное межосевое расстояние 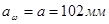
Высота зуба
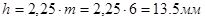
Высота головки зуба
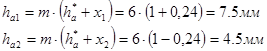
Высота ножки зуба
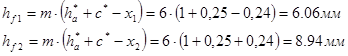
Делительный диаметр
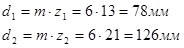
Основной диаметр
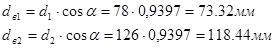
Диаметр вершин
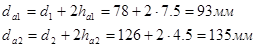
Диаметр впадин
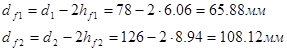
Толщина зуба по делительному диаметру
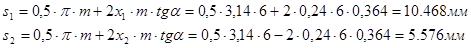
Делительный шаг
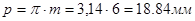
Шаг по основной окружности
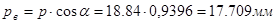
Радиус галтели
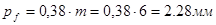
Коэффициент перекрытия
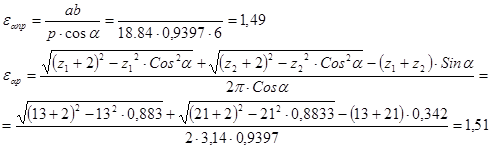
Погрешность определения коэффициента зацепления:
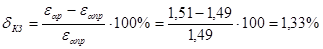
где ab и p находим из чертежа картины зацепления.
1. Масштабный коэффициент построения картины зацепления.
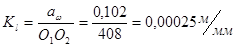
3.2 Синтез планетарного редуктора
Исходные данные:
Модуль 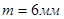
Частота вращения вала двигателя 
Частота вращения кривошипа 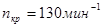
Числа зубьев 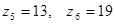
Номер схемы редуктора 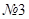
Знак передаточного отношения –
Общее передаточное отношение редуктора
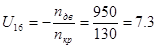
Передаточное отношение простой передачи
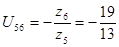
Передаточное отношение планетарной передачи
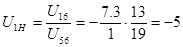
Формула Виллиса для планетарной передачи
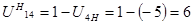
5. Передаточное отношение обращенного механизма, выраженное в числах зубьев.
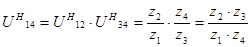
Представим полученное отношение в виде
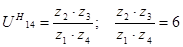
6. Подбор чисел зубьев
Выбираем числа зубьев
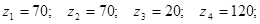
7. Условие соосности
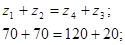
Условие соосности выполнено
8. Делительные диаметры
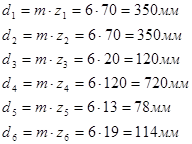
9. Угловая скорость вала двигателя
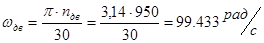
10. Линейная скорость точки A колеса z1
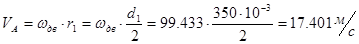
11. Масштабный коэффициент Kv
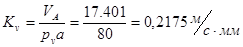
12. Масштабный коэффициент построения плана редуктора
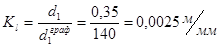
3.3 Определение частот вращения аналитическим методом.
1. Определение частот вращения аналитическим методом.
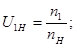
откуда
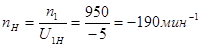
Знак плюс показывает, что водило вращается в одном направлении с валом
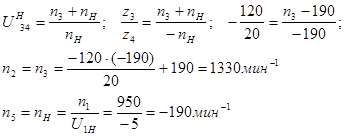
2. Определение частот вращения графическим методом.
Масштабный коэффициент плана частот вращения
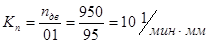
Частоты вращения, полученные графическим способом.
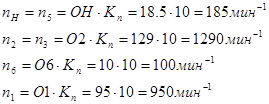
Определение погрешностей
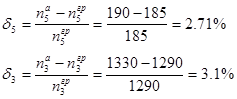
Private Sub CommandButtonl_Click()
Dim zl, z2, m, ha, C, z5, z6, xl, x2, aw, a, h, hal, ha2, hfl, hf2, dl, d2, dal, da2, dBl, dB2, dfl, df2, SI, S2, P, PB, rf, q As Double zl=CDbl(TextBoxl. Value)
z2 = CDbl(TextBox2.Value)
m = CDbl(TextBox3 .Value)
ha = CDbl(TextBox4.Value)
c = CDbl(TextBox5. Value)
q = CDbl(TextBox6.Value)
ListBoxl. Clear
ListBoxl.Addltem ("Начало отсчета")
ListBoxl.Addltem ("zl=" & zl)
ListBoxl .Addltem ("z2=" & z2)
ListBoxl.Addltem ("m=" & m)
ListBoxl.Addltem ("ha*=" & ha)
ListBoxl.Addltem ("C*=" & C)
q = (q* 3.14)/180
ListBoxl.Addltem ("угол-' & q)
xl=(17-zl)/17
ListBoxl.Addltem ("xl=" & xl)
x2 = -xl
ListBoxl.Addltem ("x2=" & x2)
a = m*(zl +z2)/2
ListBoxl .Addltem ("a=" & a)
aw=a
ListBoxl .Addltem ("aw=" & aw)
h=2.25*m
ListBoxl .Addltem ("h=" & h)
ha1=m*(ha+x1)
ListBoxl .Addltem ("ha1=" &ha1)
ha2=m*(ha+x2)
ListBoxl .Addltem ("ha2=" &ha2)
hf1=m*(ha+c-x1)
ListBoxl .Addltem ("hf1=" &hf1)
hf2=m*(ha+c-x2)
ListBoxl .Addltem ("hf2=" &hf2)
d1=m*z1
ListBoxl .Addltem ("d1=" &d1)
d2=m*z2
ListBoxl .Addltem ("d2=" &d2)
dw1=d1
ListBoxl .Addltem ("dw1=" &dw1)
dw2 = d2
ListBoxl.Addltem ("dw2=" & dw2)
dal =dl +2*hal
ListBoxl.Addltem ("dal=" & dal)
da2 - d2 + 2 * ha2
ListBoxLAddltem ("da2=" & da2)
dfl = dl - 2 * hfl
ListBoxLAddltem ("dfl=" & dfl)
df2 = d2-2*hf2
ListBoxLAddltem ("hf2=" & h£2) dBl=dl*Cos(q)
ListBoxLAddltem ("dBl=" & dBl)
dB2 = d2 * Cos(q)
ListBoxLAddltem ("dB2=" & dB2) Sl=0.5*3.14*m + 2*xl * m * Tan(q) ListBdxl.AddItem("Sl="&Sl)
S2 = 0.5 * 3.14 *m + 2*x2*m* Tan(q) ListBoxLAddltem ("S2=" & S2)
P = 3.14*m
ListBoxLAddltem ("p=" & P)
pB = p * Cos(q)
ListBoxLAddltem ("pB=" & pB) rf = 0.38 * m
ListBoxLAddltem ("r£=" & rf) End Sub
Private Sub CommandButton2_Click() UserForm 1.Hide
End Sub
Исходные данные
Угол зацепленияа =20
Коэффициент высоты головки зубаha=l
Коэффициент радиального зазораС=0,25 Модульm=6 мм
Число зубьев шестерниz 1=13
Число зубьев колеса z2=21
Результаты расчета
Начальное межосевое расстояние aw=102 мм
Высота зубаh=11,25 мм
| ШЕСТЕРНЯ |
КОЛЕСО |
| Коэффициент смещения |
Х1=0,24 |
Х2= - 0,24 |
| Высота головки зуба |
ha1=7,5мм |
ha2=4,5мм |
| Высота ножки зуба |
hf1=6,06мм |
hf2=8,94мм |
| Делительный диаметр |
d1=78мм |
d2=126мм |
| Начальный диаметр |
dw1=d1=78мм |
dw2=126мм |
| Диаметр вершин |
da1=93мм |
da2=135мм |
| Диаметр впадин |
df1=65,88мм |
df2=108,12мм |
| Основной диаметр |
db1=73,32мм |
db2=118,44мм |
| Толщина зуба |
S1=10,468мм |
S2=5,576мм |
| Шаг |
P=18,84мм |
| Основной шаг |
Pb=17,709мм |
| Радиус |
rf=2,28мм |
4. Синтез и анализ кулачкового механизма
4.1 Построение кинематических диаграмм и определение масштабных коэффициентов
Исходные данные:
а) диаграмма движения выходного звена
б) частота вращения кривошипа 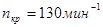
в) максимальный подъем толкателя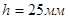
г) рабочий угол кулачка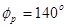
д) угол давления 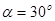
е) дезаксиал кулачка 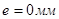
ж) число зубьев шестерни 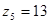
з) число зубьев колеса 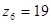
По заданному графику ускорения толкателя, графическим интегрированием по методу хорд строю 2 графика. График скорости толкателя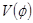 и график перемещения и график перемещения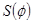 . .
Базовые величины интегрирования: 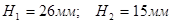
Масштабный коэффициент перемещения.
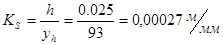
где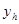 -максимальное значение ординаты графика, соответствует заданному подъему толкателя. -максимальное значение ординаты графика, соответствует заданному подъему толкателя.
Масштабный коэффициент времени
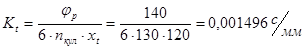
где 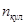 - частота вращения кулачка - частота вращения кулачка
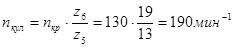
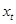 =120 мм – длина отрезка на оси абсцисс графика изображающая время поворота кулачка на рабочий угол. =120 мм – длина отрезка на оси абсцисс графика изображающая время поворота кулачка на рабочий угол.
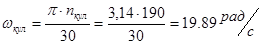
Масштабный коэффициент скорости толкателя.
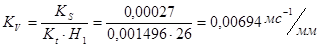
Масштабный коэффициент ускорения
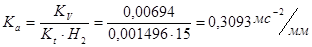
4.2 Выбор минимального радиуса и построение профиля кулачка
Минимальный радиус кулачка выбирается из условия выполнения заданного угла давления 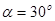 . Для этого строим совместный график . Для этого строим совместный график 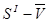 в стандартном масштабе в стандартном масштабе 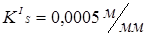 . К полученному графику проводим две касательные под углом давления и получаем зону выбора центров вращения кулачка. . К полученному графику проводим две касательные под углом давления и получаем зону выбора центров вращения кулачка.
При построении графика 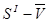 вдоль ординат и вдоль абсцисс, значения откладываем в одном и томже масштабе вдоль ординат и вдоль абсцисс, значения откладываем в одном и томже масштабе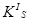 . .
Значения аналогов скорости в стандартном масштабе.
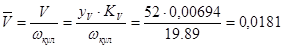
Отрезки приведенных скоростей толкателя определяем аналогичным методом, для чего находим 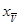
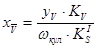
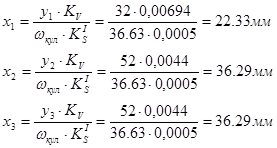
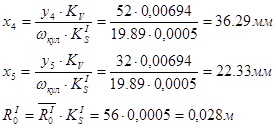
Радиус ролика
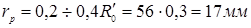
Минимальный радиус действительного профиля
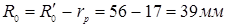
4.3 Построение профиля кулачка
Профиль кулачка строим с применением метода обращенного движения. Масштабный коэффициент построения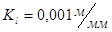 . .
Проводим окружности радиусом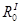 , а затем окружность радиусом дезаксиала , а затем окружность радиусом дезаксиала 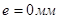 откладываем фазовый рабочий угол откладываем фазовый рабочий угол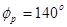 . Делим его на двенадцать частей. Делим его на двенадцать частей. К точке деления пересекшей окружность дезаксиала проводим перпендикуляры. По ним откладываем текущие перемещения. Соединяем полученные точки, получаем центровой профиль кулачка. Обкатываем ролик по центровому профилю во внутрь, получаем действительный профиль кулачка. . Делим его на двенадцать частей. Делим его на двенадцать частей. К точке деления пересекшей окружность дезаксиала проводим перпендикуляры. По ним откладываем текущие перемещения. Соединяем полученные точки, получаем центровой профиль кулачка. Обкатываем ролик по центровому профилю во внутрь, получаем действительный профиль кулачка.
4.4 Определение максимальной линейной скорости и ускорения толкателя.
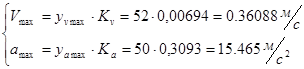
Список использованных источников
1. Машков А.А. Теория механизмов и машин. Мн., 1971.
2. Артоболевский И.И. Теория механизмов и машин. М., 1975.
3. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин под ред. К.В. Фролова М., 1986.
4. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. М., 1998.
|