Содержание
Введение
1 Синтез и анализ рычажного механизма
1.1 Структурный анализ механизма
1.2 Определение недостающих размеров
1.3 Определение скоростей точек механизма
1.4 Определение ускорений точек механизма
1.5 Диаграммы движения выходного звена
1.6 Определение угловых ускорений и скоростей
1.7 Определение ускорений центров масс звеньев механизма
1.8 Аналитический метод расчёта механизма
2 Силовой расчет рычажного механизма
2.1 Определение сил инерции
2.2 Расчет диады 4-5
2.3 Расчет диады 2-3
2.4 Расчет кривошипа
2.5 Определение уравновешивающей силы
2.6 Определение мощностей
2.7 Определение кинетической энергии и приведенного момента инерции механизма
3 Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет зубчатой передачи
3.2 Определение передаточного отношения планетарной ступени и подбор чисел зубьев колес
3.3 Определение частот вращения зубчатых колес
4 Синтез и анализ кулачкового механизма
4.1 Диаграммы движения толкателя
4.2 Определение минимального радиуса кулачка
4.3 Построение профиля кулачка
Список использованных источников
Введение
Механизм насоса с качающейся кулисой применяется в нефтеперерабатывающей промышленности и предназначен для откачки жидкости нефтяных скважин.
Подача жидкости регулируется автоматически за счёт кулачкового механизма.
Поршень получает возвратно-поступательное движение в цилиндре от электродвигателя через планетарный редуктор и рычажный механизм О1АО2С.
При движении поршня вверх осуществляется рабочий ход, при движении поршня вниз - холостой.
При рабочем ходе на поршень 5 действует сила полезного сопротивления.
Механизм насоса с качающейся кулисой - одностороннего действия.
Кулачок 6 получает вращение посредством зубчатой передачи z5-z6.
1. Синтез и анализ рычажного механизма
Схема механизма:
Исходные данные:
Q=3450 H
H=240 мм
m3=42 кг
K=1,6
m5=35 кг
nкр=150 об/мин
O1O2=625 мм
nдв=1500 об/мин
1.1 Структурный анализ механизма
Степень подвижности механизма определим по формуле:
W=3n-2p1-p2;
Где n- число подвижных звеньев,
P1- число одноподвижных кинематических пар,
P2- число двуподвижных кинематических пар,
W=3·5-2·7-0=1
Разложение механизма на группы Ассура:
Реклама

Формула строения механизма: I(0,1)→II(2,3)→II(4,5)
Механизм II класса, 2 порядка
1.2 Определение недостающих размеров
Угол размаха кулисы
b=180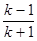 = 180∙(1,6–1)/(1,6+1)=41,53 = 180∙(1,6–1)/(1,6+1)=41,53
Длину кривошипа определяем по формуле:
lO1A=0102 ∙sin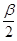 =0,625∙sin20,76=0,22м, =0,625∙sin20,76=0,22м,
Длину lO2В определим по следующей формуле:
lO2В=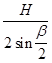 =0,24/2∙0,354=0.338 м, =0,24/2∙0,354=0.338 м,
Выберем масштабный коэффициент
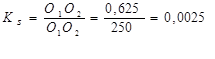
Строим 12 планов положений механизма, приняв за начало отсчета крайнее положение, соответствующее началу рабочего хода механизма.
1.3 Определение скоростей точек механизма
Определяем u точки А кривошипа:
uA=w1lO1A
где w1-угловая скорость вращения механизма, определяется по формуле:
w1=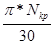 = =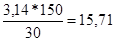 рад/с, рад/с,
Скорость точки А определим по формуле:
uA=ω1 O1A=15,71∙0,22=3,46 м/с,
План скоростей строим в масштабе:
ku=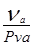 =3,46/69,2=0.05 м∙с-1/мм =3,46/69,2=0.05 м∙с-1/мм
Скорость точки A’ находим графически, решая совместно систему:
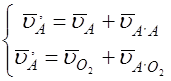
uA’= ku РuA’
По свойству подобия определяем скорость точки C’:

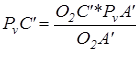
РVc’=136∙33/280=16мм
Абсолютное значение скорости точки
C’= ku puC’=0.05*17=0,85м/с
Составим систему уравнений скоростей для нахождения u в точке C:
uс’=uc’+ucc’
uc’=uc’c+uc’c
На плане puC=19мм. Абсолютное значение u в точке C:
uC= ku puC=0.05*19=0,95м/с.
Для остальных 11 положений скорости определяются аналогично, их значения приведены в таблице 1.1
Таблица 1.1 - Значения скоростей
| Скорости, м/с |
Положение механизма |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| uА |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
3,46 |
| uА’ |
1,65 |
2,95 |
3,4 |
3,4 |
3 |
2,15 |
0,7 |
1 |
2,9 |
3,15 |
1,7 |
0 |
| uC |
0,95 |
1,2 |
1,23 |
1,24 |
1,18 |
0,96 |
0,38 |
0,7 |
2,23 |
2,48 |
1,18 |
0 |
| uC’ |
0,85 |
1,24 |
1,29 |
1,26 |
1,18 |
0,96 |
0,37 |
0,65 |
2,14 |
2,42 |
1,16 |
0 |
1.4 Определение ускорений точек механизма
Ускорение точки А направлено по кривошипу к центру вращения О1.
aA=w12lO1A=15,712∙0.22=54,3м/с2
Выбираем масштабный коэффициент ускорений:
ka=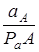 =54,3/108,6=0.25 м*с-2/мм =54,3/108,6=0.25 м*с-2/мм
На плане ускорений изображаем ускорение точки А отрезком 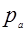 а=108 мм. Ускорение точки А’ определяем, решая совместно систему а=108 мм. Ускорение точки А’ определяем, решая совместно систему
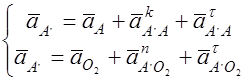
Для этого используем
aA’Ak=2∙w3 ∙VA’A=2∙VA’O2∙VA’A/A’O2=2∙Pva’∙aa’∙c/A’O2
c- коэффициент перечета определяется по формуле:
с= 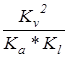 =0.052/(0.5∙0.0025)=2 =0.052/(0.5∙0.0025)=2
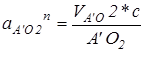
Ускорение точки С’ определим из соотношения:
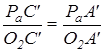
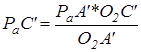
Ускорение точки С найдём, решая совместно систему
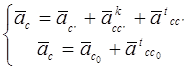
где
аCC’k=2·ω3·VCC’=2· РuA’·СС’·c/А’О2;
Ускорения всех точек механизма найдены. Ускорения для остальных положений механизма определяются аналогично. Значения ускорений сводим в таблицу 1.2.
Таблица 1.2- Значения ускорений.
| Ускорения, м/с2 |
Положение механизма |
| 1 |
3 |
5 |
7 |
9 |
11 |
0 |
| aA |
54,4 |
54,4 |
54,4 |
54,4 |
54,4 |
54,4 |
54,4 |
| aA’Ak |
14,37 |
7,74 |
12,02 |
7,55 |
24,7 |
23,56 |
0 |
| aA’O2n |
3,88 |
13,84 |
10,74 |
0,775 |
20,24 |
7,9 |
0 |
| ac’ |
15,3 |
5 |
7 |
24 |
40,6 |
48,1 |
32 |
| aCC’k |
0,75 |
0,5 |
1,25 |
0,00 |
3,45 |
1,9 |
0 |
| aC |
16,45 |
6,25 |
8,75 |
26,5 |
41,8 |
50,35 |
34 |
1.5 Диаграмма движения входного звена
Диаграмму перемещения S-t строим используя полученную из плана механизма траекторию движения точки С. Диаграммы скоростей V-t и ускорений а-t определяются из полученных 12-ти планов скоростей и планов ускорений.
Реклама

Масштабные коэффициенты диаграмм
Кs=0.0025 (м/мм)
КV=0.05 (мс-1/мм)
Ка=0,5 (мс-2/мм)
1.6 Определение угловых скоростей и ускорений
ω1=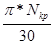 =3,14·150/30=15,71 (рад/с) =3,14·150/30=15,71 (рад/с)
ω3=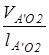 =3,46/280·0,0025=4,94 (рад/с) =3,46/280·0,0025=4,94 (рад/с)
ε1=0 (рад/с-2)
ε3=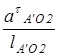 =14,88/280·0,0025=21,26 (рад/с-2) =14,88/280·0,0025=21,26 (рад/с-2)
1.7 Определение ускорений центров масс звеньев механизма
Ускорения центров масс звеньев механизма определяем из планов ускорений.
aS'=Ka·РаS3=0.5*45=22,5 м/с2
Определяем относительные угловые скорости.
ω10= ω1=15,71 рад/с;
ω30= ω3=4,94 рад/с;
ω12= ω1- ω3=10,77 рад/с;
ω45= ω3=4,94 рад/с;
1.8 Аналитический метод расчёта механизма
Исходные данные:
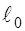 = 625 мм; = 625 мм;
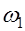 = 15,71 рад/с; = 15,71 рад/с;
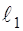 = 220 мм; = 220 мм;
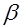 = 41,530; = 41,530;
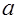 = 308 мм; = 308 мм;
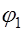 = 20,760; = 20,760;
Расчет ведется для первого положения кулисы:
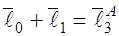 ; ;
В проекциях на координатные оси:
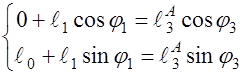 ; ;
Разделим второе уравнение ED Equation.3
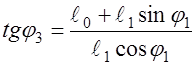 ; ;
Берем производную от левой и правой части:
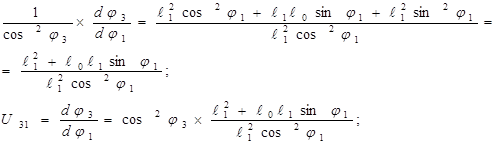
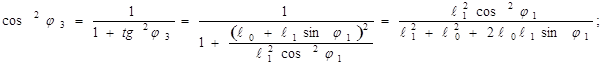
Угловая скорость кулисы:
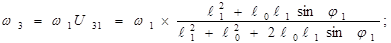 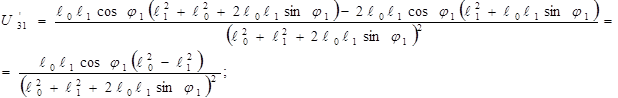
Угловое ускорение кулисы:
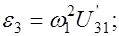
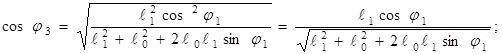
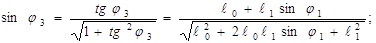
Составим векторное уравнение:
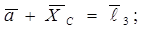
Проектируем на оси координат:
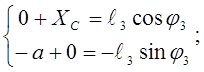
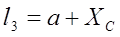 ; ;
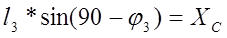 ; ;
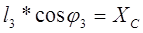 ; ;
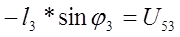 ; ;
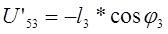 ; ;
Расчет скоростей и ускорений для первого положения механизма.
Угловая скорость кулисы:

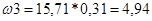
Угловое ускорение кулисы:
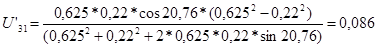 ; ;
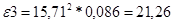  рад/с2 ; рад/с2 ;
Скорость точки С :
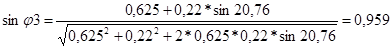 ; ;
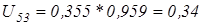 ; ;
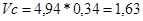 м/с; м/с;
Ускорение точки C :
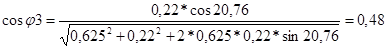
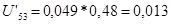  ; ;
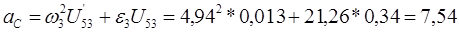 рад/с2; рад/с2;
2 Силовой анализ рычажного механизма
2.1 Определение сил инерции
Исходные данные:
w1=15,71 рад/с;
Q=3450 Н;
m5=35 кг;
m3’=12 кг;
m3’’=30 кг;
Определим силы инерции:
U5=-m5·aC;
U5= m5·PaC·Ka;
U5=35·30,6·0,5=535,5 (Н);
U3’=-m3’∙aS3’;
U3’=m3’·PaS’·Ka;
U3’=12·45·0,5=270 (Н);
U3’’=-m3’’∙aS3’’;
U3’’=m3’’·PaS’’·Ka;
U3’’=30·17·0,5=255 (Н);
Определим веса звеньев:
G5=m5·g;
G3’=m3’·g;
G3’’=m3’’·g;
G5=35·9,8=343,35 (Н);
G3’=12·9,8=117,72 (Н);
G3’’=30·9,8=294,3 (Н);
Сила полезного сопротивления Q=3450 Н.
Разбиваем механизм на группы Ассура в соответствии с формулой строения I(0,1)→II(2,3)→II (4,5). Начинаем силовой рассчёт самой удалённой от кривошипа диады.
2.2 Расчёт диады II (4,5)
Выделим из механизма диаду 4-5 и нагружаем её силами. Составляем уравнение равновесия диады 4-5:
∑Р(4,5)=, R50+Q+G5+U5+R43=0 (1)
Уравнение содержит два неизвестных- модули реакций R50 и R43, поэтому оно решается графически. Строим план сил по уравнению равновесия (1).
Для построения плана сил выбираем масштаб сил Кр
Кр= =3450/172,5=20 н/мм =3450/172,5=20 н/мм
Из плана сил определяем реакции:
R50= R50 Кр=66·20=1320 Н;
R43= R43 Кр=221·20=4420 Н;
2.3 Расчёт диады II (2,3)
Выделим диаду 2-3 и нагрузим её силами. Действие отброшенных звеньев 1,0 на третье заменяем действием реакций связей R21 и R30, которые требуется определить. Реакцию R21 направляем перпендикулярно линии движения ползуна, модуль неизвестен. Реакция R30 в шарнире О2 неизвестна ни по модулю ни по направлению; на схеме направляем её произвольно. Действие отброшенного звена 4 на третье известно: Реакция R34 равна по величине и противоположно направлена реакции R43, которая уже определена из плана сил диады II (4,5). Силы тяжести G3’ и G3’’ наносим на диаду в центрах масс стержней S3’ и S3’’. Силы инерции U3’ и U3’’ прикладываем в точках К’ и К’’, расположенных на расстоянии 2/3 длин стержней. Силы инерции направляем противоположно ускорениям центров масс согласно плана ускорений.
Составляем условия равновесия диады II(2,3):
∑Р(2,3)=0, R21+G3’+U3’+G3’’+U3’’+R34+R30=0 (2)
Данное уравнение содержит три неизвестных: модуль реакции R21, модуль и направление реакции R30. Значит уравнение (2) графически не решается. Реакция R21 может быть определена аналитически из уравнения моментов сил относительно точки О2.
∑М О2 (зв.2,3)=0, R21·AO2-U3’·hu3’+G3’·hg3’-U3’’·hu3’’-G3''·hg3’’-R34·O2C=0;
Откуда
R21= (U3’·hu3’- G3’·hg3’+ U3’’·hu3’’+ G3''·hg3’’+ R34·O2C)/ AO2
R21=(270·233-117,72·53+255·102-294,3·74+4500·132)/280=2539 Н
Теперь уравнение (2) содержит два неизвестных, а следовательно решается графически.
Строим план сил диады II(2,3) по уравнению (2). Считаем отрезки плана сил:
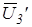 = U3’/Кр=270/20=13,5 мм. = U3’/Кр=270/20=13,5 мм.
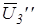 = U3’’/ Кр=255/20=12,75 мм. = U3’’/ Кр=255/20=12,75 мм.
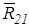 = R21/ Кр=2539/20=126,95 мм. = R21/ Кр=2539/20=126,95 мм.
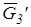 = G3’/ Кр=117,72/20=5,8 мм. = G3’/ Кр=117,72/20=5,8 мм.
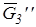 = G3''/ Кр=294,3/20=14,7 мм. = G3''/ Кр=294,3/20=14,7 мм.
Согласно уравнению (2) строим сумму векторов сил, откуда находим:
R30= 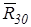 ·Кр=274·20=5480 Н. ·Кр=274·20=5480 Н.
2.4 Расчёт кривошипа
Силовой расчёт кривошипа состоит в определении реакции стойки на кривошип R10 и уравновешивающей силы Ру, имитирующей действие силы со стороны двигателя.
Реакция R21 известна, так как R12= R21. Величина Рур определиться из уравнения моментов сил относительно точки О1 кривошипа.
∑М О1 (зв.1)=0, Рур·АО1-R12·hR12=0
Рур’= R12·hR12/ АО1=2539 40/88=1154 Н
Реакция стойки на кривошип R10 определиться из условия равновесия кривошипа:
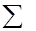 P(кр)=R21+Py+R10=0 (3) P(кр)=R21+Py+R10=0 (3)
По уравнению (3) строим план сил кривошипа, откуда определяем искомую реакцию R10
R10= R10·Кр=110·20=2200 Н.
2.5 Определение уравновешивающей силы методом Жуковского
Уравновешивающую силу можно определить с помощью план скоростей по методу рычага Жуковского.
Строим повёрнутый на 90˚план скоростей и приложим к нему все внешние силы, действующие на механизм. План скоростей рассматриваем как жёсткий рычаг с опорой в полюсе. Рычаг находится в равновесии под действием приложенных сил.
Составляем уравнение равновесия рычага в форме суммы моментов сил в форме суммы моментов сил относительно полюса плана скоростей.
∑МPv1=0
Pyp’·Pva-(Q+U5+G5)·PvC-U3’’·hU3’’-G3’’·hG3’’-U3’·hU3’+G3’·hG3’=0
Pyp’=((Q+U5+G5)·PvC+ U3’’·hU3’’+ G3’’·hG3’’+ U3’·hU3’- G3’·hG3’)/ Pva
Pyp’=((3450+535,5+343,35)·47+255·33+294,3·24+270·69-117,72·13)/179
Pyp’=1173 Н
Сравниваем значения Pyp и Pyp’, найденные двумя способами
δ=( Pyp’- Pyp)/ Pyp’
δ=(1173-1154)·100%/1173=1,62%
2.6 Определение мощности
Мгновенная потребная мощность привода насоса без учёта потерь мощности на трение определяется соотношением:
Npy=Pyp·VA=1173·3,46=4058,58 Вт
Мощность привода, затраченная на преодоления только полезной нагрузки:
NQ=Q·Vc=3450·0,95=3277,5 Вт
Потери мощности во вращательных кинематических парах:
N10=R10·f’·(ω1-ω0)·rц=2200·0,132·15,71·0,025=114,5 Вт
N12=R12·f’·(ω1-ω3)·rц=2539·0,132·10,77·0,025=90,2 Вт
N30=R30·f’·(ω3-ω0)·rц=5480·0,132·4,94·0,025=89,3 Вт
N45=R45·f’·(ω3-ω5)·rц=4420·0,132·4,94·0,025=72,05 Вт
Где rц-радиус цапфы вала, rц=0,025 м,
f’- приведенный коэффициент трения, f’=(1,2…1,5)f=0,132
Потери мощности в поступательных кинематических парах:
N23=R23·f’·VA’A=2539·0,132·1,65=553 Вт
N34=R34·f’·VC’C=4420·0,132·0,85=495 Вт
N50=R50·f’·VC=1320·0,132·0,95=165,5 Вт
Суммарная мощность трения:
Nтр=∑Ni=N10+N12+N30+N45+N23+N34+N50
Nтр=114,5+90,2+89,3+72,05+553+495+165,5=1579,2 Вт
Мгновенная потребляемая мощность двигателя:
N=NРу+Nтр
N=4058,58+1579,2=5637,78 Вт
2.7 Определение кинетической энергии и приведенного момента инерции механизма
Кинетическая энергия механизма равна сумме кинетической энергии звеньев:
Тмех=∑Тi
Для механизма насоса с заданными параметрами кинетическая энергия звена равна:
∑Тi=Т3+Т5=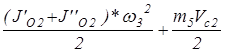
Где
JO2’=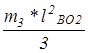 =12·0,352/3=0,49 кг·м2 =12·0,352/3=0,49 кг·м2
JO2’’=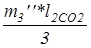 =30·0,1552/3=0,24 кг·м2 =30·0,1552/3=0,24 кг·м2
Т3=(0,49+0,24)·4,942/2=8,9 Дж
Т5=35·0,95/2=16,62 Дж
Тмех=8,9+16,62=25,52 Дж
За звено приведения обычно выбирают ведущее звено. Так как у исследуемого механизма ведущим звеном является кривошип, то кинетическая энергия определится по формуле:
Tпр=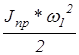
Откуда находим приведенный момент инерции:
Jпр=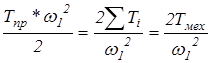
Jпр=2·25,52/15,712=0,2 кг·м2
3 Геометрический расчет зубчатой передачи. Проектирование планетарного механизма
3.1 Геометрический расчет зубчатой передачи
Исходные данные:
Число зубьев шестерни Z5=11;
Число зубьев колеса Z6=25;
Модуль m=6 мм;
Нарезание проводится методом обкатки инструментом реечного типа, который профилируется на основе исходного контура по ГОСТ 13755-81 и имеет следующие значения: угол профиля 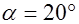 ; коэффициент высоты головки ; коэффициент высоты головки 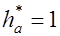 ; коэффициент радиального зазора ; коэффициент радиального зазора 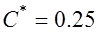 ; ;
Определяем геометрические параметры эвольвентной передаче.
Определяем минимальный коэффициент смещения:
Z5<17и Z5+Z6≥34, следовательно, передача равносмещенная,
x5=(17-Z5)/17=(17-11)/17=0,35 мм;
x6=-x5=-0,35 мм;
Определяем делительное межосевое расстояние:
а= 0,5·m·(Z5+Z6)= 0.5·6·(11+25)=108 мм;
Определяем высоту зуба:
h=m(2ha*+c*)=6(2·1+0,25)=13,5 мм;
4) Делительная высота головки зуба:
ha=m·(ha*+x);
ha5= m·(ha*+x5)= 6·(1+0,35)= 8,1 мм;
ha6=m·(ha*+x6)=6·(1-0,35)= 3,9 мм;
5) Делительная высота ножки зуба:
hf= m·(ha*+C-x);
hf5= m·(ha*+C-x5)= 6·(1+0,25-0,35)= 5,4 мм;
hf6= m·(ha*+C+x6)= 6·(1+0,25+0,35)= 9,6 мм;
Диаметр делительной окружности:
d5= m·Z5= 6·11= 66 мм;
d6= m·Z6= 6·25= 150 мм;
Диаметр основной окружности:
db5= m·Z5·cos(α)= 6·11· cos(20)= 62,05 мм;
db6= m·Z6·cos(α)= 6·25· cos(20)= 147 мм;
Диаметр окружности вершин зубьев:
da=m·Z+2m·(ha*+x);
da5=m·Z5+2m·(ha*+x5)=6∙11+2·6(1+0,35)= 82,2 мм;
da6=m·Z6+2m·(ha*+x6)=6∙25+2·6(1-0,35)= 157,8 мм;
Диаметр окружностей впадин зубьев:
df=mZ-2m(ha*+C*-x);
df5=mZ5-2m(ha*+C*-x5)=11·5-2·6(1+0,25-0,35)=55,2 мм;
df6=mZ6-2m(ha*+C*-x6)=25·5-2·6(1+0,25+0,35)=130,8 мм;
10) Делительная окружная толщина зуба:
S=0,5·π·m+2m·x·tg(α);
S5=0,5·3,14·6+2·6·0,35·tg(20)= 10,9 мм;
S6=0,5·3,14·6-2·6·0,35·tg(20)= 7,9 мм;
Делительный шаг:
P= π·m = 3,14·6=18,84 мм;
12) Основной шаг:
Pb= π·m cos(α)= 3,14·6·0,94=17,7 мм;
13) Радиус кривизны галтели
ρ=0,38m=2.28 мм;
14) Строим зубчатую передачу с масштабным коэффициентом Kl=0,00025 м/мм;
15) Проверяем коэффициент торцевого перекрытия
а) аналитический метод:
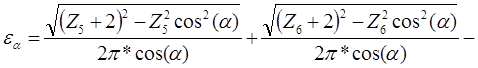
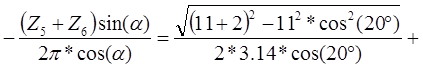
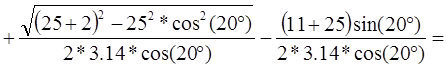 1,57 1,57
б) графический метод:
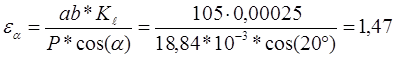
где 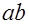 – длина активной линии зацепления. – длина активной линии зацепления.
3.2 Определение передаточного отношения планетарной ступени и подбор числа зубьев колес
Исходные данные:
nкр=150 мин-1;
nдв=1500 мин-1;
Z5=11;
Z6=25;
знак передаточного отношения привода (-)
Составляем общее передаточное отношение механизма:
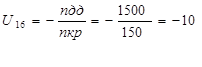
Рассчитаем передаточное отношение 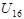 и и 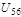 через исходные данные: через исходные данные:
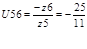
Из исходного уравнения определяем передаточное отношение планетарной ступени:
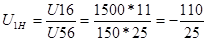  ; ;
Составляем формулу Виллиса для планетарной передачи:
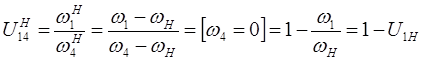 ; ;
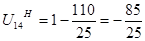  ; ;
Запишем через числа зубьев передаточное отношение обращенного механизма:
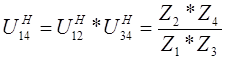 ; ;
Подбираем числа зубьев:
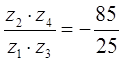 ; ; 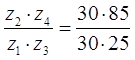 ; ;
Z1+Z2=Z4-Z3;
Z1+Z2=30+30=60
Z3+Z4=85-25=60
Z1=30, Z2=30, Z3=25, Z4=85
По выбранным числам зубьев определяем размеры колес:
d=m·Z;
d1=6·40=240 мм;
d2=6·40=240 мм;
d3=6·25=150 мм;
d4=6·85=510 мм;
d5=6·11=66 мм;
d6=6·25=150 мм
Масштабный коэффициент построения Кl=0,001 м/мм;
Для построения плана скоростей редуктора определяем скорость точки А:
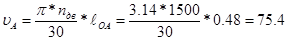 м/с; м/с;
Строим план скоростей. Масштабный коэффициент плана скоростей
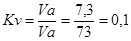 мс-1/мм; мс-1/мм;
3.3 Определение частот вращения зубчатых колес аналитическим методом
n1= nдв=1500 мин-1;
n6= nкр=150 мин-1;
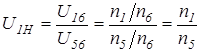 ; ;
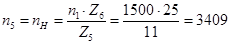 мин-1; мин-1;
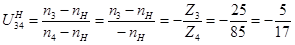 ; ;
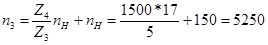 мин-1; мин-1;
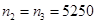 мин-1; мин-1;
Значения частот вращения получим графическим методом:
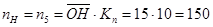 мин-1; мин-1;
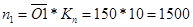 мин-1; мин-1;
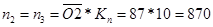 мин-1; мин-1;
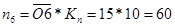 мин-1; мин-1;
4 Синтез и анализ кулачкового механизма
4.1 Диаграммы движения толкателя
Исходные данные:
Максимальный подъём толкателя h=29 мм;
Фазовый рабочий угол φ=290;
Дезаксиал е=0 мм;
nкр=150 об/мин;
Z5=11;
Z6=25
Угол давления α=25;
По заданному графику V-t графическим диференцированием получим график а-t, графическим интегрированием - S-t. Базы Н1=20 мм, Н2=25 мм. Методом исключения общего параметра t получим график V-S, a-S, a-V. Масштабные коэффициенты графиков:
Ks=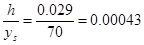 м/мм; м/мм;
Kv=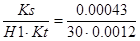 мс-1/мм мс-1/мм
Kt=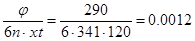 c/мм; c/мм;
Ka=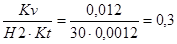 мс-2/мм мс-2/мм
4.2 Определение минимального радиуса кулачка
Минимальный радиус кулачка выбирается из условия выполнения угла давления. Для этого строим совмещённый график S’-V, где S’- текущее перемещение в стандартном масштабе КS’=0,0005 м/мм, V- аналог скорости.
На совмещённом графике на горизонтальных линиях откладываем аналоги скорости в масштабе КS’
x1=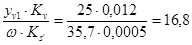 мм мм
x2=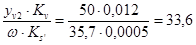
К совмещённому графику проводим две касательные под углом давления α. Ниже точки пересечения касательных выбирается центр вращения кулачка и соединяется с началом совмещённого графика. Это и будет минимальный радиус кулачка.
R0’=R0’·KS’=40·0,0005=0,02 м;
4.3 Построение профиля кулачка
Профилирование кулачка выполняется методом обращённого движения. Для этого строим кулачок в масштабе Кl=0,00025 м/мм. Проводим окружность радиусом R0’ и окружность радиуса е. Откладываем угол φр=290. Делим его на 12 частей и через точки деления проводим оси толкателя в обращённом движении. Вдоль осей толкателя откладываем текущее перемещение толкателя от окружности R0’. Соединяя полученные точки получим центровой профиль кулачка. Радиус ролика выбираем из условия:
rp=(0,2…0,4)R0’=0,25∙40=10 мм
Минимальный радиус действительного профиля:
R0=R0’-rp=40-10=30 мм
Обкатывая ролик по центровому профилю получаем действительный профиль.
Public Sub kul()
Dim I As Integer
Dim dis1, dis2, R, a1, a2, arksin1, arksin2, BETTA, BET As Single
Dim R0, FIR, FI0, FII, SHAG, E As Single
Dim S(1 To 10) As Single
R0 = InputBox("ВВЕДИТЕ МИНИМАЛЬНЫЙ РАДИУС КУЛАЧКА RO")
FIR = InputBox("ВВЕДИТЕ РАБОЧИЙ УГОЛ КУЛАЧКА FIR")
FI0 = InputBox("ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ УГЛА ПОВОРОТА КУЛАЧКА FI0")
E = InputBox("ВВЕДИТЕ ДЕЗАКСИАЛ E")
For I = 1 To 10
S(I) = InputBox("ВВЕДИТЕ СТРОКУ ПЕРЕМЕЩЕНИЙ S(" & I & ")")
Next I
FIR = FIR * 0.0174532
SHAG = FIR / 10
FI0 = FI0 * 0.0174532
FII = FI0
For I = 1 To 10
dis1 = (R0 ^ 2 - E ^ 2) ^ (1 / 2)
dis2 = S(I) ^ 2 + R0 ^ 2 + 2 * S(I) * dis1
R = dis2 ^ (1 / 2)
a1 = E / R
a2 = E / R0
arksin1 = Atn(a1 / (1 - a1 ^ 2) ^ (1 / 2))
arksin2 = Atn(a1 / (1 - a2 ^ 2) ^ (1 / 2))
BETTA = FII + arksin1 - arksin2
BETTA = BETTA * 180 / 3.1415
Worksheets(1).Cells(I, 1) = R
Worksheets(1).Cells(I, 2) = BETTA
FII = FII + SHAG
Next I
End Sub
Список использованных источников
1. Машков А.А. Теория механизмов и машин. Мн., 1971.
2. Артоболевский И.И. Теория механизмов и машин. М., 1975.
3. Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин под ред. К.В. Фролова М., 1986.
4. Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин. М., 1998.
|