МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ТЕРНОПІЛЬСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
ІМЕНІ ІВАНА ПУЛЮЯ
Тиш Євгенія Володимирівна
УДК 681.518.3+519.21
МОДЕЛЮВАННЯ ТА МЕТОДИ ОБРОБКИ
КАРДІОІНТЕРВАЛОГРАМ ПРИ ФІЗИЧНИХ НАВАНТАЖЕННЯХ
01.05.02 – Математичне моделювання та обчислювальні методи
Автореферат дисертації
на здобуття наукового ступеня кандидата технічних наук
Тернопіль – 2008
Дисертацією є рукопис.
Робота виконана в Тернопільському державного технічному університеті імені Івана Пулюя
Міністерства освіти і науки України.
Науковий керівник доктор технічних наук, професор
Бойко Іван Федорович,
Національний авіаційний університет,
професор кафедри радіоелектроніки.
Офіційні опоненти: доктор технічних наук, доцент
Яворський Богдан Іванович,
Тернопільський державний технічний університет
імені Івана Пулюя, завідувач кафедри біотехнічних систем, м.Тернопіль
доктор технічних наук, професор
Прокопенко Ігор Григорович,
Національний авіаційний університет,
завідувач кафедри авіаційних радіоелектронних комплексів, м. Київ.
Захист відбудеться “ 3 ” липня 2008 р. о 1100 годині на засіданні спеціалізованої вченої ради К58.052.01 в Тернопільському державному технічному університеті імені Івана Пулюя, 46001, м. Тернопіль, вул. Руська, 56, ауд.79
З дисертацією можна ознайомитися у науково-технічній бібліотеці Тернопільського державного технічного університету імені Івана Пулюя, 46001, м. Тернопіль, вул. Руська, 56
Автореферат розісланий “ 30 ” травня 2008 р.
Вчений секретар
спеціалізованої вченої ради К58.052.01
кандидат технічних наукГладьо В.Б.
ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОБОТИ
Актуальність теми. Організм людини – надзвичайно складна система, елементи якої тісно взаємодіють між собою. Визначення адаптивно-регулятивних характеристик живого організму є актуальною проблемою сучасної медицини, а розробка комп’ютерної системи та відповідного математичного забезпечення для автоматизованої діагностики адаптивно-регулятивних можливостей організму є важливою науково-технічною проблемою.
Одним із перспективних, високо інформаційних методів діагностики адаптивних можливостей організму є дослідження серцевого ритму за кардіоінтервалограмою (КІГ). На переваги діагностики за КІГ вказували автори багатьох наукових робіт медичного спрямування, а в сучасних автоматизованих діагностичних системах використовується математичне забезпечення, на основі робіт Баєвського Р.М., Іванова Г.Г., Меєрсона Ф.З., Саєрса Б., Жемайтіте Д. та ін. Низка праць із математичного моделювання КІГ належить Яворському Б.І., Драгану Я.П., Яворській Є.Б. Встановлено, що дослідження ритму серця в спокої не відображає приховані патології. Тому для людей (наприклад, спортсменів), в яких патологічні зміни та відхилення від норми зі сторони серцево-судинної системи нерідко можуть компенсуватися хорошою функціональною здатністю організму, необхідно для виявлення патології проводити реєстрацію та аналіз КІГ після адекватного фізичного навантаження.
Реклама

Сучасні методи аналізу КІГ та відомі діагностичні ознаки на її основі базуються на двох теоретичних підходах – детермінованому та стохастичному.
Математичні моделі КІГ у вигляді детермінованих функцій застосовуються для прогнозування стану організму. Розглядають два простих методи прогнозування, що базуються на уявленні про лінійну та експоненціальну зміну тривалостей кардіоциклів. Детерміновані моделі не враховують випадковий характер зміни тривалостей кардіоінтервалів і тому є досить спрощеними. Завдяки своїй простоті детерміновані моделі КІГ дають змогу досить легко реалізувати методи експрес-аналізу стану адаптивно-регулятивних механізмів організму, але вони не враховують стохастичний характер КІГ, що не дозволяє їх використовувати для високоінформативної діагностики.
Сучасні стохастичні методи аналізу КІГ базуються переважно на її двох математичних моделях – моделі у вигляді випадкової величини та моделі у вигляді стаціонарної дискретної послідовності. Проте такі моделі є адекватними лише для випадку, коли КІГ реєструється в стані спокою. У випадку ж реєстрації КІГ при фізичних навантаженнях необхідно враховувати нестаціонарний, перехідний характер зміни тривалостей КІГ.
Наведені аргументи вказують на актуальність побудови нової математичної моделі КІГ при фізичних навантаженнях як нестаціонарного випадкового процесу, а також визначення на її основі нового класу діагностичних ознак та методів їх оцінювання для діагностування адаптивно-регулятивних можливостей організму людини засобами сучасних інформаційних технологій.
Зв’язок роботи з науковими програмами, планами, темами. Дисертаційне дослідження проводилося в рамках наукової теми ВК 21-06 “Математичне моделювання, методи обробки та імітації біометричних циклічних сигналів в інформаційних системах”, номер держреєстрації №0106U009380, де здобувачу належить розробка програмного забезпечення для імітаційного моделювання ритмічних сигналів серця.
Реклама

Мета і задачі дослідження. Метою дисертаційної роботи є розробка математичної моделі, методів обробки, визначення діагностичних ознак та методу імітаційного моделювання КІГ для моніторингу адаптивно-регулятивних можливостей організму людини при фізичних навантаженнях. Для досягнення мети необхідно було вирішити наступні задачі:
Провести порівняльний аналіз та класифікацію існуючих математичних моделей, методів обробки, діагностичних ознак КІГ у технічних системах функціональної діагностики стану серцево-судинної системи.
Побудувати математичну модель КІГ при фізичних навантаженнях з урахуванням її перехідного випадкового характеру для розробки ефективних методів діагностування адаптивно-регулятивних можливостей організму та імітаційного моделювання КІГ засобами сучасних інформаційних технологій.
Розробити методи статистичної обробки КІГ на базі створеної математичної моделі та вибрати діагностичні ознаки, виходячи з критерію мінімуму їх кількості при збережені однакової інформативної цінності (без зниження інформативності).
Розробити метод імітаційного моделювання КІГ для потреб тестування та навчання комп’ютерних діагностичних систем.
Створити систему комп’ютерних програм обробки КІГ та проведення імітаційних експериментів для кардіоінтервалометричної діагностичної системи на базі ЕОМ.
Провести серію експериментів по обробці та моделюванню КІГ з метою апробації розроблених математичних моделей, методів обробки та імітаційного моделювання.
Об’єкт дослідження. Процес моделювання КІГ людини при фізичних навантаженнях.
Предмет дослідження. Математична модель, методи моделювання та статистична обробка КІГ.
Методи дослідження. Розв’язання задач:
теоретичного характеру – виконано з використанням методів теорії ймовірностей, теорії випадкових процесів, стохастичних інтегральних зображень, теорії ортогональних рядів;
практичного характеру – виконано з використанням математичної статистики та методів імітаційного моделювання.
Наукова новизна одержаних результатів.
Вперше побудовано математичну модель КІГ у вигляді суми дискретної детермінованої функції та стаціонарної лінійної випадкової послідовності. Побудована модель враховує як нестаціонарний (перехідний) характер, так і стохастичність КІГ при фізичних навантаженнях.
Обґрунтовано методи статистичної обробки КІГ, а саме – з використанням методу найменших квадратів побудовано алгоритм оцінювання математичного сподівання КІГ, а з використанням теорії статистичного оцінювання ймовірнісних характеристик ергодичних відносно кореляційної функції та щільності розподілу випадкових послідовностей, запропоновано алгоритм оцінювання кореляційної функції та щільності розподілу стаціонарної компоненти КІГ.
Запропоновано нові діагностичні ознаки для діагностики адаптивно-регулятивних можливостей організму людини: коефіцієнти розкладу оцінки математичного сподівання та оцінки кореляційної функції КІГ в ряди за ортогональними дискретними поліномами Чебишева, а також параметри кривої Пірсона, що апроксимує щільність розподілу КІГ.
Створено метод імітаційного моделювання КІГ при фізичних навантаженнях на основі побудованої математичної моделі.
Практичне значення одержаних результатів. Запропоновані в дисертаційній роботі методи обробки та імітаційного моделювання КІГ при фізичних навантаженнях, що ґрунтуються на їх новій математичній моделі, призначені для клінічного використання з метою проведення діагностики адаптовно-регулятивних можливостей організму людини на базі ЕОМ та дослідницької роботи в науково-експериментальних лабораторіях медичного та фізіологічного напряму.
Запропонована математична модель та обґрунтовані методи обробки на її основі вперше дають змогу проводити діагностику стану адаптивно-регулятивних можливостей організму людини за КІГ при фізичних навантаженнях, оскільки враховують як перехідний, так і стохастичний характер зміни тривалостей кардіоінтервалів. Розроблений метод імітаційного моделювання КІГ може бути використаний для потреб тестування та навчання комп’ютерних діагностичних систем.
Систему комп’ютерних програм для обробки та імітаційного моделювання КІГ при фізичних навантаженнях впроваджено в консультативному лікувально-діагностичному центрі ТОВ “Десна” ЛТД (акт впровадження від 12.02.2008 р.), в навчальний процес на кафедрі фізіології Тернопільської державної медичної академії імені І.Я. Горбачевського (акт впровадження від 15.02.2008 р.) та на кафедрі радіокомп’ютерних систем Тернопільського державного технічного університету імені Івана Пулюя (акт впровадження від 4.12.2007 р.).
Особистий внесок здобувача. Усі результати, які становлять основний зміст дисертаційної роботи, автор отримав особисто. У наукових працях, опублікованих у співавторстві, автору дисертаційної роботи належить: у [1] – побудова математичної моделі та статистична обробка КІГ; у [2] – проведення імітаційного експерименту та визначення похибок імітаційного моделювання; у [3] – проведення порівняльного аналізу методів дослідження КІГ та їх класифікація в стані спокою та при фізичних навантаженнях; у [4] – зменшення розмірності вектора діагностичних ознак за щільністю розподілу шляхом апроксимації гістограм кривими Пірсона; [6] – обґрунтування конструкції математичної моделі КІГ при фізичних навантаженнях; [7] – проведення імітаційного експерименту та визначення похибок імітаційного експерименту; [8] – обґрунтування діагностичних ознак за оцінкою математичного сподівання; [9] – класифікація та порівняльний аналіз існуючих математичних моделей, діагностичних ознак та методів їх оцінювання; [10] – уточнення типу детермінованої складової математичної моделі КІГ з урахуванням фізичного навантаження; [12] – обґрунтування вибору математичної моделі та методу імітаційного моделювання КІГ при фізичних навантаженнях.
Апробація результатів дисертації. Результати дисертаційної роботи доповідались на шостій, сьомій, восьмій, дев’ятій, десятій науково-технічних конференціях Тернопільського державного технічного університету імені Івана Пулюя (Тернопіль 2002, 2003, 2004, 2005, 2006 р.), VI міжнародній науково-практичній конференції „Наука і освіта ’2003” (Дніпропетровськ – Мелітополь 2003 р.), міжнародній науково-практичної конференції „Дні науки ’2005” (Дніпропетровськ-Бєлгород), всеукраїнській науково-практичної конференції “Медична інформатика - 2005” Тернопільського державного медичного університету ім. І.Я. Горбачевського (Тернопіль), наукових семінарах кафедри комп’ютерних наук та кафедри радіокомп’ютерних систем Тернопільського державного технічного університету імені Івана Пулюя.
Публікації. Основні результати, отримані в дисертації, опубліковано в 13 наукових працях, 5 з них – статті у наукових фахових виданнях (зокрема 1 – без співавторів), 8 – тези доповідей науково-технічних конференцій.
Структура і обсяг дисертації. Дисертація складається із вступу, чотирьох розділів, висновків, списку використаних джерел із 108 найменувань, містить 35 рисунків, 4 таблиці, 9 додатків. Повний обсяг дисертації складає 178 сторінок, основний зміст викладено на 112 сторінках.
ОСНОВНИЙ ЗМІСТ
У вступі обґрунтовано актуальність теми дисертації, відзначено зв’язок з науковими темами, сформульовано мету і задачі дослідження, показано наукову новизну отриманих результатів, їх практичне значення, також розглянуто питання апробації результатів дисертації та їх висвітлення у друкованих працях.
У першому розділі на основі аналітичного огляду літературних джерел проведено класифікацію та порівняльний аналіз існуючих математичних моделей, діагностичних ознак та методів їх оцінювання, що лежать в основі сучасних комп’ютерних систем діагностики за КІГ, принцип формування якої з електрокардіографічного сигналу зображено на рис. 1.
Виходячи із необхідності систематизації та впорядкування відомостей фізичного, математичного та технічного характеру, що стосуються моделювання та аналізу КІГ, автором окреслено нову науково-технічну область, шляхом введення поняття кардіоінтервалометрії. Кардіоінтервалометрія – це область кардіометрії, що охоплює широкий спектр проблем технічного та фізико-математичного характеру (а не медико-біологічного), науково-технічними проблемами якої є: побудова математичних моделей, вибір діагностичних ознак, обґрунтування алгоритмів обробки КІГ для проведення діагностики адаптивно-регулятивних механізмів організму; створення алгоритмів функціонування систем діагностики за КІГ; створення методів комп’ютерного імітаційного моделювання КІГ та її перетворень в технічних системах; розробка інформаційно-вимірювальних діагностичних систем за КІГ.
Проведений порівняльний аналіз відомих математичних моделей КІГ та критичний аналіз можливостей їх застосування для моделей КІГ при фізичних навантаженнях показав, що існуючі моделі мають вагомі недоліки, а тому існує об’єктивна необхідність побудови нової математичної моделі КІГ з урахуванням фізичних навантажень та розробки методів її обробки і вибору діагностичних ознак.
Враховуючи специфіку задач кардіоінтервалометрії та особливості зміни тривалостей кардіоінтервалів при фізичних навантаженнях, сформульовано вимоги до математичної моделі КІГ, що запропонована в дисертаційній роботі.
У другому розділі ґрунтуючись на особливостях формування, факті нестаціонарного (перехідного) характеру КІГ при фізичних навантаженнях (рис. 2), а також властивій стохастичності кардіоінтервалів, побудовано нову математичну модель КІГ при фізичних навантаженнях у вигляді суми дискретної детермінованої функції та стаціонарної лінійної випадкової послідовності. Розглянуто характеристики запропонованої математичної моделі. Запропоновано на основі розробленої моделі як діагностичні ознаки для прийняття рішень щодо адаптивно-регулятивних можливостей організму людини використати імовірнісні характеристики КІГ: математичне сподівання, кореляційну функцію та щільність розподілу.
Як показали результати проведених досліджень, при дії на організм людини фізичного навантаження тривалості кардіоінтервалів починають зменшуватися до певного рівня, а потім в процесі зняття фізичного навантаження зростають протягом деякого часу до попереднього рівня (стан відновлення). Це явище вимагає врахування нестаціонарності, перехідного характеру у величинах тривалостей кардіоінтервалів в математичній моделі КІГ при фізичних навантаженнях.
Враховуючи наведені вище міркування, математичну модель КІГ при фізичних навантаженнях подано у вигляді
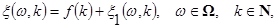 (1) (1)
де 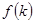 – деяка дискретна детермінована функція, яка відображає динаміку зміни (тренд) тривалостей кардіоінтервалів КІГ; – деяка дискретна детермінована функція, яка відображає динаміку зміни (тренд) тривалостей кардіоінтервалів КІГ;
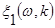 – стаціонарна лінійна випадкова послідовність, що враховує випадковий характер змін (флуктуацій) тривалостей кардіоінтервалів КІГ та яку подано у вигляді – стаціонарна лінійна випадкова послідовність, що враховує випадковий характер змін (флуктуацій) тривалостей кардіоінтервалів КІГ та яку подано у вигляді
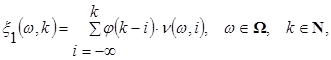 (2) (2)
де 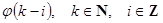 – невипадкова функція (ядро зображення (2)) двох дискретних аргументів, відносно якої виконується нерівність – невипадкова функція (ядро зображення (2)) двох дискретних аргументів, відносно якої виконується нерівність
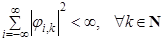 , ,
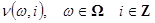 – породжуючий білий шум з дискретним часом, математичне сподіванням якого рівне нулю. – породжуючий білий шум з дискретним часом, математичне сподіванням якого рівне нулю.
Зауважимо, що у випадку реєстрації КІГ у стані спокою (без фізичних навантажень), її моделлю також буде випадковий процес (1) причому 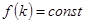 . .
Діагностичними ознаками при визначенні адаптивно-регулятивних можливостей організму людини є ймовірнісні характеристики (математичне сподівання, кореляційна функція та щільність розподілу) процесу 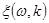 . Так, математичне сподівання процесу (1) рівне: . Так, математичне сподівання процесу (1) рівне:
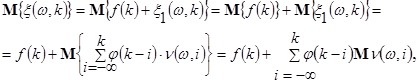 (3) (3)
але оскільки 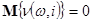 , то , то
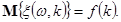 (4) (4)
Отже, для визначення математичного сподівання 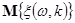 достатньо знайти функцію достатньо знайти функцію 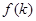 . .
Кореляційна функція процесу (1)
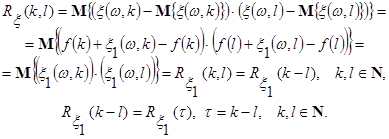 (5) (5)
Тобто, кореляційна функція випадкового процесу (1) рівна кореляційній функції стаціонарної лінійної випадкової послідовності 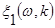 . .
Одновимірна функція щільності розподілу 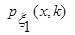 стаціонарної компоненти стаціонарної компоненти  не змінюється при зсуві за аргументом не змінюється при зсуві за аргументом 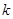 , що можна подати так: , що можна подати так:
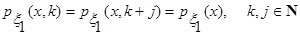 . (6) . (6)
Таким чином, діагностичними ознаками при проведенні діагностики стану адаптивно-регулятивних можливостей організму при фізичних навантаженнях на основі запропонованої в роботі моделі будуть математичне сподівання, що рівне детермінованій функції f(k), кореляційна функція 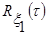 та функція щільності розподілу та функція щільності розподілу 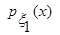 стаціонарної компоненти стаціонарної компоненти  моделі (1). моделі (1).
У третьому розділі, обґрунтовано методи статистичного оцінювання діагностичних ознак, а саме, коефіцієнтів розкладу оцінки математичного сподівання та оцінки кореляційної функції КІГ у ряди за ортогональними поліномами Чебишева, а також параметрів кривих Пірсона для оцінювання щільності розподілу, що дало можливість зменшити (оптимізувати) розмірність вектора діагностичних ознак.
Виходячи із вище запропонованих діагностичних ознак, наведено методи їх статистичного оцінювання.
Оскільки статистичне оцінювання математичного сподівання здійснюється тільки за однією реалізацією КІГ, а КІГ при фізичних навантаженнях не є стаціонарною, то оцінювання математичного сподівання, що дорівнює детермінованій складовій 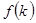 моделі (1), здійснено на основі методу найменших квадратів. моделі (1), здійснено на основі методу найменших квадратів.
У результаті оцінювання отримано послідовність значень, обсяг яких дорівнює кількості відліків КІГ. Зменшення розмірності діагностичного простору здійснено шляхом наближеного представлення функції 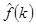 у вигляді ряду у вигляді ряду
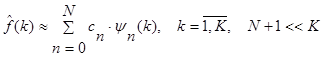 , (7) , (7)
де 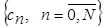 – спектральні коефіцієнти функції – спектральні коефіцієнти функції 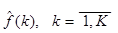 в ортогональному базисі в ортогональному базисі 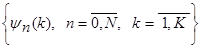 . .
У дисертаційній роботі за діагностичні ознаки прийнято декілька перших коефіцієнтів із сукупності 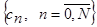 ортогонального розкладу оцінки математичного сподівання в ряди за ортогональними поліномами дискретного аргументу Чебишева, Кравчука, Лагера та за дискретними тригонометричними функціями. На основі аналізу результатів розкладу оцінки математичного сподівання КІГ в ряди за цими ортогональними базисами, виходячи з критерію мінімуму кількості членів ряду, які складають не менше 95% від повної енергії сигналу, встановлено, що за цим критерієм найменша кількість коефіцієнтів (3-4 коефіцієнти ряду) потрібно при розкладі в ряд за ортогональними поліномами Чебишева. Отже, діагностичними ознаками на основі розкладу оцінки математичного сподівання в ряди за дискретними ортогональними поліномами вибрано коефіцієнти ряду поліномів Чебишева. ортогонального розкладу оцінки математичного сподівання в ряди за ортогональними поліномами дискретного аргументу Чебишева, Кравчука, Лагера та за дискретними тригонометричними функціями. На основі аналізу результатів розкладу оцінки математичного сподівання КІГ в ряди за цими ортогональними базисами, виходячи з критерію мінімуму кількості членів ряду, які складають не менше 95% від повної енергії сигналу, встановлено, що за цим критерієм найменша кількість коефіцієнтів (3-4 коефіцієнти ряду) потрібно при розкладі в ряд за ортогональними поліномами Чебишева. Отже, діагностичними ознаками на основі розкладу оцінки математичного сподівання в ряди за дискретними ортогональними поліномами вибрано коефіцієнти ряду поліномів Чебишева.
Враховуючи отримані результати розкладу оцінки математичного сподівання, математичну модель (1) уточнено і подано у вигляді:
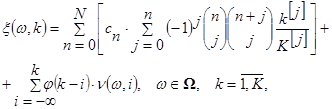 (8) (8)
де 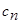 – коефіцієнти ряду Чебишева; – коефіцієнти ряду Чебишева;
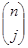 та та 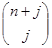 – узагальнені коефіцієнти, що дорівнюють – узагальнені коефіцієнти, що дорівнюють 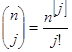 та та 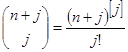
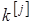 – узагальнений степінь. – узагальнений степінь.
У дисертаційній роботі побудовано гістограми стаціонарної компоненти (2) математичної моделі КІГ при фізичних навантаженнях та здійснено апроксимацію щільності розподілу КІГ системою кривих Пірсона, які визначаються як розв’язок диференціального рівняння
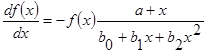 , (9) , (9)
де 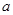 , , 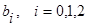 - дійсні параметри, що повністю характеризують форму (тип) кривої розподілу. Для характеристики стану адаптивно-регулятивних можливостей організму запропоновано використовувати нові діагностичні ознаки – параметри диференціального рівняння (9). Приклад побудови кривої Пірсона наведено на рис. 4. - дійсні параметри, що повністю характеризують форму (тип) кривої розподілу. Для характеристики стану адаптивно-регулятивних можливостей організму запропоновано використовувати нові діагностичні ознаки – параметри диференціального рівняння (9). Приклад побудови кривої Пірсона наведено на рис. 4.
Враховуючи ергодичність послідовності (2), статистичне оцінювання кореляційної функції здійснювалось згідно виразу
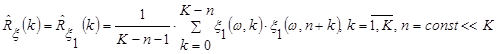 . (10) . (10)
Для зменшення діагностичного простору здійснено розклад оцінки кореляційної функції в ряд
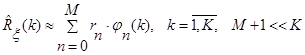 , (11) , (11)
де 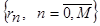 - спектральні коефіцієнти кореляційної функції - спектральні коефіцієнти кореляційної функції 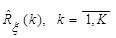 в ортогональному базисі в ортогональному базисі 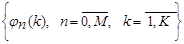 . .
В дисертаційній роботі як діагностичні ознаки за оцінкою кореляційної функції розглянуто коефіцієнти ортогональних розкладів цих оцінок в ряди за ортогональними поліномами дискретного аргументу Кравчука, Лагера, Чебишева та за дискретними тригонометричними функціями. Враховуючи енергетичний критерій, як і у випадку розкладу оцінки математичного сподівання в ряди, встановлено, що для представлення оцінки кореляційної функції стаціонарної компоненти (2) достатньо 15 перших коефіцієнтів ряду Чебишева. Таким чином, запропоновано як діагностичні ознаки за оцінкою кореляційної функції використовувати коефіцієнти ряду поліномів Чебишева.
Обгрунтовано метод прийняття рішень при діагностиці адаптивно-реглятивних механізмів організму за КІГ на основі аналізу коефіцієнтів розкладу оцінки математичного сподівання та оцінки кореляційної функції у ряди за ортогональними поліномами Чебишева, коефіцієнтів кривих Пірсона на основі критерію Неймана-Пірсона та критерію Байєса.
У четвертому розділі розглянуто питання комп’ютерного імітаційного моделювання КІГ на базі лінійних випадкових послідовностей. Проведено серію експериментів по моделюванню КІГ при фізичних навантаженнях. Розглянуто питання точності імітаційного моделювання. Розроблено систему комп’ютерних програм для проведення імітаційних експериментів та обробки кардіоінтервалограм при фізичних навантаженнях на основі запропонованих у дисертаційній роботі моделі та методів.
Алгоритм комп’ютерного моделювання КІГ полягає в моделюванні нестаціонарного випадкового процесу (1), що зводиться до імітації детермінованої складової 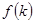 , що обчислюється на основі поліномів Чебишева за визначеними на основі спектрального розкладу оцінки математичного сподівання в ряд за поліномами Чебишева коефіцієнтами , що обчислюється на основі поліномів Чебишева за визначеними на основі спектрального розкладу оцінки математичного сподівання в ряд за поліномами Чебишева коефіцієнтами 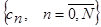 та моделювання стаціонарної лінійної випадкової послідовності (2). та моделювання стаціонарної лінійної випадкової послідовності (2).
Алгоритм моделювання реалізацій дискретної стаціонарної лінійної послідовності (2) полягає в наступному:
Будується рівняння авторегресії
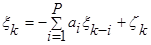 , , 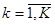 , (12) , (12)
розв’язком якого є стаціонарна лінійна послідовність (2).
Оцінюються коефіцієнти 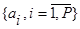 , рівняння авторегресії (12) шляхом розв’язання системи рівнянь Юла-Уокера за заданою кореляційною матрицею. , рівняння авторегресії (12) шляхом розв’язання системи рівнянь Юла-Уокера за заданою кореляційною матрицею.
Оцінюється послідовність відліків ядра 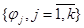 за рекурентними співвідношеннями за рекурентними співвідношеннями
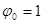 , ,
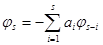 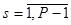 , (13) , (13)
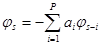 , , 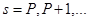 . .
Генеруються реалізації дискретного стаціонарного білого шуму з математичним сподіванням рівним нулеві та дисперсією 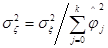 . .
Генеруються реалізації лінійної випадкової послідовності (2).
На основі математичної моделі (1) проведено серію імітаційних експериментів по моделюванню КІГ в період фізичного навантаження та в період відновлення серцевого ритму (рис. 6).
З метою перевірки адекватності, точності імітаційної моделі КІГ при фізичних навантаженнях, було проведено оцінювання абсолютних та відносних похибок комп’ютерного імітаційного моделювання. Для цього змодельовані реалізації КІГ в період фізичного навантаження та КІГ в період відновлення частоти серцевих скорочень. Отримані оцінки математичних сподівань та оцінки кореляційних функцій змодельованих КІГ порівнювались із отриманими протягом експериментальних досліджень оцінками математичних сподівань та оцінками кореляційних функцій.
Скориставшись правилом „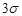 ” визначено, що з довірчою ймовірністю ” визначено, що з довірчою ймовірністю 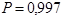 відносна похибка імітаційного моделювання КІГ на основі її моделі (10) для оцінки математичного сподівання буде належати інтервалу відносна похибка імітаційного моделювання КІГ на основі її моделі (10) для оцінки математичного сподівання буде належати інтервалу 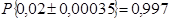 , а відносна похибка оцінки кореляційної функції буде належати інтервалу , а відносна похибка оцінки кореляційної функції буде належати інтервалу  , що дає підстави стверджувати про досить високу ступінь точності імітаційного моделювання КІГ при фізичних навантаженнях. , що дає підстави стверджувати про досить високу ступінь точності імітаційного моделювання КІГ при фізичних навантаженнях.
На базі розробленої в даній дисертаційній роботі математичної моделі та методів обробки КІГ створено систему програм для обробки, аналізу та імітаційного моделювання КІГ, яка може використовуватися в сучасних системах комп’ютерної діагностики серця.
Ця система програм реалізує такі функції:
Статистична обробка КІГ при фізичних навантаженнях.
Визначення коефіцієнтів різних ортогональних розкладів (в базисах Чебишева, Кравчука, Лагера та тригонометричних функцій) статистичних оцінок математичного сподівання та оцінок кореляційної функції КІГ, що є діагностичними ознаками.
Визначення типу кривої Пірсона та параметрів цих кривих для оцінювання щільності розподілу, що пропонуються як діагностичні ознаки.
Ідентифікація ядра лінійної випадкової послідовності та ймовірнісних характеристик її породжуючого процесу на основі методу Юла-Уокера.
Проведення імітаційного моделювання КІГ на базі лінійних випадкових послідовностей для потреб тестування та навчання комп’ютерних діагностичних систем.
Оцінювання точності імітаційного експерименту та точності визначення діагностичних ознак.
ВИСНОВКИ
У дисертаційній роботі розв’язано актуальну наукову задачу: побудовано математичну модель КІГ при фізичних навантаженнях, обґрунтовано методи її статистичної обробки та запропоновано нові класи діагностичних ознак адаптивно-регулятивних можливостей організму для комп’ютерних систем автоматизованої діагностики. Основні результати та висновки проведених теоретичних та експериментальних досліджень полягають в наступному:
Розроблено нову математичну модель КІГ з врахуванням фізичного навантаження у вигляді суми дискретної детермінованої функції та стаціонарної лінійної випадкової послідовності, що дало змогу врахувати як перехідний характер, так і стохастичність структури КІГ при фізичних навантаженнях.
Обґрунтовано методи статистичної обробки КІГ, що базуються на розробленій математичній моделі. З використанням методу найменших квадратів побудовано алгоритм оцінювання математичного сподівання КІГ, а з використанням теорії статистичного оцінювання ймовірнісних характеристик ергодичних відносно кореляційної функції та щільності розподілу випадкових послідовностей, запропоновано алгоритм оцінювання кореляційної функції та щільності розподілу стаціонарної компоненти КІГ.
Запропоновано нові класи діагностичних ознак: коефіцієнти розкладу оцінки математичного сподівання та оцінки кореляційної функції в ряди за ортогональними дискретними поліномами Чебишева та параметри кривої Пірсона, що апроксимує щільність розподілу КІГ. Запропоновані класи діагностичних ознак дають змогу мінімізувати розмірність діагностичного простору, що суттєво зменшує вимоги до обчислювальних ресурсів комп’ютерної діагностичної системи.
Розроблено метод імітаційного моделювання КІГ при фізичних навантаженнях, що базується на її математичній моделі та методі Юла-Уокера, для потреб тестування та навчання комп’ютерних діагностичних систем за КІГ.
Для апробації основних положень дисертаційного дослідження, розроблено систему комп’ютерних програм, на основі якої проведено серію натурних та імітаційних експериментів з моделювання та обробки КІГ при фізичних навантаженнях. Результати експериментів підтвердили достовірність та практичну цінність розробленої математичної моделі, методів аналізу та імітації КІГ.
СПИСОК ОПУБЛІКОВАНИХ АВТОРОМ ПРАЦЬ ЗА ТЕМОЮ ДИСЕРТАЦІЇ
Лозінська (Тиш) Є.В., Лупенко С.А., Щербак Л.М. Математична модель та методи обробки кардіоінтервалограми при фізичних навантаженнях в задачах діагностики адаптивних можливостей організму людини // Вісник Тернопільського державного технічного університету. – 2003. – Т.8, №4. – С. 97-105.
Лозінська (Тиш) Є.В., Литвиненко Я.В., Лупенко С.А., Щербак Л.М. Імітаційне моделювання кардіоінтервалограми на ЕОМ при фізичних навантаженнях // Вимірювальна та обчислювальна техніка в технологічних процесах. – Хмельницький: Навчальна книга. – 2002. – №2. – С. 120-124.
Бойко І.Ф., Лозінська (Тиш) Є.В., Лупенко С.А., Щербак Л.М. Методи аналізу кардіоінтервалограми людини в комп’ютерних діагностичних системах: класифікація та порівняльний аналіз // Вимірювальна та обчислювальна техніка в технологічних процесах. – Хмельницький: Навчальна книга. – 2004. – №1. – С.141-147.
Бойко І.Ф., Лозінська (Тиш) Є.В., Лупенко С.А. Оцінювання діагностичних ознак кардіоінтервалограми за функцією щільності розподілу // Електроніка та системи управління. – НАУ. – 2005. – №3 (5). – С. 32-38.
Лозінська (Тиш) Є.В. Уточнена математична модель кардіоінтервалограми при фізичних навантаженнях // Електроніка та системи управління. – НАУ. – 2006. – №4 (10). – С. 71-77.
Лозінська (Тиш) Є.В., Лупенко С.А., Щербак Л.М. Математична модель тривалості серцевих скорочень при фізичних навантаженнях для діагностики адаптивних можливостей організму людини по зареєстрованій електрокардіограмі // Тези доповідей шостої науково-технічної конференції Тернопільського державного технічного університету. – Тернопіль, 2002. – С. 63.
Лозінська (Тиш) Є.В., Лупенко С.А. Моделювання тривалості серцевих скорочень при фізичних навантаженнях // Тези доповідей сьомої науково-технічної конференції Тернопільського державного технічного університету. – Тернопіль, 2003. – С. 12.
Лозінська (Тиш) Є.В., Литвиненко Я.В., Лупенко С.А., Щербак Л.М. Математичне моделювання кардіоінтервалограми при фізичних навантаженнях // Тези доповідей VI міжнародної науково-практичної конференції „Наука і освіта – 2003”. – Дніпропетровськ-Мелітополь,2003. – Т.30 – С. 39-41.
Лозінська (Тиш) Є.В., Лупенко С.А. Математичне моделювання та методи обробки кардіоінтервалограми людини в сучасних комп’ютерних діагностичних системах // Тези доповідей восьмої науково-технічної конференції Тернопільського державного технічного університету. – Тернопіль, 2004. – С.63.
Лозінська (Тиш) Є.В., Лупенко С.А., Осухівська Г.М. Обґрунтування математичної моделі кардіоінтервалограми при фізичних навантаженнях // Тези доповідей дев’ятої науково-технічної конференції Тернопільського державного технічного університету. – Тернопіль, 2005. – С. 63.
Лозінська (Тиш) Є.В. Методи статистичної обробки кардіоінтервалограми та діагностичні ознаки на базі її математичної моделі // Матеріали Міжнародної науково-практичної конференції „Дні науки ’2005”, Дніпропетровськ-Бєлгород: Наука і освіта, 2005. – Т 18. – С. 37-39.
Бойко І.Ф., Лозінська (Тиш) Є.В. Математичне моделювання тривалостей серцевого ритму // Тези доповідей всеукраїнської науково-практичної конференції “Медична інформатика - 2005” Тернопільського державного медичного університету ім. І.Я. Горбачевського. – Тернопіль, 2005. – С. 48-50.
Лозінська (Тиш) Є.В. Методи прийняття рішень при діагностиці за кардіоінтервалограмою // Тези доповідей десятої науково-технічної конференції Тернопільського державного технічного університету. – Тернопіль, 2006. – С.12.
АНОТАЦІЯ
Тиш Є.В. Моделювання та методи обробки кардіоінтервалограм при фізичних навантаженнях. – Рукопис.
Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 01.05.02 - Математичне моделювання та обчислювальні методи (технічні науки) – Тернопільський державний технічний університет імені Івана Пулюя, Тернопіль, 2008 р.
Дисертацію присвячено створенню математичних, імітаційних моделей та методів обробки кардіоінтервалограм людини при фізичних навантаженнях, базуючись на теоретико-ймовірнісному підході для діагностики стану серцево-судинної системи засобами ЕОМ. Побудовано математичну модель КІГ у вигляді суми дискретної детермінованої функції та стаціонарної лінійної випадкової послідовності. Побудована модель дозволяє врахувати як нестаціонарний (перехідний) характер, так і стохастичність кардіоінтервалограми при фізичних навантаженнях, тобто є більш адекватною по відношенню до останніх. На основі створеної математичної моделі, розроблено методи статистичної обробки зареєстрованих КІГ. Запропоновано нові діагностичні ознаки для діагностики адаптивно-регулятивних можливостей організму людини: математичне сподівання, кореляційну функцію та щільність розподілу, що повністю характеризують варіативність КІГ при фізичних навантаженнях. Обґрунтовано методи статистичного оцінювання діагностичних ознак, а саме, коефіцієнтів розкладу оцінки математичного сподівання та оцінки кореляційної функції КІГ у ряд за ортогональними поліномами Чебишева, а також параметрів кривих Пірсона для оцінювання щільності розподілу, що дало можливість зменшити (оптимізувати) розмірність вектора діагностичних ознак. Розроблено методи комп’ютерного імітаційного моделювання КІГ для потреб тестування алгоритмів обробки та навчання систем розпізнавання біомедичних образів.
Ключові слова: кардіоінтервалограма, модель, лінійний випадковий процес, діагностичні ознаки, статистичні методи обробки, імітаційне моделювання.
АНОТАЦИЯ
Тыш Е.В. Моделирование и методы обработки кардиоинтервалограмм при физических нагрузках. – Рукопись.
Диссертация на соискание ученой степени кандидата технических наук по специальности 01.05.02 - Математическое моделирование и вычислительные методы (технические науки) – Тернопольский государственный технический университет имени Ивана Пулюя, Тернополь, 2008 г.
Исследование сердечного ритма за кардиоинтервалограммой (КИГ) является одним из информационных методов диагностики адаптивных возможностей организма. Современные методы анализа КИГ и известные диагностические признаки на ее основе базируются на двух теоретических подходах - детерминированному и стохастическому. Детерминированные модели не учитывают случайный характер изменения продолжительности кардиоинтервалов и поэтому являются достаточно упрощенными. Современные стохастические методы анализа КИГ базируются преимущественно на ее двух математических моделях - модели в виде случайной величины и модели в виде стационарной дискретной последовательности. Однако такие модели являются адекватными лишь для случая, когда КИГ регистрируется в состоянии покоя. В случае же регистрации КИГ при физических нагрузках необходимо учитывать нестационарный, переходной характер изменения продолжительностей КИГ.
В диссертационной работе построено математическую модель КИГ в виде суммы дискретной детерминированной функции и стационарной линейной случайной последовательности. Построенная модель позволяет учесть как нестационарный (переходной) характер, так и стохастичность КИГ, благодаря чему более адекватная по отношению к КИГ при физических нагрузках. Предложены новые диагностические признаки - вероятностные характеристики модели: математическое ожидание, корреляционная функция и плотность распределения. Выходя из выше предложенных диагностических признаков, приведено методы их статистического оценивания.
Поскольку статистическое оценивание математической ожидания осуществляется только по одной реализацией КИГ, а КИГ при физических нагрузках не является стационарной, то оценивание математического ожидания, которое равно детерминированной компоненте модели, осуществлено на основе метода наименьших квадратов. В результате оценивания получена последовательность значений, объем которых равен количеству отсчетов КИГ. Для уменьшения размерности диагностического пространства (без снижения информативности) осуществлено разложение оценки математического ожидания в ряд по ортогональным полиномам Чебишева, а в качестве диагностических признаков принято первые четыре коэффициента данного разложения.
В диссертационной работе построены гистограммы стационарной компоненты математической модели КИГ при физических нагрузках и осуществлена аппроксимация плотности распределения КИГ системой кривых Пирсона. Для характеристики состояния адаптивно-регулятивных возможностей организма на основе анализу плотности распределения предложено использовать новые диагностические признаки - параметры кривых Пирсона.
Статистическое оценивание корреляционной функции осуществлялось на основе теории статистического оценивания вероятностных характеристик эргодических относительно корреляционной функции вероятностных последовательностей. Для уменьшения размерности диагностического пространства (без снижения информативности) осуществлено разложение оценки корреляционной функции в ряд по ортогональным полиномам Чебишева, а в качестве диагностических признаков принято первые десять коэффициентов данного разложения.
Построен метод принятия решений при диагностике адаптивно-регуляционных механизмов организма за КИГ на основе анализа коэффициентов разложения оценки математической ожидание и оценки корреляционной функции в ряды за ортогональными полиномами Чебишева, коэффициентов кривых Пирсона на основе критерия Неймана-Пирсона и критерия Байеса.
Разработан метод имитационного моделирования КИГ при физических нагрузках, который базируется на ее математической модели и методе Юла-Уокера, для потребностей тестирования и обучения компьютерных диагностических систем за КИГ.
Для апробации основных положений диссертационного исследования, разработана система компьютерных программ, на основе которой проведена серия натурных и имитационных экспериментов по моделированию и обработке КИГ при физических нагрузках. Результаты экспериментов подтвердили достоверность и практическую ценность разработанной математической модели, методов анализа и имитации КИГ.
Ключевые слова: кардиоинтервалограмма, модель, линейный случайный процесс, диагностические признаки, статистические методы обработки, имитационное моделирование.
ANOTATION
Tysh E.V. Modeling and methods of cardiointervalogram processing of a man during the physical activity. – Manuscript.
Thesis for the Scientific Degree of Candidate of Technical Sciences in the specialty 01.05.02 – Mathematical Modeling and Computational methods (Technical science). – Ternopil State Ivan Pul’uj Technical University, Ternopil, 2008.
The thesis is dedicated to the creation of the mathematic imitation models and methods of processing the cardiointervalogram of a man during the physical activity basing on the theoretical probability approach to diagnosis of the cardio-vescular system by means of an electronic computer. A mathematic model of cardiointervalogram was created as a sum of a discrete determinant function and stationary linear random succession. The created model allows to consider both non-stationary (transitional) character and stochastisity of cardiointervalogram during physical activity, that is it is more adequate as to the last. Basing on the created mathematical model the methods of statistic processing of the registered cardiointervalogram were developed. New diagnosis features for the diagnosis of adaptation and regulatory possibilities of the human body were suggested: mathematic expectancy, correlation function and allocation density that fully characterize variety of cardiointervalogram during the physical activity. The methods of the mathematic evaluation of the diagnosis features were developed, in particular the decomposition coefficient of the mathematic expectancy of the correlation function of cardiointervalogram into the row with orthogonal polynoms of Chebishev and also the parameters of curves of Pirson for allocation density evaluation that allowed to diminish (optimize) the dimensions of the vector of diagnosis features. The methods of computer imitation modeling of the CIG were developed for the demands of testing the algorithms of processing and studying of the systems of identification of the biomedical images.
Key words: cardiointervalogram, cardiointerval, linear random process, diagnosis features, statistic methods of processing, imitation modeling.
|